Обработка результатов измерений
Обработка результатов измерений
ВВЕДЕНИЕ
Каждая лабораторная работа посвящена экспериментальному изучению
определенного физического явления и связана с измерением физических величин,
характеризующих это явление. Любую физическую величину невозможно измерить
абсолютно точно, т.е. в опытах, как бы точно они не проводились, невозможно
определить истинное значение измеряемой величины. Измеряемая физическая
величина может быть оценена лишь с той или иной степенью точности. Поэтому
реально задача измерений заключается не в определении истинного значения
измеряемой величины, а в установлении интервала, внутри которого находится
истинное значение этой величины. Ответ на вопрос: что взять за наилучшую
оценку истинного значения измеряемой величины, дает теория погрешностей - наука
о том, как правильно производить обработку результатов измерения.
. ТЕОРИЯ ПОГРЕШНОСТЕЙ
1.1 Классификация измерений
Существуют два типа измерений физических величин: прямое и косвенное.
В случае прямых измерений искомая величина определяется непосредственно с
помощью сравнения этой величины с соответствующей единицей измерения. Примерами
прямых измерений могут служить: измерения длины (линейкой, штангенциркулем,
микрометром), измерение массы (весы с разновесами), измерение временных
интервалов (секундомером), измерение силы тока (амперметром), измерение
температуры (термометром).
В случае косвенных измерений определяемая величина вычисляется из
полученных прямых измерений других физических величин, находящихся в известной
функциональной зависимости от искомой величины. Примерами косвенных измерений
может служить определение плотности тела по прямым измерениям массы и размеров
тела (после определения объема тела) или определение сопротивления участка
электрической цепи по прямым измерениям силы тока и напряжения и т.д.
1.2 Классификация погрешностей
При выполнении различных измерений неизбежно возникают погрешности. Это
связано с неточностью измерительных приборов, несовершенством органов чувств, с
влиянием внешних факторов, с неидеальностью самой измеряемой величины.
Погрешности подразделяются на систематические и случайные.
Систематическими называются погрешности, обусловленные одной и той же
причиной, которая может быть определена заранее. Например, шкала измерительной линейки
неравномерна, стрелка амперметра, при отсутствии тока через него, не стоит на
нуле. При многократных измерениях систематическая ошибка имеет одно и то же
значение, т.е. ошибка систематически повторяется. Такие погрешности можно
учесть и устранить.
Случайными называются погрешности, вызванные весьма большим числом
отдельных факторов, действующих в каждом случае различным образом. Случайные
погрешности могут возникать из-за неточности измерительных приборов,
несовершенства органов чувств, в результате сотрясения стола, фундамента,
движения воздуха, изменения температуры и т.д. Случайные погрешности можно
выявить и уменьшить путем проведения ряда измерений определяемой величины. Для
строгого обоснования величины случайных погрешностей используют методы теории
вероятностей.
Среди случайных погрешностей иногда могут попадаться и грубые ошибки
(промахи) величина которых заметно превышает любые значения в рассматриваемом
ряду измерений. Такие ошибки могут возникать из-за невнимательности
наблюдателя, резкого изменения условий проведения опыта, неразборчивости записи
показаний и т.д. При вычислении измеряемых величин такие ошибочные данные
следует отбрасывать и проделывать повторные (контрольные) измерения.
1.3 Оценка истинного значения измеряемой величины по
результатам эксперимента. Понятие случайной величины и вероятностного
распределения
Предварительное ознакомление с классификацией погрешностей показывает,
что измерение любой физической величины a необходимо проводить многократно.
Допустим, что проведена серия n независимых, одинаково тщательных, прямых
измерений, в результате которых получены значения x1, x2,
x3,...xn физической величины a. Тогда, как правило,
наблюдается разброс данных около истинного значения, обусловленный
существованием различных случайных факторов. Нанесем на числовую ось полученный
ряд значений x1, x2, x3,...xn в
виде черточек (рис. 1а). На числовой оси этот ряд значений займет определенное
место, и, очевидно, все значения как-то сгруппируются около искомого истинного
значения измеряемой величины, положение которого отмечено вертикальной линией.
Задача состоит в том, чтобы по данным x1, x2, x3,...xn
произвести оценку истинного значения измеряемой величины. Для решения этой
задачи можно применить законы, установленные теорией вероятности по отношению к
многократному повторению случайных явлений. В курсе теории вероятностей
доказывается, что самой лучшей оценкой истинного значения является среднее
арифметическое из числа измерений:
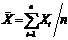 ,(1)
,(1)
т.е.
можно записать, что 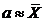 .
.
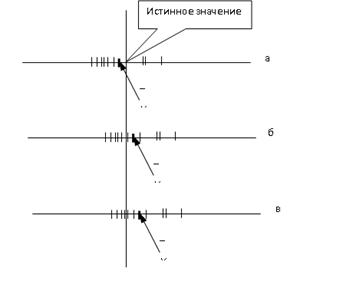
Рис.
1. Изображение трех серий измерений физической величины
Эта запись означает, что истинное значение измеряемой величины а
приближенно, но наилучшим образом оценивается по среднему арифметическому
значению. Если повторить опыт, произведя вторую серию измерений, то, очевидно,
получится новый ряд значений (рис. 1б), причем полученные значения
сгруппируются около истинного, но не повторят картину первой серии измерений.
Поскольку
на результат измерений влияют только случайные факторы, то мы не можем
утверждать, что наилучшей оценкой а будет то же, что и в первой серии
измерений, значение 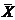 :
:

Вероятнее
всего, из расчета получится другое значение
 ,
,
которое,
также как и 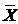 , является наилучшей оценкой а, но в новой серии
измерений. Наконец, из результатов третьей серии n измерений (рис.
1в) наилучшей приближенной оценкой истинного значения а будет
, является наилучшей оценкой а, но в новой серии
измерений. Наконец, из результатов третьей серии n измерений (рис.
1в) наилучшей приближенной оценкой истинного значения а будет
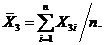
Это
значение, вообще-то, не совпадает с двумя предыдущими средними значениями
измеряемой величины. Таких серий равноточных независимых друг от друга измерений
можно провести сколько угодно. Что же в конце концов послужит оценкой величины
а? Ведь каждый раз мы будем получать среднее значение 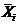 , лежащее где-то недалеко от а. Как видно из рис. 1,
приближенные оценки
, лежащее где-то недалеко от а. Как видно из рис. 1,
приближенные оценки 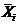 всегда более или менее отличаются друг от друга, т.е.
испытывают случайное рассеивание, несмотря на кажущуюся неизменность условий в
отдельных опытах.
всегда более или менее отличаются друг от друга, т.е.
испытывают случайное рассеивание, несмотря на кажущуюся неизменность условий в
отдельных опытах.
Таким
образом, можно сделать очень важный вывод о том, что результат измерения
является случайной величиной. Результат каждого отдельного измерения 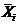 или результат расчета оценки истинного значения
или результат расчета оценки истинного значения 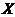 невозможно заранее предсказать, однако, это еще не
означает, что повторные измерения не обнаруживают никакой закономерности.
Закономерность в распределении измерений существует и достаточно хорошо
изучена. Она описывается законом нормального распределения Гаусса [1].
невозможно заранее предсказать, однако, это еще не
означает, что повторные измерения не обнаруживают никакой закономерности.
Закономерность в распределении измерений существует и достаточно хорошо
изучена. Она описывается законом нормального распределения Гаусса [1].
Результаты
серии измерений одной величины можно наглядно представить, построив диаграмму,
которая показала бы, как часто получались те или иные результаты. Такая
диаграмма называется гистограммой. В качестве примера рассмотрим построение
гистограммы по данным измерений величины ускорения силы тяжести методом
математического маятника. В табл. 1 приведены средние значения искомой величины
g(с точностью до сотых, всего 112 значений). Результаты
измерений распределены по группам в интервале 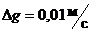 .
.
Таблица 1
|
Значение g
(м/с2) при разбиении по группам
|
Число измерений в каждом
интервале
|
Относительная доля числа
измерений
|
|
9,20-9,29
|
1
|
0,09
|
|
9,30-9,39
|
3
|
0,027
|
|
9,40-9,49
|
4
|
0,035
|
|
9,50-9,59
|
10
|
0,089
|
|
9,60-9,69
|
16
|
0,143
|
|
9,70-9,79
|
21
|
0,188
|
|
9,80-9,89
|
22
|
0,196
|
|
9,90-9,99
|
17
|
0,152
|
|
10,00-10,09
|
10
|
0,089
|
|
10,10-10,19
|
5
|
0,045
|
|
10,20-10,29
|
2
|
0,018
|
|
10,30-10,39
|
1
|
0,009
|
|
Всего 112 значений
|
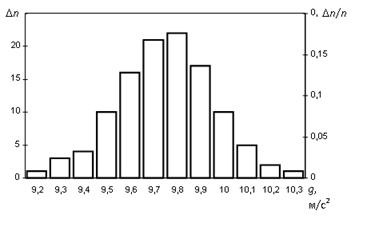
Рис. 2. Гистограмма данных, приведённых в таблице
На рис. 2 отчетливо отображена тенденция большинстваизмерений
группироваться вблизи некоторого значенияизмеряемой величины, которое и можно
принять за наилучшую оценку истинного значения.
Теперь
представим себе, что число измерений неограниченно возросло и стало очень
большим. Ширину интервалов можно сделать очень малой, но чтобы в каждом
интервале было бы много отсчётов. Если теперь вместо гистограммы построить
график, который давал бы относительную долю полного числа измерений 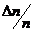 , то получится гладкая кривая, называемая кривой
распределения.
, то получится гладкая кривая, называемая кривой
распределения.
В
рассмотренном примере мы имели дело с последовательностью случайных событий,
которые обнаруживают при неограниченном увеличении их числа характерную
статистическую устойчивость. Обобщая сказанное, введем понятие случайной
величины Х, как переменной величины, принимающей различные значения, зависящие
от случайных факторов. На графике по оси абсцисс будем откладывать значения Х1,
Х2, …Хn, полученные в результате n измерений
физической величины, а по оси ординат - частоту появления 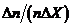 полученных значений в заданном интервале
полученных значений в заданном интервале 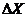 , приходящуюся на единицу этого интервала. Тогда в
пределе при
, приходящуюся на единицу этого интервала. Тогда в
пределе при 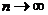 и
и 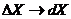 получим
плавную кривую распределения для функции
получим
плавную кривую распределения для функции 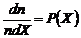 .
.
Функция
P(X) называется плотностью вероятности распределения.
Смысл введенной функции P(X) состоит в том, что P(X).dX
представляет относительную долю полного числа измерений n,
приходящуюся на интервал (X, X+dX). Другими словами, P(X).dX
есть вероятность того, что отдельное значение измеряемой величины находится в
пределах интервала (X, X+dX).
На
рис. 3 изображена типичная кривая распределения результатов измерения
физической величины, причем P(X).dX площадью фигуры,
заштрихованной наклонными линиями.
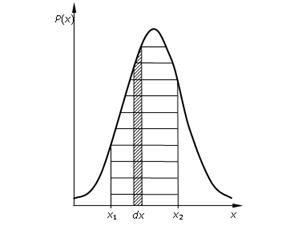
Рис.
3. Типичная кривая распределения измеренных значений
Следовательно,
вероятность того, что отдельное значение измеряемой величины окажется в
интервале от X1 до X2, равна 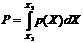 и
представлена на рис. 3 площадью фигуры, заштрихованной горизонтальными линиями.
и
представлена на рис. 3 площадью фигуры, заштрихованной горизонтальными линиями.
Как
показывает опыт, в больших совокупностях равноправных объектов, которые
называются статистическими ансамблями, существуют присущие им вероятностные
распределения (распределение Максвелла для молекул идеального газа, распределение
Ферми для электронов в металле, распределение Пуассона для распада
радиоактивных атомов, распределение Бозе - Эйнштейна для теплового излучения,
распределение Гаусса в случае большого числа измерений). Каждое из этих
распределений математически описывается своей функцией плотности вероятности
распределения P(X), имеющей конкретный математический вид в зависимости
от характера случайной величины.
.4
Распределение Гаусса и его основные характеристики
В
случае большого числа измерений (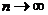 ),
случайный разброс значений измеряемой величины подчиняется закону, открытому
Гауссом.
),
случайный разброс значений измеряемой величины подчиняется закону, открытому
Гауссом.

Рис.
4. Гауссово распределение
Функция
P(X) симметрична относительно а, достигает максимума при Х = а (рис.4).
Кроме параметра а функция P(X) задается еще параметром s, который называется стандартным
отклонением.
Величина
D = s2 называется дисперсией распределения и имеет смысл
среднего значения квадрата отклонения Х от истинного значения а, т.е. 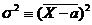 , где
, где 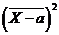 - средний
квадрат отклонения измеряемой величины от истинного значения.
- средний
квадрат отклонения измеряемой величины от истинного значения.
Р(Х) быстро стремится к нулю, когда Х становится большим по сравнению с s.
Функция нормального распределения имеет вид:
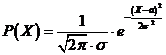 (1)
(1)
Из
рис. 5 видно, что основная часть результатов измерений группируется около
центрального значения а - истинного значения измеряемой величины.
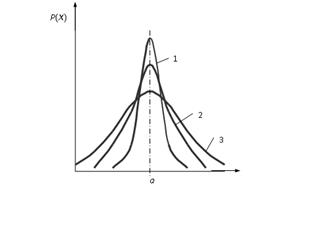
Рис. 5. Изменение формы кривой при измерениях одной и той же величины
методами различной точности: 1 - s 1; 2 - s 2; 3 - s 3; s 3>s 2>s 1
Отклонения по обе стороны от центра распределения наблюдаются тем реже,
чем больше абсолютная величина таких отклонений.
Если изменить метод измерения величины а и измерять ее другим прибором,
например, более совершенным, более точным, то разброс результатов измерений
будет около центра с прежней абсциссой а, но разброс результатов существенно
уменьшится (рис. 5, кривая 1). Если же точность метода измерений ниже, чем для
кривой 2, то разброс результатов увеличится и кривая станет более пологой (рис.
5, кривая 3). Трем кривым на рис. 5 соответствуют разные значения стандарта
отклонения s, который
характеризует размах (разброс) случайных отклонений, присущих данному методу
измерения. При этом площадь под кривыми распределения для разных s одна и та же. Параметры а и s в распределении Гаусса, как правило,
неизвестны и их нужно искать по данным значениям Х1, Х2,
…Хn, полученным из опыта. В теории
погрешностей существует метод (максимального правдоподобия), который позволяет
установить связь между параметрами распределения Гаусса а и s и набором результатов измерений
физической величины. Используя этот метод, можно строго математически доказать,
что наиболее правдоподобной оценкой истинного значения измеряемой величины
является среднее арифметическое из данных измерений, т.е.
 (2)
(2)
а
наилучшей оценкой второго параметра s является средняя
квадратичная погрешность среднего 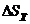 . Расчет
осуществляется по формуле:
. Расчет
осуществляется по формуле:
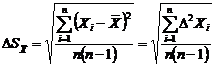 (3)
(3)
1.5 Понятие доверительного интервала и доверительной
вероятности (надежности)
Среднее
арифметическое 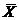 является приближенной оценкой истинного значения а
измеряемой величины. Поэтому, чтобы эта оценка была наиболее полной, надо
обязательно указать, какова погрешность полученного результата DX. Величину
абсолютного отклонения среднего
является приближенной оценкой истинного значения а
измеряемой величины. Поэтому, чтобы эта оценка была наиболее полной, надо
обязательно указать, какова погрешность полученного результата DX. Величину
абсолютного отклонения среднего 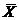 из n
измерений от истинного значения а называют абсолютной погрешностью или
доверительным интервалом среднего. Важно не то, что в результате измерений мы
получаем
из n
измерений от истинного значения а называют абсолютной погрешностью или
доверительным интервалом среднего. Важно не то, что в результате измерений мы
получаем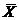 , а важно то, что наряду с
, а важно то, что наряду с 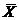 должен быть указан интервал DX, в пределах
которого где-то находится истинное значение а.
должен быть указан интервал DX, в пределах
которого где-то находится истинное значение а.
Однако
мы не может достоверно утверждать, что истинное значение а окажется внутри
интервала 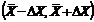 , мы можем сказать лишь следующее: имеется какая-то
вероятность того, что а лежит в пределах этого интервала. Следовательно,
доверительный интервал DX
необходимо указывать вместе с доверительной вероятностью (надежностью) a попадания истинного значения в пределы этого интервала. Без указания
вероятности a сам по себе интервал DХ не может
быть принят в качестве оценки погрешности результата. Если известен
вероятностный закон распределения Р(Х), то вероятность попадания истинного
значения в пределы этого интервала может быть рассчитана по формуле:
, мы можем сказать лишь следующее: имеется какая-то
вероятность того, что а лежит в пределах этого интервала. Следовательно,
доверительный интервал DX
необходимо указывать вместе с доверительной вероятностью (надежностью) a попадания истинного значения в пределы этого интервала. Без указания
вероятности a сам по себе интервал DХ не может
быть принят в качестве оценки погрешности результата. Если известен
вероятностный закон распределения Р(Х), то вероятность попадания истинного
значения в пределы этого интервала может быть рассчитана по формуле:
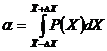 (4)
(4)
Расчет
показывает, что уже при числе измерений  выбор
погрешности
выбор
погрешности 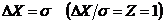 , дает величину надежности a, равную 0,68. Другими словами, если взять интервал надежности
, дает величину надежности a, равную 0,68. Другими словами, если взять интервал надежности 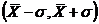 , то можно утверждать, что в 68 случаях из 100
истинная величина а попадет в указанный интервал, а в 32 случаях из 100 - не
попадет в этот интервал.
, то можно утверждать, что в 68 случаях из 100
истинная величина а попадет в указанный интервал, а в 32 случаях из 100 - не
попадет в этот интервал.
В
случае, когда 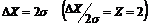 , то a получается равной 0,95. Если
, то a получается равной 0,95. Если 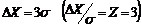 , a = 0,997, т.е. за пределы
доверительного интервала выйдет всего лишь около 3 измерений из 1000.
, a = 0,997, т.е. за пределы
доверительного интервала выйдет всего лишь около 3 измерений из 1000.
1.6 Распределение Стьюдента
Формула
(3), по которой оценивается среднеквадратичное отклонение s, является справедливой лишь при 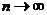 . Число
измерений в реальных опытах не может быть бесконечно большим, поэтому
использовать среднеквадратичное отклонение для ограниченного числа измерений
нельзя.
. Число
измерений в реальных опытах не может быть бесконечно большим, поэтому
использовать среднеквадратичное отклонение для ограниченного числа измерений
нельзя.
Чтобы
получить оценку доверительного интервала для величины а в случае малых n, в
теории погрешностей вместо отношения 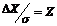 , вводят
величину
, вводят
величину
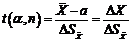 (5)
(5)
Эта
величина (коэффициент Стьюдента) является функцией числа измерений n и
величины a - доверительной вероятности, которая нам задается или
же мы ее выбираем сами.
Оказывается,
что случайная величина при малых n распределена не по нормальному закону (1), а по
закону, открытому Стьюдентом.
Вид
этого закона существенно зависит от выбора n.
Плотность
вероятности распределения P(t), соответствующая закону Стьюдента, имеет вид:
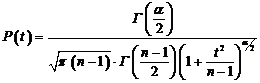 ,(6)
,(6)
где
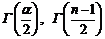 - гамма-функции
- гамма-функции
На
рис.6 приведены кривые распределения Стьюдента для различных значений n.
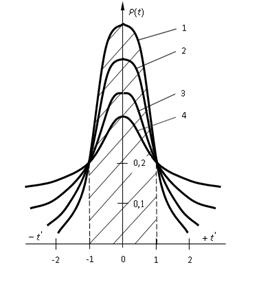
Рис.
6. Кривые распределения Стьюдента для различных n: 1 - n = ¥; 2 - n = 10; 3 - n = 5; 4 - n = 2
При
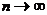 распределение Стьюдента переходит в распределение
Гаусса. Распределение Стьюдента позволяет оценить величину погрешности
результата DX при
заданной доверительной вероятности a, или, наоборот, при
заданном DX
найти величину a. Действительно, если выбрать на оси t(n,a) некоторое значение t* (рис.6), то вероятность a определяется заштрихованной площадью, причем величина a будет зависеть не только от t, но и от n.
Значение коэффициента Стьюдента t для различных значений n и a, рассчитанные в соответствии с законом Стьюдента, приведены в таблице
2.
распределение Стьюдента переходит в распределение
Гаусса. Распределение Стьюдента позволяет оценить величину погрешности
результата DX при
заданной доверительной вероятности a, или, наоборот, при
заданном DX
найти величину a. Действительно, если выбрать на оси t(n,a) некоторое значение t* (рис.6), то вероятность a определяется заштрихованной площадью, причем величина a будет зависеть не только от t, но и от n.
Значение коэффициента Стьюдента t для различных значений n и a, рассчитанные в соответствии с законом Стьюдента, приведены в таблице
2.
Задавая
надежность a, равную определенной величине, при данном значении n, по
табл.2 можно определить коэффициент t. Тогда, определив
предварительно 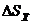 по формуле (3), можно оценить абсолютную погрешность
результата (доверительный интервал) DХ по формуле:
по формуле (3), можно оценить абсолютную погрешность
результата (доверительный интервал) DХ по формуле:
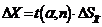 (7)
(7)
Таблица 2
|
a
|
|
n
|
0,2
|
0,4
|
0,6
|
0,8
|
0,9
|
0,95
|
0,99
|
|
2
|
0,33
|
0,73
|
1,38
|
3,1
|
6,31
|
12,7
|
63,7
|
|
3
|
0,29
|
0,62
|
1,06
|
1,9
|
2,92
|
4,30
|
9,52
|
|
4
|
0,28
|
0,58
|
0,98
|
1,6
|
2,35
|
3,18
|
5,84
|
|
5
|
0,27
|
0,57
|
0,94
|
1,5
|
2,13
|
2,78
|
4,60
|
|
6
|
0,27
|
0,56
|
0,92
|
1,5
|
2,02
|
2,57
|
4,03
|
|
7
|
0,27
|
0,55
|
0,90
|
1,4
|
1,94
|
2,45
|
3,17
|
|
8
|
0,26
|
0,55
|
0,90
|
1,4
|
1,89
|
2,36
|
3,50
|
|
9
|
0,26
|
0,54
|
0,90
|
1,4
|
1,86
|
2,31
|
3,36
|
|
10
|
0,26
|
0,54
|
0,86
|
1,4
|
1,83
|
2,26
|
3,25
|
|
15
|
0,26
|
0,54
|
0,87
|
1,3
|
1,76
|
2,14
|
2,98
|
|
20
|
0,26
|
0,53
|
0,85
|
1,3
|
1,73
|
2,09
|
2,86
|
|
30
|
0,26
|
0,53
|
0,85
|
1,3
|
1,70
|
2,05
|
2,76
|
|
40
|
0,26
|
0,53
|
0,85
|
1,3
|
1,69
|
2,02
|
2,71
|
|
60
|
0,25
|
0,53
|
0,85
|
1,3
|
1,67
|
2,00
|
2,66
|
|
∞
|
0,25
|
0,52
|
0,84
|
1,3
|
1,65
|
1,95
|
2,59
|
Истинное
значение измеряемой величины а будет находиться в пределах интервала (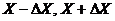 ) с вероятностью a, т.е.
) с вероятностью a, т.е.
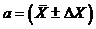 (8)
(8)
Объективным критерием качества проведенных измерений является
относительная погрешность, определяемая отношением абсолютной погрешности к
среднему значению измеряемой величины:
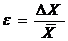 (9)
(9)
1.7 Выявление промахов
Ранее
уже говорилось, что если взять доверительный интервал 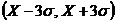 , то только в 3 случаях из 1000 измерений можно
ожидать выход измерений из указанного доверительного интервала. Если не
ставится специальная задача, где точность играет основную роль, то можно
считать данные, выходящие за доверительный интервал
, то только в 3 случаях из 1000 измерений можно
ожидать выход измерений из указанного доверительного интервала. Если не
ставится специальная задача, где точность играет основную роль, то можно
считать данные, выходящие за доверительный интервал 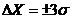 , промахами и их при чистовой обработке не учитывать.
В практических расчетах, при ограниченном числе измерений, для оценки промахов
предполагается, что
, промахами и их при чистовой обработке не учитывать.
В практических расчетах, при ограниченном числе измерений, для оценки промахов
предполагается, что  .
.
1.8 Выбор числа необходимых измерений и учет погрешности
измерительного прибора
Иногда условия работы требуют получение максимальной точности с
использованием определенного измерительного устройства, имеющего цену деления DС.
Считается,
что экспериментатор достоверно устанавливает значение показаний прибора с
точностью  (здесь d - погрешность
измерительного прибора). Если задаться доверительной вероятностью a = 0,68, то можно составить равенство для определения числа необходимых
измерений n:
(здесь d - погрешность
измерительного прибора). Если задаться доверительной вероятностью a = 0,68, то можно составить равенство для определения числа необходимых
измерений n:  .
Подставляя
.
Подставляя 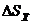 из (3), получаем:
из (3), получаем:
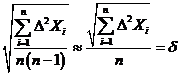
Тогда
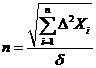 (10)
(10)
Ясно, что в результате измерений нельзя сделать ошибку меньше, чем та,
которая определяется погрешностью измерительного прибора. Поэтому в
окончательном результате в качестве абсолютной погрешности принимают случайную
погрешность только тогда, когда она существенно превышает приборную. В случае,
когда эти требования не выполняются и случайная погрешность оказывается
сравнимой с приборной погрешностью d, границы доверительного интервала определяются по формуле:
 (11)
(11)
Если
же приборная погрешность является определяющей, т.е. ее величина существенно
больше величины случайной погрешности, присущей данному методу, то в
окончательном результате учитывают только приборную погрешность. В этом случае
многократные измерения не выполняют.
1.9 Порядок обработки результатов прямых измерений
Когда физическая величина а определяется непосредственно с помощью того
или иного измерительного прибора (прямые измерения), оценка истинного значения
измеряемой величины и погрешности может быть осуществлена в следующем порядке:
. Составляется таблица результатов измерений.
2. Вычисляется среднеарифметическое значение из n измерений:
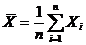
3. Определяются
погрешности отдельных измерений: 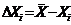
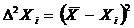
4. Вычисляются квадраты погрешностей отдельных измерений:
5. Вычисляется средняя квадратичная погрешность результата серии
измерений:
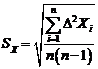
6. Если имеются резко отличающиеся от остальных значения, выясняют, не
являются ли они промахами.
7. Задаются значением доверительной вероятности a (в лабораторных работах физического
практикума обычно принимают a в пределах от 0,8 до 0,9).
. Определяют по таблице 2 коэффициент Стьюдента t(a, n) для заданной надежности a и числа проведенных измерений n.
. Определяют границы доверительного интервала:

10. Рассчитывают относительную погрешность результата серии измерений:
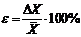
11. Окончательный результат записывается в виде:

1.10 Расчет погрешностей косвенных измерений
Как уже указывалось, косвенные измерения физической величины определяются
прямыми измерениями других физических величин, которые находятся в определенной
функциональной зависимости от искомой величины. Для определения надежности
результата косвенных измерений необходимо применять распределение вероятностей
рассматриваемой функции. Однако, такой строгий подход во многих случаях можно
заменить упрощенным.
Пусть
искомая величина Х является функцией только одной переменной, т.е. 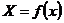 , причем, х определяется из прямых измерений
, причем, х определяется из прямых измерений  . При изменении х на dх произойдет
изменение функции Х на dX. Применяя разложение функции
. При изменении х на dх произойдет
изменение функции Х на dX. Применяя разложение функции  в ряд Тейлора:
в ряд Тейлора:
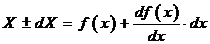 ,
,
откуда

Заменяя
значок дифференциала d значком ошибки D, получаем формулу
для абсолютной погрешности результата косвенных измерений:

Окончательный
результат можно представить в виде:
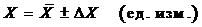
Относительная
погрешность равна:

Пусть
Х является функцией нескольких переменных, т.е. X = f(x, y, z).
Для каждой величины x, y, z,…мы имеем в результате прямых измерений следующие данные:
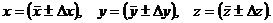 Доверительные интервалы Dx, Dy, Dz для прямых
измерений находятся методом, указанном в порядке обработки результатов прямых
измерений, придерживаясь строгого правила: все доверительные интервалы Dx, Dy, Dz определяются в
соответствии с табл. 2 для одного и того же значения доверительной вероятности a. Оценка доверительного интервала DC в этом случае, как
это следует из теории [1, 2, 4], производится по формуле:
Доверительные интервалы Dx, Dy, Dz для прямых
измерений находятся методом, указанном в порядке обработки результатов прямых
измерений, придерживаясь строгого правила: все доверительные интервалы Dx, Dy, Dz определяются в
соответствии с табл. 2 для одного и того же значения доверительной вероятности a. Оценка доверительного интервала DC в этом случае, как
это следует из теории [1, 2, 4], производится по формуле:

где
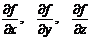 - частные производные f(x, y, z, …)
по переменным x, y, z соответственно, вычисленные для их средних значений.
- частные производные f(x, y, z, …)
по переменным x, y, z соответственно, вычисленные для их средних значений.
Частная
производная функции многих переменных по одной переменной, скажем х, является
обычной производной функции по х, причем все остальные переменные y, z,…
считаются постоянными параметрами. Относительную ошибку величины Х легко
вычислить, написав
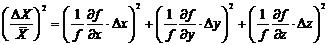
Так
как 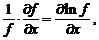
то
для относительной погрешности получаем:
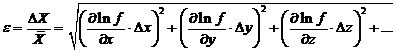
1.11 Порядок обработки результатов при косвенных измерениях
1. Вычислить
среднее значение искомой величины по результатам прямых измерений 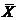 .
.
. Вычислить
относительную погрешность 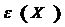 косвенных измерений, учитывая абсолютные погрешности
прямых измерений
косвенных измерений, учитывая абсолютные погрешности
прямых измерений
. Вычислить
абсолютную погрешность косвенных измерений по формуле:
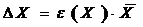
4. Окончательный результат записывается в виде:
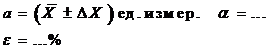
величина доверительный вероятностный погрешность
2. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
.1 Подготовка таблиц в лабораторном журнале и проведение
лабораторных измерений
Необходимость получения достаточно точного значения измеряемой физической
величины требует повторения измерения в одних и тех же условиях. Обычно
необходимое число измерений указано в описании к данной лабораторной работе или
указывается преподавателем. Однако, во всех случаях необходимо помнить, что с
ростом числа измерений возрастает и точность полученного результата. Поэтому в
большинстве лабораторных работ физического практикума необходимо проводить 5 -
10 измерений в равных условиях. Исключения допускаются только в том случае,
если есть полная уверенность в том, что измеряемая величина имеет, в принципе,
точное значение и для ее измерения используют очень точные приборы. Так, в
первой лабораторной работе по определению плотности твердого тела масса тела
является такой величиной, если для ее определения используют достаточно точный
прибор - аналитические весы с погрешностью 0,05 мг. В случае хорошо налаженных
аналитических весов массу тела можно было бы определять один раз, но
неаккуратное обращение с весами студентов, ранее выполнявшими взвешивание,
приводит к тому, что чувствительность весов резко ухудшается, и они уже не
являются достаточно точным прибором. Поэтому массу тела необходимо измерять
многократно. В первой же лабораторной работе линейные размеры (длину, высоту и
ширину) или диаметр и высоту измеряемого тела необходимо измерять многократно,
что вызвано как неточностью измерительных приборов, неточностью линейных
размеров в разных местах измеряемого тела.
Студент допускается к выполнению лабораторной работы только при наличии у
него домашней подготовки, содержащей краткий теоретический анализ
экспериментальной задачи, описание лабораторной установки и подготовленные
таблицы для записи результатов измерений. Для подготовки такой таблицы студент
должен определить количество измеряемых величин и необходимое число измерений.
Так, в первой лабораторной работе в случае цилиндрического измеряемого тела
количество измеряемых величин равно трем: масса, высота и диаметр цилиндра, а в
случае параллелепипеда количество измеряемых величин равно четырем: масса, длина,
ширина и высота параллелепипеда. Для каждой величины проводится 5 измерений.
Для оформления результатов требуется для каждой величины 3 вертикальных
колонки.
Таким образом, для цилиндрического тела таблица должна иметь десять
колонок в соответствии с примером таблицы (см. таблицу 3).
Записи результатов измерений цилиндрического тела
Таблица 3
|
№ п/п, i
|
mi, г
|
Dmi.104,
г
|
D2mi.108, г2
|
Hi, мм
|
DHi.102,
мм
|
D2Hi.104,
мм2
|
Di, мм
|
DDi.102,
мм
|
D2Di.104, мм2
|
|
1
|
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
|
å
|
|
|
|
|
|
|
|
|
|
|
dm
=…………, г
|
dH =………, мм
|
dD
=………, мм
|
|
|
|
|
|
|
|
|
|
|
|
В случае, если тело имеет форму параллелепипеда, нужно добавить еще три
колонки для третьего линейного размера.
При непосредственном выполнении лабораторной работы студент заполняет
последовательно колонки для m, H и D. Внизу таблицы студент указывает приборные погрешности dm, dH и dD, определенные, как указано далее.
2.2 Определение приборных погрешностей
При определении приборных погрешностей необходимо учитывать следующее:
. Для прецизионных, очень точных приборов имеется паспорт на прибор, в
котором указана погрешность прибора в любом диапазоне измеряемой величины.
2. Для промышленно выпускаемых механических измерительных приборов
непрецизионного класса (штангенциркули, микрометры, металлические линейки,
механические и электрические секундомеры) погрешность прибора равна половине
цены наименьшего деления прибора. Так, для микрометра с ценой деления 0,01 мм
погрешность прибора равна 0,005 мм, для аналитических весов типа А-200
минимальное деление - миллиметровое деление на высвечиваемой шкале,
соответствует 0,1 мг, и приборная погрешность равна 0,05 мг = 5.10-5
г.
. Для устройств неизмерительного назначения, но снабженных для
удобства какой-либо шкалой (треугольники, рейсшины), погрешность составляет не
менее цены деления. То же правило следует применять ко всем самодельным, не
промышленно изготовленным шкалам приборов.
4. Для
электроизмерительных приборов (вольтметры, амперметры, ваттметры) погрешность
определяется классом их точности. Класс точности указан на шкале прибора,
обычно в нижнем правом углу. В физическом практикуме МГУИЭ использованы приборы
с классом точности 4,0; 2,5; 2,0; 1,5; 1,0; 0,5; 0,2. Класс точности указывает,
какой процент от максимального значения шкалы прибора составляет погрешность
прибора. Так, для микроамперметра класса точности 1,5 с максимальным значением
измеряемого тока 300 мкА погрешность составляет: 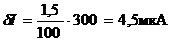 Относительная
погрешность при использовании такого прибора определяется делением абсолютной
погрешности 4,5 мкА на измеряемую величину тока.
Относительная
погрешность при использовании такого прибора определяется делением абсолютной
погрешности 4,5 мкА на измеряемую величину тока.
. При
использовании для измерения метода сравнения необходимо учитывать погрешность
изготовления «эталона», используемого в данной работе. Так, при использовании
промышленных измерительных мостов для наиболее точного измерения методом
сравнения погрешность указана на приборе. Для устройств типа «магазин
сопротивлений» погрешность определяется их классом точности, который процент от
устанавливаемого значения данной величины. Для нерегулируемых элементов (резисторы,
конденсаторы) погрешность их изготовления указана на корпусе элемента в
процентах от их номинала.
. Во
многих лабораторных работах в качестве одного из элементов измерительного
прибора используется сам экспериментатор. Он вносит определенную физиологическую
погрешность в измерения. Так, при определении интервала времени с ручным
включением хронометра с погрешностью 0,01 с, физиологическая погрешность для
человека с хорошей реакцией составит не менее 0,1 с, а с нормальной реакцией -
0,2 с. В лабораторной работе «Изучение реального соударения шаров» человек не
способен зафиксировать вследствие быстроты явления максимальное отклонение шара
точнее, чем 2о. Во всех таких случаях физиологическая погрешность
рассматривается как приборная.
2.3 Методика расчета погрешностей прямых измерений
Лабораторная работа считается выполненной после заполнения в таблице
колонок для измеренных величин и обязательного утверждения этих результатов
преподавателем. Рассмотрим теперь порядок оформления результатов на примере
расчета высоты цилиндра в лабораторной работе «Определение плотности твёрдого
тела». Сразу отметим, что заполнение остальных колонок таблицы и трудоемкость
расчетов существенно зависят от того, какой методикой расчетов будет
пользоваться студент. Первый вариант основан на использовании при расчетах
среднеарифметического значения измеряемой величины, расчет ведется по наиболее
коротким формулам, но требует длительных расчетов даже при применении
микрокалькуляторов. Второй вариант более прост, все операции производятся с
малыми числами и могут быть проделаны без применения микрокалькуляторов, но
формулы несколько более сложные.
Оформление результатов измерения (расчеты по варианту 1)
Таблица 4
|
№ п/п,
i
|
Hi, мм
|
DHi.10-3,
мм
|
D2Hi.10-6, мм2
|
|
1
|
18,37
|
-6
|
36
|
|
2
|
18,39
|
14
|
196
|
|
3
|
18,41
|
34
|
1156
|
|
4
|
18,35
|
-26
|
676
|
|
5
|
18,36
|
-16
|
256
|
|
å
|
91,88
|
0
|
2320
|
Не заполняя колонки 3 и 4, рассчитываем среднеарифметическое значение
величины H:

где
Hi - каждое из чисел в колонке 2; n -
число измерений.
Для
данных таблицы 4:
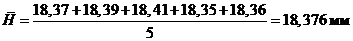
Затем находим отклонение каждого измерения от среднеарифметического значения
с учетом знака:

Эти
расчеты нужно занести в колонку 3 таблицы 4. Во избежание большого количества
нулей с последующей трудностью их учета, не следует заносить в таблицу
результаты в виде промежуточного значения (-0,006), а следует порядок (10-3)вынести
в верхнюю графу таблицы, а в самой таблице указывать только само число (-6). В
нижней строке заносится сумма отклонений (при правильном выполнении расчета она
должна быть равна нулю!). Затем находим 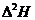 для
каждого измерения и
для
каждого измерения и 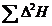 и результаты заносим в колонку 4 таблицы 4. Затем
находим квадрат среднеквадратичного отклонения
и результаты заносим в колонку 4 таблицы 4. Затем
находим квадрат среднеквадратичного отклонения

Квадрат
погрешности измерений за счет случайного разброса равен (коэффициент Стьюдента
выбран из таблицы 2 для a = 0,9 и n = 5 t(a, n) = 2,13)
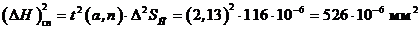
Тогда
квадрат границы доверительного интервала (приборная погрешность определена
заранее в соответствии с указаниями, изложенными выше) равен:
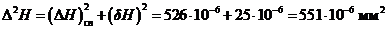
Извлекая
квадратный корень, окончательно записываем результат в виде:
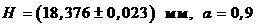
Обращаем
внимание на точность самих расчетов. Количество цифр после запятой в исходных
данных - 2. Такое повышение количества значащих цифр оправдано, так как это
значение H в дальнейшем будет использовано для расчета
плотности. Если бы H было конечной целью работы, то необходимо было
оставить столько цифр, сколько было получено в результате измерений - 2 цифры
после запятой и записать ответ в виде:

Увеличение
сверх трех количества цифр после запятой приводит только к ненужным затратам
времени и не дает никакой информации.
Вариант
2. При расчетах по этому варианту
таблицу 4 заполняют сразу, не проводя основных расчетов. Для этого выбирают
опорную, базовую величину, H0, не
сильно отличающуюся от среднеарифметического значения. Так, для нашего примера
такой величиной являлось бы одно из чисел: 18,37 или 18,38 или 18,39. Примем H0 = 18,39. Тогда DH1 = 18,37
- 18,39 = -0,02. Эти расчеты выполняют в уме и сразу заполняют таблицы 5 с
учетом замечаний о записях результатов, т.е. разность увеличивают в сто раз, а
множитель 102 заносят в верхнюю стоку таблицы. Затем заполняют
колонку 4, занося множитель 104 в верхнюю стоку таблицы. Находят
сумму.
Оформление
результатов измерения (расчеты по варианту 2)
Таблица 5
|
№ п/п,
iHi, ммDHi.10-2D2Hi.10-4, мм2
|
|
|
|
|
1
|
18,37
|
-2
|
4
|
|
2
|
18,39
|
0
|
0
|
|
3
|
18,41
|
2
|
4
|
|
4
|
18,35
|
-4
|
16
|
|
5
|
18,36
|
-3
|
9
|
|
å
|
|
-7
|
33
|
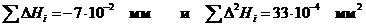
Далее
проводят расчеты по формулам:
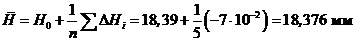
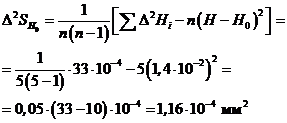
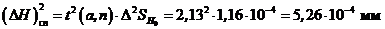

2.4 О приближенных вычислениях
При выполнении вычислений необходимо всегда руководствоваться практически
необходимой точностью. Вести вычисления с точностью большей, чем это допускают
данные задачи - бессмысленно.
Числовые данные бывают двух типов. Одни в точности задают истинную
величину, другие - приблизительно. Первые называются точными, вторые -
приближенными. Например, батарея конденсаторов состоит из 5 конденсаторов
емкостью по 50 пФ. Число 5 - точное, а число 50 пФ - приближенное.
Теория приближенных вычислений позволяет:
1. Зная степень точности данных, оценить степень точности результатов еще
до выполнения числовых операций;
2. Брать для расчетов данные с надлежащей степенью точности,
достаточной, чтобы обеспечить требуемую точность результата, и в то же время не
слишком большой, чтобы избавиться от бесполезных вычислений.
При записи приближенных чисел следует иметь в виду, что значащими
называют все цифры числа, кроме нулей, стоящих впереди числа. Например, в числе
0,00013405 пять значащих цифр; в числе 0,1200 и 5010 - четыре. Число значащих
цифр некоторого числа называется его значимостью.
В приближенных вычислениях часто приходится округлять числа как
приближенные, так и точные, т.е. отбрасывать одну или несколько цифр. Чтобы
обеспечить наибольшую близость округленного числа к округляемому, следует
соблюдать следующие правила:
1. Если первая из отбрасываемых цифр больше, чем 5, то последняя из
сохраняемых цифр увеличивается на единицу. Увеличение совершается и тогда,
когда первая из отбрасываемых цифр равна 5, а за ней одна или несколько
значащих цифр. Например, округляя приведенные ниже числа до трех значащих цифр,
получаем:
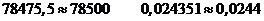
2. Если первая из отбрасываемых цифр меньше, чем 5, увеличение не
делается. Например, округляя приведенные числа до трех значащих цифр, получим
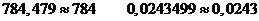
3. Если отбрасывается цифра 5, а за ней нет значащих цифр, то округление
производится на ближайшее четное число, т.е. последняя, сохраняемая цифра
остается неизменной, если она четная и увеличивается, если она нечетная. Это
связано с тем, что при многочисленных округлениях избыточные числа будут
встречаться примерно столь же часто, как и недостаточные. Взаимная компенсация
погрешностей обеспечит наибольшую точность результата. Например, округляя числа
до первого десятичного знак, получаем:
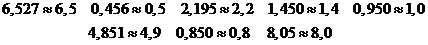
2.5 Правила приближенных вычислений
При сложении и вычитании приближенных чисел окончательный результат
округляют так, чтобы он не имел значащих цифр в тех разрядах, который
отсутствуют хотя бы в одном из приближенных данных. Например, при сложении
чисел получим
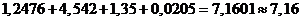
При
умножении следует округлять сомножители так, чтобы каждый из них содержал
столько значащих цифр, сколько их имеет сомножитель с наименьшим числом таких
цифр. Например, вместо выражения 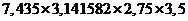 следует
вычислять выражение
следует
вычислять выражение 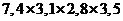
В
окончательном результате следует оставлять такое же число значащих цифр, какое
имеется в сомножителях после их округления.
В
промежуточных результатах следует сохранять на одну значащую цифру больше.
Такое же правило соблюдается и при делении приближенных чисел.
При
возведении в квадрат или куб следует в результате оставлять столько значащих
цифр, сколько их имеется в основании степени. Например, 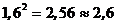
При
извлечении квадратного или кубического корней в результате нужно брать столько
значащих цифр, сколько их имеется в подкоренном выражении. Например,
 .
.
При
вычислении сложных выражений следует применять указанные правила в соответствии
с видом производимых действий. Например, 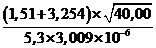
Сомножитель
5,3 имеет наименьшее число значащих цифр - две. Поэтому результаты всех
промежуточных вычислений должны округляться до трех значащих цифр:
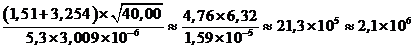
Окончательный результат округлили до двух значащих цифр.
2.6 Правила построения графиков
Возможно построения двух видов графиков: в общем виде без числовых данных
и с цифровыми данными.
Построение графиков в «общем виде» без числовых данных помогает студенту
правильно осмыслить задачу, передать общую тенденцию изменения той или иной
функции на основе математического анализа зависимости.
Построение графика с цифровыми данными производят в следующей
последовательности:
1. Графики следует вычерчивать только на подходящей специальной бумаге
(например, на миллиметровой).
2. Для заданного диапазона изменения аргумента определяют
максимальное и минимальное значения функции на границах требуемого диапазона
изменения аргумента.
Так, для построения графика X = 4t2 - 6t + 2 в диапазоне изменения t от 0 до 2 с, имеем:
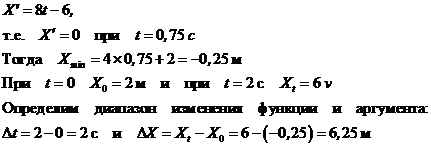
При
определении интервалов значений функции и аргумента следует округлить их последние
значащие цифры в сторону уменьшения наименьших и увеличения наибольших
возможных значений. В нашем примере t изменяется от 0 до 3 с и Х
изменяется от -1 м до +7 м.
3. Выбрать размер листа для графика так, чтобы вокруг поля координатного
угла и надписей масштабов оставались свободные поля шириной 1,5-2 см.
4. Выбрать линейный масштаб координатных осей по округленным
границам интервалов так, чтобы длины отрезков осей для функций и аргументов
были примерно одинаковыми, но чтобы деления интервалов на счетные части
образовывали шкалы, удобные для отсчета любых значений величин. Определить
масштаб для построения графика таким, чтобы поле листа было максимально
использовано. Для этого выбрать размер листа для графика таким образом, чтобы
вокруг поля координатного листа и надписей масштабов остались свободные поля
шириной 1,5 - 2 см. Далее определяют масштаб для построения графика. Например,
для вышеприведенного примера поле для построения графика оказалось равным полю
школьной тетради, то для построения графика можно использовать по горизонтали
(ось абсцисс) 10-12 см, а по вертикали (ось ординат) 8 - 10 см. Таким образом,
получим масштабы mx
и my для осей x и y
соответственно:
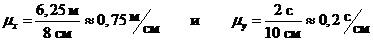
5. С началом координат совместить наименьшие округленные значения
аргумента(по оси абсцисс) и функции (по оси ординат).
6. Строят оси графика, нанося на них ряд чисел с постоянным шагом в
виде арифметической прогрессии и обозначают цифрами через равные промежутки,
удобные для отсчета значения. Эти обозначения не следует располагать слишком
часто или редко. Цифры на осях графика должны быть простыми, их не надо
связывать с расчетными значениями. Если числа очень большие или очень
маленькие, то их умножают на постоянный сомножитель типа 10n (n - целое число), вынося этот сомножитель к концу оси. Вместо
цифровых обозначений у концов осей помещают символы аргумента и функции с
наименованием единиц их измерения, отделенными запятой. Например, при
построении оси давлений Р в диапазоне от 0 до 0,003 Н/м2 целесообразно
умножить Р на 103, а ось изобразить следующим образом (рис. 7):

Рис. 7. Разметка оси координат
На график наносят расчетные или экспериментально полученные значения
величин, руководствуясь таблицей значений величин. Для построения гладкой
кривой достаточно рассчитать 5-6 точек. При теоретических расчетах точки на
графике не выделяются (рис. 8а).
Экспериментальный график строится как аппроксимированная кривая по точкам
(рис. 8б).

7. При построении графиков по экспериментальным данным необходимо на
графике указывать экспериментальные точки. При этом каждое значение величины
должно быть показано с учетом доверительного интервала. Доверительные интервалы
откладываются от каждой точки в виде отрезков прямых (горизонтальных для
аргументов и вертикальных для функций). Полная длина этих отрезков в масштабе
графика должна быть равной удвоенной абсолютной погрешности измерения. Опытные
точки можно изображать в виде крестиков, прямоугольников или эллипсов с
размерами по горизонтали 2Dх и с размерами по вертикали 2Dy. При изображении доверительных интервалов функций и аргументов на
графиках концы вертикальной и горизонтальной черточки с точкой посередине изображают
оси площади рассеяния значений (рис. 9).

Если в масштабе графика черточки доверительных интервалов за малостью
нельзя изобразить, точку значений окружают маленькой окружностью, треугольником
или ромбиком. Отметим, что экспериментальные кривые следует проводить гладкими,
с максимальным приближением к доверительным интервалам экспериментальных
значений. Рассмотренный пример на рис. 9 иллюстрирует наиболее распространенную
форму графиков, которые придется строить студенту при обработке опытных данных.
Графическое изображение величин представляет собой своеобразный язык,
обладающий наглядностью и большой информативностью при условии правильного,
неискаженного пользования им. Поэтому полезно ознакомиться с примерами ошибок в
оформлении графиков, представленных на рис. 10.

Графики двух функций одного аргумента, например F(e) и
K(e), можно совмещать на общей оси
абсцисс. В этом случае масштабы осей ординат строят слева для одной и справа
для другой функции. Принадлежность графика к одной или другой функции
показывают стрелками (рис. 11а).
Графики одной функции при различных значениях постоянной всегда совмещают
на одной плоскости координатного угла, кривые нумеруют и под графиком выписывают
значения постоянных (рис. 11б).


Приставки для образования наименований кратных и дольных
единиц
Перечисленные в табл. 6 множители и приставки используются для образования
кратных и дольных единиц от единиц Международной системы единиц (СИ), системы
СГС, а также от внесистемных единиц, допущенных государственными стандартами.
Приставки рекомендуется выбирать таким образом, чтобы числовые значения величин
находились в пределах от 0,1 до 1.103. Например, для
выражения числа 3.108 м/с лучше выбрать приставку мега, а
не кило и не гига. С приставкой кило получим: 3.108 м/с =
3.105 км/с, т.е. число, большее, чем 103.С
приставкой гига получим: 3.108 м/с = 0,3.Гм/с,
число, хотя и большее 0,1, но не целое. С приставкой мега получим: 3.108
м/с = 3.102 Мм/с.
Таблица 6
|
Кратность и дольность
|
Название
|
Обозначение
|
|
1012
|
тера
|
Т
|
|
109
|
гига
|
Г
|
|
106
|
мега
|
М
|
|
103
|
кило
|
к
|
|
101
|
дека
|
да
|
|
10-1
|
деци
|
д
|
|
10-2
|
санти
|
с
|
|
10-3
|
милли
|
м
|
|
10-6
|
микро
|
мк
|
|
10-9
|
нано
|
н
|
|
10-12
|
пико
|
п
|
Наименования и обозначения десятичных кратных и дольных единиц образуются
присоединением приставок к наименованиям исходных единиц. Присоединение двух и
более приставок подряд не допускается. Например, вместо единицы
«микромикроФарада» следует применять единицу «пикоФарада».
Обозначение приставки пишется слитно с обозначением единицы, к которой
она присоединяется. При сложном наименовании производной единицы СИ приставку
присоединяет к наименованию первой единицы, входящей в произведение или
числитель дроби. Например: кОм.м, но не Ом.км.
В виде исключения из этого правила допускается присоединение приставки к
наименованию второй единицы, входящей в произведение или в знаменатель дроби,
если ими являются единицы длины, площади или объема. Например: Вт/см3,
В/см, А/мм2 и др.
В табл. 6 указаны приставки для образования только десятичных кратных и
дольных единиц. Кроме этих единиц, государственным стандартом «Единицы
физических величин» допущены к использованию кратные и дольные единицы времени,
плоского угла и относительных единиц, не являющихся десятичными. Например,
единицы времени: минута, час, сутки; единицы угла: градус, минута, секунда.
2.5 Выражение физических величин в
одной системе единиц
Для успешного решения физической задачи необходимо уметь выразить все
имеющиеся числовые данные в одной системе единиц измерения (СИ или СГС). Такой
перевод наиболее удобно производить заменой каждого сомножителя в размерности
заданной величины на эквивалентный ему сомножитель требуемой системы единиц (СИ
или СГС) с учетом переводного коэффициента. Если последний неизвестен, то
возможен перевод в любую другую промежуточную систему единиц, для которой
переводной коэффициент известен.
Пример 1. Записать а = 0,7 км/мин2 в системе СИ.
В данном примере переводные коэффициенты заранее известны (1 км = 103
м, 1 мин = 60 с), следовательно,
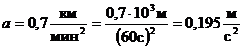
Пример
2. Записать Р = 10 л.с. (лошадиных сил) в системе СИ.
Известно,
что 1 л.с. = 75 кГм/с. Переводной коэффициент из л.с. в ватты студенту
неизвестен, поэтому используют перевод через промежуточные системы единиц:
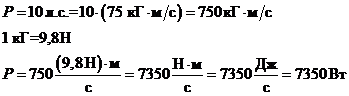
Пример
3. Перевести удельный вес d = 600 фунтов/галлон (записан в английской системе
мер) в систем СГС.
Из
справочной литературы находим:
фунт
(английский) = 0,454 кГ (килограмм силы).
галлон
(английский) = 4,546 л (литр).
Следовательно,
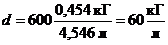
Получено
выражение с использованием внесистемных единиц, перевод которых в систему СГС,
однако, может быть студенту неизвестен. Поэтому используем промежуточные
системы единиц:
л
= 10-3 м3 (СИ) = 10-3(102 см)3
= 103см3, и
кГ
= 9,8 Н (СИ) = 9,8(105 дин) = 9,8.105 дин.
Окончательно:
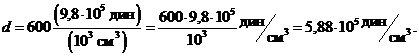
ЛИТЕРАТУРА
1. Смирнов
Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической
статистики.- М.: Наука,1959,511 с.
2. Зайдель
А.Н. Элементарные оценки ошибок измерений.- Л.: Наука, 1974, 108 с.
. Сквайрс
Д. Практическая физика.- М.: Мир,1971,246с.
. Кассандрова
О.Н., Лебедев В.В. Обработка результатов измерений.- М.: Наука, 1970, 104
ПРИЛОЖЕНИЕ
Таблица единиц измерения физических величин в СМ и переводных
коэффициентов
|
Наименование величин
|
Единицы измерения,
сокращённое обозначение
|
Определяющее уравнение
|
Коэффициенты для приведения
к единицам СИ
|
|
|
|
СГС
|
МКГСС (техническая)
|
Внесистемные единицы
|
|
Длина
|
метр, м
|
|
1 см = 10-2м
|
|
1 мкм = 10-6 м 1 Å = 10-10 м 1
дюйм = 2,54.10-2 м 1 фут = 0,305 м 1 миля = 1609,3 м 1
морская миля = 1852 м 1парсек = 3,084.1016 м
|
|
Масса
|
килограмм, кг
|
|
1 г = 10-3 кг
|
1 т.е.м. (техн. ед. массы)
= 9,81кг
|
1 ц (центнер) = 102 кг
1 а.е.м. (атомная ед. массы) = 1,6603.10-27 кг 1
фунт=0,454 кг 1 карат=2.10-4 кг
|
|
Время
|
секунда, с
|
|
|
|
1 ч = 36.102
с 1 мин = 60 с
|
|
Температура
|
Кельвин, К
|
|
|
|
|
|
Сила тока
|
Ампер, А
|
|
1 ед. силы тока СГСЭ =
1/3.10-9А
|
|
|
|
Сила света
|
кандела, кд
|
|
|
|
|
|
Плоский угол
|
радиан, рад
|
|
|
|
1о = (p/180) рад 1¢ = (p/108).10-2 рад 1² = (p/648).10-3 рад
|
|
Телесный угол
|
стерадиан, ср
|
|
|
|
1 квадр. градус ==
304,62.10-6 ср Полный телесныйугол = 4p ср= 12,567 ср
|
|
Частота
|
Герц, Гц
|
n = 1/Т
|
|
|
1 кГц = 103 Гц 1 МГц = 106
Гц
|
|
Угловая скорость
|
радиан в секунду, рад/с
|
w = j /t
|
|
|
1 об/мин = (p/30) рад/с 1 об/с = (2p) рад/с
|
|
Угловое ускорение
|
радиан на секунду в
квадрате, рад/с2
|
e = w/t
|
|
|
|
|
Скорость
|
метр в секунду, м/с
|
V = S/t
|
1 см/с = 10-2 м/с
|
|
1 км/ч = 0,278 м/с 1 узел =
0,5144 м/с
|
|
Ускорение
|
метр на секунду в квадрате,
м/с2
|
a = V/t
|
1 см/с2 = 10-4 м/с
|
|
|
|
Площадь
|
квадратный метр, м2
|
S = a . b
|
1 см2 = 10-4 м2
|
|
1 а (ар)=102 м2 1 га
(гектар) = 104 м2
|
|
Объём
|
кубический метр, м3
|
V = a . b . c
|
1 см3 = 10-6 м3
|
|
|
|
Плотность
|
килограмм на кубический
метр, м3
|
p = m/V
|
1 г/см3 = 103 кг/м3
|
1 кгс.с2/м4 = 9,807 кг/м3
|
1 т/м3 =1 кг/дм3 = 103
кг/м3 1 кг/л = 999,97 кг/м3
|
|
Сила
|
Ньютон, Н
|
F = m . a
|
1 дин = 10-5 Н
|
1 кгс = 9,807 Н
|
|
|
Момент силы
|
ньютон метр, Н.м
|
M = F .l
|
1 дин.см = 10-7 Н.м
|
1 кгс.м = 9,81 Н.м
|
|
|
Момент инерции
|
килограмм. метр в квадрате,
кг.м2
|
I = m .r2
|
1 г.см2 = 10-7 кг.м2
|
1 кгс.м.с2 = 9,807 кг.м2
|
|
|
Работа, энергия, количество
тепла
|
Джоуль,Дж
|
A=Q=F.L
|
1 эрг = 10-7 Дж
|
1 кгс.м = 9,81 Дж
|
1 кал (калория) = 4,187 Дж
|
|
Мощность
|
Ватт, Вт
|
P = A/T
|
1 эрг/с = 10-7 Вт
|
1 кгс.м/с = 9,81 Вт
|
1 л.с. = 735,499 Вт 1 кал/с
= 4,187 Вт
|
|
Давление
|
Паскаль, Па
|
p = F/S
|
1 дин/м2 = 0,1 Па
|
1 кгс/м2 = 9,81 Па
|
1 атм =1,013.105 Па 1 мм.
рт. ст. = 133 Па
|