Обработка результатов многократных измерений физической величины, проверка статистических гипотез и представление результата измерения
КУРСОВОЙ ПРОЕКТ
Обработка результатов
многократных измерений физической величины, проверка статистических гипотез и
представление результата измерения
Введение
Метрология - наука об измерениях, а
измерения - один из важнейших путей познания. Они играют огромную роль в
современном обществе. Наука, промышленность, экономика и коммуникации не могут
существовать без измерений. Каждую секунду в мире производятся миллиарды
измерительных, результаты которых используются для обеспечения качества и технического
уровня выпускаемой продукции, безопасной и безаварийной работы транспорта,
обоснования медицинских и экологических диагнозов, анализа информационных
потоков. Практически нет ни одной сферы деятельности человека, где бы
интенсивно не использовались результаты измерений, испытаний и контроля.
Примерно 15% затрат общественного труда расходуется на проведение измерений. По
оценкам экспертов, от 3 до 9% валового национального продукта передовых
индустриальных стран приходится на измерения и связанные с ними операции.
Измерения - один из важнейших путей
познания природы, объединяющий теорию с практической деятельностью человека.
Измерения являются основой научных знаний, служат для учета материальных
ресурсов и планирования, обеспечения требуемого качества продукции,
взаимозаменяемости деталей и узлов, совершенствования технологии, автоматизации
производства, стандартизации, охраны здоровья и обеспечения безопасности труда
и для многих других отраслей человеческой деятельности. Они количественно характеризуют
окружающий материальный мир, раскрывая действующие в природе закономерности.
Д.И.Менделеев очень образно выразил значение измерений для науки: "Наука
начинается... с тех пор, как начинают измерять. Точная наука невозможна без
меры".
Измерение - сложный процесс,
включающий в себя взаимодействие ряда структурных элементов - измерительной задачи,
объекта измерения, принципов, методов и средств измерения, его модели, условий
измерения, наблюдателя, результата и погрешности измерения. Сам процесс измерения
состоит из ряда последовательных этапов, включающих в себя постановку
измерительной задачи, планирование измерительного эксперимента, непосредственно
измерительный эксперимент, обработку экспериментальных данных, завершаемую
анализом и интерпретацией полученных результатов, а также записью результата в
соответствии с установленной формой представления. Грамотное и сознательное
выполнение всех этапов измерения является залогом сведения к минимуму ошибочных
выводов, сделанных по результатам измерений, и принятия решений, не приводящих
к материальным и моральным потерям.
1. Математическая
обработка результатов наблюдений
.1 Проверка нормальности
распределения результатов наблюдений
Сходимость результатов наблюдений можно
оценить наиболее полно, если их распределение является нормальным. Поэтому
исключительно важную роль при обработке результатов наблюдений играет проверка
нормальности распределения.
Эта задача представляет собой частный
случай более общей проблемы, заключающейся в подборе теоретической функции
распределения, в некотором смысле наилучшим образом согласующейся с опытными
данными.
При большом числе результатов наблюдений
(n>40) данная задача решается в следующем порядке.
Группируют результаты наблюдений в порядке
возрастания их значений: xmin - xmax. Весь диапазон результатов наблюдений разделяют
на r интервалов шириной Dxj (J=1,..., r) и подсчитывают частоты mj,
равные числу результатов, лежащих в каждом j-м интервале, т.е. меньших его
правой и больших или равных левой границе. Отношения
Pj*=mj/n (1.1)
где n-общее число наблюдений, называются
частостями и представляют собой статистические оценки вероятностей попадания
результата наблюдений в j-й интервал. Распределение частостей по интервалам
образует статистическое распределение результатов наблюдений.
Если теперь разделить частость на длину
интервала, то получим величины,
pj*= Pj*/Dxj (1.2)
являющиеся оценками средней плотности распределениям ни интервале  Dxj.
Dxj.
Если отложить вдоль оси результатов наблюдений
интервалы Dxj в порядке возрастания индекса j и на каждом
интервале построить прямоугольник с высотой, равной pj*, то получим
график, называемый гистограммой статистического распределения (рисунок 1.1).
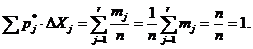

Рисунок 1.1 Гистограммой статистического
распределения
При увеличении числа интервалов r
гистограмма все больше приближается к плавной кривой, ограничивающей единичную
площадь, - к графику дифференциальной функции распределения.
При построении гистограмм рекомендуется
пользоваться следующими правилами:
) Число r интервалов выбирается в
зависимости от числа наблюдений n (при n=4-100 r=7-9; при n=100-500 r=8-12; при
n=500-1000 r=10-16; при n=1000-10000 r=12-22);
) Длины интервалов удобнее выбирать
одинаковыми. Однако если распределение крайне неравномерно, то в области
максимальной концентрации результатов наблюдений следует выбирать более узкие
интервалы;.
) Масштабы по осям гистограммы должны быть
такими, чтобы отношение ее высоты к основанию составляло примерно 5:8.
После построения гистограммы надо
подобрать теоретическую плавную кривую распределения, которая, выражая все
существенные черты статистического распределения, сглаживала бы все
случайности, связанные с недостаточным объемом экспериментальных данных.
Принципиальный вид теоретической кривой выбирают заранее, проанализировав метод
измерения или хотя бы по внешнему виду гистограммы. Тогда определение
аналитического вида кривой распределения сводится к выбору таких значений его
параметров, при которых достигается наибольшее соответствие между теоретическим
и статистическими распределениями.
Одним из методов решения этой задачи
является метод моментов. При его использовании параметрам теоретического
распределения придают такие значения, при которых несколько важнейших моментов
совпадают с их статистическими оценками. Так, если статистическое
распределение, определяемое гистограммой, приведенной на рисунке 1.1, мы хотим
описать кривой нормального распределения, то естественно потребовать, чтобы
математическое ожидание и дисперсия последнего совпадали со средним
арифметическим и оценкой дисперсии, вычисленным по опытным данным.
Далее законно возникает вопрос,
объясняются ли расхождения между гистограммой и подобранным теоретическим
распределением только случайными обстоятельствами, связанными с ограниченным
числом наблюдений, или они вызваны тем, что результаты наблюдений в
действительности распределены иначе.
Для ответа на этот вопрос используют
методы проверки статистических гипотез. Идея их применения заключается в
следующем. На основании гистограммы, полученной при обработке опытных данных,
строится гипотеза, состоящая в том, что результаты наблюдений подчиняются
распределению F(x) с плотностью р(х).
Для того чтобы принять или опровергнуть
эту гипотезу, выбирается некоторая величина U, представляющая собой меру
расхождения теоретического и статистического распределений. В качестве меры
расхождения можно принять сумму квадратов разностей частостей и теоретических
вероятностей попадания результатов наблюдений в каждый интервал, взятых с
некоторыми коэффициентами:
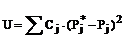 , (1.3)
, (1.3)
где Cj - коэффициенты, называемые весами разрядов, Pj
- теоретические вероятности, определяемые как
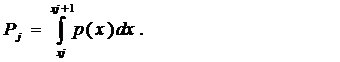 (1.4)
(1.4)
Здесь р(х)- предполагаемая плотность распределения.
Мера расхождения U является случайной величиной и, как показал
К.Пирсон, независимо от исходного распределения подчиняется c2 - распределению с k степенями свободы. Если все частоты mj
³ 5 и число измерений стремится к
бесконечности, то веса Cj выбираются равными (n / pj).
Число степеней свободы распределения k = r - s, где r- число независимых
связей, наложенных на частости pj*.
Если проверяется гипотеза о нормальности распределения, то к числу
этих связей относятся равенство среднего арифметического и точечной оценки
дисперсии соответственно математическому ожиданию и дисперсии предполагаемого
нормального распределения. Кроме того, всегда требуется, чтобы сумма частостей
по всем интервалам была равна единице. Поэтому в данном случае s=3.
Мера расхождения U, выбраним по К. Пирсону, обозначается через cк2.
Для удобства вычисления можно записать в виде
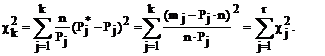 (1.5)
(1.5)
По таблице А1 можно при заданной
доверительной вероятности a=1-q найти тот доверительный интервал (cк2;q/2 и cк2;1-q/2) значений cк2 в который мера
расхождения может попасть по чисто случайным причинам.
Если вычисленная по опытным данным мера
расхождения cк2 окажется в указанном интервале, то гипотеза принимается. Это,
конечно, не значит, что гипотеза верна. Можно лишь утверждать, что она
правдоподобна, т.е. не противоречит опытным данным. Если же cк2 выходит за границы
доверительного интервала, то гипотеза отвергается как противоречащая опытным
данным.
Поскольку проверка гипотезы основывается
на опытных данных, то при принятии решения всегда возможны ошибки. Отвергая в
действительности верную гипотезу, мы совершаем ошибку первого рода. Вероятность
ошибки первого рода называется уровнем значимости и составляет q = 1- a. Принимая в
действительности неверную гипотезу, мы совершаем ошибку второго рода. Вычислить
ее вероятность невозможно, поскольку для этого нужно рассмотреть все прочие
возможные гипотезы, являющиеся альтернативой обсуждаемой гипотезы. Можно лишь
утверждать, что при уменьшении ошибки первого рода ошибка второго рода
увеличивается, поэтому не имеет смысла брать слишком высокие значения
доверительных вероятностей.
Описанная процедура проверки гипотезы о
том, что данное статистическое распределение является распределением с
плотностью р(х), называется критерием согласия c2.
1.2 Обработка
исправленных результатов прямых равнорассеянных наблюдений
Исправленными результатами наблюдений
называются результаты, не содержащие систематические погрешности измерений.
Исправленные результаты наблюдений х1,...,хn,
полученные при прямых измерениях постоянной физической величины Qx,
называются равнорассеянными (равноточными), если они являются независимыми,
одинаково распределенными случайными величинами.
Равнорассеянные результаты получают при
измерениях, проводимых одним наблюдателем или группой наблюдателей с помощью
одних и тех же средств измерений в неизменных условиях внешней среды.
Результаты обрабатывают по-разному в зависимости от того, мало (n<40) или
велико (n>40) количество наблюдений.
При количестве наблюдений n>30 наиболее часто
используют критерий «трех сигм». Более строгим является критерий, который
заключается в проверке гипотезы, что результат наблюдения хi не
будет содержать грубой погрешности, если он является одним из значений
случайной величины х с нормальным законом распределения при количестве
наблюдений n. Ф.Е. Граббсом были табулированы q-процентные точки распределения
максимальных по модулю отклонений результатов наблюдений от их среднего
значения:
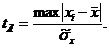 (1.7)
(1.7)
Если 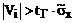 ,то такое наблюдение содержит грубую
погрешность (для уровня значимости q) и должно быть исключено при обработке
результатов наблюдений.
,то такое наблюдение содержит грубую
погрешность (для уровня значимости q) и должно быть исключено при обработке
результатов наблюдений.
Определяют оценку с.к.о. результата измерения 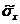 по формуле
по формуле
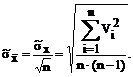 (1.8)
(1.8)
При помощи составного критерия производится проверка нормальности
распределения результатов наблюдений.
По заданной доверительной вероятности Р и числу наблюдений n
определяется коэффициент Стьюдента tp из таблицы Ж.1.
Рассчитываются доверительные границы случайной погрешности
результата измерения 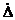 :
:
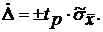 (1.9)
(1.9)
Если сравнивать значения tp для разных распределений, то оказывается, что при Р>0,85
значение tp максимальны для нормального
распределения. Поэтому при неизвестной функции распределения (или невозможности
проверки принадлежности результатов наблюдений к нормальному распределению)
рекомендуется распределение считать нормальным, так как надежность оценки 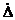 повышается.
повышается.
2. Расчетная часть
Техническое
задание:
Физическая величина - мощность, размерность - Вт;
средство измерения - ваттметр;
разрешающая способность 0,02;
количество измерений ряда наблюдений n = 100;
уровень значимости q = 0,10;
доверительная вероятность РД = 0,99.
Результаты наблюдений приведены в таблице 1 (в Вт).
равнорассеянный нормальность статистический
Таблица 1. Результаты наблюдений
многократных прямых измерений
|
i
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
xi
|
75.90
|
76.20
|
76.36
|
75.74
|
75.96
|
76.00
|
75.92
|
76.16
|
75.20
|
76.44
|
|
i
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
xi
|
75.98
|
75.68
|
76.18
|
75.54
|
76.40
|
76.74
|
75.70
|
75.96
|
75.94
|
76.24
|
|
i
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
|
xi
|
75.48
|
76.22
|
75.62
|
76.18
|
75.88
|
75.26
|
75.44
|
76.24
|
76.02
|
76.42
|
|
i
|
31
|
32
|
33
|
34
|
35
|
36
|
37
|
38
|
39
|
40
|
|
xi
|
75.94
|
76.12
|
75.78
|
75.92
|
76.48
|
75.50
|
76.66
|
76.14
|
76.10
|
75.76
|
|
i
|
41
|
42
|
43
|
44
|
45
|
46
|
47
|
48
|
49
|
50
|
|
xi
|
75.84
|
75.80
|
75.60
|
76.26
|
76.06
|
75.96
|
75.86
|
75.58
|
76.30
|
76.20
|
|
i
|
51
|
52
|
53
|
54
|
55
|
56
|
57
|
58
|
59
|
60
|
|
xi
|
75.98
|
75.82
|
75.84
|
75.72
|
75.90
|
76.36
|
76.12
|
75.82
|
75.80
|
75.64
|
|
i
|
61
|
62
|
63
|
64
|
65
|
66
|
67
|
68
|
69
|
70
|
|
xi
|
76.34
|
76.04
|
76.22
|
75.78
|
75.56
|
75.76
|
76.00
|
76.04
|
76.28
|
76.26
|
|
i
|
71
|
72
|
73
|
74
|
75
|
76
|
77
|
78
|
79
|
80
|
|
xi
|
76.02
|
76.08
|
75.74
|
75.52
|
76.46
|
75.88
|
76.62
|
75.94
|
75.72
|
76.08
|
|
i
|
81
|
82
|
83
|
84
|
85
|
86
|
87
|
88
|
89
|
90
|
|
xi
|
76.30
|
75.96
|
75.70
|
75.68
|
75.46
|
76.00
|
75.90
|
76.14
|
76.20
|
75.98
|
|
i
|
91
|
92
|
93
|
94
|
95
|
96
|
97
|
98
|
99
|
100
|
|
xi
|
76.28
|
76.16
|
75.62
|
75.30
|
75.92
|
75.66
|
76.32
|
75.86
|
75.76
|
76.06
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обработка ряда наблюдений
Находим минимальный и максимальный член ряда наблюдений:
xmin = 75,20 Вт
xmax = 76,74 Вт
Диапазон наблюдений разбиваем на r = 7 одинаковых
интервалов Δxj, равных:
Δxj = (xmax - xmin)/ r = 0,22 Вт
Δxj = h = 0,22 Вт, j = 1...7
Таблица 2. Полученные интервалы
|
1
|
75,20
|
75,42
|
|
2
|
75,42
|
75,64
|
|
3
|
75,64
|
75,86
|
|
4
|
75,86
|
76,08
|
|
5
|
76,08
|
76,30
|
|
6
|
76,30
|
76,52
|
|
7
|
76,52
|
76,74
|
Находим середины интервалов xj и подсчитываем частоту
каждого интервала:
Таблица 3. Расчетные данные
|
j
|
xj, Вт
|
mj
|
  ,1/Втηjηj2mj* ηjmj* ηj2 ,1/Втηjηj2mj* ηjmj* ηj2
|
|
|
|
|
|
|
1
|
75,31
|
3
|
0,03
|
0,14
|
-3
|
9
|
-9
|
27
|
|
2
|
75,53
|
11
|
0,11
|
0,50
|
-2
|
4
|
-22
|
44
|
|
3
|
75,75
|
21
|
0,21
|
0,95
|
-1
|
1
|
-21
|
21
|
|
4
|
75,97
|
0,29
|
1,32
|
0
|
0
|
0
|
0
|
|
5
|
76,19
|
22
|
0,22
|
1,0
|
1
|
1
|
22
|
22
|
|
6
|
76,41
|
11
|
0,11
|
0,50
|
2
|
4
|
22
|
44
|
|
7
|
76,63
|
3
|
0,03
|
0,14
|
3
|
9
|
9
|
27
|
|
Суммы:
|
100
|
-
|
-
|
-
|
-
|
1
|
185
|
Наибольшая частота приходится на пятый интервал, поэтому в
качестве «ложного нуля» принимаем:
X0 = X4 =75,97 Вт.
Вычисляем статистические оценки вероятностей попадания результата
наблюдений в j-ый интервал - частости  по формуле:
по формуле:
 =
=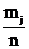
Вычисляем оценки средней плотности распределения в интервалах:
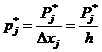
Строим гистограмму статистического распределения (рис.1).
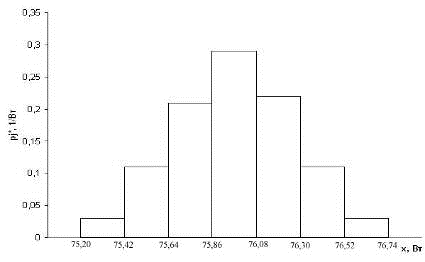
Рисунок 1. Гистограмма статистического распределения
Из вида гистограммы можно сделать предположение, что закон
распределения результатов наблюдений является нормальным.
Вычисляем для каждого интервала значение ηj:

Находим значения начальных моментов:
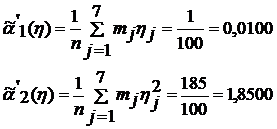
Вычисляем оценку второго центрального момента:
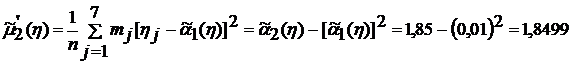
Определяем значения моментов наблюдений:
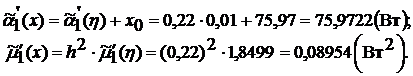
Вычисляем исправленные значения моментов:
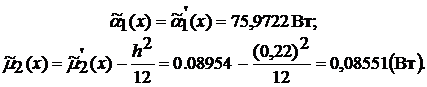
Определяем точные оценки истинного значения тока, с.к.о.
результатов наблюдений и измерений:
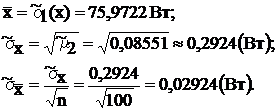
Проверяем наличие грубых погрешностей по критерию «трех сигм»:

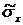 =3.
=3. 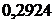 =0,8772(Вт).
=0,8772(Вт).
Наибольшие случайные отклонения равны:
|V(xmin)|=|xmin-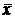 |=|75,20-75,9722|=0,7722 < 0,8772 (Вт);
|=|75,20-75,9722|=0,7722 < 0,8772 (Вт);
|V(xmax)| = | xmax-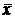 |=|76,74-75,9722|=0,7678 < 0,8772 (Вт).
|=|76,74-75,9722|=0,7678 < 0,8772 (Вт).
Таким образом, среди результатов
наблюдений нет таких, в которых были бы грубые погрешности.
Проверка нормальности закона распределения,
используя критерии Колмогорова, χ2, ω2.
1. Критерий Колмогорова.
В таблицу 4 записываем значения: x1;x1+jΔ;…; x1+kΔ, j=0,…,k, где Δ - разрешающая способность средства измерения (измеряемое приращение
интервала - Δ=0,02 Вт); k - число приращений
интервала, вычисляемое по формуле:
k = (xmax -xmin)/D
k = (76,74-75,20)/ 0,02= 77;
Записываем частоты mj+1(m1,…,mk+1), которые установлены
для значений x1,…,x1+k.Δ.
Вычисляем параметры опытного распределения:

и определяем функции опытного распределения:
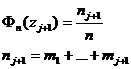
Определяем значения интегральной функции нормированного
нормального распределения. Используем для этого значения нормированной функции
Лапласа Ф’(|z|) и формулу Ф(z)=0,5+ Ф’(z), при этом Ф’(z)= Ф’(|z|) при z≥0 и Ф’(z) = - Ф’(|z|) при z<0.
По данным таблицы 6 находим максимальное абсолютное отклонение
функции опытного распределения от функции теоретического распределения:
Dmax = max|Фn(zj+1)-Ф(zj+1)|;
Dmax = 0,04433;
Вычисляем значение проверяемого параметра:
ln=Dmax*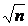 = 0,04433*10= 0,4433.
= 0,04433*10= 0,4433.
Таблица 4. Рассчитанные значения
|
j
|
x1+j*Δ
|
mj+1
|
zj+1
|
Фn(Zj+1)
|
Ф(Zj+1)
|
Фn(Zj+1)- Ф(Zj+1)
|
|
0
|
75,20
|
1
|
-2,6409
|
0,01
|
0,00415
|
0,00585
|
|
1
|
75,22
|
0
|
-2,5725
|
0,01
|
0,00508
|
0,00492
|
|
2
|
75,24
|
0
|
-2,5041
|
0,01
|
0,00621
|
0,00379
|
|
3
|
75,26
|
1
|
-2,4357
|
0,02
|
0,00734
|
0,01266
|
|
4
|
75,28
|
0
|
-2,3673
|
0,02
|
0,00889
|
0,01111
|
|
5
|
75,30
|
1
|
-2,2989
|
0,03
|
0,01072
|
0,01928
|
|
6
|
75,32
|
0
|
-2,2305
|
0,03
|
0,01287
|
0,01713
|
|
7
|
75,34
|
0
|
-2,1621
|
0,03
|
0,01559
|
0,01461
|
|
8
|
75,36
|
0
|
-2,0937
|
0,03
|
0,01831
|
0,01169
|
|
9
|
75,38
|
0
|
-2,0253
|
0,03
|
0,02118
|
0,00882
|
|
10
|
75,40
|
0
|
-1,9569
|
0,03
|
0,02500
|
0,00500
|
|
11
|
75,42
|
0
|
-1,8885
|
0,03
|
0,02938
|
0,00062
|
|
12
|
75,44
|
1
|
-1,8201
|
0,04
|
0,03438
|
0,00562
|
|
13
|
75,46
|
1
|
-1,7517
|
0,05
|
0,04006
|
0,00352
|
|
14
|
75,48
|
1
|
-1,6833
|
0,06
|
0,04648
|
0,01352
|
|
15
|
75,50
|
1
|
-1,6149
|
0,07
|
0,05370
|
0,01630
|
|
16
|
75,52
|
1
|
-1,5465
|
0,08
|
0,06057
|
0,01943
|
|
17
|
75,54
|
1
|
-1,4781
|
0,09
|
0,06944
|
0,02056
|
|
18
|
75,56
|
1
|
-1,4097
|
0,10
|
0,07927
|
0,02073
|
|
19
|
75,58
|
1
|
-1,3413
|
0,11
|
0,09012
|
0,01988
|
|
20
|
75,60
|
1
|
-1,2729
|
0,12
|
0,10204
|
0,01796
|
|
21
|
75,62
|
2
|
-1,2045
|
0,14
|
0,11507
|
0,02493
|
|
22
|
75,64
|
1
|
-1,1361
|
0,15
|
0,12714
|
0,02286
|
|
23
|
75,66
|
1
|
-1,0677
|
0,16
|
0,14231
|
0,01769
|
|
24
|
75,68
|
2
|
-0,9993
|
0,18
|
0,13567
|
0,04433
|
|
25
|
75,70
|
2
|
-0,9309
|
0,20
|
0,17619
|
0,02381
|
|
26
|
75,72
|
2
|
-0,8625
|
0,22
|
0,19489
|
0,02511
|
|
27
|
75,74
|
2
|
-0,7941
|
0,24
|
0,21476
|
0,02524
|
|
28
|
75,76
|
3
|
-0,7257
|
0,27
|
0,23270
|
0,03730
|
|
29
|
75,78
|
2
|
-0,6573
|
0,29
|
0,25463
|
0,03537
|
|
30
|
75,80
|
2
|
-0,5889
|
0,31
|
0,27760
|
0,03240
|
|
31
|
75,82
|
2
|
-0,5205
|
0,33
|
0,30153
|
0,02847
|
|
32
|
75,84
|
2
|
-0,4521
|
0,35
|
0,32636
|
0,02364
|
|
33
|
75,86
|
2
|
-0,3837
|
0,37
|
0,35197
|
0,01803
|
|
34
|
75,88
|
2
|
-0,3153
|
0,39
|
0,37448
|
0,01552
|
|
35
|
75,90
|
3
|
-0,2469
|
0,42
|
0,40129
|
0,01871
|
|
36
|
75,92
|
3
|
-0,1785
|
0,45
|
0,02142
|
|
37
|
75,94
|
3
|
-0,1101
|
0,48
|
0,45620
|
0,02380
|
|
38
|
75,96
|
4
|
-0,0417
|
0,52
|
0,48405
|
0,03595
|
|
39
|
75,98
|
3
|
0,0267
|
0,55
|
0,51197
|
0,03803
|
|
40
|
76,00
|
3
|
0,0951
|
0,58
|
0,53983
|
0,04017
|
|
41
|
76,02
|
2
|
0,1635
|
0,60
|
0,56356
|
0,03644
|
|
42
|
76,04
|
2
|
0,2319
|
0,62
|
0,59095
|
0,02905
|
|
43
|
76,06
|
2
|
0,3003
|
0,64
|
0,61791
|
0,02209
|
|
44
|
76,08
|
2
|
0,3687
|
0,66
|
0,64431
|
0,01569
|
|
45
|
76,10
|
1
|
0,4371
|
0,67
|
0,67003
|
-0,00003
|
|
46
|
76,12
|
2
|
0,5055
|
0,69
|
0,69497
|
-0,00497
|
|
47
|
76,14
|
2
|
0,5739
|
0,71
|
0,71566
|
-0,00566
|
|
48
|
76,16
|
2
|
0,6423
|
0,73
|
0,73891
|
-0,00891
|
|
49
|
76,18
|
2
|
0,7107
|
0,75
|
0,76115
|
-0,01115
|
|
50
|
76,20
|
3
|
0,7791
|
0,78
|
0,78230
|
-0,00230
|
|
51
|
76,22
|
2
|
0,8475
|
0,80
|
0,80234
|
-0,00234
|
|
52
|
76,24
|
2
|
0,9159
|
0,82
|
0,82121
|
-0,00121
|
|
53
|
76,26
|
2
|
0,9843
|
0,84
|
0,83646
|
0,00354
|
|
54
|
76,28
|
2
|
1,0527
|
0,86
|
0,85314
|
0,00686
|
|
55
|
76,30
|
2
|
1,1211
|
0,88
|
0,86864
|
0,01136
|
|
56
|
76,32
|
1
|
1,1895
|
0,89
|
0,88298
|
0,00702
|
|
57
|
76,34
|
1
|
1,2579
|
0,90
|
0,89617
|
0,00383
|
|
58
|
76,36
|
2
|
1,3263
|
0,92
|
0,90824
|
0,01176
|
|
59
|
76,38
|
0
|
1,3947
|
0,92
|
0,91924
|
0,00076
|
|
60
|
76,40
|
1
|
1,4631
|
0,93
|
0,92768
|
0,00232
|
|
61
|
76,42
|
1
|
1,5315
|
0,94
|
0,93699
|
0,00301
|
|
62
|
76,44
|
1
|
1,5999
|
0,95
|
0,94520
|
0,00480
|
|
63
|
76,46
|
1
|
1,6683
|
0,96
|
0,95254
|
0,00746
|
|
64
|
76,48
|
1
|
1,7367
|
0,97
|
0,95907
|
0,01093
|
|
65
|
76,50
|
0
|
1,8051
|
0,97
|
0,96485
|
0,00515
|
|
66
|
76,52
|
0
|
1,8735
|
0,97
|
0,96926
|
0,00074
|
|
67
|
76,54
|
0
|
1,9419
|
0,97
|
0,97381
|
-0,00381
|
|
68
|
76,56
|
0
|
2,0103
|
0,97
|
0,97778
|
-0,00778
|
|
69
|
76,58
|
0
|
2,0787
|
0,97
|
0,98124
|
-0,01124
|
|
70
|
76,60
|
0
|
2,1471
|
0,97
|
0,98422
|
-0,01422
|
|
71
|
76,62
|
1
|
2,2155
|
0,98
|
0,98679
|
-0,00679
|
|
72
|
76,64
|
0
|
2,2839
|
0,98
|
0,98870
|
-0,00870
|
|
73
|
76,66
|
1
|
2,3523
|
0,99
|
0,99061
|
-0,00061
|
|
74
|
76,68
|
0
|
2,4207
|
0,99
|
0,99224
|
-0,00224
|
|
75
|
76,70
|
0
|
2,4891
|
0,99
|
0,99361
|
-0,00361
|
|
76
|
76,72
|
0
|
2,5575
|
0,99
|
0,99477
|
-0,00477
|
|
77
|
76,74
|
1
|
2,6259
|
1,00
|
0,99573
|
0,00427
|
|
|
n=100
|
|
|
|
Dmax=0,04433
|
Так как q =0,10, то 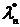 = 1,36.
= 1,36.
-q = P{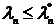 };
};
Так как 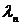 = 0,4433<
= 0,4433< 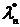 = 1,36 - то согласно критерию Колмогорова
гипотеза о нормальности закона распределения подтверждается.
= 1,36 - то согласно критерию Колмогорова
гипотеза о нормальности закона распределения подтверждается.
. Критерий χ2.
Для проверке нормальности закона распределения согласно критерию χ2 данные расчетов привели в таблице.
Аналогично интервал от хmin=75,20 Вт до хmax=76,74 Вт разбили на r=7 интервалов. Значения середин интервалов xj, частоты приведены в таблице.
Если в некоторых интервалах попало меньше пяти наблюдений, то
такие интервалы объединили с соседними.
Нашли отклонения от середин каждого из интервалов Vj=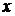 j-
j-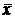 , а так же нормированные отклонения от
среднего арифметического:
, а так же нормированные отклонения от
среднего арифметического:
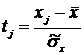 .
.
Для каждого интервала исходя из значения tj нашли дифференциальную функцию
нормированного нормального распределения p(tj). Плотность в серединах интервалов
находятся из формул:
 .
.
Нашли теоретические частоты по формуле:
n.Pj=n.hj.P(xj).
Нашли меру расхождения  ;
;
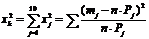
Таблица 5. Рассчитанные значения
|
j
|
xj,
мА
|
mj
|
xj- tjP(tj)P(xj)nPj=nΔxj*P(xj)x2j tjP(tj)P(xj)nPj=nΔxj*P(xj)x2j
|
|
|
|
|
|
|
1
|
75,31
|
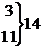 -0,6622-2,26470,03030,1036 -0,6622-2,26470,03030,1036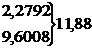 0,3783 0,3783
|
|
|
|
|
|
|
|
2
|
75,53
|
|
-0,4422
|
-1,5123
|
0,1276
|
0,4364
|
|
|
|
3
|
75,75
|
18
|
-0,2222
|
-0,7599
|
0,2989
|
1,0222
|
22,4884
|
0,0985
|
|
4
|
75,97
|
19
|
-0,0022
|
-0,0075
|
0,3977
|
1,3601
|
29,9222
|
0,0284
|
|
5
|
76,19
|
27
|
0,2178
|
0,7449
|
0,3011
|
1,0298
|
22,6556
|
0,0190
|
|
6
|
76,41
|
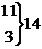 0,43781,49730,12950,4429 0,43781,49730,12950,4429 0,2888 0,2888
|
|
|
|
|
|
|
|
7
|
|
0,6578
|
2,2497
|
0,0317
|
0,1084
|
|
|
|
|
100
|
|
|
|
|
|

|
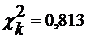
Число степеней свободы распределения k=r-s, где r=5, 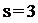 т.е. k=2.
т.е. k=2.
Так как q/2=0,05
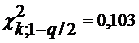
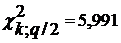
Учитывая, что:
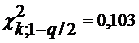 <
< 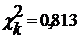 <
< 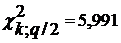
то распределение результатов можно считать нормальным.
. Критерий ω2.
Для проверки нормальности закона распределения согласно критерию ω2 данные расчетов представили в таблице.
Результаты наблюдений располагаются в порядке возрастания, т.е.
получается упорядоченная выборка ω2:
x1≤x2≤…≤xn
Вычисляем значения нормированных отклонений от среднего
арифметического:
 .
.
Исходя из zj
находим значения интегральной функции нормированного нормального распределения
Ф(zj).
Вычисляем значения критерия проверки:

Таблица 6. Рассчитанные значения
|
j
|
xj
|
zj
|
Ф(zj)
|
ln(Ф(zj))
|
ln(1-Ф(zj))
|
Aj
|
|
1
|
75,20
|
-2,640791
|
0,00415
|
-5,48465
|
-0,00416
|
-0,031561
|
|
2
|
75,26
|
-2,435601
|
0,00740
|
-4,90628
|
-0,00743
|
-0,080910
|
|
3
|
75,30
|
-2,298808
|
0,01072
|
-4,53564
|
-0,01078
|
-0,123900
|
|
4
|
75,44
|
-1,820032
|
0,03438
|
-3,37028
|
-0,03498
|
-0,151720
|
|
5
|
75,46
|
-1,751636
|
0,04006
|
-3,21738
|
-0,04088
|
-0,183827
|
|
6
|
75,48
|
-1,683240
|
0,04648
|
-3,06873
|
-0,04759
|
-0,213757
|
|
7
|
75,50
|
-1,614843
|
0,05370
|
-2,92434
|
-0,05520
|
-0,241690
|
|
8
|
75,52
|
-1,546446
|
0,06057
|
-2,80396
|
-0,06248
|
-0,268092
|
|
9
|
75,54
|
-1,478050
|
0,06944
|
-2,66729
|
-0,07197
|
-0,292571
|
|
10
|
75,56
|
-1,409653
|
0,07927
|
-2,5349
|
-0,08259
|
-0,315558
|
|
11
|
75,58
|
-1,341257
|
0,09012
|
-2,40661
|
-0,09444
|
-0,337220
|
|
12
|
75,60
|
-1,272860
|
0,10204
|
-2,28239
|
-0,10763
|
-0,357727
|
|
13
|
75,62
|
-1,204463
|
0,11507
|
-2,16221
|
-0,12225
|
-0,377243
|
|
14
|
75,62
|
-1,204463
|
0,11507
|
-2,16221
|
-0,12225
|
-0,397642
|
|
15
|
75,64
|
-1,136067
|
0,12714
|
-2,06247
|
-0,13598
|
-0,415321
|
|
16
|
75,66
|
-1,067670
|
0,14231
|
-1,94975
|
-0,15351
|
-0,431929
|
|
17
|
75,68
|
-0,999273
|
0,13567
|
-1,99753
|
-0,14580
|
-0,451336
|
|
18
|
75,68
|
-0,999273
|
0,13567
|
-1,99753
|
-0,14580
|
-0,469853
|
|
19
|
75,70
|
-0,930877
|
0,17619
|
-1,73619
|
-0,19382
|
-0,479155
|
|
20
|
75,70
|
-0,930877
|
0,17619
|
-1,73619
|
-0,19382
|
-0,494579
|
|
21
|
75,72
|
-0,862481
|
0,19489
|
-1,63532
|
-0,21678
|
-0,507578
|
|
22
|
75,72
|
-0,862481
|
0,19489
|
-1,63532
|
-0,21678
|
-0,521763
|
|
23
|
75,74
|
-0,794084
|
0,21476
|
-1,53823
|
-0,24177
|
-0,533471
|
|
24
|
75,74
|
-0,794084
|
0,21476
|
-1,53823
|
-0,24177
|
-0,546436
|
|
25
|
75,76
|
-0,725688
|
0,23270
|
-1,45801
|
-0,26488
|
-0,557194
|
|
26
|
75,76
|
-0,725688
|
0,23270
|
-1,45801
|
-0,26488
|
-0,569125
|
|
27
|
75,76
|
-0,725688
|
0,23270
|
-1,45801
|
-0,26488
|
-0,581056
|
|
28
|
75,78
|
-0,657291
|
0,25463
|
-1,36794
|
-0,29387
|
-0,589244
|
|
29
|
75,78
|
-0,657291
|
0,25463
|
-1,36794
|
-0,29387
|
-0,599984
|
|
30
|
75,80
|
-0,588894
|
0,27760
|
-1,28157
|
-0,32518
|
-0,607314
|
|
31
|
75,80
|
-0,588894
|
0,27760
|
-1,28157
|
-0,32518
|
-0,616878
|
|
32
|
75,82
|
-0,520498
|
0,30153
|
-1,19889
|
-0,35886
|
-0,623470
|
|
33
|
75,82
|
-0,520498
|
0,30153
|
-1,19889
|
-0,35886
|
-0,631870
|
|
34
|
75,84
|
-0,452101
|
0,32636
|
-1,11975
|
-0,39506
|
-0,637832
|
|
35
|
75,84
|
-0,452101
|
0,32636
|
-1,11975
|
-0,39506
|
-0,645079
|
|
36
|
75,86
|
-0,383705
|
0,35197
|
-1,04421
|
-0,43382
|
-0,650507
|
|
37
|
75,86
|
-0,383705
|
0,35197
|
-1,04421
|
-0,43382
|
-0,656611
|
|
38
|
75,88
|
-0,315308
|
0,37448
|
-0,98222
|
-0,46917
|
-0,661564
|
|
39
|
75,88
|
-0,315308
|
0,37448
|
-0,98222
|
-0,46917
|
-0,666694
|
|
40
|
75,90
|
-0,246912
|
0,40129
|
-0,91307
|
-0,51298
|
-0,671015
|
|
41
|
75,90
|
-0,246912
|
0,40129
|
-0,91307
|
-0,51298
|
-0,675016
|
|
42
|
75,90
|
-0,246912
|
0,40129
|
-0,91307
|
-0,51298
|
-0,679017
|
|
43
|
75,92
|
-0,178515
|
0,42858
|
-0,84728
|
-0,55963
|
-0,681881
|
|
44
|
75,92
|
-0,178515
|
0,42858
|
-0,84728
|
-0,55963
|
-0,684757
|
|
45
|
75,92
|
-0,178515
|
0,42858
|
-0,84728
|
-0,55963
|
-0,687634
|
|
46
|
75,94
|
0,45620
|
-0,78482
|
-0,60917
|
-0,689095
|
|
47
|
75,94
|
-0,110119
|
0,45620
|
-0,78482
|
-0,60917
|
-0,690851
|
|
48
|
75,94
|
-0,110119
|
0,45620
|
-0,78482
|
-0,60917
|
-0,692608
|
|
49
|
75,96
|
-0,041722
|
0,48405
|
-0,72557
|
-0,66175
|
-0,692699
|
|
50
|
75,96
|
-0,041722
|
0,48405
|
-0,72557
|
-0,66175
|
-0,693337
|
|
51
|
75,96
|
-0,041722
|
0,48405
|
-0,72557
|
-0,66175
|
-0,693975
|
|
52
|
75,96
|
-0,041722
|
0,48405
|
-0,72557
|
-0,66175
|
-0,694614
|
|
53
|
75,98
|
0,026675
|
0,51197
|
-0,66949
|
-0,71738
|
-0,692237
|
|
54
|
75,98
|
0,026675
|
0,51197
|
-0,66949
|
-0,71738
|
-0,691758
|
|
55
|
75,98
|
0,026675
|
0,51197
|
-0,66949
|
-0,71738
|
-0,691279
|
|
56
|
76,00
|
0,095075
|
0,53983
|
-0,6165
|
-0,77616
|
-0,687549
|
|
57
|
76,00
|
0,095075
|
0,53983
|
-0,6165
|
-0,77616
|
-0,685952
|
|
58
|
76,00
|
0,095075
|
0,53983
|
-0,6165
|
-0,77616
|
-0,684356
|
|
59
|
76,02
|
0,163468
|
0,56356
|
-0,57348
|
-0,82910
|
-0,679565
|
|
60
|
76,02
|
0,163468
|
0,56356
|
-0,57348
|
-0,82910
|
-0,677009
|
|
61
|
76,04
|
0,231864
|
0,59095
|
-0,52602
|
-0,89392
|
-0,671342
|
|
62
|
76,04
|
0,231864
|
0,59095
|
-0,52602
|
-0,89392
|
-0,667663
|
|
63
|
76,06
|
0,300261
|
0,61791
|
-0,48141
|
-0,96210
|
-0,661670
|
|
64
|
76,06
|
0,300261
|
0,61791
|
-0,48141
|
-0,96210
|
-0,656863
|
|
65
|
76,08
|
0,368657
|
0,64431
|
-0,43958
|
-1,03370
|
-0,650488
|
|
66
|
76,08
|
0,368657
|
0,64431
|
-0,43958
|
-1,03370
|
-0,644547
|
|
67
|
76,10
|
0,437054
|
0,67003
|
-0,40043
|
-1,10875
|
-0,637720
|
|
68
|
76,12
|
0,505451
|
0,69499
|
-0,36386
|
-1,18741
|
-0,631513
|
|
69
|
76,12
|
0,505451
|
0,69499
|
-0,36386
|
-1,18741
|
-0,623277
|
|
70
|
76,14
|
0,573847
|
0,71566
|
-0,33455
|
-1,25758
|
-0,616076
|
|
71
|
76,14
|
0,573847
|
0,71566
|
-0,33455
|
-1,25758
|
-0,606845
|
|
72
|
76,16
|
0,642244
|
0,73891
|
-0,30258
|
-1,34289
|
-0,599068
|
|
73
|
76,16
|
0,642244
|
0,73891
|
-0,30258
|
-1,34289
|
-0,588665
|
|
74
|
76,18
|
0,710640
|
0,76115
|
-0,27292
|
-1,43192
|
-0,580058
|
|
75
|
76,18
|
0,710640
|
0,76115
|
-0,27292
|
-1,43192
|
-0,568468
|
|
76
|
76,20
|
0,779037
|
0,78230
|
-0,24552
|
-1,52464
|
-0,558901
|
|
77
|
76,20
|
0,779037
|
0,78230
|
-0,24552
|
-1,52464
|
-0,546110
|
|
78
|
76,20
|
0,779037
|
0,78230
|
-0,24552
|
-1,52464
|
-0,533319
|
|
79
|
76,22
|
0,847433
|
0,80234
|
-0,22022
|
-1,62121
|
-0,521434
|
|
80
|
76,22
|
0,847433
|
0,80234
|
-0,22022
|
-1,62121
|
-0,507425
|
|
81
|
76,24
|
0,915830
|
0,82121
|
-0,19698
|
-1,72154
|
-0,494267
|
|
82
|
76,24
|
0,915830
|
0,82121
|
-0,19698
|
-1,72154
|
-0,479021
|
|
83
|
76,26
|
0,984227
|
0,83646
|
-0,17858
|
-1,81070
|
-0,464198
|
|
84
|
76,26
|
0,984227
|
0,83646
|
-0,17858
|
-1,81070
|
-0,447877
|
|
85
|
76,28
|
1,052623
|
0,85314
|
-0,15883
|
-1,91828
|
-0,431545
|
|
86
|
76,28
|
1,052623
|
0,85314
|
-0,15883
|
-1,91828
|
-0,413951
|
|
87
|
76,30
|
1,121020
|
0,86864
|
-0,14083
|
-2,02981
|
-0,395840
|
|
88
|
76,30
|
1,121020
|
0,86864
|
-0,14083
|
-2,02981
|
-0,376950
|
|
89
|
76,32
|
1,189416
|
0,88298
|
-0,12445
|
-2,14541
|
-0,356863
|
|
90
|
76,34
|
1,257813
|
0,89617
|
-0,10963
|
-2,26500
|
-0,335940
|
|
91
|
76,36
|
1,326210
|
0,90824
|
-0,09625
|
-2,38858
|
-0,314018
|
|
92
|
76,36
|
1,326210
|
0,90824
|
-0,09625
|
-2,38858
|
-0,291095
|
|
93
|
76,40
|
1,463002
|
0,92768
|
-0,07507
|
-2,62665
|
-0,266437
|
|
94
|
76,42
|
1,531399
|
0,93699
|
-0,06508
|
-2,76446
|
-0,240542
|
|
95
|
76,44
|
1,599796
|
0,94520
|
-0,05636
|
-2,90407
|
-0,212983
|
|
96
|
76,46
|
1,668192
|
-0,04862
|
-3,04787
|
-0,183589
|
|
97
|
76,48
|
1,736589
|
0,95907
|
-0,04179
|
-3,19589
|
-0,152185
|
|
98
|
76,62
|
2,215364
|
0,98679
|
-0,0133
|
-4,32678
|
-0,121135
|
|
99
|
76,66
|
2,352158
|
0,99061
|
-0,00943
|
-4,66811
|
-0,079314
|
|
100
|
76,74
|
2,625744
|
0,99573
|
-0,00428
|
-5,45614
|
-0,031538
|
А=-50,096205
Для уровня значимости q = 0,10 соответствующее
значение Ω2n=1,94.
Для найденного значения справедливо:
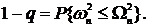
Так как:
 =1,94 и
=1,94 и 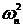 = 0,1924 <
= 0,1924 < =1,94
=1,94
то согласно критерию ω2 результаты можно принять распределенными по нормальному закону.
Определяем коэффициент Стьюдента.
Для n>30 и P=0,99 t=2,576
Рассчитываем доверительные границы случайной погрешности
результата измерения:
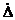 =t.
=t. =2,576·0,02924 = 0,07532 (Вт).
=2,576·0,02924 = 0,07532 (Вт).
Результат измерения согласно ГОСТ-8.207-76 представляем в виде:
I = (75,972 ± 0,076) Вт; P=0,99.
Использованная литература
1. Кострикин
А.М. Теоретическая метрология: Учеб. пособие для студентов специальности
Т.13.01 "Метрология, стандартизация и сертификация". В 3 ч. Ч.1. -
Мн.: БГУИР, 1999. - 87 с.
2. Кострикин
А.М. Теоретическая метрология: Учеб. пособие для студентов специальности
Т.13.01 "Метрология, стандартизация и сертификация". В 3 ч. Ч.2. -
Мн.: БГУИР, 1999. - 90 с.
. Сергеев
А.Г. Метрология: учебник. - М.: Логос, 2005 - 272с.: ил.
. ГОСТ
8.207-76 Прямые измерения с многократными наблюдениями. Методы обработки
результатов наблюдений