Финансовая математика
Вариант 1
Задача 1
На сколько дней можно дать в долг 1000 долл.,
исходя из 8% годовых, если возвращенная сумма будет составлять 1075 долл.?
Решение:
Модели накопления капитала по схеме простых
процентов имеет вид:
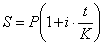
Где Р - начальная сумма, S -
наращенная сумма, t - срок вклада в днях, i -
процентная ставка, К - количество дней в году (К=365 - английская практика
начисления процентов, длительность месяцев соответствует фактической длительности
по календарю).
Р = 1000долл. S =
1075долл., i = 0,08,
К=365, t = ?дней
Найдем доходность:
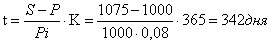
Ответ: на 342 дня
Задача 2
Сумма 10 тыс. долл. предоставлена в
долг на 5 лет под 8% годовых. Определить ежегодную сумму погашения долга.
Решение:
Определим сумму ежегодных равных платежей,
используя формулу:
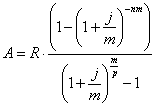
Где R - начальная
сумма вносимая ежемесячно, А - сумма кредита, n - срок
кредита, m - количество
начислений процентов, j - процентная ставка, р - количество
вкладов за год .
Где R =?., А =
10000тыс. долл., n = 5, р=1, m =1раз, j = 0,08 .
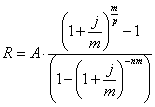
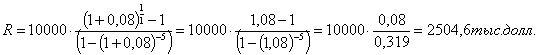
Ответ: ежегодная сумма погашения
долга 2504,6 тыс.долл.
Задача 3
Ежегодно в начале года в банк делается очередной
взнос в размере 14 тыс.руб. Банк устанавливает годовую номинальную процентную
ставку 36%. Какая сумма будет на счете по истечении шести лет, если начисление
сложных процентов происходит ежегодно.
Решение:
Найдем сумму, накопленную через 6 лет.,
используя формулу:
Где R - начальная
сумма вносимая ежемесячно, S - сумма которую нужно накопить, n - срок
вклада в годах, m - количество начислений процентов, j -
процентная ставка, р - количество вкладов за год .
В нашем случае S = ?долл. Р
= 14тыс.руб., n = 6лет, m = 1раз, р =
1 
,
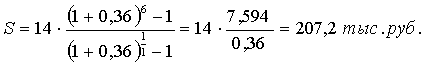
Но так как на отдельный счет
перечисляют денежные средства в начале каждого года, то
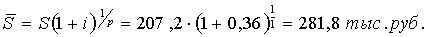
Ответ: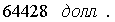
Вариант 2
Задача 1
Предприниматель хочет открыть счёт в банке,
положив такую сумму, чтобы его сын, являющийся студентом первого курса, мог
снимать с этого счёта в конце каждого года по 3600 руб., исчерпав весь вклад к
концу пятилетнего срока обучения. Какой величины должна быть сумма, если банк
начисляет сложные проценты по ставке 30% годовых?
Решение:
Определим сумму вклада, используя формулу:
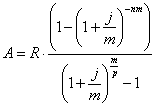
Где R - сумма
выплаты, А - сумма на счете (начальная), n - срок
выплат, m -
количество начислений процентов за год, j -
процентная ставка, р - количество выплат за год . R = 3600, А =
?, n = 5, m = 1, j = 0,30, р =
1.
Сумма вклада при снятии денег в
конце каждого месяца составит:
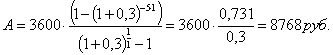
Ответ: 8768 руб.
Задача 2
Предприниматель 18 апреля обратился в банк за
ссудой до 19 ноября того же года под простую процентную ставку 25% годовых.
Банк, удержав в момент предоставления ссуды проценты за весь срок, выдал
предпринимателю 12 тыс.руб. Какую сумму необходимо будет вернуть банку, если
при расчёте использовались обыкновенные проценты с точным числом дней?
Решение:
Срок ссуды не известен, поэтому возьмем его
равным 1 году. Банку необходимо будет вернуть12 тыс.руб. т.к. проценты уде
удержаны.
В данной задаче возможно только рассчитать сумму
процентных денег, которые удержал банк.
Модели накопления капитала по схеме простых
процентов имеет вид:
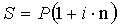
Где Р - вложенная сумма, S -
наращенная сумма, n - срок вклада в годах, i -
процентная ставка.
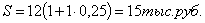
Тогда сумма процентных денег
составит: 
Ответ: Банку необходимо будет
вернуть12 тыс.руб., сумма процентных денег 3 тыс.руб.
Задача 3
Определите, что лучше: получить 16 тыс.руб.
через 2 года или 50 тыс.руб. - чрез 6 лет, если можно поместить деньги на
депозит под сложную процентную ставку 35% годовых.
Решение:
При проведении операций по сложной ставке
следует пользоваться формулой:
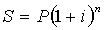
Где Р - начальная сумма, S -
наращенная сумма, n - срок вклада в годах, i -
процентная ставка.
Р = 16 тыс.руб.,
i = 35%, S = ?, n = 4 года.
Если получить 16 тыс.руб. через 2
года и поместить деньги на депозит под сложную процентную ставку 35% годовых,
то наращенная сумма за 4 года (4 года т.к. деньги на другом счете лежат 6 лет,
т.е. 6-2=4) составит:
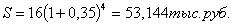
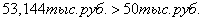- поэтому выгоднее получить 16
тыс.руб. через 2 года и поместить эти деньги на депозит под сложную процентную
ставку 35% годовых.
Ответ: выгоднее получить 16 тыс.руб. через 2
года.
Вариант 3
Задача 1
Обязательство уплатить через 100 дней сумму
долга в размере 50 тыс.руб. с начислениями на нее точными процентами по ставке
40%, было учтено за 25 дней до срока погашения по учётной ставке 25%.
Определить сумму, полученную при учёте обязательства.
Решение:
Точные проценты (дисконты) рассчитываются,
исходя из точного количества дней в календарном месяце и календарном году.
Р = 50000 руб. S
= ?, i = 0,25, К=365, t
= 100 - 25 = 75дней
При проведении операций по простой учетной
ставке d следует
пользоваться формулой:
Ответ: сумма, полученная при учёте
обязательства 52708 руб.
Задача 2
Предлагается инвестировать 300 тыс.руб. на 5 лет
при условии возврата этой суммы частями (ежегодно по 60 тыс.руб.). По истечении
5 лет выплачивается дополнительное вознаграждение в размере 120 тыс.руб.
Принимать ли это предложение, если можно депонировать деньги в банк из расчёта
20% годовых (сложных).
Решение:
Рассчитаем сколько получит инвестор от первой
сделки:
тыс.руб. на 5 лет при условии возврата этой
суммы частями (ежегодно по 60 тыс.руб.). По истечении 5 лет выплачивается
дополнительное вознаграждение в размере 120 тыс.руб.
Инвестор в результате получит 420
тыс. руб.
Рассчитаем сколько получит инвестор
от второй сделки:
При проведении операций по сложной
ставке следует пользоваться формулой:
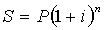
Где Р - начальная сумма, S -
наращенная сумма, n - срок вклада в годах, i -
процентная ставка.
Р = 300тыс.руб.,
i = 20%, S = ?, n = 5 лет.
Если депонировать 300 тыс.руб. в банк из расчёта
20% годовых (сложных), то полученная сумма составит 746,496 тыс. руб.
Ответ: принимать предложение не следует.
Задача 3
Определите время, за которое происходит утроение
первоначальной суммы при начислении сложных процентов, если процентная ставка
равна: 25%
Решение:
При проведении операций по сложной ставке
следует пользоваться формулой:
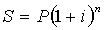
Где Р - начальная сумма, S -
наращенная сумма, n - срок вклада в годах, i -
процентная ставка.
В нашем случае должно получиться,
что 
, т.е. 
-
коэффициент наращения
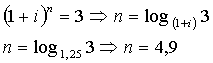
Ответ: Сумма утроится за 4,9 лет или
за 4 года и 11 месяцев.
Вариант 4
Задача 1
Через два года фирме потребуются деньги в
размере 30 млн.руб. Какую сумму необходимо срочно положить в банк, начисляющий
25% годовых, чтобы через 2 года получить требуемую сумму? ( сложные проценты)
Решение:
При проведении операций по сложной ставке
следует пользоваться формулой:
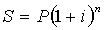
Где Р - начальная сумма, S -
наращенная сумма, n - срок вклада в годах, i -
процентная ставка.
Р = ?., i =
25%, S = 30 млн.руб.,
n = 2 года.
Сумму, которую необходимо срочно
положить в банк, начисляющий 25% годовых, чтобы через 2 года получить требуемую
сумму в 30 млн.руб. найдем по формуле:
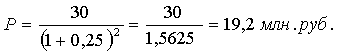
Ответ: 19,2 млн. руб.
Задача 2
Клиент хочет накопить на своем счете 80
тыс.руб., осуществляя в конце каждого года равные вклады в банк под сложную
процентную ставку 30% годовых. Какой величины должен быть каждый вклад, чтобы
клиент мог накопить требуемую сумму за а) 5 лет; б) 19 лет.
Решение:
а) Найдем сумму, которую требуется вкладывать на
счет под 30% годовых, чтобы накопить 80 тыс.руб. за 5 лет:
Где R - начальная
сумма вносимая ежемесячно, S - сумма которую нужно накопить, n - срок
вклада в годах, m - количество начислений процентов, j -
процентная ставка, р - количество вкладов за год .
В нашем случае S = 80
тыс.руб., n = 5лет, m = 1раз, р =
1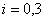 
,
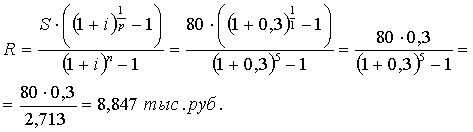
б) Найдем сумму, которую требуется
вкладывать на счет под 30% годовых, чтобы накопить 80 тыс.руб. за 19 лет:
Где R - начальная
сумма вносимая ежемесячно, S - сумма которую нужно накопить, n - срок
вклада в годах, m - количество начислений процентов, j -
процентная ставка, р - количество вкладов за год .
В нашем случае S = 80
тыс.руб., n = 5лет, m = 1раз, р =
1 ,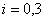
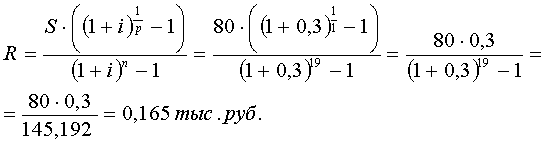
Ответ: 8,847 тыс.руб.; 0,165
тыс.руб.
Задача 3
Какое необходимо время, чтобы 28 тыс.руб.,
помещённые в банк под простую процентную ставку 20% годовых, увеличились на
такую же величину, как и 30 тыс.руб., помещенные в банк с 16 февраля по 28 июля
того же года под простую процентную ставку 25% годовых? На первый капитал
начисляются обыкновенные проценты с точным числом дней, на второй -
обыкновенные проценты с приближенным числом дней.
Решение:
Точные проценты (дисконты) рассчитываются,
исходя из точного количества дней в календарном месяце и календарном году.
Обыкновенные проценты (дисконты) рассчитываются,
исходя из приблизительного (округленного) количества дней в месяце и году.
Модели накопления капитала по схеме простых
процентов имеет вид:
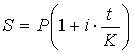
Где Р - начальная сумма, S -
наращенная сумма, t - срок вклада в днях, i -
процентная ставка, К - количество дней в году
Определим размер погасительного
платежа начисление обыкновенных процентов К=360 длительность месяцев соответствует
приблизительной длительности по календарю t =
12+30+30+30+30+28 = 160дня
Определим наращенную сумму:
Р =30 тыс. руб., S - ?, t =160, i =0,25, К =
360
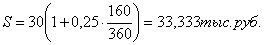
Р =30 тыс. руб., S - ?, t =160, i =0,25, К =
360
Теперь найдем какое необходимо
время, чтобы 28 тыс.руб., помещённые в банк под простую процентную ставку 20%
годовых, увеличились до 33,333 тыс. руб.
Р =28 тыс. руб., S =33,333
тыс. руб., t =?, i =0,2, К =
360
; 
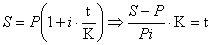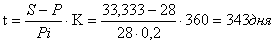
Вариант 5
Задача 1
Кредит в размере на 100 тыс. долл. получен
сроком на 3 года под 8% годовых. Определить какую сумму подлежащего возврату в
конце срока кредита, если проценты будут начисляться: а) один раз в год, б)
ежеквартально. (сложные проценты).
Решение:
Модели накопления капитала по схеме номинальной
сложной ставки имеет вид:
Где Р - начальная сумма, S -
наращенная сумма, n - срок вклада в годах, i -
процентная ставка, m - количество интервалов начисления
за год.
А) Р = 100 тыс. долл., i = 8%, S = ?, n = 2, m = 1.
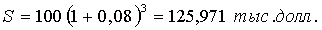
Б) Р
= 100 тыс.
долл.,
i = 8%, S = ?, n = 2, m = 4. (так как начисление процентов ежеквартально).
Ответ: сумма подлежащая возврату в конце срока
кредита а) 125,971 тыс. долл. б) 126,824 тыс. долл.
Задача 2
Определить реальную ставку при размещении
средств на год под 35% годовых, если уровень инфляции за год составляет 30%.
Решение:
Найдем индекс цен:
n = 1год, α
= 0,1
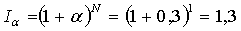
Найдем коэффициент наращения: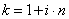 
Определим реальный коэффициент
наращения:
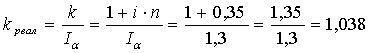
реальный коэффициент наращения.
Тогда фактическая годовая ставка
составит:
Ответ: реальная процентная ставка составляет
3,8%.
Задача 3
Перед выходом на пенсию господин N хочет обеспечить
себе дополнительный ежегодный доход в сумме 6 тыс.руб. неограниченно. Какую
сумму он должен поместить в банк, начисляющий сложные проценты по ставке 28%
годовых?
Решение:
Определим сумму вклада, используя формулу:
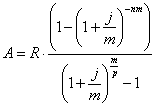
Где R - сумма
выплаты, А - сумма на счете (начальная), n - срок
выплат, m -
количество начислений процентов за год, j -
процентная ставка, р - количество выплат за год . R = 6000, А =
?, n = 40, m = 1, j = 0,28, р =
1.
Сумма вклада при снятии денег в конце
каждого месяца составит:
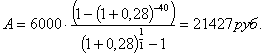
Ответ: 21427 руб.
Вариант 6
Задача 1
млн.руб. положены в банк 18 февраля не и
востребована 25 декабря того же года. Ставка банка составляет 35% годовых.
Определить сумму начисленных процентов при различной практике их начисления.
Решение:
Английская практика начисления процентов,
длительность месяцев соответствует фактической длительности по календарю
Модели накопления капитала по схеме простых
процентов имеет вид:
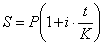
Где Р - начальная сумма, S -
наращенная сумма, t - срок вклада в днях, i -
процентная ставка, К - количество дней в году (К=365 - английская практика
начисления процентов, длительность месяцев соответствует фактической
длительности по календарю).
Р = 2 млн.руб. S = ?, i = 0,35,
К=365, длительность месяцев соответствует фактической длительности по календарю
t =
10+31+30+31+30+31+31+30+31+30+25 = 310дней
Найдем наращенную сумму:
При английской практике начисления
процентов наращенная сумма составит 2594521 руб.
Французская практика начисления процентов,
длительность месяцев соответствует фактической длительности по календарю, год
равен 360 дням
Модели накопления капитала по схеме простых
процентов имеет вид:
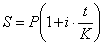
Где Р - начальная сумма, S -
наращенная сумма, t - срок вклада в днях, i -
процентная ставка, К - количество дней в году
Р = 2 млн.руб. S = ?, i = 0,35, К=360,
длительность месяцев соответствует фактической длительности по календарю
t =
10+31+30+31+30+31+31+30+31+30+25 = 310дней
Найдем наращенную сумму:
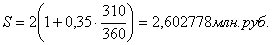
При французской практике начисления
процентов наращенная сумма составит 2602778 руб.
Немецкая практика начисления процентов,
длительность месяцев соответствует 30 дням, год равен 360 дням
Модели накопления капитала по схеме простых
процентов имеет вид:
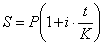
Где Р - начальная сумма, S - наращенная
сумма, t - срок
вклада в днях, i - процентная ставка, К - количество
дней в году
Р = 2 млн.руб. S = ?, i = 0,35,
К=360, длительность месяцев соответствует фактической длительности по календарю
t =
10+30+30+30+30+30+301+30+30+30+25 = 305дней
Найдем наращенную сумму:
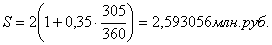
При немецкой практике начисления
процентов наращенная сумма составит 2593056 руб.
Ответ: 2594521 руб. - английская
практика, 2602778 руб. - французская практика, 2593056 руб. - немецкая
практика.
Задача 2
Банк выдал клиенту кредит на один год в размере
20 тыс.руб. по ставке 6% годовых. Уровень инфляции за год составил 18%.
Определить с учётом инфляции реальную ставку процентов по кредиту, погашенную
сумму и сумму процентов за кредит.
Решение:
Модели накопления капитала по схеме простых
процентов имеет вид:
Где Р - вложенная сумма, S -
наращенная сумма (погашенная сумма), n - срок
вклада в годах, i - процентная ставка.
Найдем наращенную сумму (погашенную
сумму):
Р = 20 тыс.руб.,
S - ?, n = 1, i = 18.
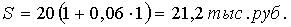- погашенная сумма.
Сумма процентов за кредит:
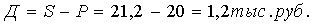
Найдем индекс цен:
n = 1год, α = 0,1
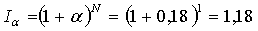
Найдем коэффициент наращения: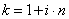
Определим реальный коэффициент
наращения:
реальный коэффициент наращения.
Тогда фактическая годовая ставка
составит:
реальная процентная ставка
составляет -10,2% - убыток для банка.
Ответ: -10,2%; 21,2 тыс. руб.; 1,2 тыс. руб.
Задача 3
Некоторая фирма хочет создать фонд в размере 500
тыс.руб. С этой целью в конце каждого года фирма предполагает вносить по 80
тыс.руб. в банк под 32% годовых. Найдите срок, необходимый для создания фонда,
если банк начисляет сложные проценты ежегодно.
Решение:
Найдем срок, необходимый для создания фонда,
если банк начисляет сложные проценты ежегодно используя формулу:
Где R - начальная
сумма вносимая ежемесячно, S - сумма которую нужно накопить, n - срок
вклада в годах, m - количество начислений процентов, j -
процентная ставка, р - количество вкладов за год .
В нашем случае S = 500
тыс.руб., n=?лет, m=1раз, р=1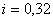 
, R=80тыс.руб.
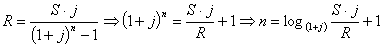
Ответ: 4 года.
Вариант 7
Задача 1
Через 150 дней с момента подписания контракта
необходимо уплатить 310 тыс.руб., исходя из 8 % годовых и временной базы 360
дней. Определить первоначальную сумму долга.
Решение:
Модели накопления капитала по схеме простых процентов
имеет вид:
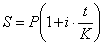
Где Р - начальная сумма, S -
наращенная сумма, t - срок вклада в днях, i -
процентная ставка, К - количество дней в году (К=360).
Р = ?. S = 310
тыс.руб., i = 0,08,
К=360, t = 150дней
Найдем первоначальную сумму долга:
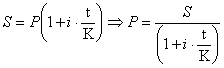
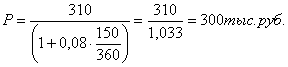
Ответ: первоначальная сумму долга
составляла 300 тыс. руб.
Задача 2
Стоит ли покупать за 5500 руб.
ценную бумагу, генерирующую ежегодный доход в размере 100 руб. в течении
двадцати лет, если банк предлагает сложную процентную ставку 18 % годовых?
Решение:
Рассчитаем сколько получит клиент от первой
сделки:
Он потратит:
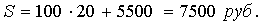
Клиент получит 7500 руб. за 20 лет
Рассчитаем сколько получит клиент от
второй сделки (если вложит 5500 в банк под сложную процентную ставку 18 %
годовых):
При проведении операций по сложной
ставке следует пользоваться формулой:
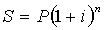
Где Р - начальная сумма, S -
наращенная сумма, n - срок вклада в годах, i -
процентная ставка.
Р = 5500 руб.,
i = 18%, S = ?, n = 20 лет.
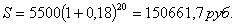
Клиент от второй сделки получит 150661,7 руб.
через 20 лет.
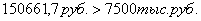
Ответ: ценную бумагу покупать не следует.
Задача 3
Вкладчик хочет положить на депозит 15 тыс.руб. И
за 5 месяцев накопить не менее 18 тыс.руб. Определите требуемую простую годовую
процентную ставку, на основании которой вкладчик должен выбрать банк для
размещения своих средств, если в расчете применяются объединенные проценты и
приближенное число дней.
Решение:
Модели накопления капитала по схеме простых
процентов имеет вид:
капитал
процент ставка
Где Р - начальная сумма, S
- наращенная сумма, n - срок
вклада в годах, i -
процентная ставка.
Р = 15 тыс.руб.
S = 18 тыс.руб.,
i = ?, n = 5/12
Найдем доходность:
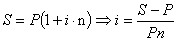
Ответ: простая годовая процентная
ставка должна составлять 48%.