Реалізація криптоалгоритму RSA
МІНІСТЕРСТВО ОСВІТИ І НАУКИ
УКРАЇНИ
НАЦІОНАЛЬНИЙ АВІАЦІЙНИЙ
УНІВЕРСИТЕТ
ІНСТИТУТ КОМПЮТЕРНИХ
ІНФОРМАЦІЙНИХ ТЕХНОЛОГІЙ
КАФЕДРА ЗАСОБІВ ЗАХИСТУ
ІНФОРМАЦІЇ
Контрольна робота
з дисципліни «Архітектура та
програмування мікропроцесорів»
на тему: «Реалізація
криптоалгоритму RSA»
Виконала:
Агафонова О.Ю.
Київ - 2014р.
Зміст
Вступ
1. Опис алгоритму RSA
2. Алгоритм створення відкритого і секретного
ключів
. Шифрування і розшифрування (приклад)
. Алгоритм шифрування сеансового ключа
. Коректність схеми RSA
. Цифровий підпис
. Використання китайської теореми про залишки
для прискорення розшифрування
. Криптоаналіз RSA
. Застосування RSA
Список використаної літератури
Вступ
(абревіатура від прізвищ Rivest,
Shamir і Adleman) - криптографічний алгоритм з відкритим ключем, що грунтується
на обчислювальній складності задачі факторизації великих цілих чисел.
Криптосистема RSA стала першою системою, придатної і для шифрування, і для
цифрового підпису. Алгоритм використовується у великому числі криптографічних
додатків, включаючи PGP, S/ MIME, TLS / SSL, IPSEC / IKE та інших.
Історія виникнення алгоритму RSA.
Опублікована в листопаді 1976 стаття
Уитфилда Діффі і Мартіна Хеллмана «Нові напрямки в криптографії» (англ. New Directions
in Cryptography) перевернула уявлення про криптографічних системах, заклавши
основи криптографії з відкритим ключем. Розроблений згодом алгоритм Діффі -
Хеллмана дозволяв двом сторонам отримати загальний секретний ключ,
використовуючи незахищений канал зв'язку. Однак цей алгоритм не вирішував
проблему аутентифікації. Без додаткових коштів користувачі не могли бути
впевнені, з ким саме вони згенерували загальний секретний ключ.
Вивчивши цю статтю, троє вчених Рональд Ривест
<#"785028.files/image001.gif"> допустимих пар відкритого та
закритого ключів 
 відповідні функції шифрування
відповідні функції шифрування  і розшифрування
і розшифрування  такі, що
такі, що  повідомлень
повідомлень  , де
, де  - безліч допустимих повідомлень,
- безліч допустимих повідомлень, 
2. Алгоритм створення відкритого і
секретного ключів
ключі генеруються таким чином:
1. Вибираються два різних випадкових простих числа
<#"785028.files/image010.gif"> і  заданого
розміру (наприклад, 1024 біта
<#"785028.files/image012.gif">,
яке називається модулем.
заданого
розміру (наприклад, 1024 біта
<#"785028.files/image012.gif">,
яке називається модулем.
. Обчислюється значення функції Ейлера
<#"785028.files/image013.gif">:

4. Вибирається ціле число  (
( ), взаємно просте
<#"785028.files/image017.gif">. Звичайно як
), взаємно просте
<#"785028.files/image017.gif">. Звичайно як  беруть
прості числа, що містять невелику кількість одиничних біт в двійковій запису
<#"785028.files/image015.gif"> називається відкритою експонентою
(public exponent)
беруть
прості числа, що містять невелику кількість одиничних біт в двійковій запису
<#"785028.files/image015.gif"> називається відкритою експонентою
(public exponent)
· Час, необхідний для шифрування з використанням
швидкого зведення в ступінь
<#"785028.files/image015.gif">.
· Занадто малі значення  ,
наприклад 3, потенційно можуть послабити безпеку схеми RSA.
,
наприклад 3, потенційно можуть послабити безпеку схеми RSA.
. Обчислюється число  ,
мультиплікативно
<#"785028.files/image015.gif">по модулю
,
мультиплікативно
<#"785028.files/image015.gif">по модулю  ,
тобто число, яке задовольняє умові:
,
тобто число, яке задовольняє умові:

· Число  називається
секретної експонентою. Зазвичай, воно обчислюється за допомогою розширеного
алгоритму Евкліда
<#"785028.files/image020.gif">публікується як відкритого ключа RSA
(RSA public key).
називається
секретної експонентою. Зазвичай, воно обчислюється за допомогою розширеного
алгоритму Евкліда
<#"785028.files/image020.gif">публікується як відкритого ключа RSA
(RSA public key).
7. Пара 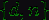 грає роль закритого ключа RSA (RSA
private key) і тримається в секреті.
грає роль закритого ключа RSA (RSA
private key) і тримається в секреті.
Припустимо, Боб хоче послати Алісі
повідомлення  .
.
Повідомленнями є цілі числа
<#"785028.files/image023.gif">до 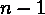 ,
т.е.
,
т.е.  .
.



. Алгоритм шифрування сеансового
ключа
Найбільш використовуваним в даний час
є змішаний алгоритм шифрування, в якому спочатку шифрується сеансовий ключ, а
потім вже з його допомогою учасники шифрують свої повідомлення симетричними
системами. Після завершення сеансу сеансовий ключ як правило знищується.
Алгоритм шифрування сеансового ключа
виглядає наступним чином:
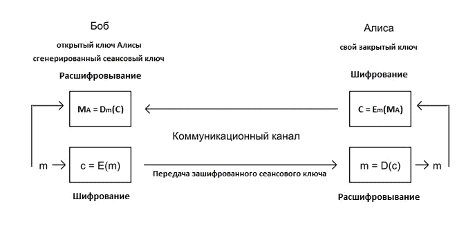


У разі, коли сеансовий ключ більше,
ніж модуль  сеансовий ключ розбивають на блоки потрібної довжини (у разі
потреби доповнюють нулями) і шифрують кожен блок.
сеансовий ключ розбивають на блоки потрібної довжини (у разі
потреби доповнюють нулями) і шифрують кожен блок.
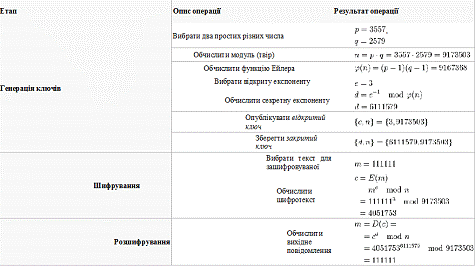
5. Коректність схеми RSA
Рівняння  і
і  ,
на яких заснована схема RSA, визначають взаємно зворотні перетворення
<#"785028.files/image034.gif">
,
на яких заснована схема RSA, визначають взаємно зворотні перетворення
<#"785028.files/image034.gif">
.
Цифровий підпис
Система RSA може використовуватися не тільки для шифрування, але і для
цифрового підпису
<#"785028.files/image036.gif">)
потрібно відправити Бобу (стороні  )
повідомлення
)
повідомлення  , підтверджене електронним цифровим підписом
<#"785028.files/image038.gif">
, підтверджене електронним цифровим підписом
<#"785028.files/image038.gif">


Оскільки цифровий підпис
<#"785028.files/image036.gif">може
переслати стороні  електронний чек. Після того як сторона
електронний чек. Після того як сторона  перевірить підпис боку
перевірить підпис боку  на
чеку, вона може передати його в свій банк, службовці якого також мають
можливість перевірити підпис і здійснити відповідну грошову операцію.
на
чеку, вона може передати його в свій банк, службовці якого також мають
можливість перевірити підпис і здійснити відповідну грошову операцію.
Зауважимо, що підписане повідомлення  НЕ
зашифровано <#"785028.files/image041.gif">представляє
основну обчислювальну складність. Це завдання може бути вирішена за допомогою
алгоритму швидкого зведення в ступінь
<#"785028.files/image042.gif">потрібно
НЕ
зашифровано <#"785028.files/image041.gif">представляє
основну обчислювальну складність. Це завдання може бути вирішена за допомогою
алгоритму швидкого зведення в ступінь
<#"785028.files/image042.gif">потрібно  операцій
множення за модулем
<#"785028.files/image020.gif">і закритий ключ
операцій
множення за модулем
<#"785028.files/image020.gif">і закритий ключ 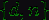 задовольняють співвідношенням
задовольняють співвідношенням  ,
,  . Тоді в процесах їх застосування
виконується відповідно
. Тоді в процесах їх застосування
виконується відповідно  і
і  умножений по модулю.
умножений по модулю.
Алгоритм RSA набагато повільніше, ніж AES
<#"785028.files/image010.gif">і  в
розкладанні
в
розкладанні  відомі зашифровувати [ відомі власнику закритого
ключа!
<#"785028.files/image049.gif">
відомі зашифровувати [ відомі власнику закритого
ключа!
<#"785028.files/image049.gif">

Оскільки  і
і  -
числа порядку
-
числа порядку 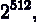 на ці дії буде потрібно два потенцирования з
показником 512 знаків за модулем 512-бітового числа. Це істотно швидше, ніж
одне потенцирование з 1024-бітовим показником за модулем числа з 1024
двійковими знаками. Далі залишилося відновити
на ці дії буде потрібно два потенцирования з
показником 512 знаків за модулем 512-бітового числа. Це істотно швидше, ніж
одне потенцирование з 1024-бітовим показником за модулем числа з 1024
двійковими знаками. Далі залишилося відновити  по
по
 і
і  що
можна зробити за допомогою китайської теореми про залишки
<#"785028.files/image054.gif">.
що
можна зробити за допомогою китайської теореми про залишки
<#"785028.files/image054.gif">.
Для обчислення  по відомим
по відомим  потрібно знайти такий
потрібно знайти такий  , щоб
, щоб

тобто

Обчислення зворотного елемента по
модулю не є складним завданням, проте зловмисникові невідомо значення . Для
обчислення функції Ейлера від відомого числа необхідно знати розкладання цього
числа на прості множники. Перебування таких множників і є складним завданням, а
знання цих множників - «потайними дверцями» (backdoor), яка використовується
для обчислення власником ключа. Існує безліч алгоритмів для знаходження
простих співмножників, так званої факторизації, найшвидший з яких на
сьогоднішній день - загальний метод решета числового поля, швидкість якого для
k-бітного цілого числа становить
 для деякого
для деякого  .
.
У 2010 році групі вчених з Швейцарії, Японії, Франції, Нідерландів,
Німеччини та США вдалося успішно обчислити дані, зашифровані за допомогою
криптографічного ключа стандарту RSA довжиною 768 біт. Знаходження простих
співмножників здійснювалося загальним методом решета числового поля
<#"785028.files/image060.gif">можна визначити  за
поліноміальний час за допомогою атаки Вінера, [18]
<#"785028.files/image061.gif">
за
поліноміальний час за допомогою атаки Вінера, [18]
<#"785028.files/image061.gif">
Оскільки НОД  то
то  підходяща
дріб в розкладанні дробу
підходяща
дріб в розкладанні дробу  в безперервну
<#"785028.files/image065.gif">
в безперервну
<#"785028.files/image065.gif">
для деякого випадкового числа  Отримавши
рівність, знайдемо
Отримавши
рівність, знайдемо  Загальне число відповідних дробів, яке доведеться
перевірити оцінюється як
Загальне число відповідних дробів, яке доведеться
перевірити оцінюється як
10. Застосування RSA
Система RSA використовується для захисту програмного забезпечення та в
схемах цифрового підпису
<http://ru.wikipedia.org/wiki/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F_%D1%86%D0%B8%D1%84%D1%80%D0%BE%D0%B2%D0%B0%D1%8F_%D0%BF%D0%BE%D0%B4%D0%BF%D0%B8%D1%81%D1%8C>.
Також вона використовується у відкритій системі шифрування PGP <http://ru.wikipedia.org/wiki/PGP>
та інших системах шифрування (наприклад, DarkCryptTC і формат xdc) у поєднанні
з симетричними алгоритмами
<http://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D0%BC%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%BD%D1%8B%D0%B9_%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC_%D1%88%D0%B8%D1%84%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F>.
Через низьку швидкість шифрування (близько 30 кбіт / с при 512 бітному
ключі на процесорі 2 ГГц), повідомлення зазвичай шифрують за допомогою більш
продуктивних симетричних алгоритмів з випадковим ключем (сеансовий ключ), а за
допомогою RSA шифрують лише цей ключ, таким чином реалізується гібридна
криптосистема
<http://ru.wikipedia.org/wiki/%D0%93%D0%B8%D0%B1%D1%80%D0%B8%D0%B4%D0%BD%D0%B0%D1%8F_%D0%BA%D1%80%D0%B8%D0%BF%D1%82%D0%BE%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0>.
Такий механізм має потенційні уразливості зважаючи на необхідність
використовувати криптостійкий генератор випадкових чисел
<http://ru.wikipedia.org/wiki/%D0%93%D0%B5%D0%BD%D0%B5%D1%80%D0%B0%D1%82%D0%BE%D1%80_%D1%81%D0%BB%D1%83%D1%87%D0%B0%D0%B9%D0%BD%D1%8B%D1%85_%D1%87%D0%B8%D1%81%D0%B5%D0%BB>
для формування випадкового сеансового ключа симетричного шифрування і ефективно
протистоїть атакам симетричний криптоалгоритм (на даний час широке застосування
знаходять AES
<http://ru.wikipedia.org/wiki/Advanced_Encryption_Standard>, IDEA
<http://ru.wikipedia.org/wiki/IDEA>, Serpent
<http://ru.wikipedia.org/wiki/Serpent>, Twofish
<http://ru.wikipedia.org/wiki/Twofish>).
Список використаної літератури
1. Bakhtiari M., Maarof MA
Serious Security Weakness In RSA Cryptosystem / /IJCSI International Journal of
Computer Science. - January 2012. - В. 1, № 3. - Т. 9. -ISSN 1694-0814.
. Whitfield Diffie, Martin E.
Hellman. New Directions in Cryptography (англ.) / / IEEE Transactions on
Information Theory. - Nov. 1976. - Т. IT-22. - С. 644-654.
. A Quarter Century Of
Recreational Mathematics, by Martin Gardner (англ.).Scientific American. -
«Ronald L. Rivest of the Massachusetts Institute of Technology allowed me to be
the first to reveal-in the August 1977 column-the« publickey »cipher system
that he co-invented» Перевірено 3 березня 2012. Фотогалерея з першоджерела 23
червня 2012.
. Перейти до:1 2 Martin
Gardner. Mathematical Games: A new kind of cipher that would take millions of
years to break (англ.) / / Scientific American. - 1977.