Основы математического анализа
1. Найдите пределы, не
пользуясь правилом Лопиталя
Решение
;
=
;
;
=
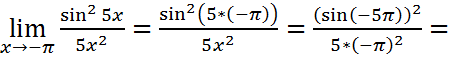
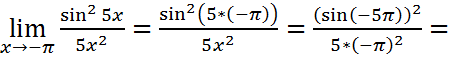
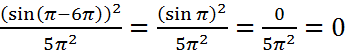
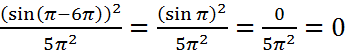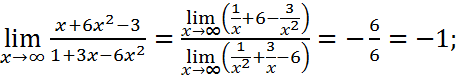
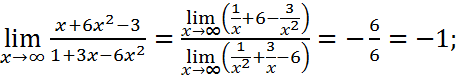
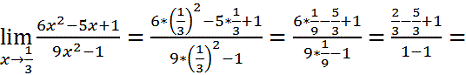
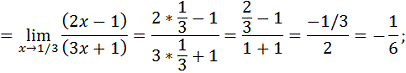
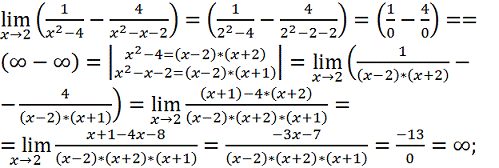
2. Исследуйте функцию на
непрерывность, постройте её график
y=
Решение
Область определения
данной функции D(y)= (−∞; +∞). В точках x=1
и x=2 функция меняет свой способ задания. В этих точках возможен
разрыв.
Исследуем на
непрерывность функцию 
в точке x=1;
=1
;
.
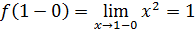
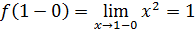Так как 
=1, заключаем что 
непрерывна в точке x=1.
Исследуем на
непрерывность функцию в точке x=2;
;
=-2.
Так как 
, но оба предела
конечны, заключаем что в точке x=2 терпит разрыв 1 рода.
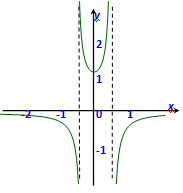
y
=;
Данная функция
определена для всех значений x,
для которых 
≠ 0, т.е. x≠±1/2.
Во всех точках своей
области определения функция непрерывна. Точки x=1/2
и x=-1/2 являются точками разрыва, так как в этих точках функция не
определена.
Определим тип точки
разрыва x=-1/2. Для этого находим односторонние пределы:
Односторонние пределы
равны бесконечности, следовательно, в точке x=-1/2
разрыв 2-го рода.
Определим тип точки
разрыва x=1/2. Для этого находим односторонние пределы;
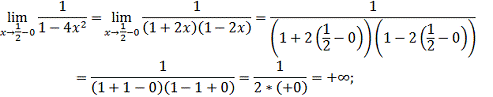
Односторонние пределы
равны бесконечности, следовательно, в точке x=1/2
разрыв 2-го рода.
Исследуем поведение
функции на бесконечности
Вычислим значения
функции в некоторых точках:
|
x
|
-1
|
-2
|
-3
|
0
|
1
|
2
|
3
|
0.25
|
|
y
|
-0.33
|
-0.066
|
-0.038
|
1
|
-0.33
|
-0.066
|
-0.038
|
1.33
|
3. Найдите производную
функции
; 
;
; 
; 
;
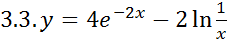
Решение
=
=
;
;
;
;
;
=
;
;
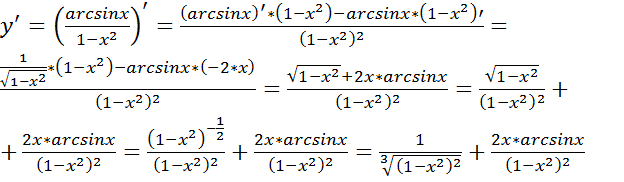
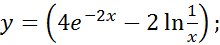
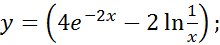
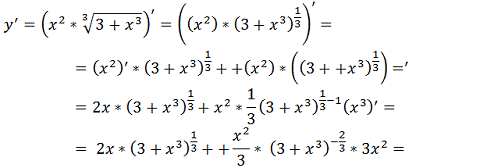
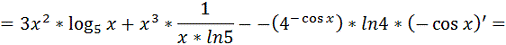
y'=
=
=
=
=
;
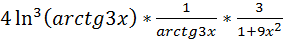
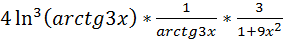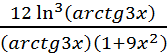
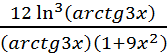4. Найдите пределы,
пользуясь правилом Лопиталя
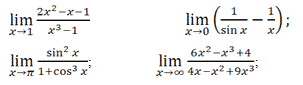
Решение
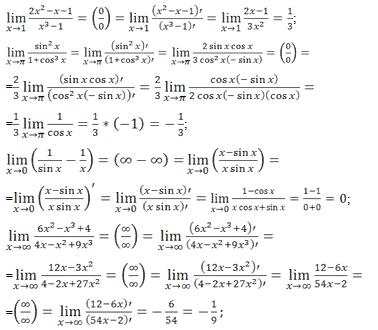
. Найдите наибольшее и
наименьшее значения функции на указанном отрезке
, [-3; 0]; 
, [2; 8].
Решение
, [-3; 0];
Найдем производную
данной функции
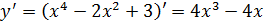
Решим уравнение 
x=0∈[-3;
0]=конец отрезка; x=-1∈[-3;
0], x=1[-3; 0]
Вычислим значение
функции в точке x=-1 и на конца отрезка.
т.е. при x=-3, и x=0
,
Следовательно,
.
.
, [2; 8].
Найдем производную
данной функции
Решим уравнение
D=b^2-4ac=
⇒
5, 
;
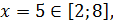
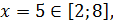
Вычислим значение
функции в точке x=5 и на концах отрезка,
т.е. при x=2, и x=8,
Следовательно,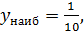
.
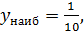
Список литературы
предел лопиталь
функция производная
1. Самочернова Л.И. Высшая математика. Часть 2: учебное
пособие / Л.И. Самочернова; Томский политехнический университет. - изд., испр.
- Томск: Издательство Томского политехнического университета, 2005. - 164 с.
. Алгебра и начала анализа. 9 и 11 выпускные классы / Е.В.
Якушева, А.В. Попов, О.Ю. Черкасов, - 416 с. - (Экзаменационные вопросы и
ответы. Экзамен на 5).
. 3000 конкурсных задач по математике. 2-е изд., испр. и
доп. - М.: Рольф, Айрис-пресс, 1998. - 624 с.