Основы эконометрики
Введение
Эконометрика - наука, исследующая количественные закономерности и
взаимозависимости в экономике на основе методов теории вероятностей и
математической статистики, адаптированных к обработке экономических данных.
Основным элементом курса является анализ и построение взаимосвязей
экономических переменных.
Математическая статистика и ее применение в экономике - эконометрика -
позволяют строить экономические модели, оценивать их параметры, проверять
гипотезы о свойствах экономических показателей и формах их связи, что в
конечном счёте служит основой для экономического анализа и прогнозирования
(основная цель эконометрики).
Экономические модели позволяют выявить особенности экономического объекта
и на основе этого предсказывать будущее поведение объекта при изменении
каких-либо параметров (повышение обменного курса, падение прибыли…).
По
своему определению любая экономическая модель абстрактна и, следовательно,
неполна. Так, например, в простейшей модели спроса предполагают, что спрос на
какой-либо товар определяется его ценой (р) и доходом потребителя (I): 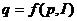 .
.
На
самом же деле на спрос влияют также другие факторы (цены на другие товары,
реклама, мода, погода и т.д.). Поэтому в модель добавляют, обычно аддитивным
образом, случайный компонент ε, интегрирующий
(объединяющий) в себе влияние всех неучтённых явно в модели факторов. Например,
модель спроса принимает вид: 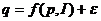 .
.
Введение
случайного компонента в модель приводит к тому, что взаимосвязь остальных её
переменных перестаёт быть строго детерминированной (функциональной) и
становится стохастической (статистической, случайной), каковая и наблюдается в
реальной действительности.
Связь
переменных, на которую накладываются воздействия случайных факторов, называется
статистической (корреляционной).
Основой
для выявления и обоснования эмпирических (опытных) закономерностей являются
статистические данные, которые обычно подразделяются на 2 вида:
перекрёстные
данные - данные по какому-либо
экономическому показателю, полученные для различных однотипных объектов (фирм,
регионов). При этом либо все данные относятся к одному периоду времени, либо
временная принадлежность несущественна.
временные
ряды - данные, характеризующие один
объект, но в разные моменты времени.
Существуют
различные методы сбора экономических данных: опрос, анкетирование, получение
официальной стат.отчётности…
Собранные
данные могут быть представлены в различной форме: в виде таблиц, диаграмм,
графиков.
Далее
подготовленные данные подставляются в теоретическую модель, представленную
аналитически (в виде некоторого уравнения) или в графическом виде.
При
этом возникает ряд проблем, важнейшими из которых являются проверка
согласованности теоретической модели с опытными данными, оценка параметров
модели и проверка предположений (гипотез), лежащих в основе модели.
Основные
этапы эконометрического исследования:
.
Постановочный этап - постановка проблемы, целей моделирования, сбор данных,
анализ их качества.
I. Спецификация
модели - выбор вида формулы зависимости.
II.
Параметризация - оценка значений параметров выбранной модели.
III. Верификация
- проверка качества полученных параметров и самой модели в целом.
IV.
Использование построенной модели для объяснения поведения экономических
показателей и прогнозирования.
Основные
типы моделей:
Экономико-математическая
модель - это математическое описание какого-либо экономического процесса или
объекта.
Математические
модели, используемые в экономике, можно подразделить на классы по ряду
признаков, относящихся к особенностям моделируемых объектов, цели моделирования
и используемого инструментария.
Макроэкономические
модели описывают экономику как единое целое, связывая между собой укрупнённые
материальные и финансовые показатели (ВВП, потребление, инвестиции, занятость,
процентную ставку…).
Микроэкономические
модели описывают взаимодействие структурных и функциональных составляющих
экономики, либо поведение отдельной такой составляющей в рыночной среде.
Теоретические
модели позволяют изучать общие свойства экономики и её характерных элементов
дедукцией (от общего к частному) выводов из формальных предпосылок.
Прикладные
модели оценивают параметры функционирования конкретного экономического объекта
и позволяют сформулировать рекомендации для практических решений. К прикладным
относятся прежде всего эконометрические модели, оперирующие числовыми
значениями экономических переменных и позволяющие статистически значимо
оценивать их на основе имеющихся наблюдений.
Особое
место в рыночной экономике занимают равновесные модели, которые описывают такие
состояния экономики, когда результирующая всех сил, стремящихся вывести их из
этого состояния, равна 0.
Статические
модели описывают состояние экономического объекта в конкретный момент или
период времени.
Динамические
модели включают взаимосвязи переменных во времени.
Детерминированные
модели предполагают строгие функциональные связи между переменными.
Стохастические
допускают наличие случайных воздействий на исследуемые показатели и используют
инструментарий теории вероятностей и математической статистики для их описания.
Приведём
3 основных класса моделей, которые применяются для анализа и
прогнозирования в эконометрике:
.
Модели временных рядов: модели тренда  и
сезонности
и
сезонности  . Они объясняют поведение временного ряда, исходя
только из его предыдущих значений. Применяются для изучения и прогнозирования
объёма продаж билетов, спроса, прогнозирования % ставки.
. Они объясняют поведение временного ряда, исходя
только из его предыдущих значений. Применяются для изучения и прогнозирования
объёма продаж билетов, спроса, прогнозирования % ставки.
.
Регрессионные модели с 1 уравнением: зависимая переменная у представляется в
виде функции одной или нескольких переменных: 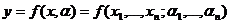 ,
где у - объясняемая (зависимая) переменная,
,
где у - объясняемая (зависимая) переменная,  -
объясняющие (независимые) переменные,
-
объясняющие (независимые) переменные, 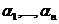 -
параметры уравнения.
-
параметры уравнения.
Регрессионные
уравнения - уравнения статистической связи между переменными.
В
зависимости от вида функции f модели делятся на линейные и нелинейные. Эти модели
применяют значительно шире, чем модели временных рядов. (Например, спрос на
мороженое как функция от времени, температуры воздуха, среднего уровня
доходов…).
.
Системы одновременных уравнений: описываются системами уравнений, могут
состоять из тождеств и регрессионных уравнений, которые кроме объясняющих переменных
могут включать в себя объясняемые переменные из других уравнений.
1. Основные
понятия теории вероятностей
1.1
Вероятностный эксперимент, событие, вероятность
Испытание
(вероятностный эксперимент) -
действие, результат которого заранее не известен (т.к. он является случайным).
Элементарный
исход - возможный результат
испытания.
Событие - один или несколько исходов.
Событие
называется случайным, если при осуществлении определенной совокупности условий S оно
может либо произойти, либо не произойти. Далее вместо того, чтобы говорить
"совокупность условий S осуществлена", будем говорить: "произведено
испытание".
Например,
строительство автомобильного завода в контексте получения прибыли -
вероятностный эксперимент (испытание). Получение прибыли - случайное событие.
Если
событие происходит всегда в условиях данного эксперимента, то оно называется
достоверным (спрос на автомобили упадет при резком повышении цен на
автомобили). Событие называется невозможным, если оно никогда не произойдет в
условиях данного эксперимента (рост спроса на автомобили приведет к снижению их
цены при прочих равных условиях - невозможное событие).
События
называются несовместными, если появление одного из них исключает появление
других событий в одном и том же испытании (увеличение налогов - рост
располагаемого дохода).
Иначе
события называются совместными (увеличение объема продаж - увеличение прибыли).
Несколько
событий образуют полную группу, если в результате испытания появится хотя бы
одно из них (появление хотя бы одного из событий полной группы есть достоверное
событие).
Если
события, образующие полную группу несовместные, то в результате испытания
появится только одно из них.
Противоположными
называют два единственно возможных события, образующих полную группу.
Противоположные события принято обозначать А и  .
.
События
называются равновозможными, если ни одно из них не является более возможным,
чем другое.
Каждый
из возможных результатов испытания называется элементарным исходом
(элементарным событием) (их нельзя разбить на более простые).
Вероятность
- число, характеризующее степень возможности появления события.
Вероятностью
события А называют отношение числа благоприятствующих этому событию исходов к
общему числу всех равновозможных несовместных элементарных исходов, образующих
полную группу.
 ,
,
где
m(A) - число благоприятствующих событию А исходов, n -
число всех возможных элементарных исходов.
Свойства
вероятности:
1. Вероятность достоверного события равна единице.
2. Вероятность невозможного события равна 0.
. Вероятность случайного события: 0 < P(A) < 1.
. Вероятность любого события удовлетворяет двойному неравенству: 0≤
P(A) ≤ 1.
5.
Если А и  - противоположные, то Р(А) = 1 - Р(
- противоположные, то Р(А) = 1 - Р( ).
).
Наряду
с классическим определением используют и другие определения вероятности, в
частности статистическое определение: в качестве статистической вероятности
события принимают относительную частоту или число, близкое к ней.
Относительной
частотой события называют отношение числа испытаний, в которых событие
появилось, к общему числу фактически произведённых испытаний.
(A) = 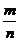 ,
,
-
число появлений события, n - общее число испытаний.
Вероятность
вычисляют до опыта, а относительную частоту - после опыта.
Пример
1. Отдел технического контроля обнаружил 3 нестандартных детали в партии из 80
случайно отобранных деталей. Относительная частота появления нестандартных
деталей W(A) =  .
.
Свойство
устойчивости относительной частоты: в
различных опытах относительная частота изменяется мало (тем меньше, чем больше
произведено испытаний), колеблясь около некоторого постоянного числа. Это
постоянное число и есть вероятность появления события.
Т.о.,
если опытным путём установлена относительная частота, то полученное число можно
принять за приближённое значение вероятности.
Статистическая
вероятность любого события также заключена между нулём и единицей:
0
≤ 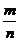 ≤ 1.
≤ 1.
Для
существования статистической вероятности требуется:
А)
возможность производить неограниченное число испытаний, в каждом из которых
событие А наступает или не наступает;
Б)
устойчивость относительных частот появления А в различных сериях достаточно
большого числа испытаний.
1.2
Случайные величины
Случайной
называют величину, которая в результате испытания примет одно и только одно
возможное значение, наперед не известное и зависящее от случайных причин, которые
сначала не могут быть учтены.
Пример
2. Число родившихся детей в городе в течение суток - СВ, которая принимает
значения 1, 2, 3, …
Пример
3. Прибыль фирмы - СВ. Возможные значения этой величины принадлежат некоторому
промежутку.
Будем
обозначать случайные величины прописными буквами X, Y, Z…, а
их возможные значения соответствующими строчными буквами x, y, z…
Различают
следующие виды случайных величин:
Дискретная
(прерывная) СВ - величина, которая принимает отдельные, изолированные числовые
значения с определенными вероятностями. Число возможных значений дискретной
случайной величины может быть конечным и бесконечным. (Пр.2)
Непрерывная
случайная величина - СВ, которая может принимать любые числовые значения из
некоторого конечного или бесконечного промежутка. Число возможных значений
непрерывной СВ бесконечно. (Пр. 3).
Для
задания дискретной СВ недостаточно перечислить все возможные ее значения, нужно
еще указать их вероятности.
Законом
распределения дискретной СВ называют соответствие между возможными значениями
этой величины и их вероятностями. Закон распределения можно задать таблично,
аналитически и графически.
При
табличном задании первая строка таблицы содержит возможные значения, а вторая -
их вероятности:
|
Х
|
х1
|
х2
|
…
|
хn
|
|
р
|
р1
|
р2
|
…
|
рn
|
Т.к. в одном испытании случайная величина принимает одно и только одно
возможное значение, то события Х = х1, Х = х2,…, Х = хn образуют полную группу. => Сумма
вероятностей этих событий равна 1:
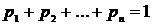 .
.
Если
множество возможных значений Х бесконечно (счетно), то ряд  сходится, и его сумма равна 1.
сходится, и его сумма равна 1.
Пример
4. В денежной лотерее выпущено 100 билетов. Разыгрывается 1 выигрыш в 50 рублей
и 10 выигрышей по 5 руб. Найти закон распределения СВ Х - стоимости возможного
выигрыша владельца лотерейного билета.
Решение.
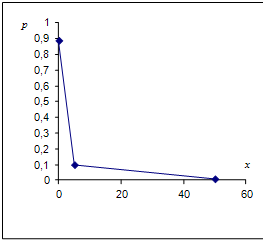
Х - дискретная СВ. Ее возможные значения: х1= 0, х2 =5, х3
= 50. Вероятности этих значений: р1= 0,89, р2 =
0,1, р3 = 0,01. (проверка: 0,89 + 0,1 + 0,01 = 1)
Тогда
закон распределения:
Для наглядности закон распределения дискретной СВ можно изобразить и
графически, для чего в прямоугольной системе координат строят точки (xi, pi), а затем соединяют их отрезками.
Полученная ломанная называется многоугольником или полигоном распределения.
Пр.4.
Аналитически СВ задается либо функцией распределения, либо плотностью
вероятностей.
Функцией
распределения СВ Х называют функцию  ,
определяющую вероятность того, что СВ Х принимает значение, меньшее, чем х:
,
определяющую вероятность того, что СВ Х принимает значение, меньшее, чем х:
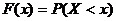 .
.
Иногда
эту функцию называют функцией накопленной вероятности или кумулятивной функцией
распределения.
Свойства
функции распределения:
1. 0
≤  ≤ 1.
≤ 1.
2.  - неубывающая функция, т.е.
- неубывающая функция, т.е. 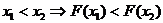 .
.
3.
 .
.
. 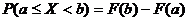 .
.
. 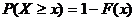 .
.
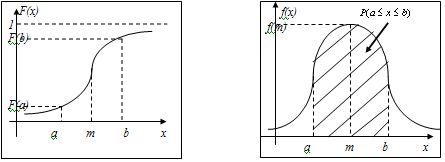
Если возможные значения СВ Х принадлежат отрезку [a, b], то

График
функции распределения даёт наглядное представление о вероятности изменения
значений СВ.
Для
примера функция распределения и её график имеют вид:
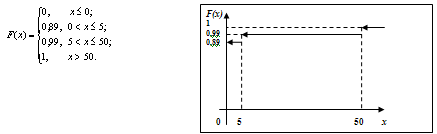
Для
непрерывной СВ нельзя определить вероятность того, что она принимает некоторое
конкретное значение, а следовательно непрерывную СВ нельзя задать таблично.
Поэтому для описания непрерывной СВ может быть использована функция
распределения. При этом она является непрерывной неубывающей функцией,
изменяющейся от 0 до 1.
Плотностью
вероятности (плотностью распределения вероятностей) непрерывной СВ Х называют
функцию  .
.
Свойства
плотности вероятности:
1.
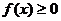 .2.
.2. 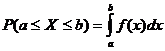 .3.
.3. 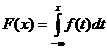 .4.
.4. 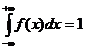 .
.
Для
непрерывной СВ справедливы равенства:
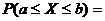
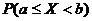 =
= =
=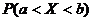 .
.
Площадь
под графиком кривой плотности вероятности равна единице.
Площадь
заштрихованной области на рисунке равна:
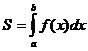 =
= .
.
Вероятность
попадания значений СВ в "хвосты" распределения, т.е. в интервалы 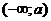 и
и  , равна 1
-
, равна 1
-  . Т.о. с помощью плотности вероятности можно
определить вероятность попадания непрерывной СВ Х в заданный интервал
. Т.о. с помощью плотности вероятности можно
определить вероятность попадания непрерывной СВ Х в заданный интервал  , что имеет большое прикладное значение.
, что имеет большое прикладное значение.
1.3
Числовые характеристики СВ
Числовыми
характеристиками СВ называют числа, которые описывают СВ суммарно. К таким
числовым характеристикам относится математическое ожидание. Оно характеризует
среднее ожидаемое значение СВ, т.е. приблизительно равно его среднему значению.
Для решения многих задач достаточно знать МО (например, при оценивании
покупательной способности населения достаточно знать средний доход).
Математическим
ожиданием дискретной СВ называют сумму произведений всех возможных ее значений
на их вероятности.
 .
.
Если
дискретная СВ принимает счетное множество всевозможных значений, то
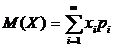
Причем
мат.ожидание существует, если ряд в правой части сходится абсолютно.
Для
непрерывной СВ:
(X) =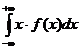 .
.
Замечание. Мат.ожидание - неслучайная постоянная величина.
Пример
5. Найти мат.ожидание дискретной СВ Х, зная закон ее распределения:
Решение. Искомое мат.ожидание М(Х) = 3∙0,1 + 5∙0,6 + 2∙0,3
= 3,9.
Мат.ожидание числа появления события в одном испытании равно вероятности
этого события.
Мат.ожидание приближенно равно (тем больше, чем больше число испытаний)
среднему арифметическому наблюдаемых значений СВ.
Замечание. МО больше наименьшего и меньше наибольшего возможных
значений СВ.
Свойства математического ожидания:
. Мат.ожидание постоянной величины равно самой постоянной: М(С) = С.
. Постоянный множитель можно выносить за знак МО: М(СХ) = СМ(Х).
. МО суммы 2-х СВ равно сумме МО слагаемых: М(Х + Y) = M(X) + M(Y).
. МО произведения двух независимых СВ равно произведению их МО:
М(ХY) = M(X)M(Y).
Зная только МО СВ нельзя судить ни о том, какие значения принимает СВ, ни
о том, как эти значения рассеяны вокруг мат.ожидания. Т.е. МО полностью не характеризует
СВ. Поэтому наряду с мат.ожиданием вводят и другие числовые характеристики.
Например, чтобы оценить, как рассеяны величины вокруг МО, используют дисперсию.
Дисперсией СВ называют мат.ожидание квадрата отклонения СВ от ее МО:
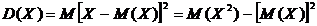 .
.
При
этом для дискретной СВ:

Для
непрерывной СВ:
 .
.
Замечание. Дисперсия СВ - неслучайная постоянная величина.
Пример
6. Найти дисперсию СВ Х, которая задана законом распределения:
Решение. Найдем МО: М(Х) = 1∙0,3 + 2∙0,5 + 5∙0,2 = 2,3.
Затем найдем возможные значения квадрата отклонения:
[х1 - M(X)]2 = (1 - 2,3)2
= 1,69; [х2 - M(X)]2 = (2 - 2,3)2
= 0,09;
[х3 - M(X)]2 = (5 - 2,3)2
= 7,29.
D(X) = 1,69∙0,3 + 0,09∙0,5+
7,29∙0,2 = 2,01.
2
способ. М(Х) = 2,3. Вычислим M(X2) = 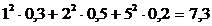 .
.
Искомая
дисперсия равна D(X) = 7,3 - (2,3)2 = 7,3 - 5,29 = 2,01.
Свойства
дисперсии:
.
Дисперсия постоянной величины равна 0: D(C) =
0.
.
Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:
(CX) =
C2D(X).
3.
Дисперсия алгебраической суммы конечного числа независимых СВ равна сумме
дисперсий этих величин:
(X ± Y) = D(X) + D(Y).
Следствие. Дисперсия суммы постоянной величины и случайной равна
дисперсии случайной величины:
(С
+ Х) = D(X).
Дисперсия
имеет размерность, равную квадрату размерности СВ.
Кроме дисперсии для оценки рассеяния СВ вокруг ее среднего значения
служат и другие характеристики, например, среднее квадратическое отклонение. Средним квадратическим отклонением СВ Х называют квадратный
корень из ее дисперсии:
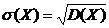 .
.
Размерность
сред.квадр.отклонения совпадает с размерностью СВ.
Пример 6. Решение.
D(X) =
2,01 =>  .
.
Чтобы
оценить разброс значений СВ в процентах относительно её среднего значения,
вводится коэффициент вариации V(X), который рассчитывается по формуле:
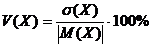 .
.
1.4
Законы распределений СВ
.
Закон равномерного распределения вероятностей
Распределение
вероятностей называется равномерным, если на интервале, которому принадлежат
все возможные значения СВ, плотность распределения сохраняет постоянное
значение.
Если
все возможные значения СВ принадлежат отрезку 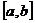 , на
котором функция f(x) сохраняет постоянное значение, то плотность
вероятности:
, на
котором функция f(x) сохраняет постоянное значение, то плотность
вероятности:
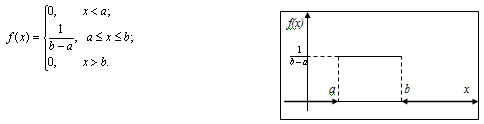
Функция
распределения

Математическое
ожидание 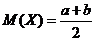 ;
;
дисперсия
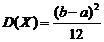 .
.
Пример 7. Поезда метрополитена идут регулярно с интервалом 2 минуты.
Пассажир выходит на платформу в случайные моменты времени. Какова вероятность,
что ждать пассажиру придется не более 0,5 мин. Найти математическое ожидание,
дисперсию и среднее квадратическое отклонение СВ Х - времени ожидания поезда.
Решение. СВ Х - время ожидания на временном отрезке 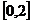 имеет равномерный закон распределения
имеет равномерный закон распределения
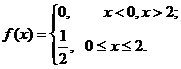 .
.
Вероятность того, что пассажир будет ждать не более 0,5 минуты равна
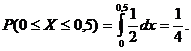
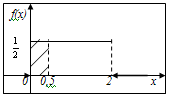
Матем.ожидание
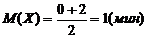 , дисперсия
, дисперсия
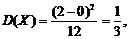

. Нормальный
закон распределения
Нормальный
закон распределения (нормальное распределение, распределение Гаусса) наиболее
часто встречается на практике. Он является предельным законом, к которому
приближаются другие законы распределения при весьма часто встречающихся
типичных условиях.
Опр. Нормальным называется распределение вероятностей
непрерывной СВ, которое описывается плотностью 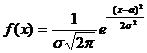 .
.
Оно
определятся двумя параметрами: а и σ.
Вероятностный
смысл этих параметров: а = М(Х), σ2 = D(X),
т.е. σ
- среднее квадратическое отклонение.
Функция
нормального распределения F(x) = 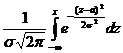 .
.
Кривую
нормального закона распределения называют нормальной (или кривой Гаусса).
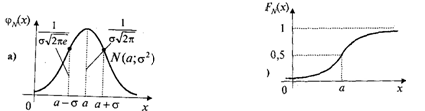
Рассмотрим
как меняется нормальная кривая при изменении параметров а и σ:

Т.о.
параметр а (т.е. М(Х)) характеризует положение, а параметр σ (среднее квадратическое отклонение ) форму нормальной
кривой.
Нормальное
распределение с параметрами а и σ обозначается N(а; σ).
Если
параметры а = 0, σ
= 1, то нормальный закон распределения
называется стандартным или нормированным N(0; 1). А
кривая - стандартной.
Плотность
нормированного распределения 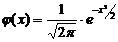 (функция
Лапласа, приложение 1)
(функция
Лапласа, приложение 1)
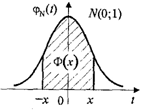
Функция
распределения 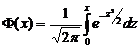 .
.
Вероятность
попадания нормированной СВ Х в интервал (0, х) можно найти, используя функцию
Лапласа Ф(х): Р(0 < Х < х) = 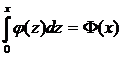 .
.
Функция
распределения СВ Х, распределенная по нормальному закону, выражается через
функцию Лапласа по формуле: 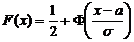 .
.
Свойства
СВ, распределённой по нормальному закону:
.
Вероятность попадания СВ Х, распределённой по нормальному закону, в интервал [x1; x2], равна
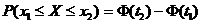
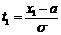 ,
,  .
.

.
Вероятность того, что отклонение СВ Х, распределенной по нормальному закону, от
МО а не превысит величину D > 0 ( по абсолютной
величине)
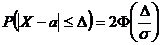
В
частности, если
D
= σ: 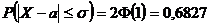 ;
;
D
= 2σ: 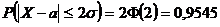 ;
;
D
= 3σ: 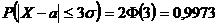 .
.
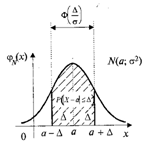
"Правило трёх сигм": Если СВ Х имеет нормальный закон N(а; σ), то практически достоверно, что её
значения заключены в интервале (а - 3σ ; а + 3σ). Нарушение правила является событием
практически невозможным
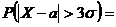
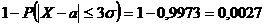 .
.
Пример 8. Полагая, что рост мужчин определённой возрастной группы имеет
нормальное распределение СВ Х с параметрами а = 173, σ2 = 36, найти:
а) долю костюмов 4-го роста (176 - 182), которые нужно предусмотреть в
общем объёме производства. б) сформулировать "правило 3-х сигм".
Решение. а) Р(176£ Х £ 182) =
Ф(t2) - Ф(t1) = Ф(1,5) - Ф(0,5) = 0,2418.
(где
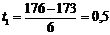 ,
, 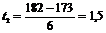 ).
).
б)
Практически достоверно, что рост мужчин данной возрастной группы заключен в
границах от а - 3σ
= 173 - 3×6 = 155 см до а + 3σ = 173 + 3×6 = 191см.
.
Распределение 
 (или
распределение Пирсона) имеет сумма квадратов n независимых СВ
(или
распределение Пирсона) имеет сумма квадратов n независимых СВ
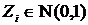 (имеющих стандартное нормальное распределение):
(имеющих стандартное нормальное распределение):  .
.
Стандартная
нормально распределенная СВ 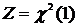 .
.
Число
степеней свободы СВ  равно n. Число степеней свободы
равно n. Число степеней свободы 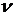 равно
числу СВ, её составляющих, уменьшенному на число линейных связей между ними.
равно
числу СВ, её составляющих, уменьшенному на число линейных связей между ними.  определяется одним числом
определяется одним числом  - числом степеней свободы (
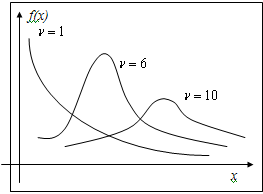
- числом степеней свободы (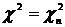 ). График плотности вероятности СВ, имеющей
). График плотности вероятности СВ, имеющей  - распределение лежит только в первой координатной
четверти и имеет асимметричный вид с вытянутым правым "хвостом".
Однако с увеличением числа степеней свободы распределение
- распределение лежит только в первой координатной
четверти и имеет асимметричный вид с вытянутым правым "хвостом".
Однако с увеличением числа степеней свободы распределение  приближается к нормальному. Распределение
приближается к нормальному. Распределение  применяется для нахождения интервальных оценок и
проверки статистических гипотез. При этом используется таблица критических
точек
применяется для нахождения интервальных оценок и
проверки статистических гипотез. При этом используется таблица критических
точек  - распределения.
- распределения.
4. Распределение Стьюдента(t -
распределение)
Пусть
СВ 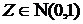 , СВ
, СВ  -
независимая от Z величина, имеющая распределение
-
независимая от Z величина, имеющая распределение  .
.
Тогда
величина  имеет распределение Стьюдента (t -
распределение) с n степенями свободы (записывают T ~
имеет распределение Стьюдента (t -
распределение) с n степенями свободы (записывают T ~ 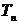 ).
).
Распределение
Стьюдента определяется только одним параметром n - числом
степеней свободы.
График
функции плотности вероятности распределения Стьюдента имеет симметричный относительно
оси ординат колоколообразный вид.

При
увеличении числа степеней свободы распределение приближается к
стандартизированному нормальному. При 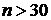 распределение
Стьюдента практически можно заменить нормальным распределением.
распределение
Стьюдента практически можно заменить нормальным распределением.
t -
распределение применяется для нахождения интервальных оценок, а также при
проверке статистических гипотез. При этом используется таблица критических
точек распределения Стьюдента.
5. Распределение Фишера (F -
распределение)
Пусть
V и W - независимые СВ, имеющие  - распределение (V ~
- распределение (V ~ 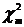 , W ~
, W ~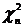 ).
).
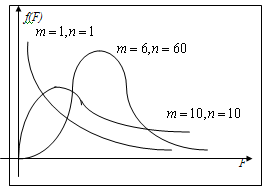
Тогда
СВ 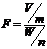 имеет
распределение Фишера (F - распределение) со степенями свободы m и n
(записывают F~
имеет
распределение Фишера (F - распределение) со степенями свободы m и n
(записывают F~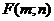 .
.
Оно определяется двумя параметрами m и n.
При
больших m и n оно приближается к нормальному. А также 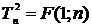 .
.
Таблица
критических значений t-критерия Стьюдента
( - число степеней свободы)
- число степеней свободы)
|
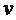 Уровень значимости- Уровень значимости-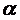 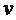 Уровень
значимости- Уровень
значимости-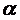
|
|
|
|
|
0,1
|
0,05
|
0,01
|
0,001
|
|
0,1
|
0,05
|
0,01
|
0,001
|
|
1
|
6,314
|
12,71
|
63,657
|
636,62
|
23
|
1,714
|
2,069
|
2,807
|
3,768
|
|
2
|
2,920
|
4,303
|
9,925
|
31,599
|
24
|
1,711
|
2,064
|
2,797
|
3,745
|
|
3
|
2,353
|
3,182
|
5,841
|
12,924
|
25
|
1,708
|
2,060
|
2,787
|
3,725
|
|
4
|
2,132
|
2,776
|
4,604
|
8,610
|
26
|
1,706
|
2,056
|
2,779
|
3,707
|
|
5
|
2,015
|
2,571
|
4,032
|
6,869
|
27
|
1,703
|
2,052
|
2,771
|
3,690
|
|
6
|
1,943
|
2,447
|
3,707
|
5,959
|
1,701
|
2,048
|
2,763
|
3,674
|
|
7
|
1,895
|
2,365
|
3,499
|
5,408
|
29
|
1,699
|
2,045
|
2,756
|
3,656
|
|
8
|
1,860
|
2,306
|
3,355
|
5,040
|
30
|
1,697
|
2,042
|
2,750
|
3,646
|
|
9
|
1,833
|
2,262
|
3,250
|
4,781
|
35
|
1,689
|
2,031
|
2,726
|
3,598
|
|
10
|
1,812
|
2,228
|
3,169
|
4,587
|
40
|
1,684
|
2,021
|
2,704
|
3,554
|
|
11
|
1,796
|
2,201
|
3,106
|
4,437
|
45
|
1,680
|
2,014
|
2,690
|
3,527
|
|
12
|
1,782
|
2,179
|
3,055
|
4,318
|
50
|
1,676
|
2,009
|
2,678
|
3,505
|
|
13
|
1,771
|
2,160
|
3,012
|
4,221
|
60
|
1,670
|
2,000
|
2,660
|
3,505
|
|
14
|
1,761
|
2,145
|
2,977
|
4,140
|
70
|
1,664
|
1,994
|
2,649
|
3,458
|
|
15
|
1,753
|
2,131
|
2,947
|
4,073
|
80
|
1,662
|
1,990
|
2,639
|
3,416
|
|
16
|
1,746
|
2,120
|
2,921
|
4,015
|
90
|
1,661
|
1,987
|
2,632
|
3,402
|
|
17
|
1,740
|
2,110
|
2,898
|
3,965
|
100
|
1,660
|
1,984
|
2,626
|
3,391
|
|
18
|
1,734
|
2,101
|
2,878
|
3,922
|
120
|
1,658
|
1,980
|
2,617
|
3,373
|
|
19
|
1,729
|
2,093
|
2,861
|
3,883
|
150
|
1,656
|
1,978
|
2,612
|
3,359
|
|
20
|
1,725
|
2,086
|
2,845
|
3,850
|
200
|
1,653
|
1,972
|
2,501
|
3,340
|
|
21
|
1,721
|
2,080
|
2,831
|
3,819
|
500
|
1,648
|
1,965
|
2,586
|
3,210
|
|
22
|
1,717
|
2,074
|
2,819
|
3,792
|
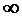 1,6451,9602,5803,291 1,6451,9602,5803,291
|
|
|
|
|
Таблица
значений 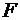 -критерия Фишера при уровне значимости
-критерия Фишера при уровне значимости 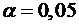
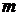
|
 12345681224 12345681224
|
|
|
|
|
|
|
|
|
|
|
|
1
|
161,5
|
199,5
|
215,7
|
224,6
|
230,2
|
233,9
|
238,9
|
243,9
|
249,0
|
254,3
|
|
2
|
18,51
|
19,00
|
19,16
|
19,25
|
19,30
|
19,33
|
19,37
|
19,41
|
19,45
|
19,50
|
|
3
|
10,13
|
9,55
|
9,28
|
9,12
|
9,01
|
8,94
|
8,84
|
8,74
|
8,64
|
8,53
|
|
4
|
7,71
|
6,94
|
6,59
|
6,39
|
6,26
|
6,16
|
6,04
|
5,91
|
5,77
|
5,63
|
|
5
|
6,61
|
5,79
|
5,41
|
5,19
|
5,05
|
4,95
|
4,82
|
4,68
|
4,53
|
4,36
|
|
6
|
5,99
|
5,14
|
4,76
|
4,53
|
4,39
|
4,28
|
4,15
|
4,00
|
3,84
|
3,67
|
|
7
|
5,59
|
4,74
|
4,35
|
4,12
|
3,97
|
3,87
|
3,73
|
3,57
|
3,41
|
3,23
|
|
8
|
5,32
|
4,46
|
4,07
|
3,84
|
3,69
|
3,58
|
3,44
|
3,28
|
3,12
|
2,93
|
|
9
|
5,12
|
4,26
|
3,86
|
3,63
|
3,48
|
3,37
|
3,23
|
3,07
|
2,90
|
2,71
|
|
10
|
4,96
|
4,10
|
3,71
|
3,48
|
3,33
|
3,22
|
3,07
|
2,91
|
2,74
|
2,54
|
|
11
|
4,84
|
3,98
|
3,59
|
3,36
|
3,20
|
3,09
|
2,95
|
2,79
|
2,61
|
2,40
|
|
12
|
4,75
|
3,88
|
3,49
|
3,26
|
3,11
|
3,00
|
2,85
|
2,69
|
2,50
|
2,30
|
|
13
|
4,67
|
3,80
|
3,41
|
3,18
|
3,02
|
2,92
|
2,77
|
2,60
|
2,42
|
2,21
|
|
14
|
4,60
|
3,74
|
3,34
|
3,11
|
2,96
|
2,85
|
2,70
|
2,53
|
2,35
|
2,13
|
|
15
|
4,54
|
3,68
|
3,29
|
3,06
|
2,90
|
2,79
|
2,64
|
2,48
|
2,29
|
2,07
|
|
16
|
4,49
|
3,63
|
3,24
|
3,01
|
2,85
|
2,74
|
2,59
|
2,42
|
2,24
|
2,01
|
|
17
|
4,45
|
3,59
|
3,20
|
2,96
|
2,81
|
2,70
|
2,55
|
2,38
|
2,19
|
1,96
|
4,41
|
3,55
|
3,16
|
2,93
|
2,77
|
2,66
|
2,51
|
2,34
|
2,15
|
1,92
|
|
19
|
4,38
|
3,52
|
3,13
|
2,90
|
2,74
|
2,63
|
2,48
|
2,31
|
2,11
|
1,88
|
|
20
|
4,35
|
3,49
|
3,10
|
2,87
|
2,71
|
2,60
|
2,45
|
2,28
|
2,08
|
1,84
|
|
21
|
4,32
|
3,47
|
3,07
|
2,84
|
2,68
|
2,57
|
2,42
|
2,25
|
2,05
|
1,81
|
|
22
|
4,30
|
3,44
|
3,05
|
2,82
|
2,66
|
2,55
|
2,40
|
2,23
|
2,03
|
1,78
|
|
23
|
4,28
|
3,42
|
3,03
|
2,80
|
2,64
|
2,53
|
2,38
|
2,20
|
2,00
|
1,76
|
|
24
|
4,26
|
3,40
|
3,01
|
2,78
|
2,62
|
2,51
|
2,36
|
2,18
|
1,98
|
1,73
|
|
25
|
4,24
|
3,38
|
2,99
|
2,76
|
2,60
|
2,49
|
2,34
|
2,16
|
1,96
|
1,71
|
|
26
|
4,22
|
3,37
|
2,98
|
2,74
|
2,59
|
2,47
|
2,32
|
2,15
|
1,95
|
1,69
|
|
27
|
4,21
|
3,35
|
2,96
|
2,73
|
2,57
|
2,46
|
2,30
|
2,13
|
1,93
|
1,67
|
|
28
|
4,20
|
3,34
|
2,95
|
2,71
|
2,56
|
2,44
|
2,29
|
2,12
|
1,91
|
1,65
|
|
29
|
4,18
|
3,33
|
2,93
|
2,70
|
2,54
|
2,43
|
2,28
|
2,10
|
1,90
|
1,64
|
|
30
|
4,17
|
3,32
|
2,92
|
2,69
|
2,53
|
2,42
|
2,27
|
2,09
|
1,89
|
1,62
|
|
35
|
4,12
|
3,26
|
2,87
|
2,64
|
2,48
|
2,37
|
2,22
|
2,04
|
1,83
|
1,57
|
|
40
|
4,08
|
3,23
|
2,84
|
2,61
|
2,45
|
2,34
|
2,18
|
2,00
|
1,79
|
1,51
|
|
45
|
4,06
|
3,21
|
2,81
|
2,58
|
2,42
|
2,31
|
2,15
|
1,97
|
1,76
|
1,48
|
|
50
|
4,03
|
3,18
|
2,79
|
2,56
|
2,40
|
2,29
|
2,13
|
1,95
|
1,74
|
1,44
|
|
60
|
4,00
|
3,15
|
2,76
|
2,52
|
2,37
|
2,25
|
2,10
|
1,92
|
1,70
|
1,39
|
|
70
|
3,98
|
3,13
|
2,74
|
2,50
|
2,35
|
2,23
|
2,07
|
1,89
|
1,67
|
1,35
|
|
80
|
3,96
|
3,11
|
2,72
|
2,49
|
2,33
|
2,21
|
2,06
|
1,88
|
1,65
|
1,31
|
|
90
|
3,95
|
3,10
|
2,71
|
2,47
|
2,32
|
2,20
|
2,04
|
1,86
|
1,64
|
1,28
|
|
100
|
3,94
|
3,09
|
2,70
|
2,46
|
2,30
|
2,19
|
2,03
|
1,85
|
1,63
|
1,26
|
|
125
|
3,92
|
3,07
|
2,68
|
2,44
|
2,29
|
2,17
|
2,01
|
1,83
|
1,60
|
1,21
|
|
150
|
3,90
|
3,06
|
2,66
|
2,43
|
2,27
|
2,16
|
2,00
|
1,82
|
1,59
|
1,18
|
|
200
|
3,89
|
3,04
|
2,65
|
2,42
|
2,26
|
2,14
|
1,98
|
1,80
|
1,57
|
1,14
|
|
300
|
3,87
|
3,03
|
2,64
|
2,41
|
2,25
|
2,13
|
1,97
|
1,79
|
1,55
|
1,10
|
|
400
|
3,86
|
3,02
|
2,63
|
2,40
|
2,24
|
2,12
|
1,96
|
1,78
|
1,54
|
1,07
|
|
500
|
3,86
|
3,01
|
2,62
|
2,39
|
2,23
|
2,11
|
1,96
|
1,77
|
1,54
|
1,06
|
|
1000
|
3,85
|
3,00
|
2,61
|
2,38
|
2,22
|
2,10
|
1,95
|
1,76
|
1,53
|
1,03
|
|
 3,842,992,602,372,212,091,941,751,521 3,842,992,602,372,212,091,941,751,521
|
|
|
|
|
|
|
|
|
|
|
2. Базовые понятия статистики
.1 Выборка и генеральная совокупность
При исследовании реальных экономических процессов приходится обрабатывать
большие объёмы экономических данных по разнообразным показателям, которые
являются случайными величинами.
Основная задача математической статистики состоит в создании методов
сбора и обработки экономических данных для получения научных и практических
выводов.
Иногда проводят сплошное обследование, т.е. исследуется каждый объект
изучаемой совокупности относительно признака, которым интересуются.
Однако изучение всей совокупности во многих случаях невозможно
(трудоёмко, дорогостояще и т.п.). Поэтому на практике вся совокупность анализируется
редко, в таких случаях проводят несплошное обследование (наблюдение). К
несплошным относится и выборочное наблюдение.
В теории выборочного наблюдения приняты следующие определения:
Генеральной совокупностью называется множество всех возможных значений
или реализаций исследуемой СВ Х при данном реальном комплексе условий.
Выборочной совокупностью (выборкой) называется часть элементов
генеральной совокупности, отобранная для изучения.
Число элементов совокупности называется её объёмом.
Например, из 1000 деталей отобрано 100 для изучения, тогда объём
ген.совокупности N = 1000, объём
выборки n=100.
Для осуществления выводов о генеральной совокупности используют выборку
ограниченного объёма. Поэтому задача математической статистики - исследование
свойств выборки и обобщение этих свойств на генеральную совокупность.
Полученный при этом вывод называют статистическим.
Выборку называют репрезентативной, если она достаточно точно отражает
изучаемые признаки и параметры генеральной совокупности.
Для репрезентативности выборки важно обеспечить случайность отбора, так,
чтобы все объекты генеральной совокупности имели равные шансы попасть в
выборку.
Для обеспечения репрезентативности выборки применяют следующие способы
отбора:
. Простой случайный отбор - объекты по одному извлекаются из
ген.совокупности. Такой отбор дают обыкновенная лотерея, жеребьёвка,
использование таблиц случайных чисел.
. Механический отбор - вся генеральная ген.совокупность делится на
столько групп, сколько объектов должно войти в выборку, а затем из каждой
группы извлекается и обследуется одна единица.
. Типический отбор - объекты отбирают пропорционально представительству
различных типов объектов в генеральной совокупности. Он нужен для того, чтобы
отразить сложную структуру ген.совокупности. При его проведении
ген.совокупность предварительно подразделяется на качественно однородные
группы, а затем из них производится случайный отбор.
. Серийный отбор - объекты отбирают не по одному, а "сериями",
которые подвергаются сплошному обследованию.
На практике часто применяется комбинированный отбор, при котором
сочетаются выше перечисленные способы.
Выборка может быть повторной, когда объект после изучения возвращается в
генеральную совокупность и могут снова попасть в выборку. И бесповторной, когда
после изучения объект не возвращается в массив.
2.2 Способы представления и обработки экономических данных
Задачей статистического описания выборки является получение такого её
представления, которое позволяет наглядно выявить вероятностные характеристики.
Различают следующие способы упорядочения данных: по возрастанию, по
совпадающим значениям, по интервалам и т.п.
Разность между максимальным и минимальным значениями выборки называется
размахом выборки:
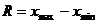 .
.
Пусть
объём выборки равен n, а число различных значений k (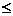 n). Тогда
значения
n). Тогда
значения 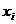 называются вариантами.
называются вариантами.
Если
значение 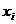 встретилось в выборке
встретилось в выборке  раз, то
число
раз, то
число  называют частотой значения
называют частотой значения 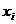 .
.
Отношение
частоты  к объёму выборки
к объёму выборки 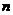 называется
относительной частотой:
называется
относительной частотой:
 .
.
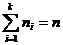 ,
,  .
.
Статистический
ряд наглядно можно представить в виде полигона частот (или полигона
относительных частот) - ломаной линии, отрезки которой соединяют (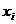 ,
, ) (или (
) (или (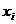 ,
,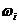 )).
)).
Пример
1. Анализируется прибыль Х предприятий отрасли. Обследованы 100 предприятий.
Данные представлены в виде статистического ряда:
|
Х
|
5
|
10
|
15
|
20
|
25
|
|
 520402510 520402510
|
|
|
|
|
|
|
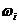 0,050,20,40,250,1 0,050,20,40,250,1
|
|
|
|
|
|
Построить полигон частот.
Решение.
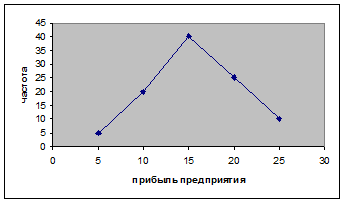
По статистическому ряду можно строить эмпирическую функцию распределения F*(x).
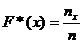 ,
,
где
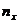 - число значений СВ Х< х,
- число значений СВ Х< х, 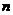 - объём выборки.
- объём выборки.
Свойства
F*(x):
1. 0
≤ 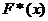 ≤ 1.
≤ 1.
. 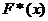 - неубывающая функция, т.е.
- неубывающая функция, т.е. 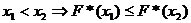 .
.
. 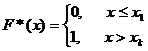 .
.
Эмпирическая
функция распределения является оценкой функции распределения 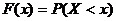 , которая называется теоретической функцией
распределения.
, которая называется теоретической функцией
распределения.
При
большом объёме выборки (или в случае непрерывного признака) её элементы могут
быть сгруппированы в интервальный статистический ряд. Для этого все 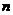 наблюдаемых значений выборки разбиваются на k
непересекающихся интервалов длиной h (- шаг разбиения). И находят
для каждого частичного интервала
наблюдаемых значений выборки разбиваются на k
непересекающихся интервалов длиной h (- шаг разбиения). И находят
для каждого частичного интервала  -
количество наблюдаемых значений СВ Х, попавших в i-й интервал.
-
количество наблюдаемых значений СВ Х, попавших в i-й интервал.  - относительная частота попадания СВ Х в i-й
интервал. Тогда интервальный статистический ряд имеет вид:
- относительная частота попадания СВ Х в i-й
интервал. Тогда интервальный статистический ряд имеет вид:
Интервальный
статистический ряд наглядно может быть представлен в виде гистограммы частот -
столбиковой диаграммы, состоящей из прямоугольников, основаниями которых служат
подынтервалы, а высота равна 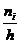 (плотность
частоты). Площадь i-го прямоугольника равна
(плотность
частоты). Площадь i-го прямоугольника равна  , а площадь всей гистограммы частот равна сумме всех
частот, т.е. объёму выборки
, а площадь всей гистограммы частот равна сумме всех
частот, т.е. объёму выборки 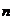 .
.
Для
построения гистограммы относительных частот основание прямоугольника также
равно h, а высота 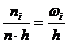 . Площадь
каждого столбика равна
. Площадь
каждого столбика равна 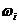 . Площадь всей гистограммы относительных частот равна
. Площадь всей гистограммы относительных частот равна  .
.
На
основании гистограммы обычно выдвигается предположение о виде закона
распределения исследуемой величины.
Пример
2. Анализируется доход населения. Извлечена выборка объёма 300 единиц. По
уровню дохода население подразделяется на 6 групп. Данные сгруппированы в
интервальный статистический ряд:
Построить гистограмму относительных частот.
Решение. Шаг h = 20. Разделив относительные частоты
на шаг разбиения, получим высоту столбиков.
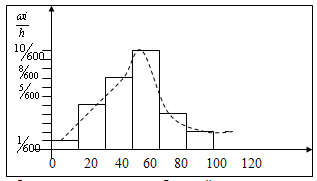
Форма гистограммы в наибольшей степени соответствует нормальному
распределению.
2.3 Статистические оценки параметров распределения
Статистической оценкой неизвестного параметра теоретического
распределения (т.е. количественного признака генеральной совокупности) называют
функцию от наблюдаемых случайных величин.
Для того чтобы оценки давали "хорошие" приближения оцениваемых
параметров, они должны удовлетворять определённым требованиям - быть
несмещёнными, состоятельными и эффективными.
Оценка генеральной средней по выборочной средней:
Генеральной
средней 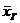 называется среднее арифметическое значений признака
генеральной совокупности:
называется среднее арифметическое значений признака
генеральной совокупности:
 .
.
Если
значения 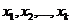 имеют частоты
имеют частоты  (
(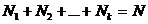 ), то
), то
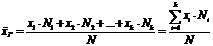 .
.
Выборочной
средней 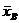 называется среднее арифметическое значений признака
выборочной совокупности:
называется среднее арифметическое значений признака
выборочной совокупности: 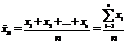 Если значения
Если значения 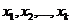 имеют
частоты
имеют
частоты 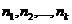 (
(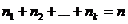 ), то
), то 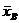
 .
.
Пусть
из генеральной совокупности извлечена повторная выборка объёма n со
значениями 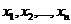 . Пусть
. Пусть 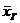 неизвестна
и требуется оценить (т.е. приближённо найти) её значение по данным выборки.
неизвестна
и требуется оценить (т.е. приближённо найти) её значение по данным выборки.
Тогда
в качестве оценки генеральной средней 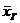 принимают
выборочную среднюю
принимают
выборочную среднюю 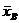 .
.
То
же и для бесповторной выборки.
Оценка
генеральной дисперсии по исправленной выборочной:
Генеральной
дисперсией 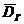 называется среднее арифметическое квадратов
отклонений значений признака генеральной совокупности от их среднего значения
называется среднее арифметическое квадратов
отклонений значений признака генеральной совокупности от их среднего значения 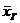 :
:
 или
или 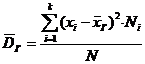
(Если
значения 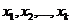 имеют частоты
имеют частоты  (
(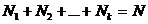 )).
)).
Генеральное
среднее квадратическое отклонение: 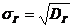 .
.
Выборочной
дисперсией  называется среднее арифметическое квадратов
отклонений наблюдаемых значений признака от их среднего значения
называется среднее арифметическое квадратов
отклонений наблюдаемых значений признака от их среднего значения 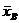 :
:

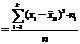 .
. 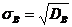 .
.
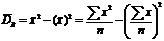 .
.
Пусть
из генеральной совокупности в результате n независимых
наблюдений над количественным признаком Х извлечена выборка объёма n. (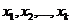 имеют частоты
имеют частоты 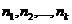 (
(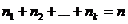 )).
)).
Требуется
по данным выборки оценить неизвестную генеральную дисперсию 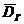 .
.
В
качестве оценки генеральной дисперсии
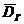 принимают исправленную дисперсию
принимают исправленную дисперсию
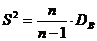
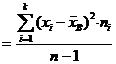 .
.
Для
оценки среднего квадратического отклонения генеральной совокупности используют
исправленное среднее квадратическое отклонение (стандартное отклонение): 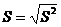 .
.
Выше
рассмотренные оценки - точечные. Они определяются одним числом.
Свойства,
выполнение которых желательно для того, чтобы оценка была признана
удовлетворительной:
1. Несмещенность. Оценка QВ
называется несмещённой оценкой параметра Q, если её математическое ожидание равно оцениваемому
параметру: М(QВ)=Q. Многократное осуществление выборок одинакового объёма
обеспечивает совпадение средненго значения оценки по всем выборкам с истинным
значением параметра. Разность М(QВ)
- Q называется смещением или
систематической ошибкой оценивания. Для несмещённых оценок систематическая
ошибка равна нулю.
. Эффективность. Оценка параметра называется эффективной, если она
имеет наименьшую дисперсию из любой другой альтернативной оценки при
фиксированном объёме выборки. Оценка называется асимптотически эффективной,
если с увеличением объёма выборки её дисперсия стремится к нулю.
. Состоятельность. Оценка называется состоятельной, если она даёт истинное
значение при достаточно большом объёме выборки.
При небольшом объёме выборки точечная оценка может значительно отличаться
от оцениваемого параметра, т.е. приводить к грубым ошибкам. В этом случае
следует пользовать интервальной оценкой.
Интервальной называют оценку, которая определяется 2 числами - концами
интервала. Она позволяет установить точность и надёжность оценок.
Пусть найденная по данным выборки статистическая характеристика QВ- оценка неизвестного параметра Q(=const).
QВ тем точнее определяет Q, чем меньше
модуль разности 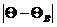 , т.е.
, т.е. 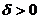 и
и 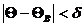 , следовательно, чем меньше
, следовательно, чем меньше 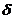 , тем оценка точнее. Т.о. положительное число
, тем оценка точнее. Т.о. положительное число 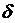 характеризует точность оценок.
характеризует точность оценок.
Однако
статистические методы не позволяют утверждать, что QВ
удовлетворяет неравенству.
Надёжностью
(доверительной вероятностью) оценки Q по QВ
называется вероятность q, с которой осуществляется неравенство 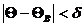 .
.
Обычно
надёжность задаётся заранее, как правило q = 0,95; 0,99
…(близкое к 1). Чем ближе доверительная вероятность к 1, тем надежнее оценка.
Доверительным
называют интервал 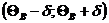 , который покрывает неизвестный параметр Q с заданной надёжностью q.
, который покрывает неизвестный параметр Q с заданной надёжностью q.
.4
Статистическая проверка гипотез
Статистической
называют гипотезу о виде закона распределения или о параметрах известного
распределения. В первом случае гипотеза непараметрическая, во втором -
параметрическая.
Гипотеза Н0, подлежащая проверке, называется нулевой
(основной). Наряду с нулевой рассматривают гипотезуН1, которая будет
приниматься, если отклоняется Н0. Такая гипотеза называется
альтернативной (конкурирующей). Например, если проверяется гипотеза о равенстве
параметра Θ некоторому значению Θ0, т.е. Н0: Θ= Θ0, то в качестве альтернативной могут рассматриваться
следующие гипотезы:
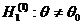 ;
; 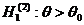 ;
; 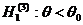 ;
; 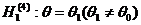 .
.
Выбор
альтернативной гипотезы определяется конкретной формулировкой задачи.
Гипотезу
называют простой, если она содержит одно конкретное предположение. Гипотезу
называют сложной, если она состоит из конечного или бесконечного числа простых
гипотез (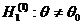 ;
; 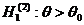 ;
; 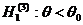 ).
).
Сущность
проверки статистической гипотезы заключается в том, чтобы установить,
согласуются или нет данные наблюдений и выдвинутая гипотеза. Эта задача
решается с помощью специальных методов математической статистики - методов
статической проверки гипотез.
При проверке гипотезы выборочные данные могут противоречить гипотезе Но.
Тогда она отклоняется. Если же статистические данные согласуются с выдвинутой
гипотезой, то она не отклоняется. В последнем случае часто говорят, что нулевая
гипотеза принимается (такая формулировка не совсем точна, однако она широко
распространена). Статистическая проверка гипотез на основании выборочных данных
неизбежно связана с риском принятия ложного решения. При этом возможны ошибки
двух родов.
Ошибка первого рода состоит в том, что будет отвергнута правильная
нулевая гипотеза.
Ошибка второго рода состоит в том, что будет принята нулевая гипотеза, в
то время как в действительности верна альтернативная гипотеза.
Возможные результаты статистических выводов представлены следующей
таблицей:
Таблица
|
Результаты про верки
гипотезы
|
Возможные состояния
гипотезы
|
|
верна Но
|
верна Н1
|
|
Гипотеза Но отклоняется
|
Ошибка первого рода
|
Правильный вывод
|
|
Гипотеза Но не отклоняется
|
Правильный вывод
|
Ошибка второго рода
|
Последствия указанных ошибок неравнозначны. Первая приводит к более
осторожному, консервативному решению, вторая - к неоправданному риску. Что
лучше или хуже - зависит от конкретной постановки задачи и содержания нулевой
гипотезы. Например, если Но состоит в признании продукции предприятия
качественной и допущена ошибка первого рода, то будет забракована годная
продукция. Допустив ошибку второго рода, мы отправим потребителю брак. Очевидно,
последствия второй ошибки более серьезны с точки зрения имиджа фирмы и ее
долгосрочных перспектив.
Исключить ошибки первого и второго рода невозможно в силу ограниченности
выборки. Поэтому стремятся минимизировать потери от этих ошибок. Отметим, что одновременное
уменьшение вероятностей данных ошибок невозможно, так как задачи их уменьшения
являются конкурирующими, и снижение вероятности допустить одну из них влечет за
собой увеличение вероятности допустить другую. В большинстве случаев
единственный способ уменьшения вероятности ошибок состоит в увеличении объема
выборки.
Вероятность совершить ошибку первого рода принято обозначать буквой α,
и ее называют уровнем
значимости. Вероятность совершить ошибку второго рода обозначают β.
Тогда вероятность не совершить
ошибку второго рода (1 - β) называется мощностью критерия.
Обычно значения α задают заранее, "круглыми" числами
(например, 0,1; 0,05; 0,01 и т.п.), а затем стремятся построить критерий
наибольшей мощности. Таким образом, если α = 0,05, то это означает, что исследователь не
хочет совершить ошибку первого рода более чем в 5 случаях из 100.
Проверку статистической гипотезы осуществляют на основании данных
выборки. Для этого используют специально подобранную СВ (статистику, критерий),
точное или приближенное значение которой известно. Эту величину обозначают:
U (или
Z) - если она имеет стандартизированное нормальное распределение;
T -
если она распределена по закону Стьюдента;
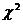 - если
она распределена по закону
- если
она распределена по закону 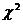 ;- если
она имеет распределение Фишера.
;- если
она имеет распределение Фишера.
В
целях общности будем обозначать такую СВ через К.
Таким
образом, статистическим критерием называют СВ К, которая служит для проверки
нулевой гипотезы. После выбора определенного критерия множество всех его
возможных значений разбивают на два непересекающихся подмножества: одно из них
содержит значения критерия, при которых нулевая гипотеза отклоняется, другое -
при которых она не отклоняется.
Совокупность
значений критерия, при которых нулевую гипотезу отклоняют, называют критической
областью. Совокупность значений критерия, при которых нулевую гипотезу не
отклоняют, называют областью принятия гипотезы.
Основной
принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое
значение критерия К (вычисленное по выборке) принадлежит критической области,
то нулевую гипотезу отклоняют. Если же наблюдаемое значение критерия К
принадлежит области принятия гипотезы, то нулевую гипотезу не отклоняют
(принимают).
Точки,
разделяющие критическую область и область принятия гипотезы, называют
критическими.
Перейдем
к определению критических точек, а следовательно, и критической области.
В
основу этого определения положен принцип практической невозможности
маловероятных событий (принцип практической уверенности): если вероятность
события А в данном испытании очень мала, то при однократном выполнении
испытания можно быть уверенным в том, что событие А не произойдёт, и в
практической деятельности вести себя так, как будто событие А вообще невозможно.
Этот принцип не может быть доказан математически, но подтверждается всем
практическим опытом человеческой деятельности. Например, отправляясь в
путешествие самолётом, мы не рассчитываем погибнуть в авиационной катастрофе,
хотя некоторая (весьма малая) вероятность такого события существует. Заметим,
что принцип сформулирован лишь "при однократном выполнении
испытания". При многократном повторении испытаний мы уже не можем считать
маловероятное событие А практически невозможным.
Пусть
для проверки нулевой гипотезы Но служит критерий К. Тогда вероятность того, что
СВ К попадет в произвольный интервал 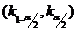 ), можно
найти по формуле:
), можно
найти по формуле: 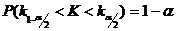 , а
, а 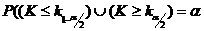 .
.
ададим
вероятность α
настолько малой (0,05; 0,01), чтобы
попадание СВ К за пределы интервала 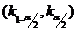 можно
было бы считать маловероятным событием. Тогда, исходя из принципа практической
невозможности маловероятных событий, можно считать, что если Но справедлива, то
при ее проверке с помощью критерия К по данным одной выборки наблюдаемое
значение К должно наверняка попасть в интервал
можно
было бы считать маловероятным событием. Тогда, исходя из принципа практической
невозможности маловероятных событий, можно считать, что если Но справедлива, то
при ее проверке с помощью критерия К по данным одной выборки наблюдаемое
значение К должно наверняка попасть в интервал 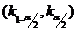 . Если же
наблюдаемое значение К попадает за пределы указанного интервала, то произойдет
маловероятное, практически невозможное событие. Это дает основание считать, что
с вероятностью 1 - α
нулевая гипотеза Н0
несправедлива.
. Если же
наблюдаемое значение К попадает за пределы указанного интервала, то произойдет
маловероятное, практически невозможное событие. Это дает основание считать, что
с вероятностью 1 - α
нулевая гипотеза Н0
несправедлива.
Точки
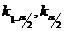 являются критическими.
являются критическими.
Критическая
область  называется двусторонней критической областью. Она
определяется в случае, когда альтернативная гипотеза имеет вид:
называется двусторонней критической областью. Она
определяется в случае, когда альтернативная гипотеза имеет вид:  .
.
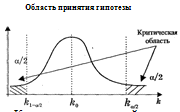
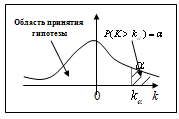
Кроме двусторонней, рассматривают также односторонние критические области
- правостороннюю и левостороннюю.
Правосторонней
называют критическую область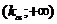 ,
определяемую из соотношения
,
определяемую из соотношения  . Она
используется в случае, когда альтернативная гипотеза имеет вид:
. Она
используется в случае, когда альтернативная гипотеза имеет вид: 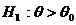 .
.
Левосторонней
называют критическую область  ,
определяемую из соотношения
,
определяемую из соотношения 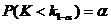 . Она
используется в случае, когда альтернативная гипотеза имеет вид:
. Она
используется в случае, когда альтернативная гипотеза имеет вид: 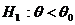 .
.

Общая
схема проверки гипотез:
.
Формулировка проверяемой (нулевой - Но) и альтернативной (Н1)
гипотез.
2.Выбор
соответствующего уровня значимости α.
3.Определение
объема выборки п.
4.Выбор критерия К
для проверки Н0.
5.Определение
критической области и области принятия гипотезы.
6.Вычисление
наблюдаемого значения критерия Кнабл.
7.Принятие
статистического решения.
3. Соотношения между экономическими переменными. Линейная связь.
Корреляция
Различные экономические явления как на микро-, так и на макроуровне не
являются независимыми, а связаны между собой (цена товара и спрос на него,
объём производства и прибыль фирмы и.т.д.).
Эта зависимость может быть строго функциональной (детермированной) и
статистической.
Зависимость
между 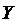 и
и  называется
функциональной, когда каждому значению одного признака соответствует одно
единственное значение другого признака. (Примером такой однозначной зависимости
может служить зависимость площади круга от радиуса).
называется
функциональной, когда каждому значению одного признака соответствует одно
единственное значение другого признака. (Примером такой однозначной зависимости
может служить зависимость площади круга от радиуса).
В
реальной действительности чаще встречается иная связь между явлениями, когда
каждому значению одного признака могут соответствовать несколько значений
другого (например, связь между возрастом детей и их ростом).
Форма
связи, при которой один или несколько взаимосвязанных показателей (факторов)
оказывают влияние на другой показатель (результат) не однозначно, а с
определенной долей вероятности, называется статистической. В частности, если
при изменении одной из величин изменяется среднее значение другой, то в этом
случае статистическую зависимость называют корреляционной.
В
зависимости от числа факторов, включаемых в модель, различают парную корреляцию
(связь двух переменных) и множественную (зависимость результата от нескольких
факторов).
Корреляционный
анализ состоит в определении направления, формы и степени связи
(тесноты) между двумя (несколькими) случайными признаками 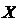 и
и 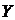 .
.
По
направлению корреляция бывает положительной (прямой), если при увеличении
значений одной переменной увеличивается значение другой, и отрицательной
(обратной), если при увеличении значений одной переменной, уменьшается значение
другой.
По
форме корреляционная связь может быть линейной (прямолинейной), когда изменение
значений одного признака приводит к равномерному изменению другого
(математически описывается уравнением прямой 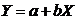 ), и
криволинейной, когда изменение значений одного признака приводит к неодинаковым
изменениям другого (математически она описывается уравнениями кривых линий,
например гиперболы
), и
криволинейной, когда изменение значений одного признака приводит к неодинаковым
изменениям другого (математически она описывается уравнениями кривых линий,
например гиперболы 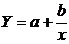 , параболы
, параболы 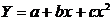 и т.д.).
и т.д.).
Простейшей
формой зависимости между переменными является линейная зависимость. И проверка
наличия такой зависимости, оценивание её индикаторов и параметров является
одним из важнейших направлений эконометрики.
Существуют
специальные статистические методы и, соответственно, показатели, значения
которых определённым образом свидетельствуют о наличии или отсутствии линейной
связи между переменными.
3.1
Коэффициент линейной корреляции
Наиболее
простым, приближенным способом выявления корреляционной связи является
графический.
При
небольшом объеме выборки экспериментальные данные представляют в виде двух
рядов связанных между собой значений 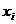 и
и 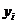 . Если каждую пару
. Если каждую пару  представить
точкой на плоскости
представить
точкой на плоскости  , то получится так называемое корреляционное поле
(рис.1).
, то получится так называемое корреляционное поле
(рис.1).
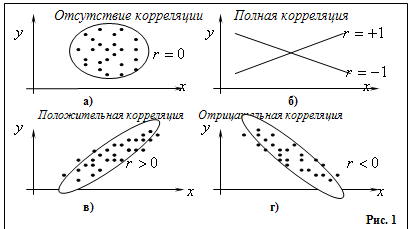
Если
корреляционное поле представляет собой эллипс, ось которого расположена слева
направо и снизу вверх (рис.1в), то можно полагать, что между признаками
существует линейная положительная связь.
Если
корреляционное поле вытянуто вдоль оси слева направо и сверху вниз (рис.1г), то
можно полагать наличие линейной отрицательной связи.
В
случае же если точки наблюдений располагаются на плоскости хаотично, т.е
корреляционное поле образует круг (рис.1а), то это свидетельствует об
отсутствии связи между признаками.
На
рис.1б представлена строгая линейная функциональная связь.
Под
теснотой связи между двумя величинами понимают степень сопряженности между
ними, которая обнаруживается с изменением изучаемых величин. Если каждому
заданному значению 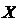 соответствуют близкие друг другу значения
соответствуют близкие друг другу значения 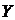 , то связь считается тесной (сильной); если же
значения
, то связь считается тесной (сильной); если же
значения 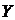 сильно разбросаны, то связь считается менее тесной.
При тесной корреляционной связи корреляционное поле представляет собой более
или менее сжатый эллипс.
сильно разбросаны, то связь считается менее тесной.
При тесной корреляционной связи корреляционное поле представляет собой более
или менее сжатый эллипс.
Количественным
критерием направления и тесноты линейной связи является коэффициент линейной
корреляции.
Коэффициент
корреляции, определяемый по выборочным данным, называется выборочным
коэффициентом корреляции. Он вычисляется по формуле:

где
 ,
,  - текущие значения признаков
- текущие значения признаков 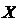 и
и 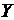 ;
;  и
и 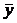 - средние арифметические значения
признаков;
- средние арифметические значения
признаков; 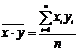 - среднее арифметическое произведений вариант,
- среднее арифметическое произведений вариант,  и
и 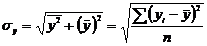 - средние квадратические отклонения этих признаков;
- средние квадратические отклонения этих признаков;  - объём выборки.
- объём выборки.
Для
вычисления коэффициента корреляции достаточно принять предположение о линейной
связи между случайными признаками. Тогда вычисленный коэффициент корреляции и
будет мерой этой линейной связи.
Коэффициент
линейной корреляции принимает значения от −1 в случае строгой линейной
отрицательной связи, до +1 в случае строгой линейной положительной связи (т.е. 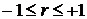 ). Близость коэффициента корреляции к 0
свидетельствует об отсутствии линейной связи между признаками, но не об
отсутствии связи между ними вообще.
). Близость коэффициента корреляции к 0
свидетельствует об отсутствии линейной связи между признаками, но не об
отсутствии связи между ними вообще.
Коэффициенту
корреляции можно дать наглядную графическую интерпретацию.
Если
 , то между признаками существует линейная
функциональная зависимость вида
, то между признаками существует линейная
функциональная зависимость вида  , что
означает полную корреляцию признаков. При
, что
означает полную корреляцию признаков. При  , прямая
имеет положительный наклон по отношению к оси
, прямая
имеет положительный наклон по отношению к оси 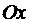 , при
, при 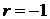 - отрицательный (рис. 1б).
- отрицательный (рис. 1б).
Если
 , точки
, точки  находятся
в области ограниченной линией, напоминающей эллипс. Чем ближе коэффициент
корреляции к
находятся
в области ограниченной линией, напоминающей эллипс. Чем ближе коэффициент
корреляции к 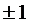 , тем уже эллипс и тем теснее точки сосредоточены
вблизи прямой линии. При
, тем уже эллипс и тем теснее точки сосредоточены
вблизи прямой линии. При 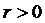 говорят о положительной корреляции. В этом случае
значения
говорят о положительной корреляции. В этом случае
значения 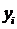 имеют тенденцию к возрастанию с увеличением
имеют тенденцию к возрастанию с увеличением 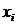 (рис.1в). При
(рис.1в). При 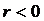 говорят
об отрицательной корреляции; значения
говорят
об отрицательной корреляции; значения  имеют тенденцию
к уменьшению с ростом
имеют тенденцию
к уменьшению с ростом 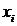 (рис.1г).
(рис.1г).
Если
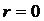 , то точки
, то точки 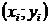 располагаются
в области, ограниченной окружностью. Это означает, что между случайными
признаками
располагаются
в области, ограниченной окружностью. Это означает, что между случайными
признаками  и
и 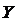 отсутствует
корреляция, и такие признаки называются некоррелированными (рис.1а).
отсутствует
корреляция, и такие признаки называются некоррелированными (рис.1а).
Также
коэффициент линейной корреляции может быть близок (равен) нулю, когда между
признаками есть связь, но она нелинейная (рис.2).
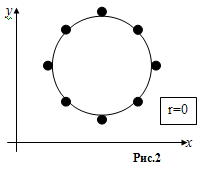
При
оценке тесноты связи можно использовать следующую условную таблицу:
|
Теснота связи
|
Величина коэффициента
корреляции при наличии
|
|
прямой связи (+)
|
обратной связи (−)
|
|
Связь отсутствует
|
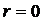 
|
|
|
Связь слабая
|
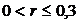 
|
|
|
Связь умеренная
|
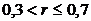 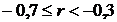
|
|
|
Связь сильная
|
 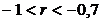
|
|
|
Полная функциональная
|
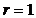 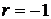
|
|
Заметим,
что в числителе формулы для выборочного коэффициента линейной корреляции
величин 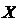 и
и 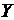 с тоит их
показатель ковариации:
с тоит их
показатель ковариации:

Этот
показатель, как и коэффициент корреляции характеризует степень линейной связи
величин 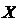 и
и 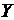 . Если он
больше нуля, то связь между величинами положительная, если меньше нуля, то
связь - отрицательная, равен нулю - линейная связь отсутствует.
. Если он
больше нуля, то связь между величинами положительная, если меньше нуля, то
связь - отрицательная, равен нулю - линейная связь отсутствует.
В
отличие от коэффициента корреляции показатель ковариации нормирован - он имеет
размерность, и его величина зависит от единиц измерения 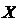 и
и 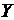 . В
статистическом анализе показатель ковариации обычно используется, как
промежуточный элемент расчёта коэффициента линейной корреляции. Т.о. формула
расчёта выборочного коэффициента корреляции приобретает вид:
. В
статистическом анализе показатель ковариации обычно используется, как
промежуточный элемент расчёта коэффициента линейной корреляции. Т.о. формула
расчёта выборочного коэффициента корреляции приобретает вид:
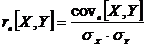
.2 Оценка
значимости (достоверности) коэффициента корреляции
Следует отметить, что истинным показателем степени линейной связи
переменных является теоретический коэффициент корреляции, который
рассчитывается на основании данных всей генеральной совокупности (т.е. всех
возможных значений показателей):
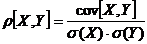 ,
,
где
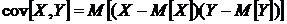 - теоретический показатель ковариции, который
вычисляется как математическое ожидание произведений отклонений СВ
- теоретический показатель ковариции, который
вычисляется как математическое ожидание произведений отклонений СВ 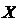 и
и 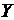 от их
математических ожиданий.
от их
математических ожиданий.
Как
правило, теоретический коэффициент корреляции мы рассчитать не можем. Однако из
того, что выборочный коэффициент не равен нулю 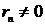 не
следует, что теоретический коэффициент также
не
следует, что теоретический коэффициент также  (т.е.
показатели могут быть линейно независимыми). Т.о. по данным случайной выборки
нельзя утверждать, что связь между показателями существует.
(т.е.
показатели могут быть линейно независимыми). Т.о. по данным случайной выборки
нельзя утверждать, что связь между показателями существует.
Выборочный
коэффициент корреляции является оценкой теоретического коэффициента, т.к. он
рассчитывается лишь для части значений переменных.
Всегда
существует ошибка коэффициента корреляции. Эта ошибка - расхождение между
коэффициентом корреляции выборки объемом 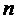 и коэффициентом
корреляции для генеральной совокупности - определяется
формулами:
и коэффициентом
корреляции для генеральной совокупности - определяется
формулами:

при
 ; и
; и  при
при 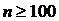 .
.
Проверка значимости коэффициента линейной корреляции означает проверку
того, насколько мы можем доверять выборочным данным.
С
этой целью проверяется нулевая гипотеза  о том,
что значение коэффициента корреляции для генеральной совокупности равно нулю,
т.е. в генеральной совокупности отсутствует корреляция. Альтернативной является
гипотеза
о том,
что значение коэффициента корреляции для генеральной совокупности равно нулю,
т.е. в генеральной совокупности отсутствует корреляция. Альтернативной является
гипотеза 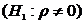 .
.
Для
проверки этой гипотезы рассчитывается  -
статистика (
-
статистика ( -критерий) Стьюдента:
-критерий) Стьюдента:
 .
.
Которая
имеет распределение Стьюдента с  степенями
свободы. По таблицам распределения Стьюдента определяется критическое значение
степенями
свободы. По таблицам распределения Стьюдента определяется критическое значение 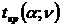 . Если рассчитанное значение критерия
. Если рассчитанное значение критерия 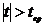 , то нуль-гипотеза отвергается, то есть вычисленный
коэффициент корреляции значимо отличается от нуля с вероятностью
, то нуль-гипотеза отвергается, то есть вычисленный
коэффициент корреляции значимо отличается от нуля с вероятностью 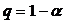 .
.
Если
же 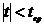 , тогда нулевая гипотеза не может быть отвергнута. В
этом случае не исключается, что истинное значение коэффициента корреляции равно
нулю, т.е. связь показателей можно считать статистически незначимой.
, тогда нулевая гипотеза не может быть отвергнута. В
этом случае не исключается, что истинное значение коэффициента корреляции равно
нулю, т.е. связь показателей можно считать статистически незначимой.
Пример
1. В таблице приведены данные за 8 лет о совокупном доходе  и расходах на конечное потребление
и расходах на конечное потребление 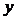 .
.
|
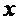 1012111214151720 1012111214151720
|
|
|
|
|
|
|
|
|
|
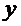 7881011121416 7881011121416
|
|
|
|
|
|
|
|
|
Изучить и измерить тесноту взаимосвязи между заданными показателями.
4. Парная линейная регрессия. Метод наименьших квадратов
Коэффициент корреляции указывает на степень тесноты взаимосвязи между
двумя признаками, но он не дает ответа на вопрос, как изменение одного признака
на одну единицу его размерности влияет на изменение другого признака. Для того
чтобы ответить на этот вопрос, пользуются методами регрессионного анализа.
Регрессионный
анализ устанавливает форму зависимости между случайной величиной 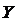 и значениями переменной величины
и значениями переменной величины 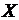 , причем, значения
, причем, значения 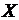 считаются
точно заданными.
считаются
точно заданными.
Уравнение
регрессии - это формула статистической связи между переменными.
Если
эта формула линейна, то речь идет о линейной регрессии. Формула статистической
связи двух переменных называется парной регрессией (нескольких переменных -
множественной).
Выбор
формулы зависимости называется спецификацией уравнения регрессии. Оценка
значений параметров выбранной формулы называется параметризацией.
Как
же оценить значения параметров и проверить надёжность сделанных оценок?
Рассмотрим
рисунок
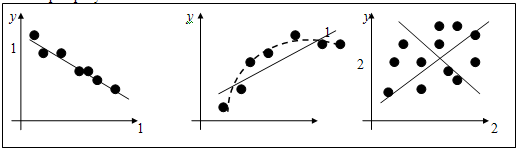
На графике (а) взаимосвязь х и у близка к линейной, прямая линия 1 здесь
близка к точкам наблюдений и последние отклоняются от неё лишь в результате
сравнительно небольших случайных воздействий.
· На графике (б) реальная взаимосвязь величин х и у описывается
нелинейной функцией 2, и какую бы мы ни провели прямую линию (например, 1),
отклонения точек от неё будут неслучайными.
· На графике (в) взаимосвязь между переменными х и у
отсутствует, и результаты параметризации любой формулы зависимости будут
неудачными.
Начальным пунктом эконометрического анализа зависимостей обычно является
оценка линейной зависимости переменных. Всегда можно попытаться провести такую
прямую линию, которая будет "ближайшей" к точкам наблюдений по их
совокупности (например, на рисунке (в) лучшей будет прямая 1, чем прямая 2).
Теоретическое уравнение парной линейной регрессии имеет вид:
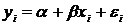 ,
,
где
 называются теоретическими параметрами (теоретическими
коэффициентами) регрессии;
называются теоретическими параметрами (теоретическими
коэффициентами) регрессии; 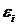 -
случайным отклонением (случайной ошибкой).
-
случайным отклонением (случайной ошибкой).
В
общем виде теоретическую модель будем представлять в виде:
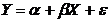 .
.
Для
определения значений теоретических коэффициентов регрессии необходимо знать все
значения переменных Х и Y, т.е. всю генеральную совокупность, что практически
невозможно.
Задача
состоит в следующем: по имеющимся данным наблюдений 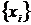 ,
, 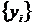 необходимо
оценить значения параметров
необходимо
оценить значения параметров  .
.
Пусть
а - оценка параметра  , b - оценка параметра
, b - оценка параметра  .
.
Тогда
оценённое уравнение регрессии имеет вид: ,
,
где
 теоретические значения зависимой переменной y,
теоретические значения зависимой переменной y, 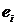 - наблюдаемые значения ошибок
- наблюдаемые значения ошибок 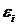 . Это уравнение называется эмпирическим уравнением
регрессии. Будем его записывать в виде
. Это уравнение называется эмпирическим уравнением
регрессии. Будем его записывать в виде 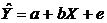 .
.
В
основе оценки параметров линейной регрессии лежит Метод Наименьших Квадратов
(МНК) - это метод оценивания параметров линейной регрессии, минимизирующий
сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной
функции.
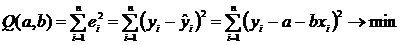 .
.
Функция
Q является квадратичной функцией двух параметров a и b.
Т.к. она непрерывна, выпукла и ограничена снизу (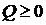 ),
поэтому она достигает минимума. Необходимым условием существования минимума
является равенство нулю её частных производных по a и b:
),
поэтому она достигает минимума. Необходимым условием существования минимума
является равенство нулю её частных производных по a и b:

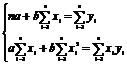 .
.
Разделив
оба уравнения системы на n, получим:
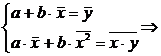
 или
или 
Иначе
можно записать:
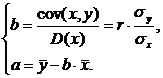
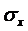 и
и 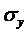 - средние квадратические
отклонения значений тех же признаков.
- средние квадратические
отклонения значений тех же признаков.
Т.о.
линия регрессии проходит через точку со средними значениями х и у 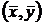 , а коэффициент регрессии b пропорционален
показателю ковариации и коэффициенту линейной корреляции.
, а коэффициент регрессии b пропорционален
показателю ковариации и коэффициенту линейной корреляции.
Если
кроме регрессии Y на X для тех же эмпирических значений найдено уравнение
регрессии X на Y (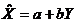 , где
, где 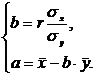 ), то произведение коэффициентов
), то произведение коэффициентов  :
:
 .
.

Коэффициент
регрессии 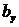 - это величина, показывающая, на
сколько единиц размерности изменится величина
- это величина, показывающая, на
сколько единиц размерности изменится величина 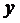 при
изменении величины
при
изменении величины  на одну единицу ее размерности. Аналогично
определяется коэффициент
на одну единицу ее размерности. Аналогично
определяется коэффициент  .
.
Как
и коэффициент корреляции, коэффициент регрессии может принимать и положительные
и отрицательные значения. Например, если коэффициент 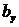 имеет знак "-", то это
означает, что при увеличении значения признака
имеет знак "-", то это
означает, что при увеличении значения признака  на
единицу его размерности значение признака
на
единицу его размерности значение признака 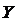 уменьшается
на величину, равную
уменьшается
на величину, равную 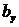 .
.
Уравнения
линейной регрессии являются уравнениями прямых линий в плоскости  , проходящих внутри соответствующего корреляционного
поля. Такие линии называются линиями регрессии.
, проходящих внутри соответствующего корреляционного
поля. Такие линии называются линиями регрессии.
Для
того, чтобы полученные МНК оценки обладали желательными свойствами, сделаем
следующие предпосылки об отклонениях 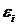 :
:
)
величина 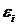 является случайной переменной;
является случайной переменной;
)
математическое ожидание 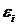 равно нулю:
равно нулю:  ;
;
)
значения 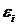 независимы между собой. Откуда вытекает, в частности,
что
независимы между собой. Откуда вытекает, в частности,
что 
)
дисперсия 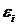 постоянна:
постоянна: 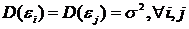 ;
;
)
ошибки 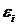 подчиняются нормальному распределению
подчиняются нормальному распределению 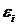 ~
~  (это
условие не является обязательным, но оно необходимо для проверки статистической
значимости найденных оценок и определения для них доверительных интервалов).
(это
условие не является обязательным, но оно необходимо для проверки статистической
значимости найденных оценок и определения для них доверительных интервалов).
Если
условия 1)-4) выполняются, то оценки, сделанные с помощью МНК, обладают
следующими свойствами:
.
Оценки являются несмещёнными (т.е. математическое ожидание каждого параметра
равно его истинному значению  ).
).
.
Оценки состоятельны (дисперсия оценок параметров при возрастании числа
наблюдений стремится к нулю: 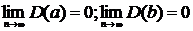 ). Иначе
говоря, надёжность оценки при возрастании выборки растёт. Если n
велико, то почти наверняка a близко к
). Иначе
говоря, надёжность оценки при возрастании выборки растёт. Если n
велико, то почти наверняка a близко к  , а b
близко к
, а b
близко к  .
.
.
Оценки эффективны, они имеют наименьшую дисперсию по сравнению с любыми другими
оценками данного параметра, линейными относительно величин  .
.
Пример
1.
По
данным примера 1 оценить параметры уравнения линейной регрессии.
5.
Оценка качества полученного уравнения (верификация)
Расчёт
значений параметров уравнения регрессии - лишь первый шаг на пути решения
проблемы количественного оценивания зависимости одной переменной от другой
(других) переменных.
Следующим
этапом решения этой проблемы является оценка качества построенного уравнения,
вынесения суждения относительно его отдельных параметров и степени пригодности
в целом.
Анализ
качества оценённой зависимости включает статистическую и содержательную
составляющие. Проверка статистического качества состоит из следующих элементов:
.
Проверка общего качества.
.
Проверка статистической значимости каждого коэффициента уравнения регрессии и
всего уравнения в целом.
.
Проверка предпосылок, лежащих в основе МНК.
Под
содержательной составляющей анализа качества понимается рассмотрение
экономического смысла оценённого уравнения регрессии: действительно ли
значимыми оказались объясняющие факторы, важные с точки зрения теории;
положительны или отрицательны коэффициенты, показывающие направление действия
этих факторов; попали ли оценки коэффициентов регрессии в предполагаемые из
теоретических соображений интервалы.
5.1 Оценка
общего качества уравнения регрессии
Для
анализа общего качества полученного уравнения регрессии на количественном
уровне используют коэффициент детерминации 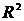 . Он
рассчитывается по формуле:
. Он
рассчитывается по формуле:
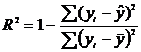 .
.
В
числителе вычитаемой из единицы дроби стоит сумма квадратов отклонений (СКО)
выборочных значений зависимой переменной от теоретических, найденных с помощью
уравнения регрессии 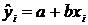 . В знаменателе - СКО наблюдений зависимой переменной
от среднего значения.
. В знаменателе - СКО наблюдений зависимой переменной
от среднего значения.
Коэффициент детерминации характеризует долю вариации
(разброса) зависимой переменной, объяснённой с помощью данного уравнения.
Замечание. В случае парной линейной регрессии коэффициент детерминации
равен квадрату коэффициента линейной корреляции.
Более точным является значение коэффициента детерминации с поправкой на
число степеней свободы.
Разделив каждую СКО на свое число степеней свободы, получим средний
квадрат отклонений, или дисперсию на одну степень свободы:
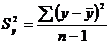 - дисперсия,
характеризующая общий разброс;
- дисперсия,
характеризующая общий разброс;
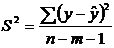 - остаточная
дисперсия, где m - число независимых (объясняющих) переменных, в
случае парной регрессии m =1 и формула имеет вид:
- остаточная
дисперсия, где m - число независимых (объясняющих) переменных, в
случае парной регрессии m =1 и формула имеет вид: 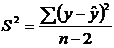 .
.
Учитывая
приведённые выше обозначения, формула коэффициента детерминации с поправкой на
число степеней свободы будет иметь вид:
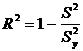 .
.
Значения
коэффициента 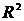 изменяются от 0 до +1 (в редких случаях значение
может быть и отрицательным числом).
изменяются от 0 до +1 (в редких случаях значение
может быть и отрицательным числом).
Близость
коэффициента детерминации к +1 свидетельствует о том, что существует
статистически значимая линейная связь между переменными, а уравнение имеет
хорошее качество.
Близость
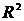 к 0 говорит о том, что просто горизонтальная прямая
к 0 говорит о том, что просто горизонтальная прямая 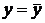 является лучшей по сравнению с найденной
регрессионной прямой.
является лучшей по сравнению с найденной
регрессионной прямой.
Самостоятельную
важность коэффициент детерминации приобретает только в случае множественной
регрессии.
5.2 Оценка существенности параметров линейной регрессии и всего уравнения в целом
После того, как найдено уравнение линейной регрессии, проводится оценка
значимости как уравнения в целом, так и отдельных его параметров.
Проверить значимость уравнения регрессии - значит установить,
соответствует ли математическая модель, выражающая зависимость между
переменными, экспериментальным данным и достаточно ли включённых в уравнение объясняющих
переменных (одной или нескольких) для описания зависимой переменной.
Проверка значимости производится на основе дисперсионного анализа.
Согласно
идее дисперсионного анализа, общая сумма квадратов отклонений (СКО) y от
среднего значения 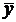 раскладывается на две части - объясненную и
необъясненную:
раскладывается на две части - объясненную и
необъясненную:

или,
соответственно:
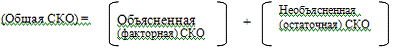
Здесь
возможны два крайних случая: когда общая СКО в точности равна остаточной и
когда общая СКО равна факторной.
В
первом случае фактор х не оказывает влияния на результат, вся дисперсия y
обусловлена воздействием прочих факторов, линия регрессии параллельна оси Ох и
уравнение должно иметь вид 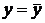 .
.
Во
втором случае прочие факторы не влияют на результат, y связан с x
функционально, и остаточная СКО равна нулю.
Однако
на практике в правой части присутствуют оба слагаемых. Пригодность линии
регрессии для прогноза зависит от того, какая часть общей вариации y
приходится на объясненную вариацию. Если объясненная СКО будет больше
остаточной СКО, то уравнение регрессии статистически значимо и фактор х
оказывает существенное воздействие на результат y. Это
равносильно тому, что коэффициент детерминации будет приближаться к единице.
Число
степеней свободы (df-degrees of freedom)
- это число независимо варьируемых значений признака.
Для
общей СКО требуется (n-1) независимых отклонений,
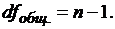
Факторная
СКО имеет одну степень свободы, и 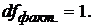
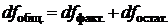
Таким
образом, можем записать: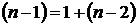
Из
этого баланса определяем, что 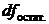 = n-2.
= n-2.
Разделив
каждую СКО на свое число степеней свободы, получим средний квадрат отклонений,
или дисперсию на одну степень свободы: 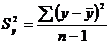 - общая дисперсия,
- общая дисперсия, 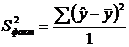 -
факторная,
-
факторная, 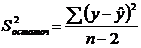 - остаточная.
- остаточная.
Анализ статистической значимости коэффициентов линейной регрессии
Хотя
теоретические значения коэффициентов  уравнения
линейной зависимости
уравнения
линейной зависимости  предполагаются постоянными величинами, оценки а и b
этих коэффициентов, получаемые в ходе построения уравнения по данным случайной
выборки, являются случайными величинами. Если ошибки регрессии имеют нормальное
распределение, то оценки коэффициентов также распределены нормально и могут
характеризоваться своими средними значениями и дисперсией. Поэтому анализ
коэффициентов начинается с расчёта этих характеристик.
предполагаются постоянными величинами, оценки а и b
этих коэффициентов, получаемые в ходе построения уравнения по данным случайной
выборки, являются случайными величинами. Если ошибки регрессии имеют нормальное
распределение, то оценки коэффициентов также распределены нормально и могут
характеризоваться своими средними значениями и дисперсией. Поэтому анализ
коэффициентов начинается с расчёта этих характеристик.
Дисперсии
коэффициентов рассчитываются по формулам:
Дисперсия
коэффициента регрессии 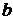 :
:
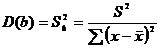 ,
,
где
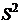 - остаточная дисперсия на одну степень свободы.
- остаточная дисперсия на одну степень свободы.
Дисперсия
параметра 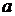 :
:
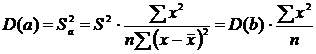
Отсюда
стандартная ошибка коэффициента регрессии 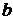 определяется
по формуле:
определяется
по формуле:
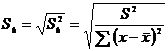 ,
,
Стандартная
ошибка параметра 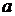 определяется по формуле:
определяется по формуле:
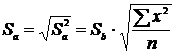 .
.
Далее
рассчитываются t - статистики:
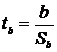 ,
, 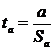
Они
служат для проверки нулевых гипотез о том, что истинное значение коэффициента
регрессии b или свободного члена a равно нулю: 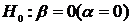 .
.
Альтернативная
гипотеза имеет вид:  .
.
t - статистики
имеют t - распределение Стьюдента с 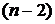 степенями свободы. По таблицам распределения
Стьюдента при определённом уровне значимости α и
степенями свободы. По таблицам распределения
Стьюдента при определённом уровне значимости α и 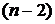 степенях
свободы находят критическое значение
степенях
свободы находят критическое значение 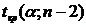 .
.
Если
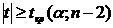 , то нулевая гипотеза должна быть отклонена,
коэффициенты считаются статистически значимыми.
, то нулевая гипотеза должна быть отклонена,
коэффициенты считаются статистически значимыми.
Если
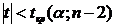 , то нулевая гипотеза не может быть отклонена. (В
случае, если коэффициент b статистически незначим, уравнение должно иметь вид
, то нулевая гипотеза не может быть отклонена. (В
случае, если коэффициент b статистически незначим, уравнение должно иметь вид 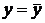 , и это означает, что связь между признаками
отсутствует. В случае, если коэффициент а статистически незначим, рекомендуется
оценить новое уравнение в виде
, и это означает, что связь между признаками
отсутствует. В случае, если коэффициент а статистически незначим, рекомендуется
оценить новое уравнение в виде 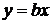 ).
).
Интервальные
оценки коэффициентов линейного уравнения регрессии:
Доверительный
интервал для а:  .
.
Доверительный
интервал для b: 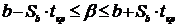
Это
означает, что с заданной надёжностью 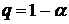 (где
(где  - уровень значимости) истинные значения а, b
находятся в указанных интервалах.
- уровень значимости) истинные значения а, b
находятся в указанных интервалах.
Коэффициент
регрессии имеет четкую экономическую интерпретацию, поэтому доверительные
границы интервала не должны содержать противоречивых результатов, например,  Они не должны включать нуль.
Они не должны включать нуль.
Анализ
статистической значимости уравнения в целом.
Распределение
Фишера в регрессионном анализе
Оценка
значимости уравнения регрессии в целом дается с помощью F-
критерия Фишера. При этом выдвигается нулевая гипотеза 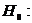 о том, что все коэффициенты регрессии, за исключением
свободного члена а, равны нулю и, следовательно, фактор х не оказывает влияния
на результат y (
о том, что все коэффициенты регрессии, за исключением
свободного члена а, равны нулю и, следовательно, фактор х не оказывает влияния
на результат y (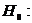
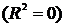 или
или 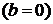 ).
).
Величина F - критерия
связана с коэффициентом детерминации. В случае множественной регрессии:
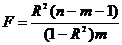 ,
,
где
m - число независимых переменных.
В
случае парной регрессии формула F - статистики
принимает вид:
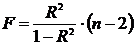 .
.
При
нахождении табличного значения F- критерия задается уровень значимости (обычно 0,05
или 0,01) и две степени свободы: 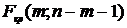 - в
случае множественной регрессии,
- в
случае множественной регрессии,  - для
парной регрессии.
- для
парной регрессии.
Если
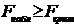 , то
, то 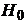 отклоняется
и делается вывод о существенности статистической связи между y и x.
отклоняется
и делается вывод о существенности статистической связи между y и x.
Если
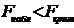 , то вероятность уравнение регрессии считается
статистически незначимым,
, то вероятность уравнение регрессии считается
статистически незначимым, 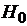 не отклоняется.
не отклоняется.
Замечание.
В парной линейной регрессии 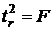 . Кроме
того,
. Кроме
того, 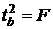 , поэтому
, поэтому 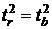 . Таким
образом, проверка гипотез о значимости коэффициентов регрессии и корреляции
равносильна проверке гипотезы о существенности линейного уравнения регрессии.
. Таким
образом, проверка гипотез о значимости коэффициентов регрессии и корреляции
равносильна проверке гипотезы о существенности линейного уравнения регрессии.
Распределение
Фишера может быть использовано не только для проверки гипотезы об одновременном
равенстве нулю всех коэффициентов линейной регрессии, но и гипотезы о равенстве
нулю части этих коэффициентов. Это важно при развитии линейной регрессионной
модели, так как позволяет оценить обоснованность исключения отдельных переменных
или их групп из числа объясняющих переменных, или же, наоборот, включения их в
это число.
Пусть,
например, вначале была оценена множественная линейная регрессия 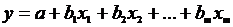 по п наблюдениям с т объясняющими переменными, и
коэффициент детерминации равен
по п наблюдениям с т объясняющими переменными, и
коэффициент детерминации равен 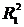 , затем
последние k переменных исключены из числа объясняющих, и по тем
же данным оценено уравнение
, затем
последние k переменных исключены из числа объясняющих, и по тем
же данным оценено уравнение 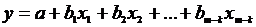 , для
которого коэффициент детерминации равен
, для
которого коэффициент детерминации равен  (
(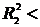
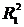 , т.к.
каждая дополнительная переменная объясняет часть , пусть небольшую, вариации
зависимой переменной).
, т.к.
каждая дополнительная переменная объясняет часть , пусть небольшую, вариации
зависимой переменной).
Для
того, чтобы проверить гипотезу об одновременном равенстве нулю всех
коэффициентов при исключённых переменных, рассчитывается величина
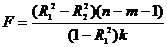 ,
,
имеющая
распределение Фишера с 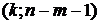 степенями свободы.
степенями свободы.
По
таблицам распределения Фишера, при заданном уровне значимости, находят 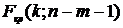 . И если
. И если 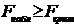 , то
нулевая гипотеза отвергается. В таком случае исключать все k
переменных из уравнения некорректно.
, то
нулевая гипотеза отвергается. В таком случае исключать все k
переменных из уравнения некорректно.
Аналогичные
рассуждения могут быть проведены и по поводу обоснованности включения в
уравнение регрессии одной или нескольких k новых
объясняющих переменных.
В
этом случае рассчитывается F - статистика
 ,
,
имеющая
распределение 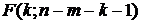 . И если она превышает критический уровень, то
включение новых переменных объясняет существенную часть необъяснённой ранее
дисперсии зависимой переменной (т.е. включение новых объясняющих переменных
оправдано).
. И если она превышает критический уровень, то
включение новых переменных объясняет существенную часть необъяснённой ранее
дисперсии зависимой переменной (т.е. включение новых объясняющих переменных
оправдано).
Замечания.
1. Включать новые переменные целесообразно по одной.
.
Для расчёта F - статистики при рассмотрении вопроса о включении
объясняющих переменных в уравнение желательно рассматривать коэффициент
детерминации с поправкой на число степеней свободы.
Пусть
имеются 2 выборки, содержащие, соответственно,  наблюдений.
Для каждой из этих выборок оценено уравнение регрессии вида
наблюдений.
Для каждой из этих выборок оценено уравнение регрессии вида 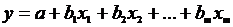 . Пусть СКО
. Пусть СКО  от линии
регрессии (т.е.
от линии
регрессии (т.е.  ) равны для них, соответственно,
) равны для них, соответственно, 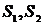 .
.
Проверяется
нулевая гипотеза 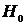 : о том, что все соответствующие коэффициенты этих
уравнений равны друг другу, т.е. уравнение регрессии для этих выборок одно и то
же.
: о том, что все соответствующие коэффициенты этих
уравнений равны друг другу, т.е. уравнение регрессии для этих выборок одно и то
же.
Пусть
оценено уравнение регрессии того же вида сразу для всех  наблюдений, и СКО
наблюдений, и СКО  .
.
Тогда
рассчитывается F - статистика по формуле:
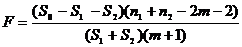
Она
имеет распределение Фишера с  степенями
свободы. F - статистика будет близкой к нулю, если уравнение для
обеих выборок одинаково, т.к. в этом случае
степенями
свободы. F - статистика будет близкой к нулю, если уравнение для
обеих выборок одинаково, т.к. в этом случае 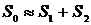 . Т.е.
если
. Т.е.
если 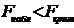
 , то
нулевая гипотеза принимается.
, то
нулевая гипотеза принимается.
Если
же 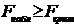 , то нулевая гипотеза отвергается, и единое уравнение
регрессии построить нельзя.
, то нулевая гипотеза отвергается, и единое уравнение
регрессии построить нельзя.
5.3 Проверка предпосылок, лежащих в основе МНК
Следующим этапом оценивания качества уравнения является проверка
выполнения предпосылок, лежащих в основе метода расчёта параметров МНК.
Предпосылками МНК являются:
. случайный характер ошибок регрессии;
. нулевая средняя величина ошибок регрессии, не зависящая от значения
объясняющих переменных;
. независимость распределения ошибок для различных наблюдений; в случае
оценки уравнения на временных рядах - отсутствие автокорреляции ошибок;
. постоянство дисперсии ошибок, её независимость от значений объясняющих
переменных - гомоскедастичность (если эта предпосылка не выполняется, то имеет
место гетероскедастичность ошибок);
. нормальность распределения ошибок регрессии.
Для проверки выполнения каждой из предпосылок применения МНК имеются
специальные тесты. Реализация многих из этих тестов предполагает значительный
объём исходных данных.
Если
распределение случайных ошибок 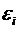 не
соответствует некоторым предпосылкам МНК, то следует корректировать модель.
не
соответствует некоторым предпосылкам МНК, то следует корректировать модель.
Проверка
первой предпосылки МНК
Прежде
всего, проверяется случайный характер остатков 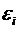 - первая
предпосылка МНК. С этой целью стоится график зависимости остатков
- первая
предпосылка МНК. С этой целью стоится график зависимости остатков 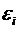 от теоретических значений результативного признака
(рис. 1). Если на графике получена горизонтальная полоса, то остатки
от теоретических значений результативного признака
(рис. 1). Если на графике получена горизонтальная полоса, то остатки  представляют собой случайные величины и МНК оправдан,
теоретические значения
представляют собой случайные величины и МНК оправдан,
теоретические значения  хорошо аппроксимируют фактические значения
хорошо аппроксимируют фактические значения  .
.

Рис.
1. Зависимость случайных остатков  от
теоретических значений
от
теоретических значений  .
.
Возможны
следующие случаи, если  зависит от
зависит от  то:
то:
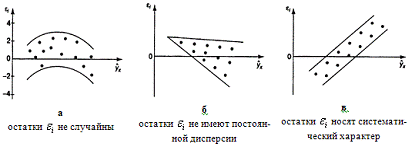
Рис.
2. Зависимость случайных остатков  от
теоретических значений
от
теоретических значений  .
.
В
этих случаях необходимо либо применять другую функцию, либо вводить дополнительную
информацию и заново строить уравнение регрессии до тех пор, пока остатки 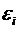 не будут случайными величинами.
не будут случайными величинами.
Проверка
второй предпосылки МНК
Вторая
предпосылка МНК относительно нулевой средней величины остатков означает, что 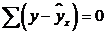 (или
(или 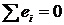 ). Это
выполнимо для линейных моделей и моделей, нелинейных относительно включаемых
переменных.
). Это
выполнимо для линейных моделей и моделей, нелинейных относительно включаемых
переменных.
Вместе
с тем, несмещенность оценок коэффициентов регрессии, полученных МНК, зависит от
независимости случайных остатков и величин 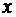 , что
также исследуется в рамках соблюдения второй предпосылки МНК. С этой целью
наряду с изложенным графиком зависимости остатков
, что
также исследуется в рамках соблюдения второй предпосылки МНК. С этой целью
наряду с изложенным графиком зависимости остатков 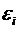 от теоретических значений результативного признака
от теоретических значений результативного признака  строится график зависимости случайных остатков
строится график зависимости случайных остатков 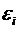 от факторов, включенных в регрессию
от факторов, включенных в регрессию 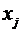 (рис. 3).
(рис. 3).

Рис.
.3. Зависимость величины остатков от величины фактора 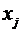 .
.
Если
остатки на графике расположены в виде горизонтальной полосы, то они независимы
от значений 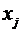 . Если же график показывает наличие зависимости
. Если же график показывает наличие зависимости 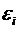 и
и 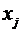 , то
модель неадекватна. Причины неадекватности могут быть разные. Возможно, что
нарушена третья предпосылка МНК и дисперсия остатков не постоянна для каждого
значения фактора
, то
модель неадекватна. Причины неадекватности могут быть разные. Возможно, что
нарушена третья предпосылка МНК и дисперсия остатков не постоянна для каждого
значения фактора 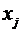 . Может быть неправильна спецификация модели и в нее
необходимо ввести дополнительные члены от
. Может быть неправильна спецификация модели и в нее
необходимо ввести дополнительные члены от 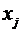 ,
например
,
например 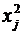 . Скопление точек в определенных участках значений
фактора
. Скопление точек в определенных участках значений
фактора 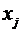 говорит о наличии систематической погрешности модели.
говорит о наличии систематической погрешности модели.
Замечание.
Предпосылка о нормальном распределении остатков (пятая предпосылка) позволяет
проводить проверку параметров регрессии и корреляции с помощью 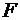 - и
- и  -критериев.
Вместе с тем, оценки регрессии, найденные с применением МНК, обладают хорошими
свойствами даже при отсутствии нормального распределения остатков, т.е. при
нарушении пятой предпосылки МНК.
-критериев.
Вместе с тем, оценки регрессии, найденные с применением МНК, обладают хорошими
свойствами даже при отсутствии нормального распределения остатков, т.е. при
нарушении пятой предпосылки МНК.
Совершенно необходимым для получения по МНК состоятельных оценок
параметров регрессии является соблюдение третьей и четвертой предпосылок.
Автокорреляция ошибок. Статистика Дарбина-Уотсона
Важной
предпосылкой построения качественной регрессионной модели по МНК является
независимость значений случайных отклонений  от
значений отклонений во всех других наблюдениях. Отсутствие зависимости
гарантирует отсутствие коррелированности между любыми отклонениями, т.е.
от
значений отклонений во всех других наблюдениях. Отсутствие зависимости
гарантирует отсутствие коррелированности между любыми отклонениями, т.е. 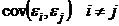 и, в частности, между соседними отклонениями
и, в частности, между соседними отклонениями 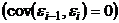 .
.
Автокорреляция
(последовательная корреляция) остатков определяется как корреляция между
соседними значениями случайных отклонений во времени (временные ряды) или в
пространстве (перекрестные данные). Она обычно встречается во временных рядах и
очень редко - в пространственных данных.
Возможны
следующие случаи:
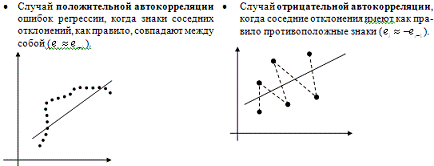
Эти
случаи могут свидетельствовать о возможности улучшить уравнение путём
оценивания новой нелинейной формулы или включения новой объясняющей переменной.
В
экономических задачах значительно чаще встречается положительная
автокорреляция, чем отрицательная автокорреляция.
Если
же характер отклонений случаен, то можно предположить, что в половине случаев
знаки соседних отклонений совпадают, а в половине - различны.
Автокорреляция в остатках может быть вызвана несколькими причинами,
имеющими различную природу.
1. Она может быть связана с исходными данными и вызвана наличием
ошибок измерения в значениях результативного признака.
2. В
ряде случаев автокорреляция может быть следствием неправильной спецификации
модели. Модель может не включать фактор, который оказывает существенное
воздействие на результат и влияние которого отражается в остатках, вследствие
чего последние могут оказаться автокоррелированными. Очень часто этим фактором
является фактор времени 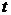 .
.
От истинной автокорреляции остатков следует отличать ситуации, когда
причина автокорреляции заключается в неправильной спецификации функциональной
формы модели. В этом случае следует изменить форму модели, а не использовать
специальные методы расчета параметров уравнения регрессии при наличии
автокорреляции в остатках.
Для обнаружения автокорреляции используют либо графический метод. Либо
статистические тесты.
Графический
метод заключается в построении графика зависимости ошибок от времени (в случае
временных рядов) или от объясняющих переменных и визуальном определении наличия
или отсутствия автокорреляции. Наиболее известный критерий обнаружения автокорреляции
первого порядка - критерий Дарбина-Уотсона. Статистика DW
Дарбина-Уотсона приводится во всех специальных компьютерных программах как одна
из важнейших характеристик качества регрессионной модели. Сначала по
построенному эмпирическому уравнению регрессии определяются значения отклонений
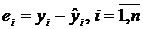 . А затем рассчитывается статистика Дарбина-Уотсона по
формуле:
. А затем рассчитывается статистика Дарбина-Уотсона по
формуле:
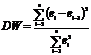 .
.
Статистика
DW изменяется от 0 до 4. DW=0
соответствует положительной автокорреляции, при отрицательной автокорреляции
DW=4. Когда автокорреляция отсутствует,
коэффициент автокорреляции равен нулю, и статистика DW = 2. Алгоритм
выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается
гипотеза  об отсутствии автокорреляции остатков.
Альтернативные гипотезы
об отсутствии автокорреляции остатков.
Альтернативные гипотезы 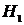 и
и 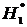 состоят,
соответственно, в наличии положительной или отрицательной автокорреляции в
остатках. Далее по специальным таблицам определяются критические значения
критерия Дарбина-Уотсона
состоят,
соответственно, в наличии положительной или отрицательной автокорреляции в
остатках. Далее по специальным таблицам определяются критические значения
критерия Дарбина-Уотсона  (- нижняя граница признания положительной
автокорреляции) и
(- нижняя граница признания положительной
автокорреляции) и 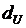 (-верхняя граница признания отсутствия положительной
автокорреляции) для заданного числа наблюдений
(-верхняя граница признания отсутствия положительной
автокорреляции) для заданного числа наблюдений  , числа
независимых переменных модели
, числа
независимых переменных модели 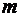 и уровня
значимости
и уровня
значимости  . По этим значениям числовой промежуток
. По этим значениям числовой промежуток 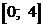 разбивают на пять отрезков. Принятие или отклонение
каждой из гипотез с вероятностью
разбивают на пять отрезков. Принятие или отклонение
каждой из гипотез с вероятностью 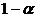 осуществляется
следующим образом:
осуществляется
следующим образом:
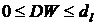 -
положительная автокорреляция, принимается
-
положительная автокорреляция, принимается 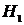 ;
;
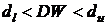 - зона
неопределенности;
- зона
неопределенности;
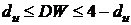 -
автокорреляция отсутствует;
-
автокорреляция отсутствует;
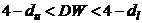 - зона
неопределенности;
- зона
неопределенности;
 -
отрицательная автокорреляция, принимается
-
отрицательная автокорреляция, принимается 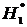 .
.
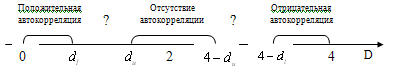
Если
фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности,
то на практике предполагают существование автокорреляции остатков и отклоняют
гипотезу 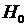 .
.
Можно
показать, что статистика DW тесно связана с коэффициентом автокорреляции первого
порядка:
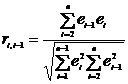
Связь
выражается формулой:
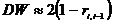 .
.
Значения
r изменяются от -1 (в случае отрицательной
автокорреляции) до +1 (в случае положительной автокорреляции). Близость r к
нулю свидетельствует об отсутствии автокорреляции.
При
отсутствии таблиц критических значений DW можно
использовать следующее "грубое" правило: при достаточном числе
наблюдений (12-15), при 1-3 объясняющих переменных, если  , то отклонения от линии регрессии можно считать
взаимно независимыми.
, то отклонения от линии регрессии можно считать
взаимно независимыми.
Либо
применить к данным уменьшающее автокорреляцию преобразование (например
автокорреляционное преобразование или метод скользящих средних).
Существует несколько ограничений на применение критерия Дарбина-Уотсона.
1. Критерий DW применяется лишь для тех моделей, которые содержат свободный
член.
2. Предполагается, что случайные
отклонения определяются по итерационной схеме
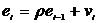 ,
,
называемой
авторегрессионной схемой первого порядка AR(1). Здесь 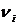 - случайный член.
- случайный член.
1. Статистические данные должны иметь
одинаковую периодичность (не должно быть пропусков в наблюдениях).
2. Критерий Дарбина - Уотсона не
применим к авторегрессионным моделям, которые содержат в числе факторов также
зависимую переменную с временным лагом (запаздыванием) в один период.
Для авторегрессионных моделей предлагается h - статистика Дарбина
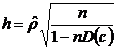 ,
,
где
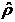 - оценка коэффициента автокорреляции первого порядка,
D(c) - выборочная дисперсия коэффициента при лаговой
переменной yt-1, n -
число наблюдений.
- оценка коэффициента автокорреляции первого порядка,
D(c) - выборочная дисперсия коэффициента при лаговой
переменной yt-1, n -
число наблюдений.
Обычно
значение 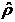 рассчитывается по формуле
рассчитывается по формуле 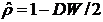 , а D(c) равна квадрату стандартной ошибки Sc оценки коэффициента с.
, а D(c) равна квадрату стандартной ошибки Sc оценки коэффициента с.
Методы
устранения автокорреляции. Авторегрессионное преобразование
В
случае наличия автокорреляции остатков полученная формула регрессии обычно
считается неудовлетворительной. Автокорреляция ошибок первого порядка говорит о
неверной спецификации модели. Поэтому следует попытаться скорректировать саму
модель. Посмотрев на график ошибок, можно поискать другую (нелинейную) формулу
зависимости, включить неучтённые до этого факторы, уточнить период проведения
расчётов или разбить его на части.
Если
все эти способы не помогают и автокорреляция вызвана какими-то внутренними
свойствами ряда {ei}, можно воспользоваться преобразованием, которое
называется авторегрессионной схемой первого порядка AR(1).
(Авторегрессией это преобазование называется потому, что значение ошибки 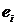 определяется значением той же самой величины, но с
запаздыванием. Т.к. максимальное запаздывание равно 1, то это авторегрессия
первого порядка).
определяется значением той же самой величины, но с
запаздыванием. Т.к. максимальное запаздывание равно 1, то это авторегрессия
первого порядка).
Формула
AR(1) имеет вид:
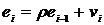 .
.
Где
 -коэффициент автокорреляции первого порядка ошибок
регрессии.
-коэффициент автокорреляции первого порядка ошибок
регрессии.
Рассмотрим
AR(1) на примере парной регрессии:
 .
.
Тогда
соседним наблюдениям соответствует формула:
 (1),
(1),
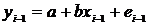 (2).
(2).
Умножим
(2) на  и вычтем из (1):
и вычтем из (1):
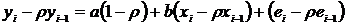 .
.
Сделаем
замены переменных
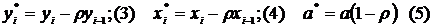
получим
с учетом
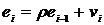 :
:
 (6).
(6).
Это
преобразование называется авторегрессионным (преобразованием Бокса-Дженкинса).
Поскольку
случайные отклонения 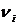 удовлетворяют предпосылкам МНК, оценки а*
и b будут обладать свойствами наилучших линейных
несмещенных оценок. По преобразованным значениям всех переменных с помощью
обычного МНК вычисляются оценки параметров а* и b, которые затем
можно использовать в регрессии.
удовлетворяют предпосылкам МНК, оценки а*
и b будут обладать свойствами наилучших линейных
несмещенных оценок. По преобразованным значениям всех переменных с помощью
обычного МНК вычисляются оценки параметров а* и b, которые затем
можно использовать в регрессии.
Т.о.
если остатки по исходному уравнению регрессии автокоррелированы, то для оценки
параметров уравнения используют следующие преобразования:
)
Преобразовать исходные переменные у и х к виду (3), (4).
)
Обычным МНК для уравнения (6) определить оценки а* и b.
)
Рассчитать параметр а исходного уравнения из соотношения (4)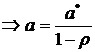 .
.
)
Записать исходное уравнение (1) с параметрами а и b (где а - из
п.3, а b берётся непосредственно из уравнения (6)).
Авторегрессионное
преобразование может быть обобщено на произвольное число объясняющих
переменных, т.е. использовано для уравнения множественной регрессии.
Для
преобразования AR(1) важно оценить коэффициент автокорреляции ρ. Это делается несколькими способами. Самое простое -
оценить ρ на основе статистики DW:
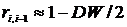 ,
,
где
r берется в качестве оценки ρ. Этот метод хорошо работает при большом числе
наблюдений.
В
случае, когда есть основания считать, что положительная автокорреляция
отклонений очень велика ( ), можно использовать метод первых разностей (метод
исключения тенденции), уравнение принимает вид
), можно использовать метод первых разностей (метод
исключения тенденции), уравнение принимает вид

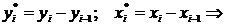
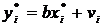 .
.
Из
уравнения по МНК оценивается коэффициент b. Параметр а
здесь не определяется непосредственно, однако из МНК известно, что 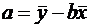 .
.
В
случае полной отрицательной автокорреляции отклонений ( )
)
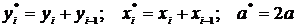 ,
,
получаем
уравнение регрессии:

или
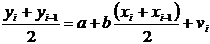 .
.
Вычисляются
средние за 2 периода, а затем по ним рассчитывают а и b. Данная модель
называется моделью регрессии по скользящим средним.
Проверка гомоскедастичности дисперсии ошибок
В
соответствии с четвёртой предпосылкой МНК требуется, чтобы дисперсия остатков
была гомоскедастичной. Это значит, что для каждого значения фактора 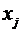 остатки
остатки 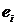 имеют
одинаковую дисперсию
имеют
одинаковую дисперсию 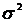 . Если это условие применения МНК не соблюдается, то
имеет место гетероскедастичность.
. Если это условие применения МНК не соблюдается, то
имеет место гетероскедастичность.
В
качестве примера реальной гетероскедастичности можно привести то, что люди с
большим доходом не только тратят в среднем больше, чем люди с меньшим доходом,
но и разброс в их потреблении также больше, поскольку они имеют больше простора
для распределения дохода.
Наличие
гетероскедастичности можно наглядно видеть из поля корреляции (- графический
метод обнаружения гетероскедастичности).

Наличие
гомоскедастичности или гетероскедастичности можно видеть и по рассмотренному
выше графику зависимости остатков 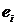 от
теоретических значений результативного признака
от
теоретических значений результативного признака  .
.
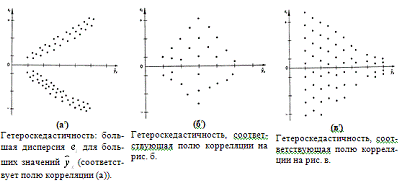
Для множественной регрессии данный вид графиков является наиболее
приемлемым визуальным способом изучения гомо- и гетероскедастичности.
При
нарушении гомоскедастичности имеем неравенства: 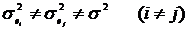 ,
где
,
где 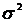 - постоянная дисперсия ошибки при соблюдении
предпосылки. Т.е. можно записать, что дисперсия ошибки при
- постоянная дисперсия ошибки при соблюдении
предпосылки. Т.е. можно записать, что дисперсия ошибки при 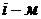 наблюдении пропорциональна постоянной дисперсии:
наблюдении пропорциональна постоянной дисперсии: 
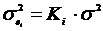 .
.
 -
коэффициент пропорциональности. Он меняется при переходе от одного значения
фактора
-
коэффициент пропорциональности. Он меняется при переходе от одного значения
фактора 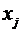 к другому.
к другому.
Задача
состоит в том, чтобы определить величину  и внести
поправку в исходные переменные. При этом используют обобщённый МНК, который
эквивалентен обычному МНК, применённому к преобразованным данным.
и внести
поправку в исходные переменные. При этом используют обобщённый МНК, который
эквивалентен обычному МНК, применённому к преобразованным данным.
Чтобы
убедиться в обоснованности использования обобщённого МНК проводят эмпирическое
подтверждение наличия гетероскедастичности.
При
малом объёме выборки, что наиболее характерно для эмпирических исследований,
для оценки гетероскедастичности может использоваться метод Гольдфельда-Квандта (в
1965 г. они рассмотрели модель парной линейной регрессии, в которой дисперсия
ошибок пропорциональна квадрату фактора).
Пусть рассматривается модель, в которой
дисперсия 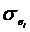 пропорциональна квадрату фактора:
пропорциональна квадрату фактора:  ,
,  . А также
остатки имеют нормальное распределение и отсутствует автокорреляция остатков.
. А также
остатки имеют нормальное распределение и отсутствует автокорреляция остатков.
Параметрический тест (критерий) Гольдфельда - Квандта:
. Все n наблюдений в выборке упорядочиваются
по величине x.
. Вся упорядоченная выборка разбивается на три подвыборки (объёмом k, С,
k.)
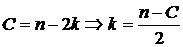 .
.
Исключаются
из рассмотрения С центральных наблюдений. (По рекомендациям специалистов, объём
исключаемых данных С должен быть примерно равен четверти общего объёма выборки
n, в частности, при n =20, С=4; при n =30, С = 8; при n =60, С=16).
.
Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и
для последней подвыборки (k последних наблюдений).
.
Определяются остаточные суммы квадратов 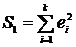 для
первой и второй
для
первой и второй  групп. Если предположение о пропорциональности
дисперсий отклонений значениям x верно, то
групп. Если предположение о пропорциональности
дисперсий отклонений значениям x верно, то 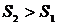 .
.
.
Выдвигается нулевая гипотеза 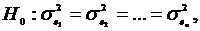 которая
предполагает отсутствие гетероскедастичности.
которая
предполагает отсутствие гетероскедастичности.
Для
проверки этой гипотезы рассчитывается отношение
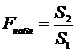 ,
,
которое
имеет распределение Фишера с 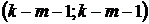 степеней
свободы (здесь m - число объясняющих переменных).
степеней
свободы (здесь m - число объясняющих переменных).
Если
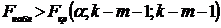 , то гипотеза об отсутствии гетероскедастичности
отклоняется при уровне значимости α.
, то гипотеза об отсутствии гетероскедастичности
отклоняется при уровне значимости α.
Этот
же тест может быть использован и при предположении об обратной
пропорциональности между дисперсией и значениями объясняющей переменной 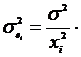 . В этом случае статистика Фишера принимает вид:
. В этом случае статистика Фишера принимает вид:
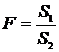 .
.
При
установлении гетероскедастичности возникает необходимость преобразования модели
с целью устранения данного недостатка. Вид преобразования зависит от того,
известны или нет дисперсии отклонений 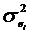 . Обобщенный
метод наименьших квадратов (ОМНК)
. Обобщенный
метод наименьших квадратов (ОМНК)
При нарушении гомоскедастичности и наличии автокорреляции ошибок
рекомендуется традиционный метод наименьших квадратов заменять обобщенным
методом наименьших квадратов (ОМНК).
Обобщенный
метод наименьших квадратов применяется к преобразованным данным и позволяет
получать оценки, которые обладают не только свойством несмещенности, но и имеют
меньшие выборочные дисперсии. Остановимся на использовании ОМНК для
корректировки гетероскедастичности. Рассмотрим ОМНК для корректировки
гетероскедастичности. Будем предполагать, что среднее значение остаточных
величин равно нулю 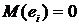 , а дисперсия пропорциональна величине
, а дисперсия пропорциональна величине 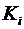 .
.
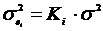 ,
,
где
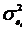 - дисперсия ошибки при конкретном
- дисперсия ошибки при конкретном 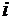 -м значении фактора;
-м значении фактора;  -
постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности
остатков;
-
постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности
остатков; 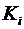 - коэффициент пропорциональности, меняющийся с
изменением величины фактора, что и обусловливает неоднородность дисперсии.
- коэффициент пропорциональности, меняющийся с
изменением величины фактора, что и обусловливает неоднородность дисперсии.
При
этом предполагается, что  неизвестна, а в отношении величин
неизвестна, а в отношении величин 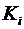 выдвигаются определенные гипотезы, характеризующие
структуру гетероскедастичности.
выдвигаются определенные гипотезы, характеризующие
структуру гетероскедастичности.
В
общем виде для уравнения  модель примет вид:
модель примет вид:
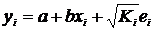 .
.
В
ней остаточные величины гетероскедастичны. Предполагая в них отсутствие
автокорреляции, можно перейти к уравнению с гомоскедастичными остатками,
поделив все переменные, зафиксированные в ходе 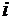 -го
наблюдения, на
-го
наблюдения, на 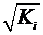 . Тогда дисперсия остатков будет величиной постоянной,
т. е.
. Тогда дисперсия остатков будет величиной постоянной,
т. е. 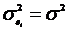 .
.
Иными
словами, от регрессии  по
по 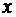 мы
перейдем к регрессии на новых переменных:
мы
перейдем к регрессии на новых переменных: 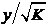 и
и  . Уравнение регрессии примет вид:
. Уравнение регрессии примет вид:
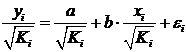 ,
,
а
исходные данные для данного уравнения будут иметь вид:
 ,
,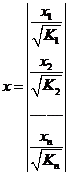 .
.
По
отношению к обычной регрессии уравнение с новыми, преобразованными переменными
представляет собой взвешенную регрессию, в которой переменные  и
и 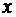 взяты с
весами
взяты с
весами  .
.
Оценка
параметров нового уравнения с преобразованными переменными приводит к
взвешенному методу наименьших квадратов, для которого необходимо минимизировать
сумму квадратов отклонений вида
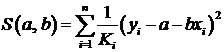 .
.
Соответственно
получим следующую систему нормальных уравнений:
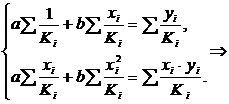
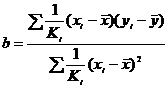 ,
,
Т.е.
коэффициент регрессии 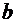 при использовании обобщенного МНК с целью
корректировки гетероскедастичности представляет собой взвешенную величину по
отношению к обычному МНК с весом
при использовании обобщенного МНК с целью
корректировки гетероскедастичности представляет собой взвешенную величину по
отношению к обычному МНК с весом 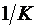 .
.
Если
преобразованные переменные 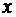 и
и  взять в отклонениях от средних уровней, то
коэффициент регрессии
взять в отклонениях от средних уровней, то
коэффициент регрессии 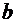 можно определить как
можно определить как
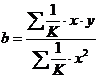 .
.
При
обычном применении метода наименьших квадратов к уравнению линейной регрессии
для переменных в отклонениях от средних уровней коэффициент регрессии 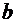 определяется по формуле:
определяется по формуле: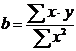 .
.
Аналогичный
подход возможен не только для уравнения парной, но и для множественной
регрессии.
Для
применения ОМНК необходимо знать фактические значения дисперсий отклонений 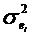 . На практике такие значения известны крайне редко.
Поэтому, чтобы применить ВНК, необходимо сделать реалистические предположения о
значениях
. На практике такие значения известны крайне редко.
Поэтому, чтобы применить ВНК, необходимо сделать реалистические предположения о
значениях 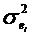 . В эконометрических исследованиях чаще всего
предполагается, что дисперсии отклонений пропорциональны или значениям xi, или значениям
. В эконометрических исследованиях чаще всего
предполагается, что дисперсии отклонений пропорциональны или значениям xi, или значениям  , т.е
, т.е 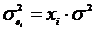 или
или  .
.
Если
предположить, что дисперсии пропорциональны значениям фактора x,
т.е. 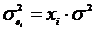 , тогда уравнение парной регрессии
, тогда уравнение парной регрессии  преобразуется делением его левой и правой частей на
преобразуется делением его левой и правой частей на  :
:
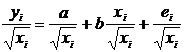
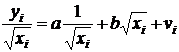 .
.
Здесь
для случайных отклонений  выполняется условие гомоскедастичности.
Следовательно, для регрессии применим обычный МНК. Следует отметить, что новая
регрессия не имеет свободного члена, но зависит от двух факторов. Оценив для
неё по МНК коэффициенты а и b, возвращаемся к исходному уравнению регрессии.
выполняется условие гомоскедастичности.
Следовательно, для регрессии применим обычный МНК. Следует отметить, что новая
регрессия не имеет свободного члена, но зависит от двух факторов. Оценив для
неё по МНК коэффициенты а и b, возвращаемся к исходному уравнению регрессии.
Если
предположить, что дисперсии  , то
соответствующим преобразованием будет деление уравнения парной регрессии
, то
соответствующим преобразованием будет деление уравнения парной регрессии  на xi:
на xi:

или,
если переобозначить остатки как 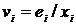 :
:
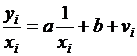 .
.
Здесь
для отклонений vi также выполняется условие гомоскедастичности.
В
полученной регрессии по сравнению с исходным уравнением параметры поменялись
ролями: свободный член а стал коэффициентом, а коэффициент b - свободным
членом. Применяя обычный МНК в преобразованных переменных
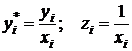 ,
,
получим оценки параметров, после чего возвращаемся к исходному уравнению.
Пример.
Рассматривая зависимость сбережений  от
дохода
от
дохода 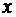 , по первоначальным данным было получено уравнение
регрессии
, по первоначальным данным было получено уравнение
регрессии
 .
.
Применяя
обобщенный МНК к данной модели в предположении, что ошибки пропорциональны
доходу, было получено уравнение для преобразованных данных:
 .
.
Коэффициент
регрессии первого уравнения сравнивают со свободным членом второго уравнения,
т.е. 0,1178 и 0,1026 - оценки параметра 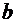 зависимости
сбережений от дохода.
зависимости
сбережений от дохода.
В
случае множественной регрессии 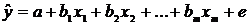 ,
,
Если
предположить 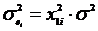 (т.е. дисперсия ошибок пропорциональна квадрату
первой объясняющей переменной), то в этом случае обобщенный МНК предполагает
оценку параметров следующего трансформированного уравнения:
(т.е. дисперсия ошибок пропорциональна квадрату
первой объясняющей переменной), то в этом случае обобщенный МНК предполагает
оценку параметров следующего трансформированного уравнения:
 .
.
Следует иметь в виду, что новые преобразованные переменные получают новое
экономическое содержание и их регрессия имеет иной смысл, чем регрессия по
исходным данным.
Пример.
Пусть  - издержки производства,
- издержки производства,  - объем продукции,
- объем продукции, 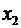 -
основные производственные фонды,
-
основные производственные фонды,  -
численность работников, тогда уравнение
-
численность работников, тогда уравнение

является
моделью издержек производства с объемными факторами. Предполагая, что  пропорциональна квадрату численности работников
пропорциональна квадрату численности работников  , мы получим в качестве результативного признака
затраты на одного работника
, мы получим в качестве результативного признака
затраты на одного работника 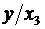 , а в
качестве факторов следующие показатели: производительность труда
, а в
качестве факторов следующие показатели: производительность труда 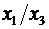 и фондовооруженность труда
и фондовооруженность труда 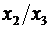 . Соответственно трансформированная модель примет вид
. Соответственно трансформированная модель примет вид
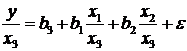 ,
,
где
параметры  ,
, 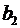 ,
, 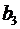 численно не совпадают с аналогичными параметрами
предыдущей модели. Кроме этого, коэффициенты регрессии меняют экономическое
содержание: из показателей силы связи, характеризующих среднее абсолютное
изменение издержек производства с изменением абсолютной величины
соответствующего фактора на единицу, они фиксируют при обобщенном МНК среднее
изменение затрат на работника; с изменением производительности труда на единицу
при неизменном уровне фовдовооруженности труда; и с изменением
фондовооруженности труда на единицу при неизменном уровне производительности
труда.
численно не совпадают с аналогичными параметрами
предыдущей модели. Кроме этого, коэффициенты регрессии меняют экономическое
содержание: из показателей силы связи, характеризующих среднее абсолютное
изменение издержек производства с изменением абсолютной величины
соответствующего фактора на единицу, они фиксируют при обобщенном МНК среднее
изменение затрат на работника; с изменением производительности труда на единицу
при неизменном уровне фовдовооруженности труда; и с изменением
фондовооруженности труда на единицу при неизменном уровне производительности
труда.
Если
предположить, что в модели с первоначальными переменными дисперсия остатков
пропорциональна квадрату объема продукции,  , можно
перейти к уравнению регрессии вида
, можно
перейти к уравнению регрессии вида
 .
.
В
нем новые переменные:  - затраты на единицу (или на 1 руб. продукции),
- затраты на единицу (или на 1 руб. продукции),  - фондоемкость продукции,
- фондоемкость продукции, 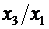 - трудоемкость продукции.
- трудоемкость продукции.
В
заключение следует отметить, что обнаружении гетероскедастичности и её
корректировка являются весьма серьёзной и трудоёмкой проблемой. В случае
применения обобщённого (взвешенного) МНК необходима определённая информация или
обоснованные предположения о величинах 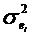 .
.
корреляция линеаризация регрессионный эконометрический
6. Множественная корреляция и линейная регрессия
Значения
экономических переменных обычно определяется влиянием не одного, а нескольких
факторов. Например, спрос на некоторое благо определяется не только ценой
данного блага, но и ценами на замещающие и дополняющие блага, доходом
потребителей и многими другими факторами. В этом случае вместо парной регрессии
рассматривается множественная регрессия  , где
, где  - зависимая переменная (результативный признак),
- зависимая переменная (результативный признак),  - независимые, или объясняющие, переменные
(признаки-факторы).
- независимые, или объясняющие, переменные
(признаки-факторы).
Множественная регрессия широко используется в решении проблем спроса,
доходности акций, при изучении функции издержек производства, в
макроэкономических расчетах и целом ряде других вопросов эконометрики. В
настоящее время множественная регрессия - один из наиболее распространенных
методов в эконометрике. Основная цель множественной регрессии - построить
модель с большим числом факторов, определив при этом влияние каждого из них в
отдельности, а также совокупное их воздействие на моделируемый показатель.
.1 Спецификация модели. Отбор факторов при построении уравнения
множественной регрессии
Построение уравнения множественной регрессии начинается с решения вопроса
о спецификации модели. Он включает в себя два круга вопросов: отбор факторов и
выбор вида уравнения регрессии.
Включение в уравнение множественной регрессии того или иного набора
факторов связано прежде всего с представлением исследователя о природе взаимосвязи
моделируемого показателя с другими экономическими явлениями. Факторы,
включаемые во множественную регрессию, должны отвечать следующим требованиям.
1. Они должны быть количественно измеримы. Если необходимо включить
в модель качественный фактор, не имеющий количественного измерения, то ему
нужно придать количественную определенность.
2. Факторы не должны быть интеркоррелированы (интеркорреляция -
корреляция между объясняющими переменными) и тем более находиться в точной
функциональной связи.
Включение в модель факторов с высокой интеркорреляцией, может привести к
нежелательным последствиям - система нормальных уравнений может оказаться плохо
обусловленной и повлечь за собой неустойчивость и ненадежность оценок
коэффициентов регрессии.
Если между факторами существует высокая корреляция, то нельзя определить
их изолированное влияние на результативный показатель и параметры уравнения
регрессии оказываются неинтерпретируемыми.
Включаемые
во множественную регрессию факторы должны объяснить вариацию независимой
переменной. Если строится модель с набором 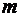 факторов,
то для нее рассчитывается показатель детерминации
факторов,
то для нее рассчитывается показатель детерминации  , который фиксирует долю объясненной вариации
результативного признака за счет рассматриваемых в регрессии
, который фиксирует долю объясненной вариации
результативного признака за счет рассматриваемых в регрессии 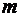 факторов. Влияние других, не учтенных в модели
факторов, оценивается как
факторов. Влияние других, не учтенных в модели
факторов, оценивается как 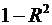 с соответствующей остаточной дисперсией
с соответствующей остаточной дисперсией 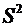 .
.
При
дополнительном включении в регрессию  фактора
коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться:
фактора
коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться:
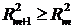 и
и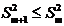 .
.
Если
же этого не происходит и данные показатели практически не отличаются друг от
друга, то включаемый в анализ фактор 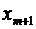 не
улучшает модель и практически является лишним фактором.
не
улучшает модель и практически является лишним фактором.
Насыщение
модели лишними факторами не только не снижает величину остаточной дисперсии и
не увеличивает показатель детерминации, но и приводит к статистической
незначимости параметров регрессии по критерию Стьюдента.
Таким
образом, хотя теоретически регрессионная модель позволяет учесть любое число
факторов, практически в этом нет необходимости. Отбор факторов производится на
основе качественного теоретико-экономического анализа. Однако теоретический
анализ часто не позволяет однозначно ответить на вопрос о количественной
взаимосвязи рассматриваемых признаков и целесообразности включения фактора в
модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой
подбираются факторы исходя из сущности проблемы; на второй - на основе матрицы
показателей корреляции определяют статистики для параметров регрессии.
Коэффициенты
интеркорреляции позволяют исключать из модели дублирующие факторы. Считается,
что две переменные явно коллинеарны, т.е. находятся между собой в линейной
зависимости, если  . Если факторы явно коллинеарны, то они дублируют друг
друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом
отдается не фактору, более тесно связанному с результатом, а тому фактору,
который при достаточно тесной связи с результатом имеет наименьшую тесноту
связи с другими факторами. В этом требовании проявляется специфика
множественной регрессии как метода исследования комплексного воздействия
факторов в условиях их независимости друг от друга.
. Если факторы явно коллинеарны, то они дублируют друг
друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом
отдается не фактору, более тесно связанному с результатом, а тому фактору,
который при достаточно тесной связи с результатом имеет наименьшую тесноту
связи с другими факторами. В этом требовании проявляется специфика
множественной регрессии как метода исследования комплексного воздействия
факторов в условиях их независимости друг от друга.
Пусть,
например, при изучении зависимости  матрица
парных коэффициентов корреляции оказалась следующей:
матрица
парных коэффициентов корреляции оказалась следующей:
Таблица
|
  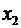 
|
|
|
|
|
 10,80,70,6 10,80,70,6
|
|
|
|
|
|
 0,810,80,5 0,810,80,5
|
|
|
|
|
|
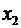 0,70,810,2 0,70,810,2
|
|
|
|
|
|
 0,60,50,21 0,60,50,21
|
|
|
|
|
Очевидно,
что факторы  и
и 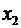 дублируют
друг друга. В анализ целесообразно включить фактор
дублируют
друг друга. В анализ целесообразно включить фактор 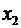 , а не
, а не  , хотя
корреляция
, хотя
корреляция 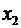 с результатом
с результатом  слабее,
чем корреляция фактора
слабее,
чем корреляция фактора  с
с 
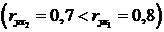 , но зато значительно слабее межфакторная корреляция
, но зато значительно слабее межфакторная корреляция 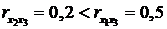 . Поэтому в данном случае в уравнение множественной
регрессии включаются факторы
. Поэтому в данном случае в уравнение множественной
регрессии включаются факторы 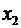 ,
,  .
.
По
величине парных коэффициентов корреляции обнаруживается лишь явная
коллинеарность факторов. Наибольшие трудности в использовании аппарата
множественной регрессии возникают при наличии мультиколлинеарности факторов,
когда более чем два фактора связаны между собой линейной зависимостью, т.е.
имеет место совокупное воздействие факторов друг на друга. Наличие
мультиколлинеарности факторов может означать, что некоторые факторы будут
всегда действовать в унисон. В результате вариация в исходных данных перестает
быть полностью независимой и нельзя оценить воздействие каждого фактора в
отдельности.
Включение
в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:
1. Затрудняется интерпретация параметров множественной регрессии как
характеристик действия факторов в "чистом" виде, ибо факторы
коррелированы; параметры линейной регрессии теряют экономический смысл.
. Оценки параметров ненадежны, обнаруживают большие стандартные
ошибки и меняются с изменением объема наблюдений (не только по величине, но и
по знаку), что делает модель непригодной для анализа и прогнозирования.
Для оценки мультиколлинеарности факторов может использоваться
определитель матрицы парных коэффициентов корреляции между факторами.
Если
бы факторы не коррелировали между собой, то матрица парных коэффициентов
корреляции между факторами была бы единичной матрицей, поскольку все
недиагональные элементы 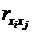
 были бы равны нулю. Так, для уравнения, включающего
три объясняющих переменных
были бы равны нулю. Так, для уравнения, включающего
три объясняющих переменных
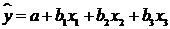
матрица
коэффициентов корреляции между факторами имела бы определитель, равный единице:
 .
.
Если
же, наоборот, между факторами существует полная линейная зависимость и все
коэффициенты корреляции равны единице, то определитель такой матрицы равен
нулю:
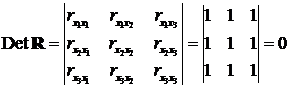 .
.
Чем
ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и ненадежнее результаты множественной регрессии.
И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции,
тем меньше мультиколлинеарность факторов.
Существует
ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь
устранения мультиколлинеарности состоит в исключении из модели одного или
нескольких факторов. Другой подход связан с преобразованием факторов, при
котором уменьшается корреляция между ними.
Одним
из путей учета внутренней корреляции факторов является переход к совмещенным
уравнениям регрессии, т.е. к уравнениям, которые отражают не только влияние
факторов, но и их взаимодействие. Так, если 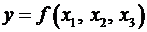 , то
возможно построение следующего совмещенного уравнения:
, то
возможно построение следующего совмещенного уравнения:
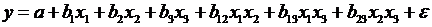 .
.
Рассматриваемое
уравнение включает взаимодействие первого порядка (взаимодействие двух
факторов). Возможно включение в модель и взаимодействий более высокого порядка,
если будет доказана их статистическая значимость по 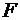 -критерию Фишера, но, как правило, взаимодействия
третьего и более высоких порядков оказываются статистически незначимыми.
-критерию Фишера, но, как правило, взаимодействия
третьего и более высоких порядков оказываются статистически незначимыми.
Отбор факторов, включаемых в регрессию, является одним из важнейших
этапов практического использования методов регрессии. Подходы к отбору факторов
на основе показателей корреляции могут быть разные. Они приводят построение
уравнения множественной регрессии соответственно к разным методикам. В
зависимости от того, какая методика построения уравнения регрессии принята,
меняется алгоритм ее решения на ЭВМ.
Наиболее широкое применение получили следующие методы построения
уравнения множественной регрессии:
1. Метод исключения - отсев факторов из полного его набора.
2. Метод включения - дополнительное введение фактора.
. Шаговый регрессионный анализ - исключение ранее введенного
фактора.
При
отборе факторов также рекомендуется пользоваться следующим правилом: число
включаемых факторов обычно в 6-7 раз меньше объема совокупности, по которой
строится регрессия. Если это соотношение нарушено, то число степеней свободы
остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения
регрессии оказываются статистически незначимыми, а 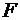 -критерий меньше табличного значения.
-критерий меньше табличного значения.
.2 Метод наименьших квадратов (МНК)
Возможны разные виды уравнений множественной регрессии: линейные и
нелинейные.
Ввиду четкой интерпретации параметров наиболее широко используется
линейная функция. Задача оценки статистической взаимосвязи переменных
формулируется аналогично случаю парной регрессии.
Теоретическое уравнение множественной линейной регрессии имеет вид:
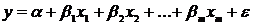 ,
,
где
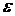 - случайная ошибка,
- случайная ошибка,  -
вектор размерности
-
вектор размерности  .
.
Для
того, чтобы формально можно было решить задачу оценки параметров должно
выполняться условие: объем выборки n должен быть не меньше
количества параметров, т.е. 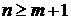 .
.
Если
же это условие не выполняется, то можно найти бесконечно много различных
коэффициентов.
Если
 (например, 3 наблюдения и 2 объясняющие переменные),
то оценки рассчитываются единственным образом без МНК путём решения системы:
(например, 3 наблюдения и 2 объясняющие переменные),
то оценки рассчитываются единственным образом без МНК путём решения системы:
 .
.
Если
же 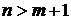 , то необходима оптимизация, т.е. выбрать наилучшую
формулу зависимости. В этом случае разность
, то необходима оптимизация, т.е. выбрать наилучшую
формулу зависимости. В этом случае разность 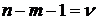 называется
числом степеней свободы. Для получения надежных оценок параметров уравнения
объём выборки должен значительно превышать количество определяемых по нему
параметров. Практически, как было сказано ранее, объём выборки должен превышать
количество параметров при xj в уравнении в 6-7 раз.
называется
числом степеней свободы. Для получения надежных оценок параметров уравнения
объём выборки должен значительно превышать количество определяемых по нему
параметров. Практически, как было сказано ранее, объём выборки должен превышать
количество параметров при xj в уравнении в 6-7 раз.
Задача
построения множественной линейной регрессии состоит в определении  -мерного вектора
-мерного вектора 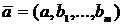 ,
элементы которого есть оценки соответствующих элементов вектора
,
элементы которого есть оценки соответствующих элементов вектора  .
.
Уравнение
с оценёнными параметрами имеет вид:
 ,
,
где
е - оценка отклонения ε.
Параметры при 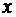 называются коэффициентами "чистой"
регрессии. Они характеризуют среднее изменение результата с изменением
соответствующего фактора на единицу при неизмененном значении других факторов,
закрепленных на среднем уровне.
называются коэффициентами "чистой"
регрессии. Они характеризуют среднее изменение результата с изменением
соответствующего фактора на единицу при неизмененном значении других факторов,
закрепленных на среднем уровне.
Классический
подход к оцениванию параметров линейной модели множественной регрессии основан
на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки
параметров, при которых сумма квадратов отклонений фактических значений
результативного признака  от расчетных
от расчетных 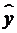 минимальна:
минимальна:
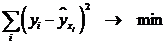 .
.
Как
известно из курса математического анализа, для того чтобы найти экстремум
функции нескольких переменных, надо вычислить частные производные первого
порядка по каждому из параметров и приравнять их к нулю.
Итак,
имеем функцию  аргумента:
аргумента:
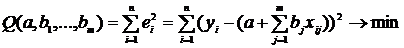
Она
является квадратичной относительно неизвестных величин. Она ограничена снизу,
следовательно имеет минимум. Находим частные производные первого порядка,
приравниваем их к нулю, и получаем систему ( )
уравнения с (
)
уравнения с ( ) неизвестным. Обычно такая система имеет единственное
решение. И называется системой нормальных уравнений:
) неизвестным. Обычно такая система имеет единственное
решение. И называется системой нормальных уравнений:

Решение
может быть осуществлено методом Крамера:
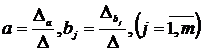 , где
, где
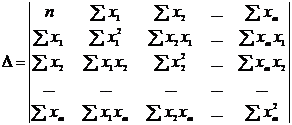 ,
,
а
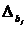 - частные определители, которые получаются из
- частные определители, которые получаются из 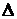 заменой соответствующего j - го столбца
столбцом свободных членов.
заменой соответствующего j - го столбца
столбцом свободных членов.
Для
двухфакторной модели (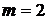 данная система будет иметь вид:
данная система будет иметь вид:
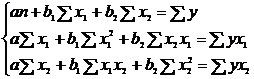
Матричный метод.
Представим данные наблюдений и параметры модели в матричной форме.
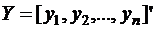 - n -
мерный вектор - столбец наблюдений зависимой переменной;
- n -
мерный вектор - столбец наблюдений зависимой переменной;
 - (m+1)
- мерный вектор - столбец параметров уравнения регрессии;
- (m+1)
- мерный вектор - столбец параметров уравнения регрессии;
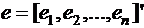 - n -
мерный вектор - столбец отклонений выборочных значений yi от
значений
- n -
мерный вектор - столбец отклонений выборочных значений yi от
значений  , получаемых по уравнению регрессии.
, получаемых по уравнению регрессии.
Для
удобства записи столбцы записаны как строки и поэтому снабжены штрихом для
обозначения операции транспонирования.
Наконец,
значения независимых переменных запишем в виде прямоугольной матрицы
размерности 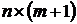 :
:
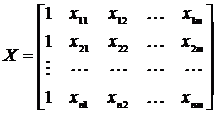
Каждому
столбцу этой матрицы отвечает набор из n значений
одного из факторов, а первый столбец состоит из единиц, которые соответствуют
значениям переменной при свободном члене.
В
этих обозначениях эмпирическое уравнение регрессии выглядит так:
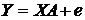 .
.
Где
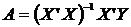 .
.
Здесь
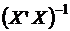 - матрица, обратная к
- матрица, обратная к 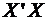 .
.
На основе линейного уравнения множественной регрессии
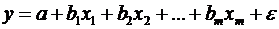
могут
быть найдены частные уравнения регрессии:
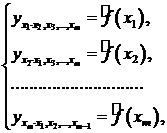
т.е.
уравнения регрессии, которые связывают результативный признак с соответствующим
фактором  при закреплении остальных факторов на среднем уровне.
В развернутом виде систему можно переписать в виде:
при закреплении остальных факторов на среднем уровне.
В развернутом виде систему можно переписать в виде:
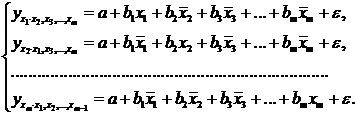
При
подстановке в эти уравнения средних значений соответствующих факторов они
принимают вид парных уравнений линейной регрессии, т.е. имеем
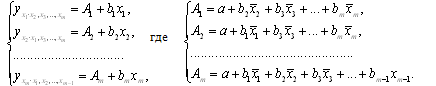
В
отличие от парной регрессии частные уравнения регрессии характеризуют
изолированное влияние фактора на результат, ибо другие факторы закреплены на
неизменном уровне. Эффекты влияния других факторов присоединены в них к
свободному члену уравнения множественной регрессии. Это позволяет на основе
частных уравнений регрессии определять частные коэффициенты эластичности:
 ,
,
где
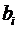 - коэффициент регрессии для фактора
- коэффициент регрессии для фактора  в уравнении множественной регрессии,
в уравнении множественной регрессии, 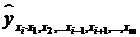 - частное уравнение регрессии.
- частное уравнение регрессии.
Наряду
с частными коэффициентами эластичности могут быть найдены средние по
совокупности показатели эластичности:
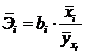 , которые
показывают на сколько процентов в среднем изменится результат, при изменении
соответствующего фактора на 1%. Средние показатели эластичности можно
сравнивать друг с другом и соответственно ранжировать факторы по силе их
воздействия на результат.
, которые
показывают на сколько процентов в среднем изменится результат, при изменении
соответствующего фактора на 1%. Средние показатели эластичности можно
сравнивать друг с другом и соответственно ранжировать факторы по силе их
воздействия на результат.
.3 Анализ качества эмпирического уравнения множественной линейной
регрессии
Проверка статистического качества оцененного уравнения регрессии
проводится, с одной стороны, по статистической значимости параметров уравнения,
а с другой стороны, по общему качеству уравнения регрессии. Кроме этого,
проверяется выполнимость предпосылок МНК.
Как и в случае парной регрессии, для анализа статистической значимости
параметров множественной линейной регрессии с m факторами, необходимо оценить дисперсию и стандартные
отклонения параметров:
Обозначим
матрицу: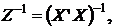
и
в этой матрице обозначим j - й диагональный элемент как 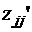 . Тогда выборочная дисперсия эмпирического параметра
регрессии равна:
. Тогда выборочная дисперсия эмпирического параметра
регрессии равна:
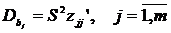 ,
,
а
для свободного члена выражение имеет вид: 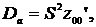
если
считать, что в матрице 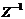 индексы изменяются от 0 до m.
индексы изменяются от 0 до m.
Здесь
S2 -
несмещенная оценка дисперсии случайной ошибки ε (среднеквадратическая ошибка регрессии):
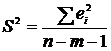 .
.
Соответственно,
стандартные ошибки (отклонения) параметров  регрессии
равны
регрессии
равны
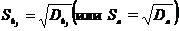 .
.
Для
проверки значимости каждого коэффициента рассчитываются t -
статистики:
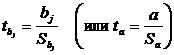 ,
,
Полученная
t - статистика для соответствующего параметра имеет
распределение Стьюдента с числом степеней свободы (n-т-1). При требуемом
уровне значимости α
эта статистика сравнивается с критической
точкой распределения Стьюдента t(α; n-т-1) (двухсторонней).
Если
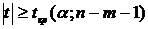 , то соответствующий параметр считается статистически
значимым, и нуль - гипотеза в виде
, то соответствующий параметр считается статистически
значимым, и нуль - гипотеза в виде 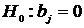 или
или  отвергается.
отвергается.
При
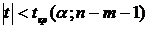 параметр считается статистически незначимым, и нуль -
гипотеза не может быть отвергнута. Поскольку bj не
отличается значимо от нуля, фактор хj линейно
не связан с результатом. Его наличие среди объясняющих переменных не оправдано
со статистической точки зрения. Не оказывая какого-либо серьёзного влияния на
зависимую переменную, он лишь искажает реальную картину взаимосвязи. Поэтому
после установления того факта, что коэффициент bj
статистически незначим, переменную хj рекомендуется
исключить из уравнения регрессии. Это не приведет к существенной потере
качества модели, но сделает её более конкретной.
параметр считается статистически незначимым, и нуль -
гипотеза не может быть отвергнута. Поскольку bj не
отличается значимо от нуля, фактор хj линейно
не связан с результатом. Его наличие среди объясняющих переменных не оправдано
со статистической точки зрения. Не оказывая какого-либо серьёзного влияния на
зависимую переменную, он лишь искажает реальную картину взаимосвязи. Поэтому
после установления того факта, что коэффициент bj
статистически незначим, переменную хj рекомендуется
исключить из уравнения регрессии. Это не приведет к существенной потере
качества модели, но сделает её более конкретной.
Строгую
проверку значимости параметров можно заменить простым сравнительным анализом.
Если
 , т.е.
, т.е. 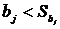 , то
коэффициент статистически незначим.
, то
коэффициент статистически незначим.
Если
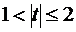 , т.е.
, т.е.  , то
коэффициент относительно значим. В данном случае рекомендуется воспользоваться
таблицей критических точек распределения Стьюдента.
, то
коэффициент относительно значим. В данном случае рекомендуется воспользоваться
таблицей критических точек распределения Стьюдента.
Если
 , то коэффициент значим. Это утверждение является
гарантированным при (n-т-1)>20 и
, то коэффициент значим. Это утверждение является
гарантированным при (n-т-1)>20 и 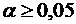 .
.
Если
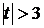 , то коэффициент считается сильно значимым.
Вероятность ошибки в данном случае при достаточном числе наблюдений не
превосходит 0,001.
, то коэффициент считается сильно значимым.
Вероятность ошибки в данном случае при достаточном числе наблюдений не
превосходит 0,001.
К
анализу значимости коэффициента bj можно подойти по - другому. Для этого строится интервальная
оценка соответствующего коэффициента. Если задать уровень значимости α, то доверительный интервал, в который с вероятностью
(1-α)
попадает неизвестное значение параметра 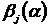 , определяется неравенством:
, определяется неравенством:
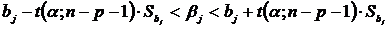
 .
.
Если
доверительный интервал не содержит нулевого значения, то соответствующий
параметр является статистически значимым, в противном случае гипотезу о нулевом
значении параметра отвергать нельзя.
Для
проверки общего качества уравнения регрессии используется коэффициент
детерминации R2. Для
множественной регрессии R2 является
неубывающей функцией числа объясняющих переменных. Добавление новой объясняющей
переменной никогда не уменьшает значение R2. Действительно, каждая следующая объясняющая
переменная может лишь дополнить, но никак не сократить информацию, объясняющую
поведение зависимой переменной.
Анализ
статистической значимости коэффициента детерминации проводится на основе
проверки нуль-гипотезы Н0: R2=0 против альтернативной гипотезы Н1: R2>0. Для проверки данной гипотезы используется
следующая F - статистика.
Задача
1. Бюджетное обследование пяти случайно выбранных семей дало следующие
результаты (в тыс. руб.):
|
Семья
|
Накопления, S
|
Доход, Y
|
Имущество, W
|
|
1
|
3
|
40
|
60
|
|
2
|
6
|
55
|
36
|
|
3
|
5
|
45
|
36
|
|
4
|
3,5
|
30
|
15
|
|
5
|
1,5
|
90
|
А) Оценить регрессию S на Y и W.
Б) Спрогнозируйте накопления семьи, имеющей доход 40 тыс.руб.и имущество
стоимостью 25 тыс.руб.
В) Предположим, что доход семьи вырос на 10 тыс.руб, в то время как
стоимость имущества не изменилась. Оцените как возрастут её накопления.
Г) Оцените как возрастут накопления семьи, если её доход вырос на 5, а
стоимость имущетва увеличилась на 15.
Задача 2. Для изучения жилья в городе по данным о 46 коттеджах было
получено уравнение множественной регрессии:
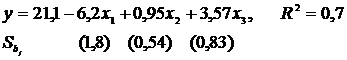
Где
у - цена объекта (тыс.дол), 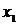 -
расстояние до центра города,
-
расстояние до центра города, 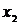 -
полезная площадь объекта (кв.м),
-
полезная площадь объекта (кв.м),  - число
этажей в доме (ед.).
- число
этажей в доме (ед.).
А)
Проверить гипотезы о равенстве нулю коэффициентов  в генеральной совокупности (т.е. проверить значимость
коэффициентов регрессии).
в генеральной совокупности (т.е. проверить значимость
коэффициентов регрессии).
Б)
Проверить гипотезу об одновременном равенстве нулю коэффициентов множественной
регрессии (или о том, что R2=0) в
ген.совокупности.
7. Прогнозирование
.1 Оценка прогнозных качеств модели
Пример 1. Рассмотрим зависимость объёма реального частного потребления в
США (С) от располагаемого дохода Y за
1971-1990 гг:
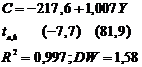
Со
статической точки зрения данная зависимость приемлема по всем показателям.
Стандартная
ошибка регрессии  при среднем значении зависимой переменной
при среднем значении зависимой переменной 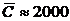 , т.е. составляет около 1%.Отклонения от линии
регрессии носят случайный характер, и их среднее значение остаётся
приблизительно постоянным.
, т.е. составляет около 1%.Отклонения от линии
регрессии носят случайный характер, и их среднее значение остаётся
приблизительно постоянным.
Отношение
стандартной ошибки регрессии к среднему значению зависимой переменной  называется средней относительной ошибкой прогноза, и
может служить критерием прогнозных качеств оценённой регрессионноё модели. Если
величина V мала и отсутствует автокорреляция ошибок (т.е.
систематичность отклонений зависимой переменной от линии регрессии, проверяемая
с помощью статистики Дарбина-Уотсона), то прогнозные качества модели высоки.
называется средней относительной ошибкой прогноза, и
может служить критерием прогнозных качеств оценённой регрессионноё модели. Если
величина V мала и отсутствует автокорреляция ошибок (т.е.
систематичность отклонений зависимой переменной от линии регрессии, проверяемая
с помощью статистики Дарбина-Уотсона), то прогнозные качества модели высоки.
Если
уравнение регрессии используется в прогнозировании, то величина V
часто рассчитывается не для того периода, на котором было построено уравнение,
а для некоторого следующего за ним "постпрогнозного" периода, для
которого имеются наблюдения зависимой и объясняющих переменных.
И
уже для последующего периода, если для него известны прогнозы значений
объясняющих переменных, может быть построен прогноз объясняемой переменной.
Считается, что период прогнозирования должен быть по крайней
мере в 3 раза короче, чем тот период, для которого было оценено уравнение
регрессии. Для
примера, оценим функцию зависимости С от Y за период не 1971-1990гг, а 1971-1986 гг., а затем построим
постпрогноз на период 1987-1990гг. Уравнение регрессии также получается
приемлемое по всем параметрам:
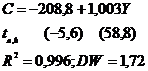
Оценим
прогнозные качества модели, рассчитав среднюю относительную ошибку прогноза V.
Поскольку для постпрогнозного периода число степеней свободы равно числу точек 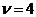 , стандартная ошибка прогноза за 1987-1990гг
рассчитывается как
, стандартная ошибка прогноза за 1987-1990гг
рассчитывается как 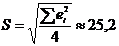 . Относительная ошибка прогноза
. Относительная ошибка прогноза 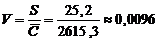 или 0,96%. Если относительную ошибку прогноза оценить
по расчётному периоду 1971-1986гг, то она окажется равной
или 0,96%. Если относительную ошибку прогноза оценить
по расчётному периоду 1971-1986гг, то она окажется равной  или 0,90%, где
или 0,90%, где 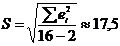 .
.
Т.о.
оценка прогнозных качеств уравнения регрессии даёт хороший результат (менее 1%
ошибки) как на расчётном, так и на контрольном (постпрогнозном) периоде.
Для
построения прогноза объёма потребления С на период после 1990г нужно оценить
уравнение за 1971-1990 г. И подставить в него прогнозируемые значения величины
располагаемого дохода Y.
7.2 Интервалы
прогноза по линейному уравнению регрессии
Прогнозирование
по уравнению регрессии представляет собой подстановку в уравнение регрессии
соответственного значения х. Такой прогноз 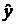 называется
точечным.
называется
точечным.
Он
не является точным, поэтому дополняется расчетом стандартной ошибки 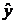 . Стандартная ошибка предсказываемого среднего
значения зависимой переменной при заданном значении
. Стандартная ошибка предсказываемого среднего
значения зависимой переменной при заданном значении 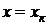 :
:
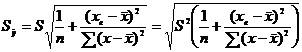
Где
 - стандартная ошибка регрессии,
- стандартная ошибка регрессии,  - остаточная дисперсия.
- остаточная дисперсия.
Величина
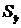 достигает минимума при
достигает минимума при  и
возрастает по мере удаления
и
возрастает по мере удаления 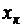 от
от 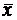 в любом направлении.
в любом направлении.
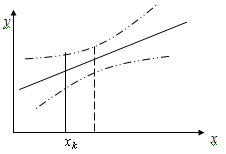
Получаем
интервальную оценку прогнозного значения 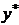 :
:
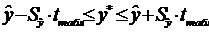
Пример
2: Уравнение зависимости затрат на производство от объёма выпускаемой продукции
по 7 предприятиям имеет вид: 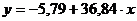 .
.
 ;
; 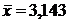 ;
; 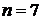 ,
, 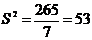 .
.
При
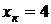 точечный прогноз затрат на производство:
точечный прогноз затрат на производство:

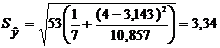 .
.
Для
прогнозируемого значения 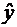 95%-ные доверительные интервалы при заданном
95%-ные доверительные интервалы при заданном 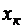 определены выражением:
определены выражением: 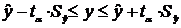 ,
,
т.е.
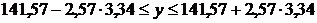 .
.
Т.о.
прогноз линии регрессии лежит в интервале: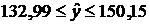 .
.
Мы
рассмотрели доверительные интервалы для среднего значения  при заданном
при заданном 
Однако
фактические значения  варьируются около среднего значения
варьируются около среднего значения  они могут отклоняться на величину случайной ошибки ε, дисперсия которой оценивается как остаточная дисперсия
на одну степень свободы
они могут отклоняться на величину случайной ошибки ε, дисперсия которой оценивается как остаточная дисперсия
на одну степень свободы 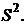 Поэтому ошибка прогноза отдельного значения
Поэтому ошибка прогноза отдельного значения  должна включать не только стандартную ошибку
должна включать не только стандартную ошибку 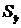 , но и случайную ошибку S. Таким
образом, средняя ошибка прогноза индивидуального значения
, но и случайную ошибку S. Таким
образом, средняя ошибка прогноза индивидуального значения  составит:
составит:
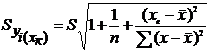
Для примера:

Доверительный
интервал прогноза индивидуальных значений  при
при 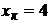 с вероятностью 0,95 составит:
с вероятностью 0,95 составит: 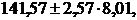 или
или 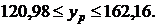
Получился
достаточно большой интервал, т.к. мало наблюдений.
Пусть
в примере с функцией издержек выдвигается предположение, что в предстоящем году
в связи со стабилизацией экономики затраты на производство 8 тыс. ед. продукции
не превысят 250 млн. руб. Означает ли это изменение найденной закономерности
или затраты соответствуют регрессионной модели?
Точечный
прогноз: 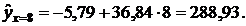
Предполагаемое
значение - 250. Средняя ошибка прогнозного индивидуального значения:

Сравним ее с предполагаемым снижением издержек производства, т.е.
250-288,93= -38,93:
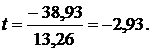
Поскольку
оценивается только значимость уменьшения затрат, то используется односторонний t-
критерий Стьюдента. При ошибке в 5 % с 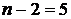
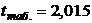 , поэтому предполагаемое уменьшение затрат значимо
отличается от прогнозируемого значения при 95 % - ном уровне доверия. Однако,
если увеличить вероятность до 99%, при ошибке 1 % фактическое значение t-критерия
оказывается ниже табличного 3,365, и различие в затратах статистически не
значимо, т.е. затраты соответствуют предложенной регрессионной модели.
, поэтому предполагаемое уменьшение затрат значимо
отличается от прогнозируемого значения при 95 % - ном уровне доверия. Однако,
если увеличить вероятность до 99%, при ошибке 1 % фактическое значение t-критерия
оказывается ниже табличного 3,365, и различие в затратах статистически не
значимо, т.е. затраты соответствуют предложенной регрессионной модели.
8. Нелинейные модели регрессии. Простейшие методы линеаризации
Если между экономическими явлениями существуют нелинейные соотношения, то
они выражаются с помощью соответствующих нелинейных функций.
Различают два класса нелинейных регрессий:
. Регрессии, нелинейные относительно включенных в анализ объясняющих
переменных, но линейные по оцениваемым параметрам.
Например,
-
полиномы различных степеней - 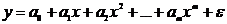 ,
,  ,
, 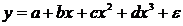 ;
;
равносторонняя
гипербола -  ;
;
полулогарифмическая
функция - 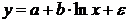 .
.
.
Регрессии, нелинейные по оцениваемым параметрам.
Например,
степенная
- 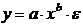 ;
;
показательная
-  ;
;
экспоненциальная
-  .
.
.
Регрессии нелинейные по включенным переменным сводятся к линейному виду с
помощью методов линеаризации простой заменой переменных, а дальнейшая оценка
параметров производится с помощью метода наименьших квадратов. Рассмотрим
некоторые функции.
Полином
второй степени 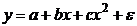 приводится к линейному виду с помощью замены:
приводится к линейному виду с помощью замены: 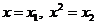 . В результате приходим к двухфакторному уравнению
. В результате приходим к двухфакторному уравнению 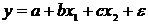 , оценка параметров которого при помощи МНК, приводит
к системе следующих нормальных уравнений:
, оценка параметров которого при помощи МНК, приводит
к системе следующих нормальных уравнений:
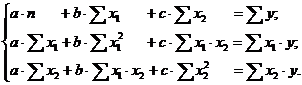
А
после обратной замены переменных получим
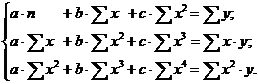
Полином
второй степени обычно применяется в случаях, когда для определенного интервала
значений фактора меняется характер связи рассматриваемых признаков: прямая
связь меняется на обратную или обратная на прямую.
Аналогично,
для полинома третьего порядка получим трёхфакторную модель.
Для
полинома степени m, получим множественную регрессию с m объясняющими
переменными
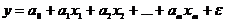 .
.
Среди
нелинейной полиномиальной модели чаще всего используется полином второй
степени, реже - третьей.
Для
равносторонней гиперболы 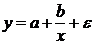 замена
замена 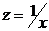 приводит
к уравнению парной линейной регрессии
приводит
к уравнению парной линейной регрессии 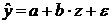 , для
оценки параметров которого используется МНК. Система линейных уравнений при
применении МНК будет выглядеть следующим образом:
, для
оценки параметров которого используется МНК. Система линейных уравнений при
применении МНК будет выглядеть следующим образом:

Такая
модель может быть использована для характеристики связи удельных расходов
сырья, материалов, топлива от объема выпускаемой продукции, времени обращения
товаров от величины товарооборота, процента прироста заработной платы от уровня
безработицы (например, кривая А.В. Филлипса), расходов на непродовольственные
товары от доходов или общей суммы расходов (например, кривые Э. Энгеля) и в
других случаях.
Аналогичным
образом приводятся к линейному виду зависимости 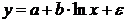 ,
,
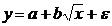 и другие.
и другие.
.
Регрессии, нелинейными по оцениваемым параметрам, делятся на два типа:
нелинейные модели внутренне линейные (приводятся к линейному виду с помощью
соответствующих преобразований, например, логарифмированием) и нелинейные
модели внутренне нелинейные (к линейному виду не приводятся). К внутренне
линейным моделям относятся, например, степенная функция - 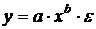 , показательная -
, показательная - 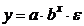 ,
экспоненциальная -
,
экспоненциальная - 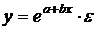 , логистическая -
, логистическая - 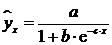 ,
обратная -
,
обратная - 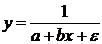 . Среди нелинейных моделей наиболее часто используется
степенная функция
. Среди нелинейных моделей наиболее часто используется
степенная функция 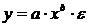 , которая приводится к линейному виду
логарифмированием:
, которая приводится к линейному виду
логарифмированием:
 ;
;
 ;
;
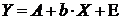 ,
,
где
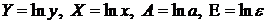 . Т.е. МНК мы применяем для преобразованных данных:
. Т.е. МНК мы применяем для преобразованных данных:
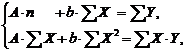
а
затем потенцированием находим искомое уравнение.
Широкое
использование степенной функции связано с тем, что параметр 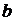 в ней имеет четкое экономическое истолкование - он
является коэффициентом эластичности. (Коэффициент эластичности показывает, на
сколько процентов измениться в среднем результат, если фактор изменится на 1%.)
Формула для расчета коэффициента эластичности имеет вид:
в ней имеет четкое экономическое истолкование - он
является коэффициентом эластичности. (Коэффициент эластичности показывает, на
сколько процентов измениться в среднем результат, если фактор изменится на 1%.)
Формула для расчета коэффициента эластичности имеет вид:
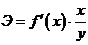 .
.
Так
как для остальных функций коэффициент эластичности не является постоянной
величиной, а зависит от соответствующего значения фактора 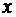 , то обычно рассчитывается средний коэффициент
эластичности:
, то обычно рассчитывается средний коэффициент
эластичности: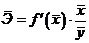 .
.
Наконец,
следует отметить зависимость логистического типа: 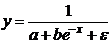 . Графиком функции является так называемая
"кривая насыщения", которая имеет две горизонтальные асимптоты
. Графиком функции является так называемая
"кривая насыщения", которая имеет две горизонтальные асимптоты 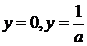 и точку перегиба
и точку перегиба  , а также
точку пересечения с осью ординат
, а также
точку пересечения с осью ординат 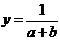 :
:

Уравнение
приводится к линейному виду заменами переменных 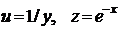 .
.
К
внутренне нелинейным моделям можно, например, отнести следующие модели: 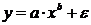 ,
, 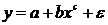 ,
,  .
.
В
случае, когда функция не поддаётся непосредственной линейной линеаризации,
можно разложить её в функциональный ряд и затем оценить регрессию с членами
этого ряда.
При
линеаризации функции или разложении её в ряд возникают и другие проблемы:
искажение отклонений  и нарушение их первоначальных свойств, статистическая
зависимость членов ряда между собой.
и нарушение их первоначальных свойств, статистическая
зависимость членов ряда между собой.
Например,
если оценивается формула  , полученная путём линеаризации или разложения в ряд,
то независимые переменные
, полученная путём линеаризации или разложения в ряд,
то независимые переменные 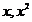 связаны между собой функционально.
связаны между собой функционально.
Поэтому
во многих случаях актуальна непосредственная оценка нелинейной формулы
регрессии. Для этого используется нелинейный МНК, идея которого основана на
минимизации суммы квадратов отклонений расчётных значений от эмпирических, т.е.
нужно оценить параметры вектора а функции 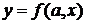 , так
чтобы ошибки
, так
чтобы ошибки  по совокупности были минимальны:
по совокупности были минимальны: .
.
Для
решения этой задачи существуют два пути:
)
непосредственная минимизация функции F с помощью методов нелинейной
оптимизации, позволяющих находить экстремум выпуклых линий (метод наискорейшего
спуска).
)
решение системы нелинейных уравнений, которая получается из необходимого
условия экстремума функции - равенство нулю частных производных по каждому из
параметров:
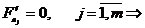 система
уравнений:
система
уравнений:
 .
.
Эта
система может быть решена итерационными методами. Однако в общем случае решение
такой системы не является более простым способом нахождения вектора а.
Существуют
методы оценивания нелинейной регрессии, сочетающие непосредственную
оптимизацию, использующую нахождение градиента, с разложением в ряд Тейлора для
последующей оценки линейной регрессии (метод Марквардта).
При
построении нелинейной регрессии более остро, чем в линейном случае, стоит
проблема правильной оценки формы зависимости между переменными.
Неточности
при выборе формы функции существенно сказываются на качестве отдельных
параметров уравнения и соответственно, на адекватности всей модели в целом.
Любое уравнение нелинейной регрессии, как и линейной зависимости,
дополняется показателем корреляции, который в данном случае называется индексом
корреляции:
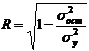
Здесь
 - общая дисперсия результативного признака y,
- общая дисперсия результативного признака y, 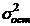 - остаточная дисперсия, определяемая по уравнению
нелинейной регрессии
- остаточная дисперсия, определяемая по уравнению
нелинейной регрессии 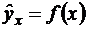 . Следует обратить внимание на то, что разности в
соответствующих суммах
. Следует обратить внимание на то, что разности в
соответствующих суммах  и
и 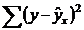 берутся не в преобразованных, а в исходных значениях
результативного признака. Иначе
говоря, при вычислении этих сумм следует использовать не преобразованные
(линеаризованные) зависимости, а именно исходные нелинейные уравнения
регрессии. По-другому можно записать так:
берутся не в преобразованных, а в исходных значениях
результативного признака. Иначе
говоря, при вычислении этих сумм следует использовать не преобразованные
(линеаризованные) зависимости, а именно исходные нелинейные уравнения
регрессии. По-другому можно записать так:
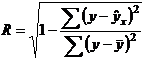
Величина
R находится в границах 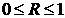 , и чем
ближе она к единице, тем теснее связь рассматриваемых признаков, тем более
надежно найденное уравнение регрессии. При этом индекс корреляции совпадает с
линейным коэффициентом корреляции в случае, когда преобразование переменных с
целью линеаризации уравнения регрессии не проводится с величинами
результативного признака. Так обстоит дело с полулогарифмической и
полиномиальной регрессией, а также с равносторонней гиперболой. Определив
линейный коэффициент корреляции для линеаризованных уравнений, например, в
пакете Excel с помощью функции ЛИНЕЙН, можно использовать его и
для нелинейной зависимости.
, и чем
ближе она к единице, тем теснее связь рассматриваемых признаков, тем более
надежно найденное уравнение регрессии. При этом индекс корреляции совпадает с
линейным коэффициентом корреляции в случае, когда преобразование переменных с
целью линеаризации уравнения регрессии не проводится с величинами
результативного признака. Так обстоит дело с полулогарифмической и
полиномиальной регрессией, а также с равносторонней гиперболой. Определив
линейный коэффициент корреляции для линеаризованных уравнений, например, в
пакете Excel с помощью функции ЛИНЕЙН, можно использовать его и
для нелинейной зависимости.
Иначе
обстоит дело в случае, когда преобразование проводится также с величиной y,
например, взятие обратной величины или логарифмирование. Тогда значение R,
вычисленное той же функцией ЛИНЕЙН, будет относиться к линеаризованному
уравнению регрессии, а не к исходному нелинейному уравнению, и величины
разностей под суммами будут относиться к преобразованным величинам, а не к
исходным, что не одно и то же. При этом, как было сказано выше, для расчета R
следует воспользоваться выражением, вычисленным по исходному нелинейному
уравнению.
Поскольку
в расчете индекса корреляции используется соотношение факторной и общей СКО, то
R2 имеет
тот же смысл, что и коэффициент детерминации. В специальных исследованиях
величину R2 для
нелинейных связей называют индексом детерминации.
Оценка
существенности индекса корреляции проводится так же, как и оценка надежности
коэффициента корреляции.
Индекс
детерминации используется для проверки существенности в целом уравнения
нелинейной регрессии по F-критерию Фишера:
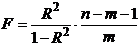 ,
,
где
n-число наблюдений, m-число
параметров при переменных х. Во всех рассмотренных нами случаях, кроме
полиномиальной регрессии, m=1, для полиномов число параметров равно m,
т.е. степени полинома. Величина m характеризует число степеней свободы для факторной
СКО, а (n-m-1) - число степеней свободы для остаточной СКО.
Индекс
детерминации R2 можно
сравнивать с коэффициентом детерминации r2 для обоснования возможности применения линейной
функции. Чем больше кривизна линии регрессии, тем больше разница между R2 и r2.
Близость этих показателей означает, что усложнять форму уравнения регрессии не
следует и можно использовать линейную функцию. Практически, если величина (R2-r2) не
превышает 0,1, то линейная зависимость считается оправданной. В противном
случае проводится оценка существенности различия показателей детерминации,
вычисленных по одним и тем же данным, через t-критерий
Стьюдента: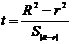 .
.
Здесь
в знаменателе находится ошибка разности (R2-r2),
определяемая по формуле:
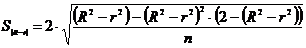
Если
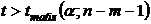 , то различия между показателями корреляции
существенны и замена нелинейной регрессии линейной нецелесообразна.
, то различия между показателями корреляции
существенны и замена нелинейной регрессии линейной нецелесообразна.
В заключение приведем формулы расчета коэффициентов эластичности для
наиболее распространенных уравнений регрессии:
9. Фиктивные
переменные в регрессионных моделях
В регрессионных моделях наряду с количественными переменными часто
используются качественные переменные, такие как профессия, пол, образование,
климатические условия и т.п.
Чтобы ввести такие переменные в регрессионную модель, им должны быть
присвоены те или иные цифровые метки, т.е. качественные переменные должны быть
преобразованы в количественные.
Такого рода переменные в эконометрике называются фиктивными
(структурными, или искусственными) переменными, а также индикатором.
Фиктивные переменные отражают два противоположных состояния качественного
фактора: фактор действует - фактор не действует. (Например, сезон летний -
сезон зимний, пол мужской - женский, есть высшее образование - нет высшего
образования).
В этом случае фиктивные переменные выражаются в двоичной форме:
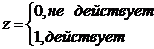 .
(Например, z=0, если потребитель не имеет высшего образования, z=1,
если потребитель имеет высшее образование).
.
(Например, z=0, если потребитель не имеет высшего образования, z=1,
если потребитель имеет высшее образование).
Таким
образом, кроме моделей, содержащих только количественные переменные 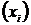 , в регрессионном анализе рассматриваются также
модели, содержащие лишь качественные переменные (обозначаемые zi), либо те и другие одновременно.
, в регрессионном анализе рассматриваются также
модели, содержащие лишь качественные переменные (обозначаемые zi), либо те и другие одновременно.
.
Регрессионные модели, содержащие лишь качественные объясняющие переменные,
называются ANOVA - моделями (моделями дисперсионного анализа).
Например,
зависимость начальной заработной платы от образования может быть записана так: ,
,
где
z=0, если претендент на рабочее место не имеет высшего
образования, z=1, если имеет. Тогда при отсутствии высшего
образования начальная заработная плата равна: 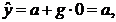
а
при его наличии: 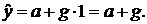
При
этом параметр а определяет среднюю начальную заработную плату при отсутствии
высшего образования. Коэффициент g показывает, на какую величину отличаются средние
начальные заработные платы при наличии и при отсутствии высшего образования у
претендента. Проверяя статистическую значимость коэффициента g с
помощью t - статистики (или значение 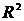 с помощью F- статистики), можно определить,
влияет или нет наличие высшего образования на начальную заработную плату.
с помощью F- статистики), можно определить,
влияет или нет наличие высшего образования на начальную заработную плату.
ANOVA - модели
представляют собой кусочно-постоянные функции. Такие модели в экономике
встречаются редко.
.
Гораздо чаще встречаются модели, содержащие как количественные, так и качественные
переменные. Такие модели называются ANCOVA - моделями (моделями
ковариационного анализа).
Рассмотрим
ANCOVA - модель при наличии у фиктивной переменной двух
альтернатив.
Простейшая
модель с одной количественной и одной качественной переменными имеет вид:
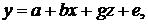
Где
у - заработная плата сотрудника фирмы, х - стаж работы, z -
пол сотрудника,
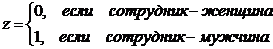
Тогда
для женщин ожидаемое значение заработной платы при х годах трудового стажа
будет: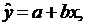
а
для мужчин -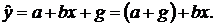
Эти
зависимости являются линейными относительно стажа работы х и различаются только
величиной свободного члена. Если коэффициент g является
статистически значимым, то можно сделать вывод, что в фирме имеет место
дискриминация в заработной плате по половому признаку. При g>0
она будет в пользу мужчин, при g<0 - в пользу женщин. На графике такие зависимости
изображаются параллельными прямыми.
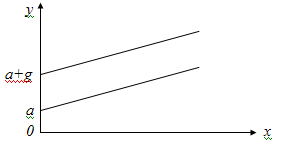
Нулевой
уровень (z = 0) качественной переменной называется базовым или
сравнительным.
Коэффициент
g в модели называется дифференциальным коэффициентом
свободного члена, т.к. он показывает, на сколько отличается свободный член в
модели при значении z = 1 от свободного члена при базовом значении
фиктивной переменной.
Кроме
того, значения фиктивных переменных можно изменять на противоположные. Суть
модели от этого не изменится. Изменится только знак коэффициента g в
модели.
.
С помощью большего числа фиктивных переменных можно обрисовать более сложные
ситуации.
В
этом случае может возникнуть ситуация, которая называется ловушкой фиктивной
переменной. Она возникает, когда для моделирования k значений
качественного признака используется ровно k бинарных (фиктивных)
переменных. В этом случае одна из таких переменных линейно выражается через все
остальные, и матрица значений переменных становится вырожденной. Тогда
исследователь попадает в ситуацию совершенной мультиколлинеарности. Избежать
подобной ловушки позволяет правило:
Если
качественная переменная имеет k альтернативных значений, то при моделировании
используется только (k-1) фиктивных переменных.
Например,
если качественная переменная имеет 3 уровня, то для моделирования достаточно
двух фиктивных переменных z1 и z2. Тогда для обозначения третьего уровня достаточно
принять, например, обе переменные равными нулю: z1=z2=0. В
частности, для обозначения уровня экономического развития страны (развитая,
развивающаяся или страна "третьего мира") можно использовать
обозначения:
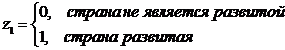
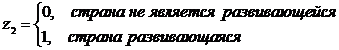
Тогда
z1=z2=0 означает страну "третьего мира".
Рассмотрим
модель с двумя объясняющими переменными, одна из которых количественная, а
другая - фиктивная, причем имеющая 3 альтернативы. Например, расходы на
содержание ребёнка могут быть связаны с доходами домохозяйств и возрастом
ребёнка: дошкольный, младший школьный и старший школьный.
Т.к.
качественная переменная связана с 3 альтернативами, то по общему правилу моделирования
необходимо использовать 2 фиктивные переменные:
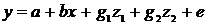 ,
,
где
у - расходы на содержание ребёнка, х - доходы домохозяйств,
 ,
,
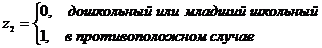 .
.
Тогда
образуются частные уравнения регрессии для отдельного возраста:
расходы
на дошкольника: 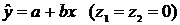 ;
;
расходы
на младшего школьника: 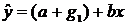
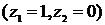 ;
;
-
расходы на старшего школьника: 
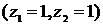 .
.
Базовым
значением качественной переменной является значение "дошкольник", 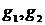 - дифференциальные свободные члены. Т.о. получаем три
параллельные регрессионные прямые:
- дифференциальные свободные члены. Т.о. получаем три
параллельные регрессионные прямые:
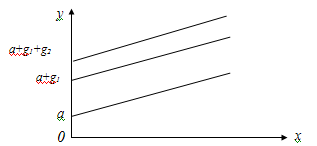
После
вычисления коэффициентов регрессий определяется статистическая значимость 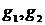 на основе обычных t - статистик.
Если они оказываются статистически незначимыми, то можно сделать вывод, что
возраст ребёнка не оказывает существенного влияния на расходы по его
содержанию.
на основе обычных t - статистик.
Если они оказываются статистически незначимыми, то можно сделать вывод, что
возраст ребёнка не оказывает существенного влияния на расходы по его
содержанию.
.
В отдельных случаях может оказаться необходимым введение двух и более фиктивных
переменных.
Для
простоты рассмотрим регрессию с одной количественной и двумя качественными
переменными. Пусть у - заработная плата сотрудников, х - стаж работы, z1 - наличие высшего образования, z2 - пол сотрудника.
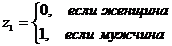 ,
, 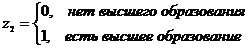 .
.
Т.о.
модель имеет вид: 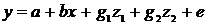 .
.
Из
неё получаем следующие зависимости:
зарплата
женщины без высшего образования: 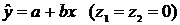 ;
;
зарплата
женщины с высшим образованием: 
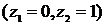 ;
;
зарплата
мужчины без высшего образования: 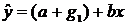
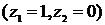 ;
;
зарплата
мужчины с высшим образованием: 
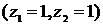 .
.
Очевидно,
что все отдельные регрессии отличаются друг от друга только свободным членом.
Определение статистической значимости коэффициентов 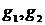 показывает, влияют ли образование и пол сотрудника на
его зарплату.
показывает, влияют ли образование и пол сотрудника на
его зарплату.
.
Фиктивные переменные широко используются и для оценки сезонных различий в
потреблении. Например, спрос на туристические путёвки, охлаждённую воду,
мороженное существенно выше летом, чем зимой. Спрос на обогреватели, шубы -
наоборот.
Обычно
сезонные колебания характерны для временных рядов. Устранение и нейтрализация
сезонного фактора позволяет сконцентрироваться на других важных количественных
и качественных характеристиках модели (тренде).
Устранение
сезонного фактора называется сезонной корректировкой. Существует
несколько методов сезонной корректировки, одним из которых является метод
фиктивных переменных.
Пусть
у зависит от количественной переменной х, причём зависимость отличается по
кварталам, тогда общую модель можно представить в виде:
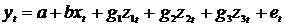 ,
,
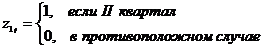 ,
, 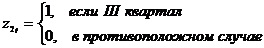 ,
,
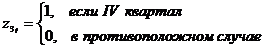
I квартал -
база.
.
Иногда (достаточно редко) фиктивные переменные могут быть использованы для
объяснения поведения зависимой переменной (т.е. зависимая переменная является
фиктивной).
Например,
исследуется зависимость наличия автомобиля от дохода, пола субъекта и т.п.
Тогда
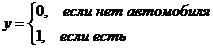 .
.
Такие
модели являются вероятностными (линейными) моделями:
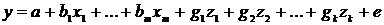 .
.
Зависимая
переменная у принимает значение 0 с вероятностью р и 1 с вероятностью (1-р).
Для
оценки параметров линейно-вероятностной модели применяются методы Logit
-, Probit-, Tobit- анализа.
.
Фиктивные переменные могут вводиться не только в линейные, но и в нелинейные
модели, приводимые путём преобразования к линейному виду.
Например,
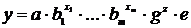 .
.
Логарифмируем,

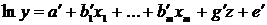 .
.
Наибольшими
прогностическими возможностями обладают модели, зависящие от нескольких количественных
факторов и от нескольких фиктивных.
Влияние
качественного фактора может сказываться не только на значении свободного члена,
но и на угловом коэффициенте линейной регрессионной модели. Обычно это
характерно для временных рядов экономических данных при изменении
институциональных условий, введении новых правовых или налоговых ограничений.
Тогда зависимость может быть выражена так:
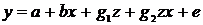 ,
,
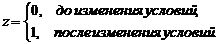
В
этой ситуации ожидаемое значение зависимой переменной определяется следующим
образом:

Коэффициенты
g1 и g2 называются соответственно дифференциальным свободным
членом и дифференциальным угловым коэффициентом. Фиктивная переменная разбивает
зависимость на две части - до и после внесения изменений в условия её действия.

Общая
зависимость имеет вид кусочно - линейной функции, а изменения условий
отображаются изменением угла наклона прямой к оси абсцисс (линии 1 - 2).
Здесь
исследователь должен принять решение, стоит ли разбивать выборку на части и
строить для каждой из них уравнение регрессии (прямые 1 и 2) или ограничиться
одной общей линией регрессии (линия 3). Для этого используют тест Чоу, который
опирается на F-статистику 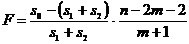 , (см.
тема "Статистика Фишера в регрессионном анализе").
, (см.
тема "Статистика Фишера в регрессионном анализе").
Если
гипотеза о структурной стабильности выборки отклоняется, то исследуется вопрос
о причинах структурных различий в подвыборках. Пусть данные в подвыборках описываются
двумя уравнениями регрессии:
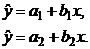
Тогда
возможны следующие варианты:
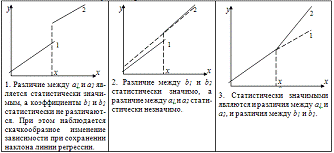
Для
тестирования всех этих ситуаций применяется следующая методика, предложенная
Гуйарати. Она основана на включении в модель регрессии фиктивной переменной z,
которая равна 1 для всех x<x* и равна 0 для всех x>x*. Далее определяются параметры следующего уравнения
регрессии:
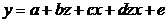 .
.
Отсюда
видно, что
а1=(а+b);b1=(c+d)(z=1),
a2=a;b2=b;(z=0).
Следовательно,
параметр b есть разница между a1 и а2, параметр d - разница
между b1 и b2. Если в уравнении b является
статистически значимым, а d - нет, то имеем первый вариант структурной
перестройки. Если, наоборот, статистически значимым является d, а b -
незначим, имеем второй вариант структурных изменений. Наконец, третий вариант
имеем в случае, если оба коэффициента b и d являются
статистически значимыми.
В
заключение следует отметить, что преимущество метода Гуйарати перед тестом Чоу
состоит в том, что нужно построить только одно, а не три уравнения регрессии.
10. Системы
эконометрических уравнений
10.1 Общее понятие о системах уравнений, используемых в эконометрике
Объектом статистического изучения в социальных науках являются сложные
системы. Построение изолированных уравнений регрессии недостаточно для описания
таких систем и объяснения механизма их функционирования.
Поэтому при моделировании экономических ситуаций часто необходимо
построение систем уравнений, когда одни и те же переменные могут выступать и в
роли объясняющих и в роли объясняемых. Так, если изучается модель спроса как
отношение цен и количества потребляемых товаров, то одновременно для
прогнозирования спроса необходима модель предложения товаров, в которой рассматривается
также взаимосвязь между количеством и ценой предлагаемых благ. Это позволяет
достичь равновесия между спросом и предложением.
Система уравнений в эконометрических исследованиях может быть построена
по-разному.
Системы уравнений здесь могут быть построены по-разному.
Возможна система независимых уравнений, когда каждая зависимая переменная
y рассматривается как функция одного и
того же набора факторов x:
 (1)
(1)
Набор
факторов xj в каждом уравнении может варьироваться.
Каждое
уравнение системы независимых уравнений может рассматриваться самостоятельно.
Для нахождения его параметров используется МНК. По существу, каждое уравнение
этой системы является уравнением регрессии.
Если
зависимая переменная  одного уравнения выступает в виде фактора
одного уравнения выступает в виде фактора 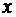 в другом уравнении, то исследователь может строить
модель в виде системы рекурсивных уравнений:
в другом уравнении, то исследователь может строить
модель в виде системы рекурсивных уравнений:
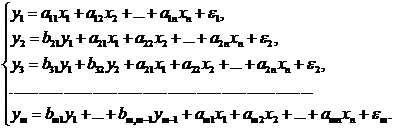 (2)
(2)
В
данной системе зависимая переменная  включает
в каждое последующее уравнение в качестве факторов все зависимые переменные
предшествующих уравнений наряду с набором факторов
включает
в каждое последующее уравнение в качестве факторов все зависимые переменные
предшествующих уравнений наряду с набором факторов 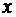 . Каждое уравнение этой системы может рассматриваться
самостоятельно, и его параметры определяются методом наименьших квадратов
(МНК).
. Каждое уравнение этой системы может рассматриваться
самостоятельно, и его параметры определяются методом наименьших квадратов
(МНК).
Наибольшее
распространение в эконометрических исследованиях получила система взаимозависимых
уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в
левую часть, а в других уравнениях - в правую часть системы:
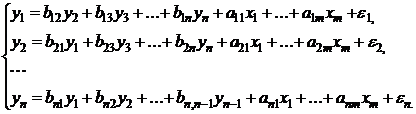 (3)
(3)
Система взаимозависимых уравнений получила название системы совместных,
одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же
переменные одновременно рассматриваются как зависимые в одних уравнениях и как
независимые в других. В эконометрике эта система уравнений называется также
структурной формой модели.
В отличие от предыдущих систем каждое уравнение системы одновременных
уравнений не может рассматриваться самостоятельно, и для нахождения его
параметров традиционный МНК неприменим. С этой целью используются специальные
приемы оценивания.
.2 Структурная
и приведенная формы модели
Экономическая модель как система одновременных уравнений может быть
представлена в структурной или приведённой форме. В структурной форме её
уравнения имеют исходный вид, отражая непосредственную связь между переменными.
Структурная форма модели обычно содержит эндогенные и экзогенные
переменные.
Эндогенные переменные (внутренние) - это зависимые переменные, число
которых равно числу уравнений в системе. Они обозначаются через y.
Экзогенные переменные (внешние) - это предопределенные переменные
(задаваемые извне, независимые), влияющие на эндогенные переменные. Они
обозначаются через x.
Классификация переменных на эндогенные и экзогенные зависит от
теоретической концепции принятой модели. Экономические переменные могут выступать
в одних моделях как эндогенные, а в других - как экзогенные переменные.
Внеэкономические переменные (например, климатические условия) входят в систему
как экзогенные переменные. В качестве экзогенных переменных можно рассматривать
значения эндогенных переменных за предшествующий период времени (лаговые
переменные). Например, потребление текущего года yt может зависеть также и от уровня
потребления в предыдущем году yt-1.
Структурная форма модели позволяет увидеть влияние изменений любой
экзогенной переменной на значения эндогенной переменной. Целесообразно в
качестве экзогенных переменных выбирать такие переменные, которые могут быть
объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые
значения эндогенных переменных.
Простейшая структурная форма модели имеет вид:
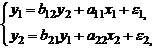 (4)
(4)
где
y1,y2 - эндогенные переменные, x1,x2 -
экзогенные.
Коэффициенты
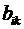 при эндогенных и
при эндогенных и 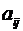 - при
экзогенных переменных называются структурными коэффициентами модели. Все
переменные в модели выражены в отклонениях
- при
экзогенных переменных называются структурными коэффициентами модели. Все
переменные в модели выражены в отклонениях  и
и 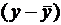 от среднего уровня, поэтому свободный член в каждом
уравнении отсутствует.
от среднего уровня, поэтому свободный член в каждом
уравнении отсутствует.
Использование
МНК для оценивания структурных коэффициентов модели дает смещенные и
несостоятельные оценки. Поэтому обычно для определения структурных
коэффициентов модели структурная форма преобразуется в приведенную.
Приведенная
форма модели представляет собой систему линейных функций эндогенных переменных
от экзогенных:
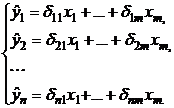 (5)
(5)
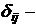 коэффициенты
приведенной формы модели.
коэффициенты
приведенной формы модели.
По
своему виду приведенная форма модели ничем не отличается от системы независимых
уравнений. Применяя МНК, можно оценить 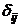 , а затем
оценить значения эндогенных переменных через экзогенные.
, а затем
оценить значения эндогенных переменных через экзогенные.
Коэффициенты
приведённой формы представляют собой нелинейные функции коэффициентов
структурной формы модели.
Рассмотрим это положение на примере простейшей структурной модели,
выразив коэффициенты приведенной формы модели через коэффициенты структурной
модели.
Для структурной модели вида (4) приведенная форма модели имеет вид
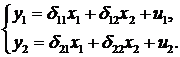 (6)
(6)
Из
первого уравнения (4) можно выразить 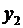 следующим
образом (ради упрощения опускаем случайную величину):
следующим
образом (ради упрощения опускаем случайную величину): .
.
Подставляя
во второе уравнение (4), имеем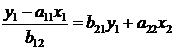 ,
,
Откуда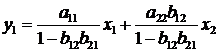 .
.
Аналогично
выразим  из второго уравнения системы (4) и подставив в
первое, получим:
из второго уравнения системы (4) и подставив в
первое, получим:
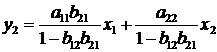 .
.
Т.о.
система (4) принимает вид:
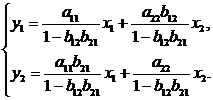
Таким
образом, можно сделать вывод о том, что коэффициенты приведенной формы модели
(6) будут выражаться через коэффициенты структурной формы следующим образом:
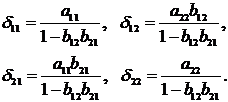
Следует
заметить, что приведенная форма модели хотя и позволяет получить значения
эндогенной переменной через значения экзогенных переменных, но аналитически она
уступает структурной форме модели, так как в ней отсутствуют оценки взаимосвязи
между эндогенными переменными.
10.3 Проблема идентификации
При переходе от приведенной формы модели к структурной исследователь
сталкивается с проблемой идентификации. Идентификация - это единственность
соответствия между приведенной и структурной формами модели.
Структурная модель (3) в полном виде, состоящая в каждом уравнении
системы из n эндогенных и m экзогенных переменных, содержит n(n-1+m)
параметров. Приведенная модель (5) в полном виде содержит nm параметров. Таким образом, в полном
виде структурная модель содержит большее число параметров, чем приведенная
форма модели. Поэтому n(n-1+m) параметров структурной модели не могут быть однозначно
определены через nm параметров
приведенной формы модели.
Чтобы получить единственно возможное решение для структурной модели,
необходимо предположить, что некоторые из структурных коэффициентов модели
равны нулю. Тем самым уменьшится число структурных коэффициентов.
С позиции идентифицируемости структурные модели можно подразделить на три
вида:
А) идентифицируемые;
Б) неидентифицируемые;
В) сверхидентифицируемые.
А) Модель идентифицируема, если все структурные ее коэффициенты
определяются однозначно, единственным образом по коэффициентам приведенной
формы модели, т.е. число параметров структурной модели равно числу параметров
приведенной формы модели.
Б) Модель неидентифицируема, если число приведенных коэффициентов меньше
числа структурных коэффициентов, и в результате структурные коэффициенты не
могут быть оценены через коэффициенты приведенной формы модели. Модель (3) в
полном виде всегда неидентифицируема.
В) Модель сверхидентифицируема, если число приведенных коэффициентов
больше числа структурных коэффициентов. В этом случае на основе приведенных
коэффициентов можно получить два или более значений одного структурного
коэффициента. Сверхидентифицируемая модель, в отличие от неидентифицируемой,
практически решаема, но требует для этого специальных методов исчисления
параметров.
Структурная модель всегда представляет собой систему совместных
уравнений, каждое из которых требуется проверять на идентификацию. Модель
считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если
хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается
неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно
сверхидентифицируемое уравнение.
Необходимое условие идентифицируемости (счётное правило проверки на
идентифицируемость): Обозначим Н - число эндогенных переменных в i- ом уравнении системы, D - число
экзогенных переменных, которые содержатся в системе, но не входят в данное
уравнение. Тогда:+1 = Н - уравнение идентифицируемо;+1 < Н - уравнение
неидентифицируемо;+1 > Н - уравнение сверхидентифицируемо.
Это счетное правило отражает необходимое, но не достаточное условие
идентификации. Более точно условия идентификации определяются, если накладывать
ограничения на коэффициенты матриц параметров структурной модели. Уравнение
идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным)
можно из коэффициентов при них в других уравнениях системы получить матрицу,
определитель которой не равен нулю, а ранг матрицы не меньше, чем число
эндогенных переменных в системе без одного.
Для оценки параметров структурной формы система должна быть
идентифицируема или сверхидентифицируема.
Пример. Проверить каждое уравнение системы на необходимое и достаточное
условия идентификации:

10.4
Оценивание параметров структурной модели
Коэффициенты
структурной модели могут быть оценены разными способами в зависимости от вида
системы одновременных уравнений. Наибольшее распространение получили два метода
оценивания коэффициентов структурной модели:
· косвенный
метод наименьших квадратов (КМНК);
· двухшаговый
метод наименьших квадратов (ДМНК);
· трёхшаговый метод наименьших квадратов МНК;
· метод максимального правдоподобия с полной информацией;
· метод максимального правдоподобия при ограниченной
информации.
Косвенный и двухшаговый методы подробно описаны в литературе и
рассматриваются как традиционные методы оценки коэффициентов структурной
модели.
КМНК применяется для идентифицируемой системы одновременных уравнений, а
ДМНК - для оценки коэффициентов сверхидентифируемой модели.
Метод максимального правдоподобия с полной информацией рассматривается
как наиболее общий метод оценивания, результаты которого при нормальном
распределении признаков совпадают с МНК. Однако при большом числе уравнений
системы этот метод приводит к достаточно сложным вычислительным процедурам.
Поэтому в качестве модификации используется метод максимального правдоподобия
при ограниченной информации (метод наименьшего дисперсионного отношения),
разработанный в 1949 г. Т.Андерсоном и Н.Рубиным.
В отличие от метода максимального правдоподобия в данном методе сняты
ограничения на параметры, связанные с функционированием системы в целом. Это
делает решение более простым, но трудоемкость вычислений остается достаточно
высокой. Несмотря на его значительную популярность, к середине 60-х годов он
был практически вытеснен двухшаговым методом наименьших квадратов (ДМНК) в
связи с гораздо большей простотой последнего. Дальнейшим развитием ДМНК
является трехшаговый МНК (ТМНК), предложенный в 1962 г. А.Зельнером и Г.Тейлом.
Этот метод оценивания пригоден для всех видов уравнений структурной модели.
Однако при некоторых ограничениях на параметры более эффективным оказывается
ДМНК. Косвенный метод наименьших квадратов (КМНК) применяется в случае точно
идентифицируемой структурной модели. Процедура применения КМНК предполагает
выполнение следующих этапов работы:
1. Структурная модель преобразовывается в приведенную форму модели.
2. Для
каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные
коэффициенты 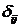 .
.
. Коэффициенты
приведенной формы модели трансформируются в параметры структурной модели.
Рассмотрим применение КМНК для модели:

Пусть
мы располагаем некоторыми данными по 5 регионам:
|
Регион
|
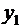 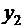 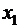 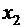
|
|
|
|
|
1
|
2
|
5
|
1
|
3
|
|
2
|
3
|
6
|
2
|
1
|
|
3
|
4
|
7
|
3
|
2
|
|
4
|
5
|
8
|
2
|
5
|
|
5
|
6
|
5
|
4
|
6
|
|
Средние
|
4
|
6,2
|
2,4
|
3,4
|
Приведенная форма модели имеет вид:

где
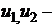 случайные ошибки приведенной формы модели.
случайные ошибки приведенной формы модели.
Для
каждого уравнения приведенной формы применим традиционный МНК и определим δ- коэффициенты. Для простоты работаем в отклонениях,
т.е. 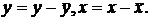 Тогда система нормальных уравнений для первого
уравнения системы составит:
Тогда система нормальных уравнений для первого
уравнения системы составит:
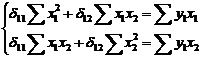
Для
приведенных данных система составит:
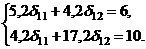
Отсюда
получаем первое уравнение (и аналогично второе):
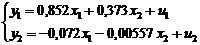
Перейдем
к структурной форме следующим образом: исключим из первого уравнения
приведенной формы x2 ,
выразив его из второго уравнения приведенной формы и подставив в первое
уравнение:
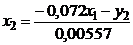 .
.
Первое
уравнение структурной формы:
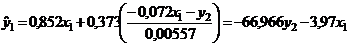 .
.
Аналогично
исключим из второго уравнения x1, выразив
его через первое уравнение и подставив во второе:
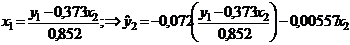 ,
,
 второе
уравнение структурной формы.
второе
уравнение структурной формы.
Структурная
форма модели имеет вид:
Эту
же систему можно записать, включив в нее свободный член уравнения, т.е. перейти
от переменных в виде отклонений от среднего к исходным переменным  и
и 
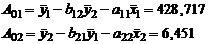
Тогда
структурная модель имеет вид:

Если
к каждому уравнению структурной формы применить традиционный МНК, то результаты
могут сильно отличаться. В данном примере будет:
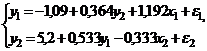
Двухшаговый
МНК. ДМНК используется для сверхидентифицируемых систем. Основная идея ДМНК: на
основе приведенной формы модели получить для сверхидентифицируемого уравнения
теоретические значения эндогенных переменных, содержащихся в правой части
уравнения. Далее, подставив их вместо фактических значений, можно применить
обычный МНК к структурной форме сверхидентифицируемого уравнения. Здесь дважды
используется МНК: на первом шаге при определении приведенной формы модели и нахождении
на ее основе оценок теоретических значений эндогенной переменной 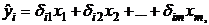 и на втором шаге применительно к структурному
сверхидентифицируемому уравнению при определении структурных коэффициентов
модели по данным теоретических (расчетных) значений эндогенных переменных.
и на втором шаге применительно к структурному
сверхидентифицируемому уравнению при определении структурных коэффициентов
модели по данным теоретических (расчетных) значений эндогенных переменных.
Сверхидентифицируемая
структурная модель может быть двух типов:
все
уравнения системы сверхидентифицируемые;
система
содержит также точно идентифицируемые уравнения.
В первом случае для оценки структурных коэффициентов каждого уравнения
используется ДМНК. Во втором случае структурные коэффициенты для точно
идентифицируемых уравнений находятся из системы приведенных уравнений.
ДМНК является наиболее общим и широко распространенным методом решения
системы одновременных уравнений. Для точно идентифицируемых уравнений ДМНК дает
тот же результат, что и КМНК.
Рассмотрим модель:
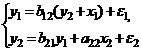
Она
получена из предыдущего примера наложением ограничения  Поэтому первое уравнение стало сверхидентифицируемым.
Поэтому первое уравнение стало сверхидентифицируемым.
На
первом шаге найдем приведенную форму модели. С использованием тех же исходных
данных получим систему:
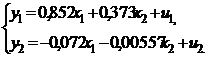
На
основе второго уравнения этой системы можно найти теоретические значения для
эндогенной переменной 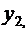 т.е.
т.е. 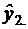 Подставим
в это уравнение значения
Подставим
в это уравнение значения  и
и  в форме
отклонений от средних значений, запишем в виде таблицы:
в форме
отклонений от средних значений, запишем в виде таблицы:
|
 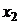    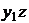 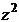
|
|
|
|
|
|
|
|
- 1,4
|
-0,4
|
0,103
|
-1,297
|
- 2
|
2,594
|
1,682
|
|
- 0,4
|
-2,4
|
0,042
|
-0,358
|
- 1
|
0,358
|
0,128
|
|
0,6
|
-1,4
|
- 0,035
|
0,565
|
0
|
0
|
0,319
|
|
- 0,4
|
1,6
|
0,02
|
-0,38
|
1
|
- 0,38
|
0,144
|
|
1,6
|
2,6
|
- 0,13
|
1,47
|
2
|
2,94
|
2,161
|
|
0
|
0
|
0
|
0
|
0
|
5,512
|
4,434
|
После
того, как найдены оценки 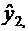 заменим в уравнении
заменим в уравнении 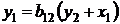 фактические
значения
фактические
значения 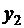 их оценками
их оценками 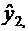 найдем
значения новой переменной
найдем
значения новой переменной 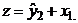 Применим МНК к уравнению:
Применим МНК к уравнению:
 .
.
Получим:
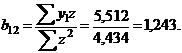
В
целом рассматриваемая система будет иметь вид:
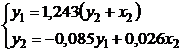
Второе
уравнение не изменилось по сравнению с предыдущим примером.
11. Временные ряды в эконометрических исследованиях
11.1 Выявление структуры временного
ряда
Временнóй ряд - это совокупность значений, какого - либо показателя
за несколько последовательных моментов или периодов времени. Каждое значение
(уровень) временного ряда формируется под воздействием большого числа факторов,
которые можно условно разделить на три группы:
- факторы, формирующие тенденцию ряда;
- факторы, формирующие циклические колебания ряда;
случайные факторы.
Тенденция характеризует долговременное воздействие факторов на динамику
показателя. Тенденция может быть возрастающей или убывающей.
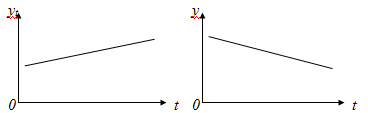
Циклические колебания могут носить сезонный характер или отражать
динамику конъюнктуры рынка, а также фазу бизнес - цикла, в которой находится
экономика страны.
Реальные
данные часто содержат все три компоненты. В большинстве случаев временной ряд
можно представить как сумму или произведение трендовой  , циклической
, циклической  и
случайной
и
случайной 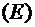 компонент. В случае суммы имеет место аддитивная
модель временного ряда:
компонент. В случае суммы имеет место аддитивная
модель временного ряда:
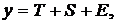 (1)
(1)
в
случае произведения - мультипликативная модель:
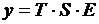 .(2)
.(2)
Основная
задача эконометрического исследования отдельного временного ряда - выявление
количественного выражения кждой из компонент и использование полученной
информации для прогноза будущих значений ряда или построение модели взаимосвязи
двух или более временных рядов.
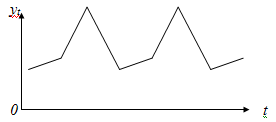
Сначала
рассмотрим основные подходы к анализу отдельного временного ряда. Такой ряд
может содержать, помимо случайной составляющей, либо только тенденцию, либо только
сезонную (циклическую) компоненту, либо все компоненты вместе. Для того, чтобы
выявить наличие той или иной неслучайной компоненты, исследуется корреляционная
зависимость между последовательными уровнями временного ряда, или
автокорреляция уровней ряда. Основная идея такого анализа заключается в том,
что при наличии во временном ряде тенденции и циклических колебаний значения
каждого последующего уровня ряда зависят от предыдущих.
Количественно
автокорреляцию можно измерить с помощью линейного коэффициента корреляции между
уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на
несколько шагов во времени.
Коэффициент
автокорреляции уровней ряда первого порядка измеряет зависимость между
соседними уровнями ряда  и
и 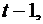 т.е. при
лаге 1.
т.е. при
лаге 1.
Он
вычисляется по следующей формуле:
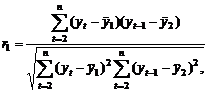 (3)
(3)
где в качестве средних величин берутся значения:
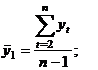
 (4)
(4)
В
первом случае усредняются значения ряда, начиная со второго до последнего, во
втором случае - значения ряда с первого до предпоследнего.
Формулу
(3) можно представить как формулу выборочного коэффициента корреляции:
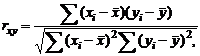 (5)
(5)
где
в качестве переменной  берется ряд
берется ряд 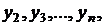 а в
качестве переменной
а в
качестве переменной  ряд
ряд 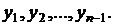
Если значение коэффициента (3) близко к единице, это указывает на очень
тесную зависимость между соседними уровнями временного ряда и о наличии во
временном ряде сильной линейной тенденции.
Аналогично
определяются коэффициенты автокорреляции более высоких порядков. Так,
коэффициент автокорреляции второго порядка характеризует тесноту связи между
уровнями 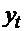 и
и 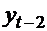 и
определяется по формуле:
и
определяется по формуле:
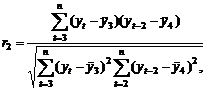 (6)
(6)
где
в качестве одной средней величины берут среднюю уровней ряда с третьего до
последнего, а в качестве другой - среднюю с первого уровня до 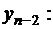
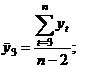
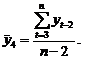 (7)
(7)
Число
периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом.
С увеличением лага число пар значений, по которым рассчитывается коэффициент
автокорреляции, уменьшается. Для обеспечения статистической достоверности
максимальный лаг, как считают некоторые известные эконометристы, не должен
превышать четверти общего объема выборки.
Коэффициент
автокорреляции строится по аналогии с линейным коэффициентом корреляции, и
поэтому он характеризует тесноту только линейной связи текущего и предыдущего
уровней ряда. По нему можно судить о наличии линейной или близкой к линейной
тенденции. Однако для некоторых временных рядов с сильной нелинейной тенденцией
(например, параболической или экспоненциальной), коэффициент автокорреляции
уровней ряда может приближаться к нулю.
Кроме
того, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей
или убывающей тенденции в уровнях ряда. Большинство временных рядов
экономических данных имеют положительную автокорреляцию уровней, однако при
этом не исключается убывающая тенденция.
Последовательность
коэффициентов автокорреляции уровней различных порядков, начиная с первого,
называется автокорреляционной функцией временного ряда. График зависимости ее
значений от величины лага называется коррелограммой. Анализ автокорреляционной
функции и коррелограммы помогает выявить структуру ряда. Здесь уместно привести
следующие качественные рассуждения.
Если
наиболее высоким является коэффициент автокорреляции первого порядка, очевидно,
исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался
коэффициент автокорреляции порядка τ, ряд
содержит циклические колебания с периодичностью в τ моментов времени. Если ни один из коэффициентов
автокорреляции не является значимым, то либо ряд не содержит тенденции и
циклических колебаний и имеет только случайную составляющую, либо ряд содержит
сильную нелинейную тенденцию, для исследования которой нужно провести
дополнительный анализ.
ряд
содержит циклические колебания с периодичностью в τ моментов времени. Если ни один из коэффициентов
автокорреляции не является значимым, то либо ряд не содержит тенденции и
циклических колебаний и имеет только случайную составляющую, либо ряд содержит
сильную нелинейную тенденцию, для исследования которой нужно провести
дополнительный анализ.
Пример
1. Пусть имеются данные об объёмах потребления электроэнергии жителями района
за 16 кварталов, млн. квт.-ч:
|
t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
yt
|
6,0
|
4,4
|
5,0
|
9,0
|
7,2
|
4,8
|
6,0
|
10,0
|
8,0
|
5,6
|
6,4
|
11,0
|
9,0
|
6,6
|
7,0
|
10,8
|
Нанесем эти значения на график:
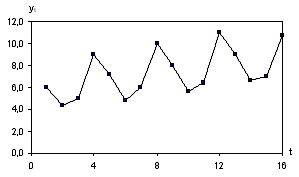
Определим автокорреляционную функцию данного временного ряда. Рассчитаем
коэффициент автокорреляции первого порядка. Для этого определим средние
значения:
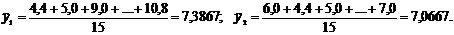
С
учетом этих значений можно построить вспомогательную таблицу:
|
t
|
yt
|
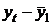 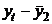 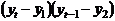  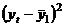
|
|
|
|
|
|
1
|
6,0
|
|
-1,0667
|
|
|
1,137778
|
|
2
|
4,4
|
-2,9867
|
-2,6667
|
3,185778
|
8,920178
|
7,111111
|
|
3
|
5,0
|
-2,3867
|
-2,0667
|
6,364444
|
5,696178
|
4,271111
|
|
4
|
9,0
|
1,6133
|
1,9333
|
-3,33422
|
2,602844
|
3,737778
|
|
5
|
7,2
|
-0,1867
|
0,1333
|
-0,36089
|
0,034844
|
0,017778
|
|
6
|
4,8
|
-2,5867
|
-2,2667
|
-0,34489
|
6,690844
|
5,137778
|
|
7
|
6,0
|
-1,3867
|
-1,0667
|
3,143111
|
1,922844
|
1,137778
|
|
8
|
10,0
|
2,6133
|
2,9333
|
-2,78756
|
6,829511
|
8,604444
|
|
9
|
8,0
|
0,6133
|
0,9333
|
1,799111
|
0,376178
|
0,871111
|
|
10
|
5,6
|
-1,7867
|
-1,4667
|
-1,66756
|
3,192178
|
2,151111
|
|
11
|
6,4
|
-0,9867
|
-0,6667
|
1,447111
|
0,973511
|
0,444444
|
|
12
|
11,0
|
3,6133
|
3,9333
|
-2,40889
|
13,05618
|
15,47111
|
|
13
|
9,0
|
1,6133
|
1,9333
|
6,345778
|
2,602844
|
3,737778
|
|
14
|
6,6
|
-0,7867
|
-0,4667
|
-1,52089
|
0,618844
|
0,217778
|
|
15
|
7,0
|
-0,3867
|
-0,0667
|
0,180444
|
0,149511
|
0,004444
|
|
16
|
10,8
|
3,4133
|
|
-0,22756
|
11,65084
|
|
|
Итого
|
|
|
9,813333
|
65,3173
|
54,0533
|
С
помощью итоговых сумм подсчитаем величину коэффициента автокорреляции первого
порядка: 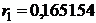 .
.
Это значение свидетельствует о слабой зависимости текущих уровней ряда от
непосредственно им предшествующих. Однако из графика очевидно наличие
возрастающей тенденции уровней ряда, на которую накладываются циклические колебания.
Продолжая аналогичные расчеты для второго, третьего и т.д. порядков,
получим автокорреляционную функцию, значения которой сведем в таблицу и
построим по ней коррелограмму:
|
Лаг
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
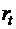 0,165150,566870,113550,983020,118710,722040,003360,97384 0,165150,566870,113550,983020,118710,722040,003360,97384
|
|
|
|
|
|
|
|
|
Из коррелограммы видно, что наиболее высокий коэффициент корреляции
наблюдается при значении лага, равном четырем, следовательно, ряд имеет
циклические колебания периодичностью в четыре квартала. Это подтверждается и
графическим анализом структуры ряда.
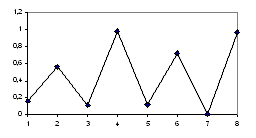
В случае если при анализе структуры временного ряда обнаружена только
тенденция и отсутствуют циклические колебания (случайная составляющая
присутствует всегда), следует приступать к моделированию тенденции. Если же во временном
ряде имеют место и циклические колебания, прежде всего, следует исключить
именно циклическую составляющую, и лишь затем приступать к моделированию
тенденции. Выявление тенденции состоит в построении аналитической функции,
характеризующей зависимость уровней ряда от времени, или тренда. Этот способ
называют аналитическим выравниванием временного ряда.
Зависимость от времени может принимать разные формы, поэтому для её
формализации используют различные виды функций:
- линейный
тренд: 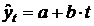 ;
;
гипербола:
 ;
;
экспоненциальный
тренд:  (или
(или 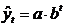 );
);
степенной
тренд: 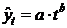 ;
;
параболический
тренд второго и более высоких порядков:
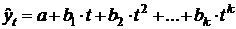 .
.
Параметры
каждого из трендов можно определить обычным МНК, используя в качестве
независимой переменной время  , а в
качестве зависимой переменной - фактические уровни временного ряда yt (или уровни за вычетом циклической составляющей, если таковая была
обнаружена). Для нелинейных трендов предварительно проводят стандартную
процедуру их линеаризации.
, а в
качестве зависимой переменной - фактические уровни временного ряда yt (или уровни за вычетом циклической составляющей, если таковая была
обнаружена). Для нелинейных трендов предварительно проводят стандартную
процедуру их линеаризации.
Существует
несколько способов определения типа тенденции. Чаще всего используют
качественный анализ изучаемого процесса, построение и визуальный анализ графика
зависимости уровней ряда от времени, расчет некоторых основных показателей
динамики. В этих же целях можно использовать и коэффициенты автокорреляции
уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов
автокорреляции первого порядка, рассчитанных по исходным и преобразованным
уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние
уровни yt и yt-1 тесно
коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней
исходного ряда должен быть высоким. Если временной ряд содержит нелинейную
тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого
порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий
коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная
тенденция в изучаемом временном ряде, тем в большей степени будут различаться
значения указанных коэффициентов.
Выбор
наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно
осуществить путем перебора основных форм тренда, расчета по каждому уравнению
скорректированного коэффициента детерминации 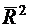 и выбора
уравнения тренда с максимальным значением этого коэффициента. Реализация этого
метода относительно проста при компьютерной обработке данных.
и выбора
уравнения тренда с максимальным значением этого коэффициента. Реализация этого
метода относительно проста при компьютерной обработке данных.
При
анализе временных рядов, содержащих сезонные или циклические колебания,
наиболее простым подходом является расчет значений сезонной компоненты методом
скользящей средней и построение аддитивной или мультипликативной модели временнóго ряда в форме (1) или (2).
Если
амплитуда колебаний приблизительно постоянна, строят аддитивную модель (1), в
которой значения сезонной компоненты предполагаются постоянными для различных
циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят
мультипликативную модель (2), которая ставит уровни ряда в зависимость от
значений сезонной компоненты.
Построение
модели (1) или (2) сводится к расчету значений Т, S или Е для каждого уровня
ряда. Процесс построения модели включает в себя следующие шаги:
1. Выравнивание исходного ряда методом
скользящей средней.
2. Расчет значений сезонной компоненты
S.
3. Устранение сезонной компоненты из
исходных уровней ряда и получение выровненных данных (Т+Е) в аддитивной или
(Т·Е) в мультипликативной модели.
4. Аналитическое выравнивание уровней
(Т+Е) или (Т·Е) и расчет значений Т с использованием полученного уравнения
тренда.
5. Расчет полученных по модели значений
(Т+S) или (Т·S)
6. Расчет абсолютных и относительных
ошибок.
Пример 2. Построение аддитивной модели временного ряда. Рассмотрим данные
об объёме потребления электроэнергии жителями района из ранее приведенного
примера. Из анализа автокорреляционной функции было показано, что данный
временнóй ряд содержит сезонные колебания
периодичностью в 4 квартала. Объёмы потребления электроэнергии в осенне -
зимний период (I и IV кварталы) выше, чем весной и летом (II и III кварталы). По графику этого ряда можно установить
наличие приблизительно равной амплитуды колебаний. Это говорит о возможном
наличии аддитивной модели. Рассчитаем её компоненты.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей
средней.
Поскольку циклические колебания имеют периодичность в 4 квартала,
просуммируем уровни ряда последовательно за каждые 4 квартала со сдвигом на
один момент времени и определим условные годовые объёмы потребления
электроэнергии (колонка 3 в таблице 1).
Разделив полученные суммы на 4, найдем скользящие средние (колонка 4
таблицы 1). Полученные таким образом выровненные значения уже не содержат
сезонной компоненты.
Поскольку скользящие средние получены осреднением четырех соседних
уровней ряда, т.е. четного числа значений, они соответствуют серединам подынтервалов,
состоящих из четверок чисел, т.е. должны располагаться между третьим и
четвертым значениями четверок исходного ряда. Для того, чтобы скользящие
средние располагались на одних временных отметках с исходным рядом, пары
соседних скользящих средних ещё раз усредняются и получаются центрированные
скользящие средние (колонка 5 таблицы 1). При этом теряются первые две и
последние две отметки временного ряда, что связано с осреднением по четырем
точкам.
Таблица 1
|
№ квартала
|
Потребление электроэнергии
yt
|
Итого за четыре квартала
|
Скользящая Средняя за
четыре квартала
|
Центрированная скользящая
средняя
|
Оценка сезонной компоненты
|
|
1
|
6,0
|
|
|
|
|
|
2
|
4,4
|
|
|
|
|
|
3
|
5,0
|
24,4
|
6,10
|
6,25
|
-1,250
|
|
4
|
9,0
|
25,6
|
6,40
|
6,45
|
2,550
|
|
5
|
7,2
|
26,0
|
6,50
|
6,625
|
0,575
|
|
6
|
4,8
|
27,0
|
6,75
|
6,875
|
-2,075
|
|
7
|
6,0
|
28,0
|
7,00
|
7,1
|
-1,100
|
|
8
|
10,0
|
28,8
|
7,20
|
7,3
|
2,700
|
|
9
|
8,0
|
29,6
|
7,40
|
7,45
|
0,550
|
|
10
|
30,0
|
7,50
|
7,625
|
-2,025
|
|
11
|
6,4
|
31,0
|
7,75
|
7,875
|
-1,475
|
|
12
|
11,0
|
32,0
|
8,00
|
8,125
|
2,875
|
|
13
|
9,0
|
33,0
|
8,25
|
8,325
|
0,675
|
|
14
|
6,6
|
33,6
|
8,40
|
8,375
|
-1,775
|
|
15
|
7,0
|
33,4
|
8,35
|
|
|
|
16
|
10,8
|
|
|
|
|
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими
уровнями ряда (колонка 2 таблицы 1) и центрированными скользящими средними
(колонка 5). Эти значения помещаем в колонку 6 таблицы 1 и используем для
расчета значений сезонной компоненты (таблица 2), которые представляют собой
средние за каждый квартал (по всем годам) оценки сезонной компоненты Si. В моделях с сезонной компонентой
обычно предполагается, что сезонные воздействия за период (в данном случае - за
год) взаимопогашаются. В аддитивной модели это выражается в том, что сумма
значений сезонной компоненты по всем точкам (здесь - по четырем кварталам)
должна быть равна нулю.
Таблица 2
|
Показатели
|
Год
|
№ квартала, i
|
|
|
I
|
II
|
III
|
IV
|
|
1
|
-
|
-
|
-1,250
|
2,550
|
|
2
|
0,575
|
-2,075
|
-1,100
|
2,700
|
|
3
|
0,550
|
-2,025
|
-1,475
|
2,875
|
|
4
|
0,675
|
-1,775
|
-
|
-
|
|
Итого за I-й
квартал (за все годы)
|
|
1,800
|
-5,875
|
-3,825
|
8,125
|
|
Средняя оценка сезонной
компоненты для I-го квартала, 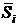
|
0,600
|
-1,958
|
-1,275
|
2,708
|
|
|
Скорректированная сезонная
компонента, 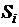 0,581-1,977-1,2942,690 0,581-1,977-1,2942,690
|
|
|
|
|
|
Для данной модели сумма средних оценок сезонной компоненты равна:
,6-1,958-1,275+2,708=0,075.
Эта сумма оказалась не равной нулю, поэтому каждую оценку уменьшим на
величину поправки, равной одной четверти полученного значения:
Δ=0,075/4=0,01875.
Рассчитаем скорректированные значения сезонной компоненты (они записаны в
последней строке таблицы 2):
 (8)
(8)
Эти
значения при суммировании уже равны нулю:
,581-1,977-1,294+2,69=0.
Шаг 3. Исключаем влияние сезонной компоненты, вычитая её значения из
каждого уровня исходного временного ряда. Получаем величины:
T+E=Y-S(9)
Эти значения рассчитываются в каждый момент времени и содержат только
тенденцию и случайную компоненту (колонка 4 следующей таблицы):
Таблица 3
|
t
|
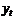 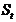 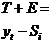 TT+S TT+S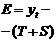 E2 E2
|
|
|
|
|
|
|
|
1
|
6,0
|
0,581
|
5,419
|
5,902
|
6,483
|
-0,483
|
0,2332
|
|
2
|
4,4
|
-1,977
|
6,377
|
6,088
|
4,111
|
0,289
|
0,0833
|
|
3
|
5,0
|
-1,294
|
6,294
|
6,275
|
4,981
|
0,019
|
0,0004
|
|
4
|
9,0
|
2,69
|
6,310
|
6,461
|
9,151
|
-0,151
|
0,0228
|
|
5
|
7,2
|
0,581
|
6,619
|
6,648
|
7,229
|
-0,029
|
0,0008
|
|
6
|
4,8
|
-1,977
|
6,777
|
6,834
|
4,857
|
-0,057
|
0,0032
|
|
7
|
6,0
|
-1,294
|
7,294
|
7,020
|
5,726
|
0,274
|
0,0749
|
|
8
|
10,0
|
2,69
|
7,310
|
7,207
|
9,897
|
0,103
|
0,0107
|
|
9
|
8,0
|
0,581
|
7,419
|
7,393
|
7,974
|
0,026
|
0,0007
|
|
10
|
5,6
|
-1,977
|
7,577
|
7,580
|
5,603
|
-0,003
|
0,0000
|
|
11
|
6,4
|
-1,294
|
7,694
|
7,766
|
6,472
|
-0,072
|
0,0052
|
|
12
|
11,0
|
2,69
|
8,310
|
7,952
|
10,642
|
0,358
|
0,1278
|
|
13
|
9,0
|
0,581
|
8,419
|
8,139
|
8,720
|
0,280
|
0,0785
|
|
14
|
6,6
|
-1,977
|
8,577
|
8,325
|
6,348
|
0,252
|
0,0634
|
|
15
|
7,0
|
-1,294
|
8,294
|
8,512
|
7,218
|
-0,218
|
0,0474
|
|
16
|
10,8
|
2,69
|
8,110
|
8,698
|
11,388
|
-0,588
|
0,3458
|
Шаг 4. Определим трендовую компоненту данной модели. Для этого проведем
выравнивание ряда (Т+Е) с помощью линейного тренда:

Подставляя
в это уравнение значения 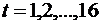 , найдем уровни Т для каждого момента времени (колонка
5 таблицы 3).
, найдем уровни Т для каждого момента времени (колонка
5 таблицы 3).
Шаг
5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого
прибавим к уровням Т значения сезонной компоненты для соответствующих
кварталов, т.е. к значениям в колонке 5 таблицы 3 прибавим значения в колонке
3. Результаты операции представлены в колонке 6 таблицы 3.
Шаг
6. В соответствии с методикой построения аддитивной модели расчет ошибки
производим по формуле:
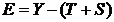 (10)
(10)
Это абсолютная ошибка. Численные значения абсолютных ошибок приведены в
колонке 7 таблицы 3. По аналогии с моделью регрессии для оценки качества
построения модели или для выбора наилучшей модели можно применять сумму
квадратов полученных абсолютных ошибок. Для данной аддитивной модели сумма
квадратов абсолютных ошибок равна 1,10. По отношению к общей сумме квадратов
отклонений уровней ряда от его среднего уровня, равной 71,59, эта величина
составляет чуть более 1,5%. Следовательно, можно сказать, что аддитивная модель
объясняет 98,5% общей вариации уровней временного ряда потребления
электроэнергии за последние 16 кварталов. Пример 3. Построение
мультипликативной модели временного ряда. Пусть имеются поквартальные данные о
прибыли компании за последние четыре года:
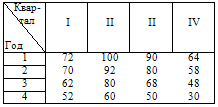
График временного ряда свидетельствует о наличии сезонных колебаний
периодичностью 4 квартала и общей убывающей тенденции уровней ряда:

Прибыль компании в весенне-летний период выше, чем в осенне-зимний
период. Поскольку амплитуда сезонных колебаний уменьшается, можно предположить
существование мультипликативной модели. Определим её компоненты.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей
средней. Методика, применяемая на этом шаге, полностью совпадает с методикой
аддитивной модели. Результаты расчетов оценок сезонной компоненты представлены
в таблице:
Таблица 5
|
№ квартала
|
Прибыль компании
|
Итого за четыре квартала
|
Скользящая средняя за
четыре квартала
|
Центрированная скользящая
средняя
|
Оценка сезонной компоненты
|
|
1
|
72
|
|
|
|
|
|
2
|
100
|
|
|
|
|
|
3
|
90
|
326
|
81,500
|
81,250
|
1,108
|
|
4
|
64
|
324
|
81,000
|
80,000
|
0,800
|
|
5
|
70
|
316
|
79,000
|
77,750
|
0,900
|
|
6
|
92
|
306
|
76,500
|
75,750
|
1,215
|
|
7
|
80
|
300
|
75,000
|
74,000
|
1,081
|
|
8
|
58
|
292
|
73,000
|
71,500
|
0,811
|
|
9
|
62
|
280
|
70,000
|
68,500
|
0,905
|
|
10
|
80
|
268
|
67,000
|
65,750
|
1,217
|
|
11
|
68
|
258
|
64,500
|
63,250
|
1,075
|
|
12
|
48
|
248
|
62,000
|
59,500
|
0,807
|
|
13
|
52
|
228
|
57,000
|
54,750
|
0,950
|
|
14
|
60
|
210
|
52,500
|
50,250
|
1,194
|
|
15
|
50
|
192
|
48,000
|
|
|
|
16
|
30
|
|
|
|
|
Шаг 2. Найдем оценки сезонной компоненты как частное от деления
фактических уровней ряда на центрированные скользящие средние (колонка 6
таблицы). Используем эти оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый
квартал оценки сезонной компоненты Si. Взаимопогашаемость сезонных воздействий в мультипликативной
модели выражается в том, что сумма значений сезонной компоненты по всем
кварталам должна равняться числу периодов в цикле. В нашем случае число
периодов одного цикла (год) равно четырем кварталам. Результаты расчетов сведем
в таблицу:
Таблица 6
|
Показатели
|
Год
|
№ квартала, i
|
|
|
I
|
II
|
III
|
IV
|
|
1
|
-
|
-
|
1,108
|
0,800
|
|
2
|
0,900
|
1,215
|
1,081
|
0,817
|
|
3
|
0,905
|
1,217
|
1,075
|
0,807
|
|
4
|
0,950
|
1,194
|
-
|
-
|
|
Итого за I-й
квартал (за все годы)
|
|
2,755
|
3,626
|
3,264
|
2,424
|
|
Средняя оценка сезонной
компоненты для I-го квартала, 
|
1,209
|
1,088
|
0,808
|
|
|
Скорректированная сезонная
компонента,  0,9131,2021,0820,803 0,9131,2021,0820,803
|
|
|
|
|
|
Здесь сумма средних оценок сезонных компонент по всем четырем кварталам
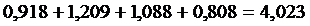
не равна четырем. Чтобы эта сумма равнялась четырем, умножим каждое
слагаемое на поправочный коэффициент
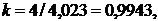 т.е.
т.е.
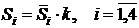 .(11)
.(11)
Значения
скорректированных сезонных компонент записаны в последней строке таблицы 6.
Теперь их сумма равна четырем. Занесем эти значения в новую таблицу (колонка 3
таблицы 7):
Таблица
7
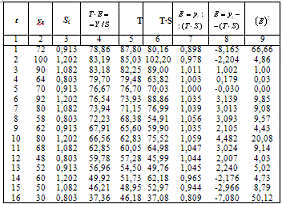
Шаг
3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной
компоненты. Тем самым мы получим величины
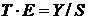 ,(12)
,(12)
которые
содержат только тенденцию и случайную компоненту (колонка 4).
Шаг
4. Определим трендовую компоненту в мультипликативной модели. Для этого
рассчитаем параметры линейного тренда, используя уровни (Т+Е). Уравнение тренда
имеет вид:
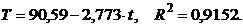
Подставляя
в это уравнение значения 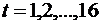 , найдем уровни Т для каждого момента времени (колонка
5 таблицы).
, найдем уровни Т для каждого момента времени (колонка
5 таблицы).
Шаг
5. Найдем уровни ряда по мультипликативной модели, умножив уровни Т на значения
сезонной компоненты для соответствующих кварталов (колонка 6 таблицы).
Шаг
6. Расчет ошибок в мультипликативной модели произведем по формуле:
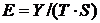 .(13)
.(13)
Численные
значения ошибок приведены в колонке 7 таблицы. Для того, чтобы сравнить
мультипликативную модель и другие модели временного ряда, можно по аналогии с
аддитивной моделью использовать сумму квадратов абсолютных ошибок. Абсолютные
ошибки в мультипликативной модели определяются как:
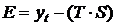 .(14)
.(14)
В
данной модели сумма квадратов абсолютных ошибок составляет 207,4. Общая сумма
квадратов отклонений фактических уровней этого ряда от среднего значения равна
5023. Таким образом, доля объясненной дисперсии уровней ряда составляет 95,9%.
Прогнозирование
по аддитивной или мультипликативной модели временного ряда сводится к расчету
будущего значения временного ряда по уравнению модели без случайной
составляющей в виде
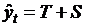 (1’)
(1’)
для
аддитивной или
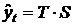 (2’)
(2’)
для
мультипликативной модели.