Активизация учебной деятельности младших школьников

Содержание

Введение

Глава 1. Теоретические основы активизации учебной деятельности младших школьников

.1 Определение понятий «учебная деятельность», «активизация учебной деятельности» в педагогической литературе

.2 Особенности учебной деятельности младших школьников

.3 Дидактические основы активизации познавательной деятельности

Глава 2. Активизация учебной деятельности младших школьников при изучении темы «Площадь фигур»

.1 Игра как средство активизации учебной деятельности младших школьников

2.2 Методика изучения темы «Площадь геометрических фигур» на уроках математики в начальной школе

2.3 Практическое обоснование проблемы активизации учебной деятельности младших школьников при изучении темы «Площадь фигур»

Заключение

Список использованных источников

Приложение

Введение

Актуальность исследования. Ключевой проблемой в решении задачи повышения эффективности и качества учебного процесса является активизация познавательной деятельности младших школьников. Ее особая значимость состоит в том, что учение, являясь отражательно-преобразующей деятельностью, направлено не только на восприятие учебного материала, но и на формирование отношения ученика к самой познавательной деятельности. Знания, полученные в готовом виде, как правило, вызывают затруднения учащихся в их применении к объяснению наблюдаемых явлений и решению конкретных задач.

Проблема активизации учебно-познавательной деятельности младших школьников не нова для ученых России она была поставлена еще в 40 - 50 годы XX века И.А. Каировым, М. А. Даниловым, Р.Г. Лембером.

Исследованием особенностей учебной деятельности учащихся, дидактических закономерностей активизации учебно-познавательной деятельности, уровней познавательной активности, ее мотивационных характеристик, методов, приемов и форм активизации познавательной деятельности занимались многие психологи, дидакты и методисты. В частности, Ю.К. Бабанский, П.Я. Гальперин, В.А. Рубинштейн, В.А. Крутецкий, Е.Н. Кабанова-Меллер, И.С. Якиманская и др.

Математика - один из самых трудных учебных предметов. Она оказывает огромное влияние на умственное и интеллектуальное развитие.

Большое значение при ознакомлении с величиной имеет использование знаний, умений и навыков, приобретаемых учащимися в связи с изучением фигур и операций над фигурами (деление фигур на части, составление фигур из других). И наоборот, использование представлений о величине, ее свойствах и измерении в процессе формирования понятия «фигура».

Так, например, на основе представлений о площадь фигуры дети знакомятся с важнейшим свойством, которое состоит в том, что площадь фигуры, составленной из нескольких частей, равна сумме площадей этих частей.

Трудность обучения состоит в том, что учителям нелегко дифференцировать материал из учебников [7, с. 12].

По учебнику «Математика. 2 класс» авторов Н.Б. Истоминой и И.Б. Нефедовой дети изучают площадь фигуры, способы сравнения площадей с помощью различных мерок, единицы площади (1 см², 1 дм², 1 м²), измерение площадей фигур, палетка, площадь и периметр прямоугольника. Изучение этих вопросов используется для разъяснения смысла действий умножения и деления, свойств этих действий, а также для формирования табличных навыков умножения и деления [14, с. 64].

По учебнику «Математика. 3 класс» авторов М.И. Моро, С.И. Волковой и И.В. Степановой дети лишь в третьем классе начинают изучение темы «Площадь. Единицы площади». Сначала учащиеся знакомятся с разными способами нахождения площадей с помощью различных мерок, на глаз. Далее идет изучение темы «Квадратный сантиметр», затем «Площадь прямоугольника» и «Квадратный дециметр». И только в четвертом классе продолжается изучение темы «Единицы площади»: квадратный метр, квадратный километр, квадратный миллиметр, ар, гектар. Позже дети учатся находить приблизительную площадь фигуры с помощью палетки. И в заключении «Нахождение искомых долей целого» [25, с. 21].

В учебнике математики Э.И. Александровой для первого класса уже с первой главы начинается изучение величин. На пятом уроке дети знакомятся через наложение предметов с понятием площадь и ее периметром. С восьмого по девятый урок идет изучение площади. И только во второй главе начинается знакомство с мерками: «Какие бывают мерки?». И лишь в разделе «Это интересно» дается подробное описание мер площади.

В учебники математики И.И. Аргинской для второго класса теме «Площадь прямоугольника» отводится отдельная глава. В ней сначала дается понятие площади фигуры, затем идет закрепление. После чего постепенно вводится мера измерения площади из вырезанных квадратиков с разными длинами сторон. Далее вводится единица измерения площади: 1см² и только в конце вводится правило нахождения площади прямоугольника [2, с. 31].

Объект исследования - процесс активизации учебной деятельности младших школьников.

Предмет исследования - активизация учебной деятельность младших школьников при изучении темы «Площади фигур».

Цель исследования - теоретически обосновать процесс активизации учебной деятельности младших школьников при изучении темы «Площадь фигур».

Задачи исследования данной темы:

1.    Изучить и проанализировать теоретическую и методическую литературу по вопросу активизации учебной деятельности младших школьников.

2.      Рассмотреть особенности использования игр на уроках математики для активизации учебной деятельности младших школьников.

.        Изучить методические особенности темы «Площадь фигур» на уроках математики в начальной школе.

.        Выявить влияние дидактических игр при изучении темы «Площадь фигур».

Гипотеза исследования: если в процессе изучения темы «Площадь фигур» использовать дидактические игры, то это будет способствовать активизации учебной деятельности младших школьников.

Методы исследования:

1.    Изучение и анализ психолого-педагогической литературы по теме исследования.

2.    Анализ и обобщение опыта учителей при проведении уроков математики по данной теме.

Глава 1. Теоретические основы формирования приемов учебной деятельности младших школьников

1.1 Определение понятий «учебная деятельность», «активизация учебной деятельности» в педагогической литературе

Учебная деятельность - один из основных (наряду с трудом и игрой) видов деятельности человека, специально направленный на овладение способами предметных и познавательных действий, обобщенных теоретических знаний. Усвоение (учение) является существенной характеристикой учебной деятельности, тем не менее, это различные явления: усвоение - это процесс, осуществляющийся в любой деятельности, Учебная деятельность - это вид деятельности, особая форма социальной активности личности.

Учебная деятельность выполняет двоякую социальную функцию. Будучи формой активности индивида, она является условием и средством его психического развития, обеспечивая ему усвоение теоретических знаний и тем самым развитие у него тех специфических способностей, которые в этих знаниях кристаллизованы. На определенном этапе психического развития (в младшем школьном возрасте) учебная деятельность играет ведущую роль в формировании личности. Как форма социально нормируемого сотрудничества ребенка со взрослыми, учебная деятельность является одним из основных средств включения подрастающих поколений в систему общественных отношений, в открыто коллективную деятельность, в ходе которой усваиваются ценности и нормы, лежащие в основе любой коллективной деятельности.

Как и игра, учебная деятельность - производный, исторически выделившийся из труда вид деятельности. Ее выделение обусловлено появлением теоретического знания, содержание которого лишь частично проявляется в отдельных практических действиях и которое, следовательно, не может быть полноценно усвоено в процессе овладения этими действиями. Развитие человеческого знания (от эмпирического уровня к теоретическому) с необходимостью вызывает развитие, перестройку учебной деятельности. Реальные масштабы этой перестройки определяются социально-экономическими условиями жизни общества, его потребностями в вооружении подрастающих поколений знаниями теоретического и эмпирического уровня. В наиболее развитых формах учебная деятельность выступает впервые в эпоху научно-технической революции.

Сущность учебной деятельности заключается в решении учебных задач, основное отличие которых в том, что их цель и результат состоят в изменении самого действующего субъекта, заключающемся в овладении определенными способами действия, а не в изменении предметов, с которыми действует субъект. Решение отдельной учебной задачи определяет целостный акт учебной деятельности, т.е. ту ее простейшую «единицу», внутри которой проявляется строение этого вида деятельности в целом. Осуществление такого акта предполагает актуализацию специфического мотива учебной деятельности - определение конечной учебной цели - предварительное определение системы промежуточных целей и способов их достижения - выполнение системы собственно учебных действий - выполнение действий контроля - оценку результатов учебной деятельности.

Как любая другая деятельность человека, учебная деятельность полимотивирована. Особое место в системе мотивов учебной деятельности принадлежит познавательному интересу, непосредственно связанному с ее содержанием и представляющему собой специфический, внутренний мотив учебной деятельности, без которого усвоение знаний из конечной цели («мотива-цели») может превратиться в условие достижения других целей, т.е. деятельность субъекта не приобретает учебного характера (или утрачивает его). Возможности и условия актуализации познавательного интереса в учебной деятельности определяются его направленностью (на результаты или способы познания) и уровнем развития (является ли он ситуационным или устойчивым, личностным).

На основе актуализированного мотива учебной деятельности определяются ее конечная и промежуточные цели. Хотя целеполагание в учебной деятельности выступает чаще всего как «принятие» субъектом поставленных извне целей, оно является не одномоментным актом, а процессом осознания предметного содержания поставленных целей, их соотнесения с актуальными мотивами, «доопределения». О сложности этого процесса свидетельствуют хорошо известные факты «переопределения» учебных целей. Одновременно с определением целей осуществляется предварительный анализ условий и способов их достижения, в результате чего формируется схема акта, ориентирующая субъекта в процессе его выполнения. Реализация целей учебной деятельности обеспечивается системой учебных действий, состав и строение которых могут значительно варьировать в зависимости от объекта усвоения (теоретическое или эмпирическое знание), способа его представления, требуемого уровня усвоения и т.п.

Описанное строение характерно для развитых форм учебной деятельности, являющихся результатом ее формирования в условиях школьного обучения. Процесс формирования учебной деятельности изучен недостаточно. На основании экспериментальных данных в нем можно выделить три основные стадии. Первая из них характеризуется освоением отдельных учебных действий - на этой основе возникает ситуационный интерес к способам действия и формируются механизмы «принятия» частных учебных целей - осуществление учебной деятельности возможно только при непосредственном взаимодействии с учителем, который ставит цели, организует действия, осуществляет их контроль и оценку. На второй стадии учебные действия объединяются в целостные акты деятельности, подчиненные достижению более отдаленной конечной цели - по мере формирования таких актов познавательный интерес приобретает устойчивый характер, начиная выполнять функцию смыслообразующего мотива учебной деятельности - с этим связано дальнейшее развитие механизмов целеполагания, обеспечивающих не только принятие поставленной извне конечной цели, но и самостоятельную ее конкретизацию - на этой основе интенсивно формируются действия контроля и оценки. Третья стадия характеризуется объединением отдельных актов учебной деятельности в целостные системы - познавательный интерес характеризуется обобщенностью, устойчивостью и избирательностью, начиная во все большей степени выполнять функцию побудительного мотива деятельности - в системе учебных действий одно из центральных мест занимают действия с различными источниками учебной информации (учебником, справочником, картой и т.п.). Хронологические рамки указанных стадий относительны и определяются в первую очередь условиями обучения. При неблагоприятных условиях развитие учебной деятельности может остановиться на первой стадии - в оптимальных условиях уже на 6-7-м году обучения учебная деятельность вступает в высшую стадию своего формирования.

Понятие «учебная деятельность» достаточно неоднозначно. При расширительном его толковании этим термином подменяются понятия научения и учения. Согласно периодизации возрастного развития Д.Б. Эльконина учебная деятельность является ведущей в младшем школьном возрасте. Однако она продолжает оставаться одним из основных видов активности и в последующие возрастные периоды - подростковый, старший школьный и студенческий. В этом смысле учебную деятельность можно определить как деятельность субъекта по овладению обобщенными способами решения жизненных задач и саморазвитию <#"650527.files/image001.gif">

Верно ли, что площадь данного прямоугольника, изображенного на рис. 2, Меньше площади этого же прямоугольника? (Свойство антирефлексивности отношения «меньше» на множестве площадей геометрических фигур). Сравните площади фигур.

Наложением фигур друг на друга дети устанавливают, что площадь квадрата меньше площади круга, а площадь круга меньше площади прямоугольника. Учащиеся убеждаются также, что площадь квадрата меньше площади прямоугольника. Учитель подводит итог этой работы: «Так как площадь квадрата меньше площади круга, а площадь круга меньше площади прямоугольника, то площадь квадрата меньше площади прямоугольника».. Упражнения, приводящие к понятию площади фигуры.

. На сколько квадратных сантиметров площадь квадрата со стороной 3 см меньше площади квадрата со стороной 5 см? (Существование разности площадей.). Упражнения, иллюстрирующие переместительное свойство сложения площадей фигур.

Чему равна площадь фигуры?

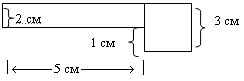
Учитель вместе с учащимися составляет выражения:

-5+3-3 (кв. см) - площадь данной фигуры;

• 3 + 2 • 5 (кв. см) - площадь этой же фигуры. В результате вычислений устанавливается, что 2 • 5 + 3 • 3 = 3 • 3 + 2 • 5.

Решение этих задач подтверждает свойство переместительности сложения во множестве площадей фигур.. Упражнения, иллюстрирующие сочетательное свойство сложения площадей фигур.

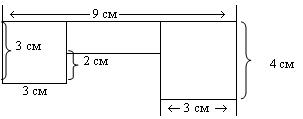
Определить площадь фигуры различными способами. Одному из способов соответствует выражение (3×3+3×1) + 4×3 (кв. см), другому - 3×3 + (3×1 + 4×3) (кв. см.).

Вычисляя значения этих выражений, учащиеся устанавливают, что сложение величин ассоциативно.. Задания, иллюстрирующие свойство монотонности сложения в множестве площадей фигур.

Найти площадь фигуры несколькими способами. Сравнить площадь всей фигуры с частью площади этой же фигуры.

В результате непосредственного счета квадратов, из которых состоит данная фигура, учащиеся устанавливают, что площадь фигуры равна (6+4) кв. см. С помощью чертежа подтверждается истинность неравенств: (6+4)>4 и (6+4)>6. (Свойство монотонности сложения в системе площадей). Задачи, неявно вводящие следующее свойство площади фигуры: площадь фигуры можно делить на любое число п одинаковых частей.

Измерение площади фигуры с помощью палетки свидетельствует о том, что любую площадь можно делить на несколько одинаковых частей.. Измерить площадь обложки учебника «Математика» в квадратных дециметрах и квадратных сантиметрах. Сравнить результаты измерения.

Учащиеся убеждаются, что площадь обложки удобнее измерять в квадратных сантиметрах [15, с. 33].

2.3 Практическое обоснование проблемы активизации учебной деятельности младших школьников при изучении темы «Площадь фигур»

Основные задачи изучения геометрические материала в 1-4 классах заключаются в том, чтобы создать у детей четкие и правильные геометрические образы, развить пространственные представления, вооружить их навыками черчения и измерения, имеющими большое жизненно-практическое значение, и тем самым подготовить учеников к успешному изучению систематического курса геометрии.

Формирование геометрических представлений является важным разделом умственного воспитания, политехнического образования, имеют широкое значение во всей познавательной деятельности человека.

Сформировав цель, задачи и выдвинув гипотезу исследования выпускной квалификационной работы, нами были три этапа исследования.

База исследования: Школа №3. В эксперименте участвовали учащиеся 3 класса в составе 20 человек.

Цель исследования: спланировать и провести исследование, доказывающее положительное влияние дидактических игр на формирование навыков вычисления площади фигур, построения геометрических фигур.

Начальный этап.

На каждом уроке математики учитель должен отводить некоторое время для заданий, которые требуют от учеников более активной, творческой умственной деятельности, связанной с анализом, сравнением, обобщением и т.д. Подобранные задания должны соответствовать теме и целям урока.

В зависимости от этого учитель определяет место таких заданий на уроке.

С детьми был проведён контрольный срез № 1. (см. приложение 4), который показал уровень развития математических способностей, навыков вычислений периметра и площади фигур, построения геометрических фигур.

Оценка «4»: 11-15 б.

Оценка «3»: 0-10 б.

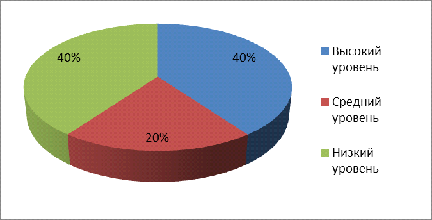
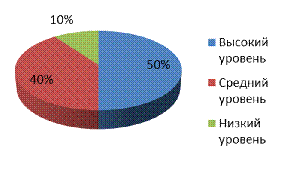
На основе результатов исследования, можно сделать выводы:

Оценка «5» - 4 чел. (40%),

Оценка «4»- 2 чел. (20%),

Оценка «3» - 4 чел. (40%) (см. рис. 1.).

Рисунок 1. Уровень развития математических способностей, навыков вычислений периметра и площади фигур, построения геометрических фигур.

Анализ выполнения заданий начального этапа.

№1.

Выполнили верно - 1 чел. (10%)

Допустили ошибки:

-  в нахождении длины квадрата - 7 чел. (70%)

-       в нахождении периметра - 6 чел. (60%)

-       в нахождении площади - 6 чел. (60%)

№2.

Выполнили верно - 1 чел. (10%)

Допустили ошибки:

в нахождении площади квадрата - 9 чел. (90%)

№3.

Выполнили верно - 1 чел. (10%)

Допустили ошибки:

-    в нахождении площади разными способами - 9 чел.(90%)

-       в построении прямоугольника, площадь которого находится аналогичным способом - 9 чел. (90%)

Вывод: на основе полученной диаграммы №1 мы видим, что из этой группы детей есть учащиеся, которые получили следующие оценки:

-    Оценка «5» - 40%;

-       Оценка «4» - 20%;

-       Оценка «3» - 40%.

Среди этой группы детей уровень математических способностей не очень высок - средний, поэтому с ними будет проводиться дальнейшая работа.

Второй этап исследования.

Цель: подобрать дидактические игры для проведения уроков математики и разработать конспекты урока с использованием дидактических игр по теме «Площадь фигур».

На данном этапе были подобраны дидактические игры (приложение 1), разработаны и проведены уроки с их использованием, позволяющие учащимся познакомиться в занимательной форме с темой «Площадь фигур», развивать интерес школьников, им легче запомнить новый материал (Приложение 2). Учащиеся активно отвечают на уроках, у них повышается работоспособность. Дети не только активно занимались учёбой, но и чувствовали себя уверенно и комфортно.

Для развития их математических способностей и повышения навыка определения площади фигур; навыка построения геометрических фигур у учащихся нами были подобраны различные задания по устранению выявленных ошибок. Работа с этими детьми проводилась как на уроках, так и во внеурочное время. На каждом уроке математики отводилось некоторое время для заданий, которые требовали от учеников более активной творческой умственной деятельности, связанной с анализом, сравнением, обобщением и т.д. Подобранные задания соответствовали теме и целям урока. В зависимости от этого учитель определял место таких заданий на уроке (см. приложение 6).

На внеклассном занятии мы закрепляли умения учащихся находить площади различных фигур. После изучения нового материала, где использовались игровые упражнения, данный материал усвоился легко, поэтому на внеклассном занятии учащиеся чувствовали себя раскованно.

Вывод второго этапа эксперимента: занятия с детьми проводились один раз в неделю после уроков. В ходе урока дети пытались решать задания с помощью учителя, сначала боялись проявить самостоятельность, не могли предложить свой вариант решения некоторых упражнений. В ходе нашей работы дети стали больше проявлять самостоятельность, не боялись допускать ошибки, предлагали интересные пути решения.

Завершающий эксперимент.

В конце нашего исследования с детьми был проведен контрольный срез №2, где в упражнения были включены задания аналогичные тем, в которых были допущены ошибки на начальном этапе (см. приложение 7).

Результаты этого среза отражены на рисунке 2.

Рисунок 2. Сравнения Уровень развития математических способностей, навыков вычислений периметра и площади многоугольников, построения геометрических фигур.

Начальный этап                                                Завершающий этап

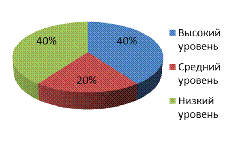
Сравнительный анализ полученных результатов.

Высокий уровень (16-21б.) - 40% Высокий уровень (20 - 21 б.) - 50%

Средний уровень (11 -15б.) - 20% Средний уровень (15 - 19 б.) - 40 %

Низкий уровень (0 -10б.) - 40% Низкий уровень (0 - 14 б.) - 10 %

Вывод контрольного этапа.

Использование заданий и упражнений, активизирующих мыслительную деятельность младших школьников при изучении геометрического материала способствует развитию математических способностей; повышению навыка вычисления периметра и площади фигур; навыка построения геометрических фигур.

Заключение

Познавательная деятельность является одной из ведущих форм деятельности ребёнка, которая провоцирует учебную, на базе познавательного энтузиазма. Поэтому активизация познавательной деятельности школьников составная часть совершенствования способов обучения

Игры и игровые упражнения - наиболее известные и часто применяемые в современной практике дошкольного воспитания виды занимательного математического материала.

Обучая маленьких детей в процессе игры, мы стремимся к тому, чтобы радость от игровой деятельности постепенно перешла в радость учения. Учение должно быть радостным. Знания нужны не ради знаний, а как важная составляющая личности, включающая умственное, нравственное, эмоциональное (этическое) и физическое воспитание.

Важнейшей задачей математического образования является вооружение учащихся общими приемами мышления, пространственного воображения, развитие способности понимать смысл поставленной задачи, умение логично рассуждать, усвоить навыки алгоритмического мышления. Каждому важно научиться анализировать, отличать гипотезу от факта, отчетливо выражать свои мысли, а с другой стороны - развить воображение и интуицию (пространственное представление, способность предвидеть результат и предугадать путь решения). Именно математика предоставляет благоприятные возможности для воспитания воли, трудолюбия, настойчивости в преодолении трудностей, упорства в достижении целей.

Одной из основных целей изучения математики является формирование и развитие мышления человека, прежде всего, абстрактного мышления, способности к абстрагированию и умения «работать» с абстрактными, «неосязаемыми» объектами.

В начальных классах рассматриваются такие величины: длина, площадь, масса, емкость, время и др. Учащиеся должны получить конкретные представления об этих величинах, ознакомиться с единицами их измерения, овладеть умениями измерять величины, научиться выражать результаты измерения в различных единицах, выполнять арифметические действия над величинами.

Среди различных систем величин, изучаемых в школе на различных этапах обучения, учащиеся уже в начальной школе знакомятся с понятием площади плоской фигуры. На первых этапах обучения речь идет об интуитивном представлении о площади, а не о строгом математическом обосновании этого понятия.

Первоначально у учащихся представление о площади плоской фигуры связывается с подсчетом числа единичных квадратов. Изучение площади в школе начинается с рассмотрения площади прямоугольника. Использование палетки позволяет сделать не только доступным для учащихся изучение вопроса об измерении площади любой плоской фигуры, но и помогает им правильно понять идею измерения площади. Переходя от непосредственного измерения площади путем сравнения ее с единицей измерения к способам косвенного измерения площадей, учителю необходимо обратить внимание учащихся на то, что для измерения площадей нет столь удобных приборов, какие были для измерения длин отрезков и величин углов. Поэтому стоит более внимательно разобраться с величиной - площадью и выявить способы ее нахождения.

Включение в процесс обучения игровых упражнений приносит заметные результаты. У детей появляются сосредоточенность, внимание, развивается мышление. Дети становятся более организованными.

Список литературы

1.   Амонашвили Ш.А. Личностно-гуманная основа педагогического процесса. - Минск: Университетское, 2000. - 560 с.

2.      Аргинская И.И. Математика. Методич. пособие к уч. 2-го кл. нач. шк. М., 2000.

3.   Берлянд И.Е. Загадки и числа: воображаемые уроки в 1-м классе: пособие для учителя. - М.: Академия, 2006.

4.      Божович Л.И. Личность и ее формирование в детском возрасте. - М.: Педагогика, 2003. - С.124.

.        Вернье Ж. Ребенок, математика и реальность: проблемы преподавания математики в начальной школе. - М.: Ин-т психологии РАН, 2000.

.        Гаркавцева Т.Ю. Геометрический материал в 1 классе как средство развития пространственного мышления учащихся. // Начальная школа. 2006. - № 10.

7.   Гейдман Б.П., Иванина Т.В., Мишарина И.Э. Математика 3 класс. - М., 2000.

8.   Глушков И.К. Методика работы над задачей в начальной школе. - Йошкар-Ола: Редакция журнала «Марий Эл учитель». - 2001.

9.      Давыдов В.В. Проблемы развивающего обучения. - М.: Педагогика, 2006. - 288 с.

.        Долбилин Н.П., Шарыгин И.Ф. О курсе наглядной геометрии в младших классах // Математика в школе. 2000. - № 6.

12.    Жиколкина Т.К. Математика. Книга для учителя. 2 кл. - М.: Дрофа, 2000.

.        Зайцев В.В. Математика для младших школьников. Методическое пособие для учителей и родителей. - М.: Владос, 2002.

.        Истомина Н.Б. Методика обучения математике в начальных классах. учеб. пособие. - М.: 2000.

.        Истомина Н.Б. Методика обучения математики в начальных классах.- М.: Академия, 2001.

.        Корешкова Т.А., Цукерман В.В. Многоугольники и их площадь в школьном курсе математики. // Математика в школе, с.70, - №3, - 2003.

17. Костицын В.Н. Моделирование на уроках геометрии: теория и методические рекомендации. - М.: Владос, 2000.

18.    Кувашова Н.Г. Тематический тестовой контроль по математике в нач. шк. - Волгоград: Учитель 2003.

19. Лавриненко Т.А. Как научить детей решать задачи. - Саратов: Лицей, 2000.

20.    Леонтьев А.И. К вопросу о развитии арифметического мышления ребенка.- М., 2000. - 109 с.

.        Матюхина М.В. Мотивация учения младших школьников. - М.: Педагогика, 2004. - 256 с.

22. Методика начального обучения математике. /Под общ. ред. А.А. Столяра, В.Л. Дроздова - Минск: Высш. школа, 2008.

23. Моро М.И. Математика: учебник для 1 класса. М.: Просвещение, 2003., 96 с.

24. Моро М.И. Математика: учебник для 2 класса. М.: Просвещение, 2012.

25. Моро М.И. Математика 3 класс. В 4 ч. Ч. 2. М., Просвещение. -Мокрушина О.А. Поурочные разработки по математике. М., «ВАКО», 2005

26. Моро М.И. Математика: учебник для 4 класса. М.: Просвещение, 2011, 112 с.

27. Моршнева Л.Г., Альхова З.И. Дидактический материал по математике. - Саратов: «Лицей», 2009.

28.    Овчинникова М.В. Методика изучения темы «Величины» на уроках математики в начальных классах: Методические рекомендации для студентов факультета «Начальное обучение. Дошкольное воспитание». - Ялта: ЦОП «Надежда», 2000. - 54 с. - ил.

.        Орлов А.Б. Психология личности и сущности человека. Парадигмы, проекции, практика / А.Б. Орлов. - М.: Академия, 2002. - 272 с.

30. Пичугин С.С. Организация творческой работы с геометрическим материалом. // Начальная школа. № 4, - 2007.

31.    Подласый И.П. Педагогика начальной школы. - М.: Владос, 2000. - 400 с.

.        Психология воспитания: пособие для методистов дошкольного и начального школьного образования, преподавателей-психологов / А.Д. Грибанова, В.К. Калиненко, Л.М. Кларина и др.; под ред. В.А. Петровского. - Изд. 2-е. - М.: Аспект-пресс, 2000. - 152 с.

.        Психология: учебник / Под. ред. А.А. Крылова. - М.: ПБОЮЛ, 2001. - 584 с.

.        Савинова Р.В., Белолюбская А.А. Логические игры и упражнения для развития интеллектуальных способностей у детей 6-7 лет: Метод. Пособие. / Р.В. Савинова, А.А. Белолюбская Я., Изд-во Департамента НиСПО МО РС (Я), - 2002. - 38 с.

35. Стойлова Л.Т. Математика: учебник для студентов высших учебных заведений. - М.: Академия, 2002. - 424 с.

36. Тихоненко А.В., Трофименко Ю.В. О развитии ключевых компетенций младших школьников при выборе рациональных способов решения геометрических задач //Начальная школа. 2007. - № 3.

37.    Фридман, Л.Н. Психология в современной школе / Л.Н. Фридман. - М.: Сфера, 2001. - 224 с.

.        Цукерман Г.А. Опыт типологического анализа младших школьников как субъектов учебной деятельности // Вопросы психологии. - 2000. - №6. - С. 24-32.

.        Шамова Т.И. Активизация учения школьников. - М.: Педагогика, 1982. - 208 с.

.        Эльконин Д.Б., В.В. Давыдов. Возрастные возможности усвоения знаний. - М.: Наука, 2000, - С. 21.

Приложение 1

Игры с геометрическими фигурами.

Игра «Чудесный мешочек» хорошо знакома дошкольникам. Она позволяет обследовать геометрическую форму предметов, упражняться в различении форм. В мешочке находятся предметы разных геометрических фигур. Ребенок обследует их, ощупывает и называет фигуру, которую хочет показать. Усложнить задание можно, если ведущий дает задание найти в мешочке какую-то конкретную фигуру. При этом ребенок последовательно обследует несколько фигур, пока не отыщет нужную. Этот вариант задания выполняется медленнее. Поэтому целесообразно, чтобы чудесный мешочек был у каждого ребенка.

Игра «Найди такой же».

Перед детьми лежат карточки, на которых изображены три-четыре различные геометрические фигуры. Воспитатель показывает свою карточку (или называет, перечисляет фигуры на карточке). Дети должны найти такую же карточку и поднять ее.

Игра «Кто больше увидит?»

На фланелеграфе в произвольном порядке расположены различные геометрические фигуры. Дошкольники рассматривают и запоминают их. Ведущий считает до трех и закрывает фигуры. Детям предлагают назвать как можно больше фигур, размещенных на фланелеграфе. Чтобы дети не повторяли ответы товарищей, ведущий может выслушивать каждого ребёнка отдельно. Выигрывает тот, кто запомнит и назовет больше фигур он становится ведущим. Продолжая игру ведущий меняет количество фигур

Игра «Посмотри вокруг» помогает закрепить представления о геометрических фигурах, учит находить предметы определенной формы. Игра проводится в виде соревнования на личное или командное первенство. В этом случае группа делится на команды. Ведущий (им может быть воспитатель или ребенок) предлагает назвать предметы круглой, прямоугольной, квадратной, четырехугольной формы, форму предметов, не имеющих углов, и т.д. За каждый правильный ответ, играющий или команда получает фишку, кружок. Правилами предусматривается, что нельзя называть два раза один и тот же предмет. Игра проводится в быстром темпе. В конце игры подводятся итоги, называется победитель, набравший наибольшее количество очков.

Игра «Геометрическая мозаика» предназначена для закрепления у детей знания о геометрических фигурах, формирует умение преобразовывать их, развивает воображение и творческое мышление, учит анализировать способ расположения частей, составлять фигуру, ориентироваться на образец. Организуя игру, воспитатель заботится об объединении детей в одну команду в соответствии с уровнем их умений и навыков. Команды получают задания разной трудности. На составление изображения предмета из геометрических фигур: работа по готовому расчлененному образцу, работа по нерасчлененному образцу, работа по условиям (собрать фигуру человека - девочка в платье), работа по собственному замыслу (просто человека). Каждая команда получает одинаковые наборы геометрических фигур. Дети должны самостоятельно договориться о способах выполнения задания, о порядке работы, выбрать исходный материал. Каждый играющий в команде по очереди участвует в преобразовании геометрической фигуры, добавляя свой элемент, составляя отдельные элементы предмета из нескольких фигур. В заключении игры дети анализируют свои фигуры, находят сходства и различия в решении конструктивного замысла.

Игра «Найди свой домик». Дети получают по одной модели геометрической фигуры и разбегаются по комнате. По сигналу ведущего все собираются у своего домика с изображением фигуры. Усложнить игру можно переместив домик. Детей учат видеть геометрическую форму в окружающих предметах: мяч, арбуз-шар, тарелка, блюдце-обруч-круг, крышка стола, стена, пол, потолок, окно-прямоугольник, платок -квадрат; косынка-треугольник; стакан- цилиндр; яйцо, кабачок- овал.

«Назови геометрическую фигуру»

Цель. Учить зрительно обследовать, узнавать и правильно называть плоскостные геометрические фигуры (круг, квадрат, треугольник, прямоугольник, овал)

Материал. Таблицы с геометрическими фигурами. На каждой таблице контурные изображения двух-трёх фигур в разных положениях и сочетаниях.

Ход игры.

Игра проводится с одной таблицей. Остальные можно закрыть чистым листом бумаги. Взрослый предлагает внимательно рассмотреть геометрические фигуры, движением руки обвести контуры фигур, назвать их. На одном занятии можно показать ребёнку 2-3 таблицы.

«Найди предмет такой же формы»

У взрослого имеются нарисованные на бумаге геометрические фигуры: круг, квадрат, треугольник, овал, прямоугольник и т.д.

Он показывает ребёнку одну из фигур, например, круг. Ребёнок должен назвать предмет такой же формы.

«Угадай, что спрятали»

На столе перед ребёнком карточки с изображением геометрических фигур. Ребёнок внимательно их рассматривает. Затем ребёнку предлагают закрыть глаза, взрослый прячет одну карточку. После условного знака ребёнок открывает глаза и говорит, что спрятано.

Приложение 2

Конспекты уроков с использованием дидактических игр

Урок математики по теме: «Квадратный сантиметр»

Цель: ознакомить учащихся с квадратным сантиметром как единицей, и научить пользоваться этой единицей измерения.

Задачи:

Образовательные - продолжать закреплять навыки решения задач и примеров; дать представление о применении новой единицы измерения.

Развивающие - развивать логическое мышление, внимание, память, наблюдательность; вычислительные умения; навыки измерения длины и площади.

Воспитательные - воспитывать умение работать в паре, усидчивость, аккуратность.

Оборудование: геометрические фигуры, карточки с заданием, записи на доске, учебник, образец кв. см.

Ход урока.

1.  Организационный момент.

2.      Индивидуальная работа.

3.  Геометрический материал.

(На наборном полотне выставлены геометрические фигуры).

Круг, прямоугольник, треугольник, квадрат, многоугольник.

-       Назовите фигуры.

-             Какое общее название можно дать этим фигурам?

-             Чем они отличаются?

-             Что знаете про стороны квадрата?

(У него все стороны равны).

4.  Сообщение новой темы и цели урока.

-       Сегодня на уроке вы познакомитесь с единицей измерения площади, которая называется квадратный сантиметр и научитесь пользоваться единицей измерения.

-       Это кв. см. - стороны которого равны 1см.

Он очень маленький, но играет огромную роль в математике.

А сейчас мы научимся чертить кв.см. в тетради.

(Учитель на доске чертит, а дети в тетради).

-       Повторяю ещё раз:

Это кв.см., при помощи которого мы будем измерять S фигур, короче можно записать так 1 кв.см.

(Учитель подписывает на доске, дети в тетрадях).

ВЫВОД: если в одном кв. см. измеряют S фигур, то в линейных см. измеряют длину отрезка.

5.  Закрепление новой темы.

-             Начерти фигуру площадью 8 см².

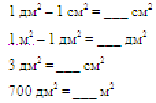
Решение задачи: Площадь одной из комнат трехкомнатной квартиры равна 20 м², а площадь второй - на 4 м² меньше. Площадь первых двух комнат на 17 м² больше площади третьей комнаты. Какова площадь третьей комнаты?

а) Чтение задачи. б) Состав схемы задачи.

(Учитель составляет схему на доске, дети в тетрадях).

в) Решение задачи.

6.  Итог урока.

С какой новой единицей измерения S вы познакомились?

Тема: «Измерение площади фигур с помощью палетки».

Цель: познакомить детей со способом нахождения площади фигур различной формы с помощью палетки.

Задачи:

Образовательная - закреплять умения учащихся заменять крупные единицы мелкими, а мелкие крупными, совершенствовать умение решать задачи. Развивающая - Развивать логическое мышление учащихся, умение точно и обоснованно аргументировать, выделять те стороны наблюдаемых явлений, которые необходимы для существа исследования и осмысления задачи.

Воспитывающая - воспитывать аккуратность, взаимоуважение друг другу.

Материал: учебник, слайды числами, с геометрическими фигурами, палеткой; индивидуальные карточки, палетки.

Ход урока. Организационный момент.

-Здравствуйте ребята. Сегодня у нас не обычный урок. К нам пришли гости. Давайте улыбнемся друг другу, гостям и мне. Садитесь. Начнем свою работу.

Мы сегодня познакомимся со способом нахождения площади фигур различной формы; вспомним единиц измерения длины и единиц измерения площади; закрепим знания по решению задач.

II. Устный счет:

а) Взяли математические тренажеры. Сегодня мы с вами повторим умножение и деление на круглых чисел. (Дети читают выражение выговаривая каждое число и говорят ответ)

б) Прочитайте числа (Показ на компьютере) 5000000; 400030; 2720532; 603010; 1005000; 100001.

Хорошо. Вспомните, какие единицы измерения длин вы знаете? (см, мм, дм, км, м)

Назовите самую маленькую: (мм). Назовите самую большую (км).

А мы на уроках пользуемся, какими единицами измерения длин? (мм, см)

А какими единицами измерения площади пользуемся? (см², мм²)

Самостоятельная работа

-Теперь выполним задание самостоятельно. (Работа с карточками). Замените мелкие единицы крупными, крупные мелкими.

Карточки:

км²= га

км²= га

км²= га

а= га

а= га 800дм²= м²

км²= м²

км²= м²

1км² 20м²= м²

Проверка фронтально с помощью сигнальных карточек

-В геометрии встречаются различные фигуры. Назовите, какие вы знаете? (треугольник, круг, прямоугольник, квадрат) (Показ на компьютере) Среди данных фигур выберите те, площадь которых умеете находить.

Теперь вспомним, как мы находим площадь квадрата? Напишите формулу на доске. S=a*a Как находим площадь прямоугольника? S=a*b. А что делать с остальными фигурами? Нам на этот вопрос предстоит ответить. Будем учиться находить площади тех фигур, которые мы не можем вычесть известными нам способами. Мы будем находить площадь разных фигур с помощью палетки (Показ). Она и у вас есть, возьмите, посмотрите внимательно. Она из чего сделана? (из пленки) А на пленке что мы видим? (Разделена на квадраты) На какие квадраты? (Они все равны) Измерьте, чему равна сторона одного квадрата? (1 см). Значит, на какие квадратные единицы разделена ваша палетка? (на квадратные сантиметры)

А как работать с ней? Может у вас есть какие-то задумки (ответы детей).

Объяснение учителя

-Чтобы найти, например площадь овала (показ на компьютере), палетку ложем на овал. И считаем полных квадратных сантиметров. Давайте считаем вместе (дети считают, учитель записывает на доске). Их 12. Потом считаем неполных. Их 16. А что же неполными делать? Как считать? (ответы детей). Договорились два неполных квадратных сантиметров считать за один полный. Значит, разделим 16:2=8. И теперь это число прибавляем к числу полных см². 12+8=20 см². Вот мы и нашли. Приблизительная площадь овала равна 20 см².

Теперь прочитаем параграф на стр. 49.

Как вы будете вычислять площадь такой фигуры? (показ на компьютере, объяснение детей)

Физкультминутка

Мы считали, мы считали И немного мы устали Дружно все тихонько встали И друг друга не задели Встали, сели, сели, встали И опять считать начнем

Повторяем алгоритм нахождения площади фигуры с помощью палетки (Дети составляют алгоритм).

Практическая работа.

-У вас на столах палетки и разные фигуры. Вы сами попробуйте найти площадь этих фигур с помощью палетки (У детей разные разноцветные геометрические фигуры. Дети находят, отвечают).

А как вы узнали? Составьте алгоритм нахождения.

. Палетку положим на фигуру.

. Считаем полных см².

. Считаем неполных см² разделим на 2.

. Число полных см² прибавим к числу неполных и находим площадь данной фигуры

Какой можно сделать вывод (повторение хором).

Закрепление

а) Теперь решим задачу. Смотрим № 262. Читаем про себя (Громко считает 1 ученик). Работа по содержанию

О чем задача? Сколько было яблок? Груш? К закрытию сколько осталось? Что спрашивает задача.

Выполнение схематичного рисунка и составление программы решения (На доске условие пишет 1 ученик, а решение самостоятельно)

1.   380-295=85кг (яблок).

2.      180-106=74кг (груш).

.        85-74=11кг (на >).

уровень - №266 (Юлия, Артур).

уровень - №265 (Ранис, Вика).

уровень - №267 (Зиля, Ника).

Каждая пара объясняет свою работу, доказывают.

Работа с тестами

У каждого ученика тестовые задания. Проверка фронтально.

Домашнее задание

№ № 261, 269 стр.50.

Итог урока

С чем мы занимались на уроке? Что нового узнали?

Тема: Площадь фигуры.

Цель: Сформировать понятие о площадях фигур и путях сравнения площадей разных фигур путём наложения одной на другую.

Задачи:

Образовательные - выявить знания учащихся о площади фигур; расширить знания о геометрических фигурах; систематизировать знания учащихся; закрепить знания путём практической деятельности; закрепить понятия «увеличить в…» и «уменьшить в…»; повторить смысл сложения.

Развивающие - развивать умение анализировать; развивать мышление, пространственные представления.

Воспитывающие - воспитывать чувства солидарности и взаимовыручки.

Форма обучения: Урок - игра.

Тип урока: «Открытие» новых знаний.

Оборудование: Учебник, карточки для устного счёта, набор геометрических фигур для учителя и для учеников, шкатулка, карточки для самостоятельной работы, компьютер.

Ход урока:

. Орг. момент. Организовать деятельность учащихся.

Здравствуйте ребята.

Прозвенел звонок,

Начинается урок.

Ваши ушки на макушке,

Слушаем, запоминаем,

На уроке не зеваем.

. Активизация знаний. Выявить знания учащихся.

Ребята, кто знает какое число является сказочным? (33)

Почему вы так считаете?

(Встречается во многих сказка, 33 богатыря, 3 - десятое царство, 3 желания)

Запишите число 33 на строку. Охарактеризуйте его. ( Двузначное число, в нём 3 десятка и 3 единицы, при счёте следует за числом 32 и предшествует числу 34.)

К нам за помощью обратился сказочный герой, чтобы узнать, кто это нужно посчитать примеры. На партах у вас лежат конверты с примерами. Найдите значения выражений. Расположите выражения в порядке убывания их значений и прочитайте спрятанное слово. Составьте из букв имя. (Царевич).

У Ивана-царевича украл Кощей-Бессмертный невесту Елену Прекрасную, унёс её в тридесятое царство. И просит нас Царевич помочь ему, вернуть невесту. Поможем Ивану, ребята?

Отправимся в путь, а перед нами мост, но на нём не хватает дощечек. Но каждое правильно выполненное задание - это одна дощечка.

1.   Найдите сумму чисел 23 и 15.

2.      Найдите произведение чисел 9 и 7.

.        На сколько число 46 больше, чем число 38.

.        Сумму чисел 36 и 15, умножьте на 0.

.        Запишите число в котором 54 десятка.

.        Уменьшаемое 86, вычитаемое 41, найдите разность.

.        По 5 взяли 7 раз.

.        Разность чисел 23 и 16, умножьте на 4.

.        Число 46, уменьшите на 2 десятка.

.        Сколько сантиметров в 5 дециметрах?

Вот и построили мы мост. Можно идти дальше. Привела нас тропинка к избушке на курьих ножках. Вошли мы в избу и кого же там увидели? (бабу Ягу) сидит Баба Яга с учебником математики и говорит: (Ученик)

- Знаю, зачем пришли, но сначала помогите мне, а потом и помогу вам. Распределите геометрические фигуры на две группы.

. Постановка проблемы урока. Подвести к выявлению темы.

Ребята, посмотрите на геометрические фигуры у вас на партах. Как вы думаете, по каким признакам их можно разделить на группы? По какому признаку, их можно разделить на две группы? (по размеру, большие и маленькие)

Разделите ваши фигуры на группы по размеру.

Назовите номера фигур, которые вы отнесли к 1 группе, ко 2 группе.

Что вы можете сказать о площади фигур первой группы, по отношению к площади фигур второй группы? Сравните их площади.

Как доказать, что у фигур из первой группы площадь меньше? (надо наложить маленькую фигуру на большую) Давайте проверим. Возьмите любую фигуру из первой группы и приложите её к фигуре из второй группы.

Итак, какой вывод можно сделать? (что у фигур первой группы площадь меньше)

На основании чего мы сделали такой вывод? (наложили фигуры друг на друга)

. «Открытие» новых знаний. Выявить знания основной теме урока.

А теперь давайте прочитаем в учебнике как сравнить площадь фигур и проверим наш вывод.

5. Вторичное закрепление. Систематизировать и закрепить знания.

Молодцы, справились с заданием и дам я вам клубок, он укажет дорогу, но чтобы узнать расстояние, которое нужно пройти, выполните задание.

Назовите номера треугольников, площади которых равны.

. Первичный контроль. Пошли мы дальше, и пришли к Кощею - Бессмертному: (Ученик)

За невестой пришёл добрый молодец? Давай договоримся, решишь задачу - заберёшь её, нет - твоя голова с плеч долой.

Давайте выручать Ивана. Задача №68.

Решили мы задачу, но не хочет Кощей отдавать Ивану невесту. Выхватил тогда Иван меч и стали они сражаться, всё ближе подбирался царевич к трону. Схватил он шкатулку, где хранилась смерть Кощеева, а на ней задание.

Что же приготовил нам Кощей?

. Итог урока. Найдите и раскрасьте одинаковым цветом фигуры, площади которых равны.

Открылась шкатулка. Взял Иван иглу и переломил её. Кощей погиб, а наш герой спас невесту, а вы ему в этом помогли. Молодцы.

Вам понравился урок? Что нового вы узнали?

. Домашнее задание. № 62. № 63 [Математика. 3 класс. Рудницкая В.Н., Юдачева Т.В.]

Приложение 3

Цель: учить находить предметы разной формы.

Содержание. Детям показывают картинку, изображающую комнату с различными предметами. В. начинает рассказ: «Однажды к мальчику прилетел Карлсон: «Ах, какая красивая комната, - воскликнул он. - Сколько тут интересных вещей! Я такого никогда не видел». «Давай я тебе все покажу и расскажу, - ответил мальчик и повел Карлсона по комнате. «Вот это стол» - начал он. «А какой он формы?» - тут же спросил Карлсон. Тогда мальчик стал очень подробно рассказывать все про каждую вещь. А теперь попробуйте вы так же, как тот мальчик, рассказать Карлсону все-все про эту комнату и предметы, которые в ней находятся.

«Сломанная лестница»

Цель: учить замечать нарушения в равномерности нарастания величин.

Материал. 10 прямоугольников, величина большого 10x15, меньшего 1xl5. Каждый последующий ниже предыдущего на 1 см; фланелеграф.

Содержание. На фланелеграфе строится лестница. Затем все дети, кроме одного ведущего, отворачиваются. Ведущий вынимает одну ступеньку и сдвигает остальные. Кто раньше других укажет, где лестница «сломана», становится ведущим. Если при первом проведении игры дети допускают ошибки, то можно использовать мерку. Ею измеряют каждую ступеньку и находят сломанную. Если дети легко справляются с задачей, можно одновременно вынуть две ступеньки в разных местах.

«Составь фигуру»

Цель: упражнять в группировке геометрических фигур по цвету, размеру.

Содержание. По просьбе В. дети достают фигуры из конверта, раскладывают их перед собой и отвечают на вопросы: «Какие у вас фигуры? Какого они цвета? Одинакового ли размера? Как можно сгруппировать фигуры, подобрать подходящие? (по цвету, форме, размеру). Составьте группу из красных, синих, желтых фигур. После того, как дети выполнять задание, В. спрашивает: «Какие получились группы? Какого они цвета? Какой формы оказались фигуры в первой группе? Из каких фигур составлена вторая группа? Сколько их всего? Сколько фигур разной формы в третьей группе? Назовите их! Сколько всего фигур желтого цвета?» Далее В. предлагает перемешать все фигуры и разложить их по форме (величине).

Приложение 4

Контрольный срез №1

Задание №1.

)        Могут ли разные прямоугольники иметь равные периметры?

)        У какого из таких прямоугольников самая большая площадь?

4 см                     2 см

см                                  3 см

)        Площадь квадрата 64 см. Какова длина его стороны? Отметь значком P правильный ответ

см                        32 см

см                        8 см

Задание №2.

)        Длина стороны квадрата 9 см. Вычисли периметр квадрата.

)        Длина сторон прямоугольника 5 см и 8 см. Какова его площадь?

)        Сравни, у какого квадрата площадь больше? Почему?

Задание №3.

)        Найти площадь фигуры разными способами:

.        __________________________________.         __________________________________.         __________________________________

)        Поставь галочку напротив того способа, который тебе кажется самым лучшим.

)        Начерти другую фигуру, для которой самым удобным будет тот же способ. Найди её площадь.

Приложение 5

Фрагменты уроков.

ТЕМА: Площадь фигуры; квадратный сантиметр.

ЦЕЛИ: Ознакомить уч-ся с квадратным сантиметром как единицей, и научить пользоваться этой единицей измерения.

ОБОРУДОВАНИЕ: геометрические фигуры, карточки с заданием, записи на доске, учебник, образец кв.см.

ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА.

На наборном полотне выставлены геометрические фигуры (Круг, прямоугольник, треугольник, квадрат, многоугольник).

Назовите фигуры.

Какое общее название можно дать этим фигурам?

Чем они отличаются?

Что знаете про стороны квадрата? (У него все стороны равны).

СООБЩЕНИЕ НОВОЙ ТЕМЫ И ЦЕЛИ УРОКА.

Сегодня на уроке вы познакомитесь с единицей измерения площади, которая называется квадратный сантиметр и научитесь пользоваться единицей измерения. (Образец на доске).

Квадратный сантиметр - это квадрат, стороны которого равны 1 см. Он очень маленький, но играет огромную роль в математике.

А сейчас мы научимся чертить кв.см. в тетради. (Учитель на доске чертит, а дети в тетради).

Повторяю ещё раз: Это кв.см., при помощи которого мы будем измерять S фигур, короче можно записать так 1 кв.см. (Учитель подписывает на доске, дети в тетрадях).

ВЫВОД: если в одном кв.см. измеряют S фигур, то в линейных см. измеряют длину отрезка.

ЗАКРЕПЛЕНИЕ НОВОЙ ТЕМЫ.

Начерти фигуру площадью 8 см².

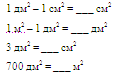
Решение задачи:

Площадь одной из комнат трехкомнатной квартиры равна 20 м², а площадь второй - на 4 м² меньше. Площадь первых двух комнат на 17 м² больше площади третьей комнаты. Какова площадь третьей комнаты?

а) Чтение задачи.

б) Составление схемы задачи.

(Учитель составляет схему на доске, дети в тетрадях).

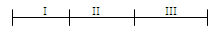
в) Решение задачи.

1) 20 - 4 = 16 (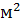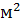) - площадь второй комнаты.

) 20 + 16 = 36 (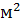) - площадь первых двух комнат.

) 36 - 17 = 19 ().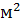

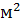Ответ: 19 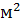 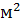площадь третьей комнаты.

Приложение 6

Единица измерения площади. Квадратный метр.

ЦЕЛИ: закрепить умение учащихся находить площади различных фигур; воспитывать чувство взаимоподдержки и выручки; продолжить работу над формированием вычислительных навыков; развивать логическое мышление.

ОБОРУДОВАНИЕ: карточки с геометрическими фигурами на парте; карточки с монетами на парте; волшебные квадратные очки, картинки фруктов; шагомер или ватерпас, рулетка, складной метр, задачники Г. Остера, его книги; задачник, тетради, линейки, простой карандаш.

ХОД ЗАНЯТИЯ:

Если к нам приходят гости,

Не здоровайся ни с кем.

Отвернись и на вопросы

Ни на чьи не отвечай.

Хороший совет я вам дала? Как называются такие советы? А чтобы совет стал хорошим, что нужно сделать? Сделайте наоборот.

Кто сочинил такие вредные советы? (Г. Остер). Какие произведения Г. Остера вы прочитали и вам понравились? (Выставка книг).

Но у нас сейчас урок математики, и чем может быть интересен Г. Остер? Этому задачнику более 10 лет. Он даже старше вас. А чтобы нам работать с этим учебником, нужно вооружиться карандашом и надеть наши волшебные очки. Что вы можете сказать о них? (Если мы посмотрим через них, все должно казаться квадратным).

Открываю доску, показываю яблоко, грушу, банан.

Какой формы будет вот то яблоко? Это груша? Это банан? Почему? Докажите.

А сейчас у вас на столах лежат листочки с фигурами квадратной формы.

Кто это может быть? Хотите дорисовать? Мне тоже интересно узнать, что же у вас получится. (Отметить разных животных). Вот какие разные у нас получились животные.

А какое задание можно предложить по этим фигурам? Что можно определить? (Определить S).

Определите разными способами (3 х 3 = 9 см², 4 х 5 = 20, 9 +20 = 29 см²). Какой способ самый рациональный? Почему?

Работа с задачником.

Теперь вы вооружились. У вас есть палетки и волшебные очки. Давайте посмотрим, что же нам предлагает Г. Остер? Откройте задачу с красной закладкой на странице 39 № 88. Прочитайте внимательно текст 88.

Длина стороны зеркала квадратной формы 10 дм. Скольким квадратным метрам будет равна площадь отражения лица царевны Несмеяны, если, когда она любуется собой, это отражение занимает как раз всю площадь зеркала?

О чем эта задача? Объясни свой ответ. Понравился вам вопрос задачи? Можно ли сократить вопрос?

Давайте уберем лишние слова. Какой вопрос тогда получится? А достаточно ли данных? (Да). Почему? (У квадрата все стороны равны). Что можно сказать о другой длине?

Прочтите еще раз вопрос задачи. В вопросе есть слова (на доске пишу слова - Квадратный метр). Квадратный метр. Найдите корень слова.

Вот квадрат. Похоже на форму зеркала Царевны-Несмеяны? (Показываю полиэтиленовую пленку размером 1м х 1м).

Что сказано в задаче о длине сторон квадратного зеркала? (10 дм - это что? 1 м). Есть у нас такая мерка, которая поможет найти площадь этого зеркала? Как это сделать? Выложим. Сколько квадратных дециметров мы выложили? 100 дм²= 1 м². А как узнаем? 10 х 10 = 100. Вот у нас получилась новая мера площади - 1 м².

Вот такое лицо было у Царевны-Несмеяны. А может быть, такое лицо у человека?

Какой литературный прием использовал Г. Остер в своей задаче? (Преувеличение). Лицо большое, как будто смотрится в увеличительное стекло.

А сейчас откройте последнюю страницу тетради, где наш справочник. Какие единицы измерения площади у нас записаны? Давайте запишем в наш справочник новую единицу измерения площади - 1 м² = 100 дм². У нас уже есть мерка, это палетка - 1 дм². Сегодня новая мерка 1 м².

А следующая задача еще интереснее. Откройте задачу с зеленой закладкой. Прочитайте.

На кухне площадью 6 кв.м. дедушка рассыпал мелочь. С каждого квадратного метра бабушка собрала по 45 рублей. Каков общий урожай?

Какие данные нам известны? S - 6 м², 1м² - по 45 р.

Что мы должны найти? Что это означает? Вот наши квадратные метры. Какой формы может быть кухня. Давайте выложим. А по-другому как можно переставить? Сколько возможных вариантов может быть?

Давайте в тетради нарисуем возможные варианты. Ребята, 1 м² войдет в тетрадь? Нет. Значит, что нужно сделать? Было преувеличение, а теперь нужно уменьшить до 1 клетки. Кто сколько вариантов найдет?

Проверка и показ нескольких работ.

У кого другая форма? Вот какие формы могли быть у кухни. А теперь разберемся с мелочью. Что в задаче сказано про рубли? С каждого метра по 45 руб. Какие сейчас у нас есть монеты? 1р., 2р., 5р., 10р. Есть ещё другие по 50коп., 10коп., 5 коп.

копеек нам понадобится? Нет. Значит отбрасываем. Какой набор рублёвых монет могла собрать бабушка с каждого метра?

Я сейчас раздам вам задание, а вы подумайте, какими монетами можно собрать 45 рублей.

Работаем в паре. Кто закончит, поднимите руку. Покажите, как вы набрали. Выложите 1 м² на полу. А теперь мы можем подсчитать, каков общий урожай монет. Найдите результат наиболее рациональным, удобным способом. Решение запишите в тетради.

Вызвать к доске учащихся, у которых разные варианты.

45 х 6 = 270р., 45 + 45 + 45 + 45 + 45 + 45 = 270р.

Как вы думаете, трудно было бабушке собрать столько мелочи?

Ну, как вам понравились задачки Г. Остера? Какой литературный прием он любит применять?

А сами смогли бы придумать такие задачки? Вот домашнее задание. Подумайте, постарайтесь придумать для соседа такие задачки на листочке (А4) с рисунком. Написать условие. Тогда у нас завтра получится свой классный задачник.

Вот теперь вы знаете, что чем можно измерять, и можете помочь своими родным измерять площади.

Урок окончен.

Приложение 7

Контрольный срез №2.

Задание №1.

1)   Вычисли площадь комнаты, длина которой 5 м, а ширина 4 м.

2)      Длина грядки прямоугольной формы 5 м, а ширина 20 дм. При перекопке грядку удлинили на 1 м. Какой площади стала грядка?

)        Вычисли периметр треугольника, если длина каждой его стороны равна 2 см 5 мм.

Задание №2.

1)   Ширина прямоугольника 8 см, а длина в 2 раза больше. Вычисли площадь прямоугольника.

2)      Длина прямоугольника равна 12 см, а ширина в 3 раза меньше. Вычисли площадь прямоугольника.

)        Периметр квадрата равен 1 дм 6 см. Вычисли площадь квадрата.

Задание №3.

)     Периметр квадрата равен 2 дм. Вычисли площадь квадрата.

2)      Длина сторон прямоугольника 6 см и 3 см. Чему равна его площадь? Выбери верный ответ и отметь его знаком P

9 см

18 см

см²

9 см²

3)   Периметр прямоугольника 20 см. Его ширина 4 см. Чему равна площадь этого прямоугольника?