Методы анализа цепей постоянного тока
Задача 1
электрический
постоянный ток цепь
Дана электрическая схема постоянного тока,
известны постоянные ЭДС E1, E2, E3. Заданы
сопротивления ветвей R1, R2, R3:
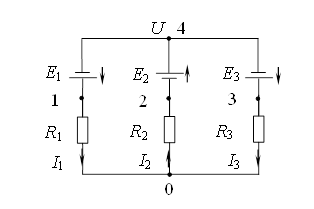
Рис.
Требуется:
) рассчитать, считая потенциал точки 0 равным
нулю, потенциалы точек схемы 1, 2, 3, 4;
) рассчитать токи в ветвях цепи I1, I2,
I3;
) проверить выполнение первого и второго законов
Кирхгофа для узлов и ветвей цепи;
) проверить данные расчетов, выполнив
компьютерное моделирование электрической цепи с помощью пакета «MC9».
Решение
. Воспользуемся методом узловых потенциалов.
Потенциал точки 4:
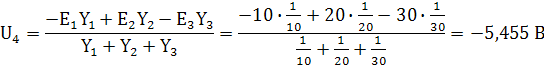
Потенциалы точек 1, 2 и 3 относительно точки
нулевого потенциала соответственно равны:
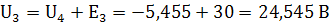
. Определим токи в ветвях 
и
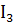по
закону Ома:
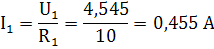
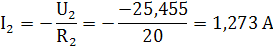
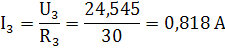
. Выполним проверку с помощью законов Кирхгофа.
По первому закону Кирхгофа:
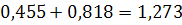
По второму закону Кирхгофа:
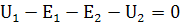
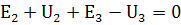
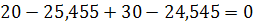
4. Выполним моделирование в системе MC9.
В результате моделирования имеем следующую схему:
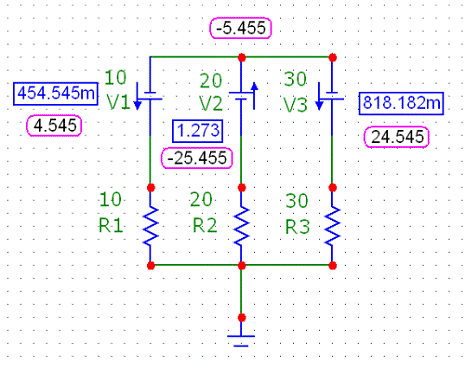
Рис.
Видно, что результат моделирования полностью
совпадает с результатами расчёта.
Задача 2
На рисунках даны два варианта электрических
цепей: двухполюсной (a) и четырёхполюсник (b). В таблице индивидуальных заданий
даны величины элементов цепей R, С и L, а также частота ω,
амплитуда Uм и начальная фаза φ
гармонического входного напряжения uвх(t).
Рис.
Требуется:
) рассчитать токи в цепях и
напряжения на элементах цепей, записать их в форме гармонических колебаний;
) построить векторные диаграммы
напряжений;
) с помощью пакета «MC9» сделать
проверку верности расчетов амплитуд токов и напряжений гармонических колебаний,
а также фазового сдвига между i(t) и uвх(t) в цепи a) и фазового
сдвига между uвх(t) и uвых(t) в цепи b).
Цепь b),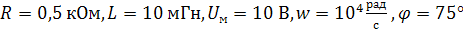 
.
Решение
. Ток в цепи i(t) определяем
символическим методом, выполняя следующие шаги.
Гармоническое воздействие 
заменяем его
комплексной амплитудой:
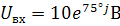
Входное сопротивление цепи:
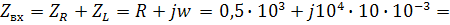
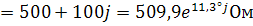
Любое комплексное число можно представить в трех
формах: алгебраической, показательной и тригонометрической. Я представил 
в
алгебраической форме, зачем требовать показательную?! Ведь когда я пишу к
примеру число 0,2, с меня же не требуют написать, что оно равно 2/10 или 1/5.
Чушь, а не замечание! Но я добавил…
Согласно закону Ома ток равен:
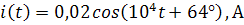
Я не округлял. Расчёты были проведены с тремя
знаками после запятой. Результат просто такой получился…
Напряжение на элементах схемы:
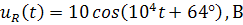
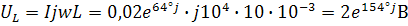
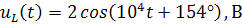
.Построим векторную диаграмму напряжений:
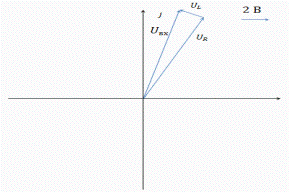
Рис.
Видно, что сумма векторов 
и
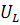равна
вектору 
.
. Выполним моделирование в системе MC9.
В результате моделирования имеем следующую схему:
Рис.
Представим временные графики сигналов:
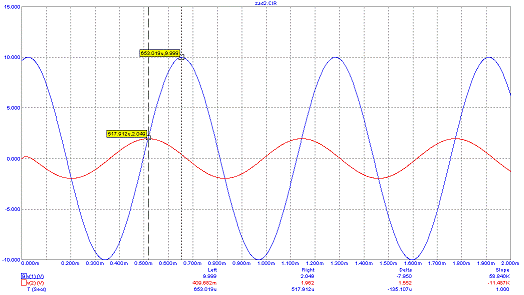
Временной сдвиг колебаний составляет:
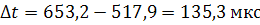
Фазовый сдвиг в радианах между входным и
выходным напряжением равен:
Этот результат подтверждает расчет:
действительно, фаза напряжения генератора равна +75°, фаза напряжения на
катушке +154°, сдвиг фаз между ними равен +79°, напряжение на катушке опережает
по фазе напряжение источника.
Задача 3
На рисунках a) и b) даны два варианта
четырёхполюсной электрической цепи. В таблице индивидуальных заданий указана
цепь для анализа и соотношения между значениями резисторов 1 и 2.
Рис.
Требуется:
) определить и построить АЧХ и ФЧХ цепи;
) определить и построить переходную и импульсную
характеристики цепи, проверить выполнение предельных соотношений;
) с помощью пакета «MC9» промоделировать
частотные и временные характеристики цепи, сравнить их с рассчитанными. При
моделировании абсолютные значения величин элементов цепи R, L и С взять равными
соответственно 1 кОм, 1 мГн и 1 нФ.
Цепь b).
- 2R
- 3R
Решение
. Запишем выражение комплексной передаточной
функции
цепи
и выделим из него модуль и аргумент:
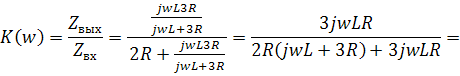
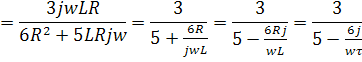
Тогда АЧХ:
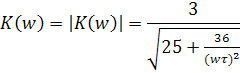
ФЧХ:
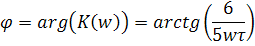
Представим схематично графики АЧХ и ФЧХ:
Рис.
Рис.
2.Определим переходную и импульсную
характеристики цепи:
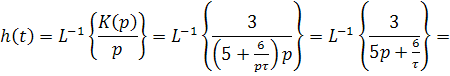
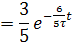
Представим графики:
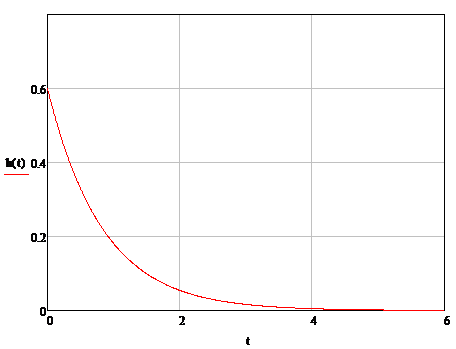
Рис.
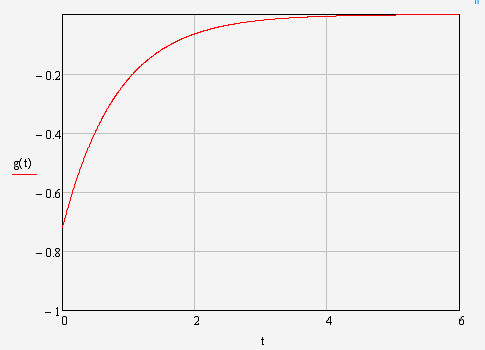
Рис.
. Выполним моделирование в системе MC9.
В результате моделирования имеем следующую схему:
Рис.
Представим графики, полученные в процессе
моделирования:
Рис.
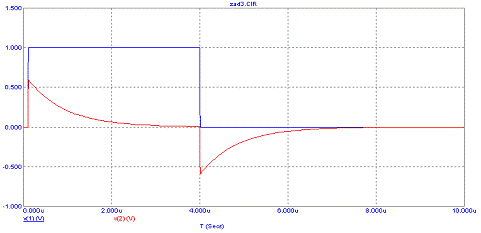
Рис.
Рис.
Видно, что результат моделирования полностью
совпадает с результатами расчёта.