Математические модели радиотехнических сигналов
Национальный
исследовательский университет "МЭИ"
Институт
информационной и экономической безопасности
Отчет
по лабораторной работе
Математические
модели радиотехнических сигналов
Выполнила
студентка гр. ИЭс-143-15
Лисовая Дарья Евгеньевна
Принял
Крутских Владислав Викторович
Москва
2015
Введение
сигнал радиотехнический mathcad
импульсный
Цель работы: Изучить основы и получить
практический навык построения математических моделей радиотехнических сигналов
с использованием программного пакета MathCad.
В работе исследуются модели гармонических,
периодических и импульсных сигналов, псевдо непрерывные и дискретные, а также
сигналы с амплитудной и частотной модуляцией.
Домашняя подготовка:
1. Ознакомьтесь с основами программирования
в пакете MathCad, способами задания функций, переменных, массивов и построением
графиков [1].
. Изучите математические модели
радиотехнических сигналов [3].
. Изучите математические основы теории
спектрального представления сигналов [3].
1. Подготовка к работе
Запустите пакет MathСad.
В начале Файла задайте параметр ORIGIN:=0 (с
этого момента нумерация элементов в матрицах и векторов будет начинаться с нуля).
. Математическая модель гармонического колебания
Задайте значение частоты f:=103 Гц, амплитуды
А:=1 и фазы j:=0.
Задайте функцию, описывающую гармонический
сигнал
(t):=Аcos(ωt+j),
где ω=2πf.
Задайте интервал аргумента функции от tmin =0 до
tmax=1 -3 с шагом Δt=10-5c (t:= 0,10-5..10-3).
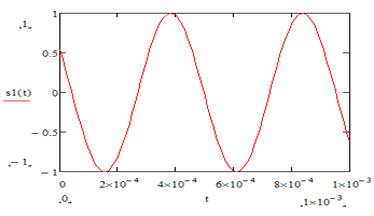
Постройте график зависимости s1(t).
Изучите вкладку "Свойства" объекта
"График".
Включите на графике сетку и единице задайте шаг
сетки пропорционально или пяти,
Исследуйте возможность выбора типа, толщины,
цвета и других параметров линии отображаемого графика.
Измените значение частоты, амплитуды сигнала и
фазы. Сделайте выводы о влиянии параметров сигнала на его график.
. Математические модели импульсных сигналов
Задайте интервал аргумента функции от tmin =0 до
tmax=11с с шагом Δt=10-1c
(t:= 0,10-1..11).
Постройте функцию включения (Хэвисайда)
s2(t,a)=Ф(t-a) для трех различных значений a= 0; 2;5 на одном графике. Формат
оси абсцисс на графике задайте от -1 до 10 и настройте сетку.

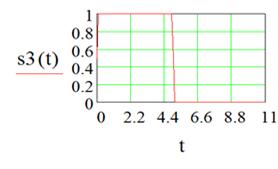
Постройте прямоугольный видеоимпульс, используя
функцию включения с разными знаками.
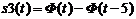

Постройте треугольный видеоимпульс


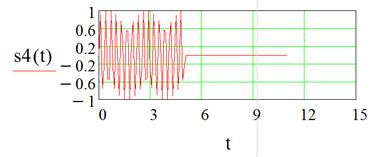
Постройте треугольный радиоимпульс


4. Математическая модель периодических сигналов
Задайте интервал аргумента функции от tmin =0 до
tmax=2*10-2 с шагом Δt=10-5c.
Постройте модель сигнала в виде суммы трех
гармонических составляющих, для этого задайте три матрицы-столбца: А - столбец
значений амплитуды (1; 0,5; 1) [В], ω - столбец
значений частоты (0; 1; 10)*103 [с-1] и φ - столбец
начальной фазы (0; 0; 0) [рад]. Используя формулу (1.1) запишите сигнал s7(t)
(n=2):
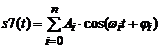 (1.1)
(1.1)

Постройте временную диаграмму сигнала s7(t) в
заданном интервале. Исследуйте особенности изменения графика, изменяя частоту
и/или амплитуду составляющих.

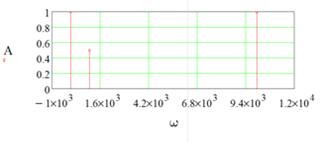
Постройте спектральную диаграмму сигнала s7(t) -
зависимость амплитуды гармоники Аi от частоты ωi (используйте
для этого матрицы А и ω). В свойствах
графика выберите параметр линии Stem.
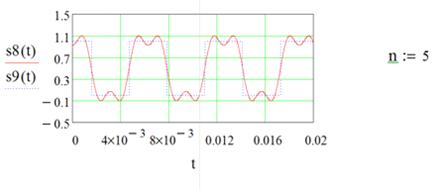
Постройте реализацию сигнала s8(t) типа меандр
(последовательность прямоугольных импульсов) используя выражение (1.1). Для
этого задайте значения параметров: А - значений амплитуды (0,5; 0,637; 0,212 ;
0,127; 0,091; 0,071) [В], ω - значений
частоты (0; 1; 3; 5;7;9)∙103 [с-1] и φ - фазы
(0; 0; π;
0; π;0)[рад], n = 5.

Постройте сигнал s9(t) типа меандр по формуле
(1.2) на том же графике.
где  с.
с.
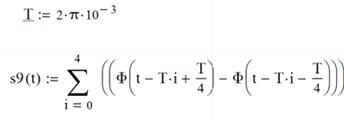
Постройте спектральную диаграмму сигнала s8(t)
так, как это было проделано в п. 3.4. Сделайте выводы.
. Математическая модель дискретного сигнала
Задайте переменную-счетчик i от 0 до 1000 и шаг
дискретизации Δt:=2π∙10-5 . Далее
переменную tti=i∙Δt.

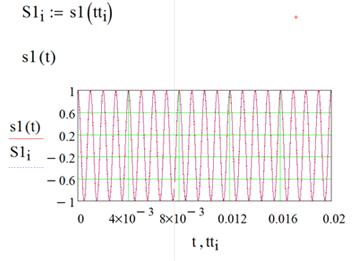
Задайте столбец S1 значений функции s1(t) (из п.
2.2) в моменты времени tti: S1i:=s(tti). Постройте графики зависимости S1i от
tti и s1(t) на одном графике.
6. Спектр сигнала. Быстрое преобразование Фурье
(БПФ)
Задайте переменные: число отсчетов N:=1000, шаг
дискретизации Δt:=10-5 , счетчик i:=0..N.
Определите переменную времени tti=i∙Δt. Рассчитайте
столбец отсчетов дискретного сигнала S7i:=s7(tti).

Постройте график зависимости отсчетных значений
сигнала S7i от отсчетов времени tti. Убедитесь, что он совпадает с графиком из
п.4.3.

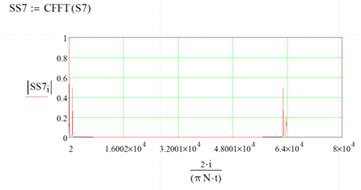
Вычислите спектральные составляющие SS7
дискретного сигнала S7, используя функцию SS7:= CFFT(S7).
Постройте амплитудно-частотное распределение
(спектральную диаграмму) сигнала S7. Для этого требуется по оси ординат взять
модуль от каждого элемента полученной матрицы SS7. Чтобы корректно представить
значения на оси частот необходимо в аргументе графика записать выражение
2i/(πNΔt) [Гц],
где i - номер отсчета, N - общее число отсчетов,
Δt
- шаг
дискретизации. Сравните полученный график с гра-фиком п.4.4.
Используя функцию обратного преобразования Фурье
(S8:=ICFFT(SS7)), восстановите сигнал S7. Постройте и сравните графики сигналов
до и после преобразования (S8 и S7).