Частично-упорядоченные множества
Содержание
Введение
. Бинарные отношения на множестве
.1 Бинарные отношения, определения
.2 Примеры бинарных отношений
. Отношение эквивалентности
.1 Рефлективность, примеры
рефлективности
.2 Симметричность
.3 Транзитивность
. Отношение порядка
. Частично-упорядоченные множества
.1 Основные определения, свойства
ч.у.м
.2 Решетки
.3 Дистрибутивность решетки
.4 Примеры дестрибутивных и
недестребутивных решеток
Заключение
Список используемой литературы
Введение
В курсовой работе будут рассматриваться решетки
со стороны теории множества как частично упорядоченные множества и со стороны
алгебры как структуры с введенной на них бинарными операциями, так же будут
введены и разобраны основные определения и свойства теории структур. Будут
разобраны вспомогательные определения операции над множествами с приведенными
примерами.
. Бинарные отношения на множестве
.1 Бинарные отношения, определения
Для начала введем несколько вспомогательных
определений.
Определение 1. Декартовым произведением множеств
X и Y называется множество XxY всех упорядоченных пар (x, y) таких, что x X, y
X, y Y.
Y.
Определение 2. Соответствием между множествами X
и Y (или соответствием из X в Y) называется любое подмножество декартова
произведения X xY. Если множества X и Y совпадают, то соответствие между
множествами X и Y называют также бинарным отношением на множестве X.
бинарные отношения наиболее часто используются в
математике, в частности, таковы равенство, неравенство, эквивалентность,
отношение порядка.
.2 Примеры бинарных отношений
Пусть X = {a, b, c, d}, Y = {1, 2, 3, 4, 5}.
Тогда множество кортежей a={(a, 1), (b, 2), (c, 3), (d, 4)} являются
соответствием из X в Y.
Отметим, что обычно соответствия задаются не
путем указания подмножества a декартова произведения X xY, а путем указания
свойства пар (x, y), принадлежащих этому подмножеству . Отношение a = {(4, 4),
(3, 3), (2, 2), (4, 2)} на множестве X = {4, 3, 2} можно определить как
свойство "Делится" на этом подмножестве целых чисел.
Отношения могут задаваться формулами:
· формулы y = x2 +5x - 6 или 
. Отношение эквивалентности
отношение множество рефлективность
решетка
Определение 3 Отношение эквивалентности ( )
на множестве
)
на множестве 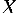 - это бинарное
отношение, для которого выполнены следующие условия:
- это бинарное
отношение, для которого выполнены следующие условия:
· Рефлексивность
<https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D1%84%D0%BB%D0%B5%D0%BA%D1%81%D0%B8%D0%B2%D0%BD%D0%BE%D0%B5_%D0%BE%D1%82%D0%BD%D0%BE%D1%88%D0%B5%D0%BD%D0%B8%D0%B5>:
 для любого
для любого  в
в 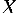 ,
,
· Симметричность
<https://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D0%BC%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%BD%D0%BE%D0%B5_%D0%BE%D1%82%D0%BD%D0%BE%D1%88%D0%B5%D0%BD%D0%B8%D0%B5>:
если  , то
, то  ,
,
· Транзитивность
<https://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B0%D0%BD%D0%B7%D0%B8%D1%82%D0%B8%D0%B2%D0%BD%D0%BE%D1%81%D1%82%D1%8C>:
если  и
и 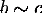 , то
, то  .
.
Запись вида « »
читается как «
»
читается как « эквивалентно
эквивалентно 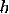 ».
».
.1 Рефлективность
Определение 4 Рефлексивное отношение - бинарное
отношение  на множестве
на множестве 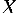 ,
при котором всякий элемент этого множества находится в отношении
,
при котором всякий элемент этого множества находится в отношении  с
самим собой.
с
самим собой.
Примеры рефлексивности:
· отношения эквивалентности:
o отношение равенства 
o отношение сравнимости по модулю
· отношения нестрогого порядка:
o отношение нестрогого неравенства 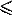
o отношение нестрогого подмножества 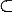
o отношение делимости 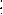
.2 Симметричность
Определение 5 Бинарное отношение  на
множестве X называется симметричным, если для каждой пары элементов множества
на
множестве X называется симметричным, если для каждой пары элементов множества 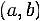 выполнение
отношения
выполнение
отношения 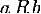 влечёт выполнение
отношения
влечёт выполнение
отношения  .
.
Примерами симметричных отношений служат
отношения типа равенства (тождества, эквивалентности, подобия)
.3 Транзитивность
Определение 6 Бинарное отношение  на
множестве
на
множестве 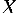 называется
транзитивным, если для любых трёх элементов множества
называется
транзитивным, если для любых трёх элементов множества  выполнение
отношений
выполнение
отношений  и
и 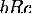 влечёт
выполнение отношения
влечёт
выполнение отношения  . Формально,
отношение
. Формально,
отношение  транзитивно, если
транзитивно, если  .
.
Пример 1. Равенство а = b
и b = c,
следует, что a = c.
Пример 2. Отношение порядка , если a
 b
и b
b
и b  c,
то a
c,
то a  c.
c.
Как видно из примеров можно привести много
примеров по свойству транзитивности. К таковым относятся операции импликации,
эквивалентности, делимости и т.д.
. Отношение порядка
Определение 7 Бинарное отношение  на
множестве
на
множестве 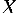 называется
отношением нестрогого частичного порядка (отношением порядка, отношением рефлексивного
порядка), если имеют место
называется
отношением нестрогого частичного порядка (отношением порядка, отношением рефлексивного
порядка), если имеют место
· Рефлексивность
<https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D1%84%D0%BB%D0%B5%D0%BA%D1%81%D0%B8%D0%B2%D0%BD%D0%BE%D1%81%D1%82%D1%8C>:
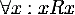
· Антисимметричность
<https://ru.wikipedia.org/wiki/%D0%90%D0%BD%D1%82%D0%B8%D1%81%D0%B8%D0%BC%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%BD%D0%BE%D0%B5_%D0%BE%D1%82%D0%BD%D0%BE%D1%88%D0%B5%D0%BD%D0%B8%D0%B5>:
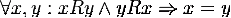 .
.
· Транзитивность
<https://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B0%D0%BD%D0%B7%D0%B8%D1%82%D0%B8%D0%B2%D0%BD%D0%BE%D1%81%D1%82%D1%8C>:
 ;
;
Определение 8 Отношение порядка R
на множестве А называется нестрогим, если оно рефлексивно на А.
Определение 9 Отношение порядка R
строгим (на A), если оно
антирефлексивно. Однако из антирефлексивности транзитивного отношения R
следует его антисимметричность, следовательно можно дать более точное
определения для строгого отношения.
Определение 9.1 Бинарное отношение R
на множество A называется строгим
порядком на А, если оно транзитивно и антирефлексивно на А.
Пример 1. Пусть P(M)
-множество всех подмножеств множества М. Отношение включения  на
множестве P(M)
есть отношение нестрого порядка.
на
множестве P(M)
есть отношение нестрого порядка.
Пример 2. Отношения ≤ и  на
множестве действительных чисел являются соответственно отношением строгого и
нестрогого порядка.
на
множестве действительных чисел являются соответственно отношением строгого и
нестрогого порядка.
Пример 3. Отношение делимости во множестве
натуральных числе есть отношение нестрого порядка.
Множество 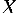 , на котором
введено отношение частичного порядка, называется частично упорядоченным
<https://ru.wikipedia.org/wiki/%D0%A7%D0%B0%D1%81%D1%82%D0%B8%D1%87%D0%BD%D0%BE_%D1%83%D0%BF%D0%BE%D1%80%D1%8F%D0%B4%D0%BE%D1%87%D0%B5%D0%BD%D0%BD%D0%BE%D0%B5_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE>.
Отношение нестрогого частичного порядка часто обозначают знаком
, на котором
введено отношение частичного порядка, называется частично упорядоченным
<https://ru.wikipedia.org/wiki/%D0%A7%D0%B0%D1%81%D1%82%D0%B8%D1%87%D0%BD%D0%BE_%D1%83%D0%BF%D0%BE%D1%80%D1%8F%D0%B4%D0%BE%D1%87%D0%B5%D0%BD%D0%BD%D0%BE%D0%B5_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE>.
Отношение нестрогого частичного порядка часто обозначают знаком  .
.
. Частично-упорядоченные множества
.1 Частично-упорядоченное множество
Определение 10: Частично
упорядоченное множество, в котором для любых элементов a и b существую inf{a,b} и sup{a,b}, называют
решеточно упорядоченным множеством.
Введем операцию +, операцией + на
частично упорядоченным множеством будем считать что a∪b = a + b =sup{a,b}. Так же
введем операцию * и будем считать, что a⋂b = a*b = inf{a,b}. (рис.1)
тогда из определения решетки как ч.у.м мы перейдем к определению решетки как
алгебраической структуры с введенной на ней бинарными операциями + и *
.2 Алгебраические решетки, свойства
Определение 11: Алгебраическая
решетка - это тройка L = [ L, +, *], где
L- непустое
множество, а + (объединение), * (пересечение) - бинарные операции на нем,
подчиняющимися парами законов коммутативности, ассоциативности, идемпотентности
и поглощения.
Из определений частично
упорядоченного множества и алгебраической решетки следует, что:
a + b =
sup{a, b}, так же
a * b = inf{a,b}.
Пусть x,
y, z
элементы и множества L,
тогда:
1. x + x = x; x * x = x;
. x + y = y + x; x * y = y *
x;
. x + (y + z) = (x + y) + z;
x * (y * z) = (x * y) * z;
. x * (x + y) = x x + (x * y)
= x;
Теорема 1. Пусть L
- множество с операциями +, *, обладающими свойствами (1 - 4). Тогда отношение
a
≤
b = a
+ b = b;
является порядком на L,
а возникающее частично упорядоченное множество оказывается
структурой(решеткой), при чем:
a + b = sup {a, b};*b = inf {a, b};
Доказательство: Рефлективность отношения ≤
вытекает из свойства (1). Если a
≤
b, и b
≤
a, т.е a
+ b = b
и b + a
= a, то в силу (3) a
= b, т.е отношение ≤
является антисимметричным. Если a
+ b = b
и b + c
= c, то применяя (3)
получим:
a + c = a + (b + c) = (a + b) + c =
b + c = c,
что доказывает транзитивность отношения ≤.
Учитывая свойства (1), (2), (3) мы получаем
a + (a + b) = (a + a) + b = a + b,+
(a + b) = b + (b + a) = b + a = a + b,
Следовательно, a
≤
a + b
и b ≤
a + b.
Если a
≤
x, b
≤
x, то используя (1)
- (3) будем иметь
(a
+ b) + x
= a + (b
+ x) = a
+ x = x,
т.е a + b
≤
x, из определения
точной верхней грани получаем что
a + b
= sup{ a,
b}.
Аналогично можно доказать, что a*b
= inf{a,
b}, (далее будем
отмечать ab = a*b)
Доказательство: Из свойств (1) - (3) вытекает,
что ab
≤
a и ab
≤
b. Если y
≤
a и y
≤
b то с помощью (3) -
(4) получаем:
y(ab) = [y ( y + b)]b = yb = y(y +
b) = y.
В силу свойств (1) и (3) получаем, что y
+ ab = y(ab)
+ ab = ab,
т.е y
≤
ab. Таким образом,
ab = inf{a,
b}.
Из теоремы 1 вытекает, что структуры образуют
многообразие универсальных алгебр с двумя бинарными операциями.
Обращая внимания на то, что свойства (1) - (4),
стоящие в левой колонке, двойственны соответствующим свойствам правой колонки.
Можно установить, что в произвольной структуре из справедливости какого - либо
свойства, записываемого в терминах структурных операций, вытекает
справедливость двойственного свойства.
Теорема 2. Если a
≤
b и c
≤
d, то a
+ b ≤
c + d
и ab ≤
cd;
Доказательство: В силу эквивалентности свойств Ia
≤
b; a
+ b = b;
ab = a;
из условия следует, что a
+ c = c,
b + d
= d; ac
= a; bd
= d;
Поэтому :
(a + b) + (c + d) = (a + c) + (b +
d) = c + d;
(ab)(cd)
= (ac)(bd)
= ab; откуда и вытекают
требуемые неравенства.
Пример 1. Пусть {a,
b, c}
элементы из множества L,
при чем, a
≤
b ≤
c. Данный набор
элементов будет являться решеткой, так как для всех этих элементов есть
наибольшее и наименьше значение, являющееся еще и inf
и sup, проверим это, для
a и b
найдем inf, т. к inf{a,b}
= ab, a
≤
b, то inf
{a,b}
= a. Для b
и c. inf{b,c}
= bc, b
≤
c, inf{b,c}
= b. используем
свойство транзитивности и получим, что inf{a,c}
= a. Из наименьших
элементов, элемент a наименьший.
Аналогично проведем проверку по свойству +, получим, что sup{a,b}
= b, sup{b,c}
= c; опять же по
свойству транзитивности получим sup{a,c}
= c; Так как множество
состоящее из трех элементов является частично упорядоченным и имеет верхнюю и
нижнюю грани, то множество L
является решеткой.
Примечание: обычно в алгебре наименьший элемент
обозначается 0. А наибольший 1. Далее в примерах можно будет это увидеть.
Пример 2 Пусть S(A)
множество всех подмножеств множества A.
при чем |A| = n,
тогда S(A)-решетка.
И n - размерность
куба.
Допустим, что множество A
состоит из 3 элементов {a,b,c}
так же оно имеет пустое множество  .
Перечислим все подмножества
.
Перечислим все подмножества  А. {a,b}
, {a,c}
, {b,c},
А. {a,b}
, {a,c}
, {b,c},
{a}
, {b} , {c}.
 Так
как n = 3, то получим 3
х мерный куб, элементы которого будут находится на разных уровнях.
Так
как n = 3, то получим 3
х мерный куб, элементы которого будут находится на разных уровнях.
Графическое представление:
.
А
.{a,b}
.{a,c}
.{b,c}
.{a}
.{b}
.
{c}
. (рис 1)
(рис 1)
Как видно на (рис 1) довольно понятно показано
что из себя представляет "множество всех подмножеств множества". На
рисунке видно что элемент {a}
не является подмножеством {b,c},
соответственно b не
подмножество {a,c}
и т.д.
Перейдем к определению дистрибутивной решетки
.2 Дистрибутивная решетка, определение
Определение 12. Дистрибутивная решётка -
решетка, в которой справедливо тождество:

равносильное тождествам
 и соответственно
и соответственно

Приведем примеры дестрибутивных и
недестрибутивных решеток, опираясь на определение
Дистрибутивной решеткой является :
.
a.
b.
0.
Как видно на (рис 2) решетка состоит из
элементов 1, a, b,
0 проверим, является ли решетка дистрибутивной, a
+ b = 1; ab
= 0, по определению решетка является дистрибутивной.
Приведем пример недестрибутивной решетки.
1.
a.
b.
c.
0.
Проверяем свойство дистрибутивности из определения12
. Имеем:
(a+ b)c = ac + bc. Проверяем
левую часть равенства. (a+b)c
, т.к a + b
= 1;
следовательно 1 * c
= c. Итак, в левой
части равенства получен результат с, следовательно в правой мы должны получить
аналогичный результат, проверяем правую часть ac
+ bc, итак, как видим
из (рис 3) ac = 0;
аналогично для bc
= 0. Получаем, с учетом левой части выражение вида с ≠ 0. Свойства
дистрибутивной решетки не выполняется, следовательно решетка недестрибутивная.
Хотя эти примеры и являются тривиальными, но они
наглядно показывают, что из себя представляют алгебраические структуры, без
лишней теоретической нагрузки, которые в основном встречаются в научной
литературе.
Заключение
В курсовой работе были введены вспомогательные
понятия и определения, необходимые для дальнейшего разбора теории структур,
были затронуты и разобраны свойства и определения касающихся решеток, как
частично упорядоченное множества с веденными на них операциями пересечения и
объединения, с наглядно приведенными примерами. Так же был разобран вопрос,
касающийся перехода от частично- упорядоченного множества к алгебраической
структуре с веденной на ней бинарными операциями + и *. Были разобраны виды
алгебраических решеток, приведены примеры с доказательствами дистрибутивных и
недестрибутивных решеток.
Список используемой литературы
.
Розен В. В. Цель - оптимальность - решение (математические модели принятия
оптимальных решений). - М.: Радио и связь, 1982.
.
Столяр А. А., Рогановский Н. М. Основы современной школьной математики. Ч. 1.
Язык. Множества. Отношения. Функции. Математические структуры. - Минск: Нар.
Асвета, 1975.
.
Мальцев А. И. Алгебраические системы. М.: Наука, 1970.