|
Критерий
сравнения
|
КФ
трапеций
|
|
Кол-во
узлов в простой КФ
|
1
|
2
|
|
Класс
функции
|
|
|
|
Число
итераций, необходимых для достижения точности 
|
4
|
5
|
|
Шаг,
необходимый для достижения точности
|
0,125
|
0,0625
|
|
Приближенное
значение интеграла (точность
= )
|
0,478441
|
0,479534
|
|
Число
итераций, необходимых для достижения точности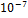 
|
11
|
11
|
|
Шаг,
необходимый для достижения точности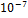
|
|
|
|
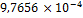
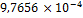
Приближенное
значение интеграла (точность
= )
|
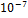0,4791634314
|
0,4791635669
|
Вывод: из таблицы мы видим, что
квадратурная формула средних прямоугольников использует меньше узлов, чем
квадратурная формула трапеций (количество узлов на единицу меньше). Этот факт
дает нам понять о том, что число арифметических операций, затрачиваемых на
выполнение одной итерации, у квадратурной формулы средних прямоугольников
меньше, чем у квадратурной формулы трапеций. У обеих квадратурных формул
функция является дважды дифференцируемой, поэтому требуемая точность
достигается приблизительно одинаково. Но на практике квадратурная формула
средних прямоугольников незначительно быстрее достигает требуемой точности, чем
квадратурная формула трапеций, если сделать еще больше опытов (для нашей
задачи). Исходя из наших заключений, мы можем с уверенностью сказать, что на
практике квадратурная формула средних прямоугольников более предпочтительна,
чем квадратурная формула трапеций, т.к. за одну итерацию она делает меньшее
количество арифметических операций.
Листинг программы для задачи №3(язык
программирования Java
6):
class Test{
public
static double e = 0.001,//0.0000001
a
= 1, b = 3;
public
static double f_x(double x){
return
Math.log(Math.sin(x)*Math.sin(x)+3)/(x*x+2*x-1);
}
public
static double f_middle_rect(int n){
double
sum = 0.0;
for(int
i=1; i<=n; i++) sum += f_x(a+(i-0.5)*(b-a)/n);
return
sum*(b-a)/n;
}
public
static double f_trap(int n){
double
sum = 0.5*(f_x(a)+f_x(b));
for(int
i=1; i<n; i++) sum += f_x(a+i*(b-a)/n);
return
sum*(b-a)/n;
}
public
static double h(int n){ return (b-a)/n;
}
public
static void main(String[] args){
int
n1 = 1, n2 = 2, i = 1; double f;
while((f
= Math.abs(h(n2)*h(n2)*(f_middle_rect(n2)-f_middle_rect(n1))/
(h(n1)*h(n1)-h(n2)*h(n2))))>e){
n1 *= 2; n2 *= 2; i++;}.out.printf("%d\n%.10f\n%.10f\n", i, h(n2),
f_middle_rect(n2)+f*h(n2)*h(n2));= 1; n2 = 2; i = 1;
while((f
= Math.abs(h(n2)*h(n2)*(f_trap(n2)-f_trap(n1))/
(h(n1)*h(n1)-h(n2)*h(n2))))>e){
n1 *= 2; n2 *= 2; i++;}.out.printf("%d\n%.10f\n%.10f\n", i, h(n2),
f_trap(n2)+f*h(n2)*h(n2));
}
}
Задача №4
Вычислить с точностью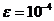 
интеграл 
.
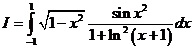Приведем исходный интеграл к более
желанному виду:
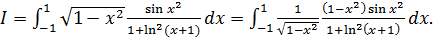
Воспользуемся формулой:
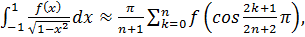
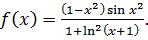
Проводим дальнейшие вычисления по предыдущей
формуле, начиная с 
=1, 
=2.
На каждой итерации увеличиваем значения ,
в
2 раза. Требуемая точность достигается при выполнении условия:
Ответ: после запуска программы
получили, что количество итераций k=4,
точность равна 0,0000145681, значение интеграла с требуемой точностью 
.
Листинг программы для задачи №4(язык
программирования Java
6):
class Test{
public
static double e = 0.0001, a = -1, b = 1;
public
static double f_x(double x){
return
(1-x*x)*Math.sin(x*x)/(1+Math.log(x+1)*Math.log(x+1));
}
public
static double f_NAST(int n){
for(int
i=0; i<=n; i++) sum += f_x(Math.cos(Math.PI*(2*i+1)/(2*n+2)));
return
sum*Math.PI/(n+1);
}
public
static void main(String[] args){
int
n1 = 1, n2 = 2, i = 1; double f;
while((f
= Math.abs(f_NAST(n2)-f_NAST(n1)))>e){ n1 *= 2;
n2 *= 2; i++; }.out.printf("%d\n%.10f\n%.10f\n", i, f, f_NAST(n2));
}
}
Задача №5
Найти с точностью 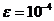решение
уравнения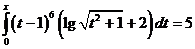 
Обозначим через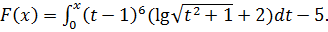 
Получили
нелинейное уравнение:
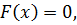
решение которого можно найти методом Ньютона по
формуле:
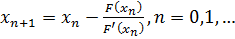
Наша расчетная формула для решения нелинейного
уравнения примет вид:
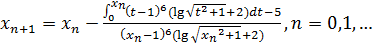
Приближенное значение интеграла, находящегося в
числителе расчетной формулы для нахождения корня уравнения, будем вычислять по
составной квадратурной формуле средних прямоугольников, используя правило Рунге
(точность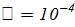 
).
Сделаем отделение корней:
1. 
с
точностью ; 
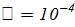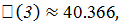с
точностью ;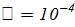 
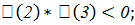
2. 
,
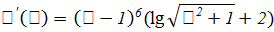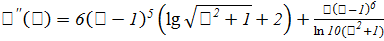не равна нулю и сохраняет знак на отрезке 
;
,
не равна нулю и сохраняет знак на отрезке ;
3. Начальное приближение 
.
Возьмем 
.
Проверим выполнение условия Фурье: 
Таким образом, мы нашли начальное приближение
для нахождения корня нашего нелинейного уравнения методом Ньютона: .
Примечание:
вычисления проводились на WolframAlpha.
Ответ: после запуска программы
получили: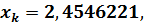 
при
количестве итераций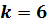 
, с
точностью 
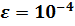(квадратичная
сходимость метода Ньютона).
|
Итерация
|
Решение
нелинейного уравнения
|
Точность
|
|
1
|
2,67254642
|
0,227453578767844
|
|
2
|
2,52436649
|
0,148179930565486
|
|
3
|
2,46362236
|
0,060744123524822
|
|
4
|
2,45478895
|
0,008833410818934
|
|
5
|
2,45462216
|
0,000166793744647
|
|
6
|
2,45462210
|
0,000000059009325
|
Листинг программы для задачи №5(язык
программирования Java
6):
class Test{
public
final static double e = 0.0001, a = 0;
public
static double f_x(double x){ //подынтегральное
выражение.
return
Math.pow(x-1, 6)*(Math.log10(Math.pow(x*x+1, 0.5))+2);
}
public
static double df_dx(double x){ //производная подынтегрального
выражения.
return
6*Math.pow(x-1, 5)*(Math.log10(Math.pow(x*x+1,
0.5))+2)+*Math.pow(x-1, 6)/(Math.log(10)*(x*x+1));
}
public
static double f_middle_rect(double b, double h, int
n){ //КФСП.
double
sum = 0.0;
for(int
i=1; i<=n; i++) sum += f_x(a+(i-0.5)*h);
return
sum*h;
}
public
static double calc_integral_acc(double b){ //правило
Рунге.
int
n1 = 1, n2 = 2;
double
f, h1 = (b-a)/n1, h2 = (b-a)/n2,= f_middle_rect(b, h1,
n1), I2 = f_middle_rect(b, h2, n2);
while((f
= Math.abs(h2*h2*(I2-I1)/(h1*h1-h2*h2)))>e){= n2; n2 *= 2; h1
= h2; h2 /= 2;= I2; I2 = f_middle_rect(b, h2, n2);
}
return
I2+f*h2*h2; //значение интеграла с точносью e.
}
public
static double calc_newton(double x){ //метод
Ньютона.
return
x-(calc_integral_acc(x)-5.0)/f_x(x);
}
double
xk = 0.0, xk1 = 2.9; int i = 0;
while(true){=
xk1; xk1 = calc_newton(xk);++;
if(Math.abs(xk1-xk)<e)
break;.out.printf("%d\n%.15f\n%.15f\n", i, xk1, Math.abs(xk1-xk));
}.out.printf("%d\n%.15f\n%.15f\n",
i, xk1, Math.abs(xk1-xk));
}
}