Типовые математические модели экономических задач линейного программирования

Федеральное Государственное образовательное учреждение

Высшего профессионального образования

Пермская государственная сельскохозяйственная академия имени академика Д.Н. Прянишникова

Кафедра Информационных систем

Контрольная работа

по дисциплине:

"Экономико-математические методы и модели"

на тему:

"Типовые математические модели экономических задач линейного программирования "

 

 

 

Выполнил: студент 2 курса заочного отделения

по специальности: 060800 "Экономика и

управление на предприятиях АПК"

шифр ЭКР-2010-404

Рудометов

Проверил: О.Ю. Вшивков

Пермь-2015

Содержание

 

1. Типовые математические модели экономических задач линейного программирования: задача об оптимальном использовании ресурсов, задача о производственных мощностях

2. Задача линейного программирования

3. Транспортная задача

Список использованной литературы

1. Типовые математические модели экономических задач линейного программирования: задача об оптимальном использовании ресурсов, задача о производственных мощностях

Многие задачи, с которыми приходится иметь дело в повседневной практике, являются многовариантными. Среди множества возможных вариантов в условиях рыночных отношений приходится отыскивать наилучшие в некотором смысле при ограничениях, налагаемых на природные, экономические и технологические возможности. В связи с этим возникла необходимость применять для анализа и синтеза экономических ситуаций и систем математические методы и современную вычислительную технику.

Такие методы объединяются под общим названием - математическое программирование.

Математическое программирование - область математики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограничениями, т.е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных.

Функцию, экстремальное значение которой нужно найти в условиях экономических возможностей, называют целевой, показателем эффективности или критерием оптимальности. Экономические возможности формализуются в виде системы ограничений. Все это составляет математическую модель. Математическая модель задачи - это отражение оригинала в виде функций, уравнений, неравенств, цифр и т.д. Модель задачи математического программирования включает:

) совокупность неизвестных величин, действуя на которые, систему можно совершенствовать. Их называют планом задачи (вектором управления, решением, управлением, стратегией, поведением и др.);

) целевую функцию (функцию цели, показатель эффективности, критерий оптимальности, функционал задачи и др.). Целевая функция позволяет выбирать наилучший вариант - из множества возможных. Наилучший вариант доставляет целевой функции экстремальное значение. Это может быть прибыль, объем выпуска или реализации, затраты производства, издержки обращения, уровень обслуживания или дефицитности, число комплектов, отходы и т.д.

Эти условия следуют из ограниченности ресурсов, которыми располагает общество в любой момент времени, из необходимости удовлетворения насущных потребностей, из условий производственных и технологических процессов. Ограниченными являются не только материальные, финансовые и трудовые ресурсы. Таковыми могут быть возможности технического, технологического и вообще научного потенциала. Нередко потребности превышают возможности их удовлетворения. Математически ограничения выражаются в виде уравнений и неравенств. Их совокупность образует область допустимых решений (область экономических возможностей). План, удовлетворяющий системе ограничений задачи, называется допустимым. Допустимый план, доставляющий функции цели экстремальное значение, называется оптимальным. Оптимальное решение, вообще говоря, не обязательно единственно, возможны случаи, когда оно не существует, имеется конечное или бесчисленное множество оптимальных решений.

Один из разделов математического программирования - линейным программированием.

Методы и модели линейного программирования широко применяются при оптимизации процессов во всех отраслях народного хозяйства: при разработке производственной программы предприятия, распределении ее по исполнителям, при размещении заказов между исполнителями и по временным интервалам, при определении наилучшего ассортимента выпускаемой продукции, в задачах перспективного, текущего и оперативного планирования и управления; при планировании грузопотоков, определении плана товарооборота и его распределении; в задачах развития и размещения производительных сил, баз и складов систем обращения материальных ресурсов и т.д.

Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий, составление смесей, раскрой материалов), производственно-транспортных и других задач.

Начало линейному программированию было положено в 1939 г. советским математиком-экономистом Л.В. Канторовичем в работе "Математические методы организации и планирования производства". Появление этой работы открыло новый этап в применении математики в экономике. Спустя десять лет американский математик Дж. Данциг разработал эффективный метод решения данного класса задач - симплекс-метод.

Общая идея симплексного метода (метода последовательного улучшения плана) для решения ЗЛП состоит в следующем:

) умение находить начальный опорный план;

) наличие признака оптимальности опорного плана;

) умение переходить к не худшему опорному плану.

Линейное программирование - раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений.

Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений. Отсюда - необходимость разработки новых методов.

Методы решения задач линейного программирования относятся к вычислительной математике, а не к экономике. Однако экономисту полезно знать о свойствах интеллектуального инструмента, которым он пользуется.

С ростом мощности компьютеров необходимость применения изощренных математических методов снижается, поскольку во многих случаях время счета перестает быть лимитирующим фактором, оно весьма мало (доли секунд).

Задача о наилучшем использовании ресурсов

Пусть некоторая производственная единица (цех, завод, объединение и т.д.), исходя из конъюнктуры рынка, технических или технологических возможностей и имеющихся ресурсов, может выпускать n различных видов продукции (товаров), известных под номерами, обозначаемыми индексом j (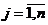). Будем обозначать эту продукцию Пj. Предприятие при производстве этих видов продукции должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т.д.).

Все эти виды ограничивающих факторов называют ингредиентами Ri. Пусть их число равно m; припишем им индекс i (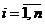). Они ограничены, и их количества равны соответственно b₁,b₂,…,b_m условных единиц.

Таким образом, 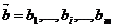 - вектор ресурсов. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т.д.

Примем в качестве такой меры, например, цену реализации с_j (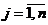), т.е.  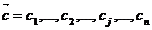- вектор цен. Известны также технологические коэффициенты а_ij, которые указывают, сколько единиц i-го ресурса требуется для производства единицы продукции >j-го вида. Матрицу коэффициентов a_ij называют технологической и обозначают буквой А. Имеем .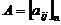

Обозначим через  план производства, показывающий, какие виды товаров П₁,…, П_j,…, П_n нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах.

Так как с_j - цена реализации единицы j-й продукции, цена реализованных x_j единиц будет равна x_jc_j, а общий объем реализации Z=x₁c₁+…+x_nc_n.

Это выражение - целевая функция, которую нужно максимизировать.

Так как a_ijx_j - расход i-го ресурса на производство x_j единиц j-й продукции, то, просуммировав расход i-го ресурса на выпуск всех n видов продукции, получим общий расход этого ресурса, который не должен превосходить  единиц:

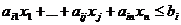
Чтобы искомый план  был реализован, наряду с ограничениями на ресурсы нужно наложить условие неотрицательности на объёмы x_j выпуска продукции:

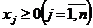
Таким образом, модель задачи о наилучшем использовании ресурсов примет вид:

 (1)

при ограничениях:

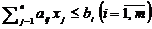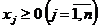 (2),  (3)

Так как переменные x_j входят в функцию  и систему ограничений только в первой степени, а показатели a_ij, b_i, c_j являются постоянными в планируемый период, то (1) - (3) - задача линейного программирования.

Задача о производственных мощностях

При планировании производства продукции на промышленном предприятии необходимо учитывать его ресурсные ограничения, а именно: фонд машинного времени по каждому виду оборудования; фонд рабочего времени, определяемый численностью персонала; фонд материальных ресурсов, которые может получить в планируемый период предприятие от поставщиков по заключенным договорам.

Модели многих задач планирования базируются на законах сохранения (балансовых соотношениях) и эмпирических закономерностях преобразования ресурсов в продукцию (производственных функциях). Математически подобные модели представляются в виде систем m линейных уравнений с n неизвестными, которые решаются с помощью известных методов линейной алгебры (например, методом Гаусса).

Общая постановка задачи об использовании мощностей (загрузке оборудования):

Предприятию задан план производства продукции по времени и номенклатуре: требуется за время T выпустить n₁, n₂,.,n_k единиц продукции P₁, P₂,.,P_k. Продукция производится на станках S₁,S₂,.,S_m, для каждого из которых известны производительность a_ij (т.е. число единиц продукции P_j, которое можно произвести на станке S_i за единицу времени) и затраты b_ij на изготовление продукции P_j на станке S_i в единицу времени.

математическая модель экономическая задача

Необходимо составить такой план работы станков (т.е. распределить выпуск продукции между станками), чтобы затраты на производство всей продукции были минимальными.

Экономико-математическая модель задачи об использовании мощностей:

Составим экономико-математическую модель задачи. Обозначим x_ij - время, в течение которого станок S_i будет занят изготовлением продукции P_{j (}i =1,2,.,m; j = 1,2,.,k).

Так как время работы каждого станка ограничено и не превышает T, то справедливы следующие неравенства:

Для выполнения плана выпуска по номенклатуре необходимо, чтобы выполнялись следующие равенства:

Кроме того, по условию задачи:

Затраты на производство всей продукции должны быть минимальны:

Экономико-математическая модель задачи об использовании мощностей (загрузке оборудования) примет вид: найти такое решение X= (x₁₁,x₁₂,.,x_mk), удовлетворяющее системам (4) и (5) и условию (6), при котором целевая функция (7) принимает минимальное значение.

2. Задача линейного программирования

Предприятие планирует выпуск двух видов продукции I и II, на производство которых расходуется три вида сырья А, В и С. Потребность a_ij i-го вида сырья на каждую единицу j-го вида продукции, запас b_i соответствующего вида сырья и прибыль c_j от реализации единицы j-го вида продукции заданы таблицей:

Таблица 1

Виды сырья	Виды продукции		Запасы сырья
	I	II
A	3	2	27
B	1	1	10
C	2	5	35
прибыль	6	5
план (ед.)	x1	x2

.        Для производства двух видов продукции I и II с планом x₁ и x₂ единиц составить математическую модель, т.е. целевую функцию прибыли F и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее n единиц обоих видов продукции.

2.      Найти оптимальный план X*= (x₁, x₂) производства продукции, обеспечивающий максимальную прибыль F_max. Определить остатки каждого вида сырья. Задачу решить симплекс-методом.

.        Построить по полученной системе ограничений многоугольник допустимых решений и найти оптимальный план производства геометрическим методом. Определить максимальную прибыль F_max.

.        Составить математическую модель двойственной задачи (систему ограничений по единичной прибыли и целевую функцию общих издержек на сырье Z); найти оптимальный набор цен на сырьё Y*= (y₁, y₂, y₃), обеспечивающий минимум общих затрат на сырье Z_min.

.        Провести анализ первоначальных и дополнительных переменных исходной и двойственной задач, сделать выводы.

.        Решить задачу оптимизации в MS Excel в режиме "поиск решения". Провести исследование полученного решения, используя отчеты по результатам, по устойчивости, по пределам; сделать выводы. Ответы, полученные в результате решений "вручную" и с помощью Excel, должны совпадать.

Решение:

Предположим, что будет использовано х₁ сырья А для изготовления продукции I, х₂ сырья для изделия II. Тогда общая прибыль составит 6х₁ + 5х₂.

Так как общее количество сырья А не может превышать 27 единиц, то должно выполняться следующее неравенство:

х₁+2х₂ ≤ 27.

Аналогичные рассуждения относительно возможно использования остального количества сырья приведут к следующим неравенствам:

х₁ + х₂ ≤ 10;

х₁ + 5х₂ ≤ 35.

При этом, так как количество изготовляемых изделий не может быть отрицательным, то:

х₁ ≥ 0, х₂ ≥ 0 (1)

Пусть F - прибыль предприятия, так как по условию необходимо составить план производства двух видов изделий, обеспечивающий максимальную прибыль, следовательно, функция F, при условии, что изготовлено х₁ единиц изделий I и х₂ единиц изделий II будет максимизироваться:

F = 6х₁ + 5х₂ → max

Таким образом, мы приходим к следующей математической задаче:

Дана система:

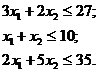 (2)

трех линейных неравенств с двумя неизвестными х_i (i=1,2). И линейная функция относительно этих же переменных:

F = 6х₁ + 5х₂ (3)

требуется среди всех неотрицательных решений системы неравенств (2), найти такое, при котором функция (3) примет максимальное значение.

Найдем решение сформулированной задачи, используя ее геометрическую интерпретацию. Сначала определим многоугольник решений. Для этого в неравенствах системы ограничений и условиях не отрицательности переменных знаки неравенств заменим на знаки точных равенств и найдем соответствующие прямые.

Прямые S1 - S3, изображены на рисунке 1.

Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой - нет. Определим искомую полуплоскость через точку О (0; 0).

Пресечение полученных плоскостей определяет многоугольник решений данной задачи

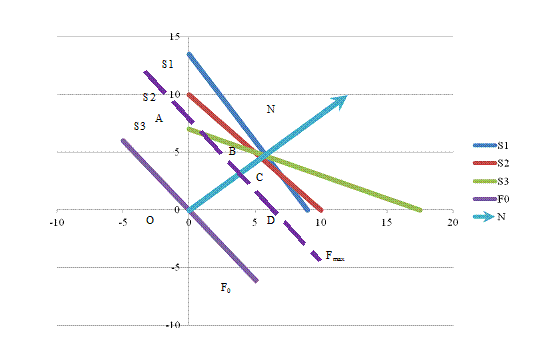
Рис. 1. Многоугольник решений

Как видно из рисунка 1, многоугольником решений является пятиугольник ОАВСD.

Таким образом, среди точек пятиугольника ОАВСD нам нужно найти такие, в которых функция F = 6х₁ + 5х₂ принимает максимальное значение. Для нахождения этих точек построим нулевую линию уровня (F₀) 6х₁ + 5х₂ = 0 и вектор N = (12;10).

Передвигая данную прямую параллельно самой себе в направлении вектора N, видим, что ее последней точкой с многоугольником решений задачи является точка C. Следовательно, в этой точке функция F принимает максимальное значение. Так как C - точка пересечения прямых S1 и S3, то ее координаты удовлетворяют уравнениям этих прямых:

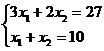
Решив эту систему уравнений мы получили: х₁ = 7 и х₂ = 3.

Таким образом, максимальное значение функции F_max = 6*7+5*3 = 42 + 15 = 57.

Решение симплекс-методом

Математическая модель задачи:

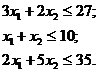
х₁, х₂ ≥ 0

F = 6х₁ + 5х₂

Запишем эту задачу в форме основной задачи ЛП:

Для этого перейдем от ограничений неравенств - к ограничениям равенствам. Введем 3 дополнительные переменные, в результате чего ограничения запишутся в виде систем ограничений:

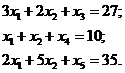
Преобразованную систему ограничений запишем в векторной форме:

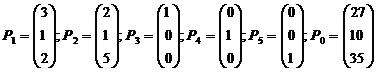
Поскольку среди векторов Р₁-Р₅ имеются 3 единичных вектора, для данной задачи можно непосредственно записать опорный план.

Таковым является план Х = (0; 0; 0; 27; 10; 35), определяемый системой трехмерных единичных векторов Р₃, Р₄, Р₅, которые образуют базис трехмерного векторного пространства.

Составим симплексную таблицу для I итерации (таб.1), подсчитав значения F₀, z_i - c_i и проверяем исходный план на оптимальность.

F₀ = (c, P₀); z₁ = (c, P₁) = 0; z₂ = (c, P₂) = 0; z₃ = (c, P₃) = 0;₄ = (c, P₄) = 0; z₅ = (c, P₅) = 0;₁ - c₁ = 0 - 6= - 6; z₂ - c₂ = 0 - 5 = - 5. Для векторов базиса z_i - c_i = 0.

Таблица 1

i	Базис	Цб	Р0	6	5	0	0	0
				Р1	Р2	Р3	Р4	Р5
1	Р3	0	27	3	2	1	0	0
2	Р4	0	10	1	1	0	1	0
3	Р5	0	35	2	5	0	0	1
4			0	-6	-5	0	0	0

Таким образом, по 4 строке таблицы 1 видно, что план не оптимален, т.к. значения z_i - c_i - отрицательны.

Далее определяем вектор, подлежащий исключению из базиса. Для этого находим Q_0min (b_i/a_i1) для a_i1>0 и Q_0min (b_i/a_i2) для a_i2>0.

Таким образом, Q_0min (b_i/a_i1) = min (27/3; 10/1; 35/2) = 27/3, а Q_0min (b_i/a_i2) = min (27/2; 10/1; 35/5) = 35/5. Min (27/3; 35/5) = 35/5.

Таким образом, мы нашли разрешающий элемент, находящийся на пересечении 2-ой строки и столбца вектора Р₂.

Следовательно, вектор Р₄ подлежит исключению из базиса.

Столбец вектора Р₂ и вторая строка являются направляющими.

Далее, составляем таблицу для итерации II (таб.2).

Сначала заполняем строку вектора вновь введенного в базис. Элементы этой строки таб.3 получаются из соответствующих элементов таб.2 делением на разрешающий элемент.

Затем, заполняем элементы столбцов для векторов, входящих в новый базис. В этих столбцах на пересечении строк и столбцов одноименных векторов проставляем единицы, а все остальные элементы полагаем равными нулю.

Для определения остальных элементов таб. 2 применяем правило прямоугольника.

Данный цикл продолжается до тех пор, пока все значения z_i - c_i - не станут положительными.

Таким образом, в таб. 2 мы запишем все итерации вычислительного процесса.

Таблица 2

i	Базис	Цб	Р0	6	5	0	0	0
				Р1	Р2	Р3	Р4	Р5
1	Р3	0	13	2,2	0	1	0	-0,4
2	Р4	0	3	0,6	0	0	1	-0,2
3	Р2	5	7	0,4	1	0	0	0,2
4			35	-4	0	0	0	1
1	Р3	0	2	0	0	1	-3,6	0,3
2	Р1	6	5	1	0	0	1,6	-0,3
3	Р2	5	5	0	1	0	-0,6	0,3
4			55	0	0	0	6,6	-0,3
1	Р5	0	6,6	0	0	3,3	-12	1
2	Р1	6	7	1	0	1	-2	0
3	Р2	5	3	0	1	-1	3	0
4			57	0	0	1	3	0

Итак, среди значений z_i - c_i нет отрицательных, следовательно, опорный план оптимален и F_max = 57.

Двойственная задача

Прямая задача имеет вид:

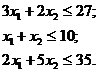
х₁, х₂ ≥ 0

F = 6х₁ + 5х₂

Хопт. = (7;3).

Max F = 57.

Составим двойственную модель и с помощью теорем двойственности найдем оптимальное решение двойственной модели:

Двойственная модель:

Z = 27y₁ + 101y₂ + 35y₃→ min

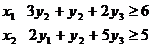
Так как мы уже нашли решение исходной задачи (таб.2), следовательно, мы нашли и решение двойственной задачи: y₁ = 1; y₂ = 3; y₃ = 0. (итерация III в симплекс-таблице 2).

Таким образом оптимальное решение двойственной задачи = y_опт (1; 3; 0).

Подставим компоненты оптимального решения двойственной задачи в функцию двойственной модели:

Z = 27*1+10*3+35*0 = 27+30+0 = 57, итак, Z = F = 57.

Отчет по результатам:

Рабочий лист: [Рудометов ЭММ - решение. xlsx]  Задача ЛП

Отчет создан: 01.10.2012 12: 12: 54

Целевая ячейка (Максимум)

Ячейка

Имя

Исходное значение

Результат

$D$10

оптимальные значения целевая функция

57

57

Изменяемые ячейки

Ячейка

Имя

Исходное значение

Результат

$B$10

оптимальные значения х1*

7

7

$C$10

оптимальные значения х2*

3

3

Ограничения

Ячейка

Имя

Значение

Формула

Статус

Разница

$D$5

коэф в 1 ограничении левая часть

27

$D$5<=$F$5

связанное

0

$D$6

коэф во 2 ограничении левая часть

10

$D$6<=$F$6

связанное

0

$D$7

коэф в 3 ограничении левая часть

29

$D$7<=$F$7

не связан.

6

$B$10

оптимальные значения х1*

7

$B$10>=0

не связан.

7

$C$10

оптимальные значения х2*

3

$C$10>=0

не связан.

3

Отчет по пределам

Microsoft Excel 12.0 Отчет по пределам
Рабочий лист: [Рудометов ЭММ - решение. xlsx]  Отчет по пределам 1
Отчет создан: 01.10.2012 12: 13: 25
		Целевое
	Ячейка	Имя	Значение
	$D$10	оптимальные значения целевая функция	57
		Изменяемое			Нижний	Целевой		Верхний	Целевой
	Ячейка	Имя	Значение		предел	результат		предел	результат
	$B$10	оптимальные значения х1*	7		0	15		7	57
	$C$10	оптимальные значения х2*	3		0	42		3	57

Отчет по устойчивости:

Microsoft Excel 12.0 Отчет по устойчивости
Рабочий лист: [Рудометов ЭММ - решение. xlsx] Задача ЛП
Отчет создан: 01.10.2012 12: 13: 13
Изменяемые ячейки
			Результ.	Нормир.
	Ячейка	Имя	значение	градиент
	$B$10	оптимальные значения х1*	7	0
	$C$10	оптимальные значения х2*	3	0
Ограничения
			Результ.	Лагранжа
	Ячейка	Имя	значение	Множитель
	$D$5	коэф в 1 ограничении левая часть	27	1
	$D$6	коэф во 2 ограничении левая часть	10	3
	$D$7	коэф в 3 ограничении левая часть	29	0

3. Транспортная задача

На трех складах А₁, А₂ и А₃ хранится а₁=100, а₂=200, а₃=60+10n единиц одного и того же груза, соответственно.

Этот груз требуется доставить трем потребителям В₁, В₂ и В₃, заказы которых b₁=190, b₂=120, b₃=10m единиц груза, соответственно. Стоимости перевозок c_ij единицы груза с i-го склада j-му потребителю указаны в соответствующих клетках транспортной таблицы:

Таблица 3

Потребности Запасы		В1	В2	В3
		b1=190	b2=120	b3=400
А1	а1 = 100	4	2	4
А2	а2 = 200	3	5	3
А3	а3 = 90	1	5	6

1.      Сравнивая суммарный запас 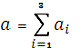 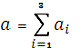и суммарную потребность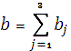 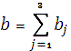 в грузе, установить, является ли модель транспортной задачи открытой или закрытой. Если модель открытая, то ее необходимо закрыть, добавив фиктивный склад А₄ с запасом а₄=b-а в случае а<b или фиктивного потребителя В₄ с потребностью b₄=a-b в случае а>b и положив соответствующие им тарифы перевозок нулевыми.

.        Составить первоначальный план перевозок методом северо-западного угла и методом наименьшей стоимости.

.        Методом потенциалов проверить первоначальный план перевозок на оптимальность в смысле суммарной стоимости перевозок, и если это не так, то составить оптимальный план

,

обеспечивающий минимальную стоимость перевозок 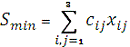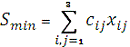. Найти эту стоимость.

4.      Решить задачу в MS Excel в режиме "поиск решения". Ответы, полученные в результате решений "вручную" и с помощью Excel, должны совпадать.

Решение:

Потребность = 190+120+400 = 710

Возможности = 100+200+90 = 390

Таким образом, данная транспортная задача (ТЗ) - открытая.

Следовательно для решения такой задачи необходимо ввести фиктивного поставщика - А4, имеющего запасы груза равные 320 единиц, тем самым мы сбалансировали спрос и предложение (таблица 4).

Таблица 4

Поставщик	Потребитель			Запасы груза
	В1	В2	В3
А1	4	2	4	100
А2	3	5	3	200
А3	1	5	6	90
А4	0	0	0	320
Потребность	190	120	400	710

Составим первоначальный план по методу северо-западного угла (таблица 5).

Таблица 5

Поставщик	Потребитель			Запасы груза
	В1	В2	В3
А1	100 4	2	4	100
А2	90 3	110 5	3	200
А3	1	10 5	80 6	90
А4	0	0	320 0	320
Потребность	190	120	400	710

n+m - 1 =4+3-1 = 6 - соответствует числу заполненных клеток

Общие транспортные издержки равны:

Z₁ = 100*4+90*3+110*5+10*5+80*6+320*0 = 400+270+550+50+480+0 = 1750

Проверим составленный план на оптимальность методом потенциалов.

Рассчитаем потенциалы, исходя из того, что потенциал строки А1 = 0 (таблица 6).

Таблица 6

Поставщик	Потребитель			Запасы груза
	В1	В2	В3
А1	100 4	2	4	100	U1=0
А2	90 3	110 5	3	200	U2=
А3	1	10 5	80 6	90	U3=
А4	0	0	320 0	320	U4=
Потребность	190	120	400	710
	V1=	V2=	V3=

Далее, рассчитаем теневые цены (таблица 7 - теневые цены выделены серым цветом).

Таблица 7

Поставщик	Потребитель			Запасы груза
	В1	В2	В3
А1	100 4	-4 2 +	-3 4	100	U1=0
А2	90 3 +	110 5	-3 3	200	U2=-1
А3	-2 1	10 5	80 6	90	U3=-1
А4	3 0	1 0	320 0	320	U4=-7
Потребность	190	120	400	710
	V1=4	V2=6	V3=7

Наличие теневых цен означает не оптимальность имеющегося плана, следовательно, для улучшения плана намечаем маршрут с наименьшей отрицательной теневой ценой и для этого маршрута определяем цикл перераспределения.

Объем перевозимого груза численно равен минимальному значению из тех объемов груза, которые указаны в клетках со знаком минус. Таким образом, min (100; 110) = 100.

Итак, составляем новый план (таблица 8).

Данный цикл длится до тех пор, пока все теневые цены не станут положительными.

Таблица 8

Поставщик	Потребитель			Запасы груза
	В1	В2	В3
А1	4 4	100 2	1 4	100	U1=0
А2	190 3	10 5	200	U2=3
А3	-2 1	10 5 +	80 6	90	U3=3
А4	3 0	1 0	320 0	320	U4=-3
Потребность	190	120	400	710
	V1=0	V2=2	V3=3

n+m - 1 =4+3-1 = 6 - соответствует числу заполненных клеток

Общие транспортные издержки равны:

Z₂ = 190*3+100*2+10*5+10*5+80*6+320*0 = 570+200+50+50+480+0 = 1350

Таблица 9

Поставщик	Потребитель			Запасы груза
	В1	В2	В3
А1	1 4	100 2	1 4	100	U1=0
А2	190 3	3 5	10 3 +	200	U2=0
А3	-5 1 +	20 5	70 6	90	U3=3
А4	0 0	1 0	320 0	320	U4=-3
Потребность	190	120	400	710
	V1=3	V2=2	V3=3

n+m - 1 =4+3-1 = 6 - соответствует числу заполненных клеток

Общие транспортные издержки равны:

Z₃ = 190*3+100*2+20*5+10*3+70*6+320*0 = 570+200+100+30+420+0 = 1320

Таблица 10

Поставщик	Потребитель			Запасы груза
	В1	В2	В3
А1	6 4	100 2	6 4	100	U1=0
А2	120 3	-2 5	80 3 +	200	U2=5
А3	70 1 +	20 5	5 6	90	U3=3
А4	0 0	-4 0 +	320 0	320	U4=2
Потребность	190	120	400	710
	V1=-2	V2=2	V3=-2

n+m - 1 =4+3-1 = 6 - соответствует числу заполненных клеток

Общие транспортные издержки равны:

Z₄ = 120*3+70*1+100*2+20*5+80*3+320*0 = 360+70+200+100+240+0 = 970

Таблица 11

Поставщик	Потребитель			Запасы груза
	В1	В2	В3
А1	6 4	100 2	6 4	100	U1=0
А2	100 3	2 5	100 3	200	U2=1
А3	90 1	4 5	5 6	90	U3=-1
А4	0 0	20 0	300 0	320	U4=-2
Потребность	190	120	400	710
	V1=2	V2=2	V3=2

n+m - 1 =4+3-1 = 6 - соответствует числу заполненных клеток

Общие транспортные издержки равны:

Z₅ = 100*3+90*1+100*2+20*0+100*3+300*0 = 300+90+200+0+300+0 = 890

В таблице 11 все теневые цены - положительные, следовательно, план оптимален.

Решение задачи в MS Excel.

Исходными данными для решения транспортной задачи являются:

-        матрица транспортных расходов;

-        предложение поставщиков;

         спрос потребителей.

Рабочий лист EXCEL с введенными исходными данными для решения транспортной задачи показан на рисунке 2.

Рис. 2 - Рабочий лист EXCEL с введенными исходными данными для решения транспортной задачи

Рабочий лист EXCEL с размеченными блоками ячеек показан на рисунке 3.

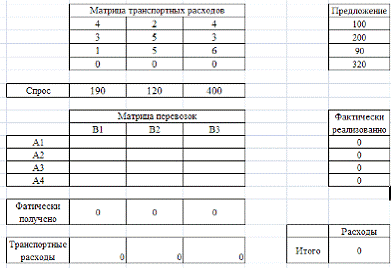
Рис. 3 - Рабочий лист EXCEL с размеченными блоками ячеек

Формирование элементов математической модели.

Элементами математической модели транспортной задачи являются следующие суммы:

фактически реализовано;

фактически получено.

Для нашей задачи m=4, n=3.

Рассмотрим процесс формирования этих сумм на рабочем листе EXCEL.

Вначале сформируем, в блоке "Фактически реализовано"

. Заполняем ячейки блока "Матрица перевозок" числом 0,01.

. Селектируем первую ячейку блока "Фактически реализовано";

. Наводим курсор на кнопку автосуммирование и щелкаем левой клавишей мыши;

. Нажимаем клавишу Delete;

. Селектируем первую строку блока "Матрица перевозок";

. Нажимаем клавишу Enter;

. Копируем формулу из первой ячейки блока "Фактически реализовано" на все остальные ячейки этого блока.

Сформируем теперь - в блоке "Фактически получено".

Для этого выполните следующие действия:

. Селектируем первую ячейку блока "Фактически получено";

. Наводим курсор на кнопку автосуммирование и щелкаем левой клавишей мыши;

. Нажимаем клавишу Delete;

. Селектируем первый столбец блока "Матрица перевозок";

. Нажимаем клавишу Enter;

. Копируем формулу из первой ячейки блока "Фактически получено" на остальные ячейки этого блока.

Для формирования целевой функции введем вначале формулы, отражающие транспортные расходы по каждому потребителю, т.е. формулы в ячейки блока "Транспортные расходы по потребителям".

Для ввода этих формул выполняем следующие действия:

. Селектируем первую ячейку блока "Транспортные расходы";

. Наводим курсор на кнопку автосуммирование и щелкаем левой клавишей мыши;

. Нажимаем клавишу Delete;

. Селектируем первый столбец блока "Матрица Транспортных расходов";

. Нажимаем клавишу *;

. Селектируем первый столбец блока "Матрица перевозок";

. Активируем строку формул, наведя на нее курсор и щелкнув затем левой клавишей мыши;

. Нажимаем одновременно три клавиши: "CTRL" + "SHIFT" + "ENTER";

. Копируем формулу в остальные ячейки блока "Транспортные расходы";

Сформируем теперь целевую функцию транспортной задачи, в ячейку "Итого расходы". Для этого:

Селектируем ячейку "Итого расходы";

. Наводим курсор на кнопку автосуммирование и щелкаем левой клавишей мыши;

. Нажимаем клавишу Delete;

. Селектируем блок ячеек "Транспортные расходы";

. Нажимаем клавишу Enter;

После формирования элементов математической модели и целевой функции транспортной задачи рабочий лист EXСEL примет вид, показанный на рисунке 4.

Рис. 4 - Формирования элементов математической модели и целевой функции транспортной задачи

Далее, приступаем к решению задачи с помощью программы "Поиск решения".

Параметры программы "Поиск решения" представлены на рисунке 5.

Рис. 5 - Параметры программы "Поиск решения"

Результаты решения представлены на рисунке 6.

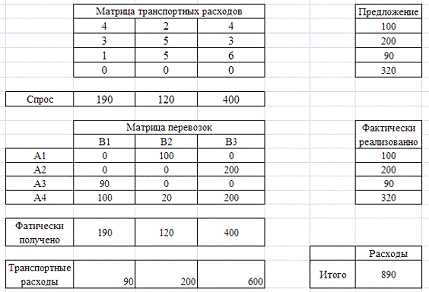
Рис. 6 - Результаты решения транспортной задачи

Список использованной литературы

1.      Венцель Е.С. Исследование операций. Задачи, принципы, методология [Текст]: учеб. пособие для вузов / Е.С. Венцель. - 3-е изд., стереотип. - М.: Дрофа, 2004.

2.      Конюховский П.В. Математические методы исследования операций в экономике [Текст]: учеб. пособие / П.В. Конюховский. - СПб.: Питер, 2000.

.        Стариков А.В. Экономико-математическое и компьютерное моделирование [Текст]: учеб. пособие / А.В. Стариков, И.С. Кущева; Фед. агентство по образованию, ГОУ ВПО "ВГЛТА". - Воронеж, 2008.

.        Хазанова Л.Э. Математические методы в экономике [Текст]: учеб. пособие / Л.Э. Хазанова. - 2-е изд., испр. и перераб. - М.: Изд-во БЕК, 2002.

.        Excel для экономистов и менеджеров [Текст] / А.Г. Дубина [и др.]. - СПб.: Питер, 2004.