Синтез и анализ комбинационных схем
Министерство
науки и образования Украины
Национальный
аэрокосмический университет им. Н.Е. Жуковского
«Харьковский
авиационный институт»
Кафедра 501
«Проектирование радиоэлектронных систем летательных аппаратов»
Лабораторная
работа №2
«Синтез и анализ
комбинационных схем»
Выполнил: студент 526 группы
Момот О.А.
г. Харьков
2014
Цель работы:
ознакомиться с методом синтеза логической схемы по заданным временным
диаграммам, закрепить знания по способам минимизации логических функций, построить
логическую схему с использованием редактора символов и смоделировать ее работу
с помощью эмулятора работы логических схем.
Теоретическая часть
Формы представления логических функций
Различают несколько способов задания ФАЛ,
основными из которых являются: табличный, аналитический, цифровой,
таблично-графический, геометрический.
Табличный способ предусматривает задание ФАЛ
таблицей истинности (рис. 1, а), в которой указывают, какие из двух возможных
значений «0» или «1» принимает функция на каждом наборе аргументов. Наборы, на
которых значение ФАЛ равно «1» называются рабочими. Наборы, на которых функция
принимает нулевое значение, называются запрещёнными.
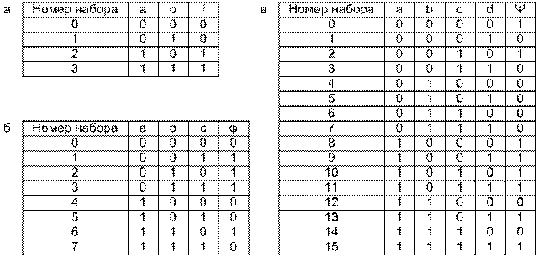
Рис. 1. Табличный способ задания функций алгебры
логики
Аналитический способ задания предполагает запись
функции в виде формализованного выражения, составленного с использованием
математического аппарата алгебры логики. Например, представленные таблицей
истинности на рис. 2.2, а-в функции могут быть записаны в виде аналитических
выражений:
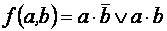 ;
;
 ;
;
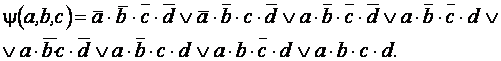
Цифровой способ задания ФАЛ реализуется
посредством записи функции в виде совокупности рабочих, запрещённых и условных наборов
аргументов. Условными наборами аргументов называются наборы, на которых
значение функции не определено или нас не интересует. При цифровом способе
задания функции f, 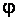 (рис. 2.2) будут
записаны в виде:
(рис. 2.2) будут
записаны в виде:
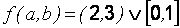 ;
; 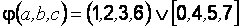 .
.
Если у функции отсутствуют условные наборы, то
указываются только рабочие наборы данной функции. Например, функция 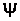 (рис.
1) при цифровом способе задания может быть записана в виде:
(рис.
1) при цифровом способе задания может быть записана в виде:
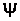 = (0,2,8 -
11,13,15).
= (0,2,8 -
11,13,15).
Таблично-графический или координатный способ
предусматривает задание ФАЛ в виде координатных карт состояний, называемых
картами Карно. При наличии n переменных карты Карно состоят из 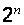 полей
и представляют собой прямоугольные таблицы, на пересечении строки и столбца
которых записывают значение функции при соответствующем наборе аргументов. При
составлении карты необходимо следить, чтобы наборы аргументов в соседних полях
(клетках) таблицы отличались только значением одной переменной. Карты Карно для
двух, трех и четырех переменных представлены на рис. 2, а-в.
полей
и представляют собой прямоугольные таблицы, на пересечении строки и столбца
которых записывают значение функции при соответствующем наборе аргументов. При
составлении карты необходимо следить, чтобы наборы аргументов в соседних полях
(клетках) таблицы отличались только значением одной переменной. Карты Карно для
двух, трех и четырех переменных представлены на рис. 2, а-в.

Рис. 2. Способы задания функций алгебры логики:
а - для двух переменных; б - трех; в - четырех; г - геометрический способ
задания ФАЛ
Каждое поле карты соответствует одной строчке
таблицы истинности, при табличном способе задания функции. Например, для
функции двух переменных, представленной на рис. 2.3, а, согласно обозначению
первому полю карты, соответствует комбинация аргументов 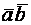 или
«00», второму -
или
«00», второму - 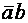 или «01», третьему
-
или «01», третьему
-  или
«11», четвёртому -
или
«11», четвёртому - 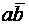 или «10». Единицы
поставлены в поля карты соответствующие рабочим наборам
или «10». Единицы
поставлены в поля карты соответствующие рабочим наборам 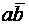 и
и
 .
В остальные поля карты, соответствующие запрещённым наборам, записаны нули.
Аналогично составляются карты для функций от трёх и четырёх переменных (рис. 2,
б, в).
.
В остальные поля карты, соответствующие запрещённым наборам, записаны нули.
Аналогично составляются карты для функций от трёх и четырёх переменных (рис. 2,
б, в).
В каждую клетку карты Карно вписываются
значения, принимаемые функцией на соответствующем данной клетке наборе
аргументов.
Графический способ задания ФАЛ предусматривает
изображение функции в виде n-мерной геометрической фигуры, вершинам которой
соответствуют наборы значений аргументов данной функции. В каждой вершине
указывается значение, принимаемое функцией на данном наборе (рис. 2 г). Данный
способ представления функций широко используется для иллюстрации основных
понятий и определений в теории кодирования.
Представление в форме временной диаграммы.
Пример:

Рис. 3
Дизъюнктивная (ДНФ) и конъюнктивная (КНФ)
нормальные формы ЛФ. Совершенные дизъюнктивная и конъюнктивная нормальные формы
представления
При записи ФАЛ в виде алгебраического выражения
удобно использовать конъюнктивную и дизъюнктивную нормальную форму
представления функции [1, 2, 5-9].
Дизъюнктивной нормальной формой (ДНФ) называется
дизъюнкция любого конечного множества попарно различных элементарных
произведений. Конъюнктивной нормальной формой (КНФ) называется произведение
любого конечного множества попарно различных элементарных дизъюнкций. Под
элементарным произведением или элементарной дизъюнкцией понимается выражение,
представляющее собой соответственно произведение или дизъюнкцию любого
конечного множества попарно различных между собой букв алфавита данной функции,
над частью которых могут быть поставлены знаки отрицания. Каждая функция может
быть представлена несколькими эквивалентными друг другу ДНФ или КНФ.
Примером задания ФАЛ в форме ДНФ могут служить
функции:

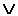
 ;
;  .
.
При представлении функций в КНФ они записываются
в виде элементарных произведений, например:
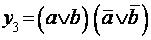 ;
;  .
.
Входящие в ДНФ элементарные произведения
называются конституентами единицы, а входящие в КНФ элементарные дизъюнкции
-конституентами нуля, если они содержат в прямом или инверсном виде все
аргументы данной функции. Любая ФАЛ
может быть записана черезконституенты единицы и конституенты нуля. Поэтому,
наряду со стандартными нормальными формами, существуют канонические совершенные
нормальные формы представления ФАЛ.
Дизъюнктивная нормальная форма называется
совершенной, если все входящие в неё элементарные произведения
являютсяконституентами единицы для одного и того же множества аргументов данной
функции. Примером представления функции в дизъюнктивной совершенной нормальной
форме (ДСНФ) может служить выражение
 .
.
Конъюнктивная нормальная форма называется
совершенной, если все входящие в неё элементарные дизъюнкции являются
конституентами нуля для одного и того же множества аргументов данной функции.
При записи в конъюнктивной совершенной нормальной форме (КСНФ) функция 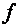 имеет
вид:
имеет
вид:
дизъюнктивный логический функция
карно
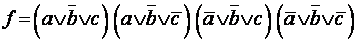 .
.
Любая ФАЛ имеет только одну ДСНФ и КСНФ. Для
получения совершенных нормальных форм существуют различные способы, основными
из которых являются: табличный и аналитический.
Табличный способ основан на использовании таблицы
истинности или карты Карно рассматриваемой функции. Для получения ДСНФ
выписываются все элементарные произведения, соответствующие наборам переменных,
на которых ФАЛ принимает единичное значение. При получении КСНФ выписываются
все элементарные дизъюнкции, соответствующие наборам переменных, на которых
функция обращается в ноль, причем каждая из входящих в элементарные дизъюнкции
переменных инвертируется. Примером могут служить ДСНФ и КСНФ функции f и 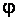 ,
записанные на основании таблиц истинности (рис. 4, а, б).
,
записанные на основании таблиц истинности (рис. 4, а, б).

Рис. 4. Совершенные нормальные формы
представления ФАЛ
Аналитический способ получения совершенных
нормальных форм основывается на использовании теоремы разложения [1, 7, 10-16],
которая при разложении ФАЛ по одной переменной (например 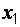 )
записывается следующим образом:
)
записывается следующим образом:
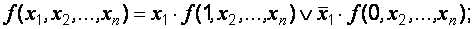 (2.1)
(2.1)
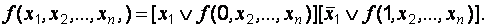 (2.2)
(2.2)
Справедливость данных тождеств доказывается
подстановкой в каждое из выражений значений: 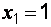 и
и
 .
.
Для получения совершенных нормальных форм
необходимо осуществить разложение ФАЛ по каждой из входящих в неё переменных.
Ниже приведен пример разложения функции 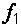 по
переменной b с использованием
формул (2.1) и (2.2) теоремы разложения:
по
переменной b с использованием
формул (2.1) и (2.2) теоремы разложения:

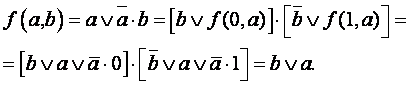
Минимизация логических функций
Работа любого КЦУ с одним выходом может быть
описана логическим выражением или системой m логических выражений, если у КЦУ m
выходов. Другими словами, всякому КЦУ с одним выходом или каждому из m выходов
многовыходного КЦУ взаимно однозначно соответствует логическое выражение, в
котором буквы соответствуют входным переменным, а знаки операций - ЛЭ,
выполняющим эти операции. Подобные логические выражения именуют уравнениями
связи «вход-выход» КЦУ.
В этих условиях упрощение схемы КЦУ сводится к
минимизации логических выражений, соответствующих этим устройствам. СДНФ и СКНФ
используются для первоначального представления логических функций, но эти
формы, как правило, неэкономичны для построения схем КЦУ. Прежде чем строить
схему, реализующую логическую функцию, ее необходимо минимизировать, т.е. найти
такую эквивалентную форму представления, при которой выражение для функции
будет состоять из наименьшего числа переменных (букв). Минимизация логических
функций может быть проведена аналитически, используя постулаты и законы булевой
алгебры.
Основными понятиями, которые вводятся на этапе
минимизации логических функций, являются понятия смежных минтермов и импликант,
а основной операцией упрощения является операция склеивания смежных минтермов.
Смежными принято называть минтермы, отличающиеся формой вхождения в них лишь
одной переменной (в один минтерм переменная входит в прямой форме, а в другой -
в инверсной). Например, смежными являются минтермы  и
и
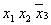 (различаются
формой вхождения только переменной х1). Два смежных минтерма СДНФ могут быть
объединены по разнящемуся аргументу, в результате чего происходит их замена
одной конъюнкцией с числом переменных на единицу меньшим, чем в исходных
минтермах. Например,
(различаются
формой вхождения только переменной х1). Два смежных минтерма СДНФ могут быть
объединены по разнящемуся аргументу, в результате чего происходит их замена
одной конъюнкцией с числом переменных на единицу меньшим, чем в исходных
минтермах. Например, 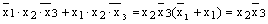
Операция объединения смежных минтермов по
разнящейся переменной именуется склеиванием. Конъюнкция, получаемая в
результате склеивания двух смежных минтермов, называется импликантой.
Импликанты с одинаковым числом переменных (рангом), в свою очередь могут
оказаться смежными, что позволяет производить их склеивание между собой.
Процесс многоступенчатого склеивания приводит к получению импликант, которые не
имеют себе смежных. Такие импликанты называют простыми. Процесс минимизации
логических функций значительно упрощают карты Карно.
Карты Карно представляют собой прямоугольную
таблицу (матрицу), разбитую горизонтальными и вертикальными линиями на клетки
(ячейки). Общее число ячеек совпадает с числом минтермов и равно 2n, где n -
число переменных упрощаемой функции. Таким образом, каждая ячейка карты
соответствует определенному минтерму, размещение которых осуществляется таким
образом, чтобы смежные минтермы находились в соседних ячейках. Соседними
считаются ячейки, имеющие общие стороны, а также расположенные на краях одних и
тех же строк или столбцов карты. Такой порядок размещения минтермов
обеспечивается принятым способом образования наборов переменных,
соответствующих различным ячейкам карты. Все переменные разбиваются на две
группы.
Наборам переменных одной группы ставят в
соответствие столбцы, наборам другой группы - строки карты. Для определенности
крайний левый столбец и верхнюю строку карты обозначают наборами с нулевыми
значениями всех переменных (это условие не является обязательным). Для функции
двух переменных карта Карно представляет собой таблицу, разделенную на четыре
ячейки, по одной на каждый входной набор (рис. 2, а). Строки карты связаны с
переменной  , столбцы - с
переменной
, столбцы - с
переменной 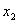 . Расположенная
слева вверху ячейка соответствует входному набору (0 0) или минтерму (
. Расположенная
слева вверху ячейка соответствует входному набору (0 0) или минтерму (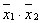 ),
расположенная ниже ее ячейка соответствует входному набору (1 0) или минтерму (
),
расположенная ниже ее ячейка соответствует входному набору (1 0) или минтерму (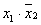 )
и т.д.
)
и т.д.

В случае функции трех переменных карта Карно
(рис. 2, б) содержит восемь ячеек, по одной для каждого входного набора,
указанного внутри ячейки. Поскольку для функции четырех переменных существует
16 входных наборов, карта Карно разделена на 16 ячеек (рис. 2, в). Наряду с
изложенным применяют и другой способ маркировки размещения минтермов: столбцы и
строки карты Карно, соответствующие переменным в прямой форме, охватывают
скобками и возле них проставляют символы переменных.
Аналогично поступают для переменных,
представленных в инверсной форме.
Алгоритм минимизации логических функций,
заданных в СДНФ при помощи карт Карно
При образовании блоков необходимо придерживаться
следующих правил: Одни и те же ячейки могут входить в несколько блоков; Блоки
должны покрывать все обозначенные ячейки; Следует стремиться к тому, чтобы
количество блоков было минимальным, а сами блоки покрывали по возможности
большее число ячеек. Для каждого блока записать логическое выражение в виде
конъюнкции тех переменных, значения которых совпадают у всех объединенных в
блок ячеек. Если блок покрывает 2, 4 или более ячеек, то онъюнкции представляют
собой импликанты склеиваемых минтермов. Ранг полученных таким образом импликант
меньше ранга минтермов, объединенных в контур, на К единиц. Логические выражения
для блоков объединить значками дизъюнкции. Полученное выражение представляет
собой минимизированную дизъюнктивную нормальную форму (МДНФ) логической
функции.
Задание
Вариант 5:

Выполнение работы
Таблица 1 Истинности
|
d
|
c
|
b
|
a
|
f
|
|
0
|
0
|
0
|
0
|
1
|
|
0
|
0
|
0
|
1
|
0
|
|
0
|
0
|
1
|
0
|
0
|
|
0
|
0
|
1
|
1
|
1
|
|
0
|
1
|
0
|
0
|
1
|
|
0
|
1
|
0
|
1
|
0
|
|
0
|
1
|
1
|
0
|
1
|
|
0
|
1
|
1
|
1
|
1
|
|
1
|
0
|
0
|
0
|
1
|
|
1
|
0
|
0
|
1
|
0
|
|
1
|
0
|
1
|
0
|
1
|
|
1
|
0
|
1
|
0
|
|
1
|
1
|
0
|
0
|
1
|
|
1
|
1
|
0
|
1
|
0
|
|
1
|
1
|
1
|
0
|
0
|
|
1
|
1
|
1
|
1
|
1
|
СКНФ: f = (
 + b + c + d)*(a +
+ b + c + d)*(a + 
 + c + d)*(
+ c + d)*(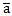
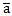 + b +
+ b + 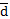
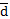 + d)*(
+ d)*(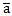
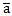 + b + c +
+ b + c + 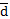
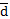 )*(
)*(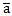
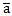 +
+ 
 + c +
+ c + 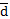
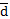 )*(
)*(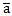
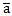 + b + +
+ b + + 
 +
+ 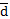
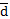 )*(a +
)*(a + 
 +
+ 
 +
+ 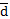
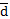 )
)
Таблица 2 Карно
|
b a
|
0 0
|
0 1
|
1 1
|
1 0
|
|
d c
|
|
|
|
|
|
0 0
|
1
|
0
|
1
|
0
|
|
0 1
|
1
|
0
|
1
|
1
|
|
1 1
|
1
|
0
|
1
|
0
|
|
1 0
|
1
|
0
|
0
|
1
|
дизъюнктивный логический карно
Минимизированная ЛФ (базис
«и-или-не»): f = (d + c + 
 + a)*(
+ a)*(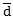
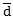 +
+ 
 +
+ 
 + a)*(
+ a)*(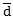
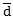 + + c +
+ + c + 
 )*(b +
)*(b + 
 )
)
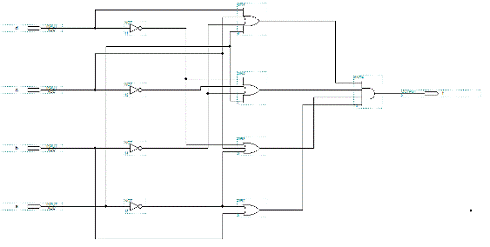
Рисунок 1 Логическая схема

Рисунок 2 Результат моделирования