Нестационарная теплопроводность
Федеральное
государственное бюджетное образовательное учреждение высшего профессионального
образования
«Уральский
институт Государственной противопожарной службы Министерства Российской
Федерации по делам гражданской обороны, чрезвычайным ситуациям и ликвидации
последствий стихийных бедствий»
Кафедра
физики и теплообмена
КОНТРОЛЬНАЯ
РАБОТА
Дисциплина:
Теплотехника
Выполнил:
слушатель ФЗО 2 Б курса
учебной
группы № 3
ст.
сержант вн. службы Гладких Р.Ю.
Екатеринбург,
2014
Теоретические ответы
Можно ли теплоту некоторого источника полностью
превратить в работу?
Ответ
Тепловой двигатель, с помощью которого можно
было бы полностью превращать в работу теплоту, полученную от какого-либо тела,
и при том так, чтобы телам с меньшей температурой, участвующим в процессе, не
передавалось сколько-нибудь теплоты, называют вечным двигателем второго рода.
С помощью вечного двигателя второго рода можно
было бы получить работу за счёт охлаждения тела (т.е. единственного источника
теплоты) без того, чтобы часть отданного источником теплоты переходила к другим
телам. Та часть теплоты, которая передаётся от источника теплоты другим телам в
процессе преобразования теплоты в работу, представляет собой «остаточное
изменение» и называется «компенсационным эффектом» или просто «компенсацией». В
этом смысле вечный двигатель второго рода может рассматриваться как
бескомпенсационный тепловой двигатель.
В связи с введением понятия о вечном двигателе
второго рода второе начало термодинамики можно сформулировать ещё и так: вечный
двигатель второго рода невозможен. Другими словами, нельзя осуществить тепловой
двигатель, единственным результатом действия которого было бы превращение
теплоты какого-либо тела в работу без того, чтобы часть этой теплоты
передавалась другим телам.
Практические задачи
Задача 1. Параметры смеси газов. Истечение газов
В помещении компрессорной станции объемом V
произошла разгерметизация трубопровода, по которому транспортируется горючий
газ под давлением P1 при
температуре Т1 через образовавшееся в трубопроводе сквозное отверстие площадью f
газ выходит в помещение.
Рассчитать, через какое время τ
во всем объеме компрессорной станции может образоваться взрывоопасная смесь, а
также среднюю молекулярную массу, плотность, удельный объем и изобарную удельную
массовую теплоемкость смеси, если ее температура Т = 293 К, а давление Р = 100
кПа. Коэффициент расхода отверстия ξ
= 0,7. Воздухообмен не учитывается. Данные, необходимые для расчетов: V
= 30∙102 м3, P1 = 1,6 МПа,
T1 = 290 К, f
= 4,1∙10-4 м2, газ - водород.
Решение
Из приложения 1 для водорода:
μ1 = 2,016 кг/моль, μСр1 = 29 
 , k = 1,4, НКПВ
= 4 %.
, k = 1,4, НКПВ
= 4 %.
Для воздуха: μ2 = 28,97
кг/моль, μСр = 29,12 
 , k = 1,4.
, k = 1,4.
Режим истечения газа: 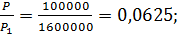
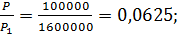

 .
.
Поскольку 
 , тогда массовый расход газа:
, тогда массовый расход газа:

 кг/с.
кг/с.
Где газовая постоянная:
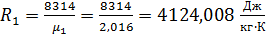
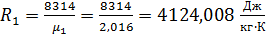 .
.
Плотность водорода в помещении:

 кг/м3.
кг/м3.
Объем водорода при НКПВ:
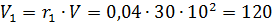
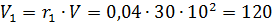 м3.
м3.
Масса водорода при НКПВ:

 кг.
кг.
Время получения взрывоопасной смеси:
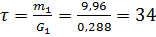
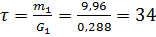 сек.
сек.
Объемные доли газов при НКПВ r1=0,04
воздуха: r=1-r1=1-0,04=0,96.
Молекулярная масса смеси:
μСМ=r1μ1+rμ=0,04∙2,016+0,96∙28,97=27,89
кг/Кмоль.
Удельная газовая постоянная смеси:

 .
.
Плотность смеси: 
 кг/м3.
кг/м3.
Удельный объем смеси: 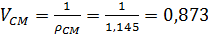
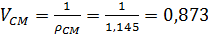 м3/кг.
м3/кг.
Массовая доля смеси:
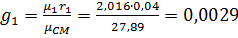
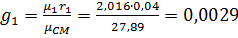 ;
;
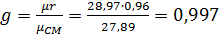
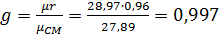 .
.
Массовые удельные теплоемкости
компонентов:

 ;
;
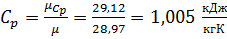
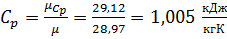 .
.
Изобарная теплоемкость смеси:

 .
.
Задача 2. Конвективный теплообмен.
Теплопередача
Рукавная линия диаметром d поперечно
обдувается воздухом со скоростью ωв. Температура воздуха tв. По
рукавной линии со скоростью ωж движется вода, температура которой
на входе в рукавную линию t'ж. рассчитать максимальную длину
рукавной линии из условия, чтобы температура на выходе из рукавной линии была t''ж ≥
10С. Толщина стенки рукавной линии δ = 4 мм. Эквивалентный
коэффициент теплопроводности материала рукава принять λ = 0,115
Вт/(м∙К). Данные, необходимые для расчетов: ωВ = 5 м/с, tB = -50 °С, ωж = 2 м/с, t´ж = 6 °С, d = 4 мм.
Решение
Средняя температура воды

 .
.
Параметры воды при 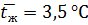
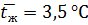 :
:
λж=55,91∙10-2 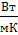
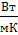 , Срж=4,205
, Срж=4,205 
 , ρж=999,8
кг/м3, νж=1,620∙10-6
м2/с.
, ρж=999,8
кг/м3, νж=1,620∙10-6
м2/с.
Параметры воздуха при tв=-50 °С:
λв=2,04∙102 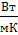
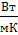 , Срв=1,013
, Срв=1,013 
 , ρв=1,584
кг/м3, νв=9,23∙10-6
м2/с.
, ρв=1,584
кг/м3, νв=9,23∙10-6
м2/с.
Число Рейнольдса для воды в рукаве

 .
.
Коэффициент теплоотдачи от воды к
рукаву:
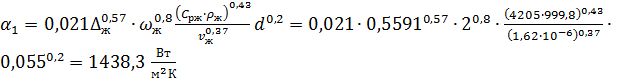

Число Рейнольдса для окружающего
воздуха:


Коэффициент теплоотдачи от рукава к
воздуху:
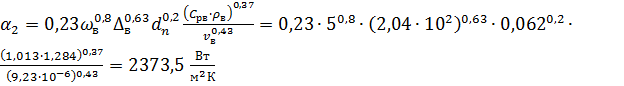

Коэффициент теплопередачи от воды к
воздуху:
Массовый расход воды:

 .
.
Допускаемое изменение энтальпии
воды:
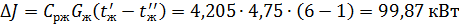
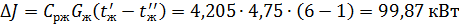 .
.
Максимальная длина рукавной линии:


Задача 3. Лучистый теплообмен
Определить минимальное расстояние,
обеспечивающее безопасность соседнего с горящим объекта, при исходных данных:
проекция факела пламени горящего объекта имеет прямоугольную форму размером d ∙ l, его
температура Тф, а степень черноты εф.
На поверхности негорящего объекта:
допустимое значение температуры Тдоп, допустимое значение плотности теплового
потока (критическая плотность) qкр, степень черноты поверхности ε.
Кроме того, оценить безопасное
расстояние от факела для личного состава, работающего на пожаре без средств
защиты, от теплового воздействия при условии: а) кратковременного пребывания;
б) длительной работы.
При кратковременном тепловом
воздействии для кожи человека qкр = 1120 Вт/м2, при длительном qкр = 560
Вт/м2. При решении задачи учитывать только теплообмен излучением. Коэффициент
безопасности принять равным β. Данные, необходимые для расчета: d=18 м, l=12 м, Тф=14∙10-2
К, εф=0,6,
Тдоп=715 К, qкр=135∙10-2
Вт/м2, ε=0,7, β=1,4.
Решение
Приведенная степень черноты:

 ;
;
Условие тепловой устойчивости:
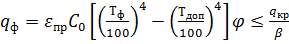
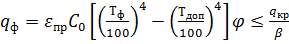
Отсюда требуемый средний коэффициент
облучаемости:
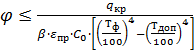
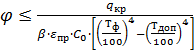 .
.
Учитывая, что φ=4φ12,
получаем:
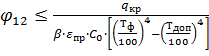
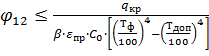 .
.
Функция φ12
описывается формулой:
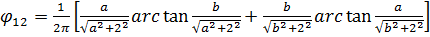
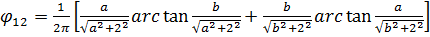 ,
,
где a=d/2=18/2=9 м;
b=l/2=12/2=6 м.
а) Для поверхности негорящего
объекта qкр=13500
Вт/м2:
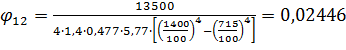
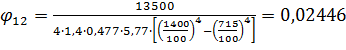 .
.
Решим уравнение φ12=0,024
относительно r методом
последовательных приближений:
Т.о. получаем r=
б) Для кратковременного пребывания людей qкр=1120
Вт/м2:

 Вт/м2.
Вт/м2.
Т.о. получаем r=
в) Для длительного пребывания людей qкр=560
Вт/м2:
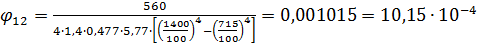
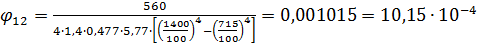 Вт/м2.
Вт/м2.
Т.о. получаем r=
Задача 4. Температурный режим при пожаре в
помещении
Производство, связанное с обращением ГЖ,
размещено в помещении размерами в плане a(м)∙b(м)
и высотой Н(м). При аварии технологических аппаратов возможны и розлив жидкости
на пол, и возникновение пожара. Предусмотрены устройства, ограничивающие
растекание жидкости на полу на площади квадрата f,
м2, расстояние от границы горения до стены с оконными и дверными проемами,
через которые будет происходить газообмен при пожаре в помещении с внешней
средой, l, м.
Механическая вентиляция при возникновении пожара
выключается. За счет естественного газообмена в помещение поступает такое
количество воздуха, что на 1 кг горящей жидкости в среднем приходится VА,
м3 воздуха.
Рассчитайте возможную температуру среды в
помещении при возникновении пожара:
а) среднеобъемную через 5, 15 и 30 мин его
развития;
б) локальную в точке над факелом под перекрытием
через 5, 15 и 30 мин его развития;
в) локальную в точках, находящихся на высоте 1,5
м от пола и расстояниях от границы горения 0,25 l,
0,5 l, 0,75 l
и l, через 2 мин его
развития.
Постройте графики:
а) изменения среднеобъемной температуры среды в
помещении при пожаре во времени;
б) изменения температуры среды в точке над
факелом под перекрытием во времени;
в) изменения температуры среды на высоте 1,5 м в
зависимости от расстояния от границы горения для 2 мин развития пожара.
По графику установите, на каком расстоянии от
выхода значение температуры среды достигает 70 0С. Данные, необходимые для
расчетов: a = 52 м, b
= 54 м, H = 12 м, l
= 26 м, f = 90 м2, VA
= 8 м2/кг, жидкость - этиловый спирт.
Решение
Из приложения 2 для этилового спирта:
QНР = 27200 мДж/кг, V0
= 6,69 м3/кг, VГ0 = 7,76 м3/кг, М0
= 3,06∙10-2 кг/(м2с). Среднее значение коэффициента избытка воздуха:
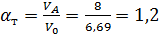
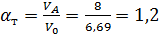 ;
;
Приведенный объем продуктов горения:
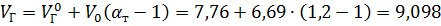
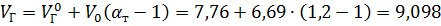 м3/кг;
м3/кг;
Масса жидкости, сгорающей при пожаре
за секунду:
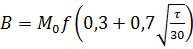
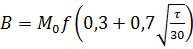 ,
,
при τ1 = 2 мин: 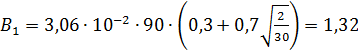
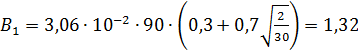 кг/с;
кг/с;
при τ2 = 5 мин: 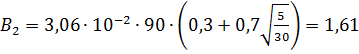
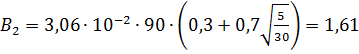 кг/с;
кг/с;
при τ3 = 15 мин: 
 кг/с;
кг/с;
при τ4 = 30 мин: 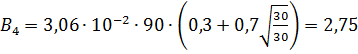
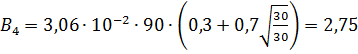 кг/с;
кг/с;
Принимаем среднеобъемную температуру
при при τ1 = 2 мин:
Тm1 = 640 K.
Удельная объемная изобарная
теплоемкость продуктов горения при при τ1 = 2 мин:
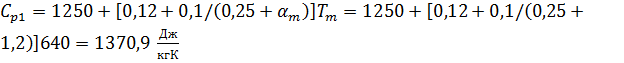
 ;
;
Приведенная степень черноты системы
«среда-поверхность ограждения»:
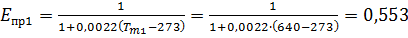
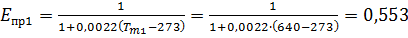 ;
;
Площадь поверхностей теплообмена:
Температура продуктов горения:
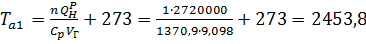
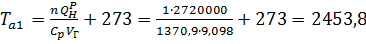 К;
К;
Проверяем среднеобъемную температуру
среды в помещении при при τ1 = 2 мин при полученных значениях:
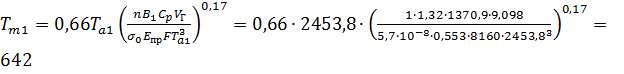
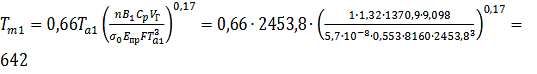 К
К
Что соотносится с ранее принятым.
Принимаем среднеобъемную температуру
при при τ2 = 5 мин:
Тm2 = 670 K.
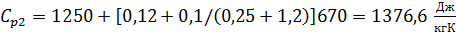
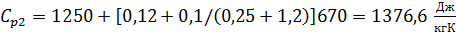


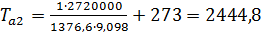
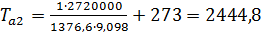 К
К

 К;
К;
Принимаем среднеобъемную температуру
при при τ3 = 15 мин:
Тm3 = 710 K.
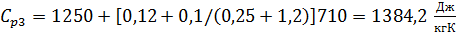
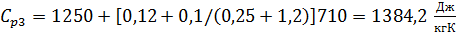 ;
;
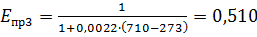
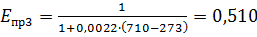 ;
;
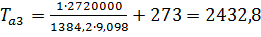
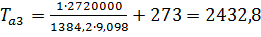 К;
К;

 К;
К;
Принимаем среднеобъемную температуру
при при τ4 = 30 мин:
Тm4 = 740 K.

 ;
;
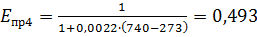
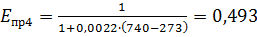 ;
;

 К;
К;
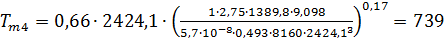
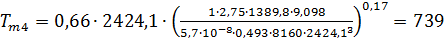 К;
К;
По результатам расчетов построим
таблицу:
|
τ, мин
|
2
|
5
|
15
|
30
|
|
Tm, К
|
642
|
667
|
707
|
739
|
Локальная температура в точке над факелом под
перекрытием:
ТО,Н,τ
= 1,6∙Тm,r
|
τ, мин
|
2
|
5
|
15
|
30
|
|
ТО,Н,τ, К
|
1027
|
1067
|
1131
|
1182
|
Локальная температура на высоте y
= 1,5 м при τ1 = 2 мин:
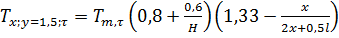
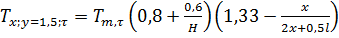 ,
,
при x = 0,25l = 0,25∙26
=6,5 м:
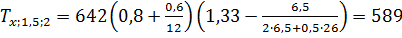
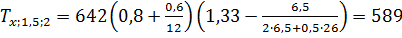 К
К
при x = 0,5l = 0,5∙26
=13 м:
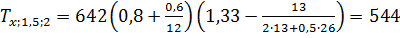
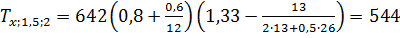 К
К
при x = 0,75l = 0,75∙26
=19,5 м:

 К
К
при x = l = 26 м:

 К
К
По результатам расчетов построим
таблицу:
|
х,
м
|
6,5
|
13
|
19,5
|
26
|
|
Т,
К
|
589
|
544
|
521
|
508
|
Задача 5. Нестационарная теплопроводность.
Изменяющиеся граничные условия 3 рода
Рассчитайте температурное поле по толщине
перекрытия через 0,5 ч после начала пожара, используя полученные при решении
задачи 4 результаты расчета температуры среды над факелом под перекрытием
(график изменения температуры среды под перекрытием). Перекрытие представляет
собой сплошную железобетонную плиту толщиной 18 см. Толщина слоя бетона λ
= 1,2 Вт/(м∙К). Начальная температура перекрытия 20 0 С, такую же
температуру имеет воздух над перекрытием.
Задачу решить графически методом конечных
разностей.
Температура факела при τ
= 30 мин, Т = 1182 К или t
= 909 °C.
Максимальное значение коэффициента теплоотдачи:
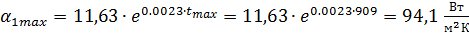
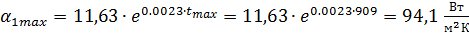 ;
;
Толщина расчетного слоя:
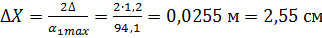
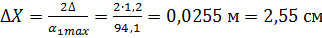 ;
;
Принимаем ∆Х = 2,6 см, тогда
число слоев:

 → n = 7
→ n = 7
Расчетный интервал времени:
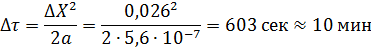
Составим расчетную таблицу:
|
τ, минТ, Кt, °Сα1,
Вт/(м2°С)X0=λ/α1,
м
|
|
|
|
|
|
0
|
941
|
668
|
54,0
|
0,0222
|
|
10
|
1098
|
825
|
77,5
|
0,0155
|
|
20
|
1152
|
879
|
87,8
|
0,0137
|
|
30
|
1182
|
909
|
94,1
|
0,0128
|
Задача 6. Нестационарная теплопроводность.
Неизменяющиеся граничные условия 3 рода
Железобетонная плита перекрытия
толщиной δ
обогревается с одной стороны средой с температурой tг в течение τ мин.
Коэффициент теплообмен а на обогреваемой поверхности плиты 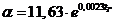 . Начальная
температура перекрытия t0 = 200C.
Коэффициент теплопроводности железобетона λ = 1,2 Вт/(м∙К),
коэффициент температуропроводности α = 5,6∙10-7 м2/с.
Рассчитать температуру на расстоянии s от
обогреваемой поверхности плиты: а) принимая перекрытие за неограниченную
пластину; б) принимая перекрытие как полуограниченное тело. Данные, необходимые
для расчетов: δ = 0,25 м, s = 0,08 м, tГ = 1000 °С,
τ = 40 мин.
. Начальная
температура перекрытия t0 = 200C.
Коэффициент теплопроводности железобетона λ = 1,2 Вт/(м∙К),
коэффициент температуропроводности α = 5,6∙10-7 м2/с.
Рассчитать температуру на расстоянии s от
обогреваемой поверхности плиты: а) принимая перекрытие за неограниченную
пластину; б) принимая перекрытие как полуограниченное тело. Данные, необходимые
для расчетов: δ = 0,25 м, s = 0,08 м, tГ = 1000 °С,
τ = 40 мин.
Решение
а) Расчет при одностороннем
нагревании плиты
Коэффициент теплообмена на
нагреваемой поверхности:

Число Био:

Число Фурье:

Характеристическое уравнение:
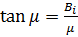
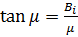
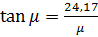
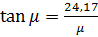
Поскольку F0<0,25,
находим первые три корня характеристического уравнения: μ1 = 1,508, μ2 = 4,528, μ3 = 7,551
Коэффициенты:
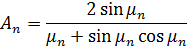
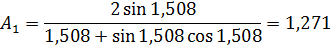
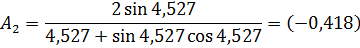
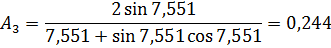
Расстояние от необогреваемой
поверхности:
х = δ - s = 0,25 -
0,08 =0,17 м
Температура в точке:
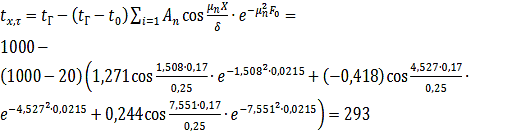
 °С
°С
б) Расчет для полуограниченного тела
Аргументы функции Крампа:
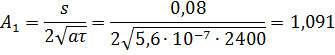

Показатель экспонанты:

Значения функции Крампа:
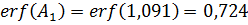

Температура в точке:
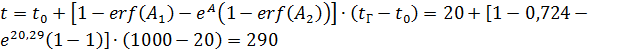
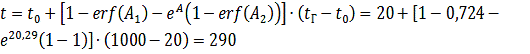 °C
°C
Результаты расчетов практически
совпадают.
конвективный газ лучистый теплообмен
Литература
1. Баранова
О.Ю., Борисенко А.В. Теплотехника: Задания и методческие указания к контрольной
работе для слушателей факультета заочного обучения, по специальности 280705
Пожарная безопасность. Екатеринбург: Уральский
институт ГПС МЧС России, 2013. 35 с.
2. Кошмаров
Ю.А., Башкирцев М.П. Термодинамика и теплопередача в пожарном деле. М.: ВИПТШ
МВД РФ, 1977 г. 444 с.
3. Задачник
по термодинамике и теплопередаче в пожарном деле. Под ред. к.т.н.
М.П.Башкирцева.- М.:ВИПТШ МВД РФ,1979 г. 217 с.