Идентификация граничных условий в задаче нестационарной теплопроводности двухкомпонентного криволинейного стержня
РЕФЕРАТ
«Идентификация граничных условий в задаче
нестационарной теплопроводности двухкомпонентного криволинейного стержня».
Выпускная работа на получение степени бакалавра по специальности «Системный
анализ».
Выделены основные положения теории теплопроводности.
Описаны элементы задачи теплопроводности с точки зрения системного анализа. В
рассматриваемой системе были определены такие характеристики как
эмерджентность, целостность, аддитивность и другие. Разработан алгоритм решения
прямой задачи теплопроводности и задачи идентификации, который реализован в
пакете MathCad.
Рассмотрены и проанализированы опасные и вредные
факторы, возникающие при работе за компьютером.
Произведен расчет цены и себестоимости
программного продукта с учетом всех необходимых трудозатрат, НДС, отчислений в
пенсионный фонд, фонд занятости и отчислений на социальное страхование,
накладных расходов.
ГРАНИЧНЫЕ УСЛОВИЯ, ЗАДАЧА ТЕПЛОПРОВОДНОСТИ,
ЗАДАЧА ИДЕНТИФИКАЦИИ, ОБРАТНАЯ ЗАДАЧА ТЕПЛОПРОВОДНОСТИ, ПОГРЕШНОСТЬ,
РАСПРОСТРАНЕНИЕ ТЕПЛА УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ, УСТОЙЧИВОСТЬ МЕТОДА.
ПЕРЕЧЕНЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ
НДС - налог на добавленную стоимость
расп-ие темп-ры - распределение температуры
тепл. п. - тепловой поток
ВВЕДЕНИЕ
Многие тепловые аппараты работают при
нестационарном режиме, поэтому тепловой расчет таких аппаратов связан с
решением задач нестационарной теплопроводности. Определение тепловых свойств
материалов также связано с нахождением температурного поля материала при
нестационарном режиме (большинство экспресс - методов определения термических
коэффициентов твердых тел основаны на определенных свойствах нестационарного
температурного поля). К подобного рода задачам относятся тепловые расчеты на
теплоустойчивость ограждающих конструкций в условиях переменных тепловых воздействий
(теплоизоляция зданий, холодильников, котлов, трубопроводов, нагревание машин,
электрокабелей, температурные напряжение в мостах и мн. др.). Таким образом,
аналитическая теория теплопроводности в настоящее время находит широкое
применение в решении различного рода технических проблем.
Процесс переноса теплоты теплопроводностью
происходит между непосредственно соприкасающимися телами или частицами тел с
различной температурой. Учение о теплопроводности однородных и изотропных тел
опирается на весьма прочный теоретический фундамент. Оно основано на простых
количественных законах и располагает хорошо разработанным математическим
аппаратом. Теплопроводность представляет собой, согласно взглядам современной
физики, молекулярный процесс передачи теплоты.
При определении переноса теплоты
теплопроводностью в реальных телах встречаются известные трудности, которые на
практике до сих пор удовлетворительно не решены. В этих задачах трудности
заключаются в том, что:
тепловые процессы развиваются в неоднородной
среде;
свойства неоднородной среды зависят от
температуры и изменяются по объему;
сложность конфигурации системы.
Важный класс прикладных проблем составляют так
же задачи управления тепловым состоянием исследуемого объекта. В этих задачах
требуется подобрать:
управляющие воздействия так, чтобы достичь
некоторого эффекта;
тепловые источники так, чтобы температура была
близка к некоторой заданной (постоянной).
В проблемах теплообмена большое значение имеют
задачи управления граничными условиями. В этих задачах имеется возможность
управлять температурой (например, температурой в некоторой области) или
тепловыми потоками на поверхности.
В руководствах по оптимальному управлению
распределенными системами в качестве наиболее характерной рассматривается задача
оптимального нагрева. Необходимо за счет некоторых управляющих воздействий
нагреть тело до некоторой заданной температуры.
Процессы переноса тепла являются одним из
основных разделов современной науки и имеют большое практическое значение в
различных отраслях. Например:
расчет тепловых аппаратов, работающих при
нестационарном режиме;
расчет ограждающих конструкций в условиях
переменных тепловых воздействий (теплоизоляция зданий, печей, трубопроводов);
приборы для измерения температуры (термопара);
нагревание машин.
Особое значение приобретают вопросы
нестационарного теплообмена в реактивной и ракетной технике, где тепловая
аппаратура работает в условиях нестационарного режима.
Задачи теплопроводности имеют широкое
практическое применение. Умение решать подобные задачи позволяет получать
важнейшие сведения о процессе. Для теплового процесса можно:
рассчитать стационарное температурное поле;
рассчитать тепловые потоки и средние значения
температур отдельных элементов конструкции и аппарата в целом;
определить характер изменения (профили,
перепады, градиенты) температур в отдельных точках конструктивных элементов
аппарата;
найти оптимальные параметры и предложить схему
управления данным аппаратом или установкой.
Таким образом, задачи теплопроводности находят
самое широкое применение в решении различных технических проблем [1].
1. ОСНОВНЫЕ
ПОЛОЖЕНИЯ ТЕОРИИ ТЕПЛОПРОВОДНОСТИ
.1 Предметное исследование
Процесс теплообмена представляет собой перенос
энергии (обмен), происходящий между телами (средами), имеющими различную
температуру.
Следует различать три механизма распределения
тепла: теплопроводность, конвекция, тепловое излучение [2].
Теплопроводность - это процесс молекулярного
переноса теплоты в твердых материалах, который происходит между непосредственно
соприкасающимися телами или частицами тел с различной температурой.
Конвекция - это процесс переноса микрочастицами
только текучей среды (жидкости или газа) из зоны с одной температурой в зону с
другой.
Тепловое излучение - представляет собой процесс
переноса энергии посредством электромагнитных колебаний, имеющих различную
длину волны
В жидкостях и газах конвекция и излучение играют
первостепенную роль, тогда как в твердых телах конвекция вообще отсутствует, а
излучение обычно пренебрежимо мало. В чистом виде теплопроводность встречается
лишь в твердых телах, а также в неподвижной среде.
По характеру переноса тепла твердые тела можно
разделить на три категории: металлы; полупроводники; непроводящие материалы
пористой и монолитной структур.
Процесс распространения теплоты в твердом теле
всегда связан с распределением температур, которые могут изменяться как по
сечению тела, так и во времени. Поэтому основной задачей теории
теплопроводности является определение пространственно-временного изменения
температуры в отдельных точках тела, т. е. нахождение зависимости вида:
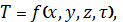
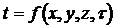 (1.1)
(1.1)
где 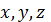
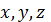 - координаты точек тела;
- координаты точек тела;
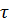
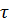 - время.
- время.
Объектом задачи теплопроводности
является температурное поле, которое обеспечивает перенос тепла от одних
участков твердого тела к другим. Температурное поле - совокупность мгновенных значений
температуры во всех точках тела. Температурное поле является скалярным. Оно
может быть стационарным и нестационарным.
Нестационарным температурным полем
называется такое поле, температура которого изменяется не только в
пространстве, но и с течением времени, или, как образно говорят, «температура
есть функция пространства и времени». Уравнение (1) есть математическая запись
нестационарного температурного поля.[6]
Стационарным температурным полем
называется такое поле, температура которого в любой его точке не изменяется во
времени, т.е. является функцией только координат [5]:
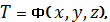
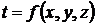

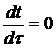 (1.2)
(1.2)
Тепловое поле характеризуется [1]:
изотермическими поверхностями;
изотермическими линиями;
градиентом;
производной по направлению.
Температурное поле дает
исчерпывающую информацию о тепловом состоянии тела и обладает следующими
свойствами [1]:
температура в теле меняется во всех
направлениях непрерывно, никаких скачков температуры в теле нет;
между точками, имеющими разные
температуры, непременно имеются точки со всеми промежуточными температурами;
изотермические поверхности всегда
замкнуты на себя или на границы тела;
любое тело может быть представлено
как совокупность бесконечного числа примыкающих друг к другу изотермических
поверхностей;
изотермические поверхности не могут
пересекать друг друга (так как одна и та же точка тела не может иметь
одновременно две температуры), но одно тело может иметь несколько одинаковых
изотерм;
поверхности максимальных градиентов
не имеют разрывов, но могут иметь изломы и, кроме того, в отличие от
изотермических поверхностей значения градиентов могут меняться скачкообразно;
в твердом изотропном теле
поверхности максимальных градиентов являются одновременно поверхностями,
совпадающими с направлением теплового потока.
Теплопроводность - это процесс
молекулярного переноса теплоты в твердых материалах, который происходит между
непосредственно соприкасающимися телами или частицами тел с различной
температурой.
Объектом задачи теплопроводности
является температурное поле, дает исчерпывающую информацию о тепловом состоянии
тела.
2. СИСТЕМНЫЙ ПОДХОД К ЗАДАЧЕ
ТЕПЛОПРОВОДНОСТИ
.1 Дерево проблем

Рисунок 2.1- Дерево проблем
Дерево проблем связано с построением
дерева целей.
2.2 Дерево целей

Рисунок 2.2 - Дерево целей
2.3 Описание системы
Структуру исследуемой системы можно представить
в линейном виде (рисунок 2.3).

Рисунок 2.3 - Структурная схема
Число уровней в системе - 6.
Для доказательства того, что исследуемый объект
является системой, рассмотрим следующие свойства системы:
Эмерджентность. При решении прямой задачи мы
находим значения температуры стержня. Решая обратную задачу теплопроводности,
находится граничная функция. То есть свойства каждой подсистемы отличается от
свойства общей системы.
Целостность. Если изменить модель тела или
граничные условия, то и дифференциальное уравнение и тепловое поле тоже
изменится. Рассматриваемая система - целостная, т.к. изменение одного элемента
влечёт за собой изменение всей системы в целом и всех её элементов в
отдельности.
Аддитивность. Температура отдельно взятого
элемента зависит только от теплофизических характеристик (плотности,
теплоемкости, коэффициента теплопроводности). Для системы в целом
характеристики зависят от характеристик всех элементов, от способа их
соединения и краевых условий.
Тип элементов: информационные.
Тип связей между элементами: информационные.
Форма модельного тела: (входная величина -
исходные данные; выходная величина-модель тела) необходима для представления
тела, которое исследуется.
Дифференциальное уравнение теплопроводности
(входная величина- модель тела; выходная величина - дифференциальное уравнение)
необходимо для математического описания процесса распространения тепла в
стержне.
Решение прямой задачи (входная величина -
дифференциальные уравнения и краевые условия, выходная величина - значения
температуры) необходимо для решения обратной задачи.
Решение обратной задачи:(входная величина -
значения температуры, выходная величина - граничное условие) необходимо для
идентификации граничного условия.
Начальное и граничное условия (входная величина
- начальное и граничное условия, выходная величина - температурное поле)
необходимы для математического описания процесса распространения тепла в
стержне.
Управление граничными условиями (входная
величина - граничное условия, выходная величина - температура) предназначено
для получения необходимой температуры.
2.3.1 Дифференциальное уравнение
теплопроводности
Связь между величинами, участвующими в передаче
теплоты теплопроводностью, устанавливается дифференциальным уравнением
теплопроводности.

Рисунок 2.5 - Допущения при выводе
дифференциального уравнения
Укажем основные типы уравнений для
случая функций двух независимых переменных [5].
. Уравнение теплопроводности
параболического типа
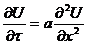 (2.1)
(2.1)
К решению этого уравнения приводят
распространение теплоты, потому его называют уравнением теплопроводности, или
уравнением Фурье.
. Уравнение теплопроводности гиперболического
типа [1]
 (2.2)
(2.2)
Это уравнение описывает процесс
переноса тепла при высокоинтенсивных нестационарных явлениях.
. Уравнение эллиптического типа -
уравнение Лапласа
 (2.3)
(2.3)
К исследованию этого уравнения
приводят решения задач о стационарном тепловом состоянии, гидродинамики,
диффузии и других.
При наличии внутреннего источника
тепла уравнение описывает перенос тепла теплопроводностью и выглядит следующим
образом:
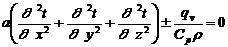 (2.4)
(2.4)
Полученное дифференциальное
уравнение описывает явления передачи теплоты теплопроводностью в самом общем
виде. Для того чтобы применить его к конкретному случаю, необходимо знать [6]:
геометрическую форму и размеры тела,
физические параметры среды и тела,
граничные условия, характеризующие
распределение температур на поверхности тела, или взаимодействие изучаемого
тела с окружающей средой.
Все эти особенности совместно с
дифференциальным уравнением дают полное описание конкретного процесса
теплопроводности.
2.3.2 Краевые условия
Совокупность начального и граничного
условий называется краевыми условиями; начальное условие называется временным
краевым условием, а граничное условие - пространственным краевым условием [1].
Начальное условие определяется задание закона распределения температуры внутри
тела в начальный момент времени, т.е.:
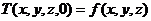 (2.5)
(2.5)
где 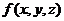 - известная функция.
- известная функция.
Во многих задачах принимают
равномерное распределение температуры в начальный момент времени, тогда:

Граничные условия могут быть заданы
4 способами.
Граничное условие первого рода
задается распределением температуры на поверхности тела для любого момента
времени.
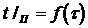 (2.6)
(2.6)
В частном случае 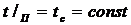 , т.е.
температура на поверхности постоянна на протяжении всего процесса теплообмена.
Граничное условие второго рода задается поверхностной плотностью теплового
потока в каждой точке поверхности тела для любого момента времени.
, т.е.
температура на поверхности постоянна на протяжении всего процесса теплообмена.
Граничное условие второго рода задается поверхностной плотностью теплового
потока в каждой точке поверхности тела для любого момента времени.
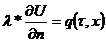 (2.7)
(2.7)
Простейший случай граничного условия
второго рода состоит в постоянстве плотности теплового потока:
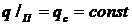
Граничное условие третьего рода
задается температурой среды, окружающей тело, и законом теплоотдачи между
поверхностями тела и окружающей средой при постоянном потоке тепла
(стационарное температурное поле). В таком случае количество тепла,
передаваемого в единицу времени с единицы площади поверхности тела в окружающую
среду, прямо пропорционально разности температур между поверхностью тела и
окружающей средой, т.е.:
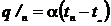 , (2.8)
, (2.8)
где a - коэффициент пропорциональности, называемый
коэффициентом теплообмена (Вт/м2·К).
Граничное условие четвертого рода
соответствует теплообмену поверхности тела с окружающей средой (конвективный теплообмен)
или теплообмену соприкасающихся твердых тел, когда температура соприкасающихся
поверхностей одинакова, т.е.: t1=t2
Помимо равенства температур, имеет
место также равенство потоков тепла:
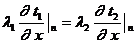 (2.9)
(2.9)
где 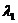 ,
, 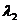 - коэффициенты теплопроводности 1-ой
и 2-ой среды.
- коэффициенты теплопроводности 1-ой
и 2-ой среды.
2.4 Классификация систем
Таблица 2.4.1 - Классификация
системы
|
№
|
Признак
классификации
|
Тип
системы по признаку
|
Определение
|
|
1
|
По
связи системы с окружающей средой
|
Открытая
|
Взаимодействует
с окружающей средой
|
|
2
|
По
происхождению
|
искусственная
|
Созданная
человеком
|
|
3
|
По
типу описания законов функционирования
|
Белый
ящик
|
Известны
законы функционирования
|
|
4
|
По
способу управления системой
|
Управление
из вне
|
Система
подчиняется внешнему управлению
|
|
5
|
По
централизации
|
Децентрализованная
|
Все
элементы равны
|
|
6
|
По
однородности структуры
|
Разнородные
|
Элементы
системы не обладают свойством взаимозаменяемости
|
|
7
|
По
типу сложности
|
Простая
|
Немного
элементов, простые связи
|
|
8
|
По
организованности
|
Хорошо
организованная
|
Удается
определить все элементы системы, связи и цели
|
|
9
|
По
непрерывности
|
Непрерывная
|
Выходная
величина изменяется плавно при плавном изменении входной величины
|
|
10
|
По
обусловленности действия
|
Детерминированная
|
Поведение
данной системы можно предсказать
|
3. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Математической моделью называется совокупность
соотношений (уравнений, неравенств, логических условий), которые с заданной
точностью описывают свойства объекта, существенные для цели исследования.
3.1 Постановка задачи
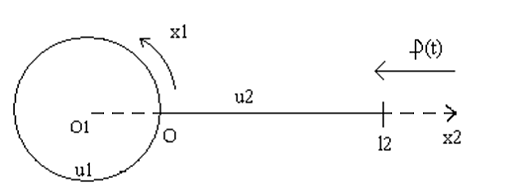
Рисунок 3.1 - Форма стержня
Уравнение теплопроводности дуги: 
Уравнение теплопроводности стержня: 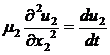
Между стержнями имеем условие
сопряжения:
Первая формула системы показывает
непрерывность температуры.
Вторая формула показывает отсутствие
источников тепла в точке соединения стержней (закон сохранения теплового
потока).
Начальное условие: 
Граничное условие: 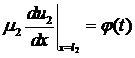
Причём 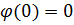 . Это
следует из
. Это
следует из 
Необходимо решить прямую и обратную
задачу.
Прямая задача заключается в том, что
при заданном тепловом потоке 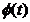 необходимо найти температуру во все
стержне.
необходимо найти температуру во все
стержне.
Обратная задача состоит в том, что
зная температуру в некоторой точке стержня в течение некоторого отрезка
времени, требуется определить тепловой поток в краевом условии, т.е. 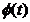
3.2 Прямая задача теплопроводности
Прямую задачу будем решать
операционным методом.
Операционное исчисление - один из
наиболее экономичных методов интегрирования линейных дифференциальных уравнений
с постоянными коэффициентами. При решении операционным методом задача
интегрирования линейного дифференциального уравнения в частных производных с
постоянными коэффициентами
<#"605857.files/image036.gif"> при всех неотрицательных x.
Преобразованием Лапласа функции f(x)
называется функция
 .
.
Функция F(p) называется изображением
функции f(x), а функция f(x) - оригиналом для F(p).

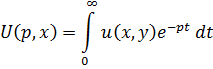
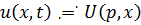
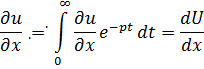
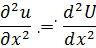
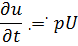
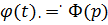

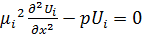 , i=1,2
, i=1,2
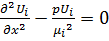
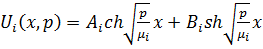
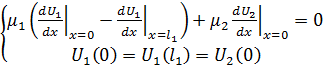
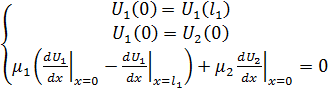


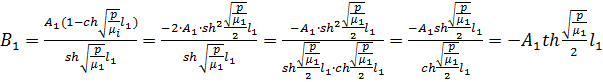

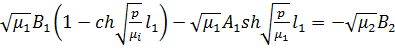
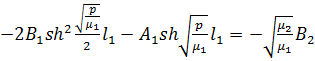
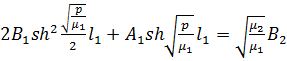
Обозначим:  ,
,


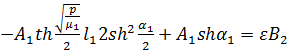

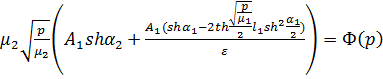
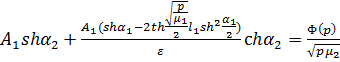

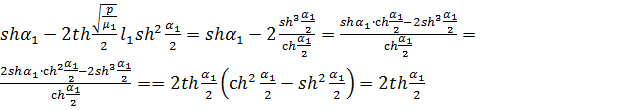


Функция  находится
при помощи формулы обращения преобразования Лапласа и теоремы Коши о вычетах. В
общем случае для этого приходится численно находить корни уравнения
находится
при помощи формулы обращения преобразования Лапласа и теоремы Коши о вычетах. В
общем случае для этого приходится численно находить корни уравнения  .
.
Для упрощения задачи положим  .
В этом случае:
.
В этом случае:
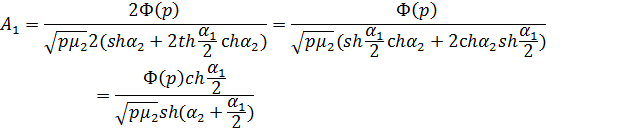




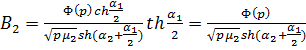 ,
,
корни знаменателя дробей находятся элементарно.
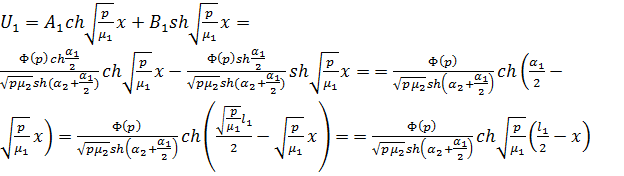

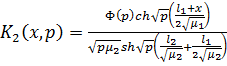

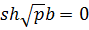 ,
, 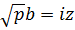
 ; n=0 - исследуем
отдельно.
; n=0 - исследуем
отдельно.
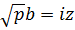
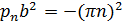
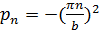
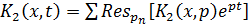
Пусть 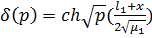 и
p=0:
и
p=0:
 ,
,
р=0 - полюс первого порядка для  .
.


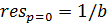
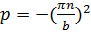 ,
,  :
:
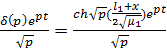
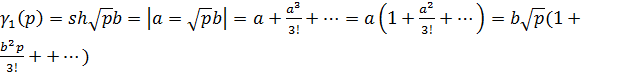
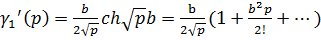
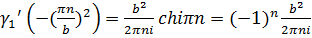



Аналогично находим:
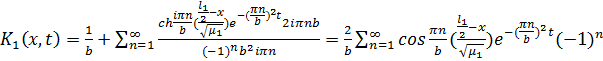
Когда t->0, то ряд сходится
медленно.
Для улучшения сходимости
проинтегрируем его по частям. Обозначим:
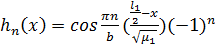 , тогда
, тогда
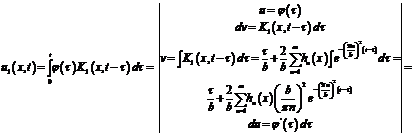

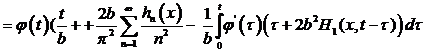


Воспользуемся суммой ряда
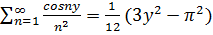 ,
, 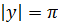
 .
.
Его сумма S(y) есть непрерывная периодическая
функция на всей оси у:

Рисунок 3.2 - График функции у
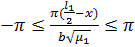
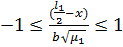
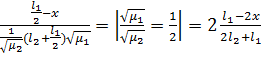

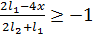

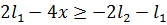
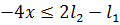
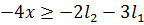
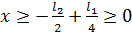
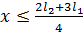
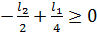 при
при 
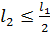
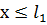
Обозначим:
теплопроводность математический
модель заземление


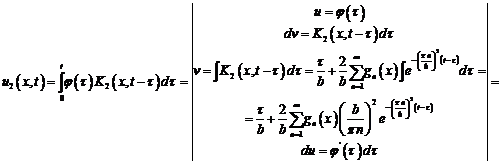
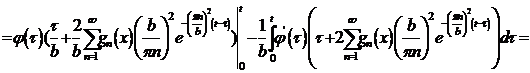
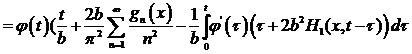
Для решения прямой задачи задаём 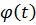 :
:

Рисунок 3.3 - График функции 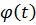
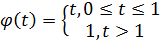
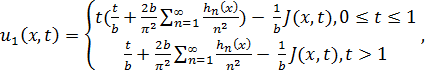
где 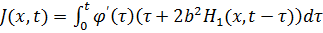
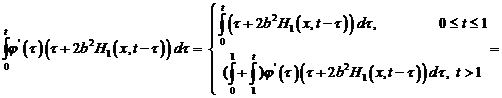
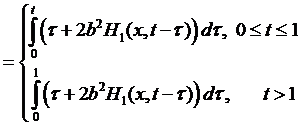
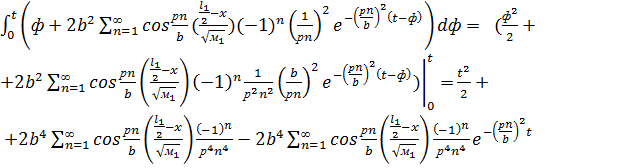


Предположим, что  .
Получим:
.
Получим:
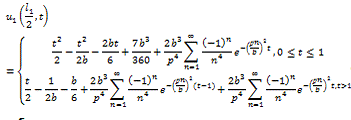
Для начала покажем
решение задачи, когда 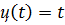 :
:
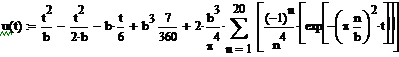

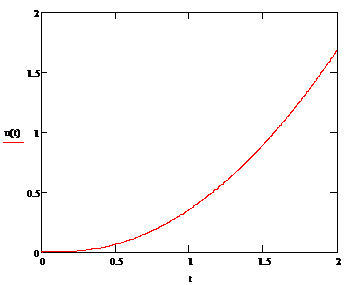
Рисунок 3.4 - График функции u(t)
Значения температуры стержня, когда 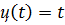 :
:
3.3 Обратная задача теплопроводности
Обратная задача состоит в том что, наблюдая
температуру в некоторой точке стержня, надо найти ту граничную функцию, которая
даёт, в рамках выбранной модели, наблюдаемую температуру.
Обозначим: 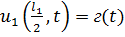 ,
т.е. наблюдение за температурой проводим в т.
,
т.е. наблюдение за температурой проводим в т.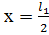 .
.
Получаем 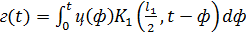 -
интегральное уравнение Вольтерра I рода.
-
интегральное уравнение Вольтерра I рода.
С помощью интегрирования по частям и условия  приведем
интегральное уравнение Вольтерра I рода к интегро-дифференциальному уравнению
Вольтерра II рода.
приведем
интегральное уравнение Вольтерра I рода к интегро-дифференциальному уравнению
Вольтерра II рода.
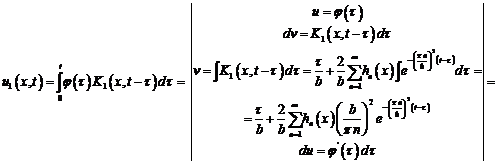
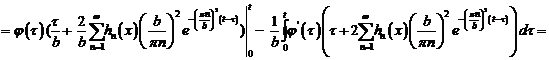

Уравнение Вольтерра второго рода
имеет вид:
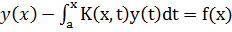 , (3.3)
, (3.3)
где 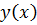 -
неизвестная функция (
-
неизвестная функция ( ),
), 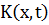 -
ядро интегрального уравнения, f(x) - свободный член.
-
ядро интегрального уравнения, f(x) - свободный член.
При 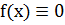 уравнение
(3.3) называют однородным, а при
уравнение
(3.3) называют однородным, а при  -
неоднородным.
-
неоднородным.
Ядро интегрального уравнения 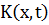 называют
вырожденным, если оно представимо в виде
называют
вырожденным, если оно представимо в виде 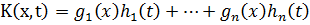 .
.
Ядро интегрального уравнения 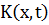 называют
разностным, если оно зависит от разности аргументов:
называют
разностным, если оно зависит от разности аргументов:  .
.
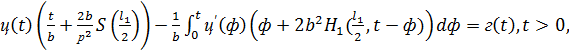
где 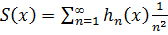
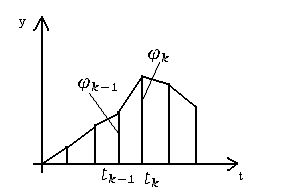
Рисунок 3.5 - Кусочно-линейное представление
функции 
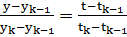
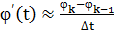
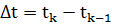
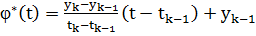 - кусочно-линейное
приближение функции
- кусочно-линейное
приближение функции 
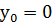
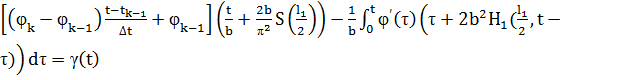 ,
,
где 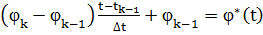

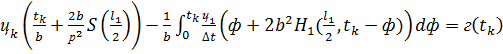
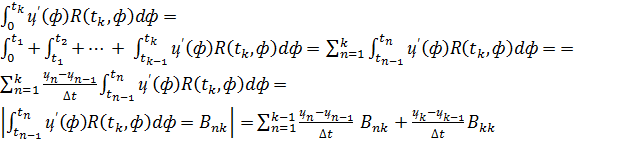 ,
,
где 
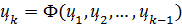
При 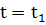 получим:
получим:
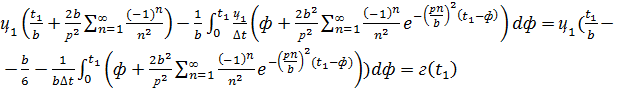
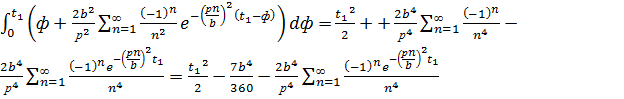
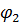

Выведем общую формулу, когда 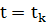 :
:

k=1,2,…
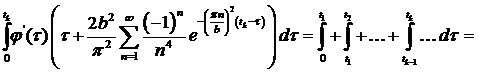
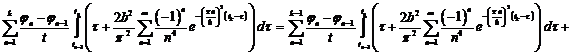

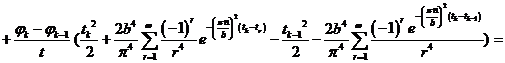
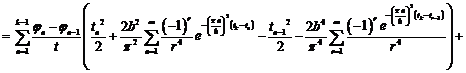

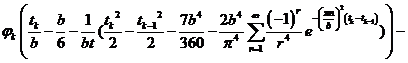
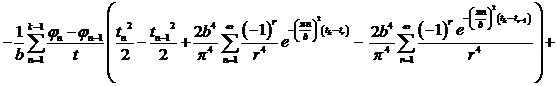
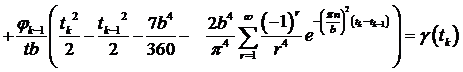
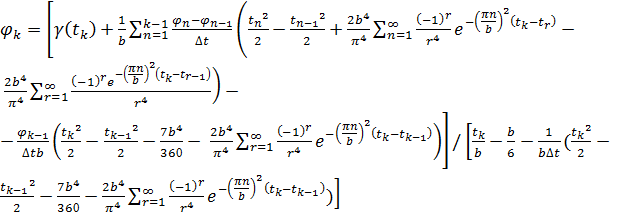
Решая обратную задачу с помощью среды MathCad,
получим:
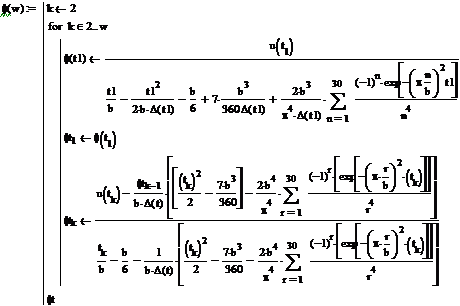
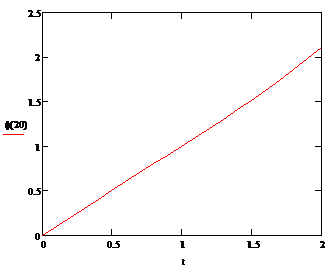
Рисунок 3.6 - График функции 
Выведем значения функции  для
20-ти точек:
для
20-ти точек:
Точные значения:
Ошибка при решении задачи увеличивается, это
видно из сравнения двух столбцов.
Решим обратную задачу другим способом:
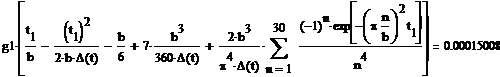

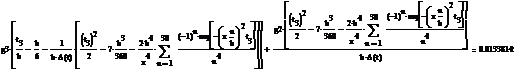
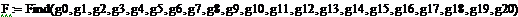
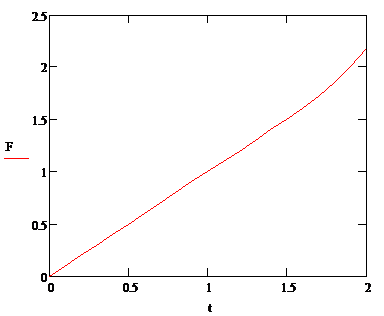
Рисунок 3.7 - График функции F
Значения функции F Точные значения:
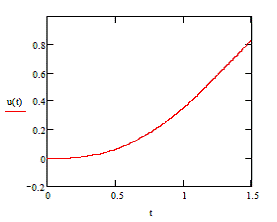
Рисунок 3.8 - График функции М
Решая обратную задачу 3-мя способами и показав,
что результаты почти совпадают, можно сказать, что граничное условие
идентифицировано приближенно, но с достаточной степенью точности.
Покажем решение задачи для функции 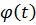 ,
когда
,
когда
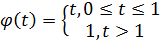
Находим температуру 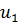 :
:

Значения температуры 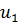 при
t=[0,2] с шагом 0.1:
при
t=[0,2] с шагом 0.1:
Решая обратную задачу, покажем, что искомая
граничная функция достаточно хорошо совпадает с той, которая была задана при
решении прямой задачи.
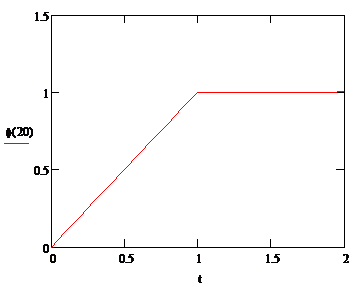
Рисунок 3.10 - График функции 
Значения функции  :
Точные значения:
:
Точные значения:
Погрешность, хотя она и маленькая, растет с
увеличением t.
Покажем результаты обратной задачи, решая ее
методом Given/Find:

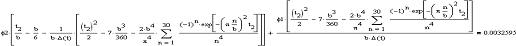
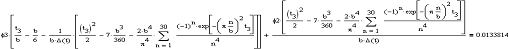
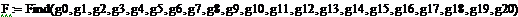
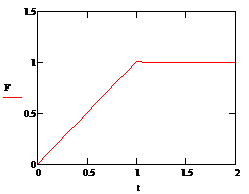
Рисунок 3.11 - График граничной функции
Выведем значения функции F: Точные значения:
Ошибка при решении задачи увеличивается, это
видно из сравнения двух столбцов.
Покажем результаты решения задачи методом
наименьших квадратов:
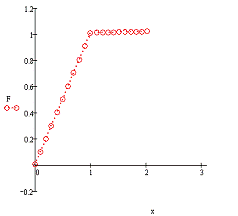
Рисунок 3.12 - График граничной функции
При решении получено точное решение задачи
теплопроводности (прямой задачи) при заданных начальных и граничных условиях и
построен алгоритм решения задачи идентификации граничного условия по измеренным
значениям температуры в некоторой точке составного стержня. Приведёны примеры
решения в среде MathCad. Сравнение найденных решений задачи идентификации
граничной функции с точными значениями показывает, что погрешности вычислений
увеличивается с увеличением промежутка времени t. Сравнение результатов решения
системы алгебраических уравнений обратной задачи тремя разными методами с
точным решением свидетельствует о хорошем их совпадении и об устойчивости
предложенного метода решения задачи идентификации, по крайней мере, для
промежутка времени 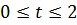 и выбранной точки
наблюдения. Дело в том, что изменение наблюдения влияет на значения ядра
интегро-дифференциального уравнения, последнее обстоятельство может привести к
плохо обусловленной системе линейных алгебраических уравнений при решении
обратной задачи. В этом случае для решения системы следует применять
регуляризующие алгоритмы Н. А. Тихонова [9]. Подойти к этому можно двояко:
можно к решению алгебраических систем, приведенных выше, применять методы
нахождения регуляризованных решений с параметрами регуляризации; можно задачу
свести к задаче минимизации квадратичного функционала:
и выбранной точки
наблюдения. Дело в том, что изменение наблюдения влияет на значения ядра
интегро-дифференциального уравнения, последнее обстоятельство может привести к
плохо обусловленной системе линейных алгебраических уравнений при решении
обратной задачи. В этом случае для решения системы следует применять
регуляризующие алгоритмы Н. А. Тихонова [9]. Подойти к этому можно двояко:
можно к решению алгебраических систем, приведенных выше, применять методы
нахождения регуляризованных решений с параметрами регуляризации; можно задачу
свести к задаче минимизации квадратичного функционала:
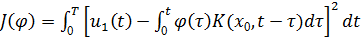 ,
,
где Т - время наблюдения, которую тоже следует
решать устойчивым методом минимизации. Рост погрешности при большом t, как это
видно из приведенных примеров, возникает из-за увеличивающегося количества
уравнений системы (итераций) и не является признаком плохой обусловленности
(некорректности) задачи.
4. БЕЗОПАСНОСТЬ ЖИЗНЕДЕЯТЕЛЬНОСТИ
Научно-технический прогресс внес серьезные
изменения в условия производственной деятельности работников умственного труда.
Их труд стал более интенсивным, напряженным, требующим значительных затрат
умственной, эмоциональной и физической энергии. Это потребовало комплексного
решения проблем эргономики, гигиены и организации труда, регламентации режимов
труда и отдыха.
В настоящее время компьютерная техника широко
применяется во всех областях деятельности человека. При работе с компьютером
человек подвергается воздействию ряда опасных и вредных производственных
факторов: электромагнитных полей (диапазон радиочастот: ВЧ, УВЧ и СВЧ),
инфракрасного и ионизирующего излучений, шума и вибрации, статического
электричества и др.
4.1 Краткое описание помещения
Написание программного продукта осуществлялось в
помещении размерами 7м ´ 9м. Таким образом, площадь
составит S=63 м2. При высоте Н=3 м объем помещения составит V=189 м3.
Естественное освещение - одностороннее.
В помещении имеется три компьютера, 4 стола и 4
стула. Компьютеры объединены в локальную сеть.
В помещении имеется один вход. Оборудование
размещается, таким образом, чтобы был обеспечен свободный проход ко всем
рабочим местам.
4.2 Выявление опасных и вредных
факторов при работе с компьютером
Производственные факторы в зависимости от
последствий, к которым может привести их действие, подразделяются на опасные и
вредные. Фактор, воздействие которого на работающего в определенных условиях
приводит к травме или другому резкому ухудшению здоровья, называется опасным
производственным фактором. Фактор, воздействие которого на работающего в
определенных условиях приводит к заболеванию или снижению работоспособности,
называется вредным производственным фактором. Опасные и вредные
производственные факторы подразделяются по своему действию на следующие группы:
физические, химические, биологические, психофизиологические.
К физическим опасным и вредным факторам
относятся:
а) воздействие вредных излучений от монитора;
б) неправильная освещенность;
в) ненормированный уровень шума;
г) нарушение микроклимата;
д) повышенный уровень вибраций, вызванный
работой вентиляторов системного блока.
К психофизическим опасным и вредным факторам
относятся:
а) тяжесть и напряженность трудового процесса;
б) эмоциональные перегрузки и умственное
перенапряжение.
Внедряемый проект не вызывает химические и
биологические опасные и вредные производственные факторы.
Работа оператора ЭВМ относится к 3 классу -
вредным условиям труда. Данный класс характеризуется наличием вредных
производственных факторов, превышающих гигиенические нормативы и оказывающих
неблагоприятное воздействие на организм работающего и/или его потомство.
Вредные условия труда по степени превышения
гигиенических нормативов и выраженности изменений в организме работающих
подразделяются на 4 степени вредности:
степень 3-го класса (3.1) - условия труда,
характеризующиеся такими отклонениями от гигиенических нормативов, которые, как
правило, вызывают обратимые функциональные изменения и обуславливают риск
развития заболевания;
степень 3-го класса (3.2) - условия труда с
такими уровнями производственных факторов, которые могут вызывать стойкие
функциональные нарушения, приводящие в большинстве случаев к росту
заболеваемости с временной утратой трудоспособности, повышению частоты общей
заболеваемости, появлению начальных признаков профессиональной патологии;
степень 3-го класса (3.3) - условия труда,
характеризующиеся такими уровнями вредных факторов, которые приводят к
развитию, как правило, профессиональной патологии в легких формах в период
трудовой деятельности, росту хронической общесоматической патологии, включая
повышенные уровни заболеваемости с временной утратой трудоспособности;
степень 3-го класса (3.4) - условия труда, при
которых могут возникать выраженные формы профессиональных заболеваний,
отмечается значительный рост хронической патологии и высокие уровни
заболеваемости с временной утратой трудоспособности.
Рабочее место оператора - это место человека в
системе «человек - машина - производственная среда», которое оснащено
средствами отображения информации, органами управления и вспомогательным
оборудованием и на котором осуществляется его трудовая деятельность.
При разработке оптимальных условий труда
оператора необходимо учитывать освещенность, шум и микроклимат. При работе на
персональном компьютере наиболее тяжелая ситуация связана с полями излучений
очень низких частот. При эксплуатации монитор компьютера излучает мягкое
рентгеновское излучение. Опасность этого вида излучения связана с его
способностью проникать в тело человека на глубину 1-2 см и поражать поверхностный
кожный покров.
На расстоянии 50 см влияние электростатического
поля уменьшается до безопасного для человека уровня. Но при работе монитора
электризуется не только его экран, но и воздух в помещении. Причем приобретает
он положительный заряд, а положительно наэлектризованные молекулы кислорода не
воспринимается организмом как кислород и не только заставляют легкие работать
впустую, но приносят в легкие микроскопические частицы пыли.
Шум оказывает вредное влияние на нервную систему
и снижает производительность труда. В частности, снижается скорость и точность
сенсомоторных процессов, увеличивается число ошибок при решении
интеллектуальных задач. Особенностью шума является то, что по мере воздействия
его во времени увеличивается его негативное влияние на нервную систему. При
увеличении уровня шума до 80дБ и более шум оказывает серьезное физиологическое
воздействие на организм. Шум уровня 90-100дБ приводит к общему утомлению,
тугоухости и глухоте, притупляется острота зрения, появляются головные боли,
повышается кровяное и внутричерепное давление, изменяется объем внутренних
органов и т.д.
4.3 Организация рабочего места
Производственная деятельность работника,
заставляет его продолжительное время находиться в сидячем положении, которое
является вынужденной позой, поэтому организм постоянно испытывает недостаток в
подвижности и активной физической деятельности. При выполнении работы сидя
большую роль играет плечевой пояс. Перемещение рук в пространстве влияет не
только на работу мышц плечевого пояса и спины, но и на положение позвоночника,
таза и даже ног.
Чтобы исключить возникновение заболеваний
необходимо иметь возможность свободной перемены поз. Необходимо соблюдать режим
труда и отдыха с перерывами, заполняемыми “отвлекающими” мышечными нагрузками
на те звенья опорно-двигательного аппарата, которые не включены в поддержание
основной рабочей позы.
Антропологические характеристики человека
определяют габаритные и компоновочные параметры его рабочего места, а также
свободные параметры отдельных его элементов.
По условиям работы рабочее место работника
относится к индивидуальному рабочему месту для работы сидя.
Рабочее место работника должно занимать площадь
не менее 6 м² , высота помещения
должна быть не менее 4 м, а объем - не менее 20 м3 на одного человека. После
проведения анализа рабочего места в лаборатории было выяснено, что площадь
данного рабочего места составляет 4 м2, а объем 12 м3, что не соответствует
приведенным требованиям. Также в результате анализа были выявлены нарушения в
организации непосредственно самого рабочего места. Высота над уровнем пола
рабочей поверхности, за которой работает оператор, должна составлять 720 мм.
Желательно, чтобы рабочий стол оператора при необходимости можно было
регулировать по высоте в пределах 680 - 780 мм. Оптимальные размеры поверхности
стола 1600 х 1000 кв. мм. Под столом должно иметься пространство для ног с
размерами по глубине 650 мм. Рабочий стол оператора должен также иметь
подставку для ног, расположенную под углом 15° к поверхности стола. Длина
подставки 400 мм, ширина - 350 мм. Удаленность клавиатуры от края стола должна
быть не более 300 мм, что обеспечит оператору удобную опору для предплечий.
Расстояние между глазами оператора и экраном видеодисплея должно составлять 40
- 80 см.
Рабочий стул работника должен быть снабжен
подъемно-поворотным механизмом. Высота сиденья должна регулироваться в пределах
400 - 500 мм. Глубина сиденья должна составлять не менее 380 мм, а ширина - не
менее 400 мм. Высота опорной поверхности спинки не менее 300 мм, ширина - не менее
380 мм. Угол наклона спинки стула к плоскости сиденья должен изменяться в
пределах 90 - 110 ° [11]
4.4 Расчет заземления
Защитным заземлением называется преднамеренное
электрическое соединение с землей металлических нетоковедущих
частей-электроустановок, которые могут оказаться под напряжением.
Защитному заземлению подлежат металлические
части электроустановок, доступные для прикосновения человека, не имеющих других
видов - защиты и обеспечивающих электробезопасность. Защитное заземление
применяется в сетях до 1000В с изолированной нейтралью и выше 1000В с любым
режимом нейтрали. Защитное действие заземления основано на том, что при
прикосновении к незаземленному корпусу электрооборудования, находящемуся под
напряжением, человек попадает под напряжение, равное разности потенциала на
корпусе электрооборудования и потенциала участка земли, на котором стоит
человек. При прикосновении к заземленному корпусу электрооборудования,
находящемуся под напряжением, человек включается в электрическую цепь параллельно
с сопротивлением заземляющего устройства. В этом случае напряжение, под
которое' попадает человек, зависит от величины сопротивления заземляющего
устройства. Таким образом, создавая между корпусом и землей металлическое
соединение большой проводимости, достигают такого уменьшения напряжения, под
которое попадает человек, что ток, проходящий через его тело, становится не
опасным для жизни.
Заземлители бывают естественные и искусственные.
К естественным заземлителям относятся различные
технологические металлоконструкции, такие как арматура железобетонных
строительных элементов, металлические оболочки кабелей (за исключением
алюминиевых) и другие, имеющие хороший контакт с землей.
Искусственные заземлители - это специально
устраиваемые для заземления металлоконструкции. Материалом искусственных
заземлителей служит сталь. Чаще всего искусственные заземлители выполняют в
виде вертикальных электродов, связанных горизонтальным электродам. Вертикальные
электроды выполняют в виде стержней диаметром 10-14 мм, длиной 5 м и более,
уголков размером от 40x40 до 60x60 мм, труб диаметром 30 - 50 мм, длиной 2-3 м.
В качестве горизонтальных электродов для связи
вертикальных заземлителей применяют полосовую сталь сечением не менее 4x12 мм й
стальные прутки диаметром не менее 6 мм. В качестве заземляющих проводников
применяет полосовую или круглую сталь.
Ток, проходящий через заземлитель в землю,
преодолевает сопротивление, называемое сопротивлением заземлителя растеканию
тока или просто сопротивлением растекания. Оно имеет три слагаемых:
сопротивление самого заземлителя, переходное сопротивление между заземлителем и
грунтом и сопротивление грунта. Две первые части по сравнению с третьей весьма
малы, поэтому ими пренебрегают и под сопротивлением заземлителя растеканию тока
понимают сопротивление грунта растеканию тока. Общее сопротивление заземляющего
устройства состоит из суммы сопротивлений растеканию; тока- с заземлителей в
землю и сопротивления заземляющих'"проводников. Нормируемые величины
сопротивления заземляющих устройств в зависимости от напряжения.
Сопротивление заземления необходимо периодически
контролировать, так как из-за коррозии заземпителей или их механических
повреждений оно может превысить допустимую величину. Поэтому контроль
заземляющих устройств проводят перед вводом в эксплуатацию и периодически во
время эксплуатации (обычно раз в год при наибольшем подсыхании или наибольшем
промерзании грунта).
Расчет заземляющего устройства осуществляют
исходя из его максимально допустимого сопротивления, установленного для
соответствующего оборудования.
Определим расчетное удельное
сопротивление  , где
, где  - удельное
сопротивление грунта, Ом*м,
- удельное
сопротивление грунта, Ом*м,  - климатический коэффициент
(выбирается из справочника в соответствии с климатическими условиями отдельных
зон). Выбираем тип грунта - чернозем с сопротивлением
- климатический коэффициент
(выбирается из справочника в соответствии с климатическими условиями отдельных
зон). Выбираем тип грунта - чернозем с сопротивлением 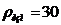 Ом*м, а
климатический коэффициент в соответствии с нашей зоной
Ом*м, а
климатический коэффициент в соответствии с нашей зоной 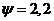 . Тогда
расчетное удельное сопротивление будет определено:
. Тогда
расчетное удельное сопротивление будет определено:
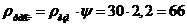 (Ом*м).
(Ом*м).
Выберем тип заземлителя и его
размеры. Искусственный заземлитель длиной 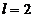 м и диаметром
м и диаметром  м.
м.
Рассчитаем сопротивление растекания
одиночного заземлителя. Заземлитель находится на поверхности грунта:
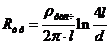 ,
,
Используя выше приведенные данные,
получим:
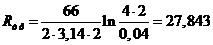 (Ом)
(Ом)
Количество параллельно соединенных
одиночных заземлителей, необходимых для получения допустимого значения
сопротивления заземления, без учета сопротивления полосы соединения, будет
составлять:
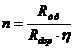 ,
,
где 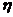 - коэффициент использования
заземлителей,
- коэффициент использования
заземлителей,  -
нормативная величина сопротивления защитного заземления. Согласно справочным
данным, количество параллельно соединенных одиночных заземлителей должно быть
не меньше двух. Из справочных таблиц выбираем
-
нормативная величина сопротивления защитного заземления. Согласно справочным
данным, количество параллельно соединенных одиночных заземлителей должно быть
не меньше двух. Из справочных таблиц выбираем 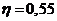 .
.
Тогда 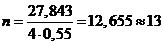 .
.
Длина полосы соединения определяется
как:
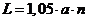 ,
,
где 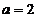 м - расстояние между вертикальными
заземлителями.
м - расстояние между вертикальными
заземлителями.
Соответственно  (м).
(м).
Рассчитываем полное значение
сопротивления растеканию тока с соединительной полосы
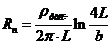 ,
,
где 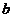 - ширина полосы.
- ширина полосы.
 (Ом).
(Ом).
Исходя из найденных значений, можно рассчитать
сопротивление всего заземляющего устройства:
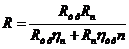 ,
,
где  - коэффициент использования
соединительной полосы, выбирается из справочника и в соответствии с заданными
условиями имеет значение
- коэффициент использования
соединительной полосы, выбирается из справочника и в соответствии с заданными
условиями имеет значение 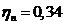 .
.
 (Ом).
(Ом).
Сопротивление R = 3,6 Ом меньше
допускаемого сопротивления, равного 4 Ом. Следовательно, диаметр заземлителя d
= 40 мм при числе заземлителей n= 13 является достаточным для обеспечения
защиты.
Работа с компьютером характеризуется
значительным умственным напряжением и нервно-эмоциональной нагрузкой
операторов, высокой напряженностью зрительной работы и достаточно большой
нагрузкой на мышцы рук при работе с клавиатурой ЭВМ. Большое значение имеет
рациональная конструкция и расположение элементов рабочего места, что важно для
поддержания оптимальной рабочей позы человека-оператора.
В процессе работы с компьютером
необходимо соблюдать правильный режим труда и отдыха. В противном случае у
персонала отмечаются значительное напряжение зрительного аппарата с появлением
жалоб на неудовлетворенность работой, головные боли, раздражительность,
нарушение сна, усталость и болезненные ощущения в глазах и пояснице.
5. ЭКОНОМИЧЕСКАЯ ЧАСТЬ: РАСЧЕТ
СЕБЕСТОИМОСТИ ПРОГРАММНОГО ПРОДУКТА
.1 Описание продукта
Разрабатываемое приложение предназначено для
проведения математического моделирования управления тепловым процессом в
модельном теле, а именно: разработка алгоритма прямой задачи теплопроводности и
задачи идентификации граничного условия (обратной). Данный проект не является
коммерческим, он разрабатывался для внутреннего использования.
Для работы с программным продуктом пользователь
описывает граничные условия модельного тела, после чего выполняется
непосредственный расчет температуры в необходимой области заданного тела.
Основными чертами разработанного программного
продукта являются:
малая погрешность вычислений;
быстродействие;
простота использования.
5.2 Расчет себестоимости
программного продукта
Чтобы оценить стоимость разрабатываемого
программного продукта необходимо:
. составить перечень работ, которые следует
выполнить, затем рассчитать трудозатраты на их выполнение;
. рассчитать заработную плату разработчиков.
В затраты на разработку программного продукта
также входят: стоимость малоценных и быстроизнашивающихся предметов, стоимость
аренды компьютера, отчисления с заработной платы и т.д.
В перечень работ, которые необходимо выполнить
входит:
формулировка постановки задачи;
проектирование программного продукта;
разработка программного продукта;
внедрение продукта.
Для руководства ходом работ и ведения всего
проекта в целом необходима должность руководителя темы. Для проектирования
подсистемы и ее последующей наладки и введения в эксплуатацию необходимо
участие программиста. Состав исполнителей приведен в таблице 5.1.
Приведем перечни работ для разработчиков
программного продукта. Продолжительность работ установлена опытным путем.
Таблица 5.1- Состав исполнителей работы
|
Должности
|
Должностные
оклады, грн.
|
|
Месячные
|
Дневные
|
|
Руководитель
|
2000
|
90.90
|
|
Программист
|
1800
|
81.81
|
Перечень работ, выполняемых сотрудниками и их
длительность приведена в таблице 5.2.
Расчет себестоимости работ начнем с расчета
фонда основной заработной платы разработчиков, с учетом трудозатрат, количества
исполнителей и среднедневной заработной платы.
 грн
грн
Таблица 5.2 - Перечень работ
|
Номер
стадии
|
Наименование
стадий и этапов
|
Продолжительность,
дни
|
Исполнители,
кол-во
|
Трудоемкость,
чел/дни
|
|
|
|
Руководитель
|
Программист
|
|
|
Разработка
технического задания
|
|
11
|
Организационная
подготовка к созданию ПрП
|
1
|
1
|
|
1
|
|
12
|
Разработка
ТЗ на постановку задачи
|
4
|
1
|
|
4
|
|
Итого
|
5
|
|
|
5
|
|
Постановка
задачи
|
|
21
|
Разработка
мат. модели и алгоритмов
|
4
|
1
|
|
4
|
|
22
|
Разработка
информационной базы
|
3
|
1
|
|
3
|
|
23
|
Техническое
обеспечение
|
1
|
1
|
|
1
|
|
24
|
Разработка
описания задачи и ТЗ
|
3
|
1
|
|
3
|
|
Итого
|
11
|
|
|
11
|
|
Разработка
ПрП
|
|
31
|
Разработка
алгоритмов
|
5
|
|
1
|
5
|
|
32
|
Разработка
документации
|
1
|
|
1
|
1
|
|
33
|
Разработка
программы
|
10
|
|
1
|
10
|
|
34
|
Проведение
экспериментов
|
30
|
|
1
|
30
|
|
Итого
|
46
|
|
46
|
|
Внедрение
|
|
42
|
Наладка
и предварительное испытание
|
1
|
|
1
|
1
|
|
Итого
|
1
|
|
1
|
|
ВСЕГО:
|
63
|
16
|
47
|
63
|
|
|
|
|
|
|
|
Рассчитаем затраты на материалы 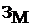 и
комплектующие, необходимые для написания программы (табл. 5.3).
и
комплектующие, необходимые для написания программы (табл. 5.3).
Таблица 5.3 - Материалы и комплектующие
|
Материалы
|
Кол-во,
шт.
|
Цена,
грн
|
Стоимость,
грн.
|
Назначение
|
|
Диски
CD-R
|
20
|
2.50
|
50
|
Хранение
резервных копий, перенос программы
|
|
Печать
документации
|
50
|
0.3
|
15
|
Документация,
распечатки, разного рода печать
|
|
Итого
|
|
|
65
|
|
Определим затраченное машинное время. Будем
считать, что руководитель пользуется компьютером в среднем 4 часа за рабочий
день, а программист, следуя нормам охраны труда, в среднем 6 часов. Получим:
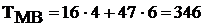 ч
ч
Стоимость часа машинного времени  будем
считать равной 2грн.
будем
считать равной 2грн.
Смета затрат на создание и внедрение
системы с группировкой затрат по статьям калькуляции приведена в табл.5.4:
Таблица 5.4 - Затраты на разработку
ПП
|
Виды
затрат
|
Формула
|
Расчет
(грн.)
|
|
|
|
|
1.
Основная заработная плата
|
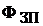 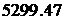
|
|
|
2.
Дополнительная заработная плата
|
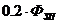 1059.89 1059.89
|
|
|
3.
Отчисления в социальные фонды:
|
|
|
|
-пенсионный
фонд
|
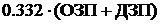 2111.31 2111.31
|
|
|
-безработица
|
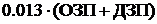 82.67 82.67
|
|
|
-социальное
страхование
|
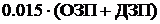 95.39 95.39
|
|
|
-страхование
от несчастных случаев
|
 54.69 54.69
|
|
|
4.
Материалы и покупные изделия
|
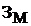 54 54
|
|
|
5.
Накладные расходы
|
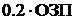 1059.89 1059.89
|
|
|
6.
Оплата услуг
|
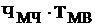 692 692
|
|
|
ИТОГО
|
|
10509.31
|
Определим цену одной копии программного
продукта.
Себестоимость=10509.31.
Прибыль составляет 2837.43 грн (27% от
себестоимости продукта).
Цена без НДС=13346.46 грн.
Цена с НДС=16015.746 грн.
В данном разделе был произведен расчет цены и
себестоимости разработанного программного продукта. Себестоимость=10509.31
гривен.
Актуальная цена программного продукта составляет
160153746 гривен. Расчет произведен с учетом и всех необходимых трудозатрат,
НДС, отчислений в пенсионный фонд, фонд занятости и отчислений на социальное
страхование, накладных расходов.
ЗАКЛЮЧЕНИЕ
В данной работе сформулирована постановка и
предложен метод решения прямой и обратной задачи теплопроводности, а также их
особенности с точки зрения системного анализа. При этом в системе выявлены
такие характеристики как эмерджентность, целостность, аддитивность.
Разработан алгоритм численного решения прямой
задачи теплопроводности и алгоритм решения задачи идентификации граничного
условия по измеренным значениям температуры в некоторой точке составного
стержня, который был реализован в пакете Mathcad.
В работе описаны основные опасные и вредные
факторы при работе на компьютере, а также выявлены мероприятия по защите.
Был проведен расчет экономической эффективности
разработанного программного продукта и определена цена, которая лежит в
диапазоне от 16015.746 грн до13346.46 грн.
ГЛОССАРИЙ
Конвекция - это процесс переноса микрочастицами
только текучей среды (жидкости или газа) из зоны с одной температурой в зону с
другой.
Краевые условия - совокупность
начального и граничного условий. Это дополнение к основному дифференциальному
уравнению, задающее его поведение в начальный момент времени или на границе
<http://ru.wikipedia.org/wiki/%D0%93%D1%80%D0%B0%D0%BD%D0%B8%D1%86%D0%B0>
рассматриваемой области соответственно.
Нестационарное температурное поле -
поле, температура которого изменяется не только в пространстве, но и с течением
времени.
Регуляризация - добавление некоторой
дополнительной информации к условию с целью решить некорректно поставленную
задачу <http://ru.wikipedia.org/wiki/%D0%9D%D0%B0%D1%87%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%B8_%D0%B3%D1%80%D0%B0%D0%BD%D0%B8%D1%87%D0%BD%D1%8B%D0%B5_%D1%83%D1%81%D0%BB%D0%BE%D0%B2%D0%B8%D1%8F>.
Стационарное температурное поле -
поле, температура которого в любой его точке не изменяется во времени, т.е.
является функцией только координат.
Температурное поле - совокупность
значений температур во всех точках рассматриваемого пространства в данный
момент времени.
Тепловое излучение - представляет
собой процесс переноса энергии посредством электромагнитных колебаний, имеющих
различную длину волны.
Теплопроводность - это процесс
молекулярного переноса теплоты в твердых материалах, который происходит между
непосредственно соприкасающимися телами или частицами тел с различной
температурой.
СПИСОК ЛИТЕРАТУРЫ
1.
Лыков А.В. Теория теплопроводности: - М, 1967, 592 с.
.
Карслоу Г., Егер Д. Теплопроводность твердых тел. - М, 1964, 487 с.
.
Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача: - М, 2003, 785 с.
.
Самарский А.А. Вычислительный эксперимент в задачах технологии // Вестник АН
СССР. - 1984. - №3. - С. 77-88.
.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. - M.: Наука,
1966. - 724 с.
.
Михлин С.Г. Уравнения математической физики: - M.: Наука, 1968.- 576 с.
.
Сурмин Ю.П. Теория систем и системный анализ: - МАУП, 2003, 368.
.
Гавва В.Н., Голованова М.А. Экономическая оценка инженерных решений: Х, ХАИ,
1999, 136 с.
.
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач: М.: Наука, 1979,
188 с.
.
Араманович И.Г., Левин В.И. Уравнения математической физики: М.: Наука, 1969,
289 с.
.
Безопасность жизнедеятельности. Безопасность технологических процессов и
производств (Охрана труда). Учеб. пособие для вузов / П.П. Кукин, В.Л. Лапин.
Е.А. Подгорных и др. - М.: Высшая школа, 1999.