Разработка системы развития логического мышления младших школьников средствами учебного предмета 'Математика'

Вид работы:

Дипломная (ВКР)
Предмет:

Педагогика
Язык:

Русский
,
Формат файла:
MS Word

646,33 Кб
Опубликовано:

2015-01-29

Все дипломные работы по педагогике

Скачать дипломную работу Читать текст online Заказать дипломную
*Помощь в написании! Посмотреть все дипломные работы

Вы можете узнать стоимость помощи в написании студенческой работы.

Разработка системы развития логического мышления младших школьников средствами учебного предмета 'Математика'

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

ТЕОРЕТИКО-МЕТОДОЛОГИЧЕСКИЙ АНАЛИЗ ИССЛЕДОВАНИЯ ЛОГИЧЕСКОГО МЫШЛЕНИЯ У МЛАДШИХ ШКОЛЬНИКОВ

.1 Аспекты изучения логики в психологии и научно-методической литературе

.2 Современные психодинамические аспекты логического мышления младших школьников

ПСИХОЛОГО-ПЕДАГОГИЧЕСКИЕ МЕХАНИЗМЫ РАЗВИТИЯ ЛОГИЧЕСКОГО МЫШЛЕНИЯ МЛАДШИХ ШКОЛЬНИКОВ

.1 Особенности логического мышления младшего школьника в изучении математики

2.2 Виды и формы дидактического материала по математике в 4 классе

3 ИССЛЕДОВАНИЕ РАЗВИТИЯ ЛОГИЧЕСКОГО МЫШЛЕНИЯ МЛАДШИХ ШКОЛЬНИКОВ СРЕДСТВАМИ УЧЕБНОГО ПРЕДМЕТА «МАТЕМАТИКА»

.1 Методический инструментарий исследования

.2 Психолого-педагогическое сопровождение в условиях эксперимента

.3 Результаты эмпирического исследования развития логического мышления младших школьников

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

ПРИЛОЖЕНИЕ

ВВЕДЕНИЕ

Актуальность. Настоящее исследование посвящено одной из актуальных проблем современной педагогики, психологии и методики преподавания математики - проблеме развития логического мышлениям младших школьников средствами учебного предмета «математика». В условиях современного общества формирование умений и навыков логического мышления учащихся можно рассматривать как одну из главных задач обучения математики в школе, так как овладение данными общедидактическими умениями обусловливает сознательное усвоение основ наук и развитие личности школьника.

Новые политические, социально-экономические и культурные изменения в Казахстане, обусловленные возрастающей ролью знаний, диктуют новые требования к качеству знаний. Качество образования в Республике Казахстан направлено на формирование в общеобразовательных школах интеллектуального, физически и духовно развитого гражданина Республики Казахстан, удовлетворение его потребности в получении образования, обеспечивающего успех в быстро меняющемся мире, развитие конкурентоспособного человеческого капитала для экономического благополучия страны[1]. Президент РК Н.А.Назарбаев в ежегодном Послании главы государства народу Казахстана озвучил пять векторов развития системы, определяющие модель новой школы, которая должна способствовать формированию человеческого потенциала государства.

Базовое звено образования - общеобразовательная школа, модернизация которой предполагает ориентацию образования не только на усвоение обучающимся определенной суммы знаний, но и на развитие его личности, его познавательных и созидательных способностей», - говорится в Государственной программе развития образования РК. В Государственном образовательном стандарте общего и среднего образования одной из целей изучения математики уже в начальных классах является формирование приемов мыслительной деятельности (анализ, синтез, сравнение, классификация, обобщение). Без способности к самостоятельному мышлению вряд ли возможно интеллектуальное развитие ребенка. Именно поэтому проблема развития логического мышления учащихся приобретает особую актуальность.

Актуальность темы исследования обусловлена потребностями современного общества в социально активной, творческой личности, формируемой в процессе обучения в школе; необходимостью решения проблемы развития мыслительных способностей учащихся в процессе обучения; важностью педагогической интерпретации достижений психологии для целей обучения и развития школьников как единого процесса на уроках математики; изыскания дидактических возможностей и методических средств формирования мыслительных операций как необходимого условия овладения системой понятий математической науки и формирования умений и навыков логического мышления как основы для развития математических умений и навыков.

В настоящее время, в период стремительного научно-технического прогресса, возросла роль математики, и поэтому приобрело большую значимость математическое образование. Большинство профессий требует определенной математической подготовки. В современных условиях математические знания, владение характерными для математики методами и специфическим языком - обязательный элемент общей культуры человека. Изучение математики способствует формированию научного мировоззрения учащихся, воспитанию трудолюбия, честности, дисциплинированности и других моральных качеств. Навыки мыслительной деятельности, приобретаемые учащимися в процессе обучения математике, готовность к упорному труду, преодоление трудностей будут нужны им в будущем независимо от того, какую профессию изберет каждый из них после окончания школы.

Анализ образовательных систем школьных курсов математики начальной школы позволяет выделить противоречия между:

требованиями, предъявляемыми к результатам учебной деятельности пятиклассников и большим объемом учебного материала, из-за чего многие учащиеся, не успев усвоить одну тему, переходят к другой со значительными пробелами, что абсолютно недопустимо при изучении математики;

уровнем развития логического мышления школьников исследуемой возрастной группы и необходимостью овладения ими приемами абстрагирования, анализа, синтеза, классификации для решения тех или иных математических задач.

Таким образом, анализ психолого-педагогической, методической литературы свидетельствует об актуальности дальнейшей разработки этой проблемы. В связи с вышеуказанным, мы определили тему исследования как «Развитие логического мышления младших школьников средствами учебного предмета «Математика».

Степень научной разработанности проблемы. Проблема развития логического мышления исследовалась психологами в общей теории мышления в первой половине XX века такими как A.B. Брушлинский, JI.C. Выготский, П.Я. Гальперин, А.Н. Леонтьев, С.Л. Рубинштейн, К.А. Славская, в теории развития мышления такие авторы как Д.Б. Богоявленская, Л.В. Занков, H.A. Менчинская, З.И. Калмыкова, Т.В. Кудрявцев, И .С. Якиманская определили значимость развития логического мышления младших школьников. Среди зарубежных психологов XX века, посвятивших этим вопросам большое количество трудов, следует выделить Ж. Пиаже, Э. Де Боне.

В исследованиях психологов второй половины XX века П.Я. Гальперин, Н.Ф. Талызина и убедительно показано, что общие приемы интеллектуальной деятельности должны выступать в процессе обучения как предмет специального усвоения и формирования.

Такие ученые, как И.Я. Лернер, И.Л. Никольская, Н.П. Партиев, H.A. Подгорецкая, A.A. Столяр и другие теоретически и экспериментально доказали, что школа не обеспечивает учащимся необходимый уровень развития логического мышления.

Необходимость дальнейшей разработки проблемы формирования логического мышления младших подростков подчеркнута в исследованиях многих ученых , таких как А.В. Николаев, А.К. Артемов, И.Л. Никольская, А.А. Столяр, К.О. Ананченко, Е.П. Коляда, Т.А. Кондрашенкова, Г.В. Краснослабоцкая, Л.А. Латотин, B.C. Нодельман, B.C. Нургалиев, Б.Д. Пайсон, Л.Н. Удовенко, О.В. Соловьева.

К различным аспектам проблемы развития логического мышления вообще и в процессе обучения в частности, обращались и продолжают обращаться многие казахстанские исследователи в области психологии, педагогики, логики К.С. Абилов, А.З. Рахимов,Методисты рассматривают пути развития логического мышления учащихся в ходе изучения различных дисциплин (О. В. Алексеева, Г. А. Бакулина, М. А. Екимова, Н. Д. Есипова, Н. В. Калягина, Е. Н. Полякова и др.).

Методические основы обеспечения базового уровня общеобразовательной математической подготовки в школах Казахстана исследованы Баймухановым Б.Б., Е.У.Медеуовым. На основе выявленных исторически тенденций школьного математического образования ими была сформирована методическая концепция национального стандарта школьного математического образования Казахстана.

Вместе с тем, несмотря на теоретическое осмысление данной проблемы, на важность развития логического мышления, на требования программ о необходимости формирования логических умений в процессе обучения, проблема развития логического мышления учащихся еще не получила должного разрешения в практике современной начальной школы. Недостаточно решены пути развития логического мышления у учащихся начальных классов, отсутствует системная технология преподавания логического мышления, нет учебного пособия для учащихся, помогающих сформировать и развить сферу логики. Таким образом, выбранная нами тема диссертационного исследования является актуальной и характеризуется научной новизной.

Цель исследования состоит в научном обосновании и разработке системы развития логического мышления младших школьников средствами учебного предмета «Математика».

Задачи исследования состоят в следующем:

провести теоретико-методологический анализ исследования логического мышления у младших школьников;

- исследовать психолого-педагогические механизмы развития логического мышления младших школьников;

разработать исследование развития логического мышления младших школьников средствами учебного предмета «математика»

Объектом исследования является процесс развития логического мышления младших школьников.

Предметом исследования является система развития логического мышления на уроках математики в 4 классе.

Методы исследования:

· теоретический анализ психолого-педагогической литературы;

· педагогический эксперимент (констатирующий, формирующий, контрольный );

· наблюдение;

· опросные методы (беседы, интервью, анкеты);

· изучение продуктов деятельности детей, педагогической документации;

· статистическо-математический метод обработки результатов.

Научная новизна состоит в том, что данное обоснование психолого-педагогических условий развития логического мышления у младшего школьника дополняет современные взгляды о психологическом потенциале педагогического развития логического мышления и обогащает психологические представления о возможностях развития логического мышления учащихся начальных классов в ситуациях на уроках математики.

В связи с этим на защиту выносятся следующие положения:

. Пояснение понятия «логическое мышление» в младшем школьном возрасте; психовозрастные особенности развития логического мышления в младшем школьном возрасте.

2. Комплекс дидактических условий, обеспечивает возможность эффективного развития логического мышления младших школьников.

. Специальная методика, отвечающая предложенному комплексу условий и направленная на комплексное обучение приёмам логического мышления. которая способствует развитию логического мышления младших школьников, так как происходит актуализация логических операции посредством памяти, восприятия, представления (на конкретном математическом содержании), получение целостного представления об исследуемом математическом объекте

Практическая значимость исследовательской работы состоит в разработке специальной методики по развитию логического мышления для 4 классов по математике способствующего эффективному развитию логического мышления. Предложенные методы исследования могут быть использованы для оценки процессов становления и развития логического мышления у младших школьников. Полученные результаты могут использоваться психологами, педагогами и родителями для диагностики и развития логического мышления младших школьников.

База исследования:

Донецкая средняя школа, 4 класс- экспериментальный класс.

Подольская средняя школа, 4 класс - контрольный класс.

Структура и объем диссертации:

Диссертация состоит из введения трех разделов, заключения, списка использованных источников, приложений. Общий объем машинописного текста работы составляет 97 страниц машинописного текста,21 таблица. 17 рисунков, 2 приложения.

Во введении обоснована актуальность темы; представлена цель исследования; определены задачи, объект и предмет, а также раскрыты научная новизна, теоретическая и практическая значимость результатов исследования; сформулированы основные положения, выносимые на защиту.

В первом разделе «Теоретико-методологический анализ исследования логического мышления у младших школьников» рассмотрены исследования в области психологии, философии и педагогики в области логического мышления младших школьников.

Во втором разделе «Психолого-педагогические механизмы развития логического мышления младших школьников» рассмотрены основные подходы к развитию логического мышления младших школьников на уроках математики.

В третьем разделе «Исследование развития логического мышления младших школьников средствами учебного предмета «математика»» проведено эмпирическое исследование развития логического мышления младших школьников, а также представлены результаты использования специальной методики по развитию логического мышления на уроках математики.

В заключении сделаны выводы по апробации результатов исследования, предложены направления развития дальнейшего изучения в данной области научного познания.

логический мышление школьник математика

1 ТЕОРЕТИКО-МЕТОДОЛОГИЧЕСКИЙ АНАЛИЗ ИССЛЕДОВАНИЯ ЛОГИЧЕСКОГО МЫШЛЕНИЯ У МЛАДШИХ ШКОЛЬНИКОВ

.1 Аспекты изучения логики в психологии и научно-методической литературе

Логика как наука зародилась в связи с риторикой (учением о красноречии) в Древней Греции и Древней Индии. Там были очень популярны публичные состязания ораторов при большом стечении зрителей. Истина и логика взаимосвязаны, поэтому значение логики невозможно переоценить. Логика помогает доказывать истинные суждения и опровергать ложные, она учит мыслить четко, лаконично, правильно. Логика нужна всем людям, работникам самых различных профессий. Преподавателям, ибо они не смогут эффективно развивать мышление учащихся, не владея логикой. Юристам, которые строят свои обвинения или защиту в соответствии с правилами логики. Врачам, ставящим диагноз на основании проявлений болезни, - логика необходима вообще всем людям как интеллектуального, так и физического труда[14].

Изучение развития логического мышления учащихся разрабатывалось в научных трудах многих ученых в области психологии и педагогики. Один из наиболее известных психологов современности, швейцарский ученый Ж.Пиаже предложил теорию развития интеллекта в детстве, которая оказала большое влияние на современное понимание его развития. В теоретическом плане он придерживался мысли о практическом, деятельностном происхождении основных интеллектуальных операций. Теория развития мышления ребенка, предложенная Ж.Пиаже, получила название «операциональной» (от слова «операция»). Операция, по Пиаже, представляет собой «внутреннее действие, продукт преобразования («интериоризации») внешнего, предметного действия, скоординированного с другими действиями в единую систему, основным свойством которой является обратимость (для каждой операции существует симметричная и противоположная операция)». В развитии операционального интеллекта у детей Ж. Пиаже выделил следующие четыре стадии[15]:

) Стадия сенсомоторного интеллекта, охватывающая период жизни ребенка от рождения до примерно двух лет. Она характеризуется развитием способности воспринимать и познавать окружающие ребенка предметы в их достаточно устойчивых свойствах и признаках.

2) Стадия операционального мышления, включающая его развитие в возрасте от двух до семи лет. На этой стадии у ребенка складывается речь, начинается активный процесс интериоризации внешних действий с предметами, формируются наглядные представления.

) Стадия конкретных операций с предметами. Она характерна для детей в возрасте от 7-8 до 11-12 лет. Здесь умственные операции становятся обратимыми.

) Стадия формальных операций. Ее в своем развитии достигают дети в среднем возрасте: от 11-12 до 14-15 лет. Данная стадия характеризуется способностью ребенка выполнять операции в уме, пользуясь логическими рассуждениями и понятиями. Внутренние умственные операции превращаются на этой стадии в структурно организованное целое.

В последнее время наиболее широкое практическое применение в обучении мыслительным действиям получила теория формирования и развития интеллектуальных операций, разработанная П.Я.Гальпериным[16]. В основу данной теории было положено представление о генетической зависимости между внутренними интеллектуальными операциями и внешними практическими действиями. Ранее это положение получило разработку во французской психологической школе и в трудах Ж.Пиаже [17]. На нем основывали свои теоретические и экспериментальные работы Л.С. Выготский[18], А.В.Запорожец[19] и многие другие.

Мышление - это социально обусловленный, неразрывно связанный с речью психический процесс поисков и открытия существенно нового, процесс опосредствованного и обобщенного отражения действительности в ходе ее анализа и синтеза. Мышление возникает на основе практической деятельности из чувственного познания и далеко выходит за его пределы. Через ощущения и восприятия мышление непосредственно связано с внешним миром и является его отражением. Правильность (адекватность) этого отражения непрерывно проверяется в процессе практического преобразования природы и общества считал А.В. Брушлинский [20].

Мыслительный процесс - процесс, которому предшествует осознание исходной ситуации (условия задачи), который является сознательным и целенаправленным, оперирует понятиями и образами, и завершается каким-либо результатом (переосмысление ситуации, нахождение решения, формирование суждения и т.п. Основные формы логического мышления - это понятия, суждения, умозаключения.

Понятие - форма мышления, отражающая существенные свойства, связи и отношения предметов и явлений, выраженная словом или группой слов. Понятия могут быть общими и единичными, конкретными и абстрактными.

Суждение - это форма мышления, отражающая связи между предметами или явлениями, это утверждение или отрицание чего-либо. Суждения могут быть ложными и истинными.

Умозаключение - форма мышления, при которой на основе нескольких суждений делается определенный вывод. Различают умозаключения индуктивные, дедуктивные, по аналогии.

Индукция - логический вывод в процессе мышления от частного к общему, установление общих законов и правил на основании изучения отдельных фактов и явлений.

Дедукция - логический вывод в процессе мышления от общего к частному, познание отдельных фактов и явлений на основании знания общих законов и правил.

Аналогия - логический вывод в процессе мышления от частного к частному (на основе некоторых элементов сходства).

Индивидуальные различия и стили мышления:

Индивидуальные различия проявляются в качествах мышления:

широта - способность охватить весь вопрос целиком, не упуская в то же время необходимых для дела частностей;

глубина - умение проникать в сущность сложных вопросов;

самостоятельность - умение выдвигать новые задачи и находить пути их решения, не прибегая к помощи других людей;

гибкость - нескованность закрепленными в прошлом приемами и способами решения задач, умение быстро менять действия при изменении обстановки;

быстрота - способность быстро разобраться в новой ситуации, обдумать и принять правильное решение;

торопливость - поспешное решение вопроса без всестороннего обдумывания, выхватывание какой-то одной стороны проблемы;

критичность - умение объективно оценивать свои и чужие мысли, тщательно и всесторонне проверять все выдвигаемые предположения и выводы.

Индивидуальные стили мышления:

синтетический - стремление создать что-то новое, оригинальное на основе обобщения разных подходов и идей; теоретическое мышление;

идеалистический - склонность к интуитивным, глобальным оценкам без осуществления детального анализа проблем;

прагматический - опора на непосредственный личный опыт, использование легко доступных материалов и информации, стремление как можно быстрее получить конкретный результат;

аналитический - систематическое и всестороннее рассмотрение вопроса на основе сбора большого объема информации и использования глубоких теорий;

реалистический - ориентация на признание фактов, конкретность, установка на исправление, коррекцию ситуаций в целях достижения определенных результатов[21].

К разрешению задачи мышление идет с помощью многообразных операций, таких как сравнение, анализ, синтез, абстракция и обобщение.

Сравнение - мышление сопоставляет вещи, явления и их свойства, выявляя сходства и различия, что приводит к классификации.

Анализ - мысленное расчленение предмета, явления или ситуации для выделения составляющих элементов. Таким образом мы отделяем несущественные связи, которые даны в восприятии.

Синтез - обратный анализу процесс, который восстанавливает целое, находя существенные связи и отношения.

Анализ и синтез в мышлении взаимосвязаны. Анализ без синтеза приводит к механическому сведению целого к сумме частей, также невозможен синтез без анализа, т. к. он должен восстановить целое из выделенных анализом частей. В складе мышления некоторых людей наблюдается склонность - у одних к анализу, у других к синтезу.

Абстракция - это выделение одной какой-либо стороны, свойства и отвлечение от остальных. Так, рассматривая предмет, можно выделить его цвет, не замечая формы, либо наоборот, выделить только форму. Начиная с выделения отдельных чувственных свойств, абстракция затем переходит к выделению нечувственных свойств, выраженных в абстрактных понятиях.

Обобщение (или генерализация) - это отбрасывание единичных признаков, при сохранении общих, с раскрытием существенных связей. Обобщение может совершиться путем сравнения, при котором выделяются общие качества. Так совершается обобщение в элементарных формах мышления. В более высших формах обобщение совершается через раскрытие отношений, связей и закономерностей. Абстракция и обобщение являются двумя взаимосвязанными сторонами единого мыслительного процесса, при помощи которого мысль идет к познанию[22].

Формирование логического мышления - важная составная часть педагогического процесса. Помочь учащимся в полной мере проявить свои способности, развить инициативу, самостоятельность, творческий потенциал - одна из основных задач современной школы. Успешная реализация этой задачи во многом зависит от сформированности у учащихся познавательных интересов. Математика даёт реальные предпосылки для развития логического мышления, задача учителя - полнее использовать эти возможности при обучении детей математике. Однако, конкретной программы логических приемов мышления, которые должны быть сформулированы при изучении данного предмета, нет. В результате работа над развитием логического мышления идёт без знания системы необходимых приёмов, без знания их содержания и последовательности формирования. Первоначальные математические знания усваиваются детьми в определённой, приспособленной к их пониманию, системе, в которой отдельные положения логически связаны одно с другим, вытекают одно из другого. При сознательном усвоении математических знаний учащиеся пользуются основными операциями мышления в достигнутом для них виде: анализом и синтезом, сравнением, абстрагированием и конкретизацией, обобщением; ученики делают индуктивные выводы, проводят дедуктивные рассуждения. Сознательное усвоение учащимися математических знаний развивает логическое мышление учащихся[23].

Овладение мыслительными операциями в свою очередь помогает учащимся успешнее усваивать новые знания. Познавая предметы и явления окружающей действительности, мы можем мысленно расчленять предмет или явление на составные части и мысленно же соединять части в одно целое. Операция мышления, направленная на расчленение целого на составляющие его части, называется анализом. Операция мышления, направленная на установление связи между предметами или явлениями, называется синтезом. Эти операции мышления взаимно связаны. Ф. Энгельс отмечает, что «…мышление состоит столько же в разложении предметов сознания на их элементы, сколько в объединении связанных друг с другом элементов в некоторое единство. Без анализа нет синтеза»[24].

Анализ и синтез, взаимно связанные операции мышления, находят постоянное применение, как при изучении элементов арифметической теории, так и при решении примеров и задач. Уже на первых шагах обучения при изучении чисел первого десятка учащиеся пользуются наглядно-действенным анализом (разложением) предметных множеств на составляющие их элементы и наглядно-действенным синтезом (соединением), группируя элементы во множества. Наглядный анализ и синтез сменяется затем анализом и синтезом по представлению: ребёнок может выполнить разложение чисел или их соединение, оперируя со зрительными образами, которые сохраняются в его памяти и могут быть воспроизведены в его сознании. Более высокой ступенью является умственный анализ и синтез, выполняемый мысленно при помощи внутренней речи. При обучении любому разделу математики приходится опираться на анализ и синтез. Анализ и синтез, как взаимосвязанные мыслительные операции находят своё применение при решении текстовых задач. Ученик под руководством учителя, прежде всего, анализирует содержание задачи, расчленяя его на числовые данные, условия и вопрос. При решении составных арифметических задач требуется применить более сложный и более тонкий анализ и синтез. Анализ содержания составной задачи, так же как и простой, сводится к расчленению его на числовые данные, условия и вопрос. Однако сами данные, условие и искомое должны подвергнутся дополнительно анализу, расчленению на составляющие их элементы [25].

В процессе обучения математике находит своё применение приём сравнения, т.е. выделение сходных и различных признаков у рассматриваемых чисел, арифметических примеров, арифметических задач. После решения задач учащиеся сравнивают, каким действием решается та или другая задача, а затем сопоставляют способы решения с различиями в условиях задач. Такое сопоставление помогает учащимся лучше осознать смысл выражений «больше на несколько единиц» и «больше в несколько раз» и прочнее установить связь между условием каждой задачи и способом её решения. Сравнение основано на анализе и синтезе: необходимо расчленить каждую задачу на составляющие её элементы, а затем мысленно соединить сходные элементы, выделив при этом существенные различия. При объяснении учащимся новой для них по способам решения задачи с многозначными числами часто используется приём аналогии: учитель предлагает решить аналогичную задачу с небольшими числами, вычисления над которыми можно выполнить устно [26].

Логическое мышление - мышление, проходящее в рамках формальной логики и отвечающее ее требованиям. Задача развития логического мышления учащихся ставится и, определенным образом, решается в массовой школе. Во всех школьных программах по математике как одна из целей обучения предмету отмечена - развитие логического мышления. Еще столетие назад Л.Н. Толстой отмечал, что математика имеет своей задачей не счисление, но обучение человеческой мысли при счислении[27]. С осознанием отдельных логических форм человек начинает более четко мыслить и выражать свои мысли в речи. Используя в обучении математике различные методы, учитель применяет их так, чтобы они содействовали активизации мышления учащихся и, тем самым, способствовали его развитию. Учитель должен владеть методикой работы над текстовой задачей, уметь заинтересовать учеников.

Мышление, отражая предметы и явления действительности, является высшей ступенью человеческого познания. При этом, имея своим единственным источником ощущения, оно раздвигает границы непосредственного отражения, что дает возможность получать знание о таких свойствах и явлениях, которые не могут быть непосредственно восприняты человеком.

Вначале логика возникла и развивалась в недрах философии как единой науки, объединявшей всю совокупность представлений людей об окружающем мире и самом человеке, его мышлении. При этом первоначально законы и формы правильного мышления изучались в границах ораторского искусства, как одного из средств воздействия на умы людей, убеждения их в целесообразности определенного поведения. Так было в Древней Индии, Древнем Китае, Древней Греции, Древнем Риме, а также средневековой России. Однако в искусстве красноречия логический аспект представляет пока еще как подчиненный, ибо логические приемы служат не столько цели достижения истины, сколько цели убеждения аудитории.

Актуальность заключается в том, что в современное время дети учатся по развивающим технологиям, где логическое мышление является основой. С начала обучения мышление выдвигается в центр психического развития писал Л.С. Выготский и становится определяющим в системе других психических функций, которые под его влиянием интеллектуализируются и приобретают произвольный характер [28]. Многочисленные наблюдения педагогов, исследования психологов убедительно показали, что ребенок, не научившийся учиться, не овладевший приемами мыслительной деятельности в начальных классах школы, в средних классах обычно переходит в разряд неуспевающих.

Деятельность человека разумна благодаря знанию законов, взаимосвязей объективной действительности. Мышление - опосредованное и обобщенное отражение существенных, закономерных взаимосвязей действительности. Это обобщенная ориентация в конкретных ситуациях действительности. Мышление человека происходит посредством репрезентаций, каждое из которых выражается словом или несколькими словами, включающими существенные свойства класса объектов или представлений, которые можно определить как понятия. Собственно эти репрезентации (понятия) являются элементами мышления, различные их сочетания дают возможность переходить от одних мыслей к другим, т.е. протекать процессу мышления в различных его формах[29].

Заметим, что на общей «лестнице» психического развития логическое мышление стоит выше образного в том смысле, что оно формируется позднее, на основе образного, и дает возможность решать более широкий круг задач, усваивать научные знания. Однако это вовсе не означает, что нужно стремиться как можно раньше сформировать у детей логическое мышление. Во-первых, усвоение логических форм мышления без достаточно прочного фундамента в виде развитых образных форм будет неполноценным. Развитое образное мышление подводит ребенка к порогу логики, позволяет ему создавать обобщенные модельные представления, на которых в значительной мере строится затем процесс формирования понятий. Во-вторых, и после овладения логическим мышлением образное нисколько не теряет своего значения. Даже в самых, казалось бы, отвлеченных видах деятельности человека, связанных с необходимостью последовательного, строго логического мышления (например, в работе ученого), огромную роль играет использование образов. Образное мышление- основа всякого творчества, оно является составной частью интуиции, без которой не обходится ни одно научное открытие.

В младшем школьном возрасте дети располагают значительными резервами развития. С поступлением ребенка в школу под влиянием обучения начинается перестройка всех его познавательных процессов. Именно младший и средний школьный возраст является продуктивным в развитии логического мышления. Это связано с тем, что дети включаются в новые для них виды деятельности и системы межличностных отношений, требующие от них наличия новых психологических качеств.

Образное мышление в максимальной степени соответствует условиям жизни и деятельности школьника, тем задачам, которые возникают перед ним в игре, в рисовании, конструировании, в общении с окружающими. Именно поэтому школьный возраст наиболее сензитивен к обучению, опирающемуся на образы. Что же касается логического мышления, то возможности его формирования следует использовать лишь в той степени, в какой это необходимо для ознакомления ребенка с некоторыми основами начальных научных знаний (например, для обеспечения полноценного овладения числом), не стремясь к тому, чтобы непременно сделать логическим весь строй его мышления [30].

В среднем школьном возрасте происходит развитие мыслительных способностей и как следствие - расширение сознания происходящего, границ воображения, диапазона суждений и проницательности. Эти возросшие возможности познания также способствуют быстрому накоплению знаний, открывающих перед дошкольником ряд вопросов и проблем, которые могут осложнить и обогатитьих жизнь.

Если говорить более конкретно, то когнитивное развитие в этом возрастном периоде характеризуется развитием абстрактного мышления и использованием метакогнитивных навыков. Оба эти фактора оказывают существенное влияние как на широту и содержание мыслей школьника, так и на его способность к моральным рассуждениям. Поставив вопрос о специфике детского мышления и о мышлении как об основном познавательном процессе личности школьника, нельзя не упомянуть о возникновении новых отличающихся от свойственных ребенку способов познания окружающей действительности.

Пиаже определил логическую сферу мышления школьника средних классов как мышление на уровне формальных операций[31]. Он считает, что развитие логики мышления до стадии формальных операций не только является основным когнитивным новообразованием, данного возраста, но и лежит в основе всей эволюции психической жизни в ребенка. Большинство современных работ по изучению когнитивного развития исходят из идей Пиаже.

Собственно, тремя существенными свойствами логики мышления являются:

- способность учитывать все комбинации переменных при поиске решения проблемы;

- способность предполагать, какое влияние одна переменная окажет на другую;

- способность объединять и разделять переменные гипотетико-дедуктивным образом [31,с.42].

Основным интеллектуальным новообразованием данного периода является способность к манипуляциям с конкретными предметами. Это свидетельствует о повороте в эволюции логики мышления, ибо способность к формулированию гипотез и следствий из них независимо от правдоподобия исходных посылок характеризует процесс суждения. Следовательно, решающее значение дошкольник может придать формальному содержанию собственных умозаключений, что было ему недоступно на предыдущих этапах развития. На стадии формальных операции логика школьника преодолевает простое освоение непосредственно доступной реальности через включение в качестве объекты рефлексии категории возможного. Отныне понимание реальности и касается также гипотетически возможного, рефлексия затрагивает не только непосредственно воспринимаемую реальность, по и гипотетические предположения, истинность или ложность которых будет определена через установление формально-логических связей между ними. Формирование логической сферы школьника включает следующие мыслительный процессы:

- более эффективное использование отдельных механизмов обработки информации, таких как ее сохранение в памяти и перенос;

- развитие стратегий для различных типов решения задач;

- более эффективные способы получения информации и ее хранения в символической форме;

- развитие исполнительных функций более высокого порядка (метафункций), в том числе планирования и принятия решений, и повышение гибкости при выборе методов из более широкой базы сценариев.

Мышление, взятое с точки зрения его дифференцированного операционального строения, выступает явлением внутренним, актуально почти неуловимым, свернутым и быстро текущим. Подсознательность и слияние операций делают их слабо доступными для рефлексии и внешнего наблюдения. Однако исследования грамматически организованных высказываний как речевых следов мысли или предметных действий как аналогов некоторых мыслительных актов позволяют реконструировать тайный динамический подтекст мышления. Одну из наиболее, убедительных реконструкций такого рода осуществил С.Л. Рубинштейн [33].

) Различение - операция выделения элементов из мыслимого целого и их отделение друг от друга. Процесс различения хорошо эксплицируется в высказываниях, перечисляющих составные части и признаки (качества, свойства, функции, связи) целостного объекта.

) Сравнение - операция мысленного сопоставления разделенных объектов или их признаков и дальнейшее установление сходства и различия между ними. Обнаруживается в высказываниях о специфических особенностях соотносимых явлений.

) Нахождение сходства (подобия, сродства) - операция, позволяющая отождествить различные объекты по одному или нескольким признакам. Раскрывается в высказываниях о разных явлениях, обладающих, однако, похожими чертами, свойствами, отношениями.

) Нахождение различий - операция, благодаря которой однородное открывается как обладающее индивидуальными или типологическими отличиями друг от друга. Бывает эксплицирована в высказываниях об отличительных признаках объектов и явлений, относящихся к одной категории.

) Объединение в целое - операция воссоединения различных, прошедших сравнение, обнаруживших тесные взаимодействия и сходные признаки объектов в новую структуру. Находит выражение в синтетических суждениях, подчеркивающих существование многого в составе одного или соотношения (причинная зависимость, воздействие, влияние и т. д.) элементов в объединяющем целом.

) Абстрагирование и обобщение - единые операции выделения существенных, то есть свободных от случайных привнесений, свойств и связей объекта и объединения объектов с данными характеристиками в общую категорию. Ярко эксплицируются высказываниями, которые подчеркивают обобщающие, отвлеченные, категориальные признаки каких-либо явлений.

) Выделение противоположностей - операция разделения оппозиционных объектов или признаков определенного объекта, находящихся в большем или меньшем противоречии друг с другом. Проявляется через высказывания, сопоставляющие противоположности.

) Синтез противоположностей - операция соединения оппозиционных объектов, свойств, связей в такое новое целое, где ранее противоречивое уравновешивается, гармонизируется, усиливается за счет единства друг с другом. Проступает через высказывания о явлениях, вещах или событиях, вбирающих в себя противоположности, погашающих одну противоположность в другой, выявляющих новые возможности их взаимодействия.

) Конкретизация - обратная операция по отношению к абстрагированию признаков, определяющих обобщенные (видовые, родовые, универсальные) различия, оппозиции и тождества исходного объекта с другими объектами. Состоит в возврате к индивидуальной специфике объекта при удержании всего богатства его абстрактных отношений. Как частный случай обнаруживается в высказываниях о конкретных явлениях, приобретающих яркую индивидуальность за счет критически полного обладания ключевыми признаками либо максимального соответствия законам тех категорий, к которым они принадлежат.

) Символизация - операция, близкая конкретизации, но предполагающая не прямое, а опосредованное соотнесение исходного единичного объекта с абстрактными параметрами общих и универсальных объектных категорий. Средством конкретизации выступает другой реальный объект, эмпирически не сравнимый с исходным, но критически полно демонстрирующий какой-то обобщенный признак, отвлеченно соединяющий оба объекта. Эксплицируется в метафорических высказываниях, а также в высказываниях, уподобляющих отдаленные явления или обладающих переносным смыслом.

По характеру операций видно, что их можно разделить на различительные, объединяющие и синтетические, причем одни из них в основном осуществляются по отношению к эмпирическим, наблюдаемым признакам объектов, а другие - по отношению к «теоретическим» признакам, являющимся эффектами абстрагирования и категориально-речевого обобщения. Эмпирические и теоретические операции различения выступают «аналитическими»; объединение эмпирических признаков и теоретический синтез принадлежат к разряду «синтетических». Подобные рассуждения стали основанием для определения С.Л. Рубинштейном единого и непрерывного мыслительного процесса как аналитико-синтетического [33,с.28].

Процесс мышления, реализующийся как последовательность разнообразных операций, складывающихся в непрерывный контур аналитико-синтетической активности, становится, благодаря опосредующим когнитивным образованиям, поступательной сменой циклов мысленной репродукции, актуализации, преобразования, прогнозирования и генерирования нового. Процессуально-структурное единство составляет, по выражению Л.М. Веккера, «формулу мысли» [34]. Операции сводятся к развитию отношений между структурными компонентами конкретной мысли и выражению этих отношений в приращениях ее структуры. В реальном взаимодействии субъекта с проблемным объектом «формулой» описываются усложняющиеся феномены осмысления, понимания, переосмысления объекта.

Отмеченные континуальность и фрагментация мыслительного процесса выступают важнейшим условием, но не главным целевым ориентиром проблемной деятельности. В ее динамике таким ориентиром чаще всего выступают «когнитивные эффекты»: репрезентации проблемы, замыслы решения, промежуточные интеллектуальные новообразования, конечные результаты процесса. Все они формируют продуктивный аспект мышления, в котором можно выделить ведущую «единицу» зрелой мысли.

Среди когнитивных образований, которыми оперирует мышление, ведущая роль принадлежит тем, которые способны интегрировать первичные и вторичные образы жизненного объекта, сделав их при этом участниками логического процесса. Придав образам и их элементам легко обратимую абстрагирующую словесную форму, эти интегральные образования сохраняют, хотя и в редуцированном виде, чувственно-фигуративную индивидуальность объекта, а также воссоздают его множественную принадлежность к различным объектным категориям и его целостное идеальное существование. Причем две последние характеристики становятся основными в мыслительном процессе. Когнитивными единицами с такими параметрами могут быть только понятия. Одна из лучших типологий, учитывающих внутреннее подобие индивидуальной и социально-исторической эволюции понятий, принадлежит Л. С. Выготскому [35]. Выделенные им разновидности становящихся понятий хорошо переводятся в план типизации концетов зрелого субъекта мышления.

Генетически самыми ранними следами во взрослом понятийном мышлении являются синкретические понятия. Они формируются способом случайного, ситуативного, ассоциативного сведения логически не соединимых вещей и событий. В синкретическую «связку» могут попасть любые элементы реальности, словно субъект бессознательно убежден, что «все в мире связано со всем» бесчисленным количеством непосредственных отношений. Синкреты обладают огромной силой субъективной убедительности, так как кажутся хранителями таинственного, иррационального знания, поднимаемого из глубин души желаниями, эмоциями и фантазиями. Синкретическими элементами понятийного строя взрослого выступают, например, мыслеобразные картины экзотических сновидений, необъяснимо влекущие идеи ритуальных, обрядовых и некоторых игровых действий, магические сцепления причин и следствий в «приметах», поэтические агглютинации шутливой «чепухи» и сказочной «небывальщины».

Детство культур и детство современного человека отмечено также развитием понятий-в-комплексах или понятий-коллекций. Такими концептами объединяются предметы, явления, события, которые или вместе объективно участвуют в каком-то практическом действии, или представляют собой различные ситуативные формы одного и того же опытно постигаемого факта. Или связаны непосредственным процессом реализации какого-то конкретного предметного желания, или же в совокупности служат материалом для словесного выделения общих свойств, полученных при первичном эмпирическом абстрагировании. Концепт «одежда» объединяет для ребенка только то, что реально носится дома или на прогулке; «игра» требует уединения с посвященными, любимых игрушек, чувства совершающегося таинства и строго ритуальных действий; «страх» означает встречу со свирепой соседской собакой, повторяющийся сон, темноту, оставленность взрослыми [36].

«Коллекционное мышление» отзывается в нашем взрослом интеллектуальном отношении к миру, когда мы непроизвольно пользуемся приемами обыденного определения вещей, «от века» задействованных в повседневной жизни, хорошо знакомых с раннего возраста, незыблемых в своей очевидности со времен, когда сказки, легенды, предания и простая житейская мудрость окружающих были для нас основным источнком знания о жизни. Особой магией обладает для нас логика древних обобщений, касающихся человеческих качеств, которую мы иногда стихийно воссоздаем, не подозревая, что ее искусные образцы появились тысячелетия назад.

К процессам образования концептов-комплексов непосредственно присоединяются процессы становления псевдопонятий, структурно и операционально сходных с истинными понятиями, но отличающимися от них относительной нестойкостью перед воздействием сенсорно-перцептивных впечатлений, невысокими порядками обобщений, прямым участием в практических действиях в виде конкретных «рецептов», указаний и регламентов. Кроме того, они отличаются «законодательным» характером в смысле руководства повседневной жизнью и негибкостью в условиях, требующих когнитивных преобразований. В производстве и воспроизводстве данных концептов задействованы самые разнообразные операции, в которых ребенок, подобно человеку магических и мифологических культур, может упражняться с настоящей страстью: различение, перечисление, сравнение, сопоставление, ассоциирование по внешнему сходству, классификация, разделение предметных противоположностей и их эмпирический синтез, установления прямых причинно-следственных отношений[37].

Развитие истинных понятий, а с ними утверждение в индивидуальной или коллективной понятийной системе законов вербализации, категоризации, иерархичности и рационализации знания является, по Выготскому, завершающим этапом нормального мыслегенеза. Согласно его логике, в процессе жизни человека современной культуры ставшее понятие должно вобрать в себя многие другие понятия и стать «теорией».

Таким образом, формирование логического мышления школьников - важная составная часть педагогического процесса. В основе системы знаний учащихся лежит сформированность системы понятий изучаемой предметной области. Владение понятийным аппаратом в большей степени определяет понимание учебного материала, его использование для решения прикладных задач учебных дисциплин.

Таким образом, логическое мышление не является врожденным, поэтому его можно и нужно развивать. Решение логических зада на уроках информатики как раз и представляет собой один из приемов развития мышления. Решение логических задач дает возможность развить внимание, память и привить навыки правильного мышления. Однако решение задач - это только один из приемов достижения цели. Наиболее эффективным методом развития абстрактного логического мышления является систематическое изучение науки логики.

Таким образом, развитие логического мышления учащихся - одна из важных и актуальных проблем педагогической науки и практики обучения в школе.

.2 Современные психодинамические аспекты логического мышления младших школьников

Формирование логического мышления - важная составная часть педагогического процесса. Помочь учащимся в полной мере проявить свои способности, развить инициативу, самостоятельность, творческий потенциал - одна из основных задач современной школы. Успешная реализация этой задачи во многом зависит от сформированности у учащихся познавательных интересов. Математика даёт реальные предпосылки для развития логического мышления, задача учителя - полнее использовать эти возможности при обучении детей математике. Однако, конкретной программы логических приемов мышления, которые должны быть сформулированы при изучении данного предмета, нет. В результате работа над развитием логического мышления идёт без знания системы необходимых приёмов, без знания их содержания и последовательности формирования. Первоначальные математические знания усваиваются детьми в определённой, приспособленной к их пониманию, системе, в которой отдельные положения логически связаны одно с другим, вытекают одно из другого [14]. При сознательном усвоении математических знаний учащиеся пользуются основными операциями мышления в достигнутом для них виде: анализом и синтезом, сравнением, абстрагированием и конкретизацией, обобщением; ученики делают индуктивные выводы, проводят дедуктивные рассуждения. Сознательное усвоение учащимися математических знаний развивает логическое мышление учащихся.

Овладение мыслительными операциями в свою очередь помогает учащимся успешнее усваивать новые знания. Познавая предметы и явления окружающей действительности, мы можем мысленно расчленять предмет или явление на составные части и мысленно же соединять части в одно целое.Операция мышления, направленная на расчленение целого на составляющие его части, называется анализом. Операция мышления, направленная на установление связи между предметами или явлениями, называется синтезом. Эти операции мышления взаимно связаны. Ф. Энгельс отмечает, что «…мышление состоит столько же в разложении предметов сознания на их элементы, сколько в объединении связанных друг с другом элементов в некоторое единство. Без анализа нет синтеза»[15].

Логическое мышление - мышление, проходящее в рамках формальной логики и отвечающее ее требованиям. Задача развития логического мышления учащихся ставится и, определенным образом, решается в массовой школе. Во всех школьных программах по математике как одна из целей обучения предмету отмечена - развитие логического мышления. Еще столетие назад Л.Н. Толстой отмечал, что математика имеет своей задачей не счисление, но обучение человеческой мысли при счислении. С осознанием отдельных логических форм человек начинает более четко мыслить и выражать свои мысли в речи. Используя в обучении математике различные методы, учитель применяет их так, чтобы они содействовали активизации мышления учащихся и, тем самым, способствовали его развитию [18]. Учитель должен владеть методикой работы над текстовой задачей, уметь заинтересовать учеников.

Актуальность заключается в том, что в современное время дети учатся по развивающим технологиям, где логическое мышление является основой. С начала обучения мышление выдвигается в центр психического развития (Л.С. Выготский) и становится определяющим в системе других психических функций, которые под его влиянием интеллектуализируются и приобретают произвольный характер[20]. Многочисленные наблюдения педагогов, исследования психологов убедительно показали, что ребенок, не научившийся учиться, не овладевший приемами мыслительной деятельности в начальных классах школы, в средних классах обычно переходит в разряд неуспевающих.

Заметим, что на общей «лестнице» психического развития логическое мышление стоит выше образного в том смысле, что оно формируется позднее, на основе образного, и дает возможность решать более широкий круг задач, усваивать научные знания. Однако это вовсе не означает, что нужно стремиться как можно раньше сформировать у ребенка логическое мышление. Во-первых, усвоение логических форм мышления без достаточно прочного фундамента в виде развитых образных форм будет неполноценным. Развитое образное мышление подводит ребенка к порогу логики, позволяет ему создавать обобщенные модельные представления, на которых в значительной мере строится затем процесс формирования понятий. Во-вторых, и после овладения логическим мышлением образное нисколько не теряет своего значения. Даже в самых, казалось бы, отвлеченных видах деятельности человека, связанных с необходимостью последовательного, строго логического мышления (например, в работе ученого), огромную роль играет использование образов. Образное мышление- основа всякого творчества, оно является составной частью интуиции, без которой не обходится ни одно научное открытие.

В младшем школьном возрасте дети располагают значительными резервами развития. С поступлением ребенка в школу под влиянием обучения начинается перестройка всех его познавательных процессов. Именно младший школьный возраст является продуктивным в развитии логического мышления. Это связано с тем, что дети включаются в новые для них виды деятельности и системы межличностных отношений, требующие от них наличия новых психологических качеств.

В младшем школьном возрасте происходит развитие мыслительных способностей и как следствие - расширение сознания происходящего, границ воображения, диапазона суждений и проницательности. Эти возросшие возможности познания также способствуют быстрому накоплению знаний, открывающих перед дошкольником ряд вопросов и проблем, которые могут осложнить - и обогатить - их жизнь.

Поставив вопрос о специфике детского мышления и о мышлении как об основном познавательном процессе личности школьника, нельзя не упомянуть о возникновении новых отличающихся от свойственных ребенку способов познания окружающей действительности. В этом вопросе авторы издавна едины и если проанализируем специфику учебных программ дошкольных учреждений, переход в которую совпадает с началом процесса обучения, то увидим, что их содержание претерпевает значительные изменения. Например, в математических науках изучение понятий и представлений, связанных операцией с числами, что необходимо предполагать способность оперировать исключительно символами. Психологические исследования подтверждают, что подобные изменения содержания дошкольных программ опираются на определенные качественные и количественные новообразования, характеризующие мышление дошкольника и его способ видения мира.

Пиаже определил логическую сферу мышления младшего школьника как мышление на уровне формальных операций. Он считает, что развитие логики мышления до стадии формальных операций не только является основным когнитивным новообразованием, данного возраста, но и лежит в основе всей эволюции психической жизни в ребенка. Большинство современных работ по изучению когнитивного развития исходят из идей Пиаже.

Собственно, тремя существенными свойствами логики мышления являются:

. Способность учитывать все комбинации переменных при поиске решения проблемы.

. Способность предполагать, какое влияние одна переменная окажет на другую.

. Способность объединять и разделять переменные гипотетико-дедуктивным образом[23].

Основным интеллектуальным новообразованием данного периода является способность к манипуляциям с конкретными

предметами. Это свидетельствует о повороте в эволюции логики мышления, ибо способность к формулированию гипотез и следствий из них

независимо от правдоподобия исходных посылок характеризует

процесс суждения. Следовательно, решающее значение дошкольник может придать формальному содержанию собственных умозаключений, что было ему недоступно на предыдущих этапах развития. На стадии формальных операции логика дошкольника преодолевает простое освоение непосредственно доступной реальности через включение в качестве объекты рефлексии категории возможного. Отныне понимание реальности и касается также гипотетически возможного, рефлексия затрагивает не только непосредственно воспринимаемую реальность, по и гипотетические предположения, истинность или ложность которых будет определена через установление формально-логических связей между ними. Формирование логической сферы младшего школьника включает следующие мыслительный процессы:

. Более эффективное использование отдельных механизмов обработки информации, таких как ее сохранение в памяти и перенос.

. Развитие стратегий для различных типов решения задач.

. Более эффективные способы получения информации и ее хранения в символической форме.

. Развитие исполнительных функций более высокого порядка (метафункций), в том числе планирования и принятия решений, и повышение гибкости при выборе методов из более широкой базы сценариев.

Одну из наиболее, убедительных реконструкций такого рода осуществил С.Л. Рубинштейн [24].

) Различение -- операция выделения элементов из мыслимого целого и их отделение друг от друга. Процесс различения хорошо эксплицируется в высказываниях, перечисляющих составные части и признаки (качества, свойства, функции, связи) целостного объекта.

) Нахождение сходства (подобия, сродства) -- операция, позволяющая отождествить различные объекты по одному или нескольким признакам. Раскрывается в высказываниях о разных явлениях, обладающих, однако, похожими чертами, свойствами, отношениями.

) Выделение противоположностей -- операция разделения оппозиционных объектов или признаков определенного объекта, находящихся в большем или меньшем противоречии друг с другом. Проявляется через высказывания, сопоставляющие противоположности.

) Конкретизация -- обратная операция по отношению к абстрагированию признаков, определяющих обобщенные (видовые, родовые, универсальные) различия, оппозиции и тождества исходного объекта с другими объектами. Состоит в возврате к индивидуальной специфике объекта при удержании всего богатства его абстрактных отношений. Как частный случай обнаруживается в высказываниях о конкретных явлениях, приобретающих яркую индивидуальность за счет критически полного обладания ключевыми признаками либо максимального соответствия законам тех категорий, к которым они принадлежат.

) Символизация -- операция, близкая конкретизации, но предполагающая не прямое, а опосредованное соотнесение исходного единичного объекта с абстрактными параметрами общих и универсальных объектных категорий. Средством конкретизации выступает другой реальный объект, эмпирически не сравнимый с исходным, но критически полно демонстрирующий какой-то обобщенный признак, отвлеченно соединяющий оба объекта. Эксплицируется в метафорических высказываниях, а также в высказываниях, уподобляющих отдаленные явления или обладающих переносным смыслом.

По характеру операций видно, что их можно разделить на различительные, объединяющие и синтетические, причем одни из них в основном осуществляются по отношению к эмпирическим, наблюдаемым признакам объектов, а другие -- по отношению к «теоретическим» признакам, являющимся эффектами абстрагирования и категориально-речевого обобщения. Эмпирические и теоретические операции различения выступают «аналитическими»; объединение эмпирических признаков и теоретический синтез принадлежат к разряду «синтетических». Подобные рассуждения стали основанием для определения С.Л. Рубинштейном единого и непрерывного мыслительного процесса как аналитико-синтетического [25].

Процесс мышления, реализующийся как последовательность разнообразных операций, складывающихся в непрерывный контур аналитико-синтетической активности, становится, благодаря опосредующим когнитивным образованиям, поступательной сменой циклов мысленной репродукции, актуализации, преобразования, прогнозирования и генерирования нового. Процессуально-структурное единство составляет, по выражению Л.М. Веккера, «формулу мысли». Операции сводятся к развитию отношений между структурными компонентами конкретной мысли и выражению этих отношений в приращениях ее структуры. В реальном взаимодействии субъекта с проблемным объектом «формулой» описываются усложняющиеся феномены осмысления, понимания, переосмысления объекта[26].

Структурная модель и виды понятий Л. С. Выготского

Одна из лучших типологий, учитывающих внутреннее подобие индивидуальной и социально-исторической эволюции понятий, принадлежит Л. С. Выготскому [27]. Выделенные им разновидности становящихся понятий хорошо переводятся в план типизации концетов зрелого субъекта мышления.

Или связаны непосредственным процессом реализации какого-то конкретного предметного желания, или же в совокупности служат материалом для словесного выделения общих свойств, полученных при первичном эмпирическом абстрагировании. Концепт «одежда» объединяет для ребенка только то, что реально носится дома или на прогулке; «игра» требует уединения с посвященными, любимых игрушек, чувства совершающегося таинства и строго ритуальных действий; «страх» означает встречу со свирепой соседской собакой, повторяющийся сон, темноту, оставленность взрослыми[28].

2 ПСИХОЛОГО-ПЕДАГОГИЧЕСКИЕ МЕХАНИЗМЫ РАЗВИТИЯ ЛОГИЧЕСКОГО МЫШЛЕНИЯ МЛАДШИХ ШКОЛЬНИКОВ

.1 Особенности логического мышления младшего школьника в изучении математики

Формирование логического мышления младших школьников - важная составная часть педагогического процесса. Помочь учащимся в полной мере проявить свои способности, развить инициативу, самостоятельность, творческий потенциал - одна из основных задач современной школы. Мышление ребёнка в той или иной мере развивает каждый общеобразовательный предмет, преподаваемый в начальной школе. Однако математика среди других предметов занимает особое место.

В словаре психологических понятий К.К. Платонова логическое мышление определяется как "вид мышления, сущность которого заключается в ориентировании понятиями, суждениями и умозаключениями с использованием законов логики" [29].В психолого-педагогической литературе "логическое мышление" недостаточно дифференцируемо от понятий "абстрактное", "теоретическое", "понятийное", "категориальное", "словесно-логическое (дискурсивное)" мышление. Иногда они рассматриваются как синонимы. Её абстрактный характер и общность методов, широко использующихся в различных областях, в наибольшей степени способствуют овладению учащимися элементарной логической грамотностью, умениями применять сформированные на уроках математики общелогические понятия, приёмы и способы действий при изучении других предметов. Многочисленные наблюдения педагогов, исследования психологов убедительно показали, что ребенок, научившийся учиться, не овладевший приемами мыслительной деятельности в начальных классах школы, в средних обычно переходит в разряд неуспевающих. Одним из важных направлений в решении этой задачи выступает создание в начальных классах условий, обеспечивающих полноценное умственное развитие, связанное с формированием устойчивых познавательных интересов, умений и навыков мыслительной деятельности, качеств ума, творческой инициативы. В основе системы знаний учащихся лежит сформированность системы понятий изучаемой предметной области. Владение понятийным аппаратом в большей степени определяет понимание учебного материала, его использование для решения прикладных задач. Каждое новое вводимое понятие должно быть четко определено, раскрыта суть изучаемого понятия, кроме того, должны быть определены связи данного понятия с другими понятиями, как уже введенными, так еще неизвестными учащимся.

В процессе обучения развивается абстрактное мышление, анализ и синтез изучаемых явлений. Например, очень большие возможности для развития логики мышления личности младшего школьника представляет математика. Переход к изучению чисел в детском саду на занятиях по математике означает переход уровню обобщения. Если в дошкольной арифметики сначала имеет место абстрагирование числа от предмета, то математику начальных классов характеризует переход к действиям с условными обозначениями чисел, т.е. обобщение обобщения, что дает возможность в абстрактной и обобщенной форме выражать отношение между величинами. Изучение математики вследствие этого дает новый толчок к развитию логической сферы[30].

Велико значение и основам геометрии в цикле математики, где имеет место абстрагирование от конкретных предметов и усвоение форм, и отношение геометрических тел в отвлеченном виде. Геометрия приучает к строгой логичности мышления, развивает умение обосновывать и доказывать, рассуждать, различать несомненное, достоверное от сомнительного, проблематичного, возможного. Все учебные предметы, изучаемые в младшем школьном возрасте, прежде всего, стимулируют развитие логической сферы мышления. Естественно, что особенностью мыслительной деятельности ребенка является нарастающая с каждым годом способность к логическому мышлению, Конечно изменение соотношения между конкретно-образным и абстрактным мышлением в пользу абстрактного мышления не должна иметь место упрощенная трактовка возрастных изменений в мышлении, согласно которым дошкольник мыслит конкретно[31].

Отмечается еще сравнительно невысокое развитие аналитико-синтетической деятельности у многих дошкольников, недостаточное владение методом рассуждения. В этом случае дети идут примитивным методом “хаотических проб-угадываний”. Некоторые младшие школьники испытывают трудности при установлении причинно-следственных связей, причем они раньше и лучше справляются с нахождением причин событий или явлений, чем с установлением следствий, т. е. прогрессивное (или прямое) рассмотрение причинно-следственных связей (от причины к следствию) вызывает, как правило, большие затруднения, чем регрессивное (или обратное- от следствия к причине). Все приведенные материалы показывают, что логическое мышление находится у дошкольников в стадии становления, быстрого развития, связанного с преодолением известных трудностей[32].

Воздействие непосредственных чувственных впечатлений на логическое мышление младшего школьника столь велико, что в ряде случаев оно оказывается сильнее воздействия слова (объяснения воспитателя, текста книжки). При неправильном использовании наглядного материала (однообразии, односторонности или ограниченности наглядного опыта) он может оказывать и отрицательное влияние - тормозить вычленение существенных признаков предмета или явления и фиксировать внимание детей на ясно выраженных, но случайных, несущественных признаках. Это часто приводит к распространенной ошибке - неправомерному сужению или расширению того или иного понятия, когда в состав понятия привносятся ярко запечатлевшиеся случайные, несущественные признаки, которые таким образом возводятся в ранг существенных. Многочисленные исследования установили, что при этом дети часто не осознают этого “привнесения”, так как одновременно дают правильные определения понятий, правильно перечисляют существенные признаки; при применении же этих понятий фактически опирается на другие, наглядно воспринятые существенные признаки. На эту тему имеется богатый и интересный материал. Наблюдалось множество подобных случаев при изучении математики. Например, младшие школьники чаще всего мыслят прямую линию только как горизонтальную, вертикальные, наклонные линии не относят к прямым, считают, что в окружности можно провести всего один или два диаметра (в вертикальном и горизонтальном положении), относят к внешним углам только тупые внешние углы.

Таким образом выясняется, что успешное формирование мышления младших школьников на уроках математики в основном будет определяться соблюдением следующих психолого-педагогических условий:

. На каждом уроке применять специальные задания, направленные на формирование мышления.

. Учитывать уровень индивидуального развития ребенка и в связи с этим осуществлять индивидуальную и дифференцированную работу с учащимися.

. Формировать словесно-логическое, абстрактное мышление на уроках математики в тесной связи с развитием практически-действенного и наглядного - образного мышления.

. При формировании словесно - логического мышления необходимо применять приём моделирования.

. Формировать словесно-логическое мышление на факультативах по математике, внеклассных занятиях[33].

Все выше изложенное говорит, о том, что формирование логического мышления является одной из актуальных проблем. Процесс воспитания культуры мышления довольно длителен.

Поэтому и начинаться он должен с первых лет обучения ребёнка в школе на уровне, соответствующем его возрасту, так как формируется не только математическая культура учащихся, но и развиваются умения по решению жизненно важных и необходимых задач.

Логическое мышление младших школьников основывается на решении нестандартных задач в их единстве: обучения, воспитания и развития. Критерием сформированности логического мышления является регулярное применение на уроках математики и во внеклассных занятиях нестандартные задачи. Регулярно используя нестандартные задачи, учитель может сформировать развитие логического мышления.

Учащиеся при анализе своей самостоятельной работы часто указывают на потребность в самоконтроле за этой работой, на необходимость в снабжении их развернутым комментарием всех сложностей, встречающихся при выполнении заданий, на затруднения в самостоятельной ориентации в теоретическом материале. В результате опроса, в частности, выяснилось, что некоторые учащиеся, не имея собранных в одном пособии всех необходимых им сведений, в поисках нужной информации чаще обращаются к преподавателю, чем к учебнику или грамматическому справочнику. Таким образом, возникает необходимость в создании специальных дидактических материалов, предназначенных для самостоятельной работы учащихся в ходе реализации проекта. Многие педагоги предпочитают использовать в своей деятельности дидактические материалы исключительно контролирующего характера. Учитывая то, что в основе любого проекта лежит, прежде всего, самостоятельная деятельность учащихся, а также то, что главное назначение дидактических материалов - использование их при самостоятельной работе, мы можем сделать вывод о том, что дидактические материалы в проекте должны играть несколько иную роль. Если это материалы контролирующего характера, то они должны обязательно предусматривать возможность самопроверки и самоконтроля[34].

Система дидактических материалов на уроке должна также предполагать последовательное, поэтапное обучение учащихся различным приемам или способам учебной деятельности, а также использование заданий различного уровня (репродуктивного, преобразующего или творческого).

Рисунок 1 - Классификация дидактического материала

Примечание: составлено автором

Современные информационные технологии позволяют разработчикам дидактических материалов оперировать таким комплексом вербальных и невербальных средств, какого в их распоряжении никогда еще не было. Эти средства позволяют создавать эстетичные, увлекательные, познавательные, проблемные материалы и тем самым повысить мотивацию и познавательный интерес учащихся. Эта психолого-педагогическая составляющая дидактического материала направлена на привлечение внимания учащегося, поддержание познавательного интереса, активизацию его мышления, на формирование оценок описываемого, создает побудительные мотивы к углубленному изучению того или иного вопроса.

В задачу учителя входит помощь обучаемому наиболее полно овладеть знаниями и использовать их в решении практических задач.

В качестве наиболее значимых принципов обучения, реализуемых при разработке дидактических материалов, хотелось бы выделить следующие:

• принцип доступности (дидактические материалы подбираются учителем согласно достигнутого уровня учащихся);

• принцип самостоятельной деятельности (работа с дидактическими материалами осуществляется самостоятельно);

• принцип индивидуальной направленности (работа с дидактическими материалами осуществляется в индивидуальном темпе, сложность и вид материалов может подбираться также индивидуально);

• принципы наглядности и моделирования (поскольку наглядно-образные компоненты мышления играют исключительно важную роль в жизни человека, использование их в обучении оказывается чрезвычайно эффективным);

• принцип прочности (память человека имеет избирательный характер: чем важнее, интереснее и разнообразнее материал, тем прочнее он закрепляется и дольше сохраняется, поэтому практическое использование полученных знаний и умений, являющееся эффективным способом продолжения их усвоения, в условиях игровой (моделирующей) компьютерной среды способствует их лучшему закреплению);

• принцип познавательной мотивации;

• принцип проблемности (в ходе работы учащийся должен решить конкретную дидактическую проблему, используя для этого свои знания, умения и навыки; находясь в ситуации, отличной от ситуации на уроке, в новых практических условиях он осуществляет самостоятельную поисковую деятельность, активно развивая при этом свою интеллектуальную, мотивационную, волевую, эмоциональную и другие сферы) [35].

Можно отметить следующее значение дидактического материала в уроке:

• Самостоятельное овладение учащимися материалом и формирование умений работать с различными источниками информации.

• Активизация познавательной деятельности учащихся.

• Формирование умений самостоятельно осмысливать и усваивать новый материал.

• Условные заменители, схемы и рисунки в дидактическом материале способствуют развитию творческого воображения, позволяют «опредметить» абстрактные понятия.

• Контроль с обратной связью, с диагностикой ошибок (появление на компьютере соответствующих комментариев) по результатам деятельности и оценкой результатов.

• Самоконтроль и самокоррекция.

• Тренировка в процессе усвоения учебного материала.

• Высвобождение учебного времени за счет выполнения на компьютере трудоемких вычислительных работ.

• Усиление мотивации обучения.

• Развитие определенного вида мышления (наглядно-образного, теоретического, логического).

• Формирование культуры учебной деятельности, информационной культуры общества.

• Активизация взаимодействие интеллектуальных и эмоциональных функций при совместном решении исследовательских (творческих) учебных задач.

Виды дидактического материала

• Дидактические тексты для обучения учащихся работе с различными источниками информации (учебником, картами, справочниками, словарями, электронными ресурсами и т.д.)

• Обобщенные планы некоторых видов познавательной деятельности: изучения научных фактов; подготовки и проведения эксперимента; изучения физического прибора; проведения научно-технического исследования; действия измерения; анализа графика функциональной зависимости; анализа таблиц.

• Памятки (инструкции) по формированию логических операций мышления: сравнение, обобщение, классификация, анализ, синтез.

• Задания по формированию умений сравнивать, анализировать, доказывать, устанавливать причинно-следственные связи, обобщать.

• Задания различного уровня сложности: репродуктивного, преобразующего, творческого.

• Задания с проблемными вопросами.

• Задания на развитие воображения и творчества.

• Экспериментальные задания.

• Инструктивные карточки, отражающие логическую схему изучения нового материала и необходимые способы учебной работы

• Карточки-консультации, дидактические материалы с поясняющими рисунками, планом выполнения заданий, с указанием типа задач и пр.

• Инструкции к лабораторным работам и фронтальным опытам.

• Листы самоподготовки учащихся к занятию.

• Справочные материалы

• Алгоритм выполнения задания.

• Указание причинно-следственных связей, необходимых для выполнения задания.

• Указание теорем, правил, формул, на основании которых выполняется задание.

• Модели и имитация изучаемых или исследуемых объектов, процессов или явлений.

• Тесты с возможностью самоконтроля.

Основные требования к дидактическому материалу:

• выбрать последовательность знакомства с информацией;

• дать ученику подробные советы о порядке самостоятельной работы и самоконтроле;

• структурировать материал таким образом, чтобы была обеспечена зрительная наглядность для сравнений и сопоставлений[36].

2.2 Виды и формы дидактического материала по математике в 4 классе

Интенсивное развитие интеллекта происходит в младшем школьном возрасте. Ребенок, особенно 7-8 летнего возраста, обычно мыслит конкретными категориями, опираясь при этом на наглядные свойства и качества конкретных предметов и явлений, поэтому в младшем школьном возрасте продолжает развиваться наглядно-действенное и наглядно-образное мышление, что предполагает активное включение в обучение моделей разного типа (предметные модели, схемы, таблицы, графики и т.п.) "Книжка с картинками, наглядное пособие, шутка учителя - все вызывает у них немедленную реакцию. Младшие школьники находятся во власти яркого факта, образы, возникающие на основе описания во время рассказа учителя или чтения книжки, очень ярки".

Младшие школьники склонны понимать буквально переносное значение слов, наполняя их конкретными образами. Ту или иную мыслительную задачу учащиеся решают легче, если опираются на конкретные предметы, представления или действия. Учитывая образность мышления, учитель принимает большое количество наглядных пособий, раскрывает содержание абстрактных понятий и переносное значение слов на ряде конкретных примеров. И запоминают младшие школьники первоначально не то, что является наиболее существенным с точки зрения учебных задач, а то, что произвело на них наибольшее впечатление: то, что интересно, эмоционально окрашено, неожиданно и ново.

Наглядно-образное мышление очень ярко проявляется при понимании, например, сложных картин, ситуаций. Для понимания таких сложных ситуаций требуется сложная ориентировочная деятельность. Понять сложную картину - это значит понять ее внутренний смысл. Понимание смысла требует сложной аналитико-синтетической работы, выделения деталей сопоставления их друг с другом. В наглядно-образном мышлении участвует и речь, которая помогает назвать признак, сопоставить признаки. Только на основе развития наглядно-действенного и наглядно-образного мышления начинает формироваться в этом возрасте формально-логическое мышление.

Мышление детей этого возраста значительно отличается от мышления дошкольников: так если для мышления дошкольника характерно такое качество, как непроизвольность, малая управляемость и в постановке мыслительной задачи, и в ее решении, они чаще и легче задумываются и над тем, что им интересней, что их увлекает, то младшие школьники в результате, обучения в школе, когда необходимо регулярно выполнять задания в обязательном порядке, научиться управлять своим мышлением.

Во многом формированию такому произвольному, управляемому мышлению способствует указание учителя на уроке, побуждающие детей к размышлению.

Учителя знают, что мышление у детей одного и того же возраста достаточно разное. Одни дети легче решают задачи практического характера, когда требуется использовать приемы наглядно-действенного мышления , например задачи, связанные с конструированием и изготовлением изделий на уроках труда. Другим легче даются задания, связанные с необходимостью воображать и представлять какие-либо события или какие-нибудь состояния предметов или явлений. Например, при написании изложений, подготовке рассказа по картинке и т.п. Третья часть детей легче рассуждает, строит условные суждения и умозаключения, что позволяет им более успешно, чем остальным детям, решать математические задачи, выводить общие правила и использовать их в конкретных случаях.

Встречаются такие дети, которым трудно и мыслить практически и оперировать образами, и рассуждать, и такие, которым все это делать легко .

Наличие такого разнообразия в развитии разных видов мышления у разных детей в значительной мере затрудняет и осложняет работу учителя. Поэтому ему целесообразно более отчетливо представлять основные уровни развития видов мышления у младших школьников.

О наличии того или иного вида мышления у ребенка можно судить по тому, как он решает соответствующие данному виду мышления задачи. Так, если при решении легких задач - на практическое преобразование предметов, или на оперирование их образами, или на рассуждение - ребенок плохо разбирается в их условии, путается и теряется при поиске их решения, то в этом случае считается, что у него первый уровень развития в соответствующем виде мышления.

Если ребенок успешно решает легкие задачи, предназначенные для применения того или иного вида мышления, но затрудняется в решении более сложных задач, в частности из-за того, что ему не удается представить все это решение целиком, поскольку недостаточно развито умение планировать, то в этом случае считается, что у него второй уровень развития в соответствующем виде мышления.

И наконец, если ребенок успешно решает и легкие и сложные задачи в рамках соответствующего вида мышления и даже может помочь другим детям в решении легких задач, объясняя причины допускаемых ими ошибок, а так же может придумывать сам легкие задачи, то этом случае считается, что у него третий уровень развития соответствующего вида мышления.

Опираясь на эти уровни в развитии мышления, учитель сможет более конкретно охарактеризовать мышление каждого ученика.

Для умственного развития младшего школьника нужно использовать три вида мышления. При этом с помощью каждого из них у ребенка лучше формируются те или иные качества ума. Так решение задач с помощью наглядно-действенного мышления позволяет развить у учеников навыки управления своими действиями, осуществление целенаправленных, а не случайных и хаотичных попыток в решении задач[58].

Такая особенность этого вида мышления следствие того, что с его помощью решаются задачи, в которых предметы можно брать в руки, чтобы изменить их состояния и свойства, а так же расположить в пространстве.

Поскольку, работая с предметами, ребенку легче наблюдать за своими действиями по их изменению, то в этом случае и легче управлять действиями, прекращать практические попытки, если их результат не соответствует требованиям задачи, или наоборот заставлять себя довести попытку до конца, до получения определенного результата, а не бросить ее выполнение, не узнав результата.

С помощью наглядно-действенного мышления удобнее развивать у детей такое важное качество ума, как способность при решении задач действовать целенаправленно, сознательно управлять и контролировать своими действиями.

Своеобразие наглядно-образного мышления заключается в том, что решая задачи с его помощью, ребенок не имеет возможности реально изменять образы и представления, а только по воображению.

Это позволяет разрабатывать разные планы для достижения цели, мысленно согласовывать эти планы, чтобы найти наилучший. Поскольку при решении задач с помощью наглядно-образного мышления, ребенку приходится оперировать лишь образами предметов (т.е. оперировать предметами лишь в мысленном плане), то в этом случае труднее управлять своими действиями, контролировать их и осознавать, чем в том случае, когда имеется возможность оперировать самими предметами.

Поэтому главная цель развития у детей наглядно-образного мышления заключается в том, чтобы с его помощью формировать умение рассматривать разные пути, разные планы, разные варианты достижения цели, разные способы решения задач.

Это следует из того, что оперируя предметами в мыслительном плате, представляя возможные варианты их изменений можно найти быстрее нужное решение, чем выполняя каждый вариант, который возможен. Тем более, что не всегда имеются условия для многократных изменений в реальной ситуации.

Своеобразие словесно-логического мышления, по сравнению с наглядно-действенным и наглядно-образным, состоит в том, что это отвлеченное мышление, в ходе которого ребенок действует не с вещами и их образами, а с понятиями о них, оформленных в словах иди знаках. При этом ребенок действует по определенным правилам, отвлекаясь от наглядных особенностей вещей и их образов.

Поэтому главная цель работы по развитию у детей словесно-логического мышления заключается в том, чтобы с его помощью формировать умение рассуждать, делать выводы из тех суждений, которые предлагаются в количестве исходных, умение ограничиваться содержанием этих суждений и не привлекать других соображений, связанных с внешними особенностями тех вещей или образов, которые отражаются и обозначают в исходных суждениях.

Итак, существует три вида мышления: наглядно-действенное, наглядно-образное, словесно-логическое. Уровни мышления у детей одного и того же возраста достаточно разные. Поэтому задача педагогов, психологов состоит в дифференцированном подходе к развитию мышления у младших школьников.

В курсе дидактики есть свои требования к современному уроку, с типами уроков и их структурой. В методике начального обучения математике всё обстоит значительно сложнее, особенно со структурой урока. Это обусловлено тем, что при построении конкретного урока необходимо учитывать не только определённые этапы обучения (актуализация знаний, объяснение нового, закрепление, контроль, повторение) и специфику математического содержания, но и основную цель урока, его логику и те методические приёмы, которые способствуют её достижению.

В связи с этим, характеризуя урок с методической точки зрения, необходимо иметь в виду не только его внешнюю, но и внутреннюю структуру может иметь различные варианты.

Первый вариант-учитель сам дважды излагает новый материал с помощью рассказа, объяснения, беседы, а затем переходит к опросу учащихся по его содержанию.

Второй вариант - учитель вначале сам объясняет новый материал, используя, методы устного изложения знаний, а затем организует самостоятельную работу учащихся над учебником с целью последующего более глубокого осмысления и запоминания новой темы.

Третий вариант - учитель определяет тему и цель урока, создает проблемную ситуацию и указывает вопросы, которые должны быть усвоены учащимися, а затем организует самостоятельную работу над учебником и проводит закрепление.

Четвертый вариант - на уроках химии, физики учитель организует лабораторную работу с целью осмысления и усвоения нового материала с использованием учебника[9].

Каким же образом передовым учителям удается дважды излагать новый материал, когда в массовой школьной практике иногда не хватает времени и для его однократного изложения? Здесь они придерживаются идеи К. Д. Ушинского, который указывал, что при первом изложении нового материала не следует нагромождать слишком много деталей и подробностей, надо объяснять только самое основное и главное, что должно быть усвоено учащимися, а расширение знаний проводить на последующих занятиях. “Рассказывая какое-нибудь событие в первый раз,-подчеркивал он,-вы должны передать только главные его черты, две, три интересные живописные подробности. Если вы в первый раз привяжете к событию слишком много объяснений и подробностей, то весь рассказ рухнет в детской голове. Утвердите в ней сначала немного, но прочно и потом уже, мало-помалу, стройте на этом укоренившемся прочном основании.

Рассказав детям событие, вы можете потом обратиться к детям с вопросами, и сначала с такими вопросами, в ответ на которые дети передали бы вам главные черты события. Затем следует другой ряд вопросов, исчерпывающих подробности ,Усвоенный детьми рассказ должен быть повторяем... и при каждом повторении наставник может что-нибудь вновь объяснить и дополнить”'.

Реализуя эту идею К. Д. Ушинского и добиваясь сжатого компактного изложения нового материала, опытные учителя и имеют возможность излагать его дважды. Больше того, на основе данной идеи они стали широко практиковать изложение нового материала укрупненными блоками, т. е. объяснять на одном уроке 3-4 и даже 5-6 новых тем, высвобождая время для последующей работы по углублению и расширению знаний и выработке практических умений и навыков. Естественно, что они прибегают к весьма сжатому изложению материала, объясняя только самое основное и главное.

Этот опыт получает распространение Естественно, учителю нужно самому настойчиво тренироваться, чтобы овладеть этой методикой.

Для успешного овладения изучаемым материалом на уроке большое значение имеет то, чтобы при его восприятии, осмыслении и усвоении учащиеся проявляли высокую познавательную активность. О различных приемах возбуждения активности учащихся в процессе устного изложения знаний учителем шла речь в предыдущей главе, посвященной методам обучения. Здесь же необходимо остановиться на проблемном изложении изучаемого материала как важном методе активизации познавательной деятельности учащихся на уроке.

Сущность этого метода состоит в том, что в процессе работы по осмыслению нового материала учитель, используя примеры и факты, ставит перед учащимися познавательные проблемы или задачи, побуждает их к размышлениям, к поиску путей решения этих проблем и раскрытию сущности изучаемых предметов и явлений, т. е. заключенных в них причинно-следственных связей. Как видим, при проблемном изложении материала учащиеся вовлекаются в познавательный поиск, что, естественно, и стимулирует их умственную активность.

Во многих случаях, когда позволяет содержание новой темы, учителя применяют проблемный способ изложения материала, побуждая учащихся к самостоятельному нахождению в нем причинно-следственных связей.

При устном изложении знаний широко применяется также прием, когда с целью возбуждения внимания и познавательной активности учащихся учитель подчеркивает противоречивые положения, заключенные в содержании учебного материала, и привлекает учащихся к их объяснению

Так путем столкновения различных суждений учащихся была создана ситуация познавательного поиска и вызвана потребность в разрешении возникшей проблемы.

Проблемность в обучении и характер познавательного поиска могут приобретать и такой вид, когда учебный материал излагает учитель, но учащимся дается задание устно или письменно расчленить его на отдельные смысловые единицы, т. е. составить план изложения. Уже в младших классах полезно приучать ребят самостоятельно выделять самое существенное в изложении учителя и формулировать важнейшие вопросы темы. В средних же и старших классах этот прием служит действенным стимулом активизации познавательной деятельности учащихся и средством развития их умственной самостоятельности.

По мере развития учащихся может применяться и такой способ изложения, когда учащимся предлагается самим найти в излагаемом учителем материале познавательную проблему, четко сформулировать и аргументировать ее решение. “Умение видеть проблемы там, где они есть,-отмечает Т. В. Кудрявцев,-свидетельство высокой степени умственного развития”.[10]

Наконец, существенной стороной учебной работы по овладению новым материалом на уроке является использование специальных методических приемов, способствующих его усвоению (запоминанию). Особенно это важно, если изучаемый материал характеризуется определенной трудностью. В этих случаях учитель может предложить учащимся ответить на вопросы учебника, устно составить тезисы по содержанию нового материала, воспроизвести про себя правила, формулы и другие теоретические положения. Весьма важно обратить внимание учащихся не только на усвоение фактов, примеров, событий и вытекающих из них теоретических выводов, но и на глубокое осмысление тех мировоззренческих и нравственно-эстетических идей, которые заключены в изучаемом материале.

Умелая организация первичного и последующего осмысления нового материала учащимися и его усвоения (запоминания) создают предпосылки для овладения знаниями непосредственно на уроке. Если учитель этого не добивается, причины нужно искать в нарушении закономерностей обучения.

Работа по выработке умений и навыков применения знаний на практике. Это весьма важный этап урока. Он связан с использованием метода устных, письменных и практических упражнений. Как отмечалось в предыдущей главе, при организации упражнений учителю следует соблюдать два положения;

во-первых, нельзя переходить на уроке к упражнениям, если учащиеся не усвоили теоретический материал, который им нужно применять на практике; во-вторых, поскольку применение знаний на практике вызывает у учащихся затруднения, следует особое внимание обращать на осмысление ими способов выполнения практических упражнений. К сожалению, на весьма многих уроках учителя организуют упражнения, предварительно не добившись усвоения теории, которую учащиеся должны применять на практике. Необходимо также владеть всем арсеналом использования упражнений в процессе обучения.

Широкое применение в учебной работе находят устные упражнения. С их помощью на уроках математики вырабатываются умения и навыки сложения, вычитания, умножения и деления целых чисел, усвоение признаков делимости чисел и т. д. Без упражнения учащиеся не усвоят валентности различных химических элементов, их атомного веса, а также буквенных обозначений химических элементов и веществ и т. д. Без специальных упражнений учащиеся не усваивают хронологические даты по истории и литературе и т. д. Устные упражнения широко применяются при выработке у учащихся орфографических и синтаксических навыков, а также при формировании умения делать морфологический и синтаксический разбор предложений. Ученик не научится грамотно писать, пока он не натренируется и не будет хорошо мысленно представлять написание того или иного слова. Поэтому устные орфографические упражнения весьма полезны для повышения грамотности учащихся.

Большое значение в овладении знаниями и выработке у учащихся умений и навыков имеют письменные упражнения. При изучении материала по языкам эти упражнения приобретают форму выполнения разнообразных упражнений по написанию и изменению слов, составлению предложений по той или иной теме, письменного морфологического разбора слов и предложений, написание диктантов, изложений и сочинений и т. д. По математике, физике и химии учащиеся упражняются в решении задач и примеров, а также выполняют различные практические измерительные работы, лабораторные опыты и т. д. Однако эффективность письменных и практических упражнений при закреплении изучаемого материала зависит от соблюдения ряда дидактических условий. Укажем на важнейшие из них.

Заслуживает внимания организация упражнений на уроке в опыте передовых учителей. В. Ф. Шаталов, переходя к организации упражнений по применению усвоенных знаний на практике, стремится к тому, чтобы все учащиеся хорошо осмыслили способы решения задач и примеров по новому материалу. С этой целью первая задача или пример решаются коллективно, и только один из учащихся ведет запись на доске. Когда решение осмысленно, учитель предлагает эту же задачу или пример решить каждому учащемуся самостоятельно.

Вторая задача или пример коллективно анализируются, а решаются самостоятельно. Последующие задачи и анализируются, и решаются каждым учащимся самостоятельно.

Очень важно, чтобы тренировочные упражнения носили творческий характер, а даваемые учителем задания побуждали учащихся к размышлениям, к применению знаний в видоизмененных условиях. На эту сторону упражнений серьезное внимание обращал проф. М. А. Данилов. “Нередко, - писал он, - закрепление пройденного материала производится неправильно. Изучив правило и выполняя на это правило те упражнения, в которых характер действий подсказан (подчеркнуть слова, вставить букву, изменить форму слова и т. п.), ученик пишет грамотно. Но, начиная писать без этих подсказок, он допускает много ошибок. Подобные упражнения слишком облегчают умственную работу школьников, вследствие чего затормаживается их умственное развитие”'.Этот этап урока может завершаться небольшой проверочной работой, показывающей, как учащиеся усвоили новый материал.

Задавание урока на дом. Как бы ни хорошо была поставлена работа по изучению нового учебного материала на уроке, все же она является формой концентрированного усвоения знаний. Для прочного же и глубокого овладения изучаемым материалом существенное значение имеет рассредоточенная во времени работа по его осмыслению и запоминанию. Вот почему на каждом уроке, как правило, учителя дают учащимся домашние задания. Обычно эти задания включают в себя:

изучение текста учебника, в котором излагается новый материал, а также различного рода письменные и практические упражнения, связанные с решением задач и примеров, ответами на вопросы, написанием сочинений и т. д. По некоторым предметам, например по биологии и географии, задания могут предусматривать наблюдение учащихся за различными явлениями природы, подготовку гербариев, схем, диаграмм и т. д. Какие же дидактические требования предъявляются к задаванию урока на дом?

Одно из этих требований состоит в том, чтобы учитель в процессе работы по изучению нового материала обращал внимание на подготовку учащихся к выполнению домашнего задания. В частности, необходимо добиваться, чтобы учащиеся хорошо осмыслили основные вопросы изучаемого материала и усвоили основные приемы применения его на практике, научились решать примеры и задачи и т. д. Обстоятельное усвоение новой темы на уроке создает предпосылки для осмысленного и самостоятельного выполнения учебного задания дома[60].

Второе требование заключается в том., чтобы домашнее задание не сводилось лишь к репродуктивной (воспроизводящей) деятельности учащихся, а включало в себя элементы творческой работы. Например, при изучении урока по учебнику можно предложить учащимся дополнить изучаемый материал своими примерами, провести наблюдение или собрать фактический материал по отдельным вопросам. Задаваемые на дом письменные задания по языку, а также задачи и примеры по математике, физике и химии должны быть видоизмененными вариантами тех, которые выполнялись или решались на уроке.

В этой связи возникает вопрос о дифференциации домашних заданий. Некоторые учителя, наряду с общим заданием для всего класса, отдельно дают более усложненные задания для учащихся, проявляющих повышенные способности в овладении знаниями по их предмету. Другие поступают иначе. Они дают трехступенчатое домашнее задание, причем за выполнение первого задания учащийся может получить только “3”, за выполнение двух заданий - “4”, а за выполнение трех заданий-“5”. Такое задание существенно увеличивает объем тренировочных упражнений и позволяет учитывать индивидуальные особенности учащихся.

Не менее существенным является и третье дидактическое требование. Задавая, урок на дом, необходимо не только указать соответствующие параграфы учебника, номера упражнений и задач, но и обратить внимание на порядок и приемы домашней работы учащихся, а также на те особенности, которыми отличаются задаваемые на дом упражнения и задачи от выполняемых и решаемых в классе. Нужно также проследить, чтобы содержание домашнего задания учащиеся записали в свои дневники.

Интерес представляет тот прием, с помощью которого В. Ф. Шаталов стимулирует учащихся к значительному увеличению объема упражнений по решению задач по математике. Он предлагает каждому ученику сделать специальную плашку, расчертить ее на клеточки и затем в эти клеточки записывать номера решенных задач. Этот прием рождает дух состязательности, стимулирует домашнюю работу учащихся и в конечном итоге способствует резкому повышению качества успеваемости.

Творческий подход к про ведению смешанных уроков. Творчество учителя при проведении уроков этого типа прежде всего касается правильной регламентации времени на его отдельные этапы. Следует исходить из того, что работа по пройденному материалу и проверка знаний учащихся не должна занимать более 15-18 мин, остальное время отводится на усвоение нового материала и выработку практических умений и навыков. К сожалению, встречаются факты, когда проверка знаний учащихся занимает 20-25 и даже 30 мин на работу же над новой темой остается 15-20 мин. Разве за это время можно усвоить новый материал, а тем более потренироваться в его применении на практике? Так и уходят учащиеся из школы без знаний, теряя интерес к учению. “Вся тяжесть школьного занятия при таком преподавании, весьма легком для учителя и потому весьма употребительном, - писал К. Д. Ушинский, - попадает на ученика. Просидев без всякой пользы шесть битых часов в классе, пропустив, по всей вероятности, половину объяснений, он должен сам приготовить урок в часы, свободные от классов. Сколько напрасно потерянного времени, сколько тяжелых усилий, и для какого ничтожного результата! Вся небольшая польза, которую приобретает ученик при таком преподавании, далеко не вознаграждает одной привычки к бездействию по целым часам и самому рабскому притворству-необходимому последствию такого препровождения времени в классах”'.

Очень важно разнообразить структуру смешанных уроков. Это разнообразие достигается с помощью использования различных методов обучения. Так, на одном уроке проверка знаний проводится методами индивидуального и уплотненного опроса, на другом - с помощью выполнения письменных заданий, аналогичных домашним, на третьем проводится небольшая творческая работа. То же самое относится к приданию работе по усвоению нового материала разнообразного характера. Как отмечено выше, не обязательно новый материал всегда излагать самому учителю. Многие новые темы учащиеся могут осмыслить и усвоить по учебнику.

Наконец, не всегда нужно начинать урок с организации повторительно - обучающей работы по пройденному материалу. Если ранее изученная тема по своему содержанию тесно связана с новым материалом, в таких случаях урок можно начать с работы по его усвоению, а проверку знаний совместить с закреплением нового материала.

Иногда ведутся дискуссии относительно того, нужно ли как-то вычленить отдельные этапы урока или же стремиться к их “слиянию”, к незаметному переходу от одного этапа к другому, так как обучение, мол, является целостным процессом. Как ответить на этот вопрос? Поскольку учащиеся должны четко осознавать задачи учебной работы на каждом этапе урока, то с психологической точки зрения эти этапы следует вычленять и подчеркивать переход от одного вида работы к другому.

Уроки сообщения новых знании. Уроки-лекции. Само их название говорит о том, что они посвящаются главным образом работе над новым материалом. Такие уроки проводятся преимущественно в средних и старших классах, когда изучается довольно объемистый материал. В средних классах они обычно проводятся методом рассказа-объяснения, сочетающегося с беседой и демонстрацией учебно-наглядных пособий. В старших классах по такому материалу проводятся уроки-лекции, включающие в себя элементы, беседы. По сравнению с комбинированными структура этих уроков выглядит проще. Для них характерны следующие этапы: а) организация учащихся к занятиям; б) краткий опрос учащихся (фронтальная беседа) по важнейшим вопросам пройденной темы с целью установления связи нового материала с ранее изученным; в) постановка темы и определение основных целей занятий, а также сообщение плана нового материала; г) изложение новой темы; д) краткий опрос учащихся по новому материалу с целью более глубокого уяснения его узловых вопросов; е) задавание урока на дом. Как видим, при проведении этих уроков основное время затрачивается на работу над новым материалом, работа же по его закреплению (запоминанию) ограничивается лишь постановкой двух-трех контрольных вопросов учащимся. В этой связи большое значение приобретают применение на этих уроках приемов активизации познавательной деятельности учащихся и, в частности, умение учителя придавать изложению нового материала проблемный характер, насыщение лекции яркими фактами и примерами, включение учащихся в беседу по анализу этих фактов и примеров, побуждение их приводить свои факты и примеры в подтверждение разъясняемых выводов, а также применение учебно-наглядных пособий и технических средств обучения. Таким образом, главным при проведении этих уроков является содержательное и глубокое разъяснение нового материала учителем и его умение поддерживать внимание и мыслительную активность школьников.[12]

Уроки закрепления изучаемого материала. Проводятся они во всех классах после изучения отдельных тем или разделов учебной программы и направлены на организацию рассредоточенного повторения пройденного материала учащимися с целью его более глубокого осмысления и усвоения. Чтобы эти занятия давали необходимый эффект, их нужно хорошо готовить. Надо, чтобы учащиеся заранее знали о времени их проведения и их основных задачах. Кроме того, учителю следует выделить основные вопросы, по которым учащиеся должны готовиться к закреплению пройденного материала. Не менее важной является и методика проведения этих уроков. Главное состоит в том, чтобы в ней правильно сочетались фронтальный и индивидуальный опрос учащихся, с письменными, устными и практическими упражнениями, а также с организацией самостоятельной учебной работы. Подобная методика работы находит свое отражение в структуре этих уроков. Как правило, начинаются они с индивидуального опроса или фронтальной беседы по пройденному материалу, затем опрос сочетается с проведением тренировочных упражнений с акцентом на закрепление более сложных вопросов темы. В конце занятий проводится небольшая самостоятельная работа. На уроках математики, физики, химии она связана с решением задач и примеров, а на занятиях по языкам учащиеся могут писать различные виды диктантов, краткие изложения, сочинения, которые затем проверяются и оцениваются учителем.

Уроки повторения, систематизации и обобщения изученного материала. Проводятся они в конце учебного года, когда пройден весь программный материал. Их специфической особенностью является то, что учитель для повторения, систематизации и обобщения знаний учащихся выделяет узловые вопросы программы, усвое-ние которых имеет решающее значение для овладения предметом. Важно, однако, не только определить вопросы для повторения пройденного материала, но и указать учащимся те параграфы и места в учебнике, которые им следует использовать при подготовке к занятиям. В качестве методов на этих уроках могут использоваться обзорные лекции учителя, беседы и устный опрос, организация упражнений по углублению практических умений и навыков.

Уроки-семинары. Уроки-конференции. В последние годы в школах широко стали применяться уроки-семинары и уроки-конференции. Их цель - активизировать самостоятельную учебную работу учащихся, стимулировать к более глубокому усвоению изучаемого материала. Учитель заранее дает вопросы для обсуждения на семинаре и указывает литературу для самостоятельной работы. Таким образом, учащиеся не только штудируют учебник, но и значительно расширяют свои знания, изучая дополнительную литературу и одновременно приобретая умение самостоятельно добывать знания. В этом состоит ценность семинарских занятий.

Уроки-конференции проводятся после изучения того или иного раздела учебной программы, для углубления знаний по которому необходимо обсудить его узловые вопросы. Готовясь к конференции, учащиеся изучают рекомендованную учителем литературу, ища ответы на поставленные вопросы и вырабатывая по ним собственную точку зрения. Вот это различие суждений учащихся по изучаемой теме служит основой дискуссии и побуждает их к активному участию в конференции.

Иногда подобные уроки могут приобретать форму школьных диспутов. 7. Развитие и воспитание учащихся на уроках Здесь же необходимо подчеркнуть следующие положения. Нередко учителя основное внимание обращают на усвоение учащимися научных фактов и вытекающих из них теоретических выводов и не всегда учат учащихся приемам произвольного внимания, а также способам мыслительной деятельности, приемам рационального запоминания, не заботятся о побуждении их к самостоятельности и творчеству в процессе овладения изучаемым материалом. Все это отрицательно сказывается на развивающей стороне обучения.

Этот же недостаток зачастую присущ и воспитательной работе на уроке. Так, отдельные учителя не всегда акцентируют внимание на раскрытии и глубоком усвоении учащимися мировоззренческих и нравственно-эстетических идей, заключенных в изучаемом материале, па использовании дискуссионных форм работы с целью выработки мировоззренческих и нравственных взглядов и убеждений, не глубоко связывают в этих целях обучение с .практикой, с жизнью.

Важной развивающей и воспитательной задачей урочных занятий является формирование интереса к учению, усидчивости и настойчивости в овладении знаниями. Однако решается она пока слабо. Учителя не используют всего арсенала методов и приемов активизации учебно-познавательной деятельности учащихся, которые стимулируют их к настойчивой учебной работе. Именно по этой причине в ряде случаев наблюдается такая парадоксальная картина: по мере перехода учащихся из младших в средние и старшие классы их интерес к учению не возрастает, как это должно было бы быть, а, наоборот, снижается, что влечет за собой и ухудшение успеваемости.

Индивидуальная работа с учащимися на уроках.

Коллективный характер урочных занятий, порождая состязательность учащихся, стимулирует их познавательную активность, содействует развитию их творческих способностей, формированию дисциплинированности, прилежания, товарищества и других нравственных качеств.

Однако, хотя урочные занятия проводятся коллективно, учебно-познавательная деятельность и усвоение знаний учащимися несут на себе отпечаток индивидуальных особенностей их мышления, памяти, сообразительности, способностей, а также мотивов и установок учения. Встает вопрос об учете этих особенностей и организации индивидуальной работы с учащимися в процессе урочных занятий.

Задача индивидуального подхода к учащимся решается более успешно, если на уроках широко практикуется самостоятельная учебная работа. Самостоятельное выполнение заданий учителя позволяет последнему видеть те трудности, с которыми сталкиваются отдельные учащиеся, и сразу же оказывать им необходимую помощь в учебной работе. Что же касается более сильных школьников, то им обычно даются несколько усложненные или дополнительные задания, отвечающие более высокому уровню их подготовки и стимулирующие развитие их способностей. Такой же характер имеет индивидуальная работа с учащимися, когда организуются занятия с учебником, а также лабораторные занятия по осмыслению нового материала и его закреплению.[13]

Индивидуальная работа с учащимися на уроке осуществляется в процессе проверки и оценки знаний. Она выражается прежде всего в том, что слабоуспевающие школьники подвергаются более частой проверке усвоения изучаемого материала. Это делается с целью побуждения их к регулярным занятиям и повышения упорства в учебной работе. Некоторая дифференциация требуется также в самом характере проверки знаний и степени ее трудности. Более сильным ученикам, как правило, ставятся более сложные вопросы, проверка их знаний чаще всего проводится по более трудному материалу. Для менее успевающих школьников ставятся вопросы попроще, а учитель чаще прибегает к наводящим и уточняющим вопросам. Все это - конечно, учитывается при выставлении оценок.

Третьим элементом индивидуальной работы на уроке является сам подход к более слабым и сильным учащимся. Общее требование о необходимости чуткого и заботливого отношения учителя к улучшению успеваемости школьников по-разному осуществляется применительно к различным категориям учащихся. Если слабый ученик проявляет некоторую леность в учении и недостаточно усидчив, учитель обязан тактично усилить контроль за его работой и соответствующим образом ориентировать его родителей. Ученик с недостаточным развитием и пробелами в знаниях нуждается не столько в контроле, сколько в оказании действенной индивидуальной помощи в учебе со стороны учителя. Школьникам, которые учатся успешно, нужно давать больше пищи для размышлений, рекомендовать для самостоятельного изучения дополнительную литературу с тем, чтобы и их учение проходило на высоком уровне трудности и развивались их способности.

Очень важным, хотя и весьма сложным, является вопрос об индивидуализации воспитательной работы с учащимися в процессе урочных занятии. Скажем, в работе со школьниками из религиозных семей необходимо больше акцентировать внимание на атеистическом материале и добиваться, чтобы они обстоятельно усваивали его. Учащихся, проявляющих индивидуалистические наклонности, нужно вовлекать в коллективные формы работы, давать им задания по оказанию помощи в учебе своим товарищам и т. д. Не меньшее значение имеет индивидуальная воспитательная работа по формированию здоровых мотивов учения у тех, кто с прохладцей относится к учебной работе или же игнорирует производственные профессии и т. д. Следует хорошо уяснить себе, что только умелое сочетание фронтальной (коллективной) и индивидуальной работы с учащимися на уроке обеспечивает высокую педагогическую действенность учебно-воспитательного процесса.

Заканчивая изложение темы об уроке, следует отметить, что в данной главе освещались дидактические, т.е. наиболее общие, вопросы проведения урочных занятий. Методика же уроков -применительно к изучению отдельных учебных предметов более детально рассматривается в курсах частных методик.

В некоторых учебных пособиях формулируются особые требования к проведению урочных занятий. В нашем же изложении, как нам кажется, нет необходимости особо выделять эти вопросы. Часть этих требований раскрыта в теме о содержании школьного образования, другая же часть четко вычленена при изложении закономерностей и принципов обучения. В данном же случае показана реализация этих требований в процессе проведения урочных занятий.

. Урок -экскурсия, которая проводится по программе природоведения в начальных классах ¾ это еще один из типов нетрадиционного урока. Особенностью урока-экскурсии является то, что процесс обучения реализуется не в условиях классного помещения, а на природе, во время непосредственного восприятия учениками ее предметов и явлений.

Уроки-экскурсии имеют огромное воспитательное влияние на детей. Восприятие красоты природы, с которой они постоянно соприкасаются, ощущение ее гармонии, влияют на развитие эстетических чувств, позитивных эмоций, доброты, отзывчивого отношения ко всему живому. Во время выполнения совместных заданий школьники учатся сотрудничать между собой.

Классифицируют уроки-экскурсии по двум признакам: по объему содержания учебного предмета (однотемный, многотемный) и по его месту в структуре изучения раздела (вступительный, текущий, итоговый). Анализ содержания уроков-экскурсий по природоведению свидетельствует о том, что в курсе этого предмета проводятся такие его виды(Рисунок 2)

Рисунок 2 - Классифицируют уроки-экскурсии

Изображенные на схеме виды уроков-экскурсий позволяют узнать макроструктуру каждого из них. Разработка методик проведения данных уроков выполняется на основе общих дидактических закономерностей, которыми руководствуется учитель во время подготовки какого-либо типа урока, однако с учетом особенностей каждого из приведенных видов.

Эффективность урока-экскурсии, прежде всего, зависит от его подготовки учителем. Эта работа выполняется в такой последовательности:

1. Указание темы урока-экскурсии по программе природоведения.

2. Указание его вида.

3. Составление логической схемы содержания урока-экскурсии по учебнику природоведения.

4. Конкретизация содержания соответственно с теми объектами, которые находятся на месте экскурсии (учитель загодя хорошо изучает маршрут и место проведения урока-экскурсии).

5. Указание учебной, развивающей и воспитательной целей данного урока.

6. Разработка методики проведения урока-экскурсии.

7. Подготовка школьников к уроку.

8. Подбор необходимого оборудования[14].

Текущий урок-экскурсия по природоведению является однотемным. По дидактической сути ¾ это комбинированный урок, то есть в его границах реализуются все этапы целевого процесса обучения с овладением младшими школьниками предметным содержанием темы, которая вмещает несколько взаимноупорядоченных элементов знаний. Соответственно макроструктура текущего урока-экскурсии слагается из таких этапов:

1. Организация класса

2. Проверка усвоенных знаний, умений и навыков.

3. Постановка цели и заданий урока. Общая мотивация.

4. Усвоение новых знаний, умений и навыков.

5. Обобщение и систематизация усвоенных знаний, умений и навыков.

6. Соотношение усвоенных знаний, умений и навыков.

7. Домашнее задание.

8. Итоги урока.

Целью текущего урока-экскурсии является формирование у учеников понятий и представлений об объектах и явлениях природы, их взаимосвязях и зависимостях, которые предопределены содержанием темы, а также освоение школьниками тех предметных, учебных и организационных умений, которые объективно возможно и необходимо сформулировать в данной теме.

Специфика текущего однотемного урока-экскурсии обусловлена тем, что усвоение каждого элемента знаний начинается с

непосредственного восприятия реальных объектов природы в условиях их существования. Предметы и явления конкретизируют микроструктуру урока.

В последние годы интерес к нетрадиционному (нестандартному) обучению в начальной школе значимо усилился. Это связано с социальными преобразованиями, происходящими в нашей стране, которые создали определенные условия для перестроечных процессов в сфере образования ¾ создания новых типов школ, активного внедрения в практику различных педагогических инноваций, авторских программ и учебников.

Организация нетрадиционного развивающего обучения предполагает создание условий для овладения школьниками приемами умственной деятельности. Овладение ими не только обеспечивает новый уровень усвоения, но и дает существенные сдвиги в умственном развитии. Овладев этими приемами, ученики становятся более самостоятельными в решении различных учебных заданий, могут рационально строить свою деятельность по усвоению новых знаний.

Внешняя структура - этапы урока, на которых решаются те или иные дидактические задачи. С точки зрения внутренней структуры каждый урок - это определённая система заданий, в процессе выполнения которых ученик овладевает ЗУНами [15].

Изучение теории развития логического мышления на уроках математики в 4 классе определились виды и формы дидактического материала на основе закономерности математических процессов, сходства и различия в математическом процессе, при постепенном усложнении заданий, задания на выявление закономерностей, зависимостей и формулировку обобщения с постепенным повышением уровня трудности заданий.

Дидактический материал на развитие логического мышления младших школьников на основе заданий алгебраического, арифметического, геометрического содержания

. Чем отличаются и чем похожи данные выражения?

+5 3+2 6-3 8-3

+6 4+2 7-3 9-4

. Найди результат, пользуясь данным равенством:

+5=8

8 -

+6=

+7=

+8=

. Сравни числа, записанные в первом и втором столбиках. Сумма чисел в первом столбике равна 18. Как быстро можно найти сумму чисел, записанных во втором столбике?

. Продолжи ряд чисел.

. 5, 7, 9, 11…

, 4, 7, 10…

Для выполнения таких заданий ученик должен не только владеть запасом определенных терминов и понятий, но и уметь устанавливать между ними взаимосвязь, проявлять наблюдательность, анализировать полученные данные. Все это способствует не только осознанному усвоению материала учащимися, но и их умственному развитию[37].

Задания для самостоятельного выявления закономерностей, зависимостей и формулировки обобщения. Для этой цели использую такие задания:

Сравни примеры, найди общее и сформулируй новое правило:

) 0+1

+ 3

+ 5

Вывод: сумма двух последовательных чисел есть число нечетное.

) I - 0

- I

-2

-3

Вывод: если из последующего числа вычесть предыдущее, то получится 1.

) 5+4-4

+ 7-7

+13- 13

Вывод: если к любому числу прибавить и затем из него вычесть одно и то же число, то получится первоначальное.

) 26: 2 х 2

: 8 х 8

: 5 х 5

9 -

Вывод: если любое число разделить и умножить на одно и то же число, то получится первоначальное число.

В процессе обучения рассуждениям учитель побуждает учащихся к поискам новых заданий - примеров, подтверждающих правильность сделанного вывода, учит сопоставлять вывод с теми фактами, на основе которых он сделан, искать и такие факты, которые могут опровергнуть вывод.

Примеры:

. Сравни выражения, найди общее в полученных неравенствах, сформулируй

вывод:

+3*2x3

+4*3x4

+5*4x5

+6*5x6

Вывод: сумма двух последовательных чисел всегда меньше произведения этих же чисел - утверждение неверное, так как

+ 1 > 0 х 1, 1 + 2 > 1 • 2.

. Слагаемое 1 2 3 4 5 6

Слагаемое 5 5 5 5 5 5

Сумма

Вывод: сумма всегда больше каждого из слагаемых опровергается подбором фактов:

+0=1

+ 0 = 2 и т.д., где суммы равны другому слагаемому.

Дидактический материал с необычными приемами устных вычислений.

. Прием, основанный на использовании свойств арифметических действий:

) 389+467+211=389+211+467=600+467=1067;

) 375+287+125+213=(375+125)+(287+213)=500+500=1000;

) 827-430-227=827-227-430=600-430=170;

) 2357+1996+3047=2357+1996+3000+43+4=(2357+43)+(1996+4)+3000

=3000+2000+3000=8000;

) 25х37х4=37х(25х4)=37х100=3700;

) 87х4+4х13=(87+13)х4=100х4=400;

)367:5-167:5=(367-167):5=200:5=40.

При нахождении значений выражений учащиеся используют следующие свойства: переместительное свойство сложения; переместительное свойство умножения; сочетательное свойство сложения; сочетательное свойство умножения; вычитание числа из суммы; умножение суммы на число; умножение разности на число.

. Прием округления:

) 399+473=400+473-1=872

) 198х3=(200-2)х3=600-6=594

) 594: 4=(600-6):4=150-1=149

. Прием умножения и деления на 5, 50, 500, 25, 250, 15, 125.

) 36х5=(36:2)х10=180

10 -

) 84х25= (84:4)х100=41300

. Приемы умножения на 9, 99, 11, 101,1001.

Используя разнообразные вычислительные приемы, помогающие значительно облегчить процесс вычисления, важно показать учащимся красоту и изящество устных вычислений. Некоторые из таких приемов не предусмотрены программой начальной школы, а между тем детей довольно легко подвести к ознакомлению с ними[38].

В работе с младшими школьниками уместно применять игровые формы в дидактическом материале. На первый план при этом выдвигается умственная задача, для решения которой следует прибегнуть к сравнению, анализу и синтезу. В этих играх дети должны делать умозаключения и высказывать суждения. Это будет содействовать не только формированию логического мышления младших школьников, но и правильной, четкой, краткой речи. Логические игры являются именно такими, в которых путем цепочки несложных умозаключений можно предвидеть, предугадать необходимый результат, ответ. В этом их притягательная сила. В играх ребенок проявляет инициативность и развивает находчивость, приучается к труду, к точности, аккуратности и настойчивости в преодолении препятствий[39]. В играх развивается и укрепляется чувство товарищеской солидарности, честность, правдивость и другие качества, необходимые для коллективной работы и воспитания сознательной дисциплины. Создание игровой атмосферы на уроке развивает познавательный интерес и активность учащихся, снимает усталость, позволяет удерживать внимание. В игре дети непроизвольно закрепляют, совершенствуют навыки вычисления Младшие школьники очень любят соревноваться. Даже самые скучные вещи, «завернутые» в соревновательную оболочку, вызывают у них интерес. Для автоматизации навыка устного счета уроках используется игра «Математический биатлон». В настоящем биатлоне нужно быстро бежать и точно стрелять - за промахи либо добавляются дополнительные круги, либо штрафные минуты. В математическом биатлоне нужно быстро вычислять, но не ошибаться: за «промах» тоже начисляются штрафные очки. В начале соревнования каждый ребенок получает листок с вариантом для решения. Ответы на каждый пример он записывает в крайнем справа столбце на листке. Закончив примеры, ученик бежит к столу учителя и получает новый вариант. Учитель отрезает ножницами полоску с ответами ученика и отдает этот «похудевший» вариант другому ученику. Полоску с ответами он оставляет у себя. В итоге к концу биатлона кто-то из детей решил два варианта, а кто-то пять. При этом за каждый пример, решенный правильно, ученику начисляется очко, а за каждый пример, решенный неправильно, очко, наоборот, снимается. Поэтому тот, кто решил больше вариантов, но допустил много ошибок, вполне может проиграть тому, кто не торопился, но и не ошибался.

Дидактический материал на развитие логического мышления при решении сюжетных задач

Как показывает опыт, в младшем школьном возрасте одним из эффективных способов развития мышления является решение школьниками нестандартных логических задач. Кроме того, решение нестандартных логических задач способно привить интерес ребенка к изучению «классической» математики. Развитие у детей логического мышления - одна из важных задач начального обучения. Умение мыслить логически, выполнять умозаключения без наглядной опоры, сопоставлять суждения по определенным правилам - необходимое условие успешного усвоения учебного материала. Основная работа по развитию логического мышления должна вестись при решении задач. Ведь в любой задаче заложены большие возможности для развития логического мышления[40].Нестандартные логические задачи - отличный инструмент для такого развития. Эффективность обучения младших школьников решению нестандартных задач зависит от нескольких условий. Во-первых, задачи следует вводить в процесс обучения в определенной системе с постепенным нарастанием сложности, так как непосильная задача мало повлияет на развитие учащихся. Во-вторых, необходимо предоставлять ученикам максимальную самостоятельность при поиске решения задач, дать им возможность пройти до конца по неверному пути, чтобы убедиться в ошибке, вернуться к началу и искать другой, верный путь решения. В-третьих, нужно помочь учащимся осознать некоторые способы, приемы и общие подходы к решению нестандартных арифметических задач. Наибольший эффект при этом может быть достигнут в результате применения различных приемов работы над задачей.

Дидактический материал для решение задач различными способами

Мало уделяется внимания решению задач разными способами в основном из-за нехватки времени. А ведь умение решать задачи разными способами свидетельствует о достаточно высоком математическом развитии. Например, детям предлагается решить задачу разными способами. При решение задачи определенным способом дети аргументируют выбор способа.

Задача. На первой грядке росло в 5 раз больше кустов клубники, чем на второй. Когда с первой грядки пересадили 22 куста на вторую грядку, то на грядках стало поровну. Сколько кустов клубники было на каждой грядке?

Решение.

Первый способ

) 5+1=6 (частей) - всего;

) 6:2=3 (части) - приходится на каждую грядку;

) 5-3=2 (части) - пересадили с первой грядки на вторую;

) 22:2=11 (к.) - столько кустов приходится на одну часть (было на второй грядке);

) 11х5=55 (к.) - столько кустов было на первой грядке.

Второй способ

) 22+22=44 (к.) - на столько меньше кустов на второй грядке, чем на первой;

) 44:4=11(к.) - столько кустов приходится на одну часть;

) 11х5=55 (к.) - столько кустов было на первой грядке.

Третий способ

Построим графическую модель условия задачи.

На первой грядке 22 куста

) 22:2=11(к.) - приходится на 1/5 всех кустов

) 11х5=55 (к.) - столько кустов было на первой грядке.

Дидактический материал для решение задач с недостающими или лишними данными.

Задачи с недостающими данными способствуют формированию критичности мышления и умению проводить мини-исследования. А также способствуют развитию умения определять структуру задачи. Например, при решении первой задачи, дети определяют, что не все данные нужны для решения задачи, При решении второй задачи дети обнаруживают недостающие данные.

Задача 1. «На столе лежали 7 груш, 3 розы, 5 яблок и 4 гвоздики. Сколько цветов лежало на столе?»

Задача 2. «Чтобы украсить класс, ребята принесли 5 ваз с цветами и еще 3 гвоздики. Сколько всего цветов принесли ребята?».

Дидактический материал для самостоятельного составления задач учащимися

Составить задачу:

) используя слова больше на, столько, сколько, меньше в, на столько больше, на столько меньше.

Задача. «У Лены 5 тетрадей в клетку, а в линейку на 2 больше. Сколько тетрадей в линейку у Лены?» После решения данной задачи учащиеся получают задания: 1) изменить в условии задачи отношение на 2 больше на отношение в 2 раза больше.

) решаемую в 1, 2, 3 действия;

) по данному ее плану решения, действиям и ответу;

) по выражению и т.д.

Дано выражение: 2+8-7. Составьте задачу по данному решению.

Дидактический материал на выбор верного решения из двух предложенных.

Задача. «У Мальвины было 12 яблок, а у Буратино на 6 яблок больше. Сколько яблок было у Буратино?». Выбери правильное решение.

а. 1) 12+6=18 (ябл.)

) 12-6=6 (ябл.)

б. 1) 12+6=18 (ябл.)

) 12+18=30 (ябл.)

При выполнении заданий такого плана у детей формируются умения анализировать условие задачи, устанавливать взаимосвязь между условием и вопросом и соотносить различные виды моделей.

Дидактический материал на решение «обратных» задач.

Детям предлагается решить исходную задачу. После решения данной задачи дети составляют тексты обратных задач. Задача. «В мультфильме про динозавров 9 серий. Коля уже посмотрел 2. Сколько серий ему осталось посмотреть?» Составь две задачи, «обратные» данной.

Систематическое использование на уроках математики специальных задач и заданий, направленных на развитие логического мышления, организованных согласно приведенной выше схеме, расширяет математический кругозор младших школьников и позволяет им более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.

Приемы развития логического мышления младших школьников, представленные в учебниках математики М.И. Моро

Чему нужно научить ребенка при обучении математике? Размышлять, объяснять получаемые результаты, сравнивать, высказывать догадки, проверять, правильны ли они; наблюдать, обобщать и делать выводы. Линия на развитие логического мышления учащихся достаточно четко прослеживается в учебниках математики М.И. Моро[41].

Дидактические материалы, направленные на развитие анализа и синтеза:

. Соединение элементов в единое целое:

Вырежи из Приложения нужные фигуры и составь из них домик, кораблик, рыбку.

.Определение признаков математического объекта

Например: Предлагается математический ряд чисел 21,12,56,65, 71,17. Что общего и что различного в данном ряду чисел? Продолжи ряд чисел

. Узнавание математического объекта по заданным признакам:

) Какое число называем при счете перед числом 6? Какое число следует за числом 6? За числом 7?

) Составь по краткой записи задачу и реши ее.

Было - 18 кг

Продали - ?

Осталось - 8 кг

. Рассмотрение данного объекта с различных точек зрения:

Например, даны выражения: 70+15, 70+17, 70+21, 70+13.

Задания: Чем похожи и чем отличаются данные выражения?

Что можно сказать о значении выражений?

. Постановка различных заданий к данному математическому объекту:

• К концу учебного года у Лиды осталось 2 чистых листа в тетради по русскому языку и 5 чистых листов в тетради по математике.

Задания: а) Поставь к этому условию вопрос, чтобы задача решалась сложением. б)

Поставь к условию вопрос, чтобы задача решалась вычитанием.

• В коробке было 10 карандашей. Когда из коробки взяли несколько карандашей, в ней осталось 6 карандашей. Сколько карандашей взяли?

Задания: а) Рассмотри краткую запись и схематический чертеж к задаче.

б) Объясни, как этот схематический чертеж составлен. Реши задачу.

Было - 10 к. 6 к. ?

Взяли - ?

Осталось - 6 к. 10 к.

Задания, направленные на формирование умения классифицировать:

При формировании приема классификации дети сначала выполняют здания на классификацию знакомых предметов.

Например: 1) разложи листочки на две группы6 а) по цвету; б) по размеру; в)по форме.

) Далее можно предлагать задание в следующей форме: По какому признаку распределили предметы.

). Найди среди следующих записей уравнения, выпиши их и реши.

+ х > 40 45 - 5 =40 60 + х = 90

- х 38 - 8 < 50 х - 8 = 10

Задания, направленные на развитие умения сравнивать:

. Выделение признаков или свойств одного объекта:

У Тани было несколько значков. Она подарила 2 значка подруге, и у нее осталось 5 значков. Сколько значков было у Тани?

Задание: Какой схематический чертеж соответствует данному условию??

зн. 5 зн. 2 зн. ?

? 7 зн.

. Установление сходства и различия между математическими объектами:

Составь задачу по краткой записи и реши ее.

Купили - 20 шт. Купили - ?

Израсходовали - 9 шт. Израсходовали - 9 шт.

Осталось - ? Осталось - 11 шт.

Чем похожи и чем отличаются эти задачи?

Задания, направленные на развитие умения обобщать:

Задания данного вида направлены на умение выделять существенные свойства предметов.

) Как можно, одним словом назвать все эти фигуры?

) Замени умножение сложением. 17х1,22х3, 15х4, 28х1, 23х3. При выполнении данного задания дети приходят к обобщению: при умножении на 1 замена на сложение невозможна.

) Замени умножение сложением. 17х0,23х2, 12х4, 28х0, 23х4. При выполнении данного задания дети приходят к обобщению: при умножении на 0 замена на сложение невозможна.

) 26:2х2 16:8х8 10:5х5

При выполнении данного задания дети приходят к обобщению6 если любое число разделить и умножить на одно и то же число, то получится первоначальное число Все предложенные задания, безусловно, направлены на формирование нескольких операций мышления, но, ввиду преобладания какой-либо из них, упражнения были разбиты на предложенные группы. Но существуют и упражнения с ярко выраженной комплексной направленностью.

) Логические задачи.

Вася выше Саши на 8 см, а Коля ниже Саши на 3 см. На сколько сантиметров самый высокий из мальчиков выше самого маленького?

) «Магические квадраты».

Расставьте числа 2; 4; 5; 9; 11; 15 так, чтобы по всем линиям в сумме получилось 24.

) Сравни уравнения в каждом столбике и, не вычисляя, скажи, в каком из них неизвестное число больше. Проверь вычислением:

х + 37 = 78 90 - х = 47 х - 28 = 32 45 + х = 63

х + 37 = 80 90 - х = 50 х - 28 = 22 45 + х = 68

Проанализировав данные дидактические материалы, взятые из учебников М.И. Моро, пришли к следующим выводам. На многих страницах учебников, на полях и на иллюстрированных разворотах размещены разнообразные развивающие упражнения, задачи, задания, построенные на изучаемом в данный момент или уже изученном математическом материале и представленные в нестандартной, но интересной и доступной для детей форме. Задания направлены на более глубокое осознание взаимосвязей между изученными вычислительными приемами.

Развитие логического мышления - одна из важнейших задач начального обучения. Такое мышление проявляется в том, что при решении задач ребенок соотносит суждения о предметах, отвлекаясь от особенностей их наглядных образов, рассуждает, делает выводы. Умение мыслить логически, выполнять умозаключение без наглядной опоры, сопоставлять суждения по определенным правилам - необходимое условие успешного усвоения учебного материала. На уроках математики при устном счете можно предлагать логические упражнения, логические упражнения, логические игры, логические задачи[42].

Устный счет можно разнообразить увлекательным материалом: задачи - шутки, задачи сказочного характера, задачи в стихах, математические лабиринты, ребусы.

Например, детям предлагается математический лабиринт «Догони-ка!».

х1 3х3 0х3 3х1

3х2 4х3 4х2 10х3 60

х2 6х3 9х3 5х3

х2 7х3 3х4 4х0

По этому лабиринту мысленно бегают два участника. Они соревнуются в расчетах: находят сумму четырех произведений несколько раз, получая каждый раз число 60. Ученики класса находят свои ходы в этом лабиринте с ответом 60 и записывают решение примеров. Составлять примеры можно на время. В конце игры выбирается победитель.

Также большую роль в формировании вычислительных навыков табличного умножения и деления играет систематическая и методически правильно построенная работа с тренинговыми карточками.

Строение и содержание дидактических тренинговых карточек по математике

Тренинговые карточки по математике можно разделить на три уровня сложности изучения отдельно взятого вычислительного приёма.

Карточки первого уровня сложности (карточка № 1) рассчитаны на закрепление изученного вычислительного приема, который на них отрабатывается до автоматизма.

Карточки повышенного уровня сложности (карточка № 2) построены так, что по ним не только отрабатывается вычислительный навык, но они предполагают и развитие логического мышления, так как содержат такие задания: сравни, вставь в окошки пропущенные числа.

Карточки высокого уровня сложности (карточка № 3) предполагают не только самые сложные задания, но и более высокий уровень самостоятельности принятия решения, так как в них имеются задания, которых не было на уроках, и они носят творческий характер[43].

Тренинговые занятия могут проводиться по-разному, в зависимости от того, на каком этапе изучения находится тот или иной вычислительный приём. Всего можно выделить два этапа.

Первый. Карточки под № 1 используются на следующем уроке после изучения вычислительного приёма. Работа по ним проходит систематически в течение 6 уроков (можно чуть больше или меньше - в зависимости от получаемых результатов). Эти карточки представляют собой, как было указано выше, перфокарты, которые по каждой теме написаны в нескольких вариантах. Раздаются они каждому учащемуся в начале урока на определённое время. Для каждого вычислительного приёма учитель сам корректирует время выполнения[44].

Цель карточек-перфокарт - довести навык решения данных приёмов до автоматизма за минимально отведённое время.

Количество ошибок, допускаемых учащимися при решении, должно сократиться до минимума: 1-3 ошибки из решённых примеров. Когда эта цель достигнута, и учащиеся всего класса справляются с заданием за минимально отведённое время, первый этап завершается.

На втором этапе учащиеся должны показать, как они могут применять изученный вычислительный приём на практике.

Урок, на котором используются тренинговые карточки № 2 и № 3, строятся следующим образом.

На каждую парту раздаются тренинговые карточки № 2, № 3. Дети знают, что должны выбрать только один лист по своим силам. Далее анализируются задания по карточкам. Особо отмечается, что учащиеся, выбравшие карточку № 2, всё делают сами, без посторонней помощи.

Дети, выбравшие карточку №3, могут один раз взять совет у товарища или у учителя. Учащиеся также знают, что выбор той или иной карточки не скажется ни на оценке, ни на отношении к нему. В журнале будут выставлены только положительные оценки.

Проводя устный счёт, особенно во втором классе, при знакомстве с понятием умножение и деление, а также при закреплении вычислительных навыков, необходимо активизировать мыслительную деятельность младших школьников, включая занимательный материал, игровые ситуации, презентации и компьютерные игры. Например, рекомендуем использовать на уроке дидактическую программу-тренажёр для школьников «Примерчик».

"Примерчик" - программа, которая будет задавать ребенку примеры на умножение и деление, помогать в запоминании таблицы умножения и соответствующих случаев деления, обучит его выполнять умножение "столбиком".

Отличительной особенностью программы "Примерчик" от других аналогичных программ является наличие принудительного режима <#"790471.files/image003.gif">

Диаграмма 1. Сравнительная характеристика логического мышления в экспериментальном и контрольном классах

Таблица 2. Сравнительная характеристика результатов логического мышления по методики «числовые ряды» в экспериментальном и контрольном классах

	Высокая	Средняя	Низкая
Экспериментальный (20 учащихся)	3	10	7
Контрольный(20учащийся)	3	11	6

Диаграмма 2. Сравнительная характеристика логического мышления в экспериментальном и контрольном классах

.Наблюдения за решением математических задач.

Учащиеся выполняли задание с интересом, большинство учащихся в обоих классах выполняли задание самостоятельно, не обращались за помощью к учителю. Слабоуспевающие учащиеся не справились с выполнением задач самостоятельно. У учащихся наблюдались затруднения в выполнении кратких записей к задачам. Результаты выглядят следующим образом:

Таблица 3. Сравнительная характеристика результатов логического мышления на основе наблюдения за решением задач в экспериментальном и контрольном классах

ВысокаяСредняяНизкая
Экспериментальный (20 учащихся)	1	12	7
Контрольный(20учащийся)	2	12	6

Диаграмма 3. Сравнительная характеристика логического мышления в экспериментальном и контрольном классах

Из данных результатов можно сделать следующий вывод: в 4 классе определенно имеются перспективы для работы по развитию логического мышления как у детей со средним уровнем, так и у детей с высоким уровнем. Дальнейшая работа будет направлена на развитие и совершенствование операций логического мышления.

3.2 Психолого-педагогическое сопровождение в условиях эксперимента

Формирующий эксперимент

В формирующем эксперименте в систему уроков математики в экспериментальном классе предлагается дидактический материал, направленный на развитие логического мышления младших школьников. В разработке дидактического материала лежат разработки М. Монтессори и логические блоки Дьенеша. Дидактический материал выполнен на основе мультимедийного оборудования.

неделя экспериментальной работы: Изучение понятии и представлений по циклу умножение двухзначного числа на двухзначное. В ходе работы с учащимися закреплялся материал по теме, исследовались вопросы, связанные с алгоритмом выполнения умножения двухзначных чисел, применением правил умножения в решении задач, определении площадей фигур. В качестве контроля за уровнем развития логического мышления учащихся применялись следующие виды работы:

· Дидактический материал по теме «Умножение двузначного числа на двузначное» (время работы - 10 минут) материал содержит схемы, «магические квадраты», «незаконченные примеры», «уравнения с пропусками», геометрический материал;

· Самостоятельная работа по теме урока. (5 заданий, 25 минут отведенного времени);

· Работа по дидактическому материалу на закрепление предыдущих тем (10 заданий в электронном материале 15 минут отведенного времени).

Критерии оценивания:

· Способность производить логические действия (анализ, синтез, сравнение)(на основании выполненных заданий в дидактическом материале )

Высокий уровень - задание выполнено полностью, без ошибок.

Средний уровень - задание выполнено с незначительными ошибками в пределах отведенного времени;

Низкий уровень - задание не выполнено полностью, допущены ошибки, ученик затратил большее количество времени, чем отведено.

· Способность производить умозаключения (на основе наблюдения за деятельностью учащихся).

Высокий уровень- ученик полностью соотносит теоретический материал с практическим.

Средний уровень - ученик не во всех заданиях видит аспекты теоретического материала.

Низкий уровень - ученик не видит в практическом задании теорию предмета.

· Формирование понятий и суждений учащихся(на основании устных ответов учащихся);

Высокий уровень - ученик полностью обосновывает ответ, соотносит итоги работы с материалом урока;

Средний уровень - ученик обосновывает ответ не полностью, допускает неточности в итогах работы;

Низкий уровень - ученик не может обосновать ответ.

Результаты работы:

В результате проведения экспериментальной работы с учащимися 4 класса определились следующие показатели:

На данном этапе работы в экспериментальном классе при выполнении заданий на основании дидактического материала большинство учащихся допускали ошибки при выполнении «геометрических» загадок, в «магических квадратах», в занимательных уравнениях. Работа по дидактическому материалу на основе мультимедийных средств затрудняет ответы у учащихся. Ученики не могли сосредоточится и быстро выполнить задание. При устном обосновании выполненных заданий практически все учащиеся допустили неточности, у многих учеников нет логической связки между темой и практическим заданием на уроке. Многие учащиеся не обладают умениями сравнивать представленные в дидактическом материале объемы и пространственные модели.

Таблица 3. Показатели логического мышления

Экспериментальный класс	высокая	Средняя	низкая
Способность производить логические действия	1	10	9
Способность производить умозаключения	2	11	7
Формирование понятий и суждений учащихся	2	10	8

Диаграмма 3. Результаты 2 недели эксперимента

Третья неделя эксперимента

Изучение понятий и представлений по теме «Решение задач с двумя неизвестными». В ходе работы с учащимися закреплялся материал по теме, исследовались вопросы, связанные с особенностью решения задач с двумя неизвестными, определялся алгоритм в решении таких задач, проводились аналогии с предыдущими темами по математики. На данном этапе применялся дидактически материал в виде задач, основанных на рисунках и схемах. 1 задача была представлена в буквенных выражениях, такой вид задания развивает у учащихся умения производить аналогии и взаимосвязи. Применение электронных дидактических заданий на основе анимации предметов и действий позволяет проследить у учащихся развитие умений анализировать и выделять главное Виды работ :

· Решение задач на основе предоставленного дидактического материала (5 задач)

· Работа по электронным карточкам (5 заданий, 10 минут отведенного времени);

· Работа по дидактическому материалу на закрепление темы уроков (10 заданий в электронном материале 15 минут отведенного времени).

Критерии оценивания:

· Способность производить умозаключения (на основе наблюдения за деятельностью учащихся).

· Формирование понятий и суждений учащихся(на основании устных ответов учащихся);

Высокий уровень - ученик полностью обосновывает ответ, соотносит итоги работы с материалом урока;

Результаты работы:

В результате проведения экспериментальной работы с учащимися 4 «А»класса определились следующие показатели :

При решении задач с двумя неизвестными у 2 учащихся не наблюдалось трудностей как в оформлении задачи, составлении краткой записи, так и в выборе варианта решения задачи. У остальной части класса наблюдались трудности в формулировании вопроса к задаче и составлении краткой записи задачи. Алгоритм выполнения задач усвоили 3 учащихся 6 учеников не имеют представлений о решении задач по алгоритму. Выполнение заданий по дидактическому материалу основанному на буквенных выражениях были интересны учащимся, большинство учащихся выполнили задания в полном объеме, применение компьютера в выполнении заданий позволил заинтересовать слабоуспевающих школьников.

Таблица 4. Показатели 3 этапа эксперимента

Экспериментальный класс	высокая	Средняя	низкая
Способность производить логические действия	2	10	8
Способность производить умозаключения	2	12	6
Формирование понятий и суждений учащихся	2	10	8

неделя эксперимента. Изучение понятии и представлений по теме «Деление трехзначного числа на двухзначное». В ходе работы с учащимися закреплялся материал по теме, исследовались вопросы, связанные с алгоритмом выполнения процесса деления чисел, закреплялись умения и навыки деления на примере решения задач. Дидактический материал на данном этапе способствовал развитию логики и скорости выполнения заданий: «математический биатлон», «Быстрый счет» и т.д.Виды работ :

· Математический диктант (на основе дидактического материала, время 7 минут);

· Практическое закрепление темы урока (на основе тренинговых карточек. 5 заданий, 25 минут отведенного времени);

· Работа по дидактическому материалу (10 заданий в электронном материале 15 минут отведенного времени).

Критерии оценивания:

· Способность производить умозаключения (на основе наблюдения за деятельностью учащихся).

· Формирование понятий и суждений учащихся(на основании устных ответов учащихся);

Результаты работы:

При решении задач у учащихся всего класса наблюдались трудности в формулировании вопроса к задаче и составлении краткой записи задачи. Алгоритм выполнения задач усвоили 3 учащихся 6 учеников не имеют представлений о решении задач по алгоритму. При работе над математическим диктантом 4 учащихся показали высокий уровень развития способности производить умозаключения. Использование тренинговых карточек по теме урока вызвал практически у всех учащихся затруднение в ответах. Интерес представили задания с геометрическими заданиями и с рисуночными изображениями на логику мышления, но скорость выполнения данных заданий занижена, учащиеся долго не могли сформулировать правильный ответ. Выполнение заданий по дидактическому материалу интересны учащимся, большинство учащихся выполнили задания в полном объеме, применение компьютера в выполнении заданий позволил заинтересовать слабоуспевающих школьников.» учащихся выполнили дидактические задания на компьютере полностью и без ошибок

Таблица 5. Показатели 4 этапа

высокая

Средняя

низкая

Способность производить логические действия

Способность производить умозаключения

Формирование понятий и суждений учащихся

неделя эксперимента. Изучение понятии и представлений по теме «Решение задач на основе уравнений». В ходе работы с учащимися закреплялся материал по теме, исследовались вопросы, связанные с составлением уравнений к задачам. Проводилась работа по учебнику и по дидактическому материалу. В составлении задач применялись схемы и таблицы, помогающие развитию логики мышления. Виды работы:

· Работа по дидактическому материалу (тестирование учащихся 10 тестов - 10 минут)

· Самостоятельная работа (5 заданий, 25 минут отведенного времени);

· Работа по электронному дидактическому материалу (10 заданий в электронном материале 15 минут отведенного времени).

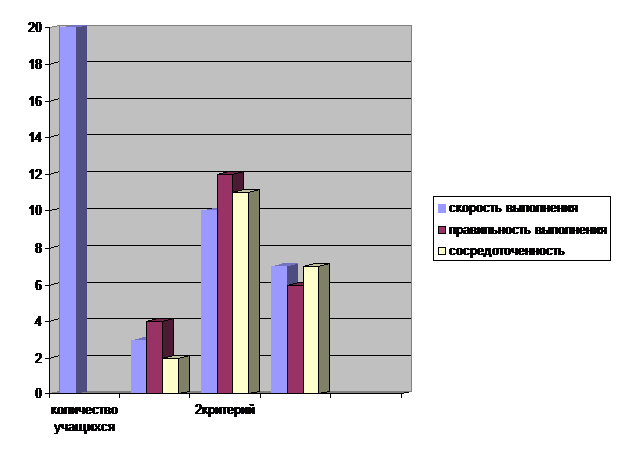
Диаграмма 5. Результаты 4недели эксперимента:

Критерии оценивания:

· Способность производить умозаключения (на основе наблюдения за деятельностью учащихся).

· Формирование понятий и суждений учащихся(на основании устных ответов учащихся);

Результаты работы:

При решении задач у учащихся всего класса наблюдались трудности в формулировании вопроса к задаче и составлении уравнения к задаче. Алгоритм выполнения задач усвоили 4 учащихся 5 учеников не имеют представлений о решении задач по алгоритму. При работе над тестами большую скорость выполнения показали учащиеся на закрытых формах тестов, открытые формы тестирования вызывали затруднение. Использование материала для тестирования из дополнительных источников вызвал практически у всех учащихся затруднение в ответах). Интерес представили тесты с заданиями и с рисуночными изображениями на логику мышления, но скорость выполнения данных тестов занижена, учащиеся долго не могли сформулировать правильный ответ. Выполнение заданий по дидактическому материалу интересны учащимся, большинство учащихся выполнили задания в полном объеме, применение компьютера в выполнении заданий позволил заинтересовать слабоуспевающих школьников.

Таблица 6. Показатели 5 этапа

Экспериментальный классвысокаяСредняя низкая
Способность производить логические действия	4	10	6
Способность производить умозаключения	4	12	4
Формирование понятий и суждений учащихся	3	11	6

неделя эксперимента. Изучение понятий и представлений по циклу «Решение «обратных» задач». В ходе работы с учащимися закреплялся материал по теме, исследовались вопросы, связанные с решением обратных задач. Проводились деловые игры с применением дидактического материала, демонстрация слайдов. В качестве контроля за развитием логического мышления»» учащихся применялись различные виды работы. Виды работы :

· Фронтальное тестирование (20 тестов - 2 варианта, 10 минут отведенного времени);

· Дидактический материал по решению «обратных задач» (5 заданий, 25 минут отведенного времени);

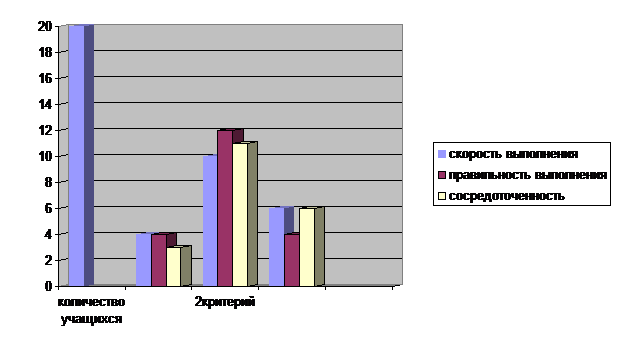
Диаграмма 6. Результаты 5 недели эксперимента

Критерии оценивания:

· Способность производить умозаключения (на основе наблюдения за деятельностью учащихся).

· Формирование понятий и суждений учащихся(на основании устных ответов учащихся);

Результаты работы:

При решении «обратных» задач у учащихся всего класса наблюдались трудности в формулировании вопроса к задаче и составлении уравнения к задаче. Алгоритм выполнения «обратной» задачи задач усвоили 5 учащихся. 4 учеников не имеют представлений о решении задач по алгоритму. При работе над тестами большую скорость выполнения показали учащиеся на закрытых формах тестов, открытые формы тестирования вызывали затруднение. Использование материала для тестирования из дополнительных источников вызвал практически у всех учащихся затруднение в ответах). Интерес представили тесты с заданиями и с рисуночными изображениями на логику мышления, но скорость выполнения данных тестов занижена, учащиеся долго не могли сформулировать правильный ответ. Выполнение заданий по дидактическому материалу интересны учащимся, большинство учащихся выполнили задания в полном объеме, применение компьютера в выполнении заданий позволил заинтересовать слабоуспевающих школьников. Дидактический материал для выполнения домашнего задания позволил определить проблемные узлы в выполнении уравнений и сложных задач у учащихся. Электронный дидактический материал способствовал развитию умения анализировать и сопоставлять растровую картинку и вид примера к ней у 5 учащихся. У 4 учащихся произошли изменения в при выполнении «магических » квадратов. Данные учащиеся не понимали алгоритм работы таких заданий, но после предоставления «магических квадратов в электронном виде поняли алгоритм работы этого дидактического материала

Таблица 7. Показатели логического мышления 6 недели эксперимента

Экспериментальный классвысокаяСредняя низкая
Способность производить логические действия	5	11	4
Способность производить умозаключения	4	12	4
Формирование понятий и суждений учащихся	5	12	3

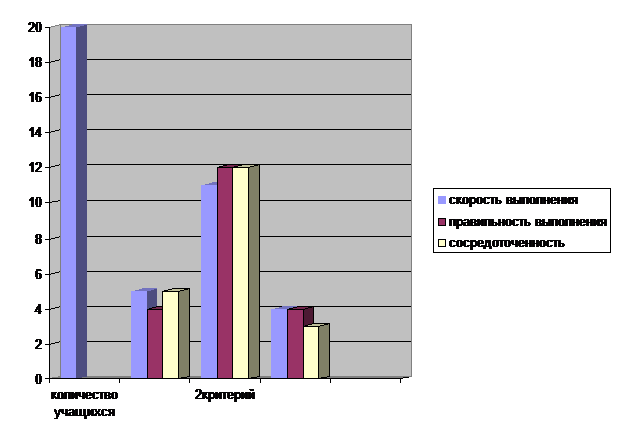
Диаграмма 7. Результаты 6недели эксперимента

неделя эксперимента. Изучение понятий и представлений по циклу умножение и деления многозначного числа на многозначное: «Задания, направленные на развитие умения сравнивать». В ходе работы с учащимися закреплялся материал по теме, исследовались вопросы, связанные с величинами, параметрами и объемами. Проводились беседа, работа по дидактическому материалу, демонстрация слайдов и изображений, представлены к изучению объемные модели. В качестве контроля за развитием логического мышления учащихся применялись различные виды работы. Виды тестирования:

· Фронтальное тестирование (20 тестов - 2 варианта, 10 минут отведенного времени);

· Контрольная работа (5 заданий, 35 минут отведенного времени);

· Работа по дидактическому материалу (10 заданий в электронном материале 15 минут отведенного времени).

Критерии оценивания:

· Способность производить умозаключения (на основе наблюдения за деятельностью учащихся).

· Формирование понятий и суждений учащихся(на основании устных ответов учащихся);

Результаты работы:

В результате проведения экспериментальной работы с учащимися на седьмой недели в 4 классе определились следующие показатели :

Таблица 7. Показатели развития логического мышления 7 этапа

Экспериментальный классвысокаяСредняя низкая
Способность производить логические действия	6	12	2
Способность производить умозаключения	4	12	4
Формирование понятий и суждений учащихся	5	12	3

Диаграмма 7 Результаты 7недели эксперимента

Итак, динамика развития логического мышления с помощью дидактического материала планомерно в экспериментальном класса повышается.

3.3 Результаты эмпирического исследования развития логического мышления младших школьников

Анализ результатов итогового этапа педагогического эксперимента

После проведения формирующего эксперимента снова проводился сравнительный анализ результатов в контрольном и экспериментальных классах. Проводились следующее мероприятия:

.Методика «Четвертый лишний»

При выполнении заданий учащиеся с интересом относились к рисуночным изображениям. Выполнение заданий проходило в быстром темпе в экспериментальном классе. Результаты выполнения заданий выглядят следующим образом:

Таблица 8. Сравнительная характеристика результатов логического мышления по методики «Четвертый лишний» в экспериментальном и контрольном классах

	Высокая	Средняя	Низкая
Экспериментальный (20 учащихся)	7	10	3
Контрольный(20учащийся)	3	11	6

. Тест Липпмана «Логическая закономерность»

При выполнении заданий учащиеся экспериментального класса выполнили задание быстрее чем в контрольном. Количество времени, затраченного на выполнение заданий не превышало временные рамки (10 минут). Слабоуспевающие ученики не справились с заданием в полном объеме.

Диаграмма 8. Сравнительная характеристика логического мышления в экспериментальном и контрольном классах

Таблица 2. Сравнительная характеристика результатов логического мышления на основании тестов Липпмана в экспериментальном и контрольном классах

	Высокая	Средняя	Низкая
Экспериментальный (20 учащихся)	7	10	3
Контрольный(20учащийся)	3	11	6

.Наблюдения за решением математических задач.

Учащиеся выполняли задание с интересом, большинство учащихся в экспериментальном классе выполняли задание самостоятельно, не обращались за помощью к учителю. Результаты выглядят следующим образом:

Диаграмма 2. Сравнительная характеристика логического мышления в экспериментальном и контрольном классах

	Высокая	Средняя	Низкая
Экспериментальный (20 учащихся)	6	12	2
Контрольный(20учащийся)	2	12	6

Из данных результатов можно сделать следующий вывод: применение дидактического материала при выполнении различных видов заданий на уроках математики способствует развитию логического мышления младших школьников.

Диаграмма 3. Сравнительная характеристика логического мышления в экспериментальном и контрольном классах

ЗАКЛЮЧЕНИЕ

Логика способствует становлению самосознания, интеллектуальному развитию личности, помогает формированию у нее научного мировоззрения. Успешное решение сложных задач обучения и воспитания молодежи в решающей степени зависит от учителя, от его интеллектуального уровня, профессионального мастерства, эрудиции и культуры. Профессия учителя требует постоянного творчества, неустанной работы мысли и совершенствования ее культуры, без чего не возможен учительский авторитет среди учащихся. Для улучшения подготовки учительских кадров рекомендуется расширить преподавание логики, изучение которой поможет поднять интеллектуальную культуру будущих учителей[46].

Актуальность проведенного исследования заключается в том, что в современное время дети учатся по развивающим технологиям, где логическое мышление является основой. С начала обучения мышление выдвигается в центр психического развития (Л.С. Выготский) и становится определяющим в системе других психических функций, которые под его влиянием интеллектуализируются и приобретают произвольный характер[47]. Многочисленные наблюдения педагогов, исследования психологов убедительно показали, что ребенок, не научившийся учиться, не овладевший приемами мыслительной деятельности в начальных классах школы, в средних классах обычно переходит в разряд неуспевающих

В повседневной жизни, в науке, в обучении каждому ежедневно приходится из одних истинных суждений выводить другие, опровергать ложные суждения или неправильно построенные доказательства. Сознательное следование законам логики дисциплинирует мышление, делает его более аргументированным, эффективным и продуктивным, помогает избежать ошибок. По мере формирования теоретического мышления учащиеся всё больше научается осознавать обобщенные закономерности явлений. Мышление начинает особенно переходить от единичного через особенное к всеобщему, от случайного к необходимому, от явлений к существенному в них, от одного определения сущности ко всё более глубокому познанию действительности, к пониманию взаимосвязи её различных моментов, сторон её сущности[48]. Точнее учащиеся не только и не столько всё глубже познаёт действительность, по мере того, как развивается его мышление, сколько его мышление всё более развивается, по мере того как углубляется его познавательное проникновение в действительность. Именно поэтому нам представилось особенно важным выявить основные закономерности развития и диагностики мышления в этом возрасте. Как известно, мышление тесно связано с обучением, поэтому развитие логического мышления, основанное на решении нестандартных задач, поможет ученикам развить логическое мышление. Последние, в свою очередь, не будут голословными утверждениями, а будут осознанными и осмысленными убеждениями каждого ученика.

Развитие логического мышления как педагогический процесс необходимо осуществлять в соответствии с законами развития детского организма, в единстве и согласии с интеллектуальным развитием ребенка[49]. Поскольку логическое мышление можно рассматривать как новое приоритетное направление педагогической теории и практики, то и его содержание сегодня - на стадии становления, пересмотра объекта изучения, определения методологических подходов. Определив основные задачи развития логического мышления младших школьников, нужно подумать, на каких общих основаниях, принципах должно строиться его содержание. Ибо они во многом определяют эффективность обучения, воспитания и развития школьников в интеллектуальном развитии[50].

Урок математики предоставляет уникальную возможность обеспечения взаимосвязи педагогического процесса с процессом освоения ребенком математических понятий, выступающей, одновременно, с основными понятиями математики. Таким образом, дидактический материал, оставаясь одним из важных направлений по развитию логического мышления, вносят свою лепту в развитие интеллекта ребенка. При достижении поставленной цели использовались следующие теоретические задачи, которые решались в первой главе:

1. Обобщить материал о развитии логического мышления младших школьников.

2. Рассмотреть виды дидактического материала, способствующие развитию логического мышления младших школьников.

. Определить особенности развития и диагностики логического мышления у детей в младшем школьном возрасте.

В основе интеллектуальной деятельности лежат конкретные мыслительные операции анализа и синтеза, классификации обобщения, аналогий, сравнения, подведение под понятие, установления причинно-следственных связей и т.п. Хотя мышление и не исчерпывается логикой, тем не менее оно оперирует логическими категориями, связями и отношениями. Для выполнения логических действий подростки должны уметь отличать существенные от несущественных свойств предметов и явлений, выявлять признаки необходимые и достаточные, выбирать основания для сравнения или классификации, владеть логико-функциональными отношениями разного типа. Перечисленные логические операции смыкаются с учебной деятельностью, в процессе которой необходимо использовать классификацию, аналогию, обобщение, нахождение числовых закономерностей и пространственные умения.

Результаты исследования показывают, младшие школьники успешнее выполняют задания, требующие пространственных умений, т.е. у них преобладает практически-действенное и образное мышление. Однако, установлено, что развитие логического мышления сопровождается умением соотношения его видов - от практически-действенного и образного к понятийному, теоретическому.

Проделанная работа по формированию развитие логического мышления у детей младшего школьного возраста, дала свои положительные результаты. Полученные данные дают возможность предположить, что у исследуемых детей произошел прирост в показателях развития логического мышления. Улучшение показателей обусловлено использованием дидактического материала на уроках математики. Стабильная, систематическая работа в данном направлении позволила повысить уровень развития логического мышления у детей младшего школьного возраста, у них был сформирован соответствующий уровень умений и навыков. В итоге можно сделать вывод, что система занятий проведенные на уроках математики, являясь оптимальной формой работы с младшими школьниками:

· повышают развитие логического мышления учащихся;

· вооружают их навыками решения нестандартных задач, уравнений, примеров;

· значительно расширяют и углубляют знания о математических процессах;

· формируют эмоциональную восприимчивость;

· формируют практические умения по решению жизненных задач.

Основной замысел данной дипломной работы состоял в том, чтобы изучить особенности развития логического мышления в младшем школьном возрасте, разработать проведённое теоретическое и экспериментальное исследование. Это доказало корректность выдвинутой гипотезы и определило возможность сделать следующие выводы:

. Изучены научно-теоретические основы развития логического мышления младшего школьника в теории педагогики, психологии и педагогической практике.

Одной из важнейших задач, стоящих перед учителем начальных классов, является развитие самостоятельной логики мышления, которое позволило бы детям строить умозаключения, приводить доказательства, высказывать суждения, логически связанные между собой, обосновывая свои суждения, делать выводы, и, в конечном счете, самостоятельно приобретать знания. Логическое мышление не является врождённым, поэтому его можно и нужно развивать. Решение логических задач в начальной школе как раз и представляет собой один из приёмов развития мышления. Во многом роль обучения математики в развитии мышления обусловлена современными разработками в области методики моделирования и проектирования, особенно в объективно ориентированном моделировании и проектировании, опирающемся на свойственно человеческое понятийное мышление.

. Положительное влияние на логическое мышление младших школьников оказали подобранный дидактический материал, в основу которых входит активное формирование основных мыслительных операций.

. Экспериментально проверили развитие логического мышления младших школьников при решении заданий на основе дидактического материала. Определили уровень развития логического мышления младших школьников, исходя из полученных данных, можно отметить следующие факты: на начале эксперимента степень сформированности логического мышления был на стартовом уровне, после появились связи между умением производить логические операции осознанно, аргументировано и умение определять структуру и организацию элементов и частей целого, ориентируясь на существенные признаки предметов.

Разумеется, работа не может претендовать на полноту и завершённость, поскольку затронутая проблема достаточно глубинна и объёмна и требует не одного года кропотливой работы не одного человека.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1 Закон об образовании РК от 2007 г.

2 Послание президента РК народу Казахстана 2013г.

Государственная программа развития образования в РК 2011-2020г.г.

4 Калмыкова З.И. Продуктивное мышление как основа обучаемости. - Автореферат на соискание степени к.п.н. Алматы., 1981

Пиаже Ж. Генетическая психология. М. Просвещение, 1983.

6 Болотина Л. Р. Развитие мышления учащихся // Начальная школа - 1994 - №11

Ковалевская С. Новый математический труд. М.: Просвещение, 1953г.

Ломоносов М.В. Избранные философские произведения - М.: Госполитиздат, 1950.

Шардаков В. С. Мышление школьников. М.: Просвещение, 1963.

10 Пиаже Жан. Речь и мышление ребёнка.М. Наука и просвещение, 1981г.

11 Гальперин П.Я. Введение в психологию - М., 2000

Брушлинский А.В. Психология мышления и проблемное обучение. - М., 1983.

13 Абилов К.С. Основы методики развития мышления школьников - Автореферат на соискание степени к.п.н. Алматы, 1987г

14 Маркова А.К., Матис Т.А., Орлов А.Б. Формирование мышления в учении школьников. - М.: Просвещение , 1991 - 300-307 с.

15 Энгельс Ф. Избранные труды,Л., 1983г.

Коломинский Я. Л. Человек: психология. М.:1986.

17 Немов Р.С. Психология. Книга 1. Общие основы психологии. М. 1998 г.

18 Толстой Л.Н. Избранное. М.: Мир, 1992г.

Сергеева В.П. Психолого-педагогические теории и технологии начального образования. Москва, 2002.

Выготский Л.С. Вопросы детской психологии. - С.-Пб.: Союз, 1999.

Выготский Л.С. Мышление и речь: собрание сочинений. В 6 т. Т.2. - М., 1982.

Марцинковская Т. Д. Диагностика психического развития детей. М.: Линка-пресс, 1998.

Пиаже Жан. Речь и мышление ребёнка.

Рубинштейн С. Л. Основы общей психологии. СПб., 1998.

Рубинштейн С.Л. Основы общей психологии. В 2 т. - Т.1. - М., 1989

26 Веккер Л.М. Психология мышления. - М.. 1965

Выготский Л.С. Мышление и речь: собрание сочинений. В 6 т. Т.2. - М., 1982.

28 Выготский Л.С. Избранные труды. М.: Просвещение,1989г.

29 Платонов К.К. «Психологический словарь» - Минск, 1985г.

30 Шаталов В.Ф. Точка опоры. - М.: Педагогика, 1987г.-160с.

31 Зотов Ю.Б. /Под редакцией Пидкасистого П.И./ Организация современного урока М.: Просвещение, 1988г.

Лордкипанидзе Д.О. Принципы организации и принципы обучения. М., 1957, с. 57.

Марев И. Методологические основы дидактики: Пер. с болг./ Предисл. И.Я. Лернера. - М.: Педагогика, 1987г. - 224с.

Гетманова А. Д.Логика

Алексеева А. В., Бокуть Е. Л., Сиделева Т. Н. Преподавание в начальных классах: Психолого - педагогическая практика. Учебно-методическое пособие. - М.: ЦГЛ, 2003. - 208 с.

Винокурова Н. К. Развиваем способности детей: 4 класс. - М.: Росмэн-Пресс, 2002. - 79 с.

Ануфриев А. Ф., Костромина С. Н. Как преодолеть трудности в обучении детей: Психодиагностические таблицы. Психодиагностические методики. Коррекционные упражнения. - М.: Ось - 89, 2001. - 272 с.

38 Развитие младших школьников в процессе усвоения знаний/Под ред. Н.В. Зверевой. М.: Педагогика, 1983.

Артёмов А.К., Истомина Н.Б. Теоретические основы методики обучения математике в начальных классах: Пособие для студентов факультета подготовки учителей начальных классов заочного отделения. - М.: Институт практической психологии, Воронеж: НПО «МОДЭК»,1996. - 224 с.

40 Забрамная С. Д., Костенкова Ю. А. Развивающие занятия с детьми: Материалы для самостоятельной работы студентов по курсу «Психолого-педагогическая диагностика и консультирование». - М.: В. Секачёв, 2001. - 80 с.

Моро М. И., Пышкало А. М. Методика обучения математике в I -III классах: Пособие для учителя. Издание второе, переработанное и дополненное. - М.: Просвещение, 1978. - 336с.

Овчинникова В. С. Методика обучения решению задач в начальной школе: Учебное пособие по курсу «Методика обучения математике» для студентов педагогических факультетов высших учебных заведений и колледжей. - М.: Мегатрон, 1998. - 67с.

Петровский А. В., Ярошевский М. Г. Психология: Учебник для студентов высших педагогических учебных заведений. - Второе издание, стереотип. - М.: Издательский центр «Академия», 2001. - 512 с.

Стойлова Л. П. Математика: Учебник для студентов высших педагогических учебных заведений. - М.: Издательский центр «Академия», 2002. - 424 с.

Тихомирова Л. Ф. Упражнения на каждый день: Логика для младших школьников: Популярное пособие для родителей и педагогов. - Ярославль: Академия развития, 2001. - 144 с

46 Методика начального обучения математике/Под. ред. В.А. Дрозд. Минск, 1988.

47 Выготский Л.С. Обучение и развитие в школьном возрасте. Вкн.: Умственное развитие детей в процессе обучения. - М., Просвещение, 1985.

Дрозд В.А. и др. Методика начального обучения математике. Минск, 1988

Развитие творческой активности школьника/Под ред. А.Н. Матюшкина. М.: Педагогика, 1991.

Стойлова Л.П., Пышкало А.М. Основы начального курса математики. М.: Просвещение, 1988.

Актуальные проблемы методики обучения математике в начальных классахю. Под ред. М И Моро и др. М. Педагогика, 1997. -С.754

Артемов А. К. Обучение математике. Пенза, 1995. - С.65

Истомина Н.Б. Активизация учащихся на уроке математики в начальных классах. М. 1986. -С.94.

Истомина Н.Б. практикум по методике преподавания математики в начальных классах. М. 1986. -С.544

Скаткин Л.Н. Методика начального обучения математики. М. 1972. -С. 667

Бантова М.А., Т.В.Бельтюкова. Методика преподавания математики в начальных классах. М., 1984. -С. 756

Бантова М.А., Т.В.Бельтюкова. Обучение в 4 классе. Пособия для учителей четырехлетней начальной школы в двух книгах. Книга 2. - С.335

Истомина Н.Б.Методика обучения математике в начальных классах. С. 45

Дидактика средней школы. Под ред. Данилова М.А. и Скатина М.Н. - М., Просвещение, 1975.

Загвязинский В.И. Пед. творчество учителя. - М., Просвещение, 1987.

Каган М.С. Человеческая деятельность. - М., Просвещение, 1974.

Краевский В.В., Лернер И.Я. Дидактика средней школы. - М., Просвещение, 1982.

Лернер И.Я. Дидактическая система методов обучения. - М., Знание,1976.

Морозова Н.Г. Учителю о познавательном интересе. - М., Знание, 1979

Абрамова Г.С. Возрастная психология: учебное пособие для студентов. - М., Академия, 1988.

Оганесян В.А., Колягин Ю.Н. и др. методика преподавания в средней школе. Общая методика. - М., Просвещение, 1980.

Поляк Г.Б. Занимательные задачи. - Учпедгаз, 1955.

Манвелова О.Н., Манвелов С.Г. Основы конструирования урока. Армавир, 1993.

Щукина Г.И. Педагогические проблемы формирования познавательных интересов учащихся. - М., Педагогика, 1988.

Азаров Ю.П. Искусство воспитывать. - М., Просвещение, 1988.

Бабанский Ю.К. Оптимизация учебно-воспитательного процесса. - М., Просвещение, 19 82.

Поляк Г.Б. Занимательные задачи. - М., Учпедгаз, 1955.

Рубинштейн С.М. Основы общей психологии. - М., Педагогика, 1946.

Химчин А.Я. О воспитательном эффекте уроков математики. - М., математическое просвещение, 1961

Гузик Н.П. Учить учится - М.: Просвещение, 1981г.

Гусарчук Д.М. Избранное .: Просвещение, 1985г.

Дашко Л.И. Наглядные пособия - М.: Просвещение, 1990г. 124с.

Занков Л.В. Наглядность и активизация учащихся в обучении - М.: Знание, 1960г. 162с.

Зотов Ю.Б. /Под редакцией Пидкасистого П.И./ Организация современного урока М.: Просвещение, 1988г.

Методика начального обучения математике. Минск, 1988.

Вербицкий А.А., Платонова Т.А. Формирование познавательной и профессиональной мотивации. - М., Просвещение, 1986.

Кордемский Б.А. Увлечь школьника математикой. - М., Просвеще-ние, 1981.

Манвелова О.Н., Манвелов С.Г. Основы конструирования урока. Армавир, 1993

Зак А.З. Развитие интеллектуальных способностей у детей 8 лет: Учебно-методическое пособие для учителей. - М.: Новая школа, 1996. - 252 с.

Зак А.З. Развитие интеллектуальных способностей у детей 9 лет: Учебно-методическое пособие для учителей. - М.: Новая школа, 1996. - 108 с.

Мерезникова Т.Д. Диагностика психологического развития детей. Пособие по практической психологии. - М.: Линка-Пресс, 1997. - 176 с.

Матюшкин А.М. Проблемная ситуация в мышлении и обучении. - М.: Педагогика, 1972. - 168 с.

Махмутов М.И. Проблемное обучение: Основные вопросы теории. - М.: Педагогика, 1975. - 368 с.

Гальперин П.Я. Котик Н.Р. К психологии творческого мышления//Вопросы психологии. - 1982. - №5.

Готсдинер А.Л. К проблеме многосторонних способностей//Вопросы психологии. - 1991. - №4.

Давыдов В.В. Проблемы развивающего обучения: Опыт теоретического и экспериментально-психологического исследования. - М.: Педагогика, 1986. - 240 с.

Дистервег. Избранные педагогические сочинения. - М.: Просвещение, 1956. - 376 с.

Уотсон Дж. Психология как наука о поведении. - Госиздат Украины, 1926.

Вертгеймер М. Продуктивное мышление: пер. с нем. - М.: Прогресс, 1987. - 336 с.

Майер Р.А. Задачи, направленные на развитие функционального стиля мышления школьников. - М., 1973. - С. 36-50.

Пиаже Ж. Природа интеллекта // Избранные психологические произведения. - М., 1994.

97 Maslow A.H. Motivation and Personality. Harper and Bros., 1954.

Сеченов И.М. Избранные философские и психологические произведения. - М.: Учпедгиз, 1947. - 419 с.

Дьюи Д. Психология и педагогика мышления/Пер. с англ. Николаевой Н.М., под ред. Виноградова Н.Д. - М.: Совершенство, 1997. - 208 с.

Ересь Е.П. Способности и их развитие. - М.: Знание, 1957.

Зак А.З. Развитие интеллектуальных способностей у детей 6-7 лет: Учебно-методическое пособие для учителей. - М.: Новая школа, 1996. - 288 с.

ПРИЛОЖЕНИЕ А

Тест Липпмана «Логическая закономерность»

Тест

. 2, 3, 4, 5, 6, 7;

. 6, 9, 12, 15, 18, 21;

. 1, 2, 4, 8, 16, 32;

. 4, 5, 8, 9, 12, 13;

. 19, 16, 14, 11, 9, 6;

. 29, 28, 26, 23, 19, 14;

. 16, 8, 4, 2, 1, 0.5;

. 1, 4, 9, 16, 25, 36;

. 21, 18, 16, 15, 12, 10;

. 3, 6, 8, 16, 18, 36.

Обработка и интерпретация результатов теста

Ключ к тесту

. 2, 3, 4, 5, 6, 7, 8, 9

. 6, 9, 12, 15, 18, 21, 24, 27

. 1, 2, 4, 8, 16, 32, 64, 128

. 4, 5, 8, 9, 12, 13, 16, 17

. 19, 16, 14, 11, 9, 6, 4, 1

. 29, 28, 26, 23, 19, 14, 8, 1

. 16, 8, 4, 2, 1, 0.5, 0.25, 0.125

. 1, 4, 9, 16, 25, 36, 49, 64

. 21, 18, 16, 15, 12, 10, 9, 6

. 3, 6, 8, 16, 18, 36, 38, 76

Интепретация результатов теста

Время выполнения задания (мин., сек.) Кол-во ошибок Баллы Уровень развития логического мышления

мин. и менее 0 5 Очень высокий уровень логического мышления

мин. 10 сек. - 4 мин. 30 сек. 0 4 Хороший уровень, выше, чем у большинства людей

мин. 35 сек. - 9 мин. 50 сек. 0 3+ Хорошая норма большинства людей

мин. 35 сек.- 9 мин. 50 сек. 1 3 Средняя норма

мин. 10 сек. - 4 мин. 30 сек. 2 - 3 3- Низкая норма

мин. 10 сек. - 15 мин. 4 - 5 2 Ниже среднего уровня развития логического мышления

мин. - 15 мин. 0-3 2+ Низкая скорость мышления, «тугодум»

Более 16 мин. Более 5 1 Дефект логического мышления у человека, прошедшего обучение в объеме начальной школы, либо высокое переутомление

В данной работе использованы четыре методики, направленные на исследование как общего уровня развития младших школьников, их способности к обучению, так и отдельных мыслительных операций, анализируя которые можно охарактеризовать отдельные особенности мышления ребёнка. Это следующие методики:

1. Методика “логико-количественные отношения”.

2. Методика “Сравнения понятий”.

. Методика “Классификация понятий”

. Методика шифровки цифровых символов.

В каждом исследовании принимало участие 10 подростков. Ниже приводится описание всех методик и анализ полученных результатов. Результаты тестирований и ответы отдельно взятого ребёнка (см. в приложениях).

Методика “логико-количественные отношения”.

Испытуемым в этой методике предлагается решить 20 задач на выяснение логико-количественных отношений. Все задачи представлены в таблице (см. материал к методике).

В каждой из этих задач необходимо определить, какая величина больше или, соответственно, меньше другой и результат записать под чертой в виде соотношения между величинами “А” и “В” с помощью знаков “ < ” или “ > ”. Решать все без исключения задачи нужно только в уме, как можно быстрее и без ошибок.

На решение всех 20 задач отводится 10 минут. По истечении этого времени психодиагностический эксперимент прерывается и определяется число правильно решенных испытуемых задач за это время.

Примечание. Ниже для контроля приводятся правильные решения всех задач с указанием номера задачи и правильного решения. В ответах вместо указанных выше знаков использованы словесные формулировки:

1. В больше А	2. В больше А	3. В больше А	4. В больше А
5. А больше В	6. В больше А	7. А больше В	8. А больше В
9. А больше В	10. А больше В	11. А больше В	12. В больше А
13. В больше А	14. В больше А	15. А больше В	16. В больше А
17. В больше А	18. А больше В	19. А больше В	20. А больше В

Оценка результатов.

За каждую правильно решенную задачу испытуемый получает 0,5 балла. Максимальная сумма баллов, которую может набрать один испытуемый за решение всех 20 задач, равна 10. если результат оказался равным целому числу баллов с половиной, то он округляется до большего ближайшего числа. Например, результат 8,5 баллов в итоге округляется до 9,0 баллов.

Выводы об уровне развития мышления

баллов - очень высокий

8 - 9 баллов - высокий

4 - 7 баллов - средний

- 3 балла - низкий

- 1 балла - очень низкий

l. А больше Б в 6 раз Б меньше В в 7 раз	2. А меньше Б в 10 раз Б больше В в 6 раз	В А
3. А больше Б в 3 раза Б меньше в 6 раз	4. А больше Б в 3 раза Б меньше В в 5 раз
В А	В А
5. А меньше Б в 3 раза больше В в 5 раз	6. А больше Б в 9 раз Б меньше В в 12 раз
В А	В А
7. А больше Б в 9 раз Б меньше В в 4 раза	8. А меньше Б в 3 раза Б больше В в 7 раз
В А	В А
9. А меньше Б в 5 раз Б больше В в 6 раз	10. А меньше Б в 2 раза Б больше В в 8 раз
В А	В А
11. А меньше Б в'3 раза Б больше В в 4 раза	12. А больше Б в 2 раза Б меньше В в 5 раз
В А	В А
13. А меньше Б в 10 раз Б больше В в 3 раза	14. А меньше Б в 5 раз Б больше В в 2 раза
В А	В А
15. А больше Б в 4 раза Б меньше В в 3 раза	16. А меньше Б в 3 раза Б.больше В в 2 раза
В А	В А
17. А больше Б в 4 раза Б меньше В в 7 раз	18. А больше Б в 4 раза Б меньше В в 3 раза

19. А меньше Б в 5 раз Б больше В в 8 раз	20. А больше Б в 7 раз Б меньше В в 3 раза
В А	В А

Методика “Сравнения понятий”.

С помощью этой методики анализируется развитие операции сравнения.

Ход выполнения задания. Метод заключается в том, что испытуемому называются два слова, обозначающие те или иные предметы или явления и просят сказать, что общего между ними и чем они отличаются друг от друга. При этом экспериментатор все время стимулирует испытуемого в поиске возможно большего количества черт сходства и различия между словами пары: “Чем еще они похожи?”, “Еще чем?”, “Чем еще они отличается друг от друга?”, “Еще чем?”, Дается примерный список слов для сравнения. Можно выделить три категории задач,которые применяются для сравнения и различения понятий (А. Р. Фурия). Во-первых, испытуемым даются два слова, явно относящиеся к одной категории (например, “корова - лошадь”). Во-вторых, предлагаются два слова, у которых общее найти трудно и которые гораздо больше отличаются друг от друга, чем в предыдущем случае (например, “ворона рыба”). Третья группа задач еще-сложнее - это задачи на сравнение и различение объектов в условиях конфликта, где различия выражены гораздо больше, чем сходство (например, “всадник - лошадь”). Различие уровней сложности этих категорий задач зависит от степени трудности абстрагирования признаков или наглядного взаимодействия объектов, от степени трудности включения этих объектов в определенную категорию. Анализ результатов. Проводится количественный и качественный анализ результатов. Количественная обработка заключается в подсчете количества выделенных испытуемым в каждой паре черт сходства и различия.

Высокий уровень развития операции сравнения отмечается в том случае, когда школьник назвал более двадцати черт, средний - десять-пятнадцать черт, низкий - менее десяти черт. В процессе обработки ответов важно учесть, какие черты отметил учащийся в большем количестве - черты сходства или различия. часто ли он употреблял родовые понятия. Этот метод имеет значение для диагностики умственного недоразвития или отсталости. Умственно отсталый ребёнок не сможет выполнить задачу на отвлечение признака и введение объектов в иерархию одной категории и всегда будет замещать такой ответ либо указанием на различие, либо введением в какую-то наглядную ситуацию. Для человека, больного шизофренией, характерно обратное - полный отрыв от наглядной ситуации и обобщение по несуществующим признакам объектов. После проведения количественного и качественного анализа результатов, можем заключить: из 10 испытуемых высокий уровень развития операций сравнения имеет только один ребёнок, 1 - выше среднего, 2 - средний и 6 человек имеют низкий уровень развития операций сравнения. Методика “Классификация понятий” Выявлялклся такие особенности мышления, как способность выделять существенные признаки (для объединения карточек в группы) й уровень обобщения, доступный школьнику или взрослому. Ход выполнения задания. Задание проходит.-втри. этапа, с тремя последовательными инстрфциями психолога. Испытуемому дается набор карточек с написанными (напечатанными) на них словами. Список слов - в материалах к методике.

Там же примерная форма фиксации результов - протокола опыта. Первый этап процедуры начинается при так называемой “глухой” инструкции: “Разложи карточки так, чтобы слова, которые подходят друг к другу, оказались в одной группе”. Количество возможных групп не оговаривается. В случае, если испытуемый задает вопросы, прежде чем приступить к выполнению задания, ему говорят: “Начинай, дальше увидишь сам”. После того как испытуемый самостоятельно сформировал несколько мелких групп карточек, у него спрашивают, почему те или иные карточки помещаются вместе и какое название им дается. Затем происходит переход ко второму этапу процедуры. Инструкция на втором этапе звучит так: “Ты верно объединил карточки в группы. Дай теперь этим группам короткие названия. Продолжай работу таким же образом”. После того, как все карточки оказались помещенными в группы и всем группам даны короткие названия, экспериментатор переходит к третьему этапу методики.

Дается следующая инструкция: “Точно так же, как ты объединял карточку с.карточкой в отдельные группы и давал им названия, объедини теперь группу с группой, не перекладывая отдельных карточек. Таких групп должно быть как можно меньше. Они также должны иметь колкие названия”. Если испытуемый на этом этапе формирует больше, .чем три группы, ему предлагается сформировать из оставшихся групп 2 - 3 основные. В протоколе фиксируются этапы выполнения работы, названия групп и карточки в них, а также вопросы и ответы испытуемого. При анализе результатов большое значение имеет то, на каком этапе допущены школьником те или иные ошибки; отстаивал ли он свои принципы объединения карточек в группы, использовал ли помощь экспериментатора, какие еще особенности мышления проявлял в классификации. Так, если испытуемый на втором этапе сформировал отдельные группы диких, домашних, летающих, водоплавающих животных и отказался объединить эти группы в одну, то это свидетельствует о степени использования конкретных, детализованных признаков в направленности его мышления. Если же подобные объединения проходили легко, самостоятельно, без указания экспериментатора на необходимость укрупнения групп, то это можно квалифицировать как достигнутый уровень обобщенности мышления, способности испытуемого ориентироваться не только на существенные признаки, но и учитывать их иерархии, т. е; использовать существенные связи между понятиями.

Показателем этого является также степень затруднений или легкости при поиске обобщающих понятий, которые фиксируют основания классификации карточек в группы. Если на третьем этапе выполнения методики испытуемый легко ' объединил группы и адекватно назвал обобщающие признаки, то есть основания считать, что мышление его характеризуется использованием обобщенных ориентиров и протекает на “категориальном уровне. Кроме того, анализ поведения школьника в ходе исследования позволяет говорить о наличии или отсутствии у него внушаемости, эмоциональной устойчивости.

Эти предположения проверяются с помощью навязывания испытуемому неадекватных оснований для объединения групп, дискредитации экспериментатором тактики работы испытуемого или похвалы при ошибках. Отсюда следует, что с методикой должен работать психолог, а не учитель ребенка; ведь в последнем случае трудно ожидать такого типа взаимодействия школьника и экспериментатора, при кагором школьник сможет принять необходимость стаивать на своем, противопоставлять свои обоснования мнению взрослого. Эта методика дает надежные результаты при использовании ее в комплексе других методик, также нацеленных на выявление доступного испытуемому уровня обобщений, или конкретно обобщенности Мышления, целенаправленности мыслительной деятельности, ригидности (как трудности переключения с одного способа рассуждений н а другой), характера опосредствующих рассуждения понятийных связей

МАТЕРИАЛ К МЕТОДИКЕ “КЛАССИФИКАЦИЯ ПОНЯТИЙ”

Список слов, каждое из которых должно быть напечатано на отдельной карточке

рубль яблоня светлячок прожектор свеча телевизор керосиновая лампа электролампа фонарь сантиметр весы часы термометр радиоприемник лев тигр слон карп голубь гусь ласточка муравей

муха кит клоп огурец капуста свекла барабан мяч компас ботинки тетрадь пароход телега лук лимон груша яблоко примус велосипед платье грузовик самолет

глобус электродуховка колесо сазан (рыба) книга кровать овощехранилище пианино скрипка щипцы топор ножницы молоток пила моряк уборщица доктор ребенок футболист солнце медведь луна электроплита

град кукла тюльпан подушка шкаф одеяло буфет дождь роза матрац стакан сосна шапка снег ложка вилка тарелка

Методика шифровки цифровых символов.

Это один из невербальных подтекстов методики, направленной на исследование интеллекта, автором которой является Векслер. От испытуемого требуется в специальной таблице (см. материал к данной методике) в соответствии с образцами в рядах случайно подобранных цифр, поставить под каждой цифрой ее обозначение-символ, т. е. про- - извести как бы перешифровку цифр. Время выполнение задания ограничивается 90 секундами. Обработка результатов: Каждое правильно выполненное задание оценивается в 1 балл.

Первые десать заданий не учитываются, они служат примером. О способности к научению новому свидетельствует выполнение последующих примеров, когда испытуемом предупреждают о начале хронометрии и необходимости выполнять задание как можно скорее. Этой методикой исследуется психомоторика, способность к обучению. В результате обработки таблиц мы выяснили, что средний показатель развития психомоторики и способности к обучению у испытуемых оказался равен 47,2 %. Причём данный показатель не превышает и 50 %, свидетельствуют о необходимости развивать способность подростков к обучению новому.

Разработка системы развития логического мышления младших школьников средствами учебного предмета 'Математика'

Разработка системы развития логического мышления младших школьников средствами учебного предмета 'Математика'

ВВЕДЕНИЕ

Похожие работы на - Разработка системы развития логического мышления младших школьников средствами учебного предмета 'Математика'