
Вычислим площадь фигуры
с пределами интегрирования а=  и b= 0.
и b= 0.
неопределенный интеграл
расходимость предел
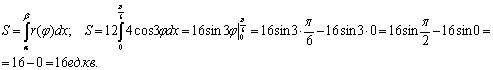
Ответ: 
5. Задание 5
В двойном интеграле расставьте
пределы интегрирования двумя способами (меняя порядок интегрирования) и
вычислите интеграл.
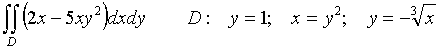
Решение
Сделаем чертеж области D:

I способ:

Расставим пределы интегрирования:

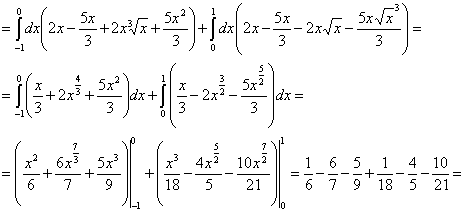
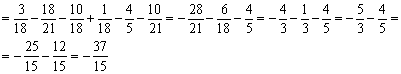
II способ:


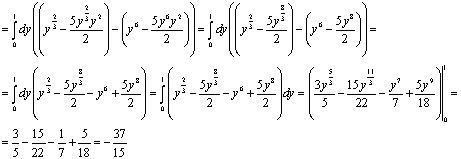
Вычислить криволинейный интеграл
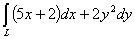 ,
,
где L - путь, соединяющий точки А (-2; 0) и В (0; 2) по
) прямой 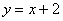 ;
;
) ломаной линии
АСВ, где С (-2; 2);
) окружности 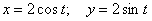
Решение
1. 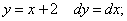
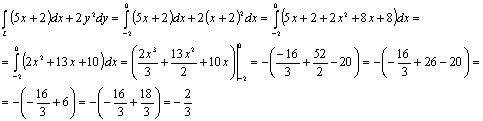
2. Разбиваем замкнутый
путь АСВА на три участка АС, СВ, ВА
На участке АС принимаем
за параметр ординату, при этом х=-2, dx=0,
на участке СВ, абсциссу, при этом у=2, dy=0,
на участке ВА ординату, при чем у=х+2, dx=dy

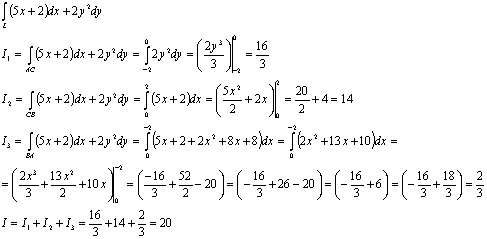
. окружности 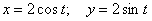
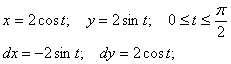
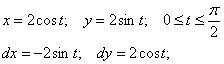
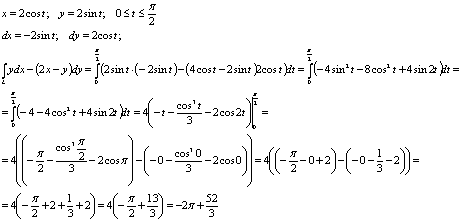
Список литературы
1. Выгодский М.Я. Справочник по высшей математике. - М.: АСТ:
Астрель, 2006. - 991 с.
. Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика.
Под ред. А.И. Кирилова. - 3-е изд., испр. - М.: ФИЗМАТЛИТ, 2006. - 368 с.
. Красс М.С., Чупрыков Б.П. Математика для экономистов. - СПб.:
Питер 2007. - 464 с.