Основы финансовых вычислений

Основы финансовых вычислений

Основы финансовых вычислений

1. Задача 1

Дана матрица последствий Q, в которой строки - возможные управленческие решения, а столбцы - исходы, соответствующие альтернативным вариантам реальной ситуации (состояниям внешней среды).

Выберите рациональную управленческую стратегию, применяя критерии (правила) максимакса, Вальда, Гурвица и Сэвиджа. Примите рекомендуемое значение α-критерия Гурвица.

Решение

Полная неопределенность означает отсутствие информации о вероятностных состояниях среды («природы»), например о вероятностях тех или иных вариантов реальной ситуации. В лучшем случае могут быть известны диапазоны значений рассматриваемых величин. Рекомендации по принятию решений в таких ситуациях сформулированы в виде определенных правил (критериев).

.        Критерий (правило) максимакса. По этому критерию определяется вариант решения, максимизирующий максимальные выигрыши (например, доходы) для каждого варианта ситуации. Это критерий крайнего («розового») оптимизма, в соответствии с которым наилучшим является решение, дающее максимальный выигрыш, равный 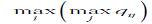. Рассматривая i-е решение, предполагают самую хорошую ситуацию, приносящую доход 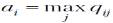, а затем выбирают решение с наибольшим значением ai. Критерий максимакса означает, что нужно по каждой строке матриц Q найти максимальное значения, а среди максимальных значений найти максимальное.

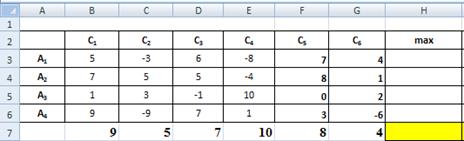
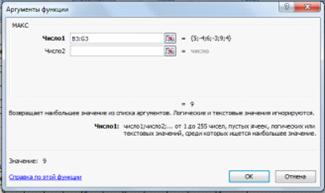
Кликнем на ячейку H3, введем в нее функцию =МАКС (B3:G3) из Категории Статистические и нажмем клавишу Enter или ОК.

В ячейке H3 появляется максимальное значение дохода для альтернативы А1 равное 7.

Для остальных альтернатив эта величина вычисляется путем протягивания ячейки H3 по столбцу (H3:H6). В ячейку H7 введем функцию =МАКС (H3:H6) и нажмем клавишу Enter: в ячейке H7 появится число 10. Сравнивая его с числами в ячейках (H3:H6), находим, что оно совпадает с максимальным значением дохода для альтернативы А₃, которая, следовательно, и является наилучшей по критерию максимакса.

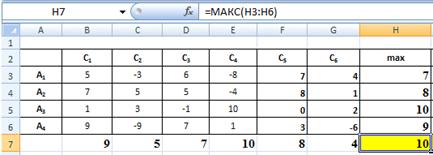
Рис. 1. Выбор рационального решения в условиях неопределенности по критерию максимакса

Делаем вывод, к какой стратегии отнесем максимальное значение 10 - к 3 стратегии.

2.      Правило Вальда (правило максимина, или критерий крайнего пессимизма). Рассматривая i-e решение, будем полагать, что на самом деле ситуация складывается наихудшая, то есть приносящая наименьший доход 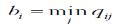. Но теперь выберем решение i₀ с наибольшим b_i0. Итак, правило Вальда рекомендует принять решение i₀ такое, что .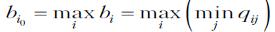

Критерий Вальда означает, что необходимо найти среднее минимальное значение по каждой строке максимальное (максимум из минимальных). В ячейку I3 (рис. 2.) введем функцию =МИН (В3:G3) из Категории Статистические, нажмем клавишу Enter или ОК и получим в ячейке I3 минимальное значение доходности для альтернативы А1, равное -8.

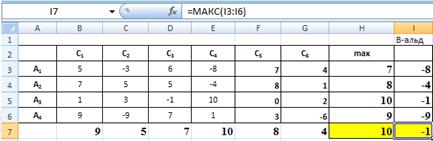
Рис. 2. Выбор рационального решения в условиях неопределенности по критерию Вальда

Рис. 3. Ввод функций

Для остальных альтернатив аналогичная величина вычисляется путем протягивания ячейки I3 по столбцу (I3:I6). В ячейку I7 введем функцию =МАКС (I3:I6) и нажмем клавишу Enter: в ячейке I7 появится число -1 Сравнивая его с числами в ячейках (I3:I6), заметим, что оно совпадает с минимальным значением дохода для альтернативы А₃, которая, следовательно, и является оптимальной по критерию Вальда.

Делаем вывод, к какой стратегии отнесем максимум из минимальных значений -1 - к 3 стратегии.

3.      Правило (α-критерий) Гурвица (взвешивающий пессимистический и оптимистический подходы к выбору решений). По данному критерию выбирают вариант решения, при котором достигается максимум выражения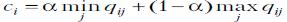, где α выражает долю пессимизма (параметр пессимизма) в характере ЛПР, причем а € [0; 1].

Таким образом, критерий Гурвица рекомендует руководствоваться некоторым средним результатом между крайним оптимизмом и крайним пессимизмом. При α = 0 критерий Гурвица совпадает с критерием максимакса, а при α = 1 - с критерием Вальда. Значение α выбирается из субъективных (интуитивных) соображений. В ячейках L3 набираем заданное значение параметра α. В ячейку H3 введем формулу =$L$3*I3+(1-$L$3)*H3 соответствующая 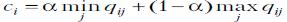 и нажмем клавишу Enter. В ячейке J3 появится значение критерия Гурвица для альтернативы А1, равное 1 при α = 0,4. Ячейку J3 протягиваем по столбцу (J3:J6), в результате будут вычислены значения критерия Гурвица для всех альтернатив и всех заданных значений параметра α.

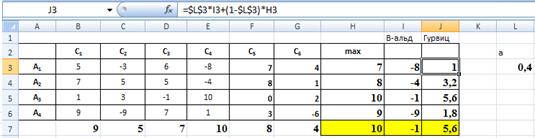
Рис. 4. Выбор рационального решения в условиях неопределенности по α-критерию Гурвица (для сравнения сохранен выбор решений по критерию максимакса и правилу Вальда)

В ячейку J7 введем функцию =МАКС (J3:J6) и нажмем клавишу Enter: в ячейке H7 появится число 5,6. Сравнивая его с числами в ячейках (J3:J6), найдем, что оно совпадает со значением критерия Гурвица для альтернативы А₃ равная 5,6, которая и является оптимальным решением при α = 0,4.

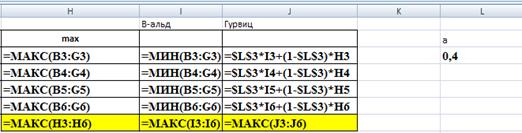
Рис. 5. Ввод функций

Делаем вывод, к какой стратегии отнесем максимум из минимальных значений 5,6 - к 3 стратегии.

4. Правило Сэвиджа (критерий минимаксного риска). Этот критерий аналогичен критерию Вальда, но ЛПР принимает решение, руководствуясь не матрицей последствий Q = {q_ij}, а матрицей рисков R = {r_ij}. По этому критерию наилучшим является решение, при котором максимальное значение риска будет наименьшим, то есть равным 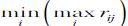. Рассматривая i-e решение, предполагают ситуацию максимального риска 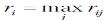 и выбирают вариант решения i₀ с наименьшим .

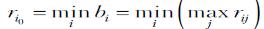Пусть принимается решение Ai. Очевидно, если бы было известно, что реальная ситуация будет Cj, то ЛПР приняло решение, дающее доход q q j i ij =max. Однако i-е решение принимается в условиях неопределенности. Значит, ЛПР рискует получить доход не qj, а только qij. Таким образом, существует реальная возможность недополучить доход, и этому неблагоприятному исходу можно сопоставить в качестве меры недополучения дохода риск rij, размер которого целесообразно оценить как разность

= qj - qij.

Матрица R = {rij} называется матрицей рисков.

Необходимо посчитать матрицу рисков.

Найдем максимальные значения элементов матрицы по столбцам. Для этого выделим ячейку В7, вызовем Мастер функций → Категория Статистические → МАКС. На панели в строке формул появляется =МАКС (В3:В6), нажимаем кнопку ОК: в ячейке В7 появляется число 9 - максимальный доход q1 для состояния среды С1. Максимальные доходы для остальных ситуаций находим, протягивая ячейку В7 по строке (В7:G7) c помощью крестика.

Для вычисления элементов матрицы рисков выделим ячейку В13, введем в нее формулу =В$7-В3 и нажмем клавишу Enter. В ячейке В13 появится вычисленное значение риска r₁₁ = 4. Ячейку В13 протягиваем по строке (В13:G13), а выделенные ячейки - по столбцу (G13:G16). Матрица рисков будет вычислена в ячейках (В13:G16).

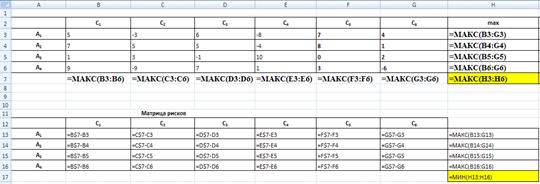
Рис. 6. Расчет матрицы рисков по матрице №1 в MS Excel

Протягивая ячейку H13 по столбцу (H13:H16), получим максимальные риски для остальных альтернатив. В ячейку H17 введем функцию =МИН (H13:H16) и нажмем клавишу Enter. В ячейке H17 появится число 8 - минимальное значение из набора максимальных рисков (критерий Сэвиджа). Сравнивая его с числами в ячейках (H13:H16), находим рациональное решение по критерию Сэвиджа - альтернативу А₃.

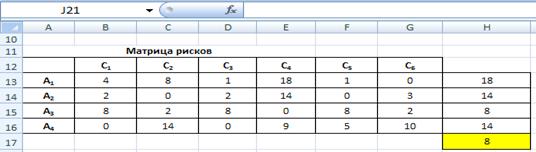
Рис. 7. Выбор рационального решения в условиях неопределенности по критерию Сэвиджа

Делаем вывод, к какой стратегии отнесем максимум из минимальных значений 8 - к 3 стратегии.

Ответ: Рациональное оптимальное значение стратегия №3

2. Задача 2

Рассматриваются два альтернативных проекта A и B. Оценив их рисковость, выберите наиболее привлекательный проект. Приняты следующие обозначения: pi - вероятности состояния внешней среды; xi - соответствующие доходности проектов.

Рис. 8. Исходные данные

Решение

Табличный способ организации выбора решений. Рассмотрим ряд распределения значений доходности ценной бумаги х_i(r_i), соответствующих определенным состояниям экономической конъюнктуры, для которых известны вероятности их реализации pi (табл. 1).

Прежде чем рассчитывать характеристики, а именно математическое ожидание и дисперсию доходности необходимо проверить: ∑P_i^A=1; ∑P_i^B=1.

Рис. 9. Проверка

Математическое ожидание доходности ценной бумаги рассчитывается по формуле 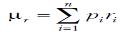. Классической мерой риска служит среднеквадратическое отклонение  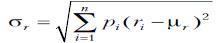(риск вложения денежных средств в проект). В расчетах часто бывает целесообразно использовать формулу 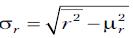, где под знаком корня находится разность между средним квадратом доходности и квадратом средней доходности.

Речь идет о выборе между двумя ценными бумагами, этих двух характеристик недостаточно. В этом случае целесообразно ввести в рассмотрение такой показатель, как коэффициент вариации 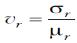, который имеет смысл риска, приходящегося на единицу ожидаемой доходности. Этот показатель находится как отношение среднего квадратического отклонения к математическому ожиданию для каждого проекта.

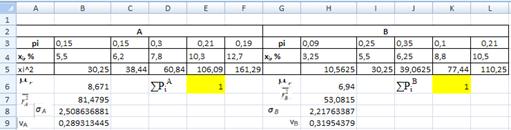
Рис. 10. Выполнение расчетов в MS Excel, позволяющих выбрать оптимальный проект

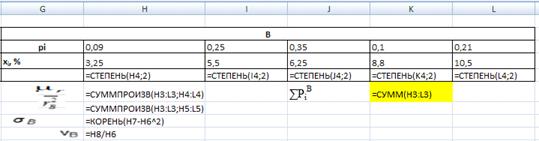
Рис. 11. Ввод функций

3. Задача 3

Найти оптимальный портфель минимального риска из двух ценных бумаг с учетом рыночного индекса и доходностью не ниже доходности по облигациям. Текущие котировки исходных данных акций, индекса рынка и облигаций представлены в таблице 1.

Таблица 1. Исходные данные

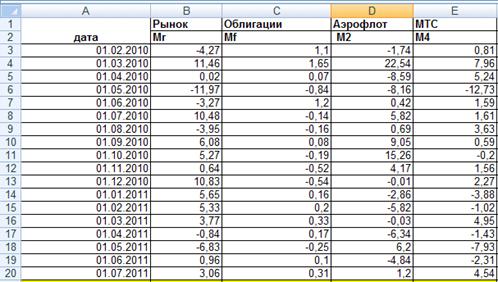
Требуется:

) рассчитать доходности соответствующих активов по месяцам;

) определить характеристики каждой ценной бумаги: ai, βi, αi R², а также общий рыночный, или систематический и собственный, или несистематический риск;

) сформировать портфель минимального риска из двух видов ценных бумаг при условии, что обеспечивается доходность портфеля не меньшая, чем по безрисковым ценным бумагам (облигациям) с учетом доходности по рыночному индексу РТС;

) построить линию рынка ценных бумаг - SML.

Решение

В таблице №1 «Исходные данные» уже рассчитаны доходности соответствующих торговых инструментов, таким образом нам не нужно рассчитывать доходность инструментов за каждый месяц по формуле

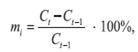
Проведем предварительные расчеты. Для дальнейших расчетов потребуются значения оценок математического ожидания доходностей по безрисковой ценной бумаге (облигации) mf и ценным бумагам, рыночному индексу РТС mr, а также квадрата риска (волатильности) доходности по рыночному индексу.

Нахождение указанных величин с помощью MS Excel проводится в несколько этапов:

Этап 1. Определение значений оценок математического ожидания доходностей по безрисковой ценной бумаге (облигации) mf и ценным бумагам, а также рыночному индексу РТС mr основывается на применении функций СРЗНАЧ и ДИСП категории Статистические.

Обращаясь к Мастеру функций, вызываем функцию СРЗНАЧ, затем аналогичным образом - функцию ДИСП.

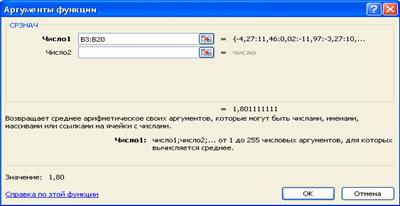
Рис. 12. Функция СРЗНАЧ

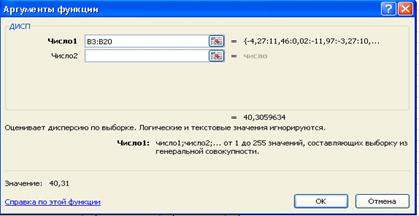
Рис. 13. Функция ДИСП

Рис. 14. Определение значений оценок математического ожидания MS Excel

Этапы 2-3. Для оценки таких характеристик каждой ценной бумаги, как ai, βi, R², а также общего рыночного и собственного риска используем инструмент Регрессия из пакета Анализа данных (Сервис →Анализ данных → Регрессия).

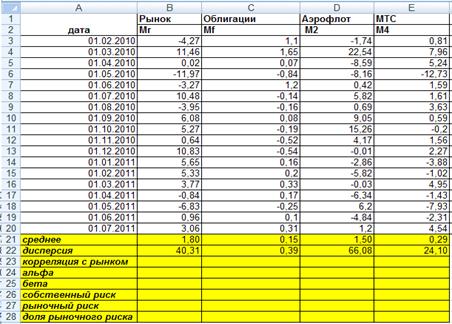
Рис. 15. Таблица для вызова инструмента Регрессия и формирования оценок на этапах 2-3 решения задачи

Найдем корреляцию с рынком с помощью Функции→Статистические→КОРРЕЛ. В Массив 1 выделяем данные индекса рынка на каждый месяц, а в Массив 2 доходы по акции М1 и М2.

Список литературы

1.      Оценка и анализ рисков. Компьютерный лабораторный практикум для студентов шестого курса, обучающихся по специальности 080105.65 «Финансы и кредит», специализация «Финансовый менеджмент». - М.: ВЗФЭИ, 2011.

.        Финансовая математика. Методические указания по выполнению лабораторной работы для студентов, обучающихся по направлениям 080200.68 «Менеджмент», программа «Финансовый менеджмент», 080100.68 «Экономика», программа «Корпоративные финансы», квалификация (степень) магистр. - М.: ВЗФЭИ, 2012.

.        Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: Учеб. пособие. - 3-е изд., перераб. И доп. - М.:Вузовский учебник: ИНФРАМ-М, 2012. - 389 с.