Метод статистических испытаний Монте-Карло

Метод статистических испытаний Монте-Карло

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственное образовательное учреждение высшего профессионального образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Институт-кибернетики

Специальность - прикладная информатика (в экономике)

Кафедра-ОСУ

Отчет по лабораторной работе №1

«Метод статистических испытаний Монте-Карло»

по дисциплине «Имитационное моделирование ЭП»

вариант

Выполнил: ст. гр. 8592

Л.С. Ковина

Томск 2012

Цель работы:

Изучение возможностей метода статистических испытаний Монте-Карло, для решения детерминированных и вероятностных задач.

Задача 1. Решение детерминированной задачи. Определение площади фигуры

Фигура ограничена следующими линиями: , , ,

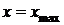.        Согласно заданному варианту, исходные данные следующие -  , , ,  ;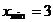

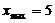.        Найти площадь фигуры аналитическим методом (с помощью вычисления определенного интеграла);

.        Построить графики для наглядной демонстрации результатов эксперимента;

.        Вычислить 95%-й доверительный интервал и сравнить его с точным значением интеграла;

.        Сделать выводы о зависимости точности вычислений от количества испытаний.

Решение

.        Найдем площадь фигуры аналитическим методом, т.е. вычислением определенного интеграла:

f(x) = -2x² + x⁴ +2

2.     
Чтобы проанализировать поведение функции на заданном интервале, построим ее график:

.        Вычислим максимальное значение функции на заданном интервале:

F(5) = -2*5² + 5⁴ + 2 = 577

4.      Вычислим площадь прямоугольника по формуле:

S _прям = (b-a) * max _f(x)

S _прям = 2*577 = 1154

5.      Рассчитаем площадь фигуры методом статистических испытаний Монте-Карло при N равном 100, 500, 1000, 5000, 10000. Для каждого N имеем 10 прогонов.

.        Построим график для наглядной демонстрации результатов эксперимента:

.        Для каждого N вычислим 95%-й доверительный интервал и сравним его с точным значением интеграла.

площадь фигура интеграл статистический

8.     
Исходя из результатов эксперимента можно сделать следующие выводы:

·        Оценка площади фигуры улучшается с увеличением числа генерируемых точек (с увеличением объема выборки).

·        Усреднение результатов 10 прогонов для каждой выборки объемом n дает более точную оценку площади, чем любой из прогонов. В таблице видно, что среднее 10 экспериментов ближе к точному значению площади, чем оценки, полученные в каждом отдельном прогоне.

·        Уменьшение величины стандартного отклонения свидетельствует о том, что «точность» среднего 10 экспериментов повышается с увеличением объема выборки n.