Линейная модель множественной регрессии

Линейная модель множественной регрессии

Контрольная работа

Линейная модель множественной регрессии

План

1.   Линейная модель множественной регрессии в скалярной и векторной формах. МНК оценки коэффициентов множественной регрессии.

2.      Ковариационная матрица оценок коэффициентов регрессии. Оценка дисперсии ошибок.

.        Теорема Гаусса-Маркова.

.        Коэффициент детерминации, скорректированный коэффициент детерминации.

.        Частная корреляция.

.        Проверка статистических гипотез, доверительные интервалы.

Литература

1.   Линейная модель множественной регрессии в скалярной и векторной формах. МНК оценки коэффициентов множественной регрессии

Включение в уравнение множественной регрессии того или иного набора факторов связано, прежде всего, с представлением о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1)      они должны быть количественно измеримы (качественные показатели могут быть проранжированы);

2)      факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной зависимости.

Включаемые факторы должны объяснять вариацию зависимой переменной. Если строится модель с р факторами, то для неё можно определить R² - коэффициент детерминации, который фиксирует долю объясненной вариации признака. Влияние других, не учтенных в модели, факторов оценивается (1-R²) с соответствующей остаточной дисперсией. При дополнительном включении в регрессию (р + 1)-го фактора коэффициент R² должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит, то включаемый фактор является лишним. Насыщение модели лишними факторами приводит к статистической незначимости параметров регрессии.

Как и в парной зависимости возможны разные виды уравнений множественной регрессии: линейные и нелинейные. Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функции (степенная легко линеаризуется).

Рассмотрим линейную модель множественной регрессии:

.

По выборке объёма n оценивается уравнение регрессии

,

где неизвестные коэффициенты оцениваются МНК, при котором минимизируется сумма квадратов остатков, позволяя получить систему нормальных уравнений:

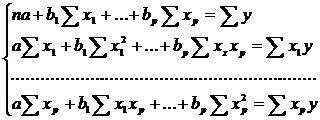
Решение системы может быть получено, например, по формулам Крамера:

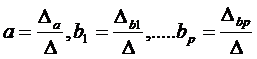, при этом

.

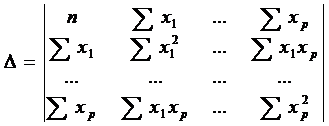Оценим коэффициенты регрессии МНК в матричной форме. Обозначим

, , , ,

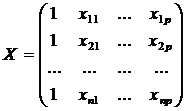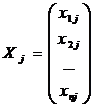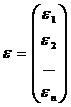Значения признака Матрица объясняющих Вектор Вектор Вектор

переменных, столбцами регрессора j случайных коэффициентов

которой являются X_j ошибок регрессии

Модель множественной регрессии примет вид

,

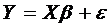где Х - детерминированная матрица, Y и 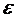 - случайные матрицы. Пусть 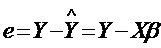, где  - вектор модельных значений. Сумма квадратов остатков минимизируется:

.

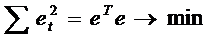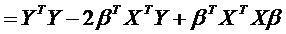
Необходимые условия получают дифференцированием  по вектору .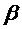

  .

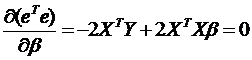
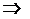
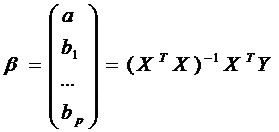Аналогично парной регрессии, можно показать, что вектор остатков е  всем независимым переменным и S = (1…1)^T, а вектор  - есть ортогональная проекция вектора Y на гиперплоскость, образованную S и Х. Кроме того,

, .

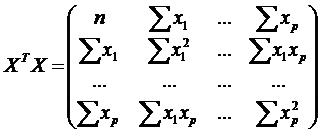Если перейти к стандартизованному масштабу:

, , … , ,

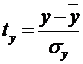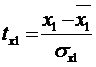уравнение регрессии примет вид:

,

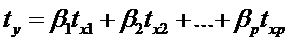где коэффициенты могут быть определены из системы уравнений

 ,

здесь 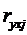 и 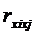 - парные коэффициенты корреляции.

Вернуться от стандартизованного масштаба к обычному можно с помощью соотношений:

, .

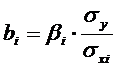И, наконец, параметры уравнения множественной регрессии можно определить с помощью ППП:

·        ППП Excel:

а) Сервис/Анализ данных/Описательная статистика

б) Сервис/Анализ данных/Корреляция

в) Сервис/Анализ данных/Регрессия

·        ППП Statgraphic:

а) Describe/Numeric Data/Multiple Variable Analysis/ в доп. меню поставить флажки на Summary Statistics, Correlations, Partial Correlations

б) Relate/Multiple Regression.

Пример. Известны следующие данные (условные) о сменной добыче угля на одного рабочего Y (т), мощности пласта Х₁ (м) и уровне механизации работ Х₂ (%), характеризующие процесс добычи угля на 7 шахтах. Предполагая, что между Y, X₁, X₂ существует линейная корреляционная зависимость, найти её аналитическое выражение.

Решение.

Проверим однородность выборки.

Так как все значения меньше 35 %, то выборка однородна, и её можно использовать для анализа.

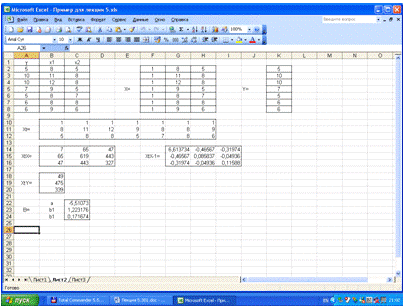
Вариант решения 1.

Расчет с помощью матричных операций.

Использование матричной формы записи формул и проведения расчетов имеет несколько преимуществ и недостатков.

Преимущества заключаются в том, что запись формул приобретает очень компактный вид: вид формул, представленных в матричном виде, не зависит от количества факторов, включенных в модель, и является очень удобным при расчетах характеристик многофакторных моделей.

Недостатком использования в расчетах матричных формул является необходимость хорошего знания матричной алгебры.

Приведем перечень используемых матричных операций.

Транспонирование - Вставка функции, Категория: Ссылки и массивы, Функции: ТРАНСП.

Вычисление обратной матрицы - Вставка функции, Категория: Математические, Функции: МОБР.

Умножение матриц - Вставка функции, Категория: Математические, Функции: МУМНОЖ.

Выполнение матричных функций имеют следующие особенности:

для результирующей матрицы нужно выделить необходимое количество ячеек;

для распространения действий на массив:

·        Выделить 1-ю ячейку с расчетами и все ячейки, на которые будет распространено действие функции;

·        Нажать и отпустить клавишу «F2»;

·        Последовательно нажать, не отпуская, клавиши «Ctrl», «Shift», «Enter», отпустить все три клавиши, и на экране появится содержимое всей матрицы.

Вариант решения 2.

1) Составим ,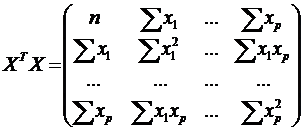

, ,

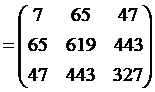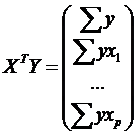
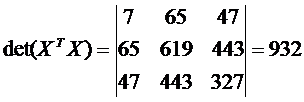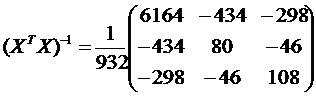 и

.

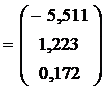Таким образом, уравнение множественной регрессии примет вид:

.

Вариант решения 3.

Вариант решения 4.

Получим уравнение регрессии в стандартизованном масштабе.

На практике часто бывает необходимо сравнение влияние на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии 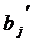и средние показатели эластичности Э_j:

, .

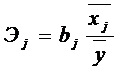Стандартизованный коэффициент регрессии показывает, на сколько величин S_y изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на S_xj, а средний показатель эластичности Э_j - на сколько % (от средней) изменится в среднем Y при увеличении только Х_j на1 %.

Пример.

Для данных предыдущего примера имеем:

)

)  ;

 .

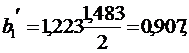
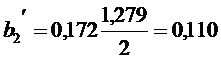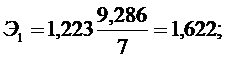
2. Ковариационная матрица оценок коэффициентов регрессии. Оценка дисперсии ошибок

Преобразуем вектор оценок 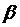 с учетом наличия случайной составляющей:

,

Т.е. оценки параметров, найденные по выборке, будут содержать случайные ошибки. регрессия дисперсия детерминация статистический

Вариации оценок параметров будут определять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматривают ковариационную матрицу К, являющуюся матричным аналогом дисперсии одной переменной

Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных. Так как  является несмещенной оценкой, то

, .

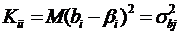В матричном виде будем иметь

,

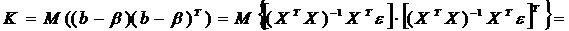
так как эти элементы Х - детерминированные величины.

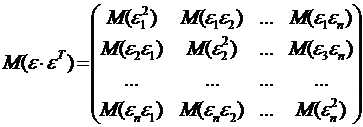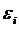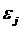В матрице  все элементы, не лежащие на главной диагонали, равны нулю в силу некоррелируемости  и  между собой, а все элементы, лежащие на главной диагонали равны одной и той же дисперсии 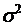: 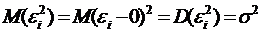. Поэтому  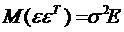и, следовательно, ковариационная матрица

.

Так как 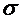² неизвестна, заменив её несмещённой оценкой - выборочной дисперсией,

,

где (n-p-1) - число степеней свободы, получим выборочную оценку ковариационной матрицы. Стандартные ошибки коэффициентов регрессии определяются:

1способ: , , 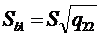…, где q_ii - диагональные элементы матрицы (Х^ТХ)^-1.

2 способ: , где R² - множественный коэффициент детерминации, R²_xix1…xp - коэффициент детерминации для зависимости x_i от остальных факторов.

3. Теорема Гаусса-Маркова

Предположим, что:

1. ;

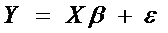. Х - детерминированная матрица 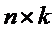, имеющая максимальный ранг k;

. ; .

Тогда оценка МНК  является наиболее эффективной (в смысле наименьшей дисперсии) оценкой в классе линейных несмещенных оценок.

Доказательство:

Обозначим , 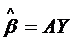. Любую другую оценку  можно представить в виде  , где С - некоторая матрица.

Докажем несмещенность оценок.

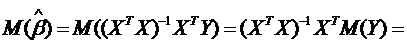
Так как оценка должна быть несмещенной, то

.

Используя СХ = 0, получим

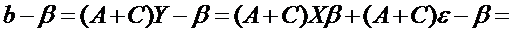
(так как AX = E и СХ = 0).

Вычислим ковариационную матрицу вектора b.

.

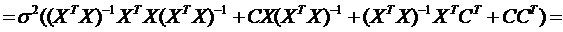
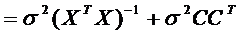Таким образом, 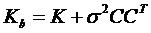 или .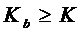

Теорема доказана.

4. Коэффициент детерминации, скорректированный коэффициент детерминации

Для оценки взаимосвязи между зависимой переменной и совокупностью объясняющих переменных используют множественный (совокупный) коэффициент (индекс) корреляции R или коэффициент детерминации R². Как и раньше коэффициент детерминации R² равен отношению  и характеризует долю вариации зависимой переменной, объясненную уравнением регрессии, 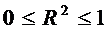. Для расчета можно использовать более удобную формулу:

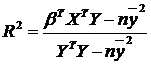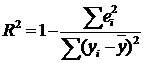 или  или ,

где 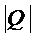 - определитель матрицы парных коэффициентов корреляции, q₁₁ - алгебраическое дополнение элемента r₁₁.

Множественный коэффициент детерминации можно рассматривать как меру качества уравнения регрессии, характеристику прогностической силы регрессионной модели. Чем ближе R² к 1, тем лучше регрессия описывает зависимость между объясняющими и зависимой переменными.

Недостаток R² состоит в том, что его значение не убывает с ростом числа объясняющих переменных. Это происходит потому, что:

) оптимизация при определении оценок происходит по критерию, отличному от R^2;

2) R² возрастает при добавлении ещё одного регрессора и всегда можно добиться R² = 1, что не будет иметь экономического смысла.

В этом смысле предпочтительней скорректированный коэффициент детерминации

,

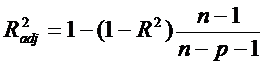который может уменьшаться при введении в регрессионную модель переменных, не оказывающих существенного влияния на зависимую переменную. Можно заметить, что 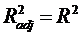 только при R² = 1.  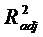может принимать отрицательные значения (например, при R² = 0). Для расчета можно использовать формулу:

.

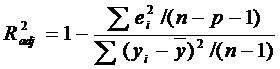Пример. Вычислим коэффициент детерминации и скорректированный коэффициент детерминации

=; R = 0,967.

5. Частная корреляция

В случае парной регрессии естественной мерой зависимости (линейной) является выборочный коэффициент корреляции между переменными. Использование многомерной регрессии позволяет обобщить это понятие на случай, когда имеется несколько независимых переменных. Корректировка здесь необходима по следующим соображениям: высокое значение коэффициента корреляции между исследуемой зависимой и какой-либо независимой переменной может означать высокую степень зависимости, но может быть обусловлено и другой причиной. Имеется третья переменная, которая оказывает сильное влияние на две первые, что и является причиной высокой корреляции.

Поэтому возникает естественная задача найти «чистую» корреляцию между двумя переменными, исключив (линейное) влияние других факторов. Это можно сделать с помощью коэффициента частной корреляции.

Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.

Пусть , 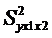- соответствующие остаточные дисперсии регрессий Y на X₁ и Y на X₁, X₂. Влияние фактора X₂ на результат можно определить коэффициентом частной корреляции

,  .

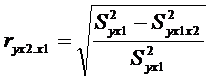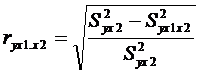Можно получить другую формулу коэффициента частной корреляции:

 ,

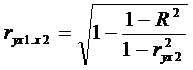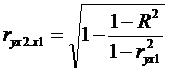
Или , .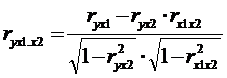

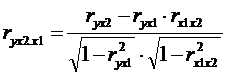Рассмотренные показатели частной корреляции называют коэффициентами частной корреляции 1-го порядка, так как они фиксируют тесноту связи двух переменных при закреплении (элиминировании) влияния одного фактора. Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Коэффициенты парной корреляции называют коэффициентами нулевого порядка. Если рассматривается регрессия с числом факторов р, то возможны частные коэффициенты корреляции 1-го, 2-го, …, (р-1)-го порядков, т.е. влияние, например, х₁ можно оценить при разных условиях независимости действия других факторов: , , 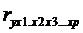. Сопоставление коэффициентов частной корреляции разного порядка по мере увеличения числа включаемых факторов показывает процесс «очищения» зависимости результативного признака с исследуемым фактором.

Выборочным частным коэффициентом корреляции между переменными x_i и x_j при фиксированных значениях остальных (р-2) переменных называют выражение

,

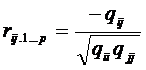где - алгебраические дополнения элементов  матрицы выборочных коэффициентов корреляции. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле:

.

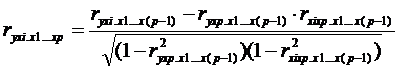В частности, при трех факторах возможно вычисление трех коэффициентов частной корреляции 2-го порядка: , , 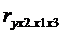, например,

.

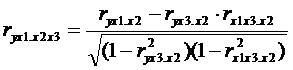Например. Составим матрицу Q парных коэффициентов корреляции, частные коэффициенты корреляции.

; ; ;

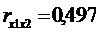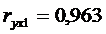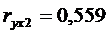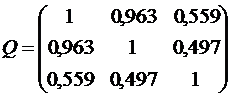; det(Q)=0,04823; q₁₁ = 1-0,497² = 0,75299;

R = ..

; ; .

Сравнивая частные коэффициенты корреляции с соответствующими парными коэффициентами, видим, что за счет «очищения» связи наибольшему изменению подвергся коэффициент корреляции между х₁ и х₂: был 0,497 - стал -0,185. Это пример ложной корреляции, так как х₁ - мощность пласта не может зависеть от х₂ - уровня механизации. А коэффициенты корреляции между у и х₁, у и х₂ после «очищения» несколько снизились от 0,963 до 0,952 и от 0,599 до 0,344, что по-видимому, соответствует действительности.

Зная частные коэффициенты корреляции, можно определить совокупный коэффициент корреляции по формуле:

.

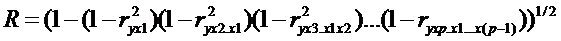6. Проверка статистических гипотез, доверительные интервалы

Проверка значимости коэффициентов регрессии.

Как и в случае парной регрессии можно показать, что вектор оценок  имеет нормальное распределение со средним 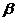 и матрицей ковариаций

, т е.

.

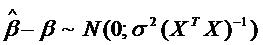Таким образом, случайные величины

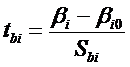 и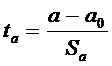

имеют распределение Стьюдента с (n-р-1) степенями свободы. В общем случае проверяются гипотезы: Н₀: а = а₀ или о значимости Н₀: а = 0

Н₀: b = b₀ Н₀: b = 0

Проверка состоит в следующем:

если 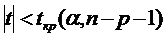, то нет оснований отвергать Н₀ (р- число факторов);

если 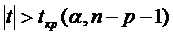, то Н₀ отвергают.

Соответствующие доверительные интервалы для оценок коэффициентов регресси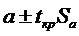и (): () и ().

Пример.

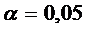, k = n - p - 1 = 7-2-1 = 4, t_kp(0,05;4) = 2,78.

значим при 5 - % -ом уровне значимости.

Доверительный интервал: (0,698; 1,748).

2)      H₀: 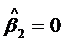,   Н₀ принимается и  не значим.

Доверительные интервалы.

Наряду с интервальным оцениванием коэффициентов регрессии весьма важным для оценки точности определения зависимой переменной является построение доверительного интервала для функции регрессии или условного математического ожидания зависимой переменной М_х(y). Обобщая соответствующие выражения на случай множественной регрессии, можно получить доверительный интервал:

,

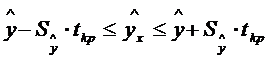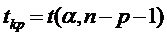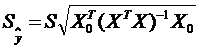, - стандартная ошибка, .

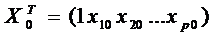Доверительный интервал для индивидуальных значений зависимой переменной y_i примет вид:

, .

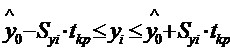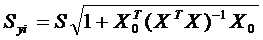Доверительный интервал для параметра 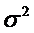 во множественной регрессии строится аналогично парной модели:

.

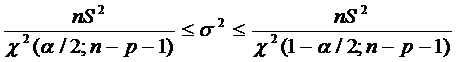Пример. Известно: S² = 0,4175; S = 0,64614;

 ; .

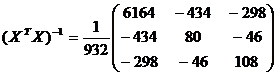По данным примера оценить сменную добычу угля на одного рабочего для шахт с мощностью пласта 10 м и уровнем механизации 6,5 %. Найти 95 % -й доверительный интервал для индивидуального и среднего значений и интервальную оценку дисперсии при .

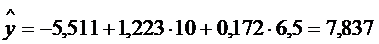) (т).

) , ,

=.

, .

) ; .

.

) ; ; ; ;

;

;

; .

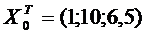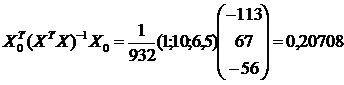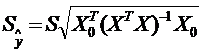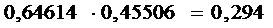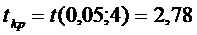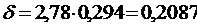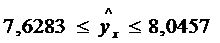
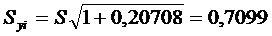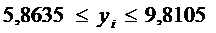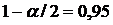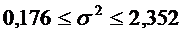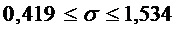Оценка надежности результатов множественной регрессии и корреляции.

Для определения статистической значимости R² проверяется гипотеза

Н₀: R² = 0 с помощью статистики F =  .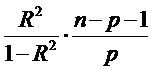

Если F < F_кр(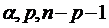), то Н₀ нет оснований отвергать или R² статистически не значим, не значимо и уравнение в целом. В противном случае - уравнение и R² значимы.

Пример.

.

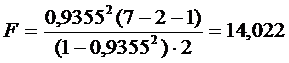F_kp (0,05;2;4) = 6,94.

Т.к. F > F_kp, то уравнение значимо.

Оценивается не только значимость уравнения в целом, но и значимость фактора, дополнительно включенного в модель. Мерой оценки включения фактора в модель служит частный F- критерий, F_xi.

Если оценивается значимость влияния фактора х_р после включения в модель факторов х₁, х₂,…,х_р-1, то формула частного F- критерия примет вид:

 .

В общем виде для x_i

.

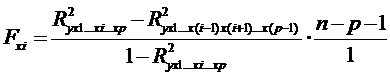С помощью частного F- критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор вводится в уравнение последним. Зная F_xi можно определить t-критерий: 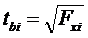. Взаимосвязь частного коэффициента корреляции, частного F-критерия и t-критерия для коэффициентов чистой регрессии можно использовать в процедуре отбора факторов (на каждом шаге исключается фактор с наименьшим незначимым значением F_xi или t_bi).

Литература

1.   Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. М.: МГУ Изд-во «ДИС», 2007.

2.      Кулинич Е.И. Эконометрия. М.: Финансы и статистика, 2001.

.        Мацкевич И.П., Свирид Г.П. Высшая математика: Теория вероятностей и математическая статистика. Мн.: Вышэйшая школа, 1993.

.        Булдык Г.М. Сборник задач и упражнений по высшей математике: Теория вероятностей и математическая статистика. Мн.: Вышэйшая школа, 1996.

.        Сошникова Л.А., Тамашевич В.Н., Уебе Г., Шефер М. Многомерный статистический анализ в экономике М.: ЮНИТИ - ДАНА, 1999.