Основы механики
1. Движение
материальной точки задано уравнением 
, где 
; 
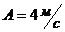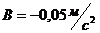. Определить момент времени, в
который скорость точки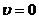 
. Найти
координату и ускорение в этот момент. Построить графики координаты, пути,
скорости и ускорения этого движения.
Дано: , , .
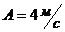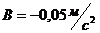Найти: t, x, a.
Решение: Мгновенная скорость -
первая производная пути по времени:
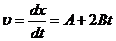
из формулы видно, что скорость
изменяется линейно и движение равноускоренное. Скорость точки будет равна нулю :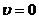
,
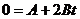Откуда время остановки:
.
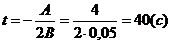Координата точки в этот момент
времени:
.
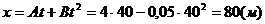Ускорение - первая производная
скорости или вторая производная пути по времени: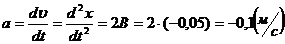 
.
Графики координаты и пути одинаковы
(до 
):
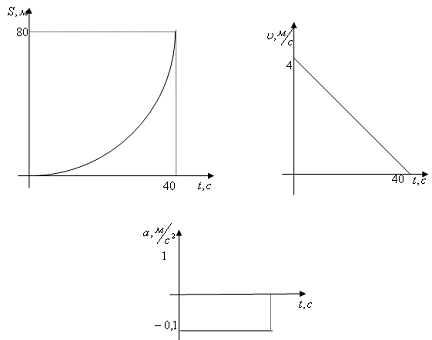
2. Колесо, вращаясь равнозамедленно,
за время 2 уменьшило свою частоту от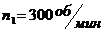 
до 
. Найти угловое ускорение колеса и
число оборотов колеса за это время.
Дано: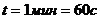 
, 
, 
.
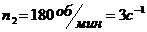Найти: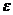 
, N.
Решение: Угловое ускорение -
изменение угловой скорости в единицу времени:
,
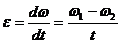Зная угловую скорость:
,
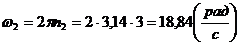найдем угловое ускорение:
.
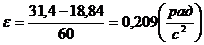Так как движение равнозамедленно, то
угол поворота:
,
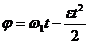С другой стороны угол поворота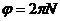 
и тогда
выразим число оборотов:
.
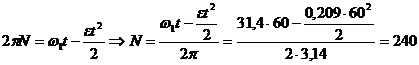Без промежуточных расчетов:
Угловое ускорение - изменение
угловой скорости в единицу времени:
,
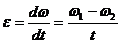Зная угловую скорость:
и
,
найдем угловое ускорение:
.
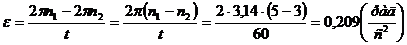Так как движение равнозамедленно, то
угол поворота:
,
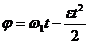С другой стороны угол поворота 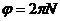и тогда
выразим число оборотов:
.
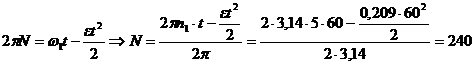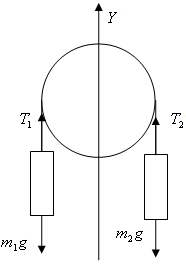
3. Через блок
перекинута нить, к концам которой подвешены грузы с массам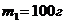и 
и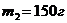 
. На какое
расстояние опустится больший груз за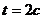 
.
Найти: S.
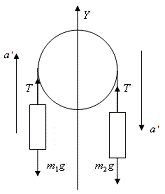
Решение: Так как второй груз по
массе больше, чем первый, то он соответственно будет двигаться вниз, а первый
вверх с таким же ускорением. (Так как о блоке ничего не сказано, считаем его
неподвижным и силы натяжения нити по разные стороны блока считаем одинаковыми).
Проекции сил на вертикальную ось OY, действующие на каждый груз по II закону
Ньютона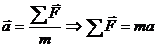 
, будут:
,
Откуда выразим силы натяжения нитей:
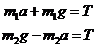
Так как силы натяжений равны с
каждой стороны блока, то:
,
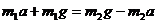Откуда выразим ускорение груза:
.
С этим ускорением груз за 2 секунды
переместился на:
.
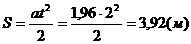ускорение
угловой инерция оборот
4. Нить с
привязанными к ее концам грузами массами m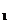
=50г и m
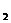=60г
перекинута через блок диаметром D=4см. Определить момент инерции
блока, если под действием силы тяжести грузов он получил угловое ускорение 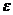=1,5рад/с
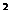. Трением
пренебречь.
Дано: 
, 
, 
, 
.
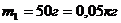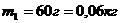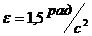Найти: J.
Решение: Так как второй груз по
массе больше, чем первый, то он соответственно будет двигаться вниз, а первый
вверх с таким же ускорением. Линейное ускорение грузов через угловое:
.
Проекции сил на вертикальную ось OY,
действующие на каждый груз по II закону Ньютона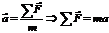 
, будут:
,
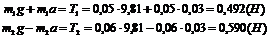
По закону динамики вращательного
движения:
.
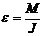Момент возникает из-за действия сил
натяжения нитей по обеим сторонам блока и поэтому:
,
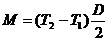тогда уравнение примет вид:
,
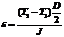Откуда выразим момент инерции блока:
.
Без промежуточных расчетов: Так как
второй груз по массе больше, чем первый, то он соответственно будет двигаться
вниз, а первый вверх с таким же ускорением. Линейное ускорение грузов через
угловое:
.
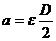Проекции сил на вертикальную ось OY,
действующие на каждый груз по II закону Ньютона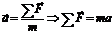 
, будут:
,
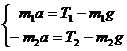откуда выразим силы натяжения нитей:
По закону динамики вращательного
движения:
.
Момент возникает из-за действия сил
натяжения нитей по обеим сторонам блока и поэтому:
,
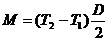тогда уравнение примет вид:
Откуда выразим момент инерции блока:
.
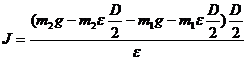Подставив численные значения:
.
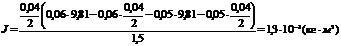