Анализ электрической цепи постоянного тока
Министерство
образования Российской Федерации
Уфимский
Государственный Авиационный Технический Университет
Кафедра
Теоретических Основ Электротехники
Анализ
электрической цепи постоянного тока
Выполнила:
студентка группы
ИКТ-203 Симбирцева
Д.С.
Проверила:
доцент Медведева Л.
С.
Уфа
2012
Задание
1. Согласно
индивидуальному заданию, составить схему электрической цепи. В распечатке
исходных данных сопротивления заданы в Омах, ЭДС - в Вольтах, ток источника
тока - в Амперах.
2. Нарисовать
ориентированный граф схемы.
3. Составить
топологические матрицы схемы: соединений А, главных контуров В .
4. Проверить
соотношение: 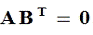
5. Составить
уравнения по законам Кирхгофа в алгебраической и матричной формах.
6. Определить
токи в ветвях схемы методом контурных токов.
7. Определить
токи в ветвях схемы методом узловых потенциалов.
8. Проверит
правильность расчетов по законам Кирхгофа.
9. Составить
баланс мощностей.
10.Для
контура, содержащего две ЭДС составить потенциальную диаграмму.
11.Для
ветви с сопротивлением R1 определить ток методом эквивалентного генератора.
электрическая цепь
ток потенциал
1.
Согласно индивидуальному заданию, составим схему электрической цепи:
Исходные данные:
E1
(04) =-10 B2
(05) =50 B
R1
(41) =90 Oм2 (53)
=60 Ом
R3
(31) =60 Ом4 (12) =50 Ом
R5 (32) =40
Ом6
(20)
=90
Ом
J1
(01)
=6
A
2.
Нарисуем ориентированный граф схемы:

3.
Составим топологические матрицы схемы
матрица соединений А:

где к - номера ветвей, g
- номера узлов.
матрица главных контуров В:
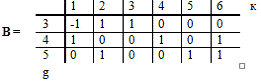
где к - номера ветвей, g
- номера хорд.
4.
Проверим соотношение 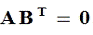
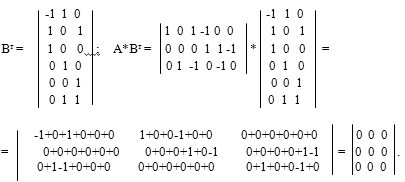
Равенство верно
. Составим
уравнения по законам Кирхгофа в алгебраической и матричной формах
Согласно составленному дереву графа, у которого
3 ветви, составим 3 уравнения по первому закону Кирхгофа, и 3 уравнения по
второму закону Кирхгофа.
запишем первый закон Кирхгофа в матричной форме:
А*I
= - А*J;
где I-
матрица-столбец неизвестных токов, J-матрица-столбец
токов источников тока.
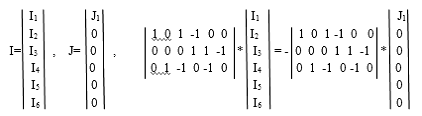
- запишем первый закон Кирхгофа в алгебраической
форме:
1 +
I3 - I4 = J1,4 + I5 - I6
= 0,2 - I3 - I5 = 0.
- запишем второй закон Кирхгофа в матричной
форме:
*U=B*E;
где U-
матрица-столбец неизвестных напряжений, Е-матрица-столбец известных источников
ЭДС.

- запишем второй закон Кирхгофа в алгебраической
форме:
-R1*I1 + R2*I2
+ R3I3 = - Е1
+ Е2,1*I1
+ R4*I4 + R6*I6 = E1,2*I2
+ R5*I5
+
R6*I6
= E2.
6. Определим токи в ветвях схемы методом
контурных токов
Данный метод основан на втором законе Кирхгофа.
Перерисуем схему: преобразуем источник тока в
эквивалентный источник ЕДС, выберем произвольно направление токов в ветвях
цепи, и произвольно выберем направление обхода контуров.
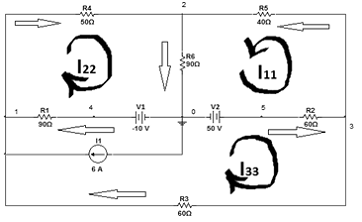
- Запишем систему уравнений для
нахождения контурных токов в общем виде:
R11* I11 +R12*I22
+ R13*I33 = E11,21*I11 +
R22*I22 + R23*I33 = E22,31*I11
+ R32*I22 + R33*I33 = E33.
- Выразим собственные и смежные
сопротивления контуров:
R11 = R2 + R5
+ R6,22 = R1 + R4+ R6,33
= R1 + R2 + R3,12 = R21
= R6,13
= R31
= R2,
R23=
R32
= -R1.
- Подставим численные значения:
11
= 190
Ом,
R22
= 230 Ом,
R33
= 210 Ом,
R12
= R21
= 90 Ом,
R23
= R32
= -90 Ом.
- Выразим контурные ЭДС:
11
= E2,22 = E1
+ J1*R1,33
= E2
-
E1
-J1*R1.
- Подставим численные значения:
11
= 50
B,22 = 530
B,33 = -480
B.
- Составим систему уравнений для нахождения
контурных токов
(R2 + R5 + R6)*I11
+ R6*I22 + R2*I33 = E2,6*I11
+ (R1 + R4+ R6)*I22 - R1*I33
= E1 + J1*R1,2*I11 - R1*I22
+ (R1 + R2 + R3)*I33 = E2 -
E1 -J1*R1.
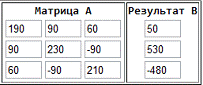
- Подставим численные значения:
Решим данную систему уравнений, используя
программу Gauss, получим
значения контурных токов:
11
= -0.08633А,
I22
= 1.74619А,
I33
= -1.51279А.
Выразим все истинные токи через контурные токи:
1
= I22 - I33 - J1,2 = I11 + I33,3
= I33,
I4 = I22,5
= I11,
I6
= I11
+ I22,
- Подставим численные значения:
1
= -2.74102 A,2 = -1.59912 A,3 = -1.51279А,4
= 1.74619А,5 =
-0.08633А,6
=1.65986 A.
7. Определим токи в ветвях схемы методом узловых
потенциалов
Данный метод основан на первом законе Кирхгофа и
на обобщенном законе Ома. По методу узловых потенциалов можно составить столько
уравнений, сколько ветвей у дерева графа, следовательно в нашем случае 3
уравнения. В схеме заземлим нулевой узел (φ0
= 0 B).
- Запишем систему уравнений для
нахождения потенциалов в общем виде:
φ1*g11
+ φ2*g12
+ φ3*g13
=
J11,
φ1*g21
+ φ2*g22
+ φ3*g23
= J22,
φ1*g31
+ φ2*g32
+ φ3*g33
= J33.
- Уравнение в матричной форме имеет вид:
φкк*gкк=
Jкк
- Посчитаем проводимости ветвей:
11
= g1 + g3 + g4 ,22 = g4
+ g5 + g6 ,33 = g2 + g3
+ g5,12
= g21
= - g4,
g13
= g31
= - g3,
g23
= g32
= - g5
,
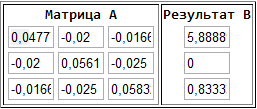
- Подставим численные значения:
11
= 1/ R1 +1/ R3 +1/ R4 =0.04777См,22
= 1/ R4 +1/ R5 +1/ R6 = 0.05611См,33
= 1/ R2 +1/ R3 +1/ R5 = 0.05832 См,
g12 = g21 = -
1/ R4 = -0.02См,
g13 = g31 = -
1/ R3 = -0.01666 См,23
= g32 = - 1/ R5 = -0.025 См,
- Посчитаем узловые токи:
11
= E1*g1+
J1,
J22
= = 0,
J33
= E2*g2.
- Подставим численные значения:
11
= 5.88889 А,
J22
= 0А,
J33
= 0.83333 А.
Cоставим
систему уравнений для нахождения потенциалов:
φ1*(1/
R1 +1/
R3 +1/
R4 )
+ φ2*(-
1/ R4 )
+ φ3*(-
1/ R3 )
= E1*g1+
J1,
φ1*(-
1/ R4 )
+ φ2*(1/
R4 +1/
R5 +1/
R6 ) +φ3*(-
1/ R5 )
= 0,
φ1*(-
1/ R3 )
+ φ2*(-
1/ R5 )+
φ3*(1/
R2 +1/
R3 +1/
R5 )
= E2*g2.
Решим данную систему уравнений, используя
программу Gauss, получим
значения потенциалов:
φ1
= 236.49459B,
φ2
= 149.42932B,
φ3
= 146.01826B.
- Подсчитаем значения токов по закону
Ома:
1
= (- φ1+
E1 )/R1,2 = (-φ3+
E2) /R2,3 = (φ3
- φ1
)/R3,4 = (φ1
- φ2
)/R4,5 = (φ3
- φ2)/R5,6
= φ2 /R6,
- Подставим численные значения:
1
= -2.73883А,
I2
= -1.6003А,
I3
= -1.50793А,
I4
= 1.7413А,
I5
= -0.08528А,
I6
= 1.66033А.
8. Проверим правильность расчетов по законам
Кирхгофа
- составим уравнения по первому и второму
законам Кирхгофа:
1 +
I3 - I4 = -J1,4 + I5 - I6
= 0,2 - I3 - I5 = 0,
R1*I1 + R2*I2
+ R3I3 = -E1 + E21*I1 +
R4*I4 + R6*I6 = E1,2*I2
+R5*I5 + R6*I6 = E2.
составим матрицу:
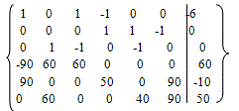
Решим данную систему уравнений, используя
программу Gauss, получим
значения силы токов:
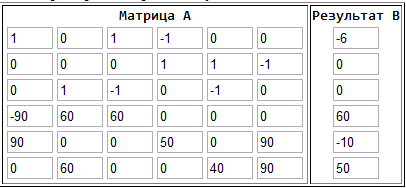
1
= -2.74111 A,2 = -1.599 A,3 = -1.51267 A,4 =
1.74619A,5 = -0.08328A,6
= 1.65989 A.
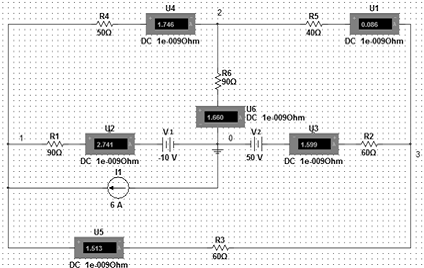
9. Составим баланс мощностей
Баланс мощностей является следствием закона
сохранения энергии и является критерием проверки правильности полученных
результатов.

Мощность, генерируемая источником ЭДС и тока
(сумма алгебраическая), равняется мощности потребляемой приемником.
Для данной схемы:
Е2*I2
+ E6*I6 + J6*φ2
= R1*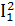 + R2*
+ R2* + R3*
+ R3* + R4*
+ R4*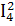 + R5*
+ R5*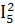 + R6*
+ R6*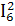 ,
,
Сравним: 1366.6373 Вт 1366.5286
Вт, следовательно, наши расчеты верны.
1366.5286
Вт, следовательно, наши расчеты верны.
10. Для контура, содержащего два ЭДС составим
потенциальную диаграмму
- Составим потенциальную диаграмму для контура
0-4-1-2-3-5-0
φ0=
0 B,
φ4
= Е1
=-10 В,
φ1
= φ4+
I1*R1 = Е1+
I1*R1= -10+2.744*90 = 236,96B,
φ2
= φ1-
I4*R4 = 236.96 - 1.746*50= 149.66 B,
φ3
= φ2 -
I5*R5 =149.66 - 0.086*40= 146.22 B,
φ5
=
φ3
- I2*R2
=
146.22 - 1.599*60=50 B,
φ0
= φ5 -
Е2= 50 - 50=0 В (См. приложение)
11. Для ветви с сопротивлением R1
определим ток методом эквивалентного генератора
Разомкнём ветвь 1 и найдем UXX,
которое
равно ЭДС генератора ЕГ. Для этого воспользуемся методом узловых
потенциалов (φ0
=0)
XX(1)=
φ1

11
= 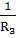 +
+
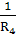 =
0.
0367 См,
=
0.
0367 См,
g22
= 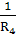 +
+
 +
+
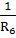 =0,0561
См ,
=0,0561
См ,
g33
= 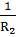 +
+
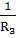 +
+
 =0,0583
См ,
=0,0583
См ,
g12
= g21
= - 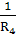 =
=-0,02 См,
=
=-0,02 См,
g13
= g31
= - 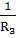 =
-0,0167 См,
=
-0,0167 См,
g23
= g32
= -  =
-0,025 См,
=
-0,025 См,
оставим систему уравнений для нахождения
потенциала φ1:
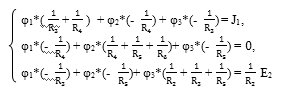
Решим данную систему уравнений, используя
программу Gauss, получим
значения потенциала φ1:
φ1
= 412 B,
ЕЭГ =UXX(
10) =412 B.
2) для нахождения Rвн
= RГ
закоротим
все источники ЭДС, а источники тока разомкнем, получим:
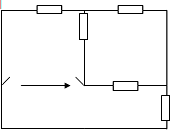
преобразуем треугольник в звезду, получим:
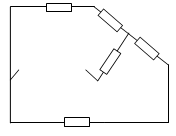
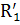 =
= 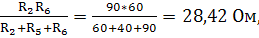
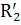 =
= 
 =
= 
Rвн=
RГ 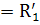 +
+
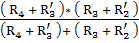 =
12,5+
=
12,5+  =63,791
Ом.
=63,791
Ом.
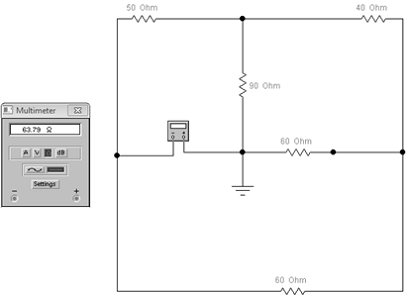
3) Найдем I1,
составим уравнение по второму закону Кирхгофа:
1*R1
+ RГ*I1
= EЭГ,1=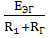 =-
=-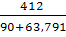 =- 2,69
А.
=- 2,69
А.
4) Определим IКЗ:
IКЗ
= 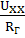 ,
,
IКЗ
=-  =
-6,559 А.
=
-6,559 А.

Вывод
В данной расчетно-графической работе был
проведен анализ электрической цепи постоянного тока, а именно:
составила схему электрической цепи;
нарисовала ориентированный граф схемы;
составила топологические матрицы схемы:
соединений А, главных контуров В, проверила соотношение А*Вт = 0;
определила токи в ветвях схемы тремя методами:
методом контурных токов, методом узловых потенциалов, методом эквивалентного
генератора. По законам Кирхгофа проверила правильность расчетов;
составила баланс мощности, для контура,
содержащего две ЭДС составила потенциальную диаграмму.
Значения силы токов, которые были определены в
каждом из трех вышеуказанных методов, совпали. Имела место быть некоторая
погрешность, в результате неточного вычисления, но она не имела большого
значения. Следует сделать вывод, что значения характеристик цепи не зависят от
метода ее исследования.