|
Себестоимость
единицы продукции, руб.
|
Число
заводов
|
|
до
1000
|
4
|
|
1000-1020
|
11
|
|
1020-1040
|
26
|
|
1040-1060
|
24
|
|
1060-1080
|
14
|
|
1080-1100
|
5
|
Решение
1. Обозначим
себестоимость единицы продукции xi,
а число заводов через fi.
а) Для начала
найдем среднюю себестоимость единицы продукции с помощью средней арифметической
взвешенной:
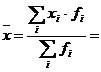 (990 * 4 + 1 010 * 11 + 1 030 * 26
+ 1 050 * 24 + 1 070 * 14 + 1 090 * 5) / (4 + 11 + 26 + 24 + 14 + 5) = 87 480
/ 84 = 1 041,43 (руб.).
(990 * 4 + 1 010 * 11 + 1 030 * 26
+ 1 050 * 24 + 1 070 * 14 + 1 090 * 5) / (4 + 11 + 26 + 24 + 14 + 5) = 87 480
/ 84 = 1 041,43 (руб.).
б) Определим моду и медиану.
Модой называют значение признака,
которое наиболее часто встречается в данной совокупности. Мода рассчитывается
по формуле:
Мо = х0 + h * 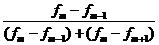 ,
,
где х0 - нижняя граница
интервала;- величина интервала;m - частота модального интервала;m-1
- частота интервала, предшествующего модальному;m+1 - частота
интервала, следующего за модальным.
В нашем случае модальным интервалом
является интервал 102 -1040.
Тогда Мо = 1 020 + 20 * (26 - 11) /
((26 - 11) + (26 - 24)) = 1037,65 руб.
По определению, медиана - это
значение варьирующего признака, которое делит исследуемый ряд на две равные
части.
Медиана вычисляется по формуле:
Ме = х0 + h * 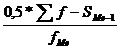 ,
,
где х0 - нижняя граница
медианного интервала;- величина интервала;
SMe-1 - сумма
частот интервалов, предшествующих медианному;
fMe - частота
медианного интервала.
Накопленная частота Si получается
суммированием частот ряда распределения, от первого до i-го
элемента. Значения накопленных частот представим в таблице:
|
Себестоимость
единицы продукции, руб.
|
до
1000
|
1000-1020
|
1020-1040
|
1040-1060
|
1060-1080
|
1080-1100
|
|
Число
заводов (Si)
|
4
|
15
|
41
|
79
|
84
|
Медианный интервал:
1040-1060.
Тогда Ме = 1040 +
20 * ((0,5 * 84 - 41) / 24) = 1040,83 руб.
Вывод: большее
число заводов имеет среднюю себестоимость единицы продукции в размере 1 041,43
руб. При этом максимальное число заводов имеют себестоимость единицы продукции
1 037,65 руб., что соответствует модальному значению. Медианное значение
размера себестоимости единицы продукции равно 1 040,83 руб., т.е. половина
числа заводов имеет размер себестоимости единицы продукции от значения до 1 000
руб. до 1 040,83 руб., а другая половина - от 1 040,83 руб. до 1 100 руб.
3. Определить
сводный индекс цен и общую экономию от изменения цен
|
Виды
изделий
|
Продано,
шт.
|
Цена,
руб.
|
|
базисный
период (q0)
|
отчетный
период
(q1)
|
базисный
период
(p0)
|
отчетный
период
(p1)
|
|
А
|
35
000
|
37
000
|
3,2
|
3,1
|
|
Б
|
14
000
|
12
500
|
2,5
|
2,8
|
|
В
|
3
500
|
3
300
|
12
|
15
|
Решение
Сводный индекс цен
рассчитывается по формуле:
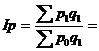 (3,1*37 000 + 2,8*12 500 + 15*3
300) / (3,2*37 000 + 2,5*12 500 + 12 * 3 300) = 199 200 / 189 250 = 1,053.
(3,1*37 000 + 2,8*12 500 + 15*3
300) / (3,2*37 000 + 2,5*12 500 + 12 * 3 300) = 199 200 / 189 250 = 1,053.
Этот индекс показывает, каким было
бы изменение цен, если бы величины продаж в базисном периоде были такими же,
как в отчетном. Данный индекс равен 1,053, т.е. изменение цен составляет 5,3%.
Общая экономия или перерасход от
изменения цен рассчитывается как разность между числителем и знаменателем:
Э = 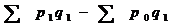 = 199 200 - 189 250 = 9 950 руб.
= 199 200 - 189 250 = 9 950 руб.
Т.е. в нашем случае был получен
перерасход в размере 9 950 руб.
4. Определить общий индекс
физического объема продукции на основе следующих данных по заводу:
|
Вид
продукции
|
Изменение
объема производства в отчетном периоде (в % к базисному)
|
Реализовано
продукции в базисном периоде, тыс.руб.
|
|
1
|
+6,4
|
140
|
|
2
|
-2,8
|
250
|
|
3
|
+3,2
|
340
|
Решение
Индекс физического
объема продукции рассчитывается по формуле:
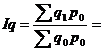 (1,064 * 140 + 0,972 * 250 + 1,032
* 340) / (140 + 250 + 340) = 742,84 / 730 = 1,018.
(1,064 * 140 + 0,972 * 250 + 1,032
* 340) / (140 + 250 + 340) = 742,84 / 730 = 1,018.
Таким образом, можно сделать вывод о
том, что стоимость продукции в отчетном периоде по сравнению с базисным периодом
возросла на 1,8% за счет увеличения физического объема продукции.
5. Определить тенденцию
динамического ряда, применив сглаживание способом скользящей средней на основе
данных о валовом сборе зерна, млн. т.
|
Годы
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
Сбор
|
7,4
|
8,6
|
8,1
|
8,8
|
9,4
|
8,9
|
9,3
|
9,7
|
9,5
|
9,6
|
9,3
|
Решение
1) Выравнивание
динамического ряда методом скользящей средней:
|
Годы
|
Сбор,
млн. т.
|
Сумма
сбора по 3-летиям, млн. т., yi
|
Трехлетняя
скользящая средняя, млн. т., ci
|
|
1
|
7,4
|
-
|
-
|
|
2
|
8,6
|
24,1
|
8,03
|
|
3
|
8,1
|
25,2
|
8,40
|
|
4
|
8,5
|
25,4
|
8,47
|
|
5
|
8,8
|
26,7
|
8,90
|
|
6
|
9,4
|
27,1
|
9,03
|
|
7
|
8,9
|
27,6
|
9,20
|
|
8
|
9,3
|
27,9
|
9,30
|
|
9
|
9,7
|
28,5
|
9,50
|
|
10
|
9,5
|
28,8
|
9,60
|
|
11
|
9,6
|
28,4
|
9,47
|
|
12
|
9,3
|
-
|
-
|
Таким образом, мы
взяли в качестве укрупненного интервала период в 3 месяца. Тогда трехлетняя
скользящая средняя рассчитывается по следующей формуле: ci
= yi / 3. Таким
образом, в данном случае имеется тенденция увеличения сбора зерна по годам.
. По приведенным
ниже данным определите внутригрупповую, межгрупповую, общую дисперсию основных
производственных фондов предприятий двух управлений, эмпирическое
корреляционное отношение
|
Группы
предприятий по стоимости основных фондов, млн. руб.
|
Число
предприятий по управлению
|
Итого
|
|
первое
|
второе
|
5
|
4
|
9
|
|
5-7
|
4
|
6
|
10
|
|
7-9
|
7
|
5
|
12
|
|
9-11
|
2
|
4
|
6
|
Решение
Для начала найдем значения средней
стоимости основных фондов по всей рассматриваемой совокупности (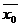 ), а также
внутригрупповые средние значения стоимости основных фондов соответственно по
первому и второму управлениям (
), а также
внутригрупповые средние значения стоимости основных фондов соответственно по
первому и второму управлениям (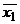 и
и 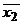 ).
).
Общую среднюю ищем по формуле
взвешенной средней арифметической:
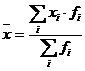 ,
,
причем при вычислении используем
значения, соответствующие серединам интервалов распределения основных фондов, а
в качестве весов берем количество предприятий, указанное в колонке «Итого»:
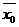 = (4*9 + 6*10 + 8*12 + 10*6) / (9 +
10 + 12 + 6) = 252 / 37 = 6,81 млн. руб.
= (4*9 + 6*10 + 8*12 + 10*6) / (9 +
10 + 12 + 6) = 252 / 37 = 6,81 млн. руб.
При вычислении внутригрупповых
средних в качестве весов берем количество предприятий, соответствующее нужной
группе:
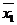 = (4*5 + 6*4 + 8*7 + 10*2) / (5 + 4
+ 7 + 2) = 120 / 18 = 6,67 (млн. руб.).
= (4*5 + 6*4 + 8*7 + 10*2) / (5 + 4
+ 7 + 2) = 120 / 18 = 6,67 (млн. руб.).
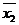 = (4*4 + 6*6 + 8*5 + 10*4) / (4 + 6
+ 5 + 4) = 132 / 19 = 6,95 (млн. руб.).
= (4*4 + 6*6 + 8*5 + 10*4) / (4 + 6
+ 5 + 4) = 132 / 19 = 6,95 (млн. руб.).
Внутригрупповая дисперсия
характеризует вариацию, обусловленную влиянием факторов, не имеющих отношения к
подразделению предприятий на группы по управлениям. Ее значение в каждой группе
рассчитывается по формуле:
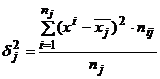 ,
,
где xi - середина i-го
интервала в группировке по стоимости основных фондов;
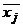 - внутригрупповая средняя величина
стоимости основных фондов в j-й группе;
- внутригрупповая средняя величина
стоимости основных фондов в j-й группе;
nij - число
предприятий, относящихся к j-й группе и одновременно попадающих
в i-й интервал
по стоимости основных фондов;
nj - общее
число предприятий в j-й группе.
Получим следующие значения для
внутригрупповых дисперсий:
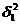 = ((4 - 6,67)2*5 + (6 -
6,67)2*4 + (8 - 6,67)2*7 + (10 - 6,67)2*2) /
(5 + 4 + 7 + 2) = 72 / 18 = 4 млн. руб.
= ((4 - 6,67)2*5 + (6 -
6,67)2*4 + (8 - 6,67)2*7 + (10 - 6,67)2*2) /
(5 + 4 + 7 + 2) = 72 / 18 = 4 млн. руб.
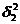 = ((4 - 6,95)2*4 + (6 -
6,95)2*6 + (8 - 6,95)2*5 + (10 - 6,95)2*4) /
(4 + 6 + 5 + 4) = 83 / 19 = 4,37 млн. руб.
= ((4 - 6,95)2*4 + (6 -
6,95)2*6 + (8 - 6,95)2*5 + (10 - 6,95)2*4) /
(4 + 6 + 5 + 4) = 83 / 19 = 4,37 млн. руб.
По совокупности в целом вариация
стоимости основных фондов под влиянием прочих факторов (кроме группировки по
управлениям) характеризуется средней из внутригрупповых дисперсий (k = 2 - число
групп (управлений)):
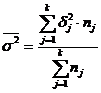 = (4 * 18 + 4,37 * 19) / (18 + 19)
= 4,19.
= (4 * 18 + 4,37 * 19) / (18 + 19)
= 4,19.
Межгрупповая дисперсия характеризует
вариацию, обусловленную влиянием фактора, положенного в основу группировки
предприятий по управлениям и находится по формуле:
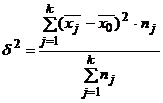 ,
,
где k - число
управлений (k = 2);
nj - число
предприятий в j-й группе;
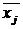 - частная средняя по j-й группе;
- частная средняя по j-й группе;
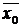 - общая средняя по всей совокупности
предприятий.
- общая средняя по всей совокупности
предприятий.
Получим межгрупповую дисперсию: 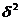 = ((6,67 -
6,81)2*18 + (6,95 - 6,81)2*19) / (18 + 19) = 0,0196.
= ((6,67 -
6,81)2*18 + (6,95 - 6,81)2*19) / (18 + 19) = 0,0196.
Общую дисперсию найдем по формуле:
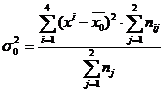 = ((4 - 6,81)2*9 + (6 -
6,81)2*10 + (8 - 6,81)2*12 + (10 - 6,81)2*6) /
(9 + 10 + 12 + 6) = 155,68 / 37 = 4,21.
= ((4 - 6,81)2*9 + (6 -
6,81)2*10 + (8 - 6,81)2*12 + (10 - 6,81)2*6) /
(9 + 10 + 12 + 6) = 155,68 / 37 = 4,21.
Проверим по правилу сложения
дисперсий: общая дисперсия равна сумме средней из внутригрупповых и
межгрупповой дисперсий:
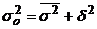 .
.
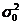 = 4,21 =
= 4,21 = 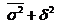 = 4,19 +0,02
= 4,21.
= 4,19 +0,02
= 4,21.
Эмпирическое корреляционное
отношение:
η = 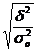 =
= 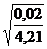 = 0,07.
= 0,07.
Вывод: дисперсия стоимости основных
фондов лишь на 0,5% ( (0,02 / 4,21) . 100%) объясняется
принадлежностью предприятия к первому или второму управлению, а на 99,5% -
влиянием остальных факторов. Величина эмпирического корреляционного отношения
положительна и близка к 0. Поэтому в подразделении предприятий по управлениям
практически нет никакой необходимости.
7. Имеются следующие данные о
распределении школ города по типам и оценке сложности учебного предмета «Основы
информатики» (тыс. чел.):
|
Тип
школы
|
Хорошее
освоение курса
|
Среднее
освоение курса
|
Проблемы
с освоением курса
|
Итого
|
|
А
|
74
|
12
|
5
|
91
|
|
Б
|
71
|
11
|
12
|
94
|
|
В
|
62
|
21
|
23
|
|
Итого
|
207
|
44
|
40
|
291
|
Рассчитайте
коэффициенты взаимной сопряженности Пирсона и Чупрова. Сформулируйте выводы.
Решение
1) Рассчитаем
теоретические частоты внутри таблицы пропорционально распределению частот в
итоговой строке:
f11’
= (91 * 207) / 291 = 64,7312’ = (91 * 44) / 291 = 13,7613’
= (91 * 40) / 291 = 12,5121’ = (94 * 207) / 291 = 66,8722’
= (94 * 44) / 291 = 14,2123’
= (94 * 40) / 291 = 12,92
f31’
= (106 * 207) / 291 = 75,40
f32’
= (106 * 44) / 291 = 16,03
f33’
= (106 * 40) / 291 = 14,57
) Расчетное
значение критерия хи-квадрат определится по формуле:
χ2 = 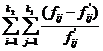 ,
,
где fij и fij’ -
соответственно эмпирические и теоретические частоты в i-той строке j-го столбца;
k1 и k2 -
соответственно число групп в строках и столбцах таблицы.
Расчетное значение критерия
составит:
χ2 = (74 -
64,73)2 / 64,73 + (12 - 13,76)2 / 13,76 + (5 - 12,51)2
/ 12,51 + (71 - 66,87)2 / 66,87 + (11 - 14,21)2 / 14,21 +
(12 - 12,92)2 / 12,92 + (62 - 75,4)2 / 75,4 + (21 -
16,03)2 / 16,03 + (23 - 14,57)2 / 14,57 = 15,9066.
) Коэффициент сопряженности Пирсона
рассчитывается по формуле:
Р = 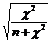 ,
,
где n - общее
число наблюдений.
Тогда Р = 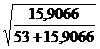 = 0,4805.
= 0,4805.
Коэффициент взаимной сопряженности
Чупрова позволяет учесть число групп по каждому признаку и определяется
следующим образом:
С = 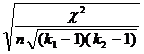 =
= 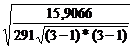 = 0,0273.
= 0,0273.
Таким образом, между типом школы и
освоением курса отмечается некоторая зависимость, но степень тесноты связи
невелика.
8. С целью определения средней
месячной заработной платы персонала гостиниц города было проведено 15%-ное
выборочное обследование с отбором единиц пропорционально численности типических
групп. Для отбора сотрудников внутри каждого типа гостиниц использовался
механический отбор.
|
Тип
гостиницы
|
Средняя
месячная заработная плата, руб.
|
Среднее
квадратическое отклонение, руб.
|
Число
сотрудников, чел.
|
|
1
|
2
270
|
120
|
35
|
|
2
|
2
410
|
163
|
56
|
|
3
|
3
420
|
240
|
125
|
|
4
|
3
840
|
255
|
104
|
С вероятностью
0,954 определите пределы средней месячной заработной платы всех сотрудников
гостиниц.
Решение
Уточним исходные данные. Объем
выборки n = 320,
объем генеральной совокупности N = 2 133. Отношение 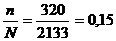 .
.
Необходимые данные представим в
таблице.
|
Средняя
месячная заработная плата, xi
|
Число
сотрудников, fi
|
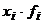 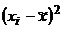 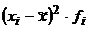
|
|
|
|
2
270
|
35
|
79
450
|
968
196,96
|
33
886 893,60
|
|
2
410
|
56
|
134
960
|
712
285,36
|
39
887 980,16
|
|
3
420
|
125
|
427
500
|
27
565,96
|
3
445 745,00
|
|
3
840
|
104
|
343
431,16
|
35
716 840,64
|
|
Итого
|
320
|
1
041 270
|
-
|
112
937 459,40
|
По условию выборка
механическая. Ее суть заключается в том, что составляется список единиц
генеральной совокупности (сотрудников гостиниц) и в зависимости от числа
отбираемых единиц устанавливается шаг отбора (интервал, через который следует
отбирать студентов). Очевидно, что такая выборка является бесповторной, поэтому
будем использовать формулы для случайной бесповторной выборки.
) Среднюю месячную
заработную плату по выборке (выборочную среднюю) найдем по формуле средней
арифметической взвешенной:
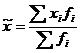 ,
,
где xi - средняя
месячная заработная плата сотрудников i-й
гостиницы;
fi - число
сотрудников i-й гостиницы
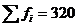 ).
).
Тогда 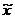 = (2 270 * 35 + 2 410*56 + 3
420*125 + 3 840*104) / 320 = 1 041 270 / 320 = 3 253,97 (руб.).
= (2 270 * 35 + 2 410*56 + 3
420*125 + 3 840*104) / 320 = 1 041 270 / 320 = 3 253,97 (руб.).
) Оценим генеральную дисперсию:
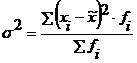 = 112 937 459,4 / 320 = 352 929,56
(руб.).
= 112 937 459,4 / 320 = 352 929,56
(руб.).
Средняя квадратическая ошибка
случайной бесповторной выборки при нахождении среднего возраста студентов
определяется по формуле:
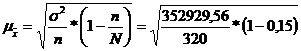 = 30,62 (руб.).
= 30,62 (руб.).
Т.е. ошибка при определении средней
месячной заработной платы персонала гостиниц исходя из выборки составляет 30,62
руб.
) Определим предельную ошибку
выборки: 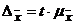 , где величина
t
определяется из условия
, где величина
t
определяется из условия 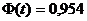 (Ф -
функция Лапласа).
(Ф -
функция Лапласа).
Получим t = 2. Тогда
предельная ошибка выборки 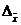 = 2 * 30,62
= 61,24 руб. Это значит, что с вероятностью 0,954 средняя месячная заработная
плата персонала всех гостиниц (генеральная средняя
= 2 * 30,62
= 61,24 руб. Это значит, что с вероятностью 0,954 средняя месячная заработная
плата персонала всех гостиниц (генеральная средняя 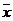 ) находится
в пределах:
) находится
в пределах:
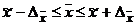
или
253,97 - 61,24 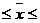 3 253,67 +
61,24
3 253,67 +
61,24
192,73 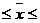 3 315,21
3 315,21
Иначе - средняя месячная заработная
плата персонала всех гостиниц колеблется в пределах от 3 192,73 до 3 315,21
руб.
9. Партия электроламп упакована в
400 коробок по 48 шт. в каждой. Средняя длительность горения электроламп
составляет 1220 ч, а межсерийная дисперсия - 150. Качество электроламп
проверяется на основе серийного 1,5%-ного случайного бесповторного отбора.
Определите: а) предельную ошибку при установлении средней длительности горения
электроламп: б) пределы контролируемого параметра в генеральной совокупности.
Выводы сделайте с вероятностью 0,954.
Решение
Число обследованных серий (коробок
по 48 электроламп) s = 6, число серий в генеральной
совокупности S = 400.
Межсерийная дисперсия 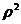 = 150,
= 150,
Средняя длительность горения
электроламп 1 220 ч.
Предельная ошибка выборки (t - уровень
доверия при вероятности 0,954 = 2) для средней рассчитывается по формуле:
D
= 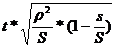 = 2 * Ö(150 / 400 *
(1 - 6 / 400) = 1,23.
= 2 * Ö(150 / 400 *
(1 - 6 / 400) = 1,23.
Отсюда с вероятностью 0,954 можно
указать пределы контролируемого параметра в генеральной совокупности:
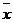 = х ± Dх = 1 220 ±
1,23, т.е. от 1 218,77 до 1 221,23 ч.
= х ± Dх = 1 220 ±
1,23, т.е. от 1 218,77 до 1 221,23 ч.
10. Измерьте тесноту связи и силу
связи между признаками. Сделайте выводы
|
Группы
рабочих по стажу, лет (xi)
|
Число
рабочих (fi)
|
Средняя
зарплата, руб. (yi)
|
Коэффициент
вариации зарплаты, %
|
|
До
3
|
14
|
1950
|
12
|
|
3-6
|
16
|
2590
|
26
|
|
6-9
|
14
|
3640
|
27
|
|
9
и более
|
8
|
4280
|
18
|
Решение
Показатель тесноты
связи - линейный коэффициент корреляции:
r = 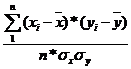
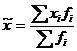 = (1,5*14 + 4,5*16 + 7,5*14 +
10,5*8) / (14 + 16 + 14 + 8) = 5,42.
= (1,5*14 + 4,5*16 + 7,5*14 +
10,5*8) / (14 + 16 + 14 + 8) = 5,42.
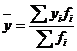 = (1 950*14 + 2 590*16 + 3 640*14 +
4 280*8) / (14 + 16 + 14 + 8) = 2 960,38.
= (1 950*14 + 2 590*16 + 3 640*14 +
4 280*8) / (14 + 16 + 14 + 8) = 2 960,38.
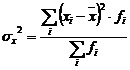 = ((1,5 - 5,42)2*14 +
(4,5 - 5,42)2*16 + (7,5 - 5,42)2*14 + (10,5 - 5,42)2*8)
/ (14 + 16 + 14 + 8) = 9,53
= ((1,5 - 5,42)2*14 +
(4,5 - 5,42)2*16 + (7,5 - 5,42)2*14 + (10,5 - 5,42)2*8)
/ (14 + 16 + 14 + 8) = 9,53
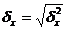 = √9,53 = 3,09.
= √9,53 = 3,09.
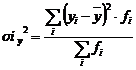 = ((1 950 - 2 960,38)2*14
+ (2 590 - 2 960,38)2*16 + (3 640 - 2 960,38)2*14 + (4
280 - 2 960,38)2*8) / (14 + 16 + 14 + 8) = 709 319,08.
= ((1 950 - 2 960,38)2*14
+ (2 590 - 2 960,38)2*16 + (3 640 - 2 960,38)2*14 + (4
280 - 2 960,38)2*8) / (14 + 16 + 14 + 8) = 709 319,08.
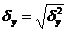 = √709 319,08 = 842,21.
= √709 319,08 = 842,21.
Тогда r = ((1,5 -
5,42) * (1 950 - 2 960,38) + (4,5 - 5,42) * (2 590 - 2 960,38) + (7,5 - 5,42) *
(3 640 - 2 960,38) + (10,5 - 5,42) * (4 280 - 2 960,38)) / (52 * 3,09 * 842,21)
= 12 418,72 / 135 326,30 = 0,09.
Парный коэффициент корреляции меньше
0,5 и больше нуля, что говорит о наличии между исследуемыми признаками (стажем
рабочих и средней зарплатой) достаточно слабой прямой зависимости