Отметим
эти точки на координатной плоскости и проведем через них плавную кривую.
Добавим линию, симметричную построенной кривой относительно начала
координат.Воспользовавшись периодичностью, достроим график до конца.
График
функции y = tgx
называют тангенсоидой. Ту ее часть, которая изображена на рис. 25, обычно
называют главной ветвью тангенсоиды.


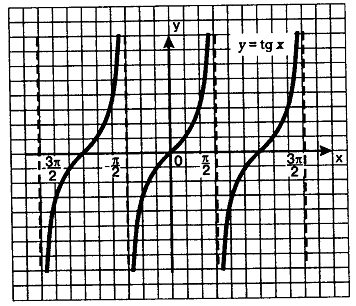

рис
25 рис 26
Отметим еще
несколько свойств функции у = tg x.
Свойство
4.
Функция возрастает на интервале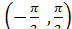 . В более общем
виде - функция возрастает на любом интервале вида
. В более общем
виде - функция возрастает на любом интервале вида  .
.
Свойство
5.
Функция у = tg х не ограничена ни сверху, ни снизу.
Свойство
6.
У функции y = tg х нет ни
наибольшего, ни наименьшего значения.
Свойство
7.
Функция у = tg x непрерывна на интервале  .
В более общем виде - функция непрерывна на любом интервале
.
В более общем виде - функция непрерывна на любом интервале 
При
значениях x =  функция
претерпевает разрыв. Каждая прямая вида
функция
претерпевает разрыв. Каждая прямая вида
x=  служит
вертикальной асимптотой графика функции.
служит
вертикальной асимптотой графика функции.
Свойство
8.
 .
.
Имеет
место тождество (формула приведения):

График
функции y = ctg х (рис. 27), как и график функции у = tg x, называют тангенсоидой.
Главной ветвью графика функции y
= ctg x обычно называют ветвь, заключенную в полосе от х = 0 до х = π.

рис
27
2.2 Введение
тригонометрических функций на уроках алгебры и
начал анализа по
учебнику М. И. Башмакова
.2.1 Вводная беседа
Мы изучаем новый класс функций - тригонометрические
функции. Они служат прежде всего для описания разнообразных процессов. С
периодически повторяющимися ситуациями человек сталкивается повсюду. Его жизнь
сопровождают различные астрономические явления - восход и заход Солнца,
изменение фаз Луны, чередование времен года, положение звезд на небе, затмения
и движения планет. Человек давно заметил, что все эти явления возобновляются
периодически. Жизнь на Земле тесно связанна с ними, и поэтому неудивительно,
что астрономические наблюдения явились источником многих математических
открытий.
Открывая утром газету, мы часто читаем сообщение
об очередном запуске искусственного спутника Земли. Обычно в сообщении
указывают наименьшее и наибольшее расстояние спутника от поверхности Земли и
период его обращения. Если сказано, что период обращения спутника составляет 92
мин, то мы понимаем, что его положение относительно Земли в какой-то момент
времени и через каждые 92 мин с этого момента будет одинаковым. Так мы приходим
к понятию периодической функции как функции, обладающей период, т.е. таким
числом Т, что значение функции при значениях аргумента, отличающихся на Т, 2Т,
3Т и т.д., будут одинаковыми.
Астрономия, которая дает нам наиболее наглядное
представление о периодических процессах, определяет положение объектов в
небесной сфере с помощью углов. Можно сказать так: в качестве аргумента
периодических функций очень часто выступает угол. Поэтому в нашей беседе мы
обсудим вопрос об измерении углов.
Геометрический угол - это
часть плоскости, ограниченная двумя лучами, выходящими из одной точки, вершины
угла. Чтобы сравнивать углы, удобно закрепить их вершины в одной точке и
вращать стороны.
В качестве единицы измерения геометрических
углов принят градус -  часть развернутого
угла. Конкретные углы удобно измерять в градусах с помощью транспортира. Углы,
получаюшиеся при непрерывном вращении, удобно измерять не в градусах, а с
помощью таких чисел, которые отображали бы сам процесс построения угла, т.е.
вращение. Поэтому удобно связать измерения углов со временем.
часть развернутого
угла. Конкретные углы удобно измерять в градусах с помощью транспортира. Углы,
получаюшиеся при непрерывном вращении, удобно измерять не в градусах, а с
помощью таких чисел, которые отображали бы сам процесс построения угла, т.е.
вращение. Поэтому удобно связать измерения углов со временем.
Развернутый угол измеряется половиной дуги
единичной окружности. Это число обозначается буквой π.
π = 3,14159265358…
Угол величиной π - самостоятельная
единица измерения углов. Прямой угол равен 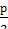 . Угол в
равностороннем треугольнике равен
. Угол в
равностороннем треугольнике равен  и т.д. Угол, мера
которого равна числу 1, называют радианом. Он соответствует некоторому
углу, чуть меньше, чем
и т.д. Угол, мера
которого равна числу 1, называют радианом. Он соответствует некоторому
углу, чуть меньше, чем  , ведь
, ведь 
Так как прямой угол равен  ,
то
,
то  ,
откуда
,
откуда 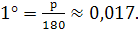
радиан можно выразить через градусы:
Представим маленький шарик, который равномерно
вращается по единичной окружности в положительном направлении (против часовой
стрелки).В момент времени t
= 0 шарик находился в т.А, за время t
= 1 он прошел расстояние, равное 1. За время, равное π,
он
прошел половину окружности, а за время 2π
- всю окружность.

Пусть t
=  . Отложим по окружности от точки А = Р0
. Отложим по окружности от точки А = Р0
в положительном направлении путь длинной  . Так
. Так
как длина всей окружности равна 2π, то
точка 
является
серединой дуги АВ (рис.28)
рис 28 Таким
образом, для каждого значения t
можно
построить
точку Pi.На
языке механики аргумент t
- это время, на языке геометрии t
- это угол.
2.2.2 Определения и
простейшие свойства тригонометрических
функций
Тригонометрические функции
определяются с помощью координат вращающейся точки. Рассмотрим на координатной
плоскости ху единичную окружность. Точка Р0 имеет координаты
(1;0), она начальная.
Определение. Синусом числа t называется ордината точки Pi, косинусом
числа t называется абсцисса точки Pi, где Pi получается поворотом начальной точки единичной окружности на угол t.
Если обозначить координаты точки Pi через х и у, то мы получим x = cos t,
y = sin t или можно записать что точка Pi имеет координаты (cos t, sin t).
Так как точка Pi лежит на окружности, то ее координаты связаны соотношением:
х2 + у2 =1,
тогда cos t и sin t будут связанны следующими соотношениями:
sin 2 t + cos 2 t = 1,
которое называют основным
тригонометрическим тождеством.
Определение. Тангенсом числа t называется отношение синуса числа t к его косинусу, т.е. по определению

Котангенсом числа t называется отношение косинуса числа t к его синусу, т.е. по определению

Тангенс числа t определен для тех значений t, для которых cos t ≠ 0. Котангенс числа t определен для тех значений t, для которых sin t ≠ 0.
Тригонометрические функции являются
периодическими.
Теорема. Число 2π является периодом синуса и косинуса.
Для доказательства необходимо
показать верность равенств:

Это доказывается с помощью координат
вращающейся точки. Точки Рt и Pt+π совпадают, то совпадают и их координаты ч.т.д.
Знаки тригонометрических функций
определяются в зависимости от того, в какой четверти лежит рассматриваемый
угол.
Синус числа t есть ордината точки Pi, поэтому синус
положителен в первой и второй четвертях и отрицателен в третьей и четвертой
четвертях.
Косинус числа t как абсцисса точки Pi положителен в
первой и четвертой четвертях и отрицателен во второй и третьей.
Тангенс и котангенс являются
отношением координат. Поэтому они положительны тогда, когда эти координаты
имеют одинаковые знаки (первая и третья четверти), и орицательны, когда разные
(вторая и четвертая четверти) (рис 29).

рис 29
Теорема. Синус - нечетная функция, т.е. при всех t выполнено равенство
sin (-t) = - sin t. Косинус - четная функция, т.е. при всех t выполнено равенство
cos (-t) = cos t.
Доказательство. Для всякого значения
t точки
Рt и Р- t симметричны друг другу относительно оси абсциссы (т.е. cos t = cos (-t)), а ординаты противоположны (т.е.
sin t = - sin (-t)), ч.т.д.
С л е д с т в и е: Тангенс и
котангенс - нечетные функции.
Действительно, 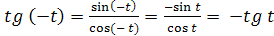 . Аналогично доказывается нечетность котангенса.
. Аналогично доказывается нечетность котангенса.
Значения тригонометрических функций
острых углов можно вычислить по таблицам с помощью прямоугольного треугольника.
Их вычисление для любого значения аргумента можно привести к вычислению
значений для аргумента t . Соответствующие формулы - формулы приведения.
. Соответствующие формулы - формулы приведения.


Из этих основных формул можно
вывести и другие формулы приведения:

Доказательство:
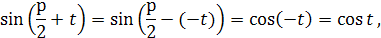

Аналогично выводятся формулы:

Мнемоническое правило для
запоминания формул приведения следующее:
) Название функции не меняется,
если к аргументу левой части добавляется
-π или
+ π, и меняется, если
добавляется 
) Знак правой части определяется
знаком левой, считая, что t
Вычислять значения
тригонометрических функций можно пользуясь следующими соображениями:
) С помощью формул приведения вычисление
значения тригонометрической функции любого числа можно свести к вычислению
функции угла, лежащего в первой четверти.
) Достаточно знать значение лишь
одной из тригонометрических функций. С помощью основных тождеств и зная
четверть, в которой лежит значение аргумента, легко найти значения остальных
функций.
) Полезно помнить значения
тригонометрических функций для углов:
Для решения простых, но важных
уравнений достаточно вспомнить определение тригонометрической функции.
Например: 1. sin t = 0.Вращающаяся точка Рt имеет нулевую ординату
в момент времени t = 0, π, 2π,…, а так
же t = -π,
-2π,… .В общем виде множество этих значений
можно записать в виде t = πk, k . Таким образом, решением уравнения sin t = 0 будут числа t = πk, k
. Таким образом, решением уравнения sin t = 0 будут числа t = πk, k .
.
2. sin t = 1, t =  πk, k
πk, k .
.
3. sin t = -1, t = 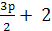 πk, k
πk, k .
.
4. cos t = 0, t =  πk, k
πk, k .
.
5. cos t = 1, t =  πk, k
πk, k .
.
6. cos t = -1, t =  πk, k
πk, k .
.
Все рассмотренные уравнения имеют
бесчисленное множество решений. Эти решения записываются в виде бесконечных
серий с помощью переменной (в наших примерах k), которая может принимать любые
целые значения.
2.2.3 Исследование
тригонометрических функций.
Рассмотрим функции у = sin x и y = cos x.
) Область определения. Синус
и косинус числа х задаются как координаты точки Рх,
получившейся из точки Р0(1;0) поворотом на угол х. Так как
поворот возможен на любой угол, то область определения синуса и косинуса
является множество R.
) Промежутки монотонности.
При х = 0 точка занимает положение Р0(1;0). Пока она движется по
окружности, оставаясь в первой четверти, ее абсцисса уменьшается, а ордината
увеличивается. При х =  точка
займет положение
точка
займет положение
 (0;1). Итак, в
первой четверти синус (ордината) возрастает от 0 до 1, а косинус (ордината)
убывает от 1 до 0.
(0;1). Итак, в
первой четверти синус (ордината) возрастает от 0 до 1, а косинус (ордината)
убывает от 1 до 0.
Когда точка переходит во вторую четверть,
ордината начинает убывать от 1 до 0. Абсцисса становится отрицательной и растет
по абсолютной величине, значит, косинус продолжает убывать от 0 до -1.
В третьей четверти синус становится
отрицательной и убывает от 0 до -1, а косинус начинает возрастать от -1 до 0.
Наконец, в четвертой четверти синус возрастает
от -1 до 0 и косинус возрастает от 0 до 1.
) Точки экстремума. Координаты вращающейся
точки меняются между -1 и +1. Эти числа являются наименьшими и наибольшими
значениями синуса и косинуса. Если требуется указать абсциссы точек экстремума,
то надо решить уравнения
sin
x = ± 1, cos
x = ± 1.
) Промежутки постоянного знака и корни
функции. Эти вопросы были рассмотрены в предыдещем параграфе.
) Множество значений. Синус и косинус
принимают любые значения от - 1 до +1, так как являются координатами точки,
движущейся по единичной окружности.
Для приближенного построения графика синусоиды
можно поступить
так:

перенести на числовые прямые все
ключевые точки и их значения для функции
у =
sin x,
(рис 30) получим точки на
координатной плоскости, принадлежащие
синусоиде, которые плавной линией
соединим.
Так мы получим график синуса
рис 30 на
промежутке  . Так как
. Так как
 ,
,
то график синуса должен быть
симметричен относительно прямой 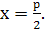 Это
позволяет построить график синуса на отрезке
Это
позволяет построить график синуса на отрезке  .
Воспользовавшись нечетностью синуса, получим график синуса на отрезке [-π,
0] симметричным
отражением построенной части синусоиды относительно начала координат. Так как
отрезок [-π, π] имеет длину, равную
периоду синуса, то график синуса на всей числовой оси можно получить
параллельными переносами построенной кривой.
.
Воспользовавшись нечетностью синуса, получим график синуса на отрезке [-π,
0] симметричным
отражением построенной части синусоиды относительно начала координат. Так как
отрезок [-π, π] имеет длину, равную
периоду синуса, то график синуса на всей числовой оси можно получить
параллельными переносами построенной кривой.
Вернемся к свойствам синуса и косинуса, и
посмотрим, как они проявляются на графике.
. Функция y
= sin x
имеет период 2π. На графике: если
разобьем ось Ох на отрезки длиной 2π, то
получим «одинаковые» части, получающиеся друг из друга параллельным переносом
вдоль оси Ох.
. Функция y
= sin x
нечетна. На графике: синусоида симметрична относительно начала координат.
. Функция y
= sin x
обращается в нуль при х = πk, k . На графике: точки пересечения с осью
абсцисс.
. На графике: точки пересечения с осью
абсцисс.
. Функция y
= sin x
положительна при 2πk
< x < (2k+1)π
и
отрицательна при
(2k+1)π
< x < (2k+2)π
, k . Указанные промежутки соответствуют первой-второй (sin
x> 0) четвертям или третьей-четвертой (sin
x< 0) четвертям.
. Указанные промежутки соответствуют первой-второй (sin
x> 0) четвертям или третьей-четвертой (sin
x< 0) четвертям.
. Функция y
= sin x
возрастает при  πk ≤ х ≤
πk ≤ х ≤  πk, и убывает при
πk, и убывает при  πk ≤ х ≤
πk ≤ х ≤ 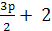 πk, k
πk, k .
.
6. Множеством значений функции y
= sin x
является отрезок [-1, 1].
График косинуса можно построить так же, как и
синуса. Или, воспользовавшись формулами приведения  построить график косинуса как синусоида, сдвинутая на
построить график косинуса как синусоида, сдвинутая на  влево по оси Ох (рис 31).
влево по оси Ох (рис 31).

Рис 31
По определению тангенс числа х задается
как отношение sin
x и cos
x. Изучим свойства
тангенса:
1.
Область определения функции у = tg
x - множество всех
действительных чисел, за исключением чисел вида  .
.
.
Тангенс - периодическая функция с основным периодом π.
.
Тангенс - нечетная функция, tg
(-x) = tg
x.
.
Функция у = tg
x обращается в нуль
одновременно с синусом, т.е. при
х
= 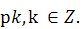
.
Функция у = tg х положительна в первой и третьей четвертях и отрицательна во
второй и четвертой.
.
Тангенс возрастает в первой четверти. Действительно, пусть 0 ≤ х1
< x2
<  Тогда
sin х1 <
sin x2
(возрастание синуса) и cos
х1 > cos
x2
(убывание косинуса). Так как значения косинуса положительны, то
Тогда
sin х1 <
sin x2
(возрастание синуса) и cos
х1 > cos
x2
(убывание косинуса). Так как значения косинуса положительны, то  Умножим
это неравенство на неравенство с положительными членами: sin
х1 < sin
x2.
Получим tg х1
< tg
x2.
Умножим
это неравенство на неравенство с положительными членами: sin
х1 < sin
x2.
Получим tg х1
< tg
x2.
Тангенс
возрастает так же и в четвертой четверти. Пусть  <
х1 < x2
≤ 0. Тогда,
<
х1 < x2
≤ 0. Тогда,
0 ≤ -х1 Б -ч2
Б  0 ≤ - х1 < - x2 <
0 ≤ - х1 < - x2 <  .
Тогда, tg (-х2) < tg (-x1). Пользуясь свойством
нечетности, получаем, - tg х2 < - tg x1. Поэтому tg х1 < tg x2.
.
Тогда, tg (-х2) < tg (-x1). Пользуясь свойством
нечетности, получаем, - tg х2 < - tg x1. Поэтому tg х1 < tg x2.
На промежутке  тангенс отрицателен и возрастает. На
тангенс отрицателен и возрастает. На  положителен и возрастает. В итоге: тангенс возрастает на
промежутке
положителен и возрастает. В итоге: тангенс возрастает на
промежутке  .
.
. Когда х возрастает от 0 до  , тангенс возрастает, при этом когда х приближается к
, тангенс возрастает, при этом когда х приближается к  , синус близок к 1, а косинус - к 0. Поэтому отношение
, синус близок к 1, а косинус - к 0. Поэтому отношение  становится сколь угодно большим.
становится сколь угодно большим.
. График тангенса. На промежутке  график можно построить по точкам, учтя, что тангенс строго
возрастает, в нуле обращается в нуль, а при приближении к
график можно построить по точкам, учтя, что тангенс строго
возрастает, в нуле обращается в нуль, а при приближении к  становится сколь угодно большим. Отразив построенную часть
относительно начала координат, получим график тангенса на промежутке
становится сколь угодно большим. Отразив построенную часть
относительно начала координат, получим график тангенса на промежутке  . Для построения полного графика разобьем числовую ось на отрезки,
перенося
. Для построения полного графика разобьем числовую ось на отрезки,
перенося  вправо и влево на π,
2π, 3 π и т.д.
вправо и влево на π,
2π, 3 π и т.д.
График тангенса (рис 32) распадается
на отдельные, не связанные между собой части. Это вызвано тем, что в точках  , k
, k тангенс не определен.
тангенс не определен.
Свойства котангенса получаются так же, как и
свойства тангенса.
. Функция у = сtg x определена при  , k
, k
. Функция у = сtg x периодична с периодом равным π.
3. Функция у = сtg x нечетна: сtg (-x) = сtg x.
4.
Функция у = tg
x обращается в нуль
одновременно с косинусом, т.е. при х =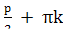 ,
k
,
k .
.
.
Функция у = сtg х положительна в первой и третьей четвертях и отрицательна во
второй и четвертой.
.
Функция у = сtg х убывает на промежутке (πk;
π+πk).
.
Область значений - множество R.
.
График котангенса на рис. 33

Рис
32 рис 33
2.3 Определение
тригонометрических функций как сумм степенных
рядов
Докажем сначала следующее простое
предложение, которым сразу будет охвачен ряд важных случаев:
Если функция f(x) в промежутке [0, Н]
или [-Н,0] (Н>0) имеет производные всех порядков, и все эти производные при
изменении х в указанном промежутке оказываются по абсолютной величине
ограниченными одним и тем же числом:
 (1)
(1)
(где L не зависит от n), то во всем промежутке имеет место
разложение

В самом деле, взяв дополнительный
член rn(х) в форме Лагранжа
 (2)
(2)
имеем, в силу (1)
 (3)
(3)
При безграничном возрастании n выражение  стремится к 0, как видно из сходимости ряда:
стремится к 0, как видно из сходимости ряда:

(это справедливо в силу сходимости
ряда, являющегося разложением числа e, т.е.

Но в таком случае и гn(х) имеет пределом 0,
что и доказывает наше утверждение.
Это предложение приложимо к
тригонометрическим функциям sin х и cos х в промежутке [-1,1 ], ибо производные их, соответственно
равные sin (х + ), cos (х +
), cos (х + ), будут в нем по абсолютной величине ограничены единицей.
), будут в нем по абсолютной величине ограничены единицей.

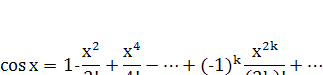
Все они имеют разложение при любом
значении х.
Коэффициенты Тейлора для этих
функций будут вычисляться
следующим образом. Если f(x) = sin х, то
f(k) (х) = sin (х + 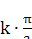 ), так что
), так что
f (0) = 0, f(2m) (0) = sin mπ = 0,
f(2m-1) (0) = sin (mπ -  )= (-1)m-1 , (m=1, 2, 3…)
)= (-1)m-1 , (m=1, 2, 3…)

Аналогично, при f(x) = cos x:
f(k) (х) = cos (х + 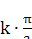 ), f (0) = 1, f(2m) (0) = (-1)m,
), f (0) = 1, f(2m) (0) = (-1)m,
f(2m-1) (0) = 0 , (m=1, 2, 3…)
Таким образом (если взять n = 2m+l)

Таким образом функции sin x и cos x можно определить как суммы
соответствующих рядов Тейлора.
Пусть теперь f(x) = arctg х. Значения всех
последовательных производных при х=0 будут находиться из равенства:
 , т.е. f'(
, т.е. f'( =1.
=1.
Возведя обе части в n-степень, получим
fn+1 (0) =
-n(n-1) fn-1.
 , f''(
, f''( =0. Ясно, что всегда f (2m) (0) = 0.
=0. Ясно, что всегда f (2m) (0) = 0.
Что касается производных нечетного
порядка, то для них из (4):
f(2m+1) = -
(2m-1)·2m· f(2m-1)
f '(0) = 1, f(2m+1)
(0) = (-1)m (2m)!
Так что разложение функции f(x) = arctg x представится в виде:

Для функции f(x) = tg
x закон образования коэффициентов в формуле Тейлора сложен. Тем не
менее, несколько первых членов ее написать нетрудно. Так как, например,

то f(0)= 0 , 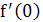 =
1,
=
1,  =
0,
=
0,  ,
,
 .
.
Так что 
2.4 Аксиоматическое
определение тригонометрических функций
В настоящем параграфе будет дано
аксиоматическое определение тригонометрических функций, как функций, обладающих
некоторыми, точно описанными характеристическими свойствами, на основании
которых могут быть установлены все прочие свойства этих функций.
Аналитическим
косинусом С(х) и аналитическим синусом S(x)
называются функции:
I. Определенные
для всех действительных значений х;
II. Удовлетворяющие
функциональному уравнению:
С (х-у) = С(х) С (у) +S(x) S(y)
(иными словами, равенство (Сх-у)
выполняется тождественно при всех значениях х и у);
III. Положительные
в интервале 0<х<λ, где λ - некоторое положительное число:
С(х) > 0 и S(x)> 0 при 0<х< λ;
IV. В
граничных точках интервала (0, λ.) имеет место следующее равенство:
V.
С(0) = S(λ) = 1.
Сформулированное определение не дает
ответа на вопрос, существует ли хотя бы одна система функций С(х) и S(x), удовлетворяющая всем условиям;
чтобы убедиться в существовании функций С(х) и S(x), достаточно построить хотя бы один
конкретный пример такой системы функций. Осуществить требуемое построение
можно различными способами. В самом
деле, при λ =  всем перечисленным условиям удовлетворяют функции cos х и sin х. При произвольном
данном λ >0, условиям I - IV удовлетворяют функции
всем перечисленным условиям удовлетворяют функции cos х и sin х. При произвольном
данном λ >0, условиям I - IV удовлетворяют функции

Не касаясь вопроса о существовании
функций С(х) и S(x), установим свойства этих функций, вытекающие из основных условий
I - IV,
т.е. будут установлены свойства функций С(х) и S(x) в предположении, что они
существуют.
1. Имеют место следующие
равенства граничных значений,
S(0) = С(λ) = 0.
Доказательство: положив в основном
тождестве II: х = у = 0, получим
С(0) = С2(0) + S2(0), откуда в силу IV, 1= 1 + S2(0) = 0 и S(0) = 0.
Положив в II: х = у = λ., получим
С(0) = С2(λ) + S2(λ),
откуда 1= 1 + С2(λ) и С(λ) = 0.
2. Имеет место тождество:
C2(x)
+ S2(x) = l.
Доказательство: достаточно положить
в основном тождестве II: х = у, и принять во внимание условие IV. Следствие:
Функции С(х) и S(x) ограничены.
| S(x) | ≤ 1, | С(х) | ≤ 1
3. Имеет
место следующие тождества, выражающие функции С(х) и S(x) одна через другую:
С(λ
-х) = S(x), S(λ -х)
= С(х).
Доказательство: заменив в основном
соотношении II х на λ, а у на х, получим:
С(λ
-х) = С(λ) С(х) + S(λ)
S(x) = S(x).
Заменив в полученном равенстве х на λ -у, получим
С(у) = S(λ -y)
4. Для
функции S(x) имеет место формула сложения:
5.
S(x+y) = S(x) С (у) + S(y) С(х).
Доказательство: воспользовавшись
доказанным свойством 3, получим:
S(x+y) = С [λ - (х+у)] = С [(λ - х) - у)]=
= С (λ - х) С (у) + S(λ -
х) S(y) = S(x) С (у) + S(y) С(х).
6. Функция
С(х) - четная, а функция S(x) - нечетная.
Доказательство: положив в основном
соотношении II х = 0, получим:
С(-у) = С(0) С(у) + S(0) S(y) = С(у).
Положив в формуле S (х+у) у = -х, получим:
= S(x-x) = S(x) С(-х) + С(х) S(-x) = С(х) [S(x) + S(-x)] + 0.
Возможны два случая:
Случай а) С(х) ≠ 0, тогда S(x) + S(-x) = 0 или S(x) = - S(-x).
Случай b) С(х) = 0. Пусть у - произвольное
число, взятое в интервале 0< у < λ; приняв во внимание, что С(-х) = С(х) = 0, получим:
С(х+у) = С[х-(-у)] = С(х) С(-у) + S(x) S(-y) = S(x) S(-y) (1)
и C(y+x) = С [y+(-x>] = C(y) C(-x) + S(y) S(-x) = S(y) S(-x)
(2)
Так как по условию III С(у) > 0, S(y) > 0, то в силу предыдущего,
S(y) = - S(-y). Приравняв выражения (1) и (2), получим:
S(x) S(-y) = S(y) S(-x) или -S(x) S(y) = S(y)
S(-x).
Так как S(y)≠0, то и случае b) имеем: S(x)= - S(-x). Функция S (х) - нечетная.
. Имеют место теоремы сложения,
выражающиеся следующими формулами:
С(х-у) = С(х) С(у) + S(x) S(y);
С(х+у) = С(х) С (у) - S(x) S(y);
S(x+y) = S(x) C(y) +
S(y) C(x);(x-y) = S(x) C(y) - S(y) C(x).
В самом деле, первая формула имеет
место по условию, третья доказана, вторая и четвертая вытекают из первой и
третьей и из доказанных свойств четности и нечетности заменой у на -y.
7. Имеют место
тождества:

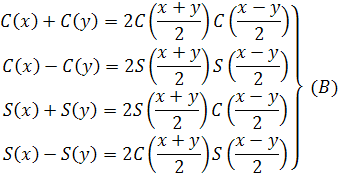 S(2x) = 2 S(x) С(х); С(2х) = С2 (х) - S2 (х). (С)
S(2x) = 2 S(x) С(х); С(2х) = С2 (х) - S2 (х). (С)
Доказательство: формулы (А)
преобразования произведения в суммы получаются из теорем сложения (пункт 6)
путем надлежащего почленного сложения и вычитания соответствующих тождеств.
Формулы (В) преобразования сумм в произведения получаются непосредственно из
теорем сложения. Так, например:
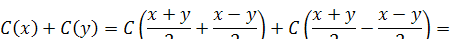


Формулы (С) двойного аргумента
получаются из формул С(х+у) и S(x+y) при х = у.
. Имеют место формулы деления
аргумента пополам:

Для доказательства достаточно
воспользоваться тождествами:

(второе тождество получается из
формулы (С) заменой х на  ).
).
9. имеют место формулы приведения:
С(х+ λ)
= - S(x); S(x+ λ) = С(х); [х + λ]
С(х+ 2 λ) = - С(х); S(x+ 2 λ) = - S(x); [х + 2 λ]
С(х+ З λ) = S(x); S(x+ З λ) = - С(х); [х + З λ]
С(х+ 4 λ) = С(х); S(x+ 4 λ) = S(x); [х + 4 λ]
Доказательство: вычислим значения
функции С(х) и S(x) в точках λ,2 λ, З λ, 4 λ.
Имеем:
С(λ) = О, S(λ)
= 1;
С(2 λ)
= С2(λ) - S2(λ) = -1, S(2 λ) = О,
С(З λ)
= С(λ) С(2 λ) - S(λ) S(2 λ) = О,
S(3 λ) = S(λ) С(2 λ) + С(λ) S(2 λ) = -1,
И, наконец:
С(4
λ) = С2(2 λ) - S2(2 λ) = 1, S(4
λ) = 2 S(2 λ) С(2 λ) = 0.
Для доказательства формул достаточно
воспользоваться теоремами сложения. Так, например:
С(х+ λ)
= С(х) С(λ) - S(x) S(λ) = - S(x).
Следствие: функции С(х) и S(x) -
периодические.
В самом деле, тождества [х + 4 λ] показывают, что число 4 λ является периодом для
каждой из этих функций.
10. В
интервале (0, 2 λ) функция С(х) убывает, а в интервале (2 λ, 4 λ) возрастает.
Доказательство: имеем
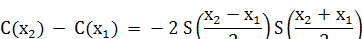
Пусть 0 <  <
< 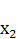 < 2
λ; тогда 0 <
< 2
λ; тогда 0 < < λ
и 0 <
< λ
и 0 <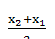 < 2
λ.
< 2
λ.
Значение функции S(x) в точках  и
и  положительны (следствие пред. пункта), следовательно:
положительны (следствие пред. пункта), следовательно:
С(х2) < C( )
)
Т.е. С(х) убывает в интервале (0, 2 λ).
Пусть 2 λ ≤  <
< 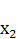 < 4 λ; тогда 0 <
< 4 λ; тогда 0 < < λ и 2 λ <
< λ и 2 λ <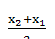 < 4
λ.
< 4
λ.
В этом случае 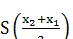 < 0, а поэтому
< 0, а поэтому
C( ) <
С(х2),
) <
С(х2),
Т.е. С(х) убывает в интервале (2 λ, 4 λ).
Тем же методом доказывается
следующее утверждение:
В интервале (-λ, λ), функция S(x) возрастает, а в
интервале (λ, З λ) убывает. В частности
заметим, что в интервале (0, λ) функция С(х) убывает, a S(x) возрастает.
. Функции С(х) и S(х) непрерывны на
интервале (-∞; +∞)
Докажем предварительно следующую
лемму.
Лемма: Функция С(х) непрерывна в точке х = 0.
Доказательство: так как С(0) = 1, то для доказательства леммы надо
установить, что:
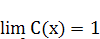
Достаточно рассмотреть правый предел
lim
С(х), считая, что х > 0, так как если этот правый предел существует, то, в
силу свойства четности функции С(х):
С(х) = С(-х),
существует и имеет то же численное
значение также и левый предел С(х) в точке 0.
Так как в интервале (0, λ) функция С(х) монотонна
(убывает) и ограниченна, то правый предел функции С(х) существует.
А следовательно, существует предел
(двусторонний) С(х) в точке х = 0; обозначим этот предел через 1:
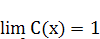
Для вычисления 1 достаточно найти
предел числовой последовательности значений функции С(х) по какой-либо частной
последовательности {хn} значений аргумента, сходящейся к нулю: lim хn = 0. В качестве такой
частной последовательности возьмем последовательность:
x0= λ, x1=  , x2 =
, x2 = 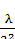 , … , xn=
, … , xn=  , …
, …
Применив последовательно формулу
деления аргумента пополам, найдем:
С(х0) = 0, C(x1) =  ,С(х2)=
,С(х2)=  , C(х3) =
, C(х3) =  ,
,
и вообще (применив метод полной
индукции):
С(хn) =  (n радикалов).
(n радикалов).
Вычислим предел последовательности {sn}, которая
определяется рекуррентной формулой sn =  , и
начальным значением s =
, и
начальным значением s =  :
:
s1= , s2=
, s2= ,..., sn=
,..., sn= ,...
,...
эта последовательность возрастает.
Покажем, что последовательность {sn} ограничена. Имеем:
s1< 2, s2= <2,
<2,
применим метод полной индукции.
Допустим, что  <
2, тогда получим также:
<
2, тогда получим также:
sn=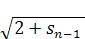 <2.
<2.
Так как последовательность {sn} возрастает и
ограничена, то lim sn = 2. Вычислим предел последовательности {С(хn)} значений функции
С(х). Имеем:
lim C(xn) = lim  =1.
=1.
Таким образом, имеем:

т.е. функция С(х) непрерывна в точке
0, ч.т.д.
Следствие: Функция S(x) непрерывна в точке х = 0.
В самом деле,
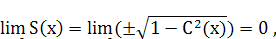
Значение функции S(x) в точке х = 0 также равно 0:

Теорема: Функции С(х) и S(x) непрерывны в каждой точке х. Доказательство: требуется доказать,
что

Докажем первое равенство. Имеем:
C(x+h)
= С(х) C(h)
- S(x)
S(h)
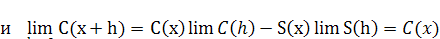
Второе равенство доказывается тем же методом,
ч.т.д.
12. На сегменте [0, 2 λ] функция С(х)
убывает от 1 до -1; На сегменте [2 λ, 4 λ] возрастает от -1 до1.
Доказательство: во-первых, в
данном интервале (0, 2 λ) функция С(х) убывает
(см. пункт 11).
во-вторых, С(0) = 1, С(2 λ) = -1.
в-третьих, пусть k -
произвольное число, взятое при условии -1<
k <1; будучи непрерывной в интервале (0, 2λ), функция С(х) имеет
значение, равное k в некоторой точке ζ (единственной в силу монотонности):
С(ζ)
= k,где 0<
ζ <2λ, ч.т.д.
Аналогично доказываются следующие
утверждения: На сегменте [2 λ, 4 λ] возрастает от -1 до 1;
На сегменте [-λ, λ] функция S(x) возрастает от -1 до 1;
На сегменте
[λ, З λ] убывает от 1 до
-1.
13. Число 4 λ есть наименьший
положительный период для функций С(х) и S(x).
Доказательство: как известно, число
4λ есть период функций
С(х) и S(x) (см. пункт 9, следствие). Если число 1 является периодом функции
С(х), то: С(1) = С(0) = 1.
Значение, равное 1, функция С(х)
имеет в точках: О, ±4 λ, ±8 λ,..., 4к λ,... Из этих возможных значений для 1 наименьшим положительным
числом является число 4 λ.
Аналогично, для функции S(x): S (λ +1) = S(λ) = 1.
Последнее равенство справедливо при
1 = 4к λ, из этих чисел наименьшее положительное есть число 4 λ.
Мы изучили свойства косинуса и
синуса, оставив в стороне две другие тригонометрические функции. Функция
аналитический тангенс Т(х) определяется формулой

Изучение её свойств не представляет
затруднений и может быть выполнено обычными способами на основании определения
и известных свойств синуса и косинуса. Это же замечание относится и к
котангенсу
2.5
Тригонометрические функции как решения линейного
дифференциального
уравнения
Тригонометрические функции могут
быть определены как частные решения некоторого линейного дифференциального
уравнения второго порядка, при этом их свойства могут быть установлены на
основании общих теорем теории дифференциальных уравнений.
Рассмотрим следующее линейное
однородное уравнение с постоянными коэффициентами:

Согласно общим теоремам теории
дифференциальных уравнений, существуют два частные решения Y1(x) и Y2(х) этого уравнения,
удовлетворяющие следующим начальным условиям:
Y1 (0) = 1,  (0) = 0, Y2 (0) = 0,
(0) = 0, Y2 (0) = 0,  (0) = 1.
(0) = 1.
Функции Y1(x) и Y2(х) линейно независимы,
так как начальное значение вронскиана отлично от нуля.

А поэтому общее решение нашего
уравнения может быть представлено в виде:
Y = C1 Y1 (x) + C2Y2(x).
Функции Y1(x) и Y2(х) непрерывны в
интервале (-∞, +∞).
Следовательно, эти функции
удовлетворяют первому характеристическому условию I, присущему аналитическому
косинусу и синусу. Дифференциальное уравнение (3) может быть заменено системой
линейных уравнений:

с постоянными коэффициентами.
Существует единственное решение этой системы:
у = у(х), z = z(x), удовлетворяющее
начальному условию:
у(0) = 0, z (0) = 1.
Функция у(х) (в силу способа составления
системы (4)) удовлетворяет дифференциальному уравнению (3) и начальным
условиям:
у(0) = 0, у' (0) = z (0) = 1.
Следовательно: у (х) = Y2 (х).
Функция z(x) также удовлетворяет уравнению (3):

и начальным условиям:
z(0)=l,z'(0) = -y(0)
= 0,
а потому:
z (x) = Y1 (x). (5)
Итак, в силу системы (4) имеем:
 (х) = Y1 (х),
(х) = Y1 (х),  (x) = -Y2(x).
(x) = -Y2(x).
Умножив первое уравнение (4) на у, а
второе на z и сложив, получим:

откуда:
у2 (х) + z2 (х) = const.
Положив у = Y2 (х), z = Y1 (х),
получим:
 (x) +
(x) +
 (x) = const;
(x) = const;
Но при х=0 значение левой части
равно 1. Cледовательно имеет место
тождество:
 (x) +
(x) +
 (x) = l.(6)
(x) = l.(6)
Следствие. Функции Y1 (х) и Y2 (х) ограничены.
Пусть ξ - произвольное действительное число. Функция: у(х) = Y1(х
- ξ), (при данном ξ) удовлетворяет уравнению (3). В самом деле:
у" (х) = - Y" (х
- ξ), а потому
у" (х) + у (х) =  (x + ξ) +
(x + ξ) +  (х- ξ) =
0.
(х- ξ) =
0.
Следовательно, функция у(х) при
некоторых значениях C1 и С2 содержится
в общем решении (у):
 (х - ξ) = C1 Y1 (х) + С2 Y2 (х). (7)
(х - ξ) = C1 Y1 (х) + С2 Y2 (х). (7)
Продифференцировав:
 (х - ξ) = - Y2 (х - ξ) = - C1 Y2 (ξ) + С2 Y1 (ξ).
(х - ξ) = - Y2 (х - ξ) = - C1 Y2 (ξ) + С2 Y1 (ξ).
И положив х = ξ , получим:
C1 Y1 (ξ) + С2 Y2(ξ) = 1;
C1 Y2 (ξ) +
C2 Y1(ξ) = 0.
Откуда (приняв во внимание (6))
получим:
C1 = Y1(ξ), С2 = Y2 (ξ).
Равенство (7) примет следующий вид:
Y1(х - ξ) = Y1 (х) Y1(ξ)+ Y2 (х) Y2 (ξ).
Последнее равенство есть тождество,
так как х и ξ
- произвольные действительные числа.
Следствие: для функций Y1(x) и Y2(x) удовлетворяется условие II, которым обладают
аналитические синус и косинус.
Теорема: существуют положительные значения аргумента х, при которых
функция Y1(x) обращается в нуль.
Доказательство: предположим
противное, что Y1(x) ≠ 0 при произвольном
значении х>0. Тогда Y1(x) >0 в интервале (0, +∞).
В самом деле, если бы существовало значение x1, при котором Y1(x) <0, то (в силу непрерывности) в
промежутке, ограниченном точками х = 0 и х = x1 существовала бы точка ξ (по крайней мере одна), в которой Y1(ξ)
= 0 (ибо Y1(x1) < 0, a Y1(0) = 1> 0), что
противоречит предположению.
Так как  (x) = Y1(x) >0, то функция Y2 (х) возрастает. Следовательно, Y2(x) >0 при х >0, ибо Y2 (0) = 0 и Y2 (0) < Y2 (х). Так как Y2 (х) - возрастающая положительная и ограниченная в интервале (0,
+∞) функция, то существует конечный предел:
(x) = Y1(x) >0, то функция Y2 (х) возрастает. Следовательно, Y2(x) >0 при х >0, ибо Y2 (0) = 0 и Y2 (0) < Y2 (х). Так как Y2 (х) - возрастающая положительная и ограниченная в интервале (0,
+∞) функция, то существует конечный предел:

Из тождества  = - Y2(x) и неравенства Y2(x) >0 следует, что
= - Y2(x) и неравенства Y2(x) >0 следует, что  <0, и значит Y1(x) убывающая функция. Будучи
убывающей и положительной (а потому ограниченной), функция Y1(x) имеет конечный предел в бесконечности:
<0, и значит Y1(x) убывающая функция. Будучи
убывающей и положительной (а потому ограниченной), функция Y1(x) имеет конечный предел в бесконечности:
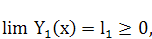
Y1(x +1) - Y1(x);
Эта разность в бесконечности имеет
предел, равный 0:

Но, с другой стороны, применив
теорему Лагранжа:

(где х <  < х+1), получим:
< х+1), получим:

Следовательно, предположение, что
функция Y2(x) отлична нуля при всех
положительных значениях аргумента, привело к противоречию, откуда следует
справедливость теоремы. Ч.т.д.
Обозначим через λ наименьший
положительный корень функции Y1(x) (наименьший положительный корень
существует, так как множество точек,
в которых непрерывная функция Y1(x) обращается в нуль, замкнуто),
тогда Y1(λ) = 0 и Y1(x) >0 при 0 < х < λ. В интервале (0,
λ)
функция Y2(x) возрастает (как имеющая
положительную производную), а потому Y2(x) >0. Это значение есть предел возрастающей
положительной в интервале (0, λ) функции:
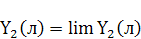
Положив х =  в тождестве (6), получим Y2(
в тождестве (6), получим Y2( ) =1.
Итак, имеем:
) =1.
Итак, имеем:
Y1(0) = Y2( ) =1, и
в интервале (0,
) =1, и
в интервале (0,  )
функции Y1(x) и Y2(x) положительны.
)
функции Y1(x) и Y2(x) положительны.
Следовательно, эти функции
удовлетворяют характеристическим условиям III - IV. Функции и Y2(x), как удовлетворяющие условиям I - IV, суть аналитический косинус и
аналитический синус:
и Y2(x), как удовлетворяющие условиям I - IV, суть аналитический косинус и
аналитический синус:
Y1(x) =
Cλ(x) , Y2(x) = Sλ(x)
Покажем, что λ=  .
Рассмотрим параметрические уравнения окружности:
.
Рассмотрим параметрические уравнения окружности:
х = Cλ(t) , у = Sλ(t), где 0 < t < 4 λ.
Вычислим длину дуги σ с началом в точке
А(1,0), соответствующей значению параметра t = 0, и с концом в точке М(х,у),
соответствующей произвольному значению параметра t. Имеем:
Следовательно, Cλ(t) и Sλ(t) суть абсцисса и ордината конца дуги длины t единичной окружности, отложенной от
точки А, а потому:
Cλ(t) =
cos t, Sλ(t) = sin t.
При t = λ имеем σ = λ =  .
.
2.6 Определение
тригонометрических функций при помощи
обращения
интегралов
Мы начинаем с определения arctg x равенством

Это уравнение однозначно определяет
значение у, соответствующего каждому действительному значению х. Так как
подинтегральная функция - четная, то у является нечетной функцией от х. Далее,
так как у непрерывна и строго возрастает, то, существует обратная функция х = х
(у), также непрерывная и строго возрастающая. Мы полагаем:
x = x(y) = tg y.
Если мы определим π уравнением:

то х (у) определена для  <y<
<y< .
.
Теперь мы полагаем

где имеется в виду положительное
значение корня. Таким образом,
cos у и sin у определены для  <y<
<y< . Когда у →
. Когда у →  , х→∞, и,
, х→∞, и,
следовательно, cos у → 0 и sin у→ -1.
Мы определяем  равенствами
равенствами

Тогда cos у и sin у определены для  <y≤
<y≤ , a
, a  для
для  <y<
<y< .
Наконец, мы определяем tg у, cos у и sin у для значений у вне интервала (
.
Наконец, мы определяем tg у, cos у и sin у для значений у вне интервала ( ,
,  ) с
помощью уравнений:
) с
помощью уравнений:

которые последовательно
распространяют наши определения на интервалы
( ,
,  ), (
), ( ,
,  ),,...,
(
),,...,
( ,
,  ), (
), ( ,
,  ),...
),...
Функция tg у тогда определена для
всех значений у, кроме (k +  )п, где
k -
целое число. Эти значения определением не охватываются; но tg у стремится к +∞
или к - ∞, когда у стремится к одному из этих значений,
соответственно, слева или справа. С другой стороны, cos у и sin у определены и
непрерывны для всех значений у.
)п, где
k -
целое число. Эти значения определением не охватываются; но tg у стремится к +∞
или к - ∞, когда у стремится к одному из этих значений,
соответственно, слева или справа. С другой стороны, cos у и sin у определены и
непрерывны для всех значений у.
Мы начали с определения acrtg x и tg y и затем определили cos у и sin у через tg у. Мы могли бы выбрать arcsin х и sin.y в качестве наших основных функций.
В этом случае мы должны были бы определить arcsin х в интервале (-1,1)
равенством

где берется положительное значение
корня; sin у - как обратную функцию; π - с помощью равенства

a cos у и tg у - соотношениями

Дальнейшее развитие теории зависит
от формул сложения. Заметим, в первую очередь, что:
(1 + x2) (1 + у2) = (1 - xy)2 + (x + y)2,
и, следовательно,

Это приводит к соотношению
arctg х + arctg у = arctg z.
Но так как эти функции многозначны,
то необходимо более внимательное рассмотрение.
Положим

так что

Таким образом, t и u изменяются в одном направлении.
Когда t возрастает от -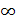 до
до  и
возрастает от
и
возрастает от  до
∞ , а когда t возрастает от
до
∞ , а когда t возрастает от  до
∞ , и возрастает от -
до
∞ , и возрастает от -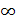 до
до  . Кроме
того, u = 0 когда t = x1, и u = -x1, когда t = 0.
. Кроме
того, u = 0 когда t = x1, и u = -x1, когда t = 0.
Предположим теперь, что х2
имеет такое значение, что интервал (-x1, x2) значений u не содержит точку u =  , в
которой t обращается в бесконечность. Если x1> 0, то х2 должно быть меньше
, в
которой t обращается в бесконечность. Если x1> 0, то х2 должно быть меньше  , а если x1< 0, то x2 должно быть больше
, а если x1< 0, то x2 должно быть больше  . В этих учловиях t монотонно возрастает или убывает от 0 до
. В этих учловиях t монотонно возрастает или убывает от 0 до  когда u возрастает или убывает от -x1 до x2. Так как
когда u возрастает или убывает от -x1 до x2. Так как

то мы имеем

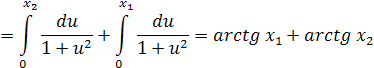
Если мы теперь положим  , то мы
имеем
, то мы
имеем
y = y1 + y2 и

что и является формулой сложения для
тангенса.
Эта формула пока доказана только при
некоторых ограничениях на значения переменных, а именно, в предположении, что x2 <  , если
х1 > 0 и x2 >
, если
х1 > 0 и x2 >  , если
, если
х1 < 0. Когда х1
> 0 и x2→  слева, то х→ +∞ и у→
слева, то х→ +∞ и у→  . Наши
предположения сводятся, таким образом, к тому, что у1, у2
и у1+у2 должны лежать в интервале (
. Наши
предположения сводятся, таким образом, к тому, что у1, у2
и у1+у2 должны лежать в интервале ( ,
,  ).
).
Эти ограничения, однако, не нужны.
Ограничения на у1+у2
возникло из нашего предположения, что интервал  не содержит
не содержит  .
Допустим, что это условие нарушено, например, предположим для определенности,
что х1 > 0 и x2 >
.
Допустим, что это условие нарушено, например, предположим для определенности,
что х1 > 0 и x2 >  . Тогда, при u возрастающем от - х1 до x2, t возрастает от 0 до ∞, затем меняет знак и возрастает от -∞
до х. Таким образом, мы имеем:
. Тогда, при u возрастающем от - х1 до x2, t возрастает от 0 до ∞, затем меняет знак и возрастает от -∞
до х. Таким образом, мы имеем:

Следовательно,
arctg х = arctg х1 + arctg x2 - π.
И, по (9)
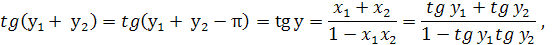
Аналогично мы можем поступить в
случае х1 < 0. Следовательно, (10) имеет место, если только у1
и у2 лежат в интервале ( ,
,  ).
).
Наконец, так как каждая часть
уравнения (10) является, по (9), периодической функцией от y1 или у2, то (10) справедливо без всяких ограничений, за
исключением того, что ни y1, ни у 2 ни y1+y2 не должно быть нечетным
кратным  , так как в этих случаях (10) теряет смысл.
, так как в этих случаях (10) теряет смысл.
Из соотношений (10) и (8) мы
заключаем, что

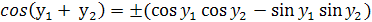
Для определения знака положим у2
= 0. Уравнение сводится к следующему: cos y1 = ± cos y1 так что при у2 = 0 следует брать положительный знак.
Так как обе части меняют знак, когда у2 увеличивается на π, то формула имеет место с
положительным знаком для всех у2 кратных π. Далее, обе части
уравнения являются непрерывными функциями от у2, так что перемена
знака может произойти только в том случае, когда обе части обращаются в нуль,
т. е. при значениях …,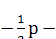 y1,
y1,  y1,
y1,  y1 ,…, каждое из которых является единственным в любом интервале
длины π . Так как мы видели, что в каждом таком интервале существует
значение у2. Для которого знак положителен, то он должен быть всегда
положительным. Следовательно,
y1 ,…, каждое из которых является единственным в любом интервале
длины π . Так как мы видели, что в каждом таком интервале существует
значение у2. Для которого знак положителен, то он должен быть всегда
положительным. Следовательно,

и соответствующая формула для sin (y1+y2) доказывается
аналогично.
2.7
Тригонометрические функции как решение системы
функциональных
уравнений
Будем исходить из следующей системы
функциональных уравнений:

Дополним эту систему соотношениями:

Предположим, что функции S(x) и С(х), удовлетворяющие
соотношениям (11) - (12) cуществуют.
Теорема. Любое нетривиальное решение системы обладает следующими
свойствами:
1) S(0) = 0, С(0) = 1.
2) |S(x)|≤ l, |С(х) | ≤ 1.
3) S(-x) = -S(x), С(-х) = С(х).
4) Справедливы
формулы сложения: С(х+у) = С(х) С(у) - S(x) S(y) и
S (х+у) = S(x) С (у) + S(y) С(х),
Доказательство:
) полагая х = у = 0 в соотношениях
(11), будем иметь: S(0) = 0, С(0) = С2(0), откуда следует, что С(0) = 0 или
С(0) = 1. Очевидно при С(0) = 0, S(x) = 0, С(х) = 0. поэтому будем рассматривать систему уравнений
(11) при С(0) = 1 и S(0) = 0.
) полагая х = у в равенстве (11),
получим:
S2(x) + С2(х) =
1 (13)
Из соотношения (13) получаем:
|S(x)|≤ l, |С(х) | ≤
1. (14)
Далее, полагая х = а в равенстве
(13), получим: S2(a) + С2(а) = 1. но S(a) = 1. Следовательно,
С(а) =
0.
(15)
) полагая х = 0 в равенстве (11),
получим: S(-y) = S(0) С(у) - С(0) S(y).
Отсюда следует, что
S(-y) = - S(y)
(16)
Полагая х = 0 в равенстве (11),
получим: С(-у) = С(0) С(у) + S(0) S(y), то есть
С(-у) = С
(у) (17)
) Теперь легко вывести формулы
сложения для функции S(x) и С(х). Действительно, заменяя у через -у в соотношениях (11),
используя четность и нечетность С(х) и S(x) (16) - (17) получим:
S(x + у)
= S(x)C(y) + C(x)S(y)
(18)
C(x + y) =
C(x)C(y)-S(x)S(y)
(19)
Что и требовалось доказать.
Из соотношений (18) и (19) вытекают
также при у = а следующие формулы:
S(x+a) = С(х)
(20)
С(х+а) = - S(x)
(21)
Эти формулы вместе с (18) и (19)
позволяют выразить значение функции S(x) и С(х) для любого действительного значения х через значения этих
функций для значения х, принадлежащего интервалу (0, а), в частности, будем иметь:
S(2a+x) = С(х+а) = - S(x) (22)
С(2а+х) = - S(x+a) = - С(х) (23)
Как следствие, выводим следующие
формулы:




Эти формулы вытекают из соотношений
(11) или формул сложения. Из (19) и (24) приходим к формулам двойного аргумента
для рассматриваемых, функций:
S(2x) = S(x)C(x) + C(x)S(x) = 2 S(x) C(x) (28)
Наконец, установим следующие
формулы:

Теорема: функции С(х) и S(x) являются периодическими и число 4а - есть наименьший
положительный период этих функций.
Доказательство: применяя доказанные
выше формулы (22) - (23):
S(x+4a) = S[2a+(2a+x)] =
- S(2a+x) = S(x)
Итак, при всяком х имеем: S(4a+x) = S(x). Т.е. Т=4а является периодом
функции согласно определению. Докажем, что при всяком х имеет место равенство:
S(x+k) = S(x)
(30)
Число к не может быть равно числу а,
2а, За. В самом деле, если k=2а, то S(2a+x) = S(x). Но S(2a+x) = - S(x). Отсюда: S(x) = - S(x). Или S(x) = 0. это противоречит условию (12). Если k=3а, то S(3a+x) = S(x), но из (20) - (21):
S(x+3a) = S[a+(2a+x)] = С(2а+х) = - С(-х) = - С(х)
Или
S(x) = - С(х)
Чего не может быть, так как в этом
случае из (11) следует, что S(x) = 0. Если k=а, то S(x+a) = S(x). С другой стороны, S(x+a) = С(х) или S(x) = С(х), чего не может быть.
Положим х = 0 в равенстве (30).
Тогда получим: S(k) = S(0).
Число к не может принадлежать
интервалу (0, а), так как в противном случае мы пришли бы в противоречие с
условием (12).
Число k не может принадлежать интервалу (а,
2а), так как в противном случае число 2а-к принадлежало бы интервалу (0, а) и
мы имели бы, согласно (16) - (17) и (22) - (26):
S(2a-k) = ...=- S(-k) = S(k) = 0, что противоречит условию
(12).
Число к не может принадлежать
интервалу (2а, 4а), так как в противном случае число 4а-к принадлежало бы
интервалу (0, 2а) и мы имели бы:
S(4a-k) = S[4a+(-k)] =
S(-k) = - S(k) = 0
Что противоречит только что
доказанному. Итак, число 4а является наименьшим положительным периодом для
функции S(x).
Для функции С(х) доказывается
аналогично. Поэтому число 4а - также является наименьшим положительным периодом
для функции С(х). Ч.т.д.
Теорема: функция С(х) положительна в
интервале (0,а).
Доказательство: если 0 < х <
а, то 0 < а-х < а. Допустим, что С(х) < 0, тогда S(a-x) < 0, а это противоречит условию
(12). Итак, С(х) > 0, если 0 < х < а. ч.т.д.
Теорема: функция S(x) возрастает, а функция С(х) убывает
на сегменте [0, а].
Доказательство: пусть числа x1 и х2 принадлежат сегменту [0, а] и x1>x2. тогда будем иметь:

Следовательно,

Вместе с тем имеем (27):
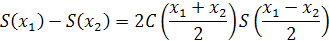
Таким образом, S(x1) - S(x2) > 0, S(x1) > S(x2), т.е. S(x) возрастает. Далее, в силу (25):

Таким образом, C(x1) - C(x2) < 0, C(x1) < C(x2)., т.е. C(x) убывает. Ч.т.д. Теорема:
при любом натуральном n имеют место равенства:
 ,
(число радикалов равно n-1), (31)
,
(число радикалов равно n-1), (31)
 ,
(число радикалов равно n-1). (32)
,
(число радикалов равно n-1). (32)
Доказательство: применим метод
математической индукции.
Действительно:


Допустим, что равенство (31)
справедливо при n=k. Имеем:
 ,
(число радикалов равно k-1), Имеем делее:
,
(число радикалов равно k-1), Имеем делее:

Следовательно,
 (число
радикалов равно k)
(число
радикалов равно k)
Итак, равенство (31) справедливо и
при n=k+l. Так как это равенство верно и при n=1, то, следовательно, оно верно при
любом натуральном n.
Аналогично доказывается и (32).
Теорема: если n - натуральное число, то  =1.
=1.
Теорема: если n - натуральное число, то = 0.
= 0.
Теорема:  =1.
=1.
Доказательство:  существует в силу монотонности и ограниченности функции С(х) в
интервале (0,а). Известно, для того, чтобы найти
существует в силу монотонности и ограниченности функции С(х) в
интервале (0,а). Известно, для того, чтобы найти  , достаточно найти
, достаточно найти 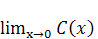 по
какой-либо последовательности, сходящейся к нулю. Имеем:
по
какой-либо последовательности, сходящейся к нулю. Имеем:


Итак,  =1.
=1.
Теорема: функции S(x) и С(х) непрерывны.
Доказательство: 1) для функции С(х).
используя (25), имеем:
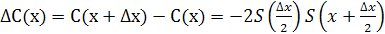
Вместе с тем, в силу (14):

Тогда 
Это значит, что С(х) - непрерывная.
) случай с S(x) доказывается аналогично.
Теорема: если число х принадлежит интервалу (0,а), то S(x) <  .
.
Далее, на основании (20) - (29),
можно доказать, что С(х) и S(x) совпадают с тригонометрическими функциями cos х и sin х соответственно и
вывести общее решение системы функциональных уравнений.
Определение: решения системы функциональных уравнений (11) называются
тригонометрическими синусом и косинусом и обозначаются соответственно:
S(x) = sin (  ) , C(x) = cos (
) , C(x) = cos ( 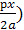 .
.
Заключение тригонометрия функция учебник школьный
В своем историческом развитии
тригонометрия прошла следующие этапы:
1) Тригонометрия
была вызвана к жизни в раннюю пору разумной деятельности людей необходимостью
производить измерения углов.
2) Первыми
шагами тригонометрии было установление связей между величиной угла и отношением
специально построенных отрезков прямых. Непосредственным результатом этого было
то, что стало возможным решать плоские треугольники, главным образом, с целью
определения расстояний до удалённых или недоступных объектов.
3) В
интересах практической астрономии и географических исследований были получены
аналогичные результаты для треугольников на сферических поверхностях. С тех пор
плоская и сферическая тригонометрии развивались как неотъемлемые части единой
науки.
4) Измерительный
характер задач тригонометрии при массовом их повторении приводил к
настоятельной необходимости табулировать значения вводимых тригонометрических
функций.
5) По мере
оформления представлений о тригонометрических функциях они превращались в
самостоятельные объекты исследований. Т.е. собственно в функции, объекты,
обладающие самостоятельным значением и своими особыми свойствами.
6) В
начале XVI в. были установлены взаимные интерпретации между решениями
определённого класса неприводимых алгебраических уравнений и задачами о делении
угла, тем самым было положено начало установлению связей между алгеброй и
тригонометрией.
7) В XVIII
в. тригонометрические функции были включены в систему математического анализа в
качестве одного из классов аналитических функций.
|
Этап
|
Основные
результаты
|
Учёные
|
|
I. (VII в. до н.э. - II в.
н.э.)
|
Определение
расстояний до удаленных или недоступных объектов; Определение небесных
координат светил, продолжительности дня и т.д.
|
Фалес
Милетский (VII - VI вв. до н.э.) Аристарх Самосский (ок. 310 - 260 гг. до
н.э.) Архимед (ок. 287 - 212 гг. до н.э.) Евклид (II в. до н.э.) Гиппарх (II
в. до н.э.) Менелай (I в. н.э.) Клавдий Птолемей (II в. н.э.) и др.
|
|
II.
(II - XII вв.)
|
Составление
тригонометрических таблиц; Появление и доказательство основных
тригонометрических тождеств; Теорема Менелая, теоремы синусов и тангенсов и
др.
|
Клавдий Птолемей (II в. н.э.) Ал-Харрани (IX в.) Ал-Хорезми (IX в.)
Ал-Фараби (X в.) Ал-Бузджани (X - XI вв.) Беруни (X - XI вв.) Ибн Ирак
(X - XI вв.) Аз-Заркали (XI вв.) Герардо Кремонский (1114 -1187 гг.)
Насирэддин Туси (1201 - 1274 гг.) Ал-Каши (XIV - XV вв.) и др.
|
|
Ш.
(XII - XV вв.)
|
Выделение
тригонометрических функций в самостоятельные объекты исследований (как
функции в виде таблиц).
|
Леонардо
Пизанский (1170 - 1250 гг.) Иоанн Сакробоско (XIII в.) Джованни Кампано
(XIII в.) Иоганн Мюллер (Региомонтан) (1436 - 1476 гг.) Николай Коперник
(1473 - 1543 гг.) и др.
|
|
IV.
(XVI - XVII вв.)
|
Выведение
новых тригонометрических формул; Установление взаимной интерпритации между
решениями определённого класса неприводимых алгебраических уравнений и
задачами о делении угла.
|
Ф. Виет (1540 - 1603 гг.) И. Кеплер (1571 - 1630 гг.) П. Ферма (1601 -
1665 гг.) и др.
|
|
V.
(XVIII - XIX вв.)
|
Включение
тригонометрических функций в систему математического анализа в качестве одного
из классов аналитических функций.
|
Леонард
Эйлер (1707 - 1783 гг.) И.Г. Ламберт (1728 - 1777 гг.) А.И. Лексель (1741 -
1784 гг.) С. Люилье (1750 - 1840 гг.) и др.
|
В данной работе были рассмотрены
различные способы построения теории тригонометрических функций: при помощи
степенных рядов, линейного дифференциального уравнения, обращения интегралов, с
помощью системы функциональных уравнений. Аксиоматическая теория является их
обобщением. С её точки зрения различные способы определения тригонометрических
функций есть лишь различные её интерпретации. Исторически эта теория является
завершающим этапом в развитии теории тригонометрических функций.
В школе при введении теории
тригонометрических функций применяется традиционный способ. Тригонометрический
материал впервые появляется в курсе планиметрии (8 кл.), во второй раз
тригонометрия предстает как часть алгебры (9 кл.), и в третий раз - в системе
начал анализа (10-11 кл.). И, прежде всего, это обусловлено тем, что именно
так, как вводятся элементы тригонометрии в средней школе, сформировалась эта
наука в своём историческом развитии.
Литература
1. Глейзер Г. И. История
математики в средней школе / Пособие для учителей. М.: Просвящение. 1961 г.
2. Клейн Ф. Элементарная
математика с точки зрения высшей (том 1) / Ф. Клейн. М.- Л. 1987 г.
3. Матвиевская Г. П. Очерки
истории тригонометрии / Г. П. Матвиевская. Ташкент. 1990 г.
4. Рыбников К. А.
Возникновение и развитие математической науки / К. А. Рыбников. М.:
Просвящение. 1987 г.
5. Энциклопедия элементарной
математики. - М., 1952 г, т.2.
6. Фихтенгольц Г. М. Курс
дифференциального и интегрального исчисления. - М., 1969 г., том 2.
7. Бохан К. А. и др. Курс
математического анализа. - М., 1972, т.2.
8. Новоселов С. И.
Специальный курс тригонометрии. - М.. 1967.
9. Харди Г. Г. Курс чистой
математики. - М., 1949 г.
10. ал-Фараби.
Математические трактаты. Алма-Ата: Наука, 1972.
11. А. Г. Мордкович Алгебра
и начала анализа 10-11 кл., 2001.
12. М. И. Башмаков Алгебра
и начала анализа 10-11 кл., 2001.