|
X
|
0
|
0.04
|
0.08
|
0.12
|
0.16
|
0.2
|
|
R
|
0.094
|
0.074
|
0.053
|
0.042
|
0.038
|
Проектирование
сверхзвукового участка сопла
Примем
согласно экспериментальным данным полуугол раструба сопла  ,тогда найдем длину сверхзвуковой части (конического
сопла). Она равна:
,тогда найдем длину сверхзвуковой части (конического
сопла). Она равна:
 .
.
Спроектируем
профилированное сопло, которое обеспечивает получение на выходе параллельного
сверхзвукового потока с заданным числом M.
проведем
через точку на стенке сопла , соответствующей критическому сечению ,прямую под
углом  к оси и продолжим ее до пересечения с осью (точка O)
к оси и продолжим ее до пересечения с осью (точка O)
из
точки O проведем близко расположенные радиальные прямые
,получим 
1 отложим от критического сечения на
оси расстояние равное длине конического сопла (точка А)
проведем
из точки А характеристики. Они проведены под углом равным 15'
15'
найдем
пересечение радиальной прямой  с
характеристикой
с
характеристикой (точка
(точка )
)
Для
сечения проходящего через А1 используя газодинамическую ф-ю  из таблицы по значению L находят
значение
из таблицы по значению L находят
значение  ,
,  и из
точки
и из
точки проводим характеристики под углом
проводим характеристики под углом  (откладывается угол от
(откладывается угол от )
аналогично для других точек
)
аналогично для других точек
Расчет
параметров течения газа по соплу
Расчет параметров на дозвуковом участке сопла ведем по следующей схеме:
1 ранее дозвуковая часть была разбита
на 6 частей, согласно данному разбиению выбираем соответствующие сечения;
считаем
 для каждого из полученных сечений;
для каждого из полученных сечений;
для
полученного значения  находим из таблицы газодинамических функций число
находим из таблицы газодинамических функций число
по
найденным числам  можно найти параметры
можно найти параметры  ,
, ,
, ,
, через газодинамические функции по сечениям
через газодинамические функции по сечениям 
Расчет параметров на сверхзвуковом участке сопла ведем следующим образом:
на
характеристике  в точках
в точках значение
числа Маха
значение
числа Маха  уже было найдено ранее; согласно данным значениям
уже было найдено ранее; согласно данным значениям  по газодинамическим функциям можно найти значение
параметров
по газодинамическим функциям можно найти значение
параметров  ,
, ,
, ,
, в точках
в точках 
значение
параметров в точках  и точках
и точках  будут
соответственно идентичны, так как соответствующие точки (например
будут
соответственно идентичны, так как соответствующие точки (например ) будут лежать на одной характеристике, по построению,
поэтому параметрам на стенке сопла будут соответствовать X
точек
) будут лежать на одной характеристике, по построению,
поэтому параметрам на стенке сопла будут соответствовать X
точек 
Найдем
величину скорости звука в зависимости от выбранного сечения по формуле: 
Величину
скорости находим из зависимости 
В результате вычислений получили следующие данные:
|
 0.040.80.120.160.20,230,280,340,440,63 0.040.80.120.160.20,230,280,340,440,63
|
|
|
|
|
|
|
|
|
|
|
|
 7. 8967.
4966.6245.5524.2241.3280.7120.4320.11920.088 7. 8967.
4966.6245.5524.2241.3280.7120.4320.11920.088
|
|
|
|
|
|
|
|
|
|
|
|
 13.7613.2712.1410.718.813.862.461.740.970.57 13.7613.2712.1410.718.813.862.461.740.970.57
|
|
|
|
|
|
|
|
|
|
|
|
 0.1370.3040.5250.7411.8272.232.5443.0703.595 0.1370.3040.5250.7411.8272.232.5443.0703.595
|
|
|
|
|
|
|
|
|
|
|
|
 1992196218941802167211981008870692556 1992196218941802167211981008870692556
|
|
|
|
|
|
|
|
|
|
|
|
 12327045863082012681418150416181700 12327045863082012681418150416181700
|
|
|
|
|
|
|
|
|
|
|
|
 895888872851820694636591527473 895888872851820694636591527473
|
|
|
|
|
|
|
|
|
|
|
Построим по полученным данным графики распределения давления, плотности,
температуры, безразмерной скорости и скорости звука по длине сопла.
Расчет
сопла Лаваля в среде Gas2
Структурная схема:
Сначала строим контур сопла. Далее мы разбиваем область внутри контура на
ячейки с помощью линейной аппроксимации. На входном сечении сопла задаем
границу втекания потока, а на выходной - границу вытекания.
Так как, задача осесимметричная берем цилиндрическую систему координат.
На границе втекания задаем давление и температуру во входном сечении
сопла. Учитываем в расчетах вязкость.
Схема распределения давления газов по соплу.

Схема распределения температуры газов по соплу.

Схема распределения плотности газов по соплу.

Высчитываем погрешность для распределения давления:



Высчитываем погрешность для распределения температуры:



Высчитываем погрешность для распределения плотности:



Расчет
крыльевого профиля методом скачков уплотнения и волн разряжения.
Профиль симметричный с хордой в = 150 мм и максимальной толщиной с= 14
мм.
Параметры потока обтекающего крыловой профиль
№ варианта № профиля M P(МПА) T(K) k 
Угол атаки
Угол атаки
|
Угол атаки
|
|
|
|
|
13
|
4
|
3.2
|
0.1
|
373
|
1.4
|
0
|
4
|
-2
|

Рис 1 Торможение потока на скачке уплотнения.

Рис 2 Ускорение потока на волне разрежения.
Расчет обтекания крыльевого профиля при заданных параметрах набегающего
потока выполняется точным методом скачков - волн разрежения.
1
Определяем параметры потока на каждом прямолинейном участке
1 рассчитываем параметры потока на
скачках уплотнения
2 рассчитываем параметры потока на
волнах расширения
Расчет
параметров потока на скачках уплотнения проводим следующим образом: при
заданном угле атаки и профиле находим угол отклонения потока (Рис 1),далее находим угол косого скачка b , который зависит от величины скорости Маха и от угла
(Рис 1),далее находим угол косого скачка b , который зависит от величины скорости Маха и от угла  (Cм газодинамические ф-ии ),затем ищем отношение
давления после отклонения потока к давлению до него(
(Cм газодинамические ф-ии ),затем ищем отношение
давления после отклонения потока к давлению до него( ),
),

Зная
значение  , находим значение
, находим значение  ,далее
находим
,далее
находим и по газодинамическим функциям находим
и по газодинамическим функциям находим  . Найдём значение скоростного напора непосредственно
перед обтеканием крыла
. Найдём значение скоростного напора непосредственно
перед обтеканием крыла
V=Ma где  -скорость звука
-скорость звука 



|
        
|
|
|
|
|
|
|
|
|
|
0°
|
3.2
|
4°
|
21°10’
|
2.9
|
1.105
|
0.1105
|
0.0105
|
0.015
|
|
4°
|
3.2
|
0°
|
18°13’
|
3.2
|
1
|
0.1
|
0
|
0
|
|
4°
|
3.2
|
8°
|
24°40’
|
2.8
|
1.394
|
0.1394
|
0.0394
|
0.055
|
|
-2°
|
3.2
|
6°
|
22°50’
|
2.95
|
1.32
|
0.132
|
0.032
|
0.045
|
|
-2°
|
3.2
|
2°
|
19°45’
|
3.1
|
1.076
|
0.1076
|
0.0076
|
0.011
|
Расчет
параметров потока на волнах разрежения проводим следующим образом: при заданном
угле атаки , профиле и скорости Маха находим углы  ,
, (смотри Рис 2),далее находим фиктивный угол
(смотри Рис 2),далее находим фиктивный угол  (из таблицы газодинамических функции)
(из таблицы газодинамических функции)
Затем
прибавляем угол  ,далее находим по таблице скорости Маха
,далее находим по таблице скорости Маха  отношение давления после отклонения потока к давлению
до него (
отношение давления после отклонения потока к давлению
до него ( )будет равно
)будет равно

Зная
значение  , находим значение
, находим значение  ,далее
находим
,далее
находим . Вычислим значение скоростного напора непосредственно
перед обтеканием крыла
. Вычислим значение скоростного напора непосредственно
перед обтеканием крыла


|
           (-1) (-1)
|
|
|
|
|
|
|
|
|
|
|
|
0°
|
2.9
|
48°
|
56°34’
|
3,34
|
17°24’
|
0.529
|
0.058
|
0.0525
|
0.073
|
|
4°
|
3.2
|
18°00’
|
54°
|
62°34’
|
3,74
|
15°30’
|
0.492
|
0.049
|
0.051
|
0.071
|
|
4°
|
2.8
|
20°48’
|
46°
|
54°34’
|
3,23
|
18°00’
|
0.539
|
0.075
|
0.0644
|
0.09
|
|
-2°
|
2.95
|
19°45’
|
49°
|
57°34’
|
3,40
|
17°05’
|
0.524
|
0.069
|
0.063
|
0.088
|
|
-2°
|
3.1
|
18°42’
|
52°
|
60°34’
|
3,60
|
16°06’
|
0.502
|
0.054
|
0.0536
|
0.075
|
На конце профиля:
|
           (-1) (-1)
|
|
|
|
|
|
|
|
|
|
|
|
0°
|
3,34
|
17°24’
|
56°
|
86°
|
6,188
|
9°18’
|
0.033
|
0.0019
|
0.0561
|
0.078
|
|
4°
|
3,74
|
15°30’
|
62°
|
92°
|
8°00’
|
0.021
|
0.001
|
0.048
|
0.067
|
|
4°
|
3,23
|
18°00’
|
54°
|
84°
|
5,875
|
9°48’
|
0.037
|
0.0028
|
0.0722
|
0.101
|
|
-2°
|
3,40
|
17°05’
|
57°
|
87°
|
6.321
|
9°06’
|
0.03
|
0.0021
|
0.0669
|
0.093
|
|
-2°
|
3,60
|
16°06’
|
60°
|
90°
|
6,845
|
8°24’
|
0.025
|
0.0013
|
0.0527
|
0.074
|
2
Вычисление нормальной и продольной сил для профиля при рассматриваемых углах
атаки
 ;
;
при 
 = 0°
= 0°
Так
как профиль симметричен и находится под нулевым углом атаки то подьемная сила .Осевая же сила
.Осевая же сила




при 
 = 4°
= 4°
Находим подъемную силу

Осевая
сила

при 
 = -2°
= -2°
Находим подъемную силу

Осевая сила

3Найдем
коэффициенты для нормальной и осевой сил для профиля при рассматриваемых углах
атаки
 ;
;
при

 = 0°
= 0° ;
;
при

 = 4°
= 4° ;
;
при

 = -2°
= -2° ;
;
4
Найдем моменты тангажа для профиля при рассматриваемых углах атаки

при

 = 0°
= 0° 
при

 =4°
=4°


при

 =-2°
=-2°


5Найдем
координаты относительного центра давлений при рассматриваемых углах атаки.


при 
 =-2°
=-2°

6
Вычисляем коэффициенты лобового сопротивления и подъемной силы при
рассматриваемых углах атаки.


при

 = 0°
= 0°


при

 = 4°
= 4°


при

 = -2°
= -2°


. Оформление чертежа
Вычертить картину обтекания профиля при заданных углах атаки . Для
каждого участка течения указать значения М, Р, Р0.
Ниже
вычертить эпюру распределения по профилю избыточных давлений  с указанием их величины. Рядом указать значение
нормальной и продольной сил, их аэродинамических коэффициентов, а также указать
графически координату центра давления.
с указанием их величины. Рядом указать значение
нормальной и продольной сил, их аэродинамических коэффициентов, а также указать
графически координату центра давления.
Расчет
крыльевого профиля в среде Gas2
Структурная схема:
Вначале строим внешний контур в виде квадрата, внутри которого строится
контур крыльевого профиля. Далее мы разбиваем область вокруг крыльевого профиля
на ячейки с помощью ступенчатой аппроксимации. На внешнем контуре задаем
границы втекания и вытекания потока.
Система координат берем плоскую.
На границе втекания задаем скорость набегающего потока и его температуру.
А для разных углов атаки профиля скорость набегающего потока раскладываем на
соответствующие оси Vx и Vy. Кроме того в расчетах учитываем
вязкость.
. Распределение давления при γ=0˚.

.Распределение давления при γ=4˚.

сопло газодинамический крыльевой уплотнение
3. Распределение давления при γ=-2˚.

Вычисление
подъемной и продольной сил для профиля при рассматриваемых углах атаки
 ;
;
при 
 = 0°
= 0°
Так
как профиль симметричен и находится под нулевым углом атаки то подъемная сила .Осевая же сила
.Осевая же сила




при 
 = 4°
= 4°
Находим подъемную силу

Осевая
сила

при 
 = -2°
= -2°
Находим подъемную силу

Осевая сила

3.Найдем
коэффициенты для нормальной и осевой сил для профиля при рассматриваемых углах
атаки
 ;
;
при

 = 0°
= 0° ;
;
при

 = 4°
= 4° ;
;
при

 = -2°
= -2° ;
;
4
Найдем моменты тангажа для профиля при рассматриваемых углах атаки

при

 = 0°
= 0° 
при

 =4°
=4°
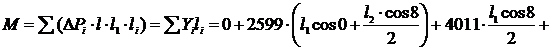

при

 =-2°
=-2°


5Найдем
координаты относительного центра давлений при рассматриваемых углах атаки.

при 
 =4°
=4°

при 
 =-2°
=-2°

6.
Вычисляем коэффициенты лобового сопротивления и подъемной силы при
рассматриваемых углах атаки.


при

 = 0°
= 0°


при
 = 4°
= 4°

при

 = -2°
= -2°


Подводя
анализ полученного результата можно отметить, что избыточное давление  полученное в среде Gas2 и с помощью
метода скачков уплотнения и волн разрежения в целом схожи, но заметно
различаются на конце профиля. Подъемная сила для углов атаки отличных от нуля
рассчитанная в Gas2 получилась несколько больше чем при использовании
метода скачков уплотнения и волн разряжения.
полученное в среде Gas2 и с помощью
метода скачков уплотнения и волн разрежения в целом схожи, но заметно
различаются на конце профиля. Подъемная сила для углов атаки отличных от нуля
рассчитанная в Gas2 получилась несколько больше чем при использовании
метода скачков уплотнения и волн разряжения.
Относительная
погрешность для подъемной и осевой силах:
При
 = 0
= 0 
При
 = 4°
= 4° 

При
 = -2°
= -2° 

Список литературы
1. Абрамович Г.Н. Прикладная газовая
динамика. М. ,Наука ,.1976г. 824 с.
2. Алемасов В.Е. Теория ракетных
двигателей М. Машиностроение 1980г. 533с.
3. Карафоли Е. Аэродинамика больших
скоростей M изд. Академия наук СССР 1960г. 740c.
4. Краснов Н.Ф. Аэродинамика в вопросах
и задачах М. Высшая школа 1985г.759c.
5. Лойцянский Л.Г. Механика жидкости и
газа M.,Наука,1973г.847c.