Исследование резонанса токов в цепи переменного тока

Исследование резонанса токов в цепи переменного тока

ЛАБОРАТОРНО - ПРАКТИЧЕСКАЯ РАБОТА № 10

«Исследование резонанса токов в цепи переменного тока»

Цель работы:

Выявить влияние активного, индуктивного и емкостного сопротивления на значения мощности и сдвиг фаз между током и напряжением в цепи переменного тока; экспериментально и теоретически исследовать резонансные явления в параллельном колебательном контуре.

Содержание отчета:

–     название лабораторно-практической работы;

–     электрические схемы;

–     заполненные таблицы;

–     все расчеты к таблицам и дополнительные расчеты;

–     основные выводы;

Правила оформления:

·        Лабораторная работа выполняется на компьютере с применением виртуальной лаборатории «Электротехника» или «Electronics WorkBench».

·        Отчет должен быть представлен печатной работой на листах формата А4, таблица заполняется шариковой ручкой от руки.

·        Расчет может выполняться от руки или на компьютере.

·        Использовать MS WORD, MS EXCEL

Требуемое оборудование:

Продолжительность работы: 2 часа

Лабораторная работа проводится в виртуальной среде «Электротехника» или «Electronics WorkBench».

Основные теоретические положения

В данной работе исследуется разветвленная электрическая цепь, состоящая из параллельно соединенных катушки индуктивности и конденсатора, и подключенная к источнику синусоидального напряжения. Схема цепи представлена на рис. 1.

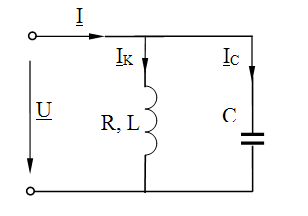
Рис. 1

Так как реальная катушка индуктивности обладает активным сопротивлением, ее целесообразно представить в виде эквивалентной схемы замещения. В данном случае удобнее воспользоваться параллельной схемой замещения катушки индуктивности, где параллельно включены резистивный элемент с активной проводимостью G и индуктивный элемент с индуктивной проводимостью B_L (рис. 2). При этом, вектор I_K тока катушки представляет собой сумму двух векторов: вектора I_KА, проходящего через резистивный (активный) элемент, и вектора I_KР, проходящего через индуктивный (реактивный) элемент. Конденсатор обладает емкостной проводимостью В_С.

Рис. 2

Активная и реактивная проводимости связаны с соответствующими сопротивлениями следующими соотношениями:

G = R/Z_K, B_L = X_L/Z_K, B_C = 1/X_C.

где: Z =

В соответствии c законом Ома полная проводимость цепи Y=I/U. Соотношение активной G, реактивной B = B_C - B_L и полной Y проводимостей определяется треугольником проводимостей (рис. 3). откуда следует:

=  или Y = .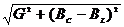

Кроме того, справедливо: G = Y*cos φ, B = Y*sin φ φ = arctg (B/G).

Аналогичный треугольник связывает вектора: тока всей цепи, тока I_KA, протекающего через активное сопротивление цепи, и тока I_P, протекающего через реактивное сопротивлении цепи, действующее значение которого определяется соотношением I_P = I_KP - I_C,(рис .4). Поэтому угол сдвига фаз φ между векторами тока I и напряжения U цепи может быть также определен с помощью формулы

φ = arctg (I_P/I_KA) = arctg [(I_KP-I_C)/I_KA].

В соответствии с первым законом Кирхгофа вектор тока цепи I определяется выражением: I = I_K + I_C или I = I_KA + I_KP + I_C.

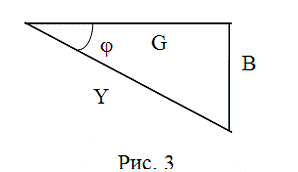
Рис. 3

Необходимо отметить, что:

· вектор активной составляющей тока катушки I_KA совпадает по фазе с вектором напряжения U. Действующее значение этого тока I_KA = G*U;

· вектор реактивной (индуктивной) составляющей тока катушки I_KP отстает по фазе от вектора напряжения U на угол α. Действующее значение этого тока

I_KP = B_L*U;

· вектор тока конденсатора I_С опережает по фазе вектор напряжения U на угол α Действующее значение этого тока I_C = B_C*U;

Рис. 4

Таким образом, возможны три режима работы параллельной цепи синусоидального тока, определяемые соотношением между величинами индуктивной B_L и емкостной B_C проводимостями:> BC, тогда IKA > IC, и вектор напряжения U опережает по фазе вектор тока I на угол φ, лежащий в пределах  0 < j < p/2.. Такая цепь (нагрузка) называется активно-индуктивной (рис. 5).< BC, тогда IKA < IC, и вектор напряжения U отстает по фазе от вектор тока I на угол φ.  -p/2 < j < 0. Такая цепь (нагрузка) называется активно-емкостной (рис. 6).= BC, тогда IKA = IC, и вектор напряжения U совпадает по фазе с вектором тока I. Такой режим работы параллельной цепи синусоидального тока называется резонансом токов (рис. 7).

Из выражения B_L = B_C следуют условия, с помощью которых можно добиться возникновения резонанса в цепи:

1.  путем подбора частоты w_рез питающего напряжения;

2.  путем подбора индуктивности L_рез катушки;

3.  путем подбора емкости C_рез конденсатора (в данной работе резонанса добиваются именно этим способом).

Очевидно, что при резонансе напряжений величина реактивной проводимости B_рез = B_C - B_L равна нулю, а полная проводимость цепи Y_рез = G, то есть принимает минимальное значение. Поэтому, действующее значение резонансного тока (величина которого минимальна) определяется формулой:

I_рез = U*Y_рез = U*G min.

При этом, вектора токов I_KP и I_C численно равны между собой, и противоположны по направлению. Следовательно ток цепи, при резонансе токов, равен активной составляющей тока, т.е. I = I_KA (рис. 7). Отметим, что при условии G<<B_L(C) токи через реактивные элементы будут во много раз превышать ток всей цепи.

Полная мощность параллельной цепи синусоидального тока может быть определена по одной из следующих формул:

S = UI, S = YU², S =  ;

соответственно активная мощность:

P = U I_KA, P = GU², P = UI cos , P = S cos ;

и реактивная мощность:

Q = Q_L - Q_C = (I_KP - I_C) U, Q = BU² = (B_C -B_L) U², Q = UI sin j, Q = S sinj.

В режиме резонанса токов Q_L = Q_C, следовательно полная мощность цепи будет равна активной мощности S_рез= P, а cos j= cos 0 = 1..

Порядок выполнения работы:

Собрать цепь в соответствии со схемой на рис. 1

Рис. 1

Установить амплитудное значение синусоидального напряжения на выходе генератора равным 5 В.

Плавно изменяя частоту генератора, снять зависимости напряжения V1, V2 и угла сдвига фаз φ в зависимости от частоты f поочередно для трех значений сопротивлений резистора R1=1 кОм, R2=2.2 кОм, R3=470 Ом.

Данные эксперимента занести в таблицы 1, 2 и 3

Таблица 1

Таблица 2

Таблица 3

По результату эксперимента построим графики (Рисунок 2,3,4) зависимости U_r , U и φ в цепи от частоты при R = 2.2 кОм, R=470 Ом, R=1 кОм.

Рисунок 2- Зависимость напряжения U_r от частоты.

Рисунок 3- Зависимость тока U от частоты.

Рисунок 4- Зависимость угла сдвига фаз φ от частоты.

Собрали цепь в соответствии с рисунком 5. Повторили эксперимент при R1= 10 кОм, R2=10 кОм. Результаты экспериментов записали в таблицу 4.

Рисунок 5- Схема цепи для эксперимента 2

Таблица 4

По результату эксперимента построим графики (Рисунок 6) зависимости U_r , U и φ в цепи от частоты при R=10 кОм, R=10 кОм.

Рисунок 6- Зависимость напряжения U_r от частоты.

Рисунок 7- Зависимость тока (U/R) от частоты.

Рисунок 8- Зависимость угла сдвига фаз φ от частоты.

переменный ток резонансный

Вывод

Мы исследовали зависимость напряжения от частоты на колебательном контуре. На частоте 500 Гц наблюдается резонанс, при котором наблюдается увеличение напряжения на колебательном контуре. При этом напряжение на резисторе уменьшается. При резонансе угол сдвига фаз становится равным нулю.