Переходные процессы

Переходные процессы

Министерство образования и науки Республики Казахстан

Карагандинский Государственный Технический университет

Контрольная работа

По дисциплине: Электротехника

тема: «Переходные процессы»

Караганда 2012

Введение

Переходным процессом называется процесс перехода от одного режима работы электрической цепи (обычно периодического) к другому (обычно также периодическому), чем-либо отличающемуся от предыдущего, например амплитудой, фазой, формой или частотой, действующей в схеме ЭДС, значениями параметров схемы, а также вследствие изменения конфигурации цепи.

Периодическими являются режимы синусоидального и постоянного тока, а также режим отсутствия тока в ветвях цепи.

Переходные процессы вызываются коммутацией в цепи. Коммутация - это процесс замыкания или размыкания выключателей.

Физически переходные процессы представляют собой процессы перехода от энергетического состояния, соответствующего докоммутационному режиму, к энергетическому состоянию, соответствующему послекоммутационному режиму.

Переходные процессы обычно являются быстро протекающими; длительность их составляет десятые, сотые, а иногда даже миллиардные доли секунд; сравнительно редко длительность переходных процессов достигает секунд и десятков секунд. Тем не менее, изучение переходных процессов важно, так как оно дает возможность установить, как деформируются по форме и амплитуде сигналы при прохождении их через усилители и другие устройства, позволяет выявить превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изоляции установки, увеличения амплитуды токов, которые могут в десятки раз превышать амплитуду токов установившегося периодического процесса (и вызвать недопустимые механические усилия), а также определить продолжительность переходного процесса.

Задание 1

Дана электрическая цепь, в которой происходит коммутация. В цепи действует постоянная ЭДС Е. Параметры цепи приведены в табл. 1. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).

Задачу следует решать классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t=0 до t=, где |Pmin| -меньший по модулю корень характеристического уравнения.

Таблица 1 - Исходные данные

Рисунок 1 - Исходная схема

Задание 2

Дана электрическая схема, на входе которой действует напряжение, изменяющееся во времени по заданному закону U1(t). Требуется определить закон изменения во времени тока в одной из ветвей схемы или напряжения на заданном участке схемы. В таблице 3.2 в соответствии с номером варианта указан номер рисунка, на котором приведен график изменения во времени входного напряжения. Параметры цепи R, L, C заданны в буквенном виде.

Задачу требуется решить с помощью интеграла Дюамеля. Искомую величину следует определить (записать ее аналитическое выражение) для всех интегралов времени. В зависимости от условий задачи полный ответ будет содержать два или три соотношения, каждое из которых справедливо лишь в определенном диапазоне времени.

В каждом ответе следует выполнить приведение подобных членов относительно е-b1t, е-b2t, t и выделить постоянную составляющую.

Таблица 2 - Исходные данные

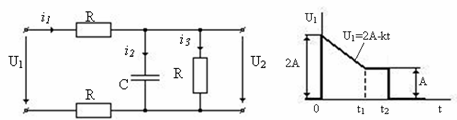
Рисунок 2 - Вариант задания

Расчет переходного процесса классическим методом:

Суть классического метода состоит в том, что решением дифференциального уравнения является сумма принужденной и свободной составляющей, а определения постоянных интегрирования, входящих в выражение для свободного тока (напряжения), производят путем совместного решения системы линейных уравнений по известным значения корней характеристического уравнения, а так же по известным значениям свободной составляющей тока (напряжения) и ее производных при

Записываем искомую величину как сумму двух слагаемых: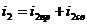

Находим принужденную составляющую (при ),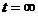

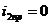
Методом входного сопротивления составляем характеристическое уравнение (при ),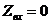

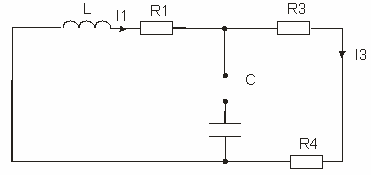
Рисунок 3 - Схема для нахождения Zвх

вх====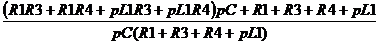0CL1 (R3+R4) + p(R1R3C+R1R4C+L1) + R1 + R3 + R4 = p2*1670*10-6*2*10-3 * 6 + p (2 * 1670 * 10-6+4*1670*10-6+2*10-3) +7=p2*20040*10-9+p12.02*10-3+7= 0*20040*10-9+p12.02*10-3+7= 0

.0002p2+0.01202p+7=0,2=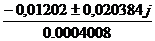=-300.5±509.35j

Записываем полное значение : (1)

Записываем производную от уравнения (1):

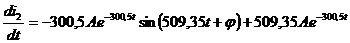cos (509.35+φ) (2)

Составим систему уравнений из (1) и (2) при :

i2(0)=Asinφ

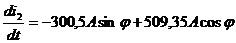
Рассчитываем цепь до коммутации, находим ток в катушке и напряжение на конденсаторе:

На основании начальных условий из пункта 7 строим схему замещения.

Рисунок 4 - Схема замещения

По схеме замещения находим интересующие значения:

A

Для первоначальной схемы составляем уравнения по законам Кирхгофа:

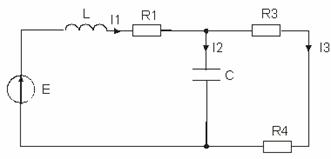
Рисунок 5 - Первоначальная схема

i1-i2-i3=0(R3+R4)-UC(0)=0

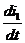+i1R1+UC=E

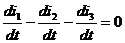
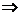
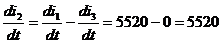
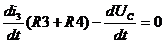
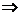
(0)= 33.36В

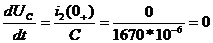
Подставляем значения в систему пункта 6

=Asinφ

sin φ=0

=509.35Acos0

=509.35A==10.837

Записываем закон изменения тока:

Построим график изменения искомой величины в функции времени в интервале от t=0 до t=

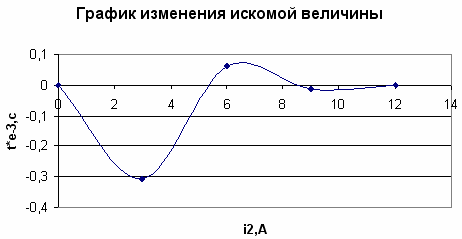
Рисунок 6 - График изменения исходной величины

Расчет переходных процессов операторным методом

Суть операторного метода сводится к преобразованию дифференциальных уравнений относительно функции вещественного переменного, например, времени t,в алгебраическое уравнение относительно нового переменного, пользуясь прямым преобразованием Лапласа, то есть из оригинала в изображение этой функции. Затем полученное уравнение преобразуется обратно в функцию времени с помощью обратного преобразований Лапласа.

Рассчитываем цепь до коммутации и определяем начальные условия:

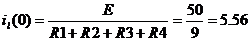А С(0)=*(R3+R4) =5.56*6=33.36В

Составляем операторную схему с учетом ЭДС, т.е сопротивления всех ветвей, источники ЭДС и тока схемы заменяем их изображениями, а ненулевые начальные условия учитываем введением новых источников энергии:

Рисунок 7 - Операторная схема

Из схемы замещения находим изображение искомой величины:

Используя законы Кирхгоффа, составляем систему трех уравнений:(p)-I3(p)-I2(p)=0

Из первого уравнения выражаем I1(p):(p)-I3(p)-I2(p)=0 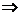 I1(p)=I3(p)+I2(p)

Подставив полученное выражение во второе уравнение, получим:

Из третьего уравнения выражаем I3(p):

Подставив полученное выражение во второе уравнение, получим:

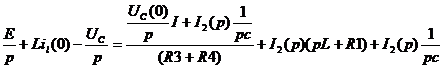
Выразим искомую величину:

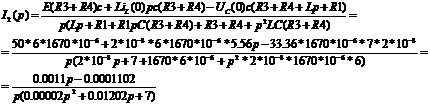
Определяем оригинал искомой величины:

=0,00004(-300.5+509.35j)+0.01202=

.01202+0,020374j +0,01202=0,020374j(p) =0.001112(-300.5+509.35j) -0, 0001102=0, 001324-0,003154j

так как:

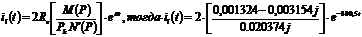= -2e-300.5t=10.8694 e-300.5t(p)=10.79e-300.5tcos(509.35t-90.010)=10.79 e-300.5tsin(509.35t-90.010+900)=10.79 e-300.5tsin(509.35t)

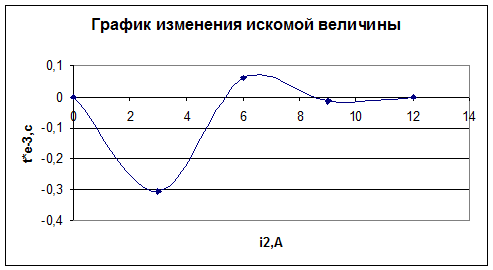
Рисунок 8 - График изменения исходной величины

Расчет переходных процессов с помощью интеграла Дюамеля

Интеграл Дюамеля применяется для расчета процессов в ветвях при подключении к источнику ЭДС сложной формы. Для этого необходимо знать переходные характеристики схемы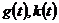.g(t) b k(t) - это соответственно ток и напряжение в исследуемой чисти ветви, если схема питается от напряжения в1 В. Метод расчета сводится к определению этих переходных характеристик классическим или операторным методом; вычислению производной подынтегральной функции интеграла Дюамеля., для чего сначала определяют производную по времени 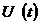, а затем заменяем переменные интегрирования на; завершающий этап включает в себя подстановку полученных ранее функций в формулу интеграла Дюамеля, интегрирование по переменной 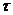 и подстановка пределов.

Таблица 3 - Исходные данные

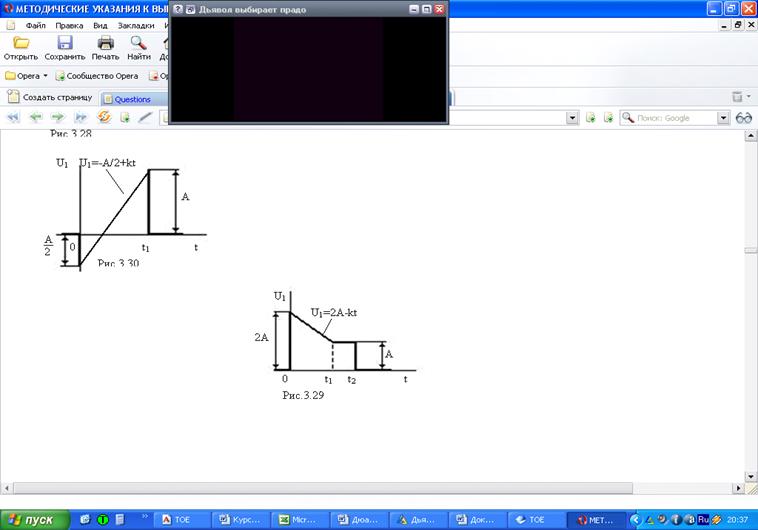
Рисунок 9 - Вариант задания

Рисунок 10 - Исходная схема

. Составляем схему замещения:

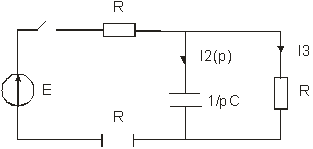
Рисунок 11 - Схема замещения

Для расчета требуемого значения тока i1 найдем переходную характеристику по току i(t), используя классический метод.

i1(t)=i1прин(t)+i св (t)

Находим i1прин:прин=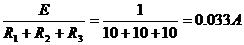

. Для нахождения iсв находим корни характеристического уравнения:

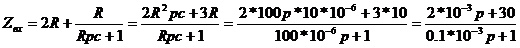
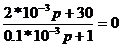
*10-3p=-30

тогда:(t)=0.033+A*e-15*10-3t(0)=0.033+A

. Находим значение тока и напряжения в первый момент после коммутации:

Рисунок 12 - Схема после коммутации

(0)=0(0+)=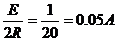

.05=0.033+A=0.017

тогда:(t)=0.033+0.017e-15*10-3t

. Рассчитаем время интегрирования t1 и t2==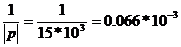

. Найдем закон изменения напряжения на участке 0<t< t1

=20-0.066*10-3k

=20-151.5*10-3t

. Находим интеграл Дюамеля на первом участке

=

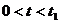
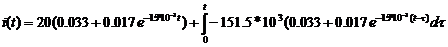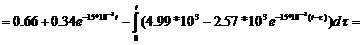
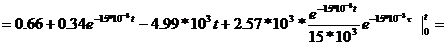
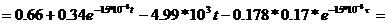
. Находим интеграл Дюамеля на втором участке

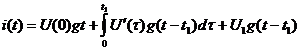
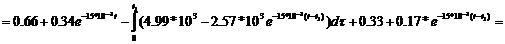
. Находим интеграл Дюамеля на третьем участке

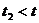
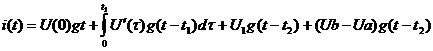
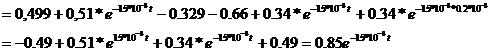
Рисунок 13 - График изменения исходной величины

Таблица 4 - Значения для графика изменения тока

Таблица 5 - Значения для графика изменения напряжения

Заключение

переходной процесс интеграл дюамель

В ходе выполнения данной контрольной работы, для решения заданий, были применены три метода: классический метод, операторный метод и метод интеграла Дюамеля.

Классическим методом расчёта переходных процессов называют метод расчёта, в котором решение дифференциального уравнения представляет собой сумму принужденной и свободной состовляющих, а определение постоянной интегрирования, входящих в выражение для свободного тока (напряжения), производят путём совместного решения системы линейных алгебраических уравнений по известным значениям корней характеристического уравнения, а также по известным значения свободной состовляющей тока (напряжения) и её производных, взятых при t=0+.

Операторный метод основан на использовании понятия об изображении функций времени. В операторном методе каждой функции ρ, и наоборот - функции переменной ρ отвечает определённая функция времени.

Переход от функции времени к функции ρ осуществляют с помощью преобразования (прямого) Лапласа.

Таким образом, операторный метод расчёта переходных процессов представляет собой метод расчёта, основанный на преобразовании Лапласа.

Операторный метод позволяет свести операцию дифференцирования к умножению, а операцию интегрирования - к делению. Это облегчает интегрирование дифференциальных уравнений.

При методе интеграла Дюамеля для того, что бы найти ток в момент времени t, заменяют плавную кривую зависимости величины на ступенчатую и просуммируют токи от начального напряжения u(0) и от всех ступенек напряжения, вступающих в действие с запозданием во времени. Очевидно, что чем большее число ступенек, тем лучше ступенчатая кривая заменяет плавную кривую. С этой целью заменяют интервал времени Δτ на бесконечно малый dτ и переходят от суммы к интегралу:

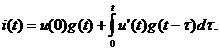
Данную формулу называют интегралом Дюамеля.

Вот в этом суть использованных методик для решения переходных процессов в линейных электрических цепях, которые применялись для решения заданий курсовой работы.

Список использованной литературы

1. Теоретические основы электротехники. Электрические цепи: учебник [текст] / Л.А.Бессонов. - 11-е изд., перераб. И доп. - М.: Гардарики, 2006. - 231 - 310 с.