Математическое моделирование в маркетинге
Оглавление
Введение
Глава 1. Обзор состояния в области математического
моделирования проблем, рассматриваемых в работе
1.1 Распределение бюджета рекламных кампаний
1.2 Дизайн рекламного баннера
Глава 2. Задача распределения имеющегося бюджета по видам рекламы
2.1 Постановка и математическая формулировка задачи
2.2 Получение модельных параметров и подходы к решению задачи
2.3 Требования к исходной информации, построение и решение
примера на модельных данных
Глава 3. Задача оптимизации дизайна визуального рекламного
объявления
3.1 Постановка и математическая формулировка задачи
3.2 Подходы к решению задачи
3.3 Получение модельных параметров
Глава 4. Нерешенные проблемы и перспективные направления в
области математического моделирования рекламы
Заключение
Библиографический список
Введение
В настоящее время реклама является очень востребованным, используемым
способом продвижения бренда, способствующим улучшению отношения к нему у людей,
усилению узнаваемости его, а также способом увеличения числа продаж продуктов
деятельности фирм. На неё тратится большое количество денег, однако,
недостаточно лишь вложить деньги случайным образом в некоторое средство рекламы
или набор таких средств, чтобы достичь поставленных целей. Перед
рекламодателями стоит задача грамотного распределения бюджета по различным
доступным медиа с целью получения наилучшего результата, максимального числа
продаж. Помимо этого требуется в зависимости от конкретного медиа средства и от
целевой аудитории оптимальным образом составлять дизайн рекламного объявления.
Существуют различные подходы к решению задач оптимизации распределения бюджета
по средствам медиа, основанные на построенных математических моделях и на
нахождении точки максимума описанной целевой функции (количество продаж или
прибыль, которые требуется максимизировать). Также есть работы, посвященные тем
факторам, которые положительно или отрицательно влияют на осведомленность о
бренде людей, видевших рекламное объявление, которые влияют на вероятность
перейти по ссылке, указанной в рекламном баннере, появившемся перед
пользователями на сайте, или появившейся при поиске пользователем информации в
поисковике. Многие из этих работ, к сожалению, не представляют большой
значимости, поскольку дают плохие результаты вследствие, например, допущенных
предположений, которые на практике не всегда выполняются, или маленького
коэффициента детерминации в построенной регрессионной модели. Необходимо
максимально точно описать процесс покупки товара в рамках задачи оптимизации
распределения бюджета рекламной кампании на средства рекламы, описать все
стадии этого процесса, начиная с взаимодействия с некоторой комбинацией
рекламных средств и заканчивая покупкой рекламируемого товара в магазине. Для
этого требуется сделать ряд предположений, описывающих поведение людей, их
взаимодействие с рекламой. После этого нужно построить математическую модель
задачи и решить ее для некоторого товара. То же самое необходимо проделать для
задачи оптимизации дизайна визуального рекламного сообщения за исключением
решения задачи на модельных параметрах для некоторого рекламируемого продукта
(в данном случае предполагается лишь построение модели). В рамках данной работы
будет выбран определенный товар, для которого будет смоделирована рекламная
кампания, включающая в себя как нахождение наилучшего распределения бюджета по
разным средствам рекламы, так и построение математической модели для
определения наилучшего дизайна рекламы.
Глава 1.
Обзор состояния в области математического моделирования проблем,
рассматриваемых в работе
.1
Распределение бюджета рекламных кампаний
реклама дизайн
математический моделирование
Пан, Хисе [2015] решали задачу оптимального выделения бюджетных средств
на исследование рынка и на рекламные средства, утверждая, что первое уменьшает
стандартное отклонение от математического ожидания прибыли от продажи товара,
что рекламные средства увеличивают это математическое ожидание. Они строили
функцию количества продукции и прибыли, зависящие от денег, потраченных на
рекламу и на исследование рынка. Авторы заключили, что с ограниченным бюджетом
фирме лучше больше денег выделять на исследование рынка, чем на рекламу,
особенно, если она несет большие убытки от того, что не продали всю продукцию
или не оказались готовы к высокому спросу. Когда стоимость продукции высока,
большую часть средств стоит выделять на рекламу. Также авторы выяснили, что с
ростом издержек на единицу продукции уменьшается часть бюджета, отводящаяся на
рекламу, притом, когда эти издержки высоки, много бюджетных средств стоит
выделить на исследование рынка, чтобы избежать больших потерь от нераспроданной
продукции. Когда средние издержки низки, проще произвести больше продукции, чем
инвестировать много денег в исследование рынка. Однако, такая стратегия может
быть применима и для случая, когда средние издержки высоки, тогда потери от
перепроизводства значительнее, чем от неудовлетворения потребительского спроса,
поэтому важнее увеличить математическое ожидание спроса посредством рекламы.
Бельтран-Ройо, Цханг [2013] привели метод стохастического моделирования
оптимизации распределения бюджета на разные средства рекламирования продуктов.
Авторы заключили, что ожидаемая прибыль с учетом неопределенности как минимум
не меньше прибыли при детерминированном подходе, что результаты оптимального
распределения бюджета надежнее при стохастическом подходе.
Беленький А. С. [2001] сформулировал математически задачу распределения
бюджета рекламной кампании по средствам рекламы и построил математическую
модель. Поиск оптимального распределения бюджетных средств в рамках построенной
модели сводился к решению задачи геометрического программирования. С целью
получения лучших результатов возможна модификация модели, включающая в себя
принятие во внимание существования неопределенности, связанной с восприятием
рекламы потенциальными покупателями товара. Это непосредственно повлияет на
численные значения вероятностей того, что у некоторого человека из
рассматриваемого региона, который подвергся некоторой комбинации средств
рекламы, возникает желание приобрести рекламируемый продукт при условии, что
решающее воздействие на него оказало определенное средство, в зависимости от
количества денег, выделяемых на рекламирование через это средство.
.2 Дизайн
рекламного баннера
Хэлен Робинсон [2007] исследовала зависимость показателя CTR баннера от таких элементов дизайна,
как размер, тон цвета, присутствие «специальных предложений» (купонов, скидок),
наличие анимации, клише, логотипа на основе случайной выборки из 209 баннеров,
размещенных на одном портале с онлайн-играми, на основе данных касательно CTR этих баннеров, полученных от
рекламного агентства. Было выяснено, что эффективными характеристиками
рекламного объявления являются наибольший из всех возможных размер, длинное
сообщение, отсутствие специальных предложений, логотипа, бренда, клише.
Результаты были получены с помощью множественного регрессионного анализа. Стоит
отметить, что результаты сложно назвать надежными, поскольку коэффициент
детерминации модели ниже 0.7, то есть значительная доля дисперсии CTR не объясняется моделью.
Хершбергер [2003] рассматривал зависимость CTR рекламного баннера от его характеристик, учитывая то,
на кого направлена реклама, на физические лица или на юридические, то есть,
учитывая вид взаимодействия B2B или B2C. Он сравнил
эффект рассмотренных характеристик на CTR при этих типах взаимодействия рекламодателя и объектов рекламы. Было
выявлено, что эффект специальных предложений сильнее, когда реклама направлена
на компании, чем когда объекты - физические лица. В первом случае CTR становится ниже при наличии таких
предложений, во втором значительный рост или падение показателя не наблюдался.
Аналогичные результаты были получены и для зависимости числа переходов по
ссылке в рекламе от ее интерактивности с поправкой на то, что в случае В2С взаимодействия
CTR также снижается в случае, когда
рекламное объявление интерактивно. Также было обнаружено, что эмоциональные
обращения к объектам рекламы эффективны лишь в том случае, когда в качестве
объектов выступают физические лица, в случае взаимодействия В2В воздействие
этой характеристики на «кликабельность» баннера негативное. Цвета средних тонов
благоприятно воздействуют на CTR,
наличие анимации также увеличивает этот показатель, но только при В2С
взаимодействии, снижая его в случае, если рекламное сообщение адресовано к
юридическим лицам. Исходя из полученных результатов, можно заключить, что при
В2В взаимодействии эффективность рекламы выше.
Майкл Дален [2001] изучал зависимости эффективности рекламного баннера в
терминах CTR и осведомленности о рекламируемом
бренде, отношения к нему от того, известный ли бренд, от опыта использования
Интернета людей, подвергающихся воздействию рекламы, а также то, как меняется
эффективность от повторных появлений рекламного объявления перед посетителями
сайта, на котором размещен баннер, в случаях, когда бренд знаком им или,
наоборот, незнаком. Дален получил следующие результаты. Когда реклама
показывается впервые посетителям, показатель CTR значительно выше в случае, если рекламируется
известный бренд. В случае повторяющихся появлений баннера перед посетителями
сайта CTR уменьшается, если бренд известен, и,
наоборот, увеличивается, если бренд незнаком. Была отклонена гипотеза о том,
что отношение к незнакомому бренду и осведомленность о нем улучшается у
человека, который неоднократно видел рекламное сообщение. В случае со знакомым
брендом отношение к нему не изменяется при неоднократном подвергании людей
рекламе. Не были отклонены гипотезы о том, что менее опытные пользователи
Интернета сильнее подвержены рекламе: они чаще переходят по ссылке на баннере,
их отношение к бренду и осведомленность о нем улучшаются в большей степени,
нежели у более опытных пользователей. Также было заключено, что чем больше
посетитель сайта подвергается рекламе известного бренда, тем хуже его отношение
к нему (осведомленность, очевидно, не меняется). Если же рекламируется
неизвестный бренд, то отношение к нему будет наилучшим, если человек
подвергается рекламе либо один раз, либо не менее пяти (значительные изменения
в осведомленности не наблюдались).
Джоффри Аткинсон [2014] изучал зависимость эффективности поисковой
рекламы, показателя CTR, от ее
различных характеристик. Было обнаружено, что слова в рекламе должны начинаться
с заглавной буквы, только когда находятся в первой строке, иначе этот прием
производит негативный эффект на CTR.
Авторы установили обратную зависимость между эффективностью рекламы и
использованием бренда ритейлера и прямую между CTR и наличием в объявлении бренда производителя. Также
был выявлен позитивный эффект приема «value puffery»
(акцентирование на цене, не уточняя ее) на число переходов по рекламе. Также,
исходя из результатов, можно заключить, что наличие специальных предложений и
вопросов к пользователям Интернета только снижает CTR поисковой рекламы, в отличие от присутствия цены
рекламируемого продукта. Главным вкладом исследования, по мнению авторов,
является обнаружение того, что элементы рекламы по-разному влияют на ее
эффективность в зависимости от местоположения в сообщении. Например, призыв к
действию, покупке не производит в целом значительный позитивный эффект, однако
если рассмотреть его наличие лишь во второй строке сообщения, то использование
этого приема является оправданным. Стоит отметить, что исследование проводилось
в определенной стране, лишь на одном рынке и что не учитывалась рекламная
деятельность конкурентов и воздействие комбинации всех используемых ключевых
слов на CTR.
Чанг-Хоан Чо [2001] изучал влияние уровня принудительности рекламы на ее
эффективность в терминах отношению к бренду, рекламному баннеру, возникновения
желания приобрести рекламируемый продукт и показателя CTR. Был сформулирован ряд гипотез. Первая заключалась в
том, что чем выше уровень принудительности, тем больше информации
воспринимается людьми из баннера. Очевидно, она не была отклонена. Вторая
гипотеза, которую также не отклонили, содержала в себе следующее утверждение:
чем выше уровень принудительности, тем выше показатель CTR рекламного объявления. Неожиданно для авторов были
отклонены гипотезы, заключающиеся в том, что больший уровень принудительности
рекламы вызывает неблагоприятное для рекламодателей отношение посетителей сайта
отношение к рекламному объявлению, бренду и маловероятное появление желания
приобрести рекламируемый продукт. Однако результаты исследования сложно с
уверенностью назвать достоверными, поскольку выборка людей не являлась
репрезентативной, в нее входили люди, подписавшиеся на обсуждение LISTSERVs (как предположили авторы, это были
более активные пользователи Интернета, чем большинство), то есть генеральной ее
нельзя назвать. Также недостатком исследования является небольшой объем выборки
баннеров и то, что точное количество переходов по ссылке в рекламе неизвестно,
оно оценивалось на основе опросов людей, подвергавшихся рекламе.
Таким образом, можно отметить, что подходов с математической точки зрения
к решению оптимизации распределения бюджета рекламной кампании по средствам
рекламы и оптимизации дизайна визуального рекламного сообщения немного, в
большей степени это относится ко второй задачи. Работы, в которой она бы
формулировалась именно как оптимизационная задача, найдены не были ввиду
коммерческой тайны прежде всего.
Глава 2.
Задача распределения имеющегося бюджета по видам рекламы
.1 Постановка
и математическая формулировка задачи
Первоначально требуется привести математическую модель проблемы: ввести
требующиеся обозначения, учесть и верно сформулировать в ней все имеющиеся
ограничения (на бюджет, на использование средств рекламы и т. д.), а также на
основе сделанных ранее предположений касательно, например, поведения людей
построить целевую функцию, описывающую прибыль, или выручку, или количество
единиц проданной рекламируемой продукции, которая должна быть максимизирована.
С целью максимизации будет использован метод в соответствии с видом целевой
функции, с тем, проблема какого вида оптимизации требует решения. В данной
работе для поиска наилучшего распределения бюджета будет использована модель,
описанная Беленьким А. С. [2000].
Пусть есть n видов рекламы, с
помощью которых можно информировать людей о продукте фирмы, который может быть
приобретен в текущем периоде под воздействием этих средств в представительстве
компании в рассматриваемом регионе или в Интернет-магазине. Делается ряд
предположений:
. Кампания проводится в определенном регионе в определенный период
времени для определенного продукта.
. Взаимодействие человека с некоторой комбинацией рекламных
средств происходит случайно независимо от других людей из рассматриваемого
региона, вероятности каждого такого взаимодействия одинаковы для всех людей из
региона.
. Каждый центр продаж обладает достаточным количеством продукции,
чтобы удовлетворить спрос покупателей, однако существует вероятность того, что
приобрести товар по тем или иным причинам не выходит.
. Выбор центра продаж любым человеком происходит случайным образом
независимо от поведения других жителей региона и местоположения магазина,
вероятность пойти в тот или иной центр одинакова для всех людей, как и
вероятность совершить покупку при выборе некоторого центра.
. Если продукт приобрести не получается с первой попытки при
выборе некоторого центра продаж, то возникшее желание купить товар у человека
пропадает.
. Чем больше на потребителя воздействует отдельный вид рекламы или
вся комбинация, тем выше становится значение вероятности того, что у человека
возникнет желание совершить покупку. Притом усиление этого желания под
воздействием одного средства рекламы происходит независимо от усиления под
воздействием другого. Максимальное значение, которое может достигнуть эта вероятность,
меньше 1, на самом деле, так как существует некоторая сумма денег для каждого
средства рекламы, такая, что если выделить на них больше этой суммы, то эта
вероятность не увеличивается.
. Возникновение желания приобрести рекламируемый продукт у потребителя
после взаимодействия с некоторой комбинацией средств рекламы не зависит от
возможности реализовать его в центрах продаж.
. Вероятность возникновения желания приобрести рекламируемый
продукт у потребителя после взаимодействия с некоторой комбинацией средств
рекламы не зависит от вероятности появления этого желания вследствие
взаимодействия с другими комбинациями типов рекламы. Кроме того она одинакова
для любого человека, получившего информацию о продукте из рекламы.
Введем следующие обозначения:
qi -максимальное
количество денег, которое можно выделить на i-е средство рекламы, i=1,…,n. q возможно выделить на всю рекламную
кампанию.
k0 -
число имеющихся центров продаж в регионе.
В данном регионе имеются вопросники, собранные в ходе определенного числа
экспериментов (рекламных кампаний), позволяющие выявить величину pjm
= φjm(xj) - вероятность появления желания приобрести продукт
вследствие воздействия комбинации рекламных средств j=1,…,n при
потраченных средствах xj в
рамках эксперимента m=1,…,l. В случае, если нет таких
вопросников, есть эксперты, способные вычислить эти величины.
Кроме этих вопросников есть и другие, позволяющие найти вероятности
покупки продукта с первой попытки в любом магазине, а также и такие вопросники,
с помощью которых можно выявить значения вероятностей воздействия на людей
каждой комбинации видов рекламы. Иначе же требуются услуги экспертов, способных
вычислить эти значения.
Пусть Ai - событие воздействия на человека
комбинации рекламных средств i=1,…,2n-1;
D/Ai - появление у человека желания
приобретения продукта при воздействии на него комбинации i=1,…,2n-1;
Bk -
событие, при котором человек решает идти покупать продукт в центр продаж k=1,…,k0;
C/Bk - событие приобретения продукта
человеком при том, что он пошел в k-й центр продаж, k=1,…,k0;
C/Ai - приобретение продукта человеком
при том, что на него оказала воздействие комбинация i и он может себе это позволить, i=1,…,2n-1;
C -
приобретение продукта человеком, получившим информацию о нем из рекламы и
имеющим возможность себе это позволить;
C/B - покупка продукта человеком,
узнавшим о нем из рекламы, в одном из центров продаж региона;
(D/Ai)j - появление
желание у человека приобрести продукт вследствие воздействия на него комбинации
i, а именно, средства j, i=1,…,2n-1, j=1,…,n;
Событие, противоположное событию Q, обозначается ⌐Q.
P(Q) - вероятность события Q.
Процесс приобретения некоторым человеком рекламируемого продукта можно
визуализировать с помощью блок-схемы, описывающей его:
Используя формулу полной вероятности, получим следующие вероятности:
P(C) =  P(Ai)P(C/Ai)(C/Ai) = P(D/Ai)P(C/B)(C) =
P(Ai)P(C/Ai)(C/Ai) = P(D/Ai)P(C/B)(C) =  P(Ai) P(D/Ai) P(Bk) P(C/Bk)
P(Ai) P(D/Ai) P(Bk) P(C/Bk)
Обратим внимание на то, что P(D/Ai) = 1-P(⌐(D/Ai)), P(⌐(D/Ai))= 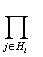 P(⌐(D/Ai)j), где Hi - множество видов рекламы из
комбинации i, воздействовавших на потребителя.
P(⌐(D/Ai)j), где Hi - множество видов рекламы из
комбинации i, воздействовавших на потребителя.
Таким образом, получаем следующую формулу:
P(C) =  P(Ai) (1-
P(Ai) (1-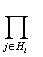 P(⌐(D/Ai)j)) P(Bk) P(C/Bk)
P(⌐(D/Ai)j)) P(Bk) P(C/Bk)
Затем обозначим за Т случайную величину - количество людей, которые были
проинформированы о продукте из рекламы и решили купить его.
η - численность целевой аудитории.

Исходя из сделанных предположений о том, что воздействие комбинациям
рекламных средств на человека происходит независимо от других людей и случайно,
воспользуемся известной схемой испытаний Бернулли:
P(T=t) = Cηt [P(C)]t [1-P(C)]η - t
Тогда математическое ожидание числа людей, которые купят продукт, из
целевой аудитории находится по следующей формуле:
M(T) = 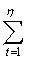 Cηt [P(C)]t [1-P(C)]η
- t t .
Cηt [P(C)]t [1-P(C)]η
- t t .
Пусть P(D/Ai)j = ψj(xj) ≤ 1 - монотонная, неубывающая функция от xj, постоянная при xj ≥  , где
, где  - предельное значение. То есть, выделять на вид рекламы
денег больше, чем
- предельное значение. То есть, выделять на вид рекламы
денег больше, чем  , не имеет смысла.
, не имеет смысла.
P(⌐(D/Ai)j)) = 1- ψj(xj).
Обозначим ξi = P(Ai), θk = P(Bk), γk = P(C/Bk), эти величины будем считать
постоянными и не зависящими от xj, j = 1,…,n.
Затем сформулируем математическое ожидание Т в новых обозначениях:
M(T) = f(x1,…,xn) =
Теперь выведем существующие ограничения на денежные средства, которые
будут выделяться в рамках кампании:
 ≤ q;
≤ q;
cjxj ≤
qj, где cj - стоимость единицы измерения рекламного средства (секунда
ТВ-рекламы, клик на рекламный баннер, размещенный на некотором сайте, и т. д.).
Обозначим за Ω множество всех возможных решений системы линейных
неравенств, описывающих бюджетные ограничения. Тогда сформулируем задачу
планирования рекламной кампании:
f(x1,…,xn) → 
Предположим, что (x*1,…,x*n) - найденный максимум целевой функции. Также допустим, что
каждый человек в регионе купит не более одной единицы продукта, и обозначим
стоимость каждой единицы за τ. В таком случае максимальная выручка
компании составит w
= τf(x*1,…,x*n). Ожидаемая прибыль от кампании
вычисляется по формуле: SP =  , где w0 - ожидаемая выручка в случае, если рекламная кампания не
проводится. В случае, когда SP>1,
проведенная рекламная кампания может считаться удачной.
, где w0 - ожидаемая выручка в случае, если рекламная кампания не
проводится. В случае, когда SP>1,
проведенная рекламная кампания может считаться удачной.
.2 Получение
модельных параметров и подходы к решению задачи
На данной стадии подготавливаются входные параметры с целью решить
задачу:
cj -
известные цены использования рекламных средств, j=1,…,n.
qj, q - известные суммы денег, которые
возможно потратить на виды рекламы и на саму кампанию соответственно.
Коэффициенты ξi, θk , γk будут вычислены экспертами, в
распоряжении которых будут вопросники.
Зависимости ψj(xj) будут найдены экспертами, исходя из результатов опроса. Они
могут быть получены с помощью метода наименьших квадратов для пар чисел (ψj(xjm), xjm), xjm - мощность рекламного средства j, использованного в m-м эксперименте, m=1,..,l, j=1,…,n, ψj(xj) - доля целевой аудитории региона, которая была подвержена j-му виду рекламы, благодаря чему у
нее возникло желание приобрести продукт.
Итак, поиск максимума целевой функции сводится к решению задачи
нелинейного программирования, для этой цели уже разработаны определенные
методы.
Есть несколько способов искать глобальный максимум целевой функции.
Во-первых, можно имеющуюся область определения разбить на подобласти, на
которых функция выпукла или вогнута. Затем на каждой из областей, где функция
вогнута, можно найти точки максимума. Поиск этих точек функции нескольких
переменных может быть организован при помощи уже разработанных с этой целью
пакетов программ, таких как, например, PTC MathCAD. После этого останется сравнить значения функции в
найденных экстремумах. Во-вторых, можно аппроксимировать имеющуюся функцию
такой функцией, для максимизации которой в условиях тех же ограничений на
переменные уже существуют методы решений, например, позиномом. В таком случае
оптимизационная задача была бы сведена к задаче геометрического
программирования, для решения которой также уже существуют пакеты программ,
таких как, например, GGPLAB
- набор инструментов для решения задач геометрического программирования в среде
Matlab.
В данном случае на сегменте x  [0,
[0,  ], j=1,…,n, ψj(xj) может быть приближена одночленом
], j=1,…,n, ψj(xj) может быть приближена одночленом 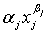 ,
αj
> 0, βj > 0 так, что P(D/Ai)j =
,
αj
> 0, βj > 0 так, что P(D/Ai)j =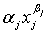 и P(⌐(D/Ai)j) = 1-
и P(⌐(D/Ai)j) = 1-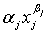 .
.
Тогда М(Т) = f(x1,…,xn) =
 [
[ ξi(1-
ξi(1- 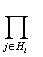 (1-
(1-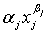 )) θk γk)]t
)) θk γk)]t  [1-
[1-  ξi(1-
ξi(1- 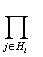 (1-
(1-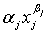 )) θk γk)]
η-t
)) θk γk)]
η-t  Cηt t
Cηt t
zj = 1
- 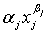 , j=1,…,n
, j=1,…,n
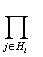 (1-
(1-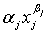 ) = ui,
) = ui,
1-ui = vi ,
 - w = 0,
- w = 0,
 = p,
= p,
- pw = s.
Теперь задача может быть сформулирована следующим образом (наиболее
компактным):
c1x1+…+cnxn ≤ q,
cjxj ≤
qj, j=1,…,n,
zj + 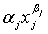 =1,
=1,
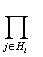 zj = ui, i=1,…,2n-1
zj = ui, i=1,…,2n-1
-ui = vi ,
 = p,
= p,
s + pw = 1,

2.3
Требования к исходной информации, построение и решение примера на модельных
данных
В качестве примера будет взята задача оптимизации распределения бюджета
рекламной кампании по двум видам рекламы (n=2): ТВ-реклама и поисковая реклама в сети Интернет.
Рекламируемым товаром будет новая модель мужских бутс для игры в футбол
некоторой компании в некотором регионе, численность целевой аудитории которого
Т равна 100000 человек (η = 100000). Соответственно, целевой аудиторией
можно назвать группу людей, а именно, мужчин, увлекающихся футболом.
Предполагается, что рекламирование товара будет проводиться в ближайшее
время в течение месяца, когда во Франции будет проходить чемпионат Европы по
футболу (в этом случае рейтинги телеканалов, по которым будут транслироваться
игры, будут очень высоки), когда тема футбола будет особенно актуальна.
Евро-2016 будет проходить в течение месяца с 10 июня по 10 июля. Поскольку
внимание телезрителей будет приковано к трансляции игр, в рассматриваемый
период времени стоимость показа рекламного ролика длительностью до десяти
секунд во время рекламной паузы между таймами матчей будет завышена. Допустим,
ролик будет показываться по Первому каналу и России 1. В обычное время цена
показа в среднем для этих каналов составляет приблизительно 100000 рублей,
тогда в данном случае она составит 200000 рублей (с1 = 200000).
Поисковая реклама будет показываться в течение месяца через несколько
поисковиков, притом будет задействована как контекстная, так и семантическая
реклама. В данном случае в качестве единицы измерения выступит запрос, при
печатании которого пользователем поисковиков будет показываться реклама,
поскольку число запросов в большей степени нежели остальные критерии влияет на
вероятность взаимодействия людей с этим типом рекламы, а также, в особенности,
на вероятности событий, заключающихся в том, что при воздействии на человека
некоторой комбинации средств рекламы, включающих в себя этот, именно поисковая
реклама сыграет решающую роль в появлении желания приобрести бутсы. Допустим, в
виду указанных выше причин стоимость одного запроса составляет 200000 (с2 =
200000).
Важнейшим вопросом является вопрос формирования бюджета рекламной
кампании, от ответа на него непосредственно зависит, какую часть целевой
аудитории получится осведомить о рекламируемом продукте, у какой части
осведомленных людей возникнет желание купить товар. Есть несколько способов
сформировать бюджет рекламной кампании. Одним из самых востребованных является
вычисление процента от товарооборота (от ожидаемой в этом году выручки или от
выручки за прошлый год). Если отталкиваться от ожидаемого дохода в этом году,
то такой метод позволяет оценить потенциальную эффективность рекламной
кампании. Требуется определить, какой именно процент выделять на рекламу. Ответ
на этот вопрос зависит от того, насколько необходимо рекламирование продуктов,
услуг фирмы. В рассматриваемом случае фирмой является производитель спортивной
экипировки, а значит, на рекламу выделится значительная часть товарооборота.
Допустим, бюджет составит 7000000 (q = 7000000).
Что касается ограничений на бюджетные средства, выделяемые на каждый из
типов рекламы, то они определяются зависимостями эффективностей этих видов
рекламы от сумм денег, вложенных в них, рекомендациями специалистов,
существующими исследованиями на тему планирования рекламных кампаний. Также
очень важную роль играет то, при каких затратах эффективность средств рекламы
перестает расти. Предположим, что если в перерыве матчей один раз показывается
рекламный ролик в течение 2 недель (в день проводится по 2 игры), то все люди,
кто мог его посмотреть, осведомлены о рекламируемом продукте, поэтому
показывать ролик больше 2 недель не имеет смысла. Тогда  = 5600000. Также можно предположить,
что нет смысла тратить средства более чем на 10 поисковых запросов, при
введении которых в поисковик пользователи Интернета будут подвергаться рекламе.
Это объясняется тем, что 10 запросов - более чем достаточно для того, чтобы
описать все возможные наборы ключевых слов, используемых с целью добычи
информации о продающихся в регионе бутсах для игры в футбол. В таком случае
= 5600000. Также можно предположить,
что нет смысла тратить средства более чем на 10 поисковых запросов, при
введении которых в поисковик пользователи Интернета будут подвергаться рекламе.
Это объясняется тем, что 10 запросов - более чем достаточно для того, чтобы
описать все возможные наборы ключевых слов, используемых с целью добычи
информации о продающихся в регионе бутсах для игры в футбол. В таком случае  = 2000000. Учтя полученные значения,
установим бюджетные ограничения на использование ТВ и поисковой рекламы равными
5300000 и 1800000, соответственно. Итак, q1 = 5300000 и q2 =
1800000.
= 2000000. Учтя полученные значения,
установим бюджетные ограничения на использование ТВ и поисковой рекламы равными
5300000 и 1800000, соответственно. Итак, q1 = 5300000 и q2 =
1800000.
Далее требуется найти вероятности взаимодействия людей, относящихся к
целевой аудитории, с каждой комбинацией средств рекламы. Всего может быть три типа
взаимодействия: человек просмотрел рекламный ролик (А1), столкнулся с рекламой
при поиске некоторой информации в Интернете (А2), а также одновременное
воздействие на него обоих рекламных средств (А3). Эти вероятности можно
определить при помощи проведения экспериментов, опрашивания людей из региона и
использования их ответов в вопросниках. Предположим, что Р(А1) = 0.8, так как
практически вся целевая аудитория будет просматривать матчи Чемпионата Европы
по футболу, притом большинство - по телевизору, поскольку игры будут
транслироваться по Первому каналу и России 1, общедоступным телеканалам. Пусть,
Р(А2) = 0.1, тогда Р(А3) = 0.1 0.8 = 0.08, так как события независимы (если человек
встречает рекламу при просмотре футбольного матча во время перерыва, то это не
влияет на вероятность того, что он случайно столкнется с поисковой рекламой
того же продукта).
0.8 = 0.08, так как события независимы (если человек
встречает рекламу при просмотре футбольного матча во время перерыва, то это не
влияет на вероятность того, что он случайно столкнется с поисковой рекламой
того же продукта).
Теперь требуется построить функции, определяющие зависимости вероятности
событий, заключающихся в том, что у потребителя возникает желание совершить
покупку рекламируемого продукта, бутс, при воздействии на него i-й комбинации средств рекламы, в
которой решающую роль сыграло j-е
средство, от суммы денег, выделенной на j-е средство. Всего таких функций будет 4: по одной для первых
двух видов взаимодействия (в них задействовано по одному виду рекламы), два при
третьем виде (потребитель столкнулся с поисковой и ТВ-рекламой). Функции имеют
вид одночленных позиномов, как и было предположено ранее. Возможно построение
их с использованием статистических данных, полученных с помощью опросов людей.
Предположим, что функции имеют следующий вид:

Параметры α, β (αхβ) получены, исходя из предположений о
значениях вероятности в двух случаях, когда выделяется  и некоторая, отличная от
и некоторая, отличная от  , сумма денег.
, сумма денег.
Ниже приведен скрипт с описанием целевой функции в среде Matlab.

Разумеется, при планировании реальной рекламной кампании требуется
экспериментально найти неизвестные параметры (выше было описано, как могут быть
получены модельные параметры), такие, как  , j = 1,2, αl,
βl, l = 1,…,4, P(C/Bk), k =
1,…,k0, P(Ai), i = 1,…,3, а не назначать им
соответствующие значения, исходя из предположений. Конечно, на проведение
вычислений искомых значений на основе проведенных экспериментов и собранных
опросников требуется большая сумма денег и немало времени, поэтому в рамках
этой работы численные значения были найдены на основе предположений.
, j = 1,2, αl,
βl, l = 1,…,4, P(C/Bk), k =
1,…,k0, P(Ai), i = 1,…,3, а не назначать им
соответствующие значения, исходя из предположений. Конечно, на проведение
вычислений искомых значений на основе проведенных экспериментов и собранных
опросников требуется большая сумма денег и немало времени, поэтому в рамках
этой работы численные значения были найдены на основе предположений.
Глава 3.
Задача оптимизации дизайна визуального рекламного объявления
.1 Постановка
и математическая формулировка задачи
Перед дизайнерами рекламного объявления стоит задача создать его таким
образом, чтобы максимизировать его способность привлечь внимание потенциальных
покупателей, заинтересовать их. Решим задачу на примере рекламного баннера в
Интернете. Требуется увеличить CTR,
отношение числа переходов по ссылке к числу показов сообщения, которое принято
считать показателем эффективности баннера. В качестве рекламируемого продукта
возьмем бутсы для игры в футбол, производящиеся некоторой компанией. Рекламное
объявление будет расположено на некотором спортивном портале.
Сделаем ряд предположений:
. Рассматриваемая рекламная кампания проводится в определенный
период времени в определенной стране.
. Переход человека по ссылке вследствие воздействия рекламе
происходит независимо от остальных людей в регионе.
. Баннер размещен на спортивном портале, соответственно, все
посетители сайта - потенциальные покупатели.
. Если реклама появляется перед человеком, не относящимся к
целевой аудитории, заинтересованность в предложении не возникает.
. Бюджет, доступный для создания рекламного баннера, ограничен.
. Сайт, на котором расположено объявление, посещают люди от 10 до
80 лет. Те, чей возраст не входит в этот диапазон, либо не пользуются
Интернетом, либо посещают его крайне редко, кроме того спорт им не интересен,
вероятнее всего, поэтому эти люди в качестве целевой аудитории рассмотрены не
будут.
. Чаще всего рассматриваемый продукт, бутсы, покупают мужчины, чей
возраст до 45 лет, так как, исходя из статистических данных, известно, что
женщины намного реже играют в футбол, тем более, крайне редко покупают бутсы
так же, как и мужчины старше 45 лет.
CTR = t/M,
где t - дискретная случайная величина,
характеризующая число переходов по ссылке, указанной в баннере, а M - число появлений рекламного
объявления перед посетителями. Поскольку М - постоянная величина, задача
увеличения показателя CTR
сводится к максимизации математического ожидания t.
Посетителей сайта необходимо разбить на группы, участники которых бы вели
себя схоже друг с другом по отношению к рекламе. Исходя из предположения №7,
будем рассматривать мужчин до 45 лет. Введем три возрастные категории:
несовершеннолетние (до 18 лет), 18-25 лет, 25-45 лет. Отметим, что в рамках
каждой группы ее участники имеют примерно одинаковый опыт пользования
Интернетом, также чаще всего участники первой группы (школьники, не работающие)
имеют значительно больше свободного времени, нежели остальные люди. Во вторую
группу входят преимущественно студенты, обладающие меньшим запасом времени,
которое можно уделить игре в футбол, в третьей возрастной категории преимущественно
люди, работающие, несущие ответственность за свои семьи, соответственно,
имеющие меньше всех остальных время и желание играть в футбол. Также
восприимчивость к рекламе зависит от образованности человека. Рассмотрим 3
категории. Уровень образования может быть следующим: неполное среднее или
среднее, среднее профессиональное или неполное высшее, высшее или ученая
степень. По степени обеспеченности люди могут быть классифицированы как низший,
средний и высший класс. Таким образом, имеется 27 групп посетителей спортивного
портала.
Тогда число переходов по ссылке на сайт организации-рекламодателя может
быть представлено в следующем виде:
t = t1 + … +t27
Делается предположение, что в каждой небольшой группе (например, в группе
несовершеннолетних людей с неполным средним образованием и низким уровнем
достатка) вероятность перейти по ссылке одинакова для всех ее участников. Это
предположение обосновано тем, что люди в такой достаточно узкой группе
находятся в приблизительно равных условиях (примерно одинаковый уровень
образованности, благосостояния, количество свободного времени), обладают
приблизительно одинаковым опытом пользования Интернетом.
Допустим, численность некоторой группы N. Рассмотрим дискретную случайную величину tk, где k - номер рассматриваемой группы людей. Выпишем ряд
распределения этой случайной величины:
|
tk
|
0
|
1
|
…
|
T
|
|
pk
|
pk0
|
pk1
|
…
|
pkT
|
Обратим внимание на то, что рассматриваемая случайная величина имеет
биномиальное распределение, поскольку, исходя из сделанных предположений,
известно, что люди подвергаются рекламе независимо друг от друга, есть всего
два исхода взаимодействия человека с рекламным баннером, и вероятности этих
исходов одинаковы для каждого человека. Значит, tk ~ Bi(N,p), где р - вероятность посетителя сайта, принадлежащего рассматриваемой
группе, перейти по ссылке (соответственно, вероятность того, что у посетителя
сайта не возникает желания перейти на сайт рекламодателя равна 1-р).
Математическое ожидание tk
равно: Etk = Np. Тогда математическое ожидание CTR вычисляется следующим образом:
Разумеется, вероятности pk, k=1,…,27, зависят непосредственно от
дизайна визуального рекламного сообщения, от того, какими характеристиками
будет наделен баннер.
Переход по ссылке зависит от следующих факторов:
. Баннер заметен, привлекает внимание.
. Рекламное предложение выгодно.
. Рекламируется известный (возможно, небезразличный) для человека
бренд.
. Визуальный эффект баннера приятный.
. Баннер является интерактивным, реагирует на действия посетителя.
Необязательно выполнение всех условий сразу, чтобы максимальное число
посетителей сайта кликнули на баннер. Целью в задаче дизайна визуального
рекламного сообщения является нахождение оптимального распределения бюджетных
средств на характеристики баннера так, чтобы его показатель CTR был наибольшим. Также отметим, что в
данной работе не ищутся ответы на следующие вопросы: стоит ли помещать на
баннер логотип компании, стоит ли указывать на нем цену продукта, делать
специальные предложения или совершать призывы перейти на сайт, какие цветовые
тона должны преобладать и т. д. Причина этого состоит в том, что уже есть
исследования на эту тему (в том числе те, что представлены в главе «Обзор
состояния в области математического моделирования проблем, рассматриваемых в
работе»), соответственно, уже найдены ответы на эти вопросы.
Введем следующие обозначения:
F -
событие, заключающееся в переходе человека, увидевшего рекламу, по ссылке;
N -
событие, заключающееся в том, что баннер замечен человеком, посетившим сайт, на
котором размещено рекламное сообщение;
D -
событие, состоящее в том, что у человека возникает желание перейти на сайт
рекламодателя;
D/N - событие, состоящее в том, что у
человека возникает желание перейти на сайт рекламодателя при условии, что он
заметил рекламный баннер;
E -
событие, заключающееся в том, что эффект, который производит рекламный баннер,
приятен для человека, который увидел рекламное сообщение;
I -
событие, заключающееся в том, что человек, поучаствовав в игре, размещенной на
баннере, захотел перейти по ссылке.
Событие I возможно в том случае, когда баннер
является интерактивным, то есть реагирует на действия пользователя. Возможное
использование интерактивности: посетитель видит баннер, двигающуюся картинку,
на которой стоит футболист напротив футбольных ворот и предлагает человеку
пробить пенальти. Посетитель кликает мышкой на мяч, футболист бьет, забивает
гол, и за это пользователю предлагается скидка на товар или подарок, который он
может забрать при покупке товара. Участие в такой игре однозначно улучшит
отношение человека к рекламному объявлению, а также предоставит ему лишний
стимул перейти по ссылке.
Представим событие F
следующим образом:
 . Тогда
. Тогда 
В свою очередь,  . События Е и I
являются совместными (возможно сделать баннер таким образом, что сначала
показывается картинка, создающая благоприятный визуальный эффект, после чего
появляется игра, которая создаст положительное отношение к объявлению и
предоставит стимул для перехода по ссылке). Тогда
. События Е и I
являются совместными (возможно сделать баннер таким образом, что сначала
показывается картинка, создающая благоприятный визуальный эффект, после чего
появляется игра, которая создаст положительное отношение к объявлению и
предоставит стимул для перехода по ссылке). Тогда

Добавим, что события E, I являются независимыми, так как
появление желания перейти на сайт с рекламируемым продуктом после участия в
игре не зависит от того, насколько сильно понравилось пользователю оформление
баннера, его дизайн, изображение на нем. Вероятность события I зависит в первую очередь от того,
какие эмоции он получил от игры, каким образом (призы, скидка) он награжден за
участие и как он стимулирован. Поэтому

Характеристики рекламного баннера, которыми его наделяют при создании
дизайна, определяют вероятности упомянутых выше событий.
Введем следующие переменные:
s -
размер рекламного баннера (см2), влияющий на то, заметит ли посетитель
рекламное объявление. Очевидно, чем больше размер, тем более заметен баннер;
a -
объем памяти, выделяющийся на анимацию (кБ), присутствующую на рекламном
баннере, она привлекает внимание посетителя, так как он с большей долей
вероятности обратит внимание на меняющиеся или двигающиеся картинки, чем на
статичный баннер;
z -
продолжительность звука (сек), раздающегося из динамика посетителя сайта при
появлении баннера. Он, с одной стороны, привлекает внимание, но, с другой, -
негативно сказывается на эффекте, который производится рекламным сообщением,
так как раздражает;
с - сумма денег ($), выделенная на размещение на баннере фото известного
футболиста. Знаменитость может держать в руках рекламируемые бутсы, либо может
быть в них на фото. Подсознательно люди стремятся быть похожими на своих
кумиров, поэтому наличие популярного футболиста благоприятно сказывается на
эффекте, который производится рекламным объявлением. Разумеется, чем больше
сумма денег, которую выделяют на приглашение поучаствовать в кампании
знаменитости, тем более известный и популярный футболист будет на фото;
m -
сумма денег ($), выделенная на создание игры, от которой зависит
реалистичность, детализация картинки.

Далее требуется описать имеющиеся параметры, обосновать имеющиеся
зависимости вероятностей событий от введенных переменных.
Разумеется, вероятности упомянутых выше событий ограничены снизу 0,
сверху - 1, они возрастают при увеличении переменных s, a, z в первом случае, с - во втором и m - в третьем. Р(Е) уменьшается при увеличении значения
переменной z. Соответственно, параметры α1,
α2, α3, λ1, λ2 больше 0, разность  .
γ1 также больше 0,
поскольку наличие анимации делает баннер заметнее.
.
γ1 также больше 0,
поскольку наличие анимации делает баннер заметнее.
В случае большинства вероятностей их «отдача от масштаба» убывающая в том
смысле, что функции, описывающие зависимости вероятностей от имеющихся
переменных, вогнутые.
Для того, чтобы наглядно описать процесс перехода по ссылке посетителя
сайта, приведем следующую блок-схему:

Например, вероятность того, что баннер будет замечен, при увеличении его
площади с 25 до 30 см2 увеличивается в большей степени, чем в случае, когда
площадь увеличивается с 50 до 55 см2, так как во втором случае изменения в
размере менее значительны, чем в первом. Поэтому параметр 0<β1<1.
Размер баннера также
влияет на воздействие анимации на вышеупомянутую вероятность, при том
положительно, так как чем большую площадь занимает рекламное объявление, тем
заметнее смена картинок на нем для посетителя сайта. Если баннер статичен, то a=0,  . Если же нет, то P(N) возрастает на величину
. Если же нет, то P(N) возрастает на величину  , которая положительно зависит от
размера объявления.
, которая положительно зависит от
размера объявления.
Вероятность благоприятного эффекта, создаваемого баннером, увеличивается,
если на баннере присутствует популярный футболист, чем он популярнее притом,
тем выше вероятность. Наблюдается зависимость вероятности благоприятного
эффекта баннера на посетителя сайта от суммы средств, выделяющейся на участие в
кампании известного футболиста, на некоторых интервалах описывающаяся выпуклой
функцией, на некоторых - вогнутой. При низких значениях суммы скорость роста
вероятности больше 0. Это объясняется тем, что стоимость привлечения известных
местных футболистов в кампанию растет менее быстро, чем их популярность, за
исключением небольшого числа самых популярных игроков. Обратная ситуация
наблюдается, когда при небольшом увеличении суммы удается достичь необходимого
количества денег для того, чтобы было возможно пригласить игрока, относящегося
к лучшим футболистам в мире, - тогда наблюдается резкий скачок вероятности. На
остальных интервалах функция ведет себя подобно линейной. Значит, β2≈1, однако то, насколько больше
или меньше этот параметр единицы, нельзя сказать, не имея обучающей выборки, не
проведя эксперимент. В то же время чем дольше звуковое сопровождение баннера,
тем сильнее портится впечатление посетителя сайта от рекламного сообщения, тем
сильнее снижается вероятность. При этом скорость роста раздражения человека от
звука, желание скрыть рекламу больше 0, поэтому логично предположить, что
вычитаемая функция  выпукла, соответственно, σ2>1.
выпукла, соответственно, σ2>1.
При увеличении количества денег, выделяемых на интерактивность баннера,
скорость роста вероятности того, что у посетителя сайта возникнет желание
перейти по ссылке, благодаря этой интерактивности, благодаря тому, что у
человека сформируется положительное впечатление вследствие участия в игре,
отрицательна, то есть функция, описывающая эту зависимость, является вогнутой.
Это объясняется тем, что чем больше выделено средств на интерактивность
баннера, тем искуснее сделана игра, тем более реалистичной она получается. Соответственно,
дополнительные вливания денег оказываются менее заметны, чем когда на
интерактивность тратятся небольшие суммы, поэтому рост вероятности уменьшается.
По этой причине β3<1.
Допустим, бюджет рекламный кампании равен b. Тогда бюджетное ограничение выглядит так:

Здесь сs, ca, cz - стоимости
использования единицы площади баннера (см2), анимации (кБ) и звукового
сопровождения (сек). Предполагается, что бюджетное ограничение линейное при
условии, что поставщики этих услуг предлагают цены, линейно зависящие от
объема. Очевидно, что нет необходимости делать звук, появляющийся при загрузке
баннера на сайте, слишком долгим, так как это не имеет смысла (вероятность
того, что объявление будет замечено, почти не увеличивается при увеличении
продолжительности звука при условии, что он и так долгий). К тому же чем он
дольше, тем быстрее растет раздражение посетителя портала и тем быстрее
портится его впечатление от баннера. Тогда можно ввести дополнительное
ограничение на z: z ≤ σc,
σ < 1. Оно также
будет отвечать за то, чтобы Р(Е) была положительной. Помимо этого стоит
учитывать вогнутость функций, описывающих зависимость P(N) от s, P(I) от m, то, также то, что рост P(N) при росте значения переменной а замедляющийся. Тогда необходимы
следующие ограничения:

В таком случае вероятность того, что посетитель сайта, относящийся к
группе k, перейдет по ссылке, может быть
представлена следующим образом:
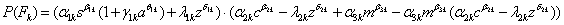

Тогда задача оптимизации дизайна визуального рекламного сообщения может
быть сформулирована следующим образом:

3.2 Подходы к
решению задачи
Таким образом, решение задачи оптимизации дизайна визуального рекламного
сообщения сводится к решению задачи нелинейного программирования. Притом эта не
относится к классу задач геометрического программирования, как могло показаться
на первый взгляд, поскольку коэффициенты перед некоторыми одночленными
позиномами отрицательны. Ограничения на независимые переменные выражаются с
помощью системы линейных неравенств. Есть несколько способов искать глобальный
максимум целевой функции. Во-первых, можно имеющуюся область определения
разбить на подобласти, на которых функция выпукла или вогнута. Затем на каждой
из областей, где функция вогнута, можно найти точки максимума. Поиск этих точек
функции нескольких переменных может быть организован при помощи уже
разработанных с этой целью пакетов программ, таких как, например, PTC MathCAD. После этого останется сравнить значения функции в
найденных экстремумах. Во-вторых, можно аппроксимировать имеющуюся функцию
такой функцией, для максимизации которой в условиях тех же ограничений на
переменные уже существуют методы решений, например, позиномом. В таком случае
оптимизационная задача была бы сведена к задаче геометрического
программирования, для решения которой также уже существуют пакеты программ,
таких как, например, GGPLAB
- набор инструментов для решения задач геометрического программирования в среде
Matlab.
.3 Получение
модельных параметров
Перед тем, как переходить к поиску максимума целевой функции при наличии
ограничений на переменные, требуется получить численные значения для всех
параметров модели. Некоторые из них искать не нужно, они известны сразу. Это
касается бюджета рекламной кампании b, стоимости размещения баннера площадью 1см2 - сs, цены исходящего от него звука продолжительностью в одну
секунду - сz, стоимости 1 кБ анимации - ca.
Что касается остальных параметров, то они могут быть найдены с помощью
проведения опросов и экспериментов. Например, чтобы найти значения α3k, β3k, возможно собрать достаточно большое количество людей,
относящихся к группе k (k = 1,…,27), начать наблюдать за их
взаимодействием с интерактивными рекламными баннерами, продвигающими те же
самые бутсы для игры в футбол. Отличаться эти баннеры друг от друга должны лишь
суммой денег, потраченной на интерактивность, в остальном же затраты должны
быть минимально возможными. Далее требуется, исходя из полученных данных,
построить приближение функции P(I) одночленом  . С этой целью возможно использование
метода наименьших квадратов. В итоге будут получены пары значений (x, y), где х - сумма денег, потраченная на интерактивность
баннера, а у - частота переходов по ссылке, указанной в баннере, или же частота
ответов «да» на вопрос, появилось ли у пользователя желание проследовать по
ссылке. Аналогичным образом можно получить все остальные параметры. Помимо
этого возможно использовать результаты проведенных исследований касательно
взаимодействия человека и баннерной рекламы.
. С этой целью возможно использование
метода наименьших квадратов. В итоге будут получены пары значений (x, y), где х - сумма денег, потраченная на интерактивность
баннера, а у - частота переходов по ссылке, указанной в баннере, или же частота
ответов «да» на вопрос, появилось ли у пользователя желание проследовать по
ссылке. Аналогичным образом можно получить все остальные параметры. Помимо
этого возможно использовать результаты проведенных исследований касательно
взаимодействия человека и баннерной рекламы.
Приведенные выше способы нахождения численных значений параметров
касаются не только поиска параметров, находящихся в формуле математического
ожидания числа переходов по ссылке, но и тех, которые находятся в системе
ограничений переменных, то есть bs, ba, bm, σ. Они также могут быть получены с
учетом рекомендаций для создания рекламных баннеров в Интернете, с учетом
имеющихся научных трудов и, обязательно, с учетом полученных параметров,
находящихся в формуле математического ожидания числа переходов по ссылке.
Глава 4.
Нерешенные проблемы и перспективные направления в области математического
моделирования рекламы
При математической формулировке задач оптимизации распределения бюджета
рекламной кампании по средствам рекламы и оптимизации дизайна визуального
рекламного объявления не удалось построить модели, в которых целевые функции
были бы такого вида, что можно было бы без аппроксимации отнести задачи к
определенному классу задач программирования. Тогда было бы возможно применить
соответствующие методы и найти точки максимума целевых функций. В случае с
полученными целевыми функциями же необходимо искать их приближение и уже для
приближающих функций искать точку максимума. Безусловно, невозможно настолько
точно построить модель, что она будет в полной мере отражать реальность, поскольку
практически всегда при наличии человеческого фактора нельзя учесть абсолютно
все детали, влияющие на его поведение, восприятие рекламы. Поэтому полученные
результаты при решении задач стоит расценивать скорее как направление, в
котором нужно двигаться при распределении бюджета по видам рекламы и при
дизайне рекламного баннера в Интернете. Однако желательно избегать таких
случаев, когда приходится искать приближающую функцию, поскольку тогда
погрешность результатов увеличивается.
Также к нерешенным проблемам следует отнести то, что при математической
формулировке обеих задач не были учтены дисперсии величин числа продаж
рекламируемого продукта и числа переходов по ссылке, указанной в рекламном
объявлении. При максимизации математического ожидания случайной величины
максимизируется среднее значение, которое принимает эта величина. Однако это не
означает, что число продаж продукта, например, совпадет с этим средним
значением. При наличии модели, идеально описывающей взаимодействие людей с
рекламой, при проведении большого числа кампаний можно было бы утверждать, что
число продаж товара приблизительно равно значению математического ожидания.
Соответственно, для одной или нескольких кампаний это не так. Тогда встает
соответствующий вопрос: как сильно значение случайной величины отличается от
математического ожидания? Очевидно, что не имеет смысла такая модель, при
построении которой и нахождении точки максимума целевой функции число продаж
продукта было бы в 5 раз меньше, чем значение функции в найденной точке.
Поэтому для надежности результатов требуется не только максимизировать
математическое ожидание, но и минимизировать дисперсию.
Помимо этого при построении математических моделей обеих задач было
сделано немало допущений, упрощающих эти модели. Сначала приведем те, которые
относятся к первой задаче. Во-первых, предполагается, что вероятности
взаимодействия человека с некоторой комбинацией средств рекламы - постоянные
величины, не зависящие от средств, выделенных на каждый из видов рекламы,
состоящих в этих комбинациях, и эти величины одинаковы для всех людей,
проживающих в рассматриваемом регионе. Здесь опять же играет роль человеческий
фактор, так что предположение не всегда истинно. Кроме того предположение,
заключающееся в том, что люди взаимодействуют с рекламой независимо друг от
друга, также не всегда верно. Ведь возможны такие ситуации, например, когда
компания друзей вместе смотрит по телевизору рекламный ролик, в котором
восхваляется новая коллекция одежды в каком-нибудь модном магазине, или просматривает
трейлер нового фильма, а после этого друзья делятся между собой впечатлениями о
рекламе. Также следует отметить, что вероятность того, что желание приобрести
рекламируемый продукт возникает при взаимодействии человека с комбинацией
рекламных средств i, где решающую
роль играет средство j,
зависит не только от того, какая сумма денег была выделена на это средство j. Она также определятся тем, какая
именно эта комбинация i,
сколько в ней находится типов рекламы и сколько на них выделено денег.
Во второй задаче имело бы смысл разбить все множество посетителей сайта
на категории не только по возрасту, уровню образования и благосостояния, но и
по национальности, роду деятельности и т. д. Но в таком случае получилось бы
слишком большое число групп, что очень усложнило бы нахождение оптимального
дизайна визуального рекламного объявления. Поэтому было принято решение
сконцентрироваться на 27 группах потребителей, разбив все множество посетителей
спортивного портала на категории по возрасту, уровню образования и
благосостояния, так как именно эти 27 групп представляют наибольший интерес.
Также обе модели не учитывают, что зависимости, описывающие вероятности
того, что желание приобрести рекламируемый продукт возникает при взаимодействии
человека с комбинацией рекламных средств i, где решающую роль играет средство j (в первом случае), и того, что баннер будет замечен,
произведет благоприятный эффект, побудит кликнуть на него за счет своей
интерактивности (во втором случае), могут быть не всегда лучше всего приближены
одночленными позиномами или их комбинацией.
Разумеется, все приведенные выше упрощения были приняты, потому что без
них обойтись невозможно, так как невозможно абсолютно точно описать
взаимодействие людей с рекламой ввиду наличия человеческого фактора, так как
иначе можно получить целевую функцию, точку максимума которой было бы
непонятно, каким образом искать. Кроме того не стоит забывать, что цель работы
- нахождение направления, в котором нужно двигаться, в большей степени, чем
сама точка.
Из описанных выше нерешенных проблем вытекают следующие перспективные
направления в области математического моделирования рекламы. Во-первых, следует
не только максимизировать математическое ожидание величины числа переходов по
ссылке, продаж рекламируемого товара и т. д., но и минимизировать дисперсию
этой величины, соответственно, было бы более эффективно решать
двухкритериальные задачи. Также перспективным направлением является нахождение
подходов к решению подобных задач с нелинейными ограничениями переменных.
В-третьих, возможна модификация математической модели первой задачи,
заключающая в учете того, что вероятность возникновения желания приобрести
рекламируемый продукт вследствие взаимодействия человека с комбинацией
рекламных средств i, где решающую
роль играет средство j,
зависит не только от того, какая сумма денег была выделена на это средство j, также от того, какие рекламные
средства входят в эту комбинацию i.
Заключение
В настоящее время на рекламу выделяются компаниями большие деньги. Перед
рекламодателями стоит задача выделять на рекламные кампании денежные средства
максимально эффективно, максимизировать свою прибыль. В данной работе были
выбраны две проблемы из числа тех, что стоят перед рекламодателями, а именно:
оптимизация распределения бюджета рекламной кампании по видам рекламы и
оптимизация дизайна визуального рекламного объявления. В обоих случаях была
поставлена и математически сформулирована задача, построена математическая
модель (для первой задачи за основу взята модель Беленького А. С., для второй
задачи построена новая), описан процесс получения модельных параметров и
подходы к решению задач (нелинейного программирования в данном случае). В
случае первой задачи подразумевалось её решение на модельных параметрах.
Удалось вычислить приблизительные значения параметров. Точка максимума найдена
не была. Дальнейшее развитие подходов к оптимизации распределения бюджета
рекламной кампании по видам рекламы и оптимизации дизайна визуального
рекламного объявления в рамках приведенных моделей подразумевает включение в
них второго критерия - дисперсии числа продаж рекламируемого товара и
показателя CTR, соответственно. Оно также включает
в себя учет в модели случаев, когда ограничения на переменные не линейны.
Библиографический
список
. Atkinson
G., Driesener C., Corkindale D. (2014). “Search Engine Advertisement Design
Effects on Click-Through Rate”. Journal of Interactive Advertising, 14(1):
24-30.
2. Belenky
A. S. (2000). “An Approach to Planning an Advertising Campaign of Goods and
Services”. Computers and Mathematics with Applications, 42: 993-1008.
. Beltran-Royo
C., Zhang H., Blanco L. A., Almagro J. (2013). “Multistage multiproduct
advertising budgeting”. Annals of Operations Research, 207(1): 261-278.
. Cho
C., Lee J., Tharp M. (2001). “Different Forced-Exposure Levels to Banner
Advertisements”. Journal of Advertising Research, 41(4): 45-56.
. Dahlen
M. (2001). “Banner Advertisements through a New Lens”. Journal of Advertising
Research, 41(4): 23-30.
. Hershberger
E. K., Lohtia R., Donthu N. (2003). “The Impact of Content and Design Elements
on Banner Advertising Click-Through Rates”. Journal of Advertising Research,
43(4): 410-418.
. Pun
H., Heese S. H. (2015). “A note on budget allocation for market research and
advertising”. International Journal of Production Economics, 166: 85-89.
. Robinson
H., Wysocka A., Hand C. (2007). “Internet Advertising Effectiveness: The Effect
of Design on Click-Through Rates for Banner Ads”. International Journal of
Advertising, 26(4): 527-541.