|
Способы
Распила i
|
Получаемые
брусья
|
Количество
бревен, распиливаемых по i-му способу
|
отходы
|
|
1.5
|
2.4
|
3.2
|
|
|
|
1
2 3 4
|
3
1 1 0
|
0
1 0 2
|
0
0 1 0
|
x1 x2 x3
x4
|
0.5
1.1 0.3 0.2
|
Количество бревен, распиливаемых по каждому
способу, обозначим х1, х2, х3, х4 соответственно.
Составим математическую модель задачи. Поскольку общее количество бревен,
поступающих на распил, неизвестно, будем искать их количество в процентах.
Тогда
x1+х2+х3+х4=1
(где 1 означает 100%).
линейный программирование симплекс
метод
Учитывая количество брусьев каждого размера,
получаемых при распиле одним из четырех способов и условие комплектности
(1:2:3), получим следующие уравнения:
x1+х2+х3=х
- для брусьев длиной 1.5 м;
х2+2х4=2х- для брусьев
длиной 2.4 м;
х3=3х- для брусьев длиной 3.2 м.
Из последнего уравнения  ,
подставив в предыдущие уравнения, получим
,
подставив в предыдущие уравнения, получим
 или
или 
При этом 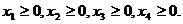
Общая величина отходов составит 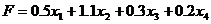 .
Необходимо найти минимум этой функции при заданных условиях.
.
Необходимо найти минимум этой функции при заданных условиях.
Итак, имеем задачу линейного программирования:


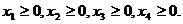
Из второго уравнения системы ограничений
следует, что х1=х2=х3=0, а при четвертом
способе распила получаются только бруски в 2.4 м, что не удовлетворяет условию
задачи. Таким образом данная задача не имеет допустимых решений.
Введем в рассмотрение способы распила, при
которых отход превышает возможную величину бруска. Получим следующую таблицу.
|
Способы
Распила i
|
Получаемые
брусья
|
Количество
бревен, распиливаемых по i-му способу
|
отходы
|
|
1.5
|
2.4
|
3.2
|
|
|
|
1
2 3 4 5 6 7 8
|
3
1 1 0 2 1 0 0
|
0
1 0 2 0 0 1 0
|
0
0 1 0 0 0 0 1
|
x1 x2 x3
x4
х5 х6 х7 х8
|
0.5
1.1 0.3 0.2 2 3.5 2.6 1.8
|
Запишем новую систему ограничений, учитывая
условие комплектности
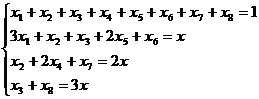
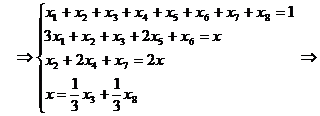
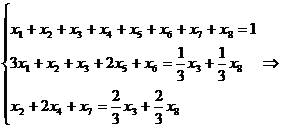
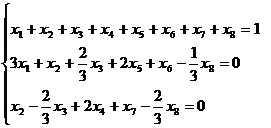
При этом 
Функция отходов примет вид
 .
.
Получаем следующую задачу линейного
программирования:
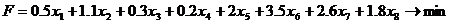
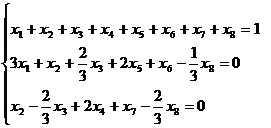

Решим ее симплекс методом.
Будем искать 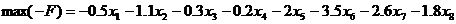 .
Запишем данные задачи в таблицу.
.
Запишем данные задачи в таблицу.
)
|
Базисные
переменные
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
х8
|
bi
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
¾
|
3
|
1
|
|
0
|
2
|
1
|
0
|
|
0
|
|
¾
|
0
|
1
|
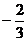
|
2
|
0
|
0
|
1
|
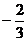
|
0
|
|
-F
|
0.5
|
1.1
|
0.3
|
0.2
|
2
|
3.5
|
2.6
|
1.8
|
0
|
Элементы таблицы (коэффициенты при х) обозначим 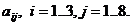
Найдем начальное базисное решение.
) Выбираем четвертый столбец разрешающим.
Вычислим симплекс-отношения для положительных
элементов четвертого столбца 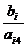 и выберем
наименьшее полученное число
и выберем
наименьшее полученное число
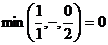 , поэтому
разрешающий элемент а34=2.
, поэтому
разрешающий элемент а34=2.
Элементы второй строки делим на а34=2.
Элементы четвертого столбца заменяем 0.
На месте а34 ставим 1.
х4 переходит в столбец базисных
переменных.
Остальные элементы таблицы пересчитываем по
формуле  ,
,
где 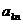 -
разрешающий элемент.
-
разрешающий элемент.
|
Базисные
переменные
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
х8
|
bi
|
|
¾
|
1
|
0.5
|
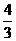
|
0
|
1
|
1
|
0.5
|
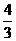
|
1
|
3
|
1
|
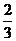
|
0
|
2
|
1
|
0
|
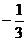
|
0
|
|
х4
|
0
|
0.5
|
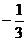
|
1
|
0
|
0
|
0.5
|
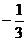
|
0
|
|
-F
|
0.5
|
1
|
0.367
|
0
|
2
|
3.5
|
2.5
|
1.867
|
0
|
) Выберем шестой столбец. Находим  ,
тогда разрешающий элемент а26=1.
,
тогда разрешающий элемент а26=1.
Пользуясь вышеизложенными правилами, заполняем
следующую таблицу.
|
Базисные
переменные
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
х8
|
bi
|
|
¾
|
-2
|
-0.5
|
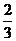
|
0
|
-1
|
0
|
0.5
|

|
1
|
|
х6
|
3
|
1
|
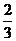
|
0
|
2
|
1
|
0
|
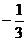
|
0
|
|
х4
|
0
|
0.5
|
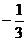
|
1
|
0
|
0
|
0.5
|
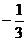
|
|
-F
|
-10
|
-2.5
|
-1.97
|
0
|
-5
|
0
|
2.5
|
3.034
|
0
|
4) Теперь нужно записать базисную переменную в
первую строку. В восьмом столбце единственный положительный элемент  ,
поэтому а18=
,
поэтому а18= - разрешающий.
- разрешающий.
|
Базисные
переменные
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
х8
|
bi
|
|
х8
|
-1.2
|
-0.3
|
0.4
|
0
|
-0.6
|
0
|
0.3
|
1
|
0.6
|
|
х6
|
2.6
|
0.9
|
0.8
|
0
|
1.8
|
1
|
0.1
|
0
|
0.2
|
|
х4
|
-0.4
|
0.4
|
-0.2
|
1
|
-0.2
|
0
|
0.6
|
0
|
0.2
|
|
-F
|
-6.36
|
-1.59
|
-3.18
|
0
|
-3.18
|
0
|
1.59
|
0
|
-1.82
|
Получили первоначальное базисное решение х4=0.2,
х6=0.2, х8=0.6, х1=х2=х3=х5=х7=0,
F(х)=1.82. Это
решение не является оптимальным, поскольку в F
- строке есть отрицательные элементы.
) Перейдем к новому решению.
Наибольший по модулю отрицательный элемент в F
- строке - это -6.36. Поэтому разрешающий столбец - первый.
Единственный положительный элемент в первом
столбце а21=2.6, он и будет разрешающим.
х1 занимает место х6 среди
базисных переменных. Далее выполняем еще один шаг симплекс-метода и получаем
новую таблицу.
|
Базисные
переменные
|
х1
|
х2
|
х3
|
х5
|
х6
|
х7
|
х8
|
bi
|
|
х8
|
0
|
0.115
|
0.769
|
0
|
0.231
|
0.461
|
0.346
|
1
|
0.692
|
|
х1
|
1
|
0.346
|
0.308
|
0
|
0.692
|
0.385
|
0.038
|
0
|
0.077
|
|
х4
|
0
|
0.538
|
-0.077
|
1
|
0.077
|
0.154
|
0.615
|
0
|
0.231
|
|
-F
|
0
|
0.612
|
-1.223
|
0
|
1.223
|
2.446
|
4.77
|
0
|
-1.33
|
) Полученное решение не является оптимальным,
поскольку в последней строке есть отрицательный элемент. Третий столбец
разрешающий. Находим симплексное отношение : 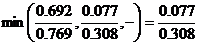 .
Разрешающий элемент а23=0.308.
.
Разрешающий элемент а23=0.308.
|
Базисные
переменные
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
х8
|
bi
|
|
х8
|
-2.5
|
-0.23
|
0
|
0
|
-1.5
|
-0.5
|
0.25
|
1
|
0.5
|
|
х3
|
3.25
|
1.12
|
1
|
1.27
|
1.25
|
0.12
|
0
|
0.25
|
|
х4
|
0.25
|
0.63
|
0
|
1
|
0.25
|
0.25
|
0.63
|
0
|
0.25
|
|
-F
|
4
|
2
|
0
|
0
|
4
|
4
|
5
|
0
|
-1.025
|
Так как в последней строке целевой функции нет
отрицательных оценок, то найденное решение оптимально:
х3=0.25, х4=0.25, х8=0.5,
х1=х2=х5=х6=х7=0, 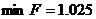 .
.
Ответ: чтобы
выполнить условие задачи, необходимо 25% бревен распиливать третьим способом,
25%- четвертым способом и 50% восьмым способом. При этом минимальная средняя
величина отходов составит 1.025 м с каждого бревна.