Функционалы
Контрольная
работа
Функционалы
Введение
Функционалом называется отображения ¦:
М1 ®
М2 , определенное на множестве М1 произвольной природы и действующее в
некоторое множество чисел М2 . Повседневная жизнь наполнена функционалами.
Приведем лишь несколько примеров, оставляя читателю возможность неограниченного
продолжения предлагаемого списка:
1) длина или вес (М1 - некоторое множество
предметов, подвергаемых измерению или взвешиванию, М2 =(0,+¥));
2) ассортимент магазина или склада с
указанием количества единиц товара данного вида ( М1 - множество видов товара,
М2=NÈ{0}
);
3) прирост населения (М1
-множество городов, регионов или стран, М2=Z);
Во всех областях математики,
как и любой другой естественной науки, многочисленные функционалы присутствуют
прежде всего в качестве структурных элементов аппарата исследования. Например,
) число решении (М1 -множество
уравнений или систем уравнений, М2=NÈ{0});
) ранг матрицы (М1 - множество
матриц, М2=NÈ{0});
) длина вектора (М1 -множество
векторов, М2 =[0,+¥));
) определенный интеграл по
фиксированному отрезку (М1-некоторое множество действительных функций, М2=R);
) расстояние между векторами в
евклидовом пространстве E(R)
(М1=E(R)´E(R),
М2=[0,+¥
) );
) скалярное произведение в
евклидовом пространстве E(R)
(М1=E(R)´E(R),
М2 =R);
В примерах 8) и 9) в отличие от
примеров 4)-7) функционалы зависят не от одной, а от двух переменных. Название
вида числового множества М1, в которое действует данный функционал часто
заменяется соответствующим названием функционала: целочисленный, положительный,
действительный, комплексный, булевский и т.д. Например, длина вектора это
неотрицательный (действительный) функционал, определенный на множество
векторов.
Обилие и разнообразие
функционалов, встречающихся в различных разделах математики, давно поставило
задачу самостоятельного изучения их важнейших классов. Предметом линейной
алгебры являются, в первую очередь, функционалы от одной или нескольких
переменных , являющихся векторами из линейного пространства L(P),
действующие в числовое поле P.
При этом от функционала требуется выполнение свойства линейности по каждой
переменной, состоящее в том, что линейную комбинацию векторов функционал,
отображает в линейную комбинацию образов этих векторов с теми же
коэффициентами. Такие функционалы от одной переменной называются линейными, от
двух переменных билинейными, в общей случае - полилинейными.
Целевая функция в
симплекс-методе линейного программирования, неевклидовы метрики в специальной
теории относительности, теория кривых и поверхностей второго порядка - вот
первые примеры, скорее оправдывающие существование теории линейных и билинейных
функционалов, чем иллюстрирующие ее. Эти примеры будут рассмотрены позже.
1. Линейные функционалы
линейный квадратичный билинейный
функционал
Пусть L=L(P) линейное
пространство над полем P. Линейным функционалом на
пространстве L называется
отображение 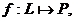
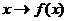 ,
удовлетворяющее условию
,
удовлетворяющее условию
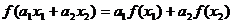 ,
,
где 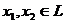 ,
, 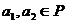 .
.
Множество всех линейных функционалов
на пространстве L обозначим через L*=L*(P). Сумму f1+f2 линейных
функционалов и произведение af линейного функционала на
скаляр определим равенствами:
 ,
,
 .
.
Предложение 1. Если  ,
, 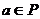 тогда
тогда 
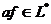 . Введенные операции сложения и
умножения на скаляр порождают на L* структуру линейного пространства
над полем Р. Ä
. Введенные операции сложения и
умножения на скаляр порождают на L* структуру линейного пространства
над полем Р. Ä
В дальнейшем будем считать, что
пространство L
конечномерно и dimL=n.
Зафиксируем в пространстве L базис 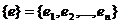 . Тогда
. Тогда
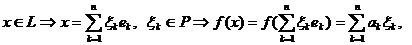
где 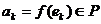 .
.
Вводя обозначения 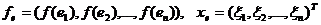 , получаем,
что
, получаем,
что
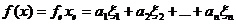 . (1)
. (1)
Последнее выражение будем называть
координатной формой записи линейного функционала f в базисе  или кратко
"линейной формой f в базисе
или кратко
"линейной формой f в базисе  ". Так
как переменные
". Так
как переменные 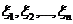 входят в
запись (1) в первой степени, это выражение часто называют линейной функцией от переменных
входят в
запись (1) в первой степени, это выражение часто называют линейной функцией от переменных
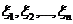 .
.
Отметив, что коэффициенты  в (1)
зависят от базиса
в (1)
зависят от базиса  , выясним
правило, по которому они изменяются при переходе от одного базиса к другому.
Пусть
, выясним
правило, по которому они изменяются при переходе от одного базиса к другому.
Пусть 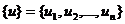 еще один
базис в пространстве L и
еще один
базис в пространстве L и 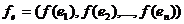 ,
, 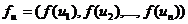 . Следующее
предложение устанавливает связь между векторами
. Следующее
предложение устанавливает связь между векторами 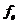 и
и 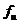 .
.
Предложение 2. Пусть 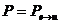 -матрица
перехода от базиса
-матрица
перехода от базиса  к базису
к базису 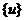 . Тогда
. Тогда
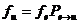 . (2)
. (2)
В самом деле, так как для любого 
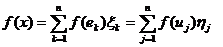 ,
,
где 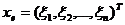 ,
, 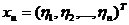 и
и 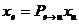 , то в силу равенства (1)
, то в силу равенства (1)  , т. е.
, т. е. 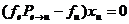 для любых
векторов
для любых
векторов 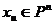 . Откуда и
следует равенство (2).
. Откуда и
следует равенство (2).
Пусть 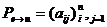 , тогда равенство (2) можно
расписать в виде
, тогда равенство (2) можно
расписать в виде
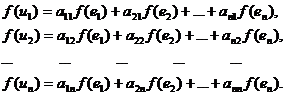
Если теперь сравнить полученные
формулы с формулами (1.20) из [9], стр. 31, выражающими связь между векторами
базисов 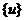 и
и  , то можно
сделать вывод, что коэффициенты линейной формы в базисе преобразуются при
переходе к другому базису так же, как векторы базиса.
, то можно
сделать вывод, что коэффициенты линейной формы в базисе преобразуются при
переходе к другому базису так же, как векторы базиса.
Предложение3. Отображение 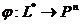 ,
, 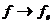 , где
, где  -
фиксированный базис пространства L, является изоморфизмом векторных пространств
над полем Р.
-
фиксированный базис пространства L, является изоморфизмом векторных пространств
над полем Р.
w Вначале
покажем биективность отображения j.
Пусть 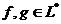 и
и 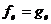 , то есть
, то есть 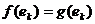 ,
, 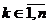 . Тогда
. Тогда
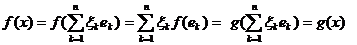
для любых  , то есть ƒ=g. Отсюда
следует инъективность отображения j.
Теперь покажем сюръективность отображения j.
Пусть
, то есть ƒ=g. Отсюда
следует инъективность отображения j.
Теперь покажем сюръективность отображения j.
Пусть 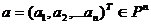 . Функционал
ƒ(х)
определим равенством
. Функционал
ƒ(х)
определим равенством
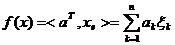 .
.
В силу свойств координат вектора в
базисе [9], стр.31,
 .
.
для любых 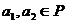 ,
, 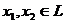 .
.
Поэтому
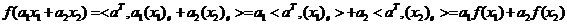
Следовательно, 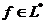 . Кроме
того,
. Кроме
того,
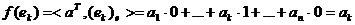 ,
,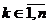 ,
,
то есть 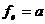 . Þ j -биекция.
. Þ j -биекция.
Осталось показать, что отображение j сохраняет операции сложения
функционалов и умножения функционала на скаляр. Действительно, если
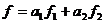
где 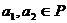 ,
,  , то
, то
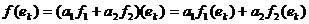 Þ
Þ 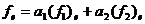 Þ j
-изоморфизм.
Þ j
-изоморфизм.
Следствие. dimL*(P)= dimL(P) и L*(P)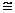 L(P)
L(P)
По критерию изоморфности двух
линейных пространств [1], §1, dimL*(P)= dimPn=n. Так как n= dimL(P), то L*(P)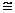 L(P) .
L(P) .
Пример 1. Рассмотрим
основную задачу линейного программирования. Предприятие производит продукт n
видов, цена единицы продукта k-ого вида равна  , количество произведенной продукции
k-ого вида равно
, количество произведенной продукции
k-ого вида равно 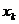 , стоимость
S всей произведенной продукции (за определенный период времени) выражается
формулой
, стоимость
S всей произведенной продукции (за определенный период времени) выражается
формулой
 .
.
Требуется при некоторых ограничениях
на 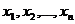 , связанных
с ресурсами сырья, спросом, производственными возможностями и так далее, найти
такое значение вектора
, связанных
с ресурсами сырья, спросом, производственными возможностями и так далее, найти
такое значение вектора  , при
котором функционал S(х) является линейным функционалом на пространстве Rn и
называется целевой функцией.
, при
котором функционал S(х) является линейным функционалом на пространстве Rn и
называется целевой функцией.
Пример 2. Пусть 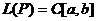 . Тогда
. Тогда
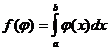
является линейным функционалом на
пространстве  , так как в
силу известных свойств определенного интеграла
, так как в
силу известных свойств определенного интеграла
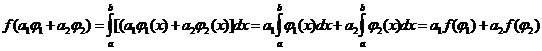
Оптимизация (т. е. нахождение
минимума или максимума) функционалов в бесконечномерном пространстве,
представимых в виде интегралов, является предметом специальной дисциплины -
вариационного исчисления.
Пример 3. В том же пространстве  рассмотрим
функционал g(j), представляющий собой
значение функции j(x0) в
произвольной, (но фиксированной!) точке x0 отрезка
[а,b], a£ x0 £b, g(j)=j(x0).
рассмотрим
функционал g(j), представляющий собой
значение функции j(x0) в
произвольной, (но фиксированной!) точке x0 отрезка
[а,b], a£ x0 £b, g(j)=j(x0).
Так как 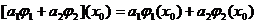 , для любых
, для любых 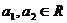 и
и 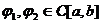 , то
функционал g является линейным. Функционал g имеет специальное обозначение
, то
функционал g является линейным. Функционал g имеет специальное обозначение 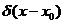 , называется
, называется
 - функцией
Дирака, сосредоточенной в точке x0, и играет большую роль в
математической физике.
- функцией
Дирака, сосредоточенной в точке x0, и играет большую роль в
математической физике.
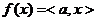 (3)
(3)
Ввиду аксиом скалярного произведения
[10], стр. 3, ƒ является
линейным функционалом на пространстве Е. Более того, любой линейный функционал
на пространстве Е может быть представлен в виде (3) [2], стр. 190.
. Билинейные функционалы
Пусть L=L(P) линейное
пространство над полем Р. Билинейным функционалом на пространстве L называется
отображение b: L×L 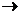 P, (х,y)
P, (х,y) 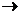 b(x,y)
b(x,y)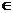 P,
удовлетворяющее условиям:
P,
удовлетворяющее условиям:
) 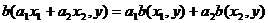
) 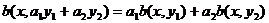
где 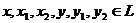 ,
, 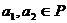 . Условия 1)
и 2) называются условиями линейности функционала по переменной х (условие 1)) и
по переменной y (условие 2)).
. Условия 1)
и 2) называются условиями линейности функционала по переменной х (условие 1)) и
по переменной y (условие 2)).
Множество всех билинейных
функционалов на пространстве L обозначим через B(L)=B(L(P)). Сумму b1+b2 билинейных
функционалов и произведение ab билинейного функционала на скаляр определим
равенствами:
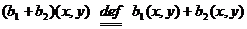
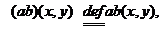
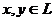 .
.
Предложение 4. Если 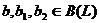 ,
, 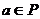 , тогда
, тогда 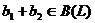 ,
, 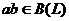 . Введенные
операции сложения и умножения на скаляр порождают на B(L) структуру линейного
пространства над полем Р. Ä
. Введенные
операции сложения и умножения на скаляр порождают на B(L) структуру линейного
пространства над полем Р. Ä
Пусть 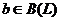 , тогда отображение
, тогда отображение 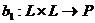 ,
, 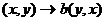 , является
билинейным функционалом на пространстве L , вообще говоря, отличным от b. Если
, является
билинейным функционалом на пространстве L , вообще говоря, отличным от b. Если 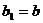 , т. е.
, т. е. 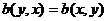 ,
, 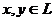 , функционал
b называется симметрическим билинейным функционалом. Множество всех
симметрических билинейных функционалов на пространстве L обозначим через
, функционал
b называется симметрическим билинейным функционалом. Множество всех
симметрических билинейных функционалов на пространстве L обозначим через 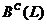 .
.
Предложение 5. Множество 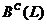 является
подпространством в пространстве B(L). Ä
является
подпространством в пространстве B(L). Ä
Предложение 6. Пусть 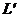 -
подпространство в пространстве L и
-
подпространство в пространстве L и 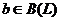 , тогда отображение
, тогда отображение 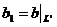 , является
билинейным функционалом на пространстве
, является
билинейным функционалом на пространстве 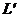 . В частности, если
. В частности, если 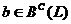 , то
, то 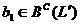 . Ä
. Ä
В дальнейшем будем считать, что
пространство L конечномерно и dimL=n.
Зафиксируем в пространстве L базис 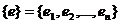 . Тогда
. Тогда
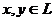 Þ
Þ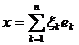 ,
, 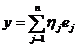 ,
, 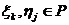 Þ
Þ
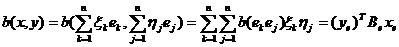 ,
,
где 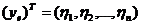 ,
,  ,
, 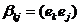 ,
, 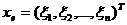 .
.
Выражение
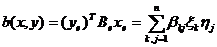 (4)
(4)
будем называть координатной формой
записи билинейного функционала b в базисе  или кратко "билинейной формой
b в базисе
или кратко "билинейной формой
b в базисе  ".
Матрица
".
Матрица 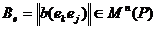 называется
матрицей билинейного функционала в базисе
называется
матрицей билинейного функционала в базисе  .
.
Если 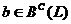 , то
, то 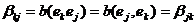 ,
, 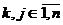 . Следовательно, матрица
. Следовательно, матрица  является
симметрической,
является
симметрической, 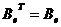 . На самом
деле справедливо более сильное утверждение.
. На самом
деле справедливо более сильное утверждение.
Предложение 7. Для того, чтобы
функционал 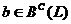 , необходимо
и достаточно, чтобы его матрица
, необходимо
и достаточно, чтобы его матрица  в произвольном базисе
в произвольном базисе  пространства
L была симметрической.
пространства
L была симметрической.
В доказательстве нуждается лишь
вторая ("достаточная") часть утверждения. Пусть
 Û
Û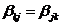 ,
, 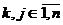 Û
Û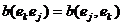 ,
, 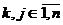 , Þ
, Þ 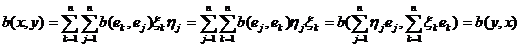 ,
, 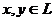 Þ
Þ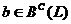
Предложение 8. 1. Отображение  ,
,  , где
, где  -фиксированный
базис пространства L, является изоморфизмом векторных пространств над полем Р.
-фиксированный
базис пространства L, является изоморфизмом векторных пространств над полем Р.
. Отображение 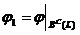 ,
, 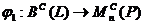 , является
изоморфизмом векторных пространств над полем Р.
, является
изоморфизмом векторных пространств над полем Р.
Здесь 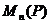 - линейное пространство квадратных
матриц над полем Р,
- линейное пространство квадратных
матриц над полем Р, 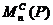 - его
подпространство, состоящее из всех симметрических матриц.
- его
подпространство, состоящее из всех симметрических матриц.
. В доказательстве прежде всего
нуждается обратимость отображения j.
Пусть 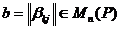 . Построим
билинейный функционал b,
. Построим
билинейный функционал b, 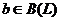 , матрица которого
, матрица которого  совпадает с
матрицей В. Искомый функционал действует по формуле
совпадает с
матрицей В. Искомый функционал действует по формуле
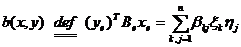 (5)
(5)
Покажем его линейность по переменной
х:
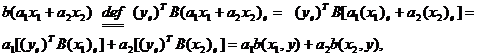
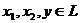 ,
, 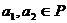 .
.
Линейность по переменной y
доказывается аналогично. Ä
Таким образом, 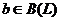 . Кроме
того,
. Кроме
того,
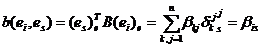 ,
,  (6)
(6)
т. е. матрица В совпадает с матрицей
функционала b в базисе  .
.
Для справедливости первой части
утверждения остается проверить, что отображение j сохраняет операции сложения и умножения на
скаляр в пространстве В(L) Ä.
. Справедливость этого утверждения
является следствием равенства (5) и (6). В самом деле, если матрица В
симметрическая, т. е. 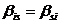 ,
,  , тогда
, тогда
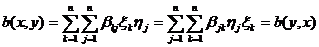 ,
, 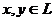 ,
,
т. е. отображение  обратимо.
Сохранение им операций пространства
обратимо.
Сохранение им операций пространства 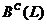 вытекает из аналогичного свойства
отображения j.
вытекает из аналогичного свойства
отображения j.
Пусть 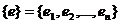 и
и 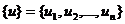 базисы в пространстве L и
базисы в пространстве L и 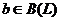 . Следующее
предложение устанавливает связь между матрицами
. Следующее
предложение устанавливает связь между матрицами  и
и 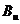 функционала b.
функционала b.
Предложение 9. Пусть 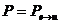 матрица
перехода от базиса
матрица
перехода от базиса  к базису
к базису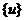 . Тогда
. Тогда
 (7)
(7)
В самом деле, поскольку для любых 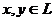
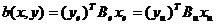
где 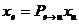 ,
, 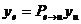 ,
, 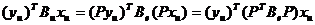
т. е. 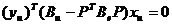
для любых векторов 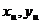 из Pn . Откуда и
следует равенство (7).
из Pn . Откуда и
следует равенство (7).
Верно и обратное утверждение.
Предложение 10. Пусть Р
невырожденная матрица,  , а
, а  матрица
билинейного функционала b в базисе
матрица
билинейного функционала b в базисе  . Тогда матрица
. Тогда матрица  является
матрицей функционала b в базисе
является
матрицей функционала b в базисе  к
к 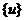 ,
обладающего тем свойством, что Р есть матрица перехода от
,
обладающего тем свойством, что Р есть матрица перехода от  к
к 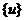 ,
, 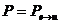 . Ä
. Ä
Следствием предложений 8 и 9
является следующее утверждение для симметрических билинейных функционалов.
Предложение 11. Пусть 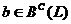 . Для того,
чтобы матрица В ,
. Для того,
чтобы матрица В , 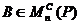 , была
матрицей функционала b в некотором базисе пространства L, необходимо и
достаточно, чтобы нашлись такая невырожденная матрица Р,
, была
матрицей функционала b в некотором базисе пространства L, необходимо и
достаточно, чтобы нашлись такая невырожденная матрица Р,  , и такой
базис
, и такой
базис  пространства
L, что
пространства
L, что
 .
.
Необходимость является следствием
равенства (7). Достаточность является следствием предложения 9 и симметричности
матрицы В при любой матрице Р,
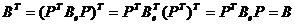 .
.
Пример 5. Примером билинейного
функционала на евклидовом пространстве Е является скалярное произведение
<x,y>, 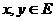 . Проверка
ее линейности по переменным x и y осуществляется на основании аксиом скалярного
произведения [10], стр. 3.
. Проверка
ее линейности по переменным x и y осуществляется на основании аксиом скалярного
произведения [10], стр. 3.
Пример 6. Примером билинейного
функционала на пространстве С[a,b] является интеграл
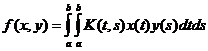 ,
,
где K(t,s) -фиксированная
непрерывная функция двух переменных t и s, изменяющихся на отрезке [a,b], 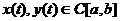 . Линейность
функционала I(x,y) по каждой переменной доказывается на основании соответствующих
свойств определенного интеграла, так же как и в примере 2.
. Линейность
функционала I(x,y) по каждой переменной доказывается на основании соответствующих
свойств определенного интеграла, так же как и в примере 2.
3. Квадратичные функционалы
Пусть 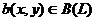 . Пологая x=y, получаем
функционал q(x)=b(x,x), который
называется квадратичным функционалом. Таким образом, квадратичный функционал на
пространстве L это отображение вида
. Пологая x=y, получаем
функционал q(x)=b(x,x), который
называется квадратичным функционалом. Таким образом, квадратичный функционал на
пространстве L это отображение вида
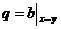 , q:L(P)®P, x®q(x).
, q:L(P)®P, x®q(x).
Множество всех квадратичных
функционалов на пространстве L обозначим через Q(L). На самом деле, любой
квадратичный функционал на L совпадает с ограничением некоторого
симметрического билинейного функционала на L на диагональ {x=y} декартова
квадрата L×L. Более
того, справедливо следующее предложение.
Предложение 12. Отображение 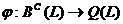 ,
действующее по правилу
,
действующее по правилу
 ,
,
является биекцией.
Пусть q(x)=b(x,x),где 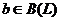 . Рассмотрим
функционал b1(x,y),
определенным равенством
. Рассмотрим
функционал b1(x,y),
определенным равенством
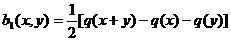 .
.
Так как
для любых 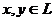 , то
, то 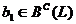 . Кроме
того,
. Кроме
того,
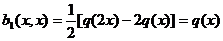 .
.
Таким образом, для любого
квадратичного функционала q на пространстве L существует функционал 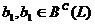 , такой, что
, такой, что
 . Кроме
того, такой функционал
. Кроме
того, такой функционал  единственный.
В самом деле, если
единственный.
В самом деле, если 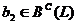 и
и 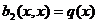 , тогда
, тогда
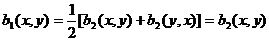 для любых
для любых 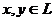
Зафиксируем в пространстве L базис  , получаем в
силу предложения 12 из равенства (1) следующую форму записи квадратичного
функционала q в базисе
, получаем в
силу предложения 12 из равенства (1) следующую форму записи квадратичного
функционала q в базисе  :
:
 (8)
(8)
где _ - симметрическая матрица, 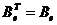 . Кратко эту
форму записи будем называть квадратичной формой q в базисе
. Кратко эту
форму записи будем называть квадратичной формой q в базисе  . Матрицу
. Матрицу  назовем
матрицей квадратичного функционала q в базисе
назовем
матрицей квадратичного функционала q в базисе  (или матрицей квадратичной формы q в
базисе
(или матрицей квадратичной формы q в
базисе  ). Матрицы
). Матрицы  и
и 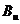 квадратичного
функционала в базисах
квадратичного
функционала в базисах  и
и 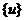 связаны
равенством (7).
связаны
равенством (7).
На множестве 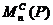 введем
следующее бинарное отношение: матрицу В назовем эквивалентной матрице А, если
существует такая невырожденная матрица Р,
введем
следующее бинарное отношение: матрицу В назовем эквивалентной матрице А, если
существует такая невырожденная матрица Р,  , что
, что
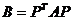 .
.
Введенное бинарное отношение
обладает свойствами:
) рефлексивность 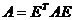 ,
,
) симметричность 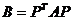 Þ
Þ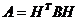 , где
, где 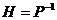 .
.
) транзитивность 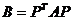 ,
, 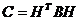 Þ
Þ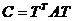 , где
, где 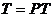 ,
,
т. е. является отношением
эквивалентности. Введенное отношение эквивалентности разбивает множество 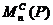 на классы
эквивалентных между собой матриц. Ниже будет показано, что число этих классов в
случае P=C равно n+1,
а в случае P=R равно (n+2)/2. Пусть
В фиксированная матрица из
на классы
эквивалентных между собой матриц. Ниже будет показано, что число этих классов в
случае P=C равно n+1,
а в случае P=R равно (n+2)/2. Пусть
В фиксированная матрица из 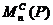 ,
,  фиксированный базис в L. Пара {B,e} порождает
квадратичный функционал q на пространстве L, обладающий тем свойством, что его
матрица в базисе
фиксированный базис в L. Пара {B,e} порождает
квадратичный функционал q на пространстве L, обладающий тем свойством, что его
матрица в базисе  совпадает с
матрицей В, а все матрицы, эквивалентные матрице В, и только они, являются
матрицами функционала q во всевозможных базисах пространства L.
совпадает с
матрицей В, а все матрицы, эквивалентные матрице В, и только они, являются
матрицами функционала q во всевозможных базисах пространства L.
Замечание. Введенное отношение
эквивалентности на множестве 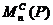 порождает следующее отношение
эквивалентности на множестве Q(L) : два функционала q1 и q2 объявляем
эквивалентными, если их матрицы в каком-нибудь базисе пространства L эквивалентны.
Ä
порождает следующее отношение
эквивалентности на множестве Q(L) : два функционала q1 и q2 объявляем
эквивалентными, если их матрицы в каком-нибудь базисе пространства L эквивалентны.
Ä
Нашей ближайшей задачей является
классификация квадратичных функционалов на пространстве L с точностью до их
эквивалентности.
. Приведение квадратичной формы к
каноническому виду
Пусть q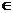 Q(L). Будем
говорить, что квадратичная форма q в базисе
Q(L). Будем
говорить, что квадратичная форма q в базисе  имеет канонический вид, если ее
матрица в этом базисе, диагонально, т. е.
имеет канонический вид, если ее
матрица в этом базисе, диагонально, т. е.
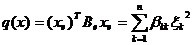 ,
,  . (9)
. (9)
Целью этого пункта является
доказательство утверждения, что для любого квадратичного функционала существует
базис, в котором его форма записи имеет канонический вид. Это утверждение
равносильно утверждению о том, что в любом классе эквивалентных между собой
симметрических матриц из 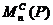 существует
матрица диагонального вида.
существует
матрица диагонального вида.
Прежде, чем доказать отмеченные
утверждения, введем ряд определений [8].
Согласованными элементарными
преобразованиями назовем следующие пары элементарных преобразований:
) 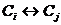 и
и  ,
,
) 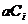 и
и  , а¹0,
, а¹0,
) 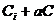 и
и 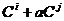 ,
, 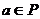 ,
, 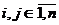 .
.
Отметим, что элементарные матрицы,
отвечающие двум согласованным элементарным преобразованиям, взаимно транспонированы.
Поскольку применение к матрице одного элементарного преобразования равносильно
умножению ее слева или справа на соответствующую элементарную матрицу e, то применение к квадратной
симметрической матрице А пары согласованных элементарных преобразований не
выводит ее из своего класса эквивалентности:
 .
.
Пусть 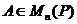 . Минор М матрицы А называется
главным минором, если множества номеров строк и столбцов матрицы А, на
пересечении которых стоит этот минор, одинаковы,
. Минор М матрицы А называется
главным минором, если множества номеров строк и столбцов матрицы А, на
пересечении которых стоит этот минор, одинаковы, 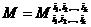 . Следующие главные миноры матрицы А
называются ее угловым минорами
. Следующие главные миноры матрицы А
называются ее угловым минорами
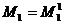 ,
, 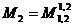 ,…,
,…,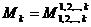 ,…,
,…,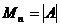 .
.
Заметим, что если к некоторой
матрице применить конечное число элементарных преобразований третьего типа
(трансвекций), то ввиду свойства 3 определителей ([13], стр.11) все ее миноры,
в том числе и угловые, останутся неизменными.
Предложение 13. Пусть 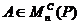 .Существует
конечное число согласованных элементарных преобразований, приводящих матрицу А
к диагональному виду.
.Существует
конечное число согласованных элементарных преобразований, приводящих матрицу А
к диагональному виду.
Вначале рассмотрим частный случай,
когда все угловые миноры матрицы А отличны от нуля. 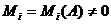 ,
, 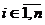 . Пусть
. Пусть 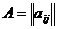 ,
, 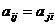 ,
, 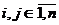 . Так как
. Так как 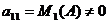 , в матрице
А можно провести следующую цепочку согласованных элементарных преобразований
, в матрице
А можно провести следующую цепочку согласованных элементарных преобразований
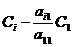 ,
,  ,
, 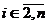 .
.
В результате из матрицы А получается
симметрическая матрица В,
 ~
~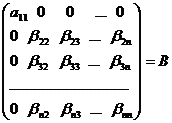 ,
,
эквивалентная ей и обладающая тем
свойством, что 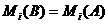 ,
,  .
.
В частности, 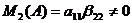 Þ
Þ 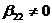 . В матрице
В проведем цепочку согласованных элементарных преобразований:
. В матрице
В проведем цепочку согласованных элементарных преобразований:
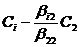 ,
,  ,
, 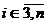 .
.
В результате получаем симметрическую
матрицу С,
А~В~С=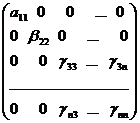 ,
,
эквивалентную матрице А и обладающую
свойством 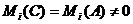 ,
, 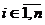 Þ
Þ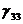 ¹ 0.
Продолжая этот процесс на n-1 шаге получим диагональную матрицу
¹ 0.
Продолжая этот процесс на n-1 шаге получим диагональную матрицу
 ,
,
эквивалентную матрице А. При этом 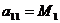 ,
,  ,…,
,…, 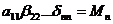 , откуда
следует, что
, откуда
следует, что
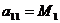 ,
, 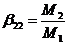 , …,
, …, 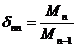 (10)
(10)
Перейдем к общему случаю. Если 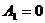 , можно
переходить к строке А. Пусть
, можно
переходить к строке А. Пусть 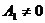 , но
, но 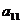 =0. Рассмотрим два случая: первый -
для которого
=0. Рассмотрим два случая: первый -
для которого 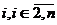 ,
, 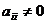 , второй -
для любого
, второй -
для любого 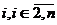 ,
,  . В первом
случае следующая пара согласованных элементарных преобразовании
. В первом
случае следующая пара согласованных элементарных преобразовании 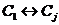 ,
, 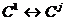 позволяет
получить матрицу, эквивалентную матрице А, у которой на месте элемента
позволяет
получить матрицу, эквивалентную матрице А, у которой на месте элемента 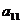 стоит
стоит 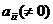 . Во втором
случае в первой строке матрицы А существует элемент
. Во втором
случае в первой строке матрицы А существует элемент  , отличный
от нуля,
, отличный
от нуля, 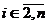 . Теперь
пара согласованных элементарных преобразований
. Теперь
пара согласованных элементарных преобразований 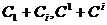 приводит к матрице, эквивалентной
матрице А, у которой на месте элемента
приводит к матрице, эквивалентной
матрице А, у которой на месте элемента 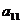 стоит
стоит 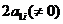 .
.
После этого осуществляется цепочка
согласованных элементарных преобразований, аналогичных тем, которые проведены
на первом шаге предыдущего случая. Если вторая строка полученной при этом
матрицы В нулевая, то переходим к третьей строке, если же 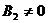 , но
, но 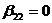 , проводится
пара согласованных элементарных преобразований, выводящих на место элемента
, проводится
пара согласованных элементарных преобразований, выводящих на место элемента 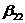 ненулевое
число и т. д. После конечного числа шагов и в этом случае будет получена
диагональная матрица, эквивалентная матрице А.
ненулевое
число и т. д. После конечного числа шагов и в этом случае будет получена
диагональная матрица, эквивалентная матрице А.
Замечание 1. Строго говоря, при
доказательстве предложения 13 следует провести индукцию по n как в частном, так
и в общем случаях. Предлагаем читателю в целях тренировки проделать этот
формализм самостоятельно.
Замечание 2. Из доказательства
предложения 13 следует, что для любой симметрической матрицы А существует
конечное число согласованных элементарных преобразований, приводящих матрицу А
к диагональному виду D, удовлетворяющему условию 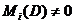 ,
,  ,
, 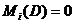 ,
, 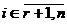 , где
, где 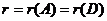 . Действительно, если A~D, то
. Действительно, если A~D, то 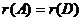 и
согласованными переменами строк и столбцов можно добиться того, чтобы первые r
элементов главной диагонали матрицы D были отличны от нуля, а остальные n-r ее
элементов равнялись нулю.
и
согласованными переменами строк и столбцов можно добиться того, чтобы первые r
элементов главной диагонали матрицы D были отличны от нуля, а остальные n-r ее
элементов равнялись нулю.
Предложение 14. Пусть 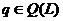 . Существует
базис, в котором квадратичная форма q имеет канонический вид.
. Существует
базис, в котором квадратичная форма q имеет канонический вид.
Возьмем произвольный базис  пространства
L и матрицу
пространства
L и матрицу  функционала
q в этом базисе. Поскольку
функционала
q в этом базисе. Поскольку 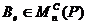 , в силу предложения 13 найдется
конечное число согласованных элементарных преобразований, приводящих матрицу
, в силу предложения 13 найдется
конечное число согласованных элементарных преобразований, приводящих матрицу  к
диагональному виду
к
диагональному виду 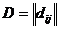 ,
, 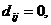
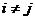 ,
,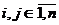 . Если через
. Если через 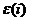 обозначить
элементарную матрицу, отвечающую соответствующему i-тому столбцовому
элементарному преобразованию, то матрицы
обозначить
элементарную матрицу, отвечающую соответствующему i-тому столбцовому
элементарному преобразованию, то матрицы  и D будут связаны равенством:
и D будут связаны равенством:
 .
.
Введем матрицу  . Матрица Р
не вырождена как произведение обратимых матриц и
. Матрица Р
не вырождена как произведение обратимых матриц и
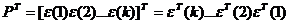 .
.
Следовательно, 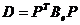 . В качестве
. В качестве
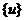 возьмем
базис:
возьмем
базис:
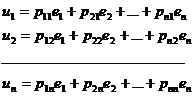 (11)
(11)
построенный по матрице 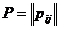 , которая
является матрицей перехода от базиса
, которая
является матрицей перехода от базиса  к базису
к базису 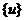 ,
, 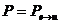 . Тогда
матрица D является матрицей функционала q в базисе
. Тогда
матрица D является матрицей функционала q в базисе 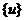 , вследствие
чего квадратичная форма q в этом базисе имеет канонический вид.
, вследствие
чего квадратичная форма q в этом базисе имеет канонический вид.
Замечание 3. Если квадратичная форма
q в базисе  имеет вид
имеет вид
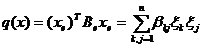 (12)
(12)
а в базисе 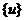 -
канонический вид
-
канонический вид
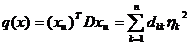 , где
, где 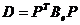 (13)
(13)
тогда в силу предложения 11 связь
между векторами 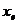 и
и 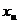 задается
равенствами
задается
равенствами 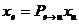 и в
координатной записи
и в
координатной записи
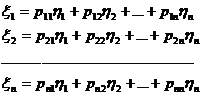 (14)
(14)
Часто говорят, что формулы (14)
определяют линейное невырожденное преобразование координат, которое приводит
квадратичную форму (12) к каноническому виду (13).
Замечание 4. Если все угловые миноры
матрицы  отличны от
нуля,
отличны от
нуля, 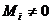 ,
, 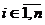 , как
следует из доказательства предложения 13, диагональные элементы матрицы D
определяются по формулам (10), т. е. квадратичная форма q в этом случае имеет
канонический вид
, как
следует из доказательства предложения 13, диагональные элементы матрицы D
определяются по формулам (10), т. е. квадратичная форма q в этом случае имеет
канонический вид
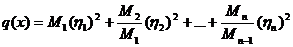 (15)
(15)
Эта формула называется формулой
Якоби.
Пример 6. Квадратичную форму
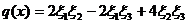 (16)
(16)
линейным невырожденным
преобразованием координат 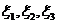 привести к
каноническому виду.
привести к
каноническому виду.
Необходимо найти невырожденную
матрицу
такую, что преобразование координат 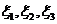
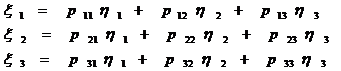
приводит форму (16) к виду
 .
.
Считая 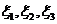 координатами
вектора х в некотором базисе
координатами
вектора х в некотором базисе  трехмерного действительного пространства
R3 , запишем
равенство (16) виде
трехмерного действительного пространства
R3 , запишем
равенство (16) виде
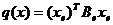 , где
, где 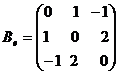
и найдем матрицу Р, приводящую
матрицу  к
диагональному виду
к
диагональному виду 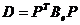 . Так как из
доказательства предложения 14 следует, что
. Так как из
доказательства предложения 14 следует, что
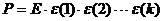 ,
,
т.е. матрица Р является результатом
применения к матрице Е столбцовых элементарных преобразований , приводящих
вместе с соответствующими строчными элементарными преобразованиями матрицу  к виду D,
то для отыскания матрицы Р достаточно составить матрицу
к виду D,
то для отыскания матрицы Р достаточно составить матрицу
 ~
~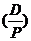
и провести в ней согласованные
элементарные преобразования, приводящие блок  к виду D. Тогда на месте блока Е
появится матрица Р. На практике более удобным является отыскание матрицы
к виду D. Тогда на месте блока Е
появится матрица Р. На практике более удобным является отыскание матрицы 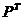 . Для этого
достаточно составить матрицу (
. Для этого
достаточно составить матрицу ( |Е) и привести блок
|Е) и привести блок  к виду D
строчными элементарными преобразованиями, тогда на месте блока Е появится
матрица
к виду D
строчными элементарными преобразованиями, тогда на месте блока Е появится
матрица 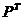 .
.
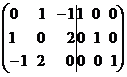
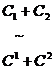

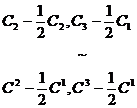

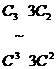
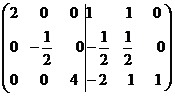 .
.
Откуда следует, что
 ,
,
канонический вид формы q
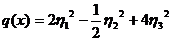 (17)
(17)
а искомое линейное невырожденное
преобразование координат, приводящее форму (13) к виду (14), имеет вид
 (18)
(18)
Замечание 5. Для контроля за
вычислительными ошибками целесообразно формулы (18) подставить в равенство (16)
и получить канонический вид (17).
5. Классификация комплексных и
вещественных квадратичных функционалов
Прежде всего заметим, что если 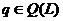 , то ввиду
равенства (7) матрицы
, то ввиду
равенства (7) матрицы  и
и 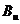 функционала
q в базисах
функционала
q в базисах  и
и 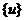 имеют
одинаковый ранг. Поэтому корректным является следующее определение.
имеют
одинаковый ранг. Поэтому корректным является следующее определение.
Рангом квадратичного функционала на
пространстве L называется ранг его матрицы в произвольном базисе  пространства
L,
пространства
L,
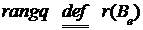
Теперь мы можем доказать следующий
критерий эквивалентности двух квадратичных функционалов на пространстве L(C).
Предложение 15. Пусть 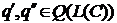 и
и  . Следующие
утверждения эквивалентны:
. Следующие
утверждения эквивалентны:
) 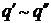 ;
;
) 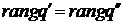 ;
;
) для каждого из функционалов 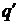 и
и  существует
базис, в котором его матрица имеет вид
существует
базис, в котором его матрица имеет вид
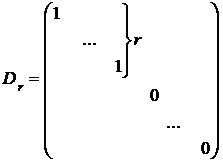 (19)
(19)
По определению 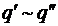 Û
Û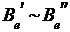 для любого
базиса
для любого
базиса  пространства
L. Поэтому для справедливости доказываемого утверждения достаточно показать,
что
пространства
L. Поэтому для справедливости доказываемого утверждения достаточно показать,
что 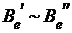 Û
Û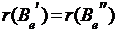 Û
Û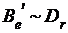 ,
, 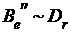 .
.
В самом деле, в силу предложения 13
каждая симметрическая матрица 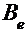 эквивалентна матрице
эквивалентна матрице 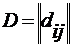 . Так как
. Так как 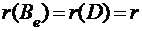 , то можно
считать что
, то можно
считать что 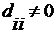 ,
, 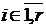 ,
, 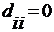 ,
, 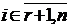 (см.
Замечание 2). Но
(см.
Замечание 2). Но
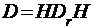
Где  , а
, а  - любое из двух значений квадратного
корня из комплексного числа
- любое из двух значений квадратного
корня из комплексного числа 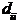 ,
, 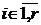 , т.е.
, т.е. 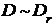 , где
, где 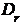 имеет вид
(19).
имеет вид
(19).
Если  , тогда
, тогда
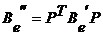
где 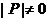 , Þ
, Þ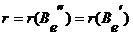 Þ
Þ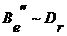 ,
, 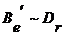 . Обратно
. Обратно 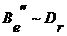 ,
, 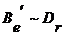 Þ
Þ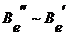 Þ
Þ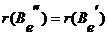 .
.
Замечание 6. Из предложения 15
следует, что множество 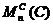 распадается
на n+1 класс
эквивалентных между собой матриц. Две матрицы при этом являются эквивалентными,
тогда и только тогда, когда они имеют одинаковый ранг. Представителями каждого
класса эквивалентности является матрицы
распадается
на n+1 класс
эквивалентных между собой матриц. Две матрицы при этом являются эквивалентными,
тогда и только тогда, когда они имеют одинаковый ранг. Представителями каждого
класса эквивалентности является матрицы 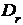 вида (19),
вида (19), 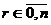 ,
, 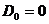 ,
, 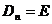 .
.
Для любого функционала 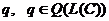 , существует
базис
, существует
базис  в котором
квадратичная форма q имеет вид
в котором
квадратичная форма q имеет вид
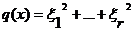 где r=rangq,
где r=rangq, 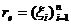 (20)
(20)
Этот вид комплексной квадратичной
формы называется нормальным и в силу предложения 15 является единственным для
любого комплексного функционала на пространстве L(C).
Теперь рассмотрим случай P=R. Прежде чем
провести классификацию вещественных квадратичных функционалов, заметим, что для
вещественного квадратичного функционала, вообще говоря, не существует базис  , в котором
он может быть записан в виде (20). Это связано с тем, что не существует
вещественного числа, являющегося квадратным корнем из отрицательного числа. В
связи с этим дадим следующее определение.
, в котором
он может быть записан в виде (20). Это связано с тем, что не существует
вещественного числа, являющегося квадратным корнем из отрицательного числа. В
связи с этим дадим следующее определение.
Будем говорить, что функционал  , в базисе
, в базисе  пространства
L(R) имеет нормальный вид, если
пространства
L(R) имеет нормальный вид, если
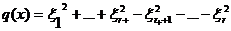 , (21)
, (21)
 ,
, 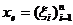 ,
,  .
.
Предложение 16. Пусть 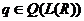 , тогда
существует базис в пространстве L(R), в котором квадратичная форма q имеет
нормальный вид.
, тогда
существует базис в пространстве L(R), в котором квадратичная форма q имеет
нормальный вид.
В силу предложения 14 существует
базис  , в котором
матрица функционала q диагонально.
, в котором
матрица функционала q диагонально. 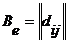 ,
, 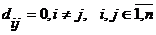 . Можем считать, что
. Можем считать, что 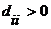 ,
, 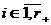 ,
, 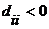 ,
,  ,
,  ,
, 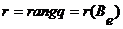 .
.
В противном случае, как и при
доказательстве предложения 15, добьемся выполнения этих условий с помощью
конечного числа согласованных перемен местами строк и столбцов. Но
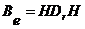 ,
,
Где  ,
,
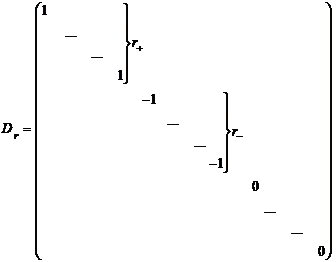 (22)
(22)
где  . Откуда следует, что в базисе
. Откуда следует, что в базисе 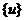 :
: ,
,  ,
, ,
, 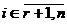 квадратичная
форма q имеет вид (21).
квадратичная
форма q имеет вид (21).
Следующее предложение усиливает
только что доказанный результат для вещественных квадратичных форм и, по существу,
является теоремой единственности нормального вида для таких квадратичных форм.
Предложение 16. (Закон инерции
вещественных квадратичных форм.) Пусть 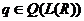 . Тогда число положительных и
отрицательных квадратов нормального вида квадратичной формы q не зависит от
базиса, в котором квадратичная форма имеет этот вид.
. Тогда число положительных и
отрицательных квадратов нормального вида квадратичной формы q не зависит от
базиса, в котором квадратичная форма имеет этот вид.
Предположим, что
квадратичная форма ранга r в базисе  имеет вид:
имеет вид:
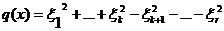 (23)
(23)
где 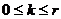 , а в базисе
, а в базисе 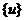 имеет вид
имеет вид
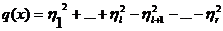 (24)
(24)
где 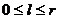 . Покажем, что k=l.
Действительно, допустим, что l<k, рассмотрим
в L подпространство
. Покажем, что k=l.
Действительно, допустим, что l<k, рассмотрим
в L подпространство 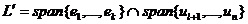 .
.
Так как система векторов 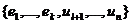 состоит из n+(k-l) векторов,
она линейно зависима
состоит из n+(k-l) векторов,
она линейно зависима
Þ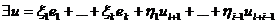 Þ
Þ
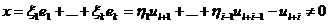
ввиду линейной независимости системы
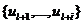 Þ
Þ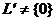 .
.
Пусть 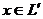 , x¹0.Тогда
, x¹0.Тогда
 ,
, 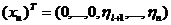 .
.
Вычислим значение q(х) двумя
способами по формулам (23) и (24), получаем, что
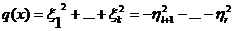 .
.
что возможно лишь в случае 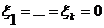 Þ
Þ  Þx=0 .
Þx=0 .
Аналогичным рассуждением
доказывается, что невозможно неравенство l>k.
Таким образом, l=k.
Число 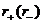 положительных (отрицательных)
квадратов канонического вида вещественного квадратичного функционала q
называется его положительным (отрицательным) индексом инерции. Ясно, что
положительных (отрицательных)
квадратов канонического вида вещественного квадратичного функционала q
называется его положительным (отрицательным) индексом инерции. Ясно, что 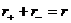 , где r=rang q.
, где r=rang q.
Предложение 18. Пусть 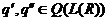 и dimL(R)=n. Следующие
утверждения равносильны:
и dimL(R)=n. Следующие
утверждения равносильны:
) 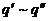 ,
,
) 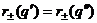 ,
,
)для каждого из функционалов 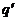 и
и 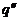 существует
базис, в котором его матрица имеет вид (22). Ä
существует
базис, в котором его матрица имеет вид (22). Ä
Замечание 7. Сигнатурой
вещественного квадратичного функционала q называется число 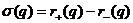 .Числа
.Числа 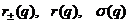 называются
инвариантами q. Знание любых двух инвариантов квадратичного функционала q из
отметенного множества инвариантов однозначно определяет класс эквивалентности
как в Q(L(R)), так и в
называются
инвариантами q. Знание любых двух инвариантов квадратичного функционала q из
отметенного множества инвариантов однозначно определяет класс эквивалентности
как в Q(L(R)), так и в  . Предлагаем
читателю показать самостоятельно, что число классов эквивалентности, в данном
случае совпадающее с числом различных матриц вида (22), равно
. Предлагаем
читателю показать самостоятельно, что число классов эквивалентности, в данном
случае совпадающее с числом различных матриц вида (22), равно
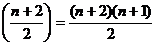 .
.
. Определенные вещественные
квадратичные функционалы
Среди квадратичных функционалов на
пространстве L (R) особый
интерес представляют так называемые положительно определенные функционалы, т.е.
такие функционалы  , что
, что
(x)>0,  , x¹0.
, x¹0.
Этот интерес связан с тем, что
связанные с такими функционалами q симметрические билинейные
функционалы вида
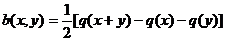
удовлетворяют аксиомам скалярного
произведения и поэтому каждый из этих билинейных функционалов порождает на
пространстве L(R) структуру
евклидова пространства, различную для различных функционалов.
Будем говорить, что матрица  ,
удовлетворяет условию Сильвестра, если все ее угловые миноры положительны,
,
удовлетворяет условию Сильвестра, если все ее угловые миноры положительны,
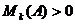 ,
, 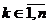 .
.
Следующая теорема дает описание
класса всех положительно определенных квадратичных функционалов на пространстве
L(R).
Предложение 19. Пусть 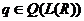 и dimL (R)=n. Следующие
утверждения равносильны:
и dimL (R)=n. Следующие
утверждения равносильны:
) q- положительно определенный
функционал;
) 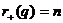 ;
;
) матрица  функционала
q в произвольном базисе е пространства L(R) удовлетворяет условию Сильвестра;
функционала
q в произвольном базисе е пространства L(R) удовлетворяет условию Сильвестра;
) матрица  функционала
q в фиксированном базисе е пространства L(R) удовлетворяет условию Сильвестра.
функционала
q в фиксированном базисе е пространства L(R) удовлетворяет условию Сильвестра.
Выберем произвольный базис 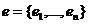 , в котором
квадратичная форма q(х) имеет нормальный вид
, в котором
квадратичная форма q(х) имеет нормальный вид
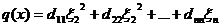 ,
,
где 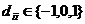 ,
, 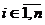 , и заметим, что
, и заметим, что
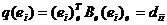 .
.
Пусть q(x)>0, 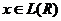 ,
, 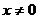 . Тогда
. Тогда 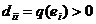 , т. е.
, т. е. 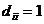 ,
, 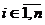 ,
, 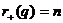 . Обратно,
пусть
. Обратно,
пусть 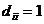 Û
Û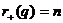 . Тогда
. Тогда
 ,
, 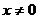 ,
,
т. е. q- положительно определен.
)Þ3) Заметим, что определители матриц функционала
q в любом базисе {e} отличны от нуля и имеют одинаковый
знак, так как
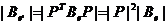 .
.
Пусть 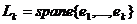 ,
, 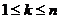 . Обозначим через
. Обозначим через 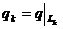 и заметим,
что
и заметим,
что  , поскольку
, поскольку 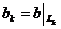 , где
b-симметрический билинейный функционал, порождающий функционал q, является
симметрическим билинейным функционалом на пространстве Lk и
, где
b-симметрический билинейный функционал, порождающий функционал q, является
симметрическим билинейным функционалом на пространстве Lk и 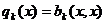 . Ясно, что
для любого k,
. Ясно, что
для любого k, 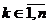 ,
функционалы qk являются
положительно определенным и, следовательно, существует базис в Lk, в котором
матрица qk имеет вид
единичной матрицы порядка k. Но тогда определитель матрицы функционала qk в базисе
,
функционалы qk являются
положительно определенным и, следовательно, существует базис в Lk, в котором
матрица qk имеет вид
единичной матрицы порядка k. Но тогда определитель матрицы функционала qk в базисе 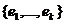 также
положителен. Остается отметить, что он совпадает с
также
положителен. Остается отметить, что он совпадает с 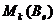 . Таким
образом, матрица
. Таким
образом, матрица  функционала
q в произвольном базисе е удовлетворяет условию Сильвестра.
функционала
q в произвольном базисе е удовлетворяет условию Сильвестра.
) Þ 4)
Очевидно.
) Þ 2) Пусть
матрица  в
фиксированном базисе е удовлетворяет условию Сильвестра. В силу замечания 4 к
предложению 14 существует базис{u}, в котором квадратная форма q(x)
имеет канонический вид (15).
в
фиксированном базисе е удовлетворяет условию Сильвестра. В силу замечания 4 к
предложению 14 существует базис{u}, в котором квадратная форма q(x)
имеет канонический вид (15).
Так как Mk>0, 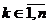 , в силу
предложений 16 и 17 r+ =n.
, в силу
предложений 16 и 17 r+ =n.
Функционал  , называется
положительным полуопределенным, если
, называется
положительным полуопределенным, если
(x)³0, 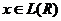 .
.
Предложение 20. Пусть 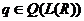 и dimL (R)=n. Следующие
утверждения эквивалентны:
и dimL (R)=n. Следующие
утверждения эквивалентны:
) q- положительно полуопределенный,
) r-(q)=0,
) матрица  в
произвольном базисе {e} пространства L(R) удовлетворяет
слабому условию Сильвестра, т. е. все ее угловые миноры неотрицательны.
в
произвольном базисе {e} пространства L(R) удовлетворяет
слабому условию Сильвестра, т. е. все ее угловые миноры неотрицательны.
) матрица  в фиксированном
базисе {e}
пространства L(R) удовлетворяет слабому условию Сильвестра. Ä
в фиксированном
базисе {e}
пространства L(R) удовлетворяет слабому условию Сильвестра. Ä
Функционал  называется
отрицательно определенным (отрицательно полуопределенным), если
называется
отрицательно определенным (отрицательно полуопределенным), если
q(x)<0, 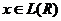 ,
, 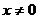 (
(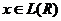 q(x)£ 0,
q(x)£ 0, 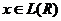 ).
).
Предлагается читателю сформулировать
и доказать аналоги предложений 10 и 20 для отрицательно определенных
квадратичных функционалов.
Указание. q(x)≥0, 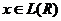 Û - q(x)£0,
Û - q(x)£0, 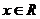 .
.
Функционал  называется
неопределенным, если существуют такие
называется
неопределенным, если существуют такие  , что
, что 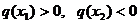 .
.
Предложение 21. Пусть 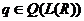 и dimL (R)=n. Для того,
чтобы функционал q был неопределенным, необходимо и достаточно, чтобы
функционал q был неопределенным,
необходимо и достаточно, чтобы
и dimL (R)=n. Для того,
чтобы функционал q был неопределенным, необходимо и достаточно, чтобы
функционал q был неопределенным,
необходимо и достаточно, чтобы
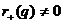 и
и 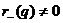 . Ä
. Ä
7. Алгоритмы и примеры
Рассмотрим основные практические
задачи, возникающие в теории квадратичных форм:
) построение линейного невырожденного
преобразовании координат, приводящего квадратичную форму к каноническому (или
нормальному) виду;
) вычисление инвариантов
квадратичной формы (это задача опирается на предыдущую ,так как требует знания
канонического или нормального вида квадратичной формы);
) выяснение эквивалентности (или
неэквивалентности) двух квадратичных форм и построение линейного невырожденного
преобразования координат, переводящего одну квадратичную форму в другую;
) исследование вещественной
квадратичной формы на положительную определенность.
Выше в разделе 4 изложен
универсальный алгоритм решения задачи!) (см. пример:), основанный на приведении
симметрической матрицы согласованными элементарными преобразованиями к
диагональному виду.
В добавление к этому рассмотрим
метод Лагранжа решение задачи1), который ввиду своей простоты в стандартных
ситуациях обладает преимуществом перед описанным выше методом.
Метод Лагранжа использует процедуру
выделения полного квадрата линейной формы, которая встречается в школьном курсе
математики при изучении квадратичных трехчленов, и опирается на следующее
тождество
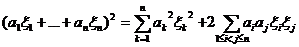 (25)
(25)
Если нам дана квадратичная форма
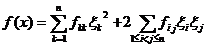 ,
,
то при 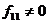 мы можем,
воспользовавшись формулой (25), выделить полный квадрат
мы можем,
воспользовавшись формулой (25), выделить полный квадрат
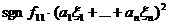 ,
,
где 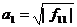 , включающий все слагаемые,
содержащие
, включающий все слагаемые,
содержащие 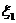 . В
результате
. В
результате
 ,
,
где 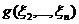 - квадратичная форма от переменных
- квадратичная форма от переменных 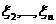 . Применяя
после этого аналогичный прием к форме g, выделяем в полный квадрат все ее
слагаемые, содержащие
. Применяя
после этого аналогичный прием к форме g, выделяем в полный квадрат все ее
слагаемые, содержащие 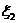 и т. д.
После конечного числа шагов исходная квадратичная форма f будет представлена в
виде линейной комбинации полных квадратов от некоторых линейных форм, что
позволяет с помощью соответствующей замены переменных получить ее канонический
вид.
и т. д.
После конечного числа шагов исходная квадратичная форма f будет представлена в
виде линейной комбинации полных квадратов от некоторых линейных форм, что
позволяет с помощью соответствующей замены переменных получить ее канонический
вид.
Пример 7. Следующую квадратичную
форму
 (26)
(26)
привести методом Лагранжа к
каноническому виду.
На первом шаге выделим полный
квадрат, содержащий все слагаемые с
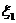 ,
,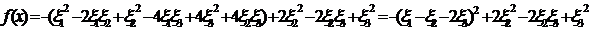 .
.
После этого выделяя полный квадрат,
содержащий все слагаемые с 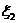 , получим, что
, получим, что
Проводя замену
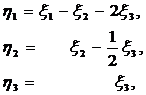
и выражая из полученных формул 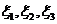 через
через 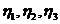 , выписываем
линейное невырожденное преобразование координат
, выписываем
линейное невырожденное преобразование координат
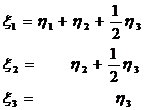 (27)
(27)
с матрицей
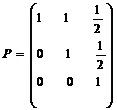 ,
,
приводящее исходную квадратичную
форму к каноническому виду,
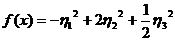 (28)
(28)
Нетрудно заметить, что метод
Лагранжа позволяет на очередном шаге исключить лишь ту переменную 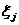 , квадрат
которой
, квадрат
которой 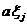 имеет
ненулевой коэффициент (т. е. a≠0). Если же в рассматриваемой записи
квадратичной формы нет ни одного квадрата переменных, нужно провести
вспомогательное линейное невырожденное преобразование координат, приводящее к
появлению нужных квадратов.
имеет
ненулевой коэффициент (т. е. a≠0). Если же в рассматриваемой записи
квадратичной формы нет ни одного квадрата переменных, нужно провести
вспомогательное линейное невырожденное преобразование координат, приводящее к
появлению нужных квадратов.
Пример 8. Применим метод Лагранжа к
квадратичной форме вида (16).
Так как она не содержит ни одного
квадрата переменной, проведем следующее невырожденное преобразование координат
,
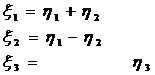 (29)
(29)
с матрицей
 .
.
После замены переменных форма (16)
принимает вид
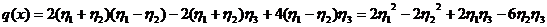 .
.
Исключая последовательно переменные 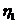 и
и 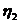 методом
Лагранжа, получаем, что
методом
Лагранжа, получаем, что
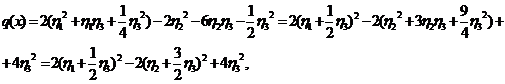 (30)
(30)
Где 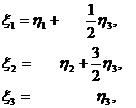
Выражая из этих формул  через
через 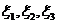 , находим,
что
, находим,
что

Наконец, подставляя найденные
выражения для  в формулу
(29), выписываем линейное невырожденное преобразование координат
в формулу
(29), выписываем линейное невырожденное преобразование координат

с матрицей
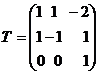 ,
,
приводящее квадратичную форму вида
(16) к каноническому виду (30).
Замечание. В целях вычислительного
контроля рекомендуется подставить найденные выражения для 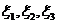 в формулу
(16) и получить канонический вид (30).
в формулу
(16) и получить канонический вид (30).
Пример 9. Показать, что вещественные
квадратичные формы q в виде (16) и f вида (26) эквивалентны и построить
линейное невырожденное преобразование, переводящее форму q в форму
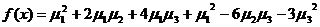 (31)
(31)
Из решения примера 6 следует, что 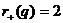 ,
, 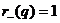 (см.
формулу (17)), а из решения примера 7 следует, что
(см.
формулу (17)), а из решения примера 7 следует, что 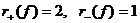 (см.
формулу (27)). Но тогда в силу предложения 18 q~f. Остается построить линейное
невырожденное преобразование, переводящее форму q в форму f.
(см.
формулу (27)). Но тогда в силу предложения 18 q~f. Остается построить линейное
невырожденное преобразование, переводящее форму q в форму f.
Из формул (17) и (18) следует, что
преобразование
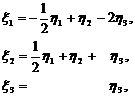 (32)
(32)
приводит форму (16) к каноническому
виду
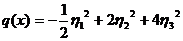 (33)
(33)
(проведена замена 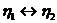 в формулах
(17) и (18)).
в формулах
(17) и (18)).
Но тогда преобразование
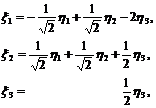 (34)
(34)
приводит форму (16) к каноническому
виду
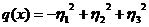 (35)
(35)
(проведена замена 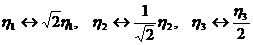 формулах
(32) и (33)).
формулах
(32) и (33)).
Далее, из формул (27) и (28)
следует, что преобразование
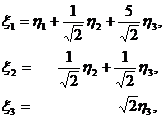
приводит форму (26) к виду (35)
(проведена замена ( в формулах
(27) и (28)).
в формулах
(27) и (28)).
Легко проверить, что обратное
преобразование имеет вид

и переводит форму вида (35) в форму
вида (26). Но тогда линейное невырожденное преобразование

переводит форму вида (35) в форму
вида (31). Подставляя найденные выражения для 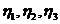 в формулы (34), получаем линейное
невырожденное преобразование
в формулы (34), получаем линейное
невырожденное преобразование
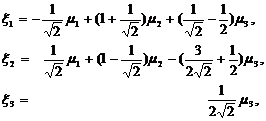
переводящее форму q вида (16) в
форму f вида (31).
Пример 10. Выяснить, при каких
значениях параметра l является
положительно определенной следующая квадратичная форма,
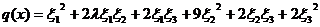 .
.
Из предложения 19 следует, что форма
q будет положительно определенной в том и только в том случае, если все угловые
миноры ее матрицы
 ,
,
положительны, т. е. (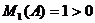 )
)
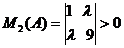 ,
, 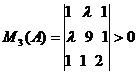 .
.
Раскрывая определители как
многочлены относительно l, получаем
следующую систему неравенств.
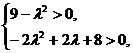 Û
Û 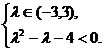
Так как корни квадратного трехчлена 
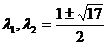 по модулю больше 3, множество
решений системы неравенств совпадает с интервалом (-3,3). Таким образом,
квадратичная форма q является положительно определенной при |l|<3.
по модулю больше 3, множество
решений системы неравенств совпадает с интервалом (-3,3). Таким образом,
квадратичная форма q является положительно определенной при |l|<3.
Историческая справка.
Фундаментальные понятия теории
квадратичных форм фактически появились уже вместе с евклидовой геометрией.
Однако, ее формирование и развитие в современном виде восходит ко второй
половине XVIII в. в связи
с потребностями арифметики, анализа и механики. Приведение к каноническому виду
(Лагранж, 1759), закон инерции (Якоби, Гаусс, 1846-1850).
Литература
1. Гельфанд
И.М. Лекции по линейной алгебре. - М. : Наука,1971.
2. Головина
Л.И. Линейная алгебра и некоторые ее приложения. - М.: Наука, 1975.
. Беклемишев
Д.В. Курс аналитической геометрии и линейной алгебры.- М.: Наука, 1971.
. Воеводин
В.В. Линейная алгебра. - М.: Наука, 1974.
. Ильин
В.А., Поздняк Э.Г. Линейная алгебра. - М.: Наука, 1984.
. Ланкастер
К. Математическая экономика. - М.: Советское радио, 1972.
. Дыбин
В.Б. Лекции по линейной алгебре, Ч I,
Вып. I, Алгебра матриц.
Ростов-на-Дону: Изд. РГУ, 1995.
. Дыбин
В.Б. Лекции по линейной алгебре, Ч I,
Вып.2, Матрицы и системы уравнений.- Ростов-на-Дону: Изд. РГУ, 1995.
. Дыбин
В.Б. Евклидовы пространства, Методические указания Вып.VI.-
Ростов-на-Дону: Изд. РГУ, 2005.
. Дыбин
В.Б., Семигук В.М. Алгебра матриц. Методические указания. Вып.1.-
Ростов-на-Дону: Изд. РГУ, 2004.
. Дыбин
В.Б., Семигук В.М. Метод Гаусса решения систем линейных алгебраических
уравнений. Методические указания. Вып. II.-
Ростов-на-Дону: Изд. РГУ, 1996.
. Дыбин
В.Б., Семигук В.М. Теория определителей. Методические указания. Вып.3.-
Ростов-на-Дону: Изд. РГУ, 2006.
. Дыбин
В.Б., Семигук В.М. Линейные пространства. Базисы и координаты. Методические
указания. Вып. V.- Ростов-на-Дону:
Изд. РГУ, 2005.
. Дыбин
В.Б., Семигук В.М. Подпространства. Методические указания. Вып.VII.-
Ростов-на-Дону: Изд. РГУ, 2007.
. Проскуряков
И.В. Сборник задач по линейной алгебре.- М.: Наука, 1984.
. Дыбин
В.Б. Лекции по линейной алгебре, Ч I,
Вып. III,
Определители. - Ростов-на-Дону: Изд. РГУ, 2007.
. Бурбаки
Н. Очерки по истории математики.- М.: ИЛ, 1963.
. Кряквин
В.Д. Линейная алгебра в задачах и упражнениях.- М.: Вузовская книга, 2006.