Исследование системы регистрации быстрых сигналов
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное
образовательное учреждение
высшего профессионального образования
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Физико-технический институт
Кафедра электроники и автоматики
физических установок
Отчёт по лабораторной работе на тему:
«Исследование системы регистрации
быстрых сигналов»
Выполнил: студент группы 0712 Столповский Алексей Евгеньевич
Принял: преподаватель Михалевич Сергей Сергеевич
Томск 2014
Теоретическая часть
Определение функционала:
Переменная величина V
называется функционалом, определенным на некотором классе функций M, если каждой функции y(x) из
класса M ставится в соответствие определенное
число V ∈ R (v ∈ C), а сам класс M называется областью определения
функционала. Для значений функционала v на элементе y = y(x) ∈ M используется символ V = V[y(x)].
Здесь в качестве функционального пространства M рассматривается пространство Ck([a, b]),
состоящее из всех функций, определенных на отрезке [a, b] и имеющих
непрерывные производные до k-го порядка включительно. Здесь k -
некоторое фиксированное число. При k = 0 пространство C0([a, b])
= C([a, b]) есть пространство всех непрерывных на [a, b]
функций.
Нормой элемента y(x) ∈ Ck([a, b]) называется неотрицательное число
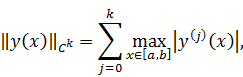


Две
функции y1(x) и y2(x) из пространства Ck[a,
b] называются близкими в смысле близости k-го порядка, если норма их
разности 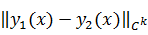
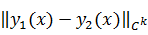 мала на
отрезке [a, b]. Другими словами, близость функций y(x)
и y1(x) в пространстве Ck ([a, b]) с заданной
точностью δ
> 0 означает, что
мала на
отрезке [a, b]. Другими словами, близость функций y(x)
и y1(x) в пространстве Ck ([a, b]) с заданной
точностью δ
> 0 означает, что 
 , т.е.
что близки не только сами функции, но и их производные до k-го порядка
включительно.
, т.е.
что близки не только сами функции, но и их производные до k-го порядка
включительно.
Функционал
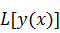
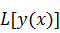 называется
линейным, если для любого λ ∈ R (λ ∈ C) и любых y1(x), y2(x) ∈ K справедливо
называется
линейным, если для любого λ ∈ R (λ ∈ C) и любых y1(x), y2(x) ∈ K справедливо
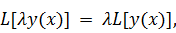
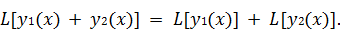

называется
действием, а 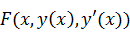
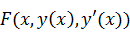 -
функцией Лагранжа (или лагранжианом).
-
функцией Лагранжа (или лагранжианом).
Каждой
функции (траектории) 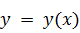
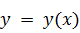 ставится
в соответствие действие
ставится
в соответствие действие 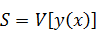
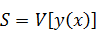 . Здесь
. Здесь 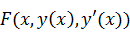
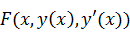 -
непрерывная функция вместе со всеми своими частными производными до второго
порядка включительно. Свойства именно этого функционала и его обобщений обычно
изучаются.
-
непрерывная функция вместе со всеми своими частными производными до второго
порядка включительно. Свойства именно этого функционала и его обобщений обычно
изучаются.
Исследуем
поведение данного функционала при изменении функции y(x). Пусть y(x)
- некоторая исходная функция, а y1(x) - некоторая другая функция,
близкая (например, в смысле близости k-го порядка) к y(x).
Функцию y1(x) будем называть проварьированной (изменённой, от
латинского variatio - изменение) функцией. Существует несколько представлений
проварьированной функции y1(x).
Можно,
например, ввести понятие вариации аналогично тому, как вводится понятие дифференциала
в дифференциальном исчислении.
Приращением, или вариацией, «аргумента» y(x)
функционала V[y(x)] называется разность между
функциями y1(x) − y(x), y(x),
y1(x) ∈ M. Для обозначения используется символ
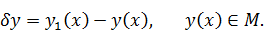
Тогда
проварьированную функцию можно записать как
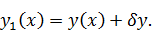
Символ

 ,
согласно определению следует понимать как единый, причём
,
согласно определению следует понимать как единый, причём 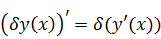
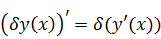 ,
поскольку производная разности равна разности производных:
,
поскольку производная разности равна разности производных:
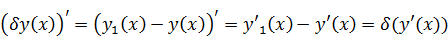
Другой
подход состоит в том, что функция y(x) в функционале V[y(x)]
рассматривается как однопараметрическое семейство
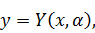
в
котором изменение параметра α меняет
функцию y(x), т.е. варьирует её. В этом случае сам функционал
становится функцией от α,
т.е 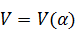
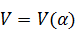 , и его
изменение в зависимости от вариации функции y(x) определяется
параметром α.
При этом вариацию
, и его
изменение в зависимости от вариации функции y(x) определяется
параметром α.
При этом вариацию 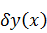
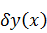 можно
определить как:
можно
определить как:
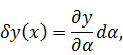
и
для её произвольности семейство 
 предполагать
произвольным, а не фиксированным.
предполагать
произвольным, а не фиксированным.
Обозначим
через
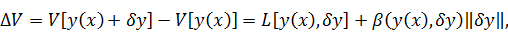
где
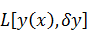
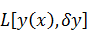 -
линейный по отношению к
-
линейный по отношению к 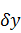
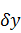 функционал,
а для функции
функционал,
а для функции 
 при
выбранной
при
выбранной 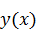
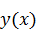 справедливо
соотношение
справедливо
соотношение

Этот
предел соответствует оценке
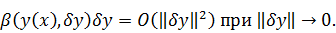
Фнукционал
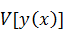
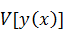 , имеющий
вариацию при
, имеющий
вариацию при 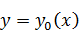
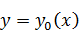 ,
называется дифференцируемым при
,
называется дифференцируемым при 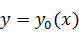
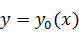 . Для
обозначения вариации функционала используется символ
. Для
обозначения вариации функционала используется символ 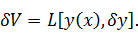
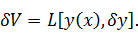
Теорема
Если
функционал 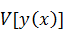
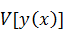 дифференцируем
в точке
дифференцируем
в точке 
 , то при
любом
, то при
любом 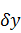
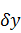 функция
функция 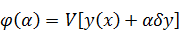
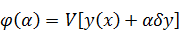 как
функция числа
как
функция числа 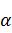
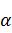 (при
фиксированных
(при
фиксированных 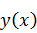
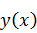 и
и 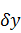
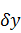 )
дифференцируема по
)
дифференцируема по 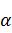
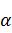 при
при 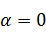
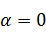 . Причём
вариацию функционала можно определить равенством
. Причём
вариацию функционала можно определить равенством
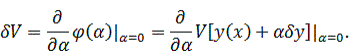
Доказательство
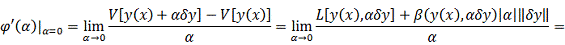
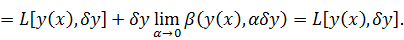
Что
и требовалось доказать. Здесь мы воспользовались свойством линейности
функционала 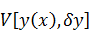
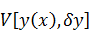 по
по 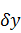
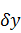 .
.
Ход
работы
вариационный исчисление
wolfram mathematica
Задание № 1
В
первом задании мы нашли в символьной форме и вычислили приращение функционала,
определённого на пространстве C1([a, b]) при различных 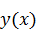
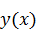 и
и 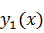
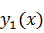
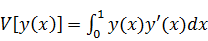
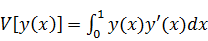


Вычисляем приращение аргумента:
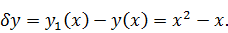
Вычисляем
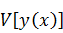
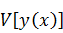 :
:

Вычисляем
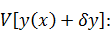
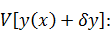
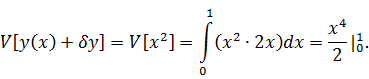
Вычисляем
приращение функционала:
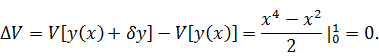
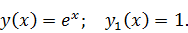
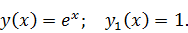

Вычисляем
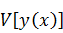
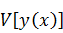 :
:
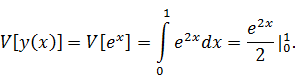
Вычисляем
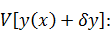
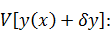
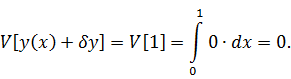
Вычисляем
приращение функционала:
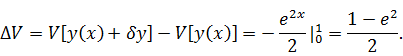
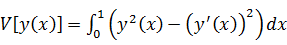
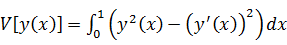 при
при 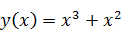
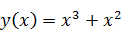 и
и 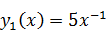
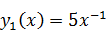 .
.
Вычисляем приращение аргумента:

Вычисляем
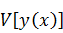
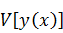 :
:

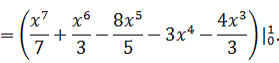
Вычисляем
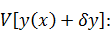
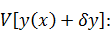

Вычисляем
приращение функционала:
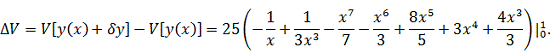
Очевидно,
что на промежутке 
 данный
интеграл расходится за счёт слагаемых с
данный
интеграл расходится за счёт слагаемых с 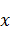
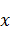 в
знаменателе.
в
знаменателе.
Задание
№ 2
Во
втором задании мы доказали, что функционал, определённый на пространстве C1([a,
b]) является дифференцируемым в каждой точке этого пространства, то есть он
имеет линейную относительно 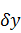
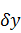 часть в
своём приращении (вариацию).
часть в
своём приращении (вариацию).
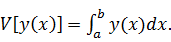
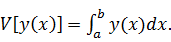
Вычисляем приращение функционала:
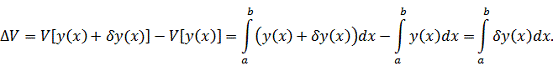
Очевидно,
что в силу свойства линейности определённого интеграла, приращение функционала
линейно относительно 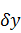
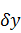 , а
значит, данный функционал является дифференцируемым на
определённом пространстве.
, а
значит, данный функционал является дифференцируемым на
определённом пространстве.
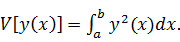
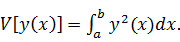
Вычисляем приращение функционала:
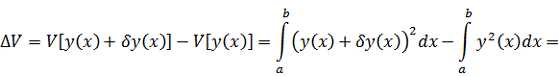

Снова используя свойство линейности определённого интеграла, можно
показать, что из приращения данного функционала возможно легко выделить
линейную часть:
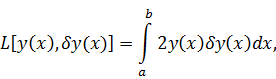
а следовательно данный функционал является дифференцируемым на
определённом пространстве.
Можно справедливо заметить, что изучаемый в данной лабораторной
функционал - действие (см. теоретическую часть) является дифференцируемым в C1([a,
b]) при общем виде лагранжиана, а следовательно, достаточно рассмотреть
общий случай.
Задание № 3
В третьем задании мы вычислили и графически изобразили приращение и
вариацию функционала.
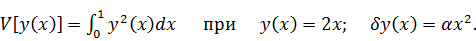
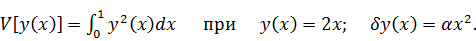
Вычисляем
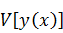
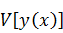 :
:
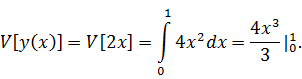
Вычисляем
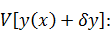
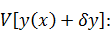
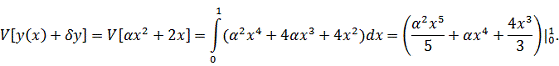
Вычисляем
приращение функционала:

Находим
вариацию функционала (т.е. выделяю линейную относительно 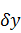
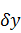 , а
следовательно и относительно α часть):
, а
следовательно и относительно α часть):
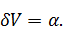
Вычисляем
значение данных функций при различных α:
Таблица
1. Значения функций в точках
|
α
|
-1
|
-0,6
|
-0,3
|
-0,1
|
-0,05
|
-0,01
|
-0,005
|
-0,001
|
|
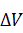
|
-0,8
|
-0,528
|
-0,282
|
-0,098
|
-0,0495
|
-0,0099
|
-0,005
|
-0,001
|
|
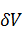
|
-1
|
-0,6
|
-0,3
|
-0,1
|
-0,05
|
-0,01
|
-0,001
|
|
α
|
0,001
|
0,005
|
0,01
|
0,05
|
0,1
|
0,3
|
0,6
|
1
|
|
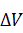
|
0,001
|
0,005
|
0,01002
|
0,0505
|
0,102
|
0,318
|
0,672
|
1,2
|
|
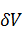
|
0,001
|
0,005
|
0,01
|
0,05
|
0,1
|
0,3
|
0,6
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Рисунок 1. График приращения и вариации функционала
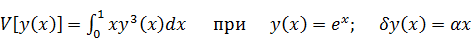
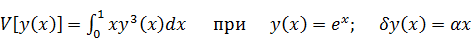 .
.
Вычислем
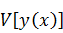
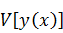 :
:
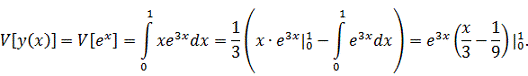
Вычислем
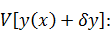
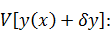

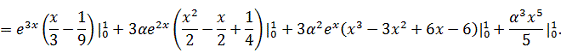
Вычислем
приращение функционала:
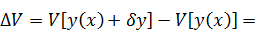
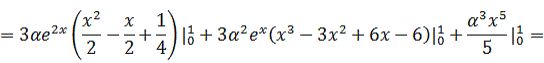
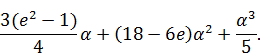
Находим
вариацию функционала (т.е. выделяю линейную относительно 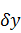
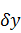 , а
следовательно и относительно α часть):
, а
следовательно и относительно α часть):
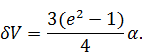
Вычисляем
значение данных функций при различных α:
Таблица
2. Значения функций в точках
|
α
|
-1
|
-0,6
|
-0,3
|
-0,1
|
-0,05
|
-0,01
|
-0,005
|
-0,001
|
|
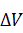
|
-3,3
|
-2,309
|
-1,291
|
-0,462
|
-0,235
|
-0,048
|
-0,024
|
-0,005
|
|
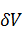
|
-4,8
|
-2,875
|
-1,437
|
-0,479
|
-0,239
|
-0,048
|
-0,024
|
|
α
|
0,001
|
0,005
|
0,01
|
0,05
|
0,1
|
0,3
|
0,6
|
1
|
|
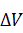
|
0,005
|
0,024
|
0,048
|
0,244
|
0,496
|
1,595
|
3,527
|
6,7
|
|
|
0,005
|
0,024
|
0,048
|
0,24
|
0,479
|
1,437
|
2,875
|
4,8
|
|
|
|
|
|
|
|
|
|
|
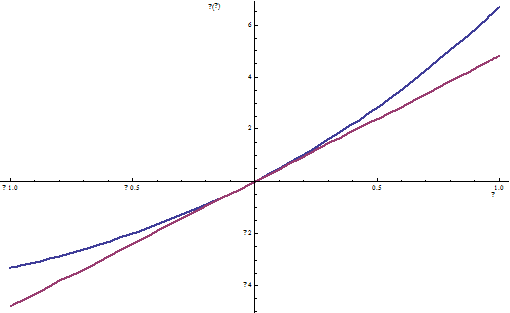
Рисунок 2. График приращения и вариации функционала
Из полученных данных следует, что при малых α,
а следовательно, при
малых приращениях аргумента функционала (подробнее - см. вывод), приращение функционала можно заменить
вариацией с незначительной погрешностью.
Задание № 4
При помощи теоремы, описанной в теоретической части нашли вариации
заданных функционалов.
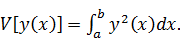
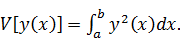
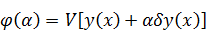
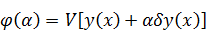 :
:
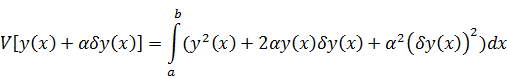
Здесь
и в дальнейшем предполагаем, что функция 
 является
непрерывной в области определения и имеет непрерывную первую производную по α. Это необходимое условие внесения операции
дифференцирования под знак интеграла.
является
непрерывной в области определения и имеет непрерывную первую производную по α. Это необходимое условие внесения операции
дифференцирования под знак интеграла.
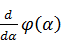
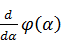 :
:
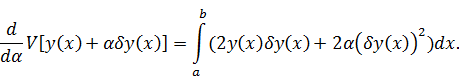
Положив
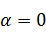
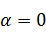 ,
записываем вариацию функционала:
,
записываем вариацию функционала:
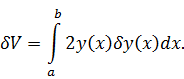
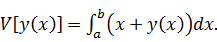
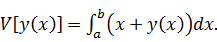
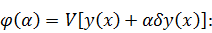
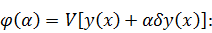
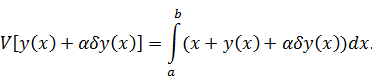
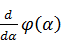
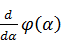 :
:
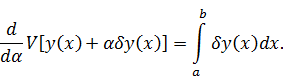
Итак,
вариация функционала имеет вид:
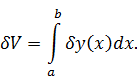
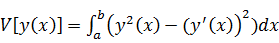
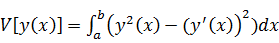
Вычисляем
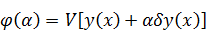
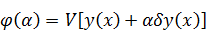 :
:
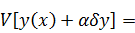
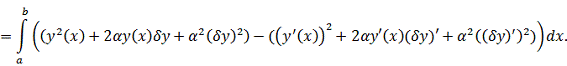
Вычисляем
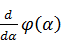
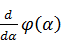 :
:
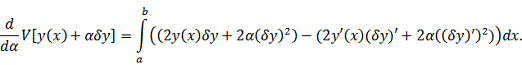
Положив
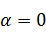
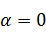 записываем
вариацию функционала:
записываем
вариацию функционала:
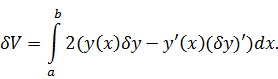
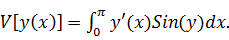
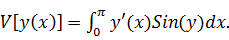
Вычисляем
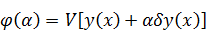
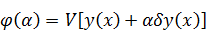 :
:
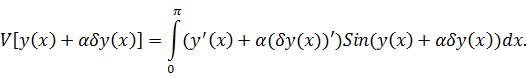
Вычисляем
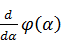
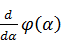 :
:
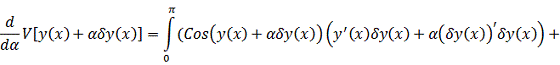
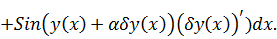
Положив
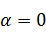
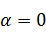 записываем
вариацию функционала:
записываем
вариацию функционала:
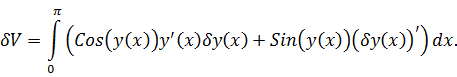
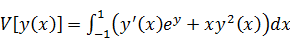
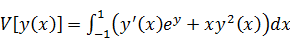 .
.
Вычисляем
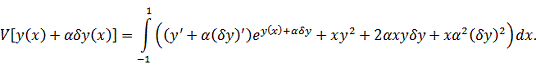
Вычисляем
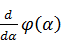
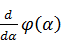 :
:
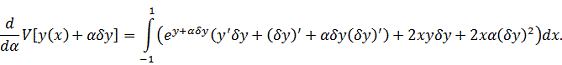
Положив
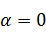
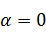 записываем
вариацию функционала:
записываем
вариацию функционала:
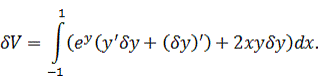
Вывод
В
ходе данной работы были изучены и проверены на практике основные постулаты
вариационного исчисления, а также закреплены навыки работы с программным
пакетом Wolfram Mathematica, то есть, цели работы
были достигнуты. Более конкретные выводы приведены ниже:
1. Как мы убедились функционал - действие не всегда имеет приращение.
Например в случае, если на заданном пространстве интеграл функционала
расходится. Однако это не означает, что при этом он не имеет вариации.
2. Можно доказать, и мы убедились на частных случаях, что функционал
- действие является дифференцируемым в C1([a, b]) при общем виде
лагранжиана, то есть, имеет вариацию.
3. При достаточно малых приращениях аргумента функционала (в нашем
случае при приращении аргумента в 1% и менее) его нелинейное приращение может
быть с достаточной степенью точности (до 4 знака после запятой) заменено
линейной вариацией. Этот факт может быть использован при выведении
теоретических закономерностей и при практических вычислениях.
4. Взяв во внимание результаты вычисления вариаций функционалов 4 и
5 четвёртого задания, можно заметить, что функционал, линейную часть приращения
которого выделить нельзя, всё равно может иметь вариацию. Иными словами, как
написано в методическом пособии, «второе определение [вариации] является более
широким».
. Все данные примеры также были посчитаны в пакете Mathematica, их с подробными комментариями можно
увидеть в приложении к данной работе. Сразу замечу, что все результаты
полностью повторили полученные в данной работе. Для большей наглядности помимо
вариаций функционалов четвёртого задания были посчитаны также их приращения.