Задачи и алгоритмы дискретной математики

КУРСОВАЯ РАБОТА

Задачи и алгоритмы дискретной математики

Введение

Актуальность данной работы заключается в необходимости для любого программиста знаний в области дискретной математики и различных ее алгоритмов, для использования при реализации разрабатываемых программных продуктов и для решения поставленных задач.

Изучение представленных алгоритмов в теории, а так же их реализация на языке программирования высокого уровня позволяют судить об эффективности данных алгоритмов и дают важный опыт.

алгоритм программный дискретный математика

1. Потоки в сетях: алгоритм Форда-Фалкерсона

.1      Формулировка задания

­    изучить теоретические аспекты вопроса построения алгоритма Форда-Фалкерсона;

­    ручная реализация решения задачи нахождения максимального потока в транспортной сети;

­    по средствам выбранного мною языка программирования C# осуществить программную реализацию алгоритма Форда-Фалкерсона.

.2      Изучение алгоритма

Так как алгоритм Форда-Фалкерсона решает задачу нахождения максимального потока в транспортной сети, следует ввести несколько понятий.

Транспортная сеть - это ориентированный граф, ребра которого имеют определенную не отрицательную пропускную способность и поток. Выделяют две такие вершины s (исток) и t (сток), что любые другие вершины находятся на пути из s в t.

Целочисленная транспортная сеть - транспортная сеть, все пропускные способности ребер которой - целые числа.

Остаточная сеть - это сеть, состоящая из тех ребер (называемых также остаточными) исходной сети, поток по которым можно увеличить. Заметим, что остаточное ребро не обязано быть ребром исходной сети. Такие ребра образуются, когда имеется поток в обратном направлении - ведь такие потоки можно уменьшить.

Идея алгоритма Форда-Фалкерсона заключается в том, чтобы выбрать произвольный путь от источника (s) к стоку (t), найти на этом пути минимальное значение остаточных пропускных способностей и увеличиваем поток на каждом ребре этого пути на найденное значение. Такие действия проделываются для всех возможных путей.

Алгоритм Фода-Фалкерсона способен отыскать максимальный поток, не зависимо от того, какой метод выбран для нахождения аугументальных путей, а так же независимо от того, какой путь мы найдем, он всегда оканчивается определением сечения, поток которого равен пропускной способности, а значит, равен величине потока сети, который является максимальным потоком.

Пошаговое описание алгоритма:

.        Обнуляем все потоки. Остаточная сеть изначально совпадает с исходной сетью;

.        В остаточной сети находим любой путь из источника в сток. Если такого пути нет, останавливаемся;

.        Пускаем через найденный путь (он называется увеличивающим путём или увеличивающей цепью) максимально возможный поток;

.        На найденном пути в остаточной сети ищем ребро с минимальной пропускной способностью C_min;

.        Для каждого ребра на найденном пути увеличиваем поток на C_min, а в противоположном ему - уменьшаем на C_min;

.        Модифицируем остаточную сеть. Для всех рёбер на найденном пути, а также для противоположных им рёбер, вычисляем новую пропускную способность. Если она стала ненулевой, добавляем ребро к остаточной сети, а если обнулилась, стираем его;

.        Возвращаемся на шаг 2.

Для поиска пути будем использовать метод «поиска в глубину» (или DFS, от англ. Depth-first search). Для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них.

Пусть задан граф G = (V, E), где V - множество вершин графа, E - множество ребер графа. Предположим, что в начальный момент времени все вершины графа окрашены в белый цвет. Выполним следующие действия:

1.   Из множества всех белых вершин выберем любую вершину, обозначим её V₁.

2.      Выполняем для неё процедуру DFS(V₁).

.        Повторяем шаги 1-3 до тех пор, пока множество белых вершин не пусто.

Процедура DFS (параметр - вершина )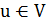

.     Перекрашиваем вершину u в черный цвет.

2.      Для всякой вершины w, смежной с вершиной u и окрашенной в белый цвет, выполняем процедуру DFS(w).

Для наглядности рассмотрим пример транспортной сети, и поиск в ней максимального потока.

Исходные данные

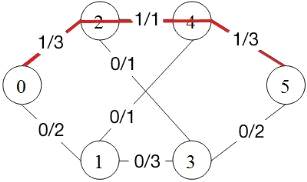
.        Проложим случайный путь и увеличим все потоки на 1 - максимально возможное, т.к. емкость 2-4 равна 1.

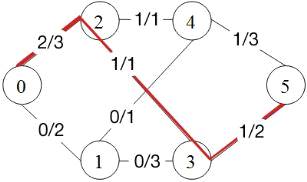
2.      Проложим следующий путь

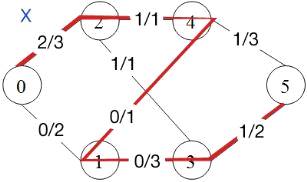
3.      Проложим следующий путь. По этому пути поток не может следовать, т.к. 4-1 является «обратным» путем, и мы не можем сделать его меньше 0.

4.      Следующий путь

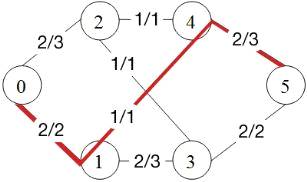
.        Следующий путь

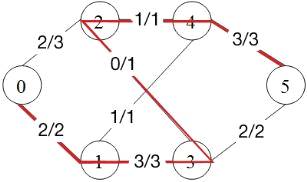
6.      Следующий путь

Больше аугументальных путей не осталось. Максимальный поток данной транспортной сети равен 7.

1.3    Реализация алгоритма программным методом

Исходными данными в программной реализации будет матрица смежности. Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) - это квадратная матрица A размера n, в которой значение элемента a_ij равно числу рёбер из i-й вершины графа в j-ю вершину.

В первой строке будет указано кол-во вершин нашего графа, например, 6.

10 5 0 0 8 0

0 0 5 3 0 4

0 0 4 5 10 0

0 0 0 4 0 9

0 0 0 0 5 6

0 0 0 0 0 0

Описание алгоритма работы программы:

.        Подключаются необходимые библиотеки и объявляются переменные

.        Считываются данные из текстового файла, который должен находиться в той же директории, что и исполняемый файл и называться data.txt

.        Заполняется матрица пропускных способностей из файла

.        Затем вызывается ф-ция max_flow (0, n-1) - это значит обход от 0, до (кол-во вершин - 1)

.        В max_flow объявляется ряд переменных, обнуляется значение «maxflow» - максимальный поток.

.        Создаем матрицу с нулевыми пропускными способностями

.        Осуществляем обход в глубину, причем проходим зануленную матрицу

.        Затем находится минимальный поток в сети и на его значение увеличиваются пропускные способности выбранного пути.

.        Цикл выполняется n раз.

.        Вывод результатов

Работа программы показана на рисунке 1.

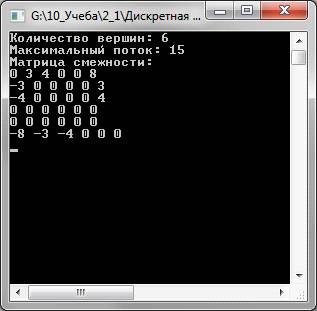
Рисунок 1 - результат работы программы.

2. Минимальные остовные деревья: алгоритм Борувки

2.1 Формулировка задания

Изучить задачу «минимального остовного дерева в графе» алгоритмом Борввки и решить ее ручным, а так же программными методами.

2.2 Изучение задачи

Пусть G (V; E) связный неориентированный, тогда A - промежуточный остовный лес для графа V. На первом шаге A состоит из всех вершин G и пустого множества ребер. В начале очередной фазы алгоритма Борувки, для каждой компоненты связности промежуточного остовного леса выбирается «лидер» или «корень» - вершина, сопоставляемая каждой компоненте. Сделать это можно с помощью обхода A в глубину: вершина, с которой начинается обход очередной компоненты, и будет ее лидером.

Безопасным ребром E относительно некоторой компоненты связности K из A назовем ребро с минимальным весом, ровно один конец которого лежит в K.

После того, как лидеры выбраны, для каждой компоненты связности находится безопасное для нее ребро методом полного перебора. Как только все такие ребра отобраны, они добавляются к A. Процесс продолжается до тех пор, пока в A присутствует больше одной компоненты связности.

Схема работы алгоритма представлена на рисунках 2-6.

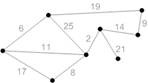
Рисунок 2. Начальная фаза. Минимальный покрывающий лес состоит из всех вершин графа и пустого множества ребер

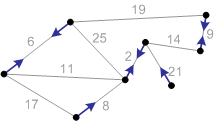
Рисунок 3. Для каждой компоненты связности (для каждой вершины) находим безопасные ребра. Они отмечены стрелками от компоненты вдоль безопасного ребра

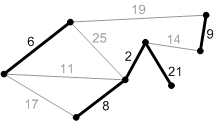
Рисунок 4. Добавляем безопасные ребра к минимальному остовному лесу

Рисунок 5. Находим безопасные ребра для каждой компоненты связности

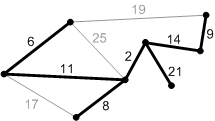
Рисунок 6. Добавляем найденные ребра. Минимальное остовное дерево построено

2.3 Программная реализация алгоритма

A ← (V, 0)(пока) в A больше одной компоненты связности

do CHOOSE-LEADERS(A)SAFE-EDGES(G)

foreach (для каждого) лидера v'

добавить safe(v') в AA

Вот простой возможный вид процедуры поиска безопасных ребер:

FIND-SAFE-EDGES(G)(для каждого) лидера v'(v') ← ∞

foreach (для каждого) ребра (u, v) ∈ E

u' ← leader(u)' ← leader(v)u' ≠ v' thenw (u, v) < w (safe(u')) then(u') ← (u, v)w (u, v) < w (safe(v')) then

safe(v') ← (u, v)

Заключение

Итогом выполнения курсовой работы по дисциплине «Дискретная математика» на тему «Алгоритм Форда-Фалкерсона» является разработка программы, реализующей заданный алгоритм.

Список используемых источников

1.   Седжвик Р. Алгоритмы на C++. - Пер. с англ. - М.: Вильямс, 2011. - 1056 с.

2.      Скиена С. Алгоритмы. Руководство по разработке. - 2-е изд.: пер. с англ. - СПб.: БХВ-Петербург, 2011. - 720 с.

.        Кристофидес Н. Теория графов. Алгоритмический подход. - Пер. с англ. - М.: Мир, 1978. - 432 с.

.        Окулов С.М. Дискретная математика. Теория и практика решения задач по информатике: учебное пособие. - М.: БИНОМ. Лаборатория знаний, 2008. - 422 с.

.        Акулич И.Л. C#. Программирование на языке высокого уровня: Учебник для вузов. - 1-е изд. - Санкт-Петербург.: Питер, 2010. - 423 с.

.        Подбельский В.В. Язык С#. Базовый курс. - 2- е изд., доп. - М.: Информ-Студио, 2011. - 384 с.

.        Мурлин А.Г., Мурлина В.А., Янаева М.В. Программирование с использование компонентов Windows Forms. Учебное пособие. Издательский дом ЮГ, 126 с.

.        Официальная документация по Visual C# и Visual Studio [Электронный ресурс] - Режим доступа: URL: - http://msdn.microsoft.com/ru-ru/library/kx37x362 (v=vs.90).aspx