Идеальные системы
Контрольная работа
Идеальные системы
Содержание
1. Термодинамические функции классического идеального газа
. Распределение атомов идеального газа в пространстве
квантовых состояний. Распределения Ферми и Бозе
. Электронный газ в металлах
. Сверхплотный ферми-газ и гравитационное равновесие звезд
. Вырожденный Бозе-газ. Экспериментальное наблюдение
Бозе-Эйнштейновской конденсации
. Черное излучение
. Связь квантовых и классических распределений Гиббса
. Двухатомный газ с молекулами из различных атомов. Вращение
молекул
. Двухатомный газ. Колебания атомов
. Флуктуации. Распределение Гаусса
.Флуктуации термодинамических величин
. Флуктуации в квазизамкнутой системе
. Флуктуации идеальных полимерных цепей
. Флуктуации изгиба длинных молекул
. Высокоэластичность полимеров с точки зрения статистической
физики
Литература
. Термодинамические функции классического идеального газа
Из опыта известно, что любой разряженный газ ведет себя как идеальный.
Взаимодействие (в этом приближении) не учитывается. Член с потенциальной
энергией в функции Гамильтона учитывает действие внешних полей (например,
тяжести).
Пусть газ заключен в сосуд объема V со стенками, непроницаемыми для атомов. Наличие стенок можно
учесть в функции Гамильтона путем введения потенциальной энергии следующего
вида:
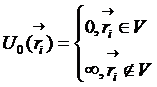 .
.
Если
такую потенциальную энергию подставить в канонического распределение Гиббса, то
это приведет к тому, что если хотя бы один атом находился вне объема, то
функция распределения равна нулю. Из термодинамики следует, что для нахождения
уравнения состояния надо знать свободную энергию (а значит  ). Многомерный интеграл по переменным всех частиц
сводится к произведению интегралов, поскольку все N частиц равноправны:
). Многомерный интеграл по переменным всех частиц
сводится к произведению интегралов, поскольку все N частиц равноправны:
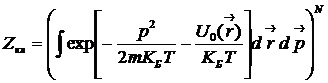 ,
, 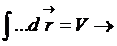
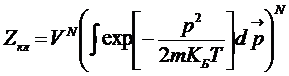
(указанный
интеграл - интеграл Пуассона),
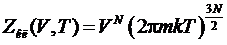 ,
,
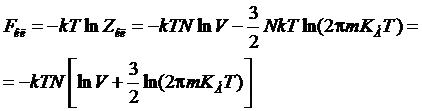
свободная
энергия классического газа.
Из
термодинамики: 
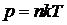 - это уравнение состояния идеального газа, которое
совпадает с экспериментальным.
- это уравнение состояния идеального газа, которое
совпадает с экспериментальным.
Энтропия:
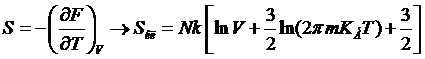 .
.
Однако
результаты для 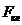 ,
, 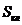 не
являются удовлетворительными т.к. в термодинамическом пределе (
не
являются удовлетворительными т.к. в термодинамическом пределе (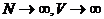 , но
, но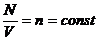 ) они
должны быть
) они
должны быть 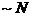 , поскольку эти величины аддитивные. Но у нас
получается, что
, поскольку эти величины аддитивные. Но у нас
получается, что 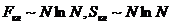 . Одним из следствий такого противоречия является
Парадокс Гиббса.
. Одним из следствий такого противоречия является
Парадокс Гиббса.
Парадокс
Гиббса
Пусть
имеется сосуд, разделенный перегородкой на две равные части, каждые объема V.
Число частиц в каждой части N. Обе половины наполнены одним и тем же газом. Если
убрать перегородку, то физическое состояние системы останется неизменным.
Естественно ожидать, что энтропия системы не изменится, поскольку нет никаких необратимых
процессов в такой системе. Однако, расчет энтропии по классической формуле
противоречит этому предположению.
При
наличии перегородки: 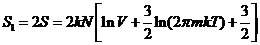 , где
, где  - вся,
- вся, 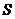 - одной половины (здесь использовано свойство
аддитивности для энтропии).
- одной половины (здесь использовано свойство
аддитивности для энтропии).
После
снятия перегородки:
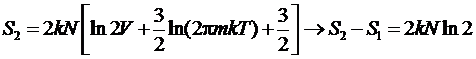 .
.
Положительная
разность энтропий означает, что при снятии перегородки энтропия системы
возрастает! Для разных газов будет такое же изменение энтропии.
Для
решения парадокса Гиббс предположил, что константа, с точностью до которой
определяется энтропия  зависит от N, причем так, что изменение
энтропии после снятия перегородки будет равно нулю. Однако очевидно, что такое
решение парадокса является искусственным, поскольку ниоткуда не следует, что
константа должна иметь именно такой вид. Строгое решение парадокса оказалось
возможным только в рамках квантовой статистической физики.
зависит от N, причем так, что изменение
энтропии после снятия перегородки будет равно нулю. Однако очевидно, что такое
решение парадокса является искусственным, поскольку ниоткуда не следует, что
константа должна иметь именно такой вид. Строгое решение парадокса оказалось
возможным только в рамках квантовой статистической физики.
2. Распределение атомов идеального газа в пространстве квантовых
состояний. Распределения Ферми и Бозе
Рассмотрим
теперь идеальный квантовый газ, в котором нет взаимодействия между частицами.
Рассмотрим пространство квантовых чисел K. Обозначим
через 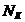 число атомов, квантовые числа которых
число атомов, квантовые числа которых 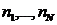 равны K, то есть:
равны K, то есть:
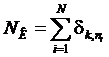 ,
, 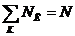
где
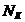 - случайная функция в пространстве квантовых чисел.
Для системы с заданным числом частиц, находящейся в термостате, распределение
- случайная функция в пространстве квантовых чисел.
Для системы с заданным числом частиц, находящейся в термостате, распределение 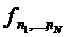 определяется квантовым каноническим распределением
Гиббса. Перепишем его в другом виде (используя
определяется квантовым каноническим распределением
Гиббса. Перепишем его в другом виде (используя 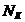 ). Для
идеального газа энергия
). Для
идеального газа энергия 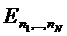 равна сумме энергий отдельных атомов:
равна сумме энергий отдельных атомов:
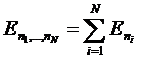 .
.
С
другой стороны можно записать:
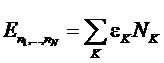 .
.
Переходя
к потенциалу (большой термодинамический потенциал)  запишем распределение Гиббса в виде:
запишем распределение Гиббса в виде:
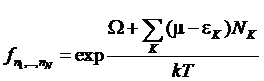 ,
, 
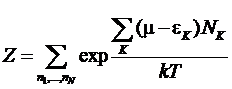 ;
; 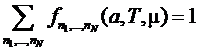 .
.
представим
в виде:
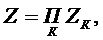
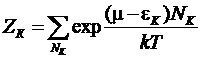 (*)
(*)
и
перейдем к суммированию по Nk.
Соответственно:
 ,
,  .
.
Тогда
можно ввести функцию распределения по числам частиц на уровне k:
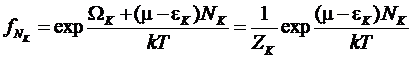 ,
,
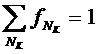 .
.
С
помощью этой функции получим искомое выражение для 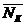 - среднего числа частиц в квантовом состоянии К:
- среднего числа частиц в квантовом состоянии К:
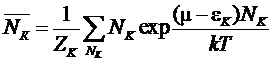 .
.
Используя
определение 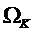 , можно записать:
, можно записать:
 . (**)
. (**)
 - это
условие позволяет установить при заданных
- это
условие позволяет установить при заданных  связь
связь  с
с 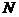 :
:
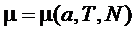 .
.
Распределения
Бозе и Ферми
Системы
частиц с целым спином называются системами Бозе (статистика Бозе). Для таких
систем числа заполнения 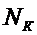 состояний К могут быть произвольными:
состояний К могут быть произвольными:
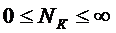 .
.
При
этом условии сумма по 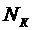 в выражении для
в выражении для  (*)
представляет из себя геометрическую прогрессию, тогда:
(*)
представляет из себя геометрическую прогрессию, тогда:
 .
.
Дифференцируем
по 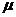 (**) и получим
(**) и получим
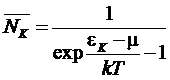 -
распределение Бозе (Бозе - Эйнштейна).
-
распределение Бозе (Бозе - Эйнштейна).
Такое
распределение впервые было предложено Шатьендранатом Бозе для фотонов, Эйнштейн
же обобщил его на произвольные системы частиц с целым спином.
Частицы
с полуцелым спином удовлетворяют принципу Паули, согласно которому величина 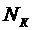 может принимать лишь два значения:
может принимать лишь два значения: 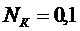 .
.
В
этом случае (*) примет вид
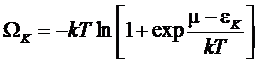 ,
,
тогда
из (**) получим
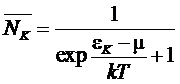 -
распределение Ферми (Ферми - Дирака).
-
распределение Ферми (Ферми - Дирака).
В
случае, когда 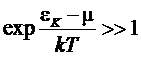 формулы Бозе и Ферми сводятся к одной
формулы Бозе и Ферми сводятся к одной
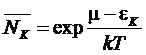 .
.
Это
ни что иное, как распределение Больцмана.
Можно
показать, что это неравенство соответствует другому:
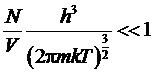 .
.
При
выполнении этого неравенства газ называется невырожденным. В этом случае можно
использовать распределения Максвелла и Больцмана. При выполнении обратного
неравенства газ называется вырожденным и для его описания используются
распределения Ферми и Бозе.
3. Электронный газ в металлах
Валентные электроны в большинстве металлов свободно перемещаются. Они
представляют собой почти идеальный квантовый Ферми-газ. Несмотря на их
заряженность, электростатическое взаимодействие между электронами и ионами в
значительной степени компенсируется. В результате кинетическая энергия
электронов оказывается значительно больше потенциальной. Уровни энергии
электронов в металле могут быть получены в результате решения стационарного
уравнения Шредингера.
Рассмотрим электронный газ при абсолютном нуле Т = 0 (полностью
вырожденный Ферми-газ). Электроны будут распределены в таком газе таким
образом, чтобы полная энергия газа имела минимально возможное значение. Так как
(согласно принципу Паули) в каждом квантовом состоянии может находится не более
одного электрона, то электроны заполнят все состояния с энергией от наименьшей
(равной нулю) до некоторой наибольшей, величина которой определяется числом
электронов в газе. С учетом двукратного спинового вырождения уровней, число квантовых
состояний электронов, движущегося в объеме V с абсолютной величиной импульса в интервале {p, p+dp} (в сферических
координатах) равно
 . (*)
. (*)
В
числителе стоит объем в пространстве импульсов и координат, в знаменателе -
элементарный объем;
Электроны
заполняют все состояния с импульсами от 0 до граничного значения р = рF. Об
этом значении говорят как о радиусе ферми-сферы в импульсном пространстве.
Полное
число электронов в этих состояниях:
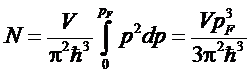 .
.
Откуда
для граничного импульса имеем
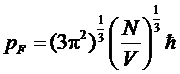 .
.
И
для граничной энергии (для большинства систем энергия рассчитывается по
классической формуле, однако есть и исключения - для очень плотных систем
энергия должна рассчитывается по релятивистской формуле):
 .
.
Эта
энергия называется энергией Ферми. Это энергия имеет простой термодинамический
смысл. Функция распределения (число заполнения) Ферми по квантовым состояниям
(с определенными значениями импульса p и проекцией спина)

Проанализируем
полученное выражение при Т®0. Видно, что при ε < µ это выражение стремится к единице, а при ε > µ стремится к нулю. Тогда можно изобразить график
зависимости среднего числа электронов на уровне от энергии электрона:

Сравнивая
полученную зависимость с распределением электронов при Т = 0, можно видеть, что
химический потенциал электронного газа при Т = 0 совпадает с граничной энергией
электронов (энергией Ферми): µ = εF. Полная
энергия газа получается умножением числа состояний (*) на р2/2m и
интегрированием по всем импульсам
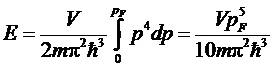
или,
подставив выражения для pF , получим
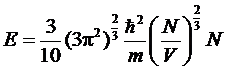 . (**)
. (**)
Найдем
уравнение состояние электронного газа (любого Ферми- газа) при температуре T
> 0.
Число
частиц в элементе фазового пространства dpxdpydpzdV
получится умножением величины
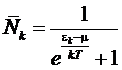 на
на  ,
,
откуда
получим
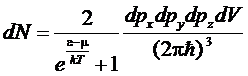
Интегрируя
по dV, получим распределение по компонентам импульса
частиц, а переходя к сферическим координатам в пространстве импульсов, найдем
распределение по абсолютной величине импульса
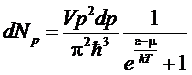 .
.
Удобно
перейти к одной переменной - энергии
 .
.
Эта
формула заменяет классическое распределение Максвелла для случая электронного
газа. Интегрируя по de, получим полное число частиц в газе:
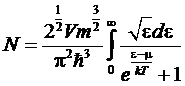 .
.
Эта
формула определяет в неявном виде (поскольку интеграл не берется) химический
потенциал газа как функцию от температуры Т и концентрации N/V.
Формулу
для большого термодинамического потенциала в случае электронного газа можно
представить в виде:
 .
.
Совершая
такой же переход от суммирования к интегрированию, который был выполнен при
расчете числа электронных состояний, получим выражение для потенциала
 .
.
Интегрируя
по частям, находим
 .
.
Это
выражение совпадает с точностью до множителя -2/3 с полной энергией газа
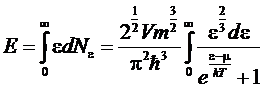 .
.
Имея
также в виду, что:
Ω=F - µN=U - TS + PV - PV- µN = G - µN -PV =
- PV,
Получим
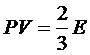 .
.
Это
соотношение должно выполняться и в предельном случае больцмановского газа.
Действительно, подставляя больцмановское значение  , получим
, получим  , то есть
уравнение Менделеева - Клапейрона.
, то есть
уравнение Менделеева - Клапейрона.
Подставим
полученное соотношение в выражение для полной энергии (**), находим уравнение
состояния электронного газа (при Т= 0К):
 .
.
Таким
образом, давление Ферми-газа при абсолютном нуле температуры пропорционально
его концентрации в степени 5/3. Полученная формула применима приближенно также
и при температурах, достаточно близких (при данной концентрации газа) к
абсолютному нулю. Условие ее применимости (условия «сильного вырождения» газа)
требует, очевидно, малости kТ по сравнению с граничной энергией eF:
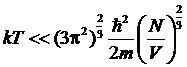 .
.
Температуру
ТF = eF/k называют температурой вырождения (температурой
Ферми). Оказывается, что для большинства металлов эта температура составляет
приблизительно 104 К. Отсюда можно сделать вывод, что в металлах электронный
газ всегда вырожден.
При
температуре, большей 0К график функции распределения Ферми будет иметь
следующий вид:

Примером
двумерного Ферми-газа является недавно открытый графен.
Рассмотрим
теперь теплоемкость Ферми-газа. В случае, когда температура газа много меньше
температуры Ферми, все термодинамические величины можно разложить в ряд:
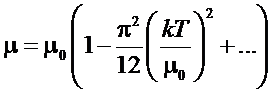 ,
,
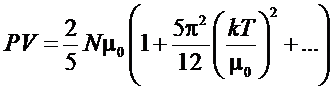 ,
,
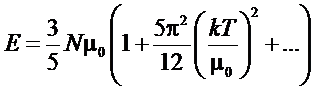 .
.
Зная
энергию, можно вычислить теплоемкость:
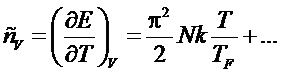 .
.
Из
этого соотношения видно, что теплоемкость электронного газа в металлах при
комнатной температуре очень мала по сравнению с теплоемкостью решетки (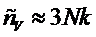 - закон Дюлонга-Пти).
- закон Дюлонга-Пти).
.
Сверхплотный ферми-газ и гравитационное равновесие звезд
Эволюция звезд. Белые карлики. Фаулер. Принципиальный интерес
представляет исследование свойств вещества при чрезвычайно больших плотностях.
Проследим качественно за изменением этих свойств по мере постепенного
увеличения плотности.
Когда объем, приходящийся на один атом, становится меньше обычных атомных
размеров, атомы теряют свою индивидуальность, так что вещество превращается в
сильно сжатую электронно-ядерную плазму. Если температура вещества не слишком
высока, то электронная компонента этой плазмы представляет собой вырожденный
ферми-газ. Электронный ферми-газ обладает своеобразным свойством: его
идеальность возрастает по мере увеличения плотности. Это происходит потому, что
кинетическая энергия электронов пропорциональна концентрации в степени 2/3, а
кулоновская энергия - лишь 1/3. Поэтому при достаточном сжатии вещества роль
взаимодействия электронов с ядрами (и друг с другом) становится несущественной,
так что можно пользоваться формулами идеального ферми-газа. Можно показать, что
это наступает при выполнении неравенства

где
пе - плотность числа электронов, те - масса электрона, Z- некоторый
средний атомный номер вещества. Отсюда получаем для полной плотности массы
вещества неравенство
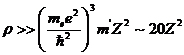 г/см3,
г/см3,
где
m’ - масса, приходящаяся на один электрон. Примем, что
эта масса равна удвоенной массе нуклона. Что касается «ядерного газа», то
благодаря большой массе ядра он еще может быть далек от вырождения, но его
вклад, например, в давление вещества совершенно несуществен по сравнению с
давлением электронного газа.
Таким
образом, термодинамические величины вещества в рассматриваемых условиях
определяются формулами, примененными к электронной компоненте. В частности, для
давления имеем
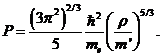
Условие
для плотности дает для давления численное неравенство 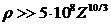 атм.
атм.
В
написанных формулах электронный газ предполагается нерелятивистским. Это
требует малости граничного импульса Ферми ρF по сравнению с тс, что приводит к численным
неравенствам

Когда
плотность и давление газа становятся сравнимыми с указанными значениями,
электронный газ делается релятивистским, а при выполнении обратных неравенств -
ультрарелятивистским. В последнем случае уравнение состояния вещества
определяется формулой
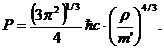
Дальнейшее
повышение плотности приводит к состояниям, в которых термодинамически выгодными
оказываются ядерные реакции, заключающиеся в захвате электронов ядрами (с
одновременным испусканием нейтрино). В результате такой реакции уменьшается
заряд ядра.
При
еще больших плотностях и давлениях будет происходить дальнейший захват
электронов ядрами, сопровождающийся дальнейшим уменьшением заряда последних.
Здесь начинается область плотностей, в которой вещество можно рассматривать в
основном как вырожденный нейтронный ферми-газ с небольшой примесью электронов и
различных ядер, концентрации которых определяются условиями равновесия
соответствующих ядерных реакций. Уравнение состояния вещества в этой области
есть
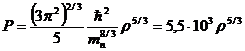 атм,
атм,
где
mn - масса нейтрона.
Наконец,
при плотностях 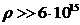 г/см3 вырожденный нейтронный газ станет
ультрарелятивистским, а уравнение состояния будет определяться формулой
г/см3 вырожденный нейтронный газ станет
ультрарелятивистским, а уравнение состояния будет определяться формулой
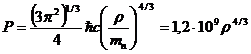 атм.
атм.
Рассмотрим
тело очень большой массы, части которого удерживаются вместе силами
гравитационного притяжения. Реальные тела большой массы известны нам в виде
звезд, непрерывно излучающих энергию и отнюдь не находящихся в состоянии
теплового равновесия. Представляет, однако, принципиальный интерес рассмотрение
равновесного тела большой массы. При этом мы будем пренебрегать влиянием
температуры на уравнение состояния, т.е. будем рассматривать тело находящимся
при абсолютном нуле («холодное» тело). Это можно сделать потому, что для сильно
вырожденного ферми-газа температуру можно считать равной нулю.
Будем
далее предполагать тело невращающимся; тогда в равновесии оно будет иметь
сферическую форму, и распределение плотности в нем будет центрально-симметричным.
Равновесное
распределение плотности (и других термодинамических величин) в теле будет
определяться следующими уравнениями. Ньютоновский гравитационный потенциал φ удовлетворяет дифференциальному уравнению

где
ρ - плотность вещества, G - ньютоновская
гравитационная постоянная; в центрально-симметричном случае имеем
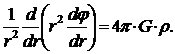
В
гравитационном поле потенциальная энергия частицы с массой т' есть т'φ, так что имеем
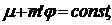
где
т' - масса частицы тела, а у химического потенциала вещества в отсутствие поля
для краткости опущен индекс нуль. Выразив φ через µ и подставив в уравнение для потенциала, мы
можем написать последнее в виде
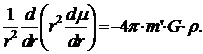
При
увеличении массы гравитирующего тела возрастает, естественно, и его средняя
плотность (это обстоятельство будет подтверждено следующими ниже вычислениями).
Поэтому при достаточно большой полной массе М тела можно рассматривать вещество
тела как вырожденный электронный ферми-газ - сначала нерелятивистский, а затем,
при еще больших массах, релятивистский.
Химический
потенциал (энергия Ферми) нерелятивистского вырожденного электронного газа
связан с плотностью тела ρ равенством
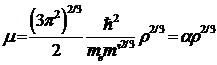 .
.
Выразив
отсюда ρ через µ, получим следующее уравнение:
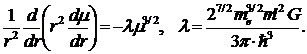 (*)
(*)
Обладающие
физическим смыслом решения этого уравнения не должны иметь особенности в начале
координат: µ -> const при r -> 0. Это требование автоматически приводит к
условию для первой производной
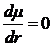 при r =
0.
при r =
0.
Ряд
существенных результатов можно получить уже путем применения к уравнению (*)
простых соображений размерности. Решения уравнения (*) содержат лишь два
постоянных параметра - постоянную λ и, например, радиус тела R, заданием
которого однозначно определяется выбор решения. Из этих двух величин можно
образовать всего одну величину с размерностью длины - самый радиус R, и
одну величину с размерностью энергии: 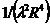 (постоянная
λ имеет размерность м-2 • Дж-1/2). Поэтому ясно, что
функция µ(r) должна иметь вид
(постоянная
λ имеет размерность м-2 • Дж-1/2). Поэтому ясно, что
функция µ(r) должна иметь вид
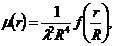
где
f- некоторая функция только от безразмерного отношения r/R.
Поскольку плотность ρ
пропорциональна µ3/2, то распределение плотности должно иметь вид
 .
.
Таким
образом, при изменении размеров сферы распределение плотности в ней меняется
подобным образом, причем в подобных точках плотность меняется обратно
пропорционально R6. В частности, средняя плотность сферы будет просто
обратно пропорциональна R6:
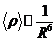 .
.
Полная
же масса М тела, следовательно, обратно пропорциональна кубу радиуса:
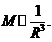
Эти
два соотношения можно написать также в виде
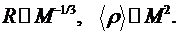
Таким
образом, размеры равновесной сферы обратно пропорциональны кубическому корню из
ее полной массы, а средняя плотность пропорциональна квадрату массы. Последнее
обстоятельство подтверждает сделанное выше предположение о том, что плотность
гравитирующего тела растет с увеличением его массы.
Тот
факт, что гравитирующая сфера из нерелятивистского вырожденного ферми-газа
может находиться в равновесии при любом значении полной массы М, можно было
усмотреть заранее из следующих качественных соображений. Полная кинетическая
энергия частиц такого газа пропорциональна N(N/V)2/3,
или, что то же самое, М5/3 / R2, а гравитационная энергия газа в целом отрицательна
и пропорциональна M2/R. Сумма двух выражений такого типа может иметь минимум
(как функция от R) при любом М, причем в точке минимума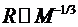 .
.
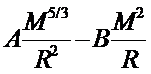 .
.
Для
безразмерной переменной ξ = r / R получим, что функция f(ξ) удовлетворяет уравнению

с
граничными условиями f ‘(0) = 0; f ‘(1) = 0. Это уравнение не
может быть решено в аналитическом виде и должно интегрироваться численно (см,
рис). Наконец, для отношения центральной плотности ρ(0) к средней плотности 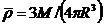 легко
найти
легко
найти

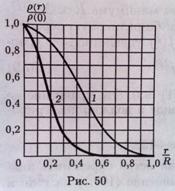
На
рисунке изображен график отношения ρ(r)/ρ(0) как функции r/R.
Перейдем
к исследованию равновесия сферы, состоящей из вырожденного
ультрарелятивистского электронного газа. Полная кинетическая энергия частиц
такого газа пропорциональна N(N/V)1/3, или иначе M 4/3 / R;
гравитационная же энергия пропорциональна -M2/R.Таким
образом, обе эти величины зависят от R одинаковым образом, и их сумма
тоже будет иметь вид const • R-1. Отсюда следует, что тело вообще не сможет
находиться в равновесии: если const > 0, то оно будет стремиться расширяться (до тех
пор, пока газ не станет нерелятивистским); если же const < 0, то
уменьшению полной энергии будет соответствовать стремление R к
нулю, т.е. тело будет неограниченно сжиматься. Лишь в особом случае const
= 0 тело может находиться в равновесии, причем в безразличном равновесии с
произвольными размерами R.
Эти
качественные соображения, разумеется, полностью подтверждаются точным
количественным анализом. Химический потенциал рассматриваемого релятивистского
газа связан с плотностью соотношением
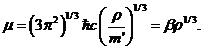
Вместо
уравнения (*) получаем теперь
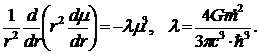
Имея
в виду, что λ обладает теперь размерностью Дж-2 • м-2, находим, что
химический потенциал как функция от r должен иметь вид
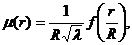
а распределение плотности
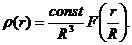
Таким
образом, средняя плотность будет теперь обратно пропорциональна R3, а
полная масса оказывается не зависящей от размеров постоянной:
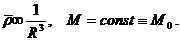
0
есть единственное значение массы, при котором возможно равновесие; при М >
М0 тело будет стремиться неограниченно сжиматься, а при М < М0 оно будет
расширяться.
Для
точного вычисления «критической массы» М0 необходимо произвести численное
интегрирование уравнения
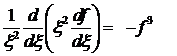 .
.
Положив
m’ = 2mn, получим M0 = 1,45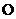 .
.
На
рисунке (кривая 2) дан график ρ(r)/ρ(0) в ультрарелятивистском случае как функции r/R.
Полученные
результаты о зависимости между массой и радиусом равновесного «холодного»
сферического тела можно представить во всей области измерения R в
виде единой кривой, определяющей зависимость М = M(R).
При больших R (и соответственно малых плотностях тела) электронный
газ можно рассматривать как нерелятивистский, и функция M(R)
спадает по закону 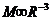 . При достаточно же малых R плотность
настолько велика, что имеет место ультрарелятивистский случай, и функция M(R)
имеет почти постоянное (равное М0) значение (строго говоря, M(R)
-> M0 при R -> 0).
. При достаточно же малых R плотность
настолько велика, что имеет место ультрарелятивистский случай, и функция M(R)
имеет почти постоянное (равное М0) значение (строго говоря, M(R)
-> M0 при R -> 0).
Сделанный
вывод имеет фундаментальное значение для эволюции звезд. Сейчас ученые уверены,
что при достижении звездой определенной массы она превращается в черную дыру.
Сверхмассивные черные дыры находятся в центре практически каждой галактики.
Полученную оценку критической массы звезды можно рассматривать лишь как
приближенную, поскольку точное решение уравнения для гравитационного поля можно
получить лишь в рамках общей теории относительности. Кроме того, после первых
оценок модели нейтронных звезд были существенно уточнены.
Белые
карлики представляют собой компактные звёзды с массами, сравнимыми с массой
Солнца, но с радиусами в ~100 км и, соответственно, светимостями в ~10 000 раз
меньшими солнечной. Плотность белых карликов составляет 108-1012 кг/м³, что почти в миллион раз выше плотности обычных звёзд
главной последовательности.
Высокая
плотность белых карликов оставалась необъяснимой в рамках классической физики и
астрономии и нашла объяснение лишь в рамках квантовой механики
<#"866454.files/image128.gif"> (*)
будет
увеличиваться, т.е. будучи отрицательным, уменьшатся по абсолютной величине.
Он
достигает значения μ
= 0 при температуре, определяемой
соотношением
 ,
,
где
z = ε/kТ - новая переменная.
Входящий
сюда интеграл выражается через ξ - функцию
Римана (табличный). Обозначая искомую температуру через Т0, получим
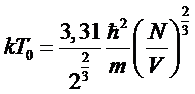 .
.
Заметим,
что по структуре полученная формула напоминает выражение для энергии Ферми, но
поскольку масса бозонов, как правило, значительно больше массы электронов, то
температура T0 будет значительно меньше, чем температура Ферми для
электронного газа.
При
Т < Т0 уравнение (*) не имеет отрицательных решений, между тем как в
статистике Бозе химический потенциал должен быть отрицательным при всех
температурах (в противном случае число заполнения уровня окажется
отрицательным).
Это
кажущееся противоречие связано с тем, что в данных условиях не законен переход
от суммирования к интегрированию, который выполнялся выше для статистики Ферми.
Действительно,
при этом переходе первый член суммы eк = 0 умножается на 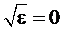 , то есть выпадает из суммы. Между тем при понижении
температуры частицы должны скапливаться именно в этом состоянии с наименьшей
энергией, пока при Т = 0 туда не попадут все они.
, то есть выпадает из суммы. Между тем при понижении
температуры частицы должны скапливаться именно в этом состоянии с наименьшей
энергией, пока при Т = 0 туда не попадут все они.
Математически
это обстоятельство проявляется в том, что в сумме
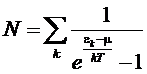
при
переходе к пределу µ®0 сумма всех членов ряда, за исключением первого
стремится к конечному пределу, определяемому интегралом
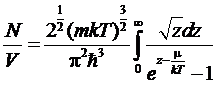 ,
,
а
первый член с εк = 0 стремится к бесконечности. Устремляя µ не к
нулю, а к некоторому малому конечному значению, можно, следовательно, предать
указанному первому члену суммы требуемое конечное значение.
Поэтому
в действительности при Т < T0 дело будет обстоять следующим образом. Частицы с
энергией ε
> 0 будут распределены по функции:

с
µ = 0
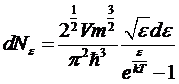 .
.
Полное
число частиц с энергиями ε > 0 будет, следовательно, равно
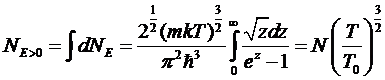 .
.
Остальные
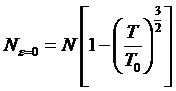
частицы
находятся в низшем состоянии, т.е. имеют энергию e = 0. Это
явление называют конденсацией Бозе-Эйнштейна. Название происходит от аналогии с
конденсацией газа в жидкость, однако здесь имеется в виду конденсация в
импульсном пространстве.
Заметим,
что само это явление было предсказано Эйнштейном, на основе полученного им
ранее распределения для произвольных частиц с целым спином.
Энергия
газа при Т < Т0 определяется, конечно только теми частицами, которые имеют
энергию больше ноля.
Полагая
в
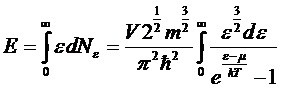
µ=0,
имеем
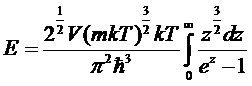 .
.
Этот
интеграл приводится к табличному, тогда получим
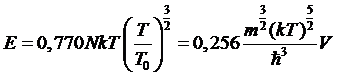 .
.
Отсюда
теплоемкость
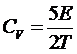 ,
,
То
есть теплоемкость пропорциональна Т3/2. Интегрируя теплоемкость, находим
энтропию
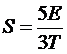 ,
,
и
свободную энергию
=
E-TS = -2/3 E
Последний
результат вполне естественен, так как при µ=0
F= Nµ+Ω=Ω.
Для
давления P = - (∂F/∂V)T
имеем
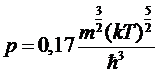 .
.
Мы
видим, что при Т < Т0 давление пропорционально Т5/2 и не зависит вовсе от
объема. Это обстоятельство - естественно следствие того, что частицы,
находящиеся в состоянии с e=0, не обладая импульсом, не
дают никакого вклада в давление. В самой точке Т = Т0 все перечисленные
термодинамические величины непрерывны. Можно, однако, что производная от
теплоемкости по температуре испытывает в этой точке скачок.
Аналогия
с давлением в двухфазной системе для газа Ван-дер-Ваальса.
Удельная
теплоемкость идеального Бозе-газа.
В
каких системах можно наблюдать явление Бозе-конденсации? Во-первых, это должны
быть бозоны с неравным нулю химическим потенциалом. Как будет показано ниже, фотоны,
являясь бозонами, имеют химический потенциал, равный нулю. Поэтому для
излучения такой эффект не имеет места. С другой стороны, это должна быть
идеальная система, в которой взаимодействие между частицами мало (все
полученные нами формулы выведены именно в этом предположении). Последнее
означает, что переход к сверхтекучему состоянию в жидком гелии, происходящий
при T » 2,2 К не может быть
интерпретирован как конденсация Бозе-Эйнштейна, поскольку в жидкости
взаимодействие между атомами велико. И хотя связь между Бозе-конденсацией и
переходом гелия в сверхтекучее состояние существует, этот случай требует
отдельного рассмотрения.
Экспериментальное
наблюдение Бозе-Эйнштейновской конденсации
Шведская
Королевская академия наук присудила Нобелевскую премию 2001 г. по физике
работающим в США ученым Э.Корнеллу, В.Кеттерле и К.Вайману “за
экспериментальное обнаружение конденсации Бозе-Эйнштейна в разреженных газах
щелочных металлов и фундаментальные исследования свойств конденсата”.
С
тех пор как Альберт Эйнштейн в предсказал новое интересное явление, история его
изучения была очень непростой. В 1924 г. Эйнштейн сделал первый весьма
неординарный шаг: перенес статистику, предложенную индийским физиком
Шатьендранатом Бозе для фотонов, на материальные частицы. В следующем году,
анализируя поведение системы таких частиц, Эйнштейн обнаружил, что в ней
возможно явление, которое сейчас получило название конденсации Бозе-Эйнштейна.
Утверждение
Эйнштейна нетривиально по двум причинам. Во-первых, рассматривается газ
невзаимодействующих частиц. Во-вторых, речь идет о конечной температуре, и в
этом случае естественно думать, что все частицы “размазаны” по разным
энергетическим состояниям. Не случайно после опубликования данной работы очень
крупные физики-теоретики высказывали сомнения в ее достоверности. Достаточно
вспомнить Дж. Уленбека, который считал этот результат артефактом, или
П.Эренфеста, близкого друга Эйнштейна, который писал в своем письме последнему,
что предсказанное им явление неявно предполагает наличие взаимодействия между
частицами. В ответном письме Эйнштейн признавал, что это, по-видимому, так, и
он затрудняется это интерпретировать, но не сомневается: конденсация - прямой
результат статистических свойств газа независимых частиц.
Чтобы
понять, почему возникали такие сомнения, надо упомянуть ряд обстоятельств. К
тому моменту еще не существовало двух статистик, которые мы теперь знаем под
именами Бозе-Эйнштейна и Ферми-Дирака, т.е. не было раздельного описания для
частиц с целочисленным спином (первая статистика) и полуцелым спином (вторая).
Не было и осознания решающего факта, что в квантовой механике волновая функция,
соответствующая двум или более идентичным частицам, при перестановке их местами
не должна меняться (статистика Бозе-Эйнштейна) или, наоборот, должна менять
знак (статистика Ферми-Дирака). Именно эта обязательная симметризация -
исключительно нетривиальное обстоятельство - фактически вводит некое
виртуальное взаимодействие между частицами в случае, когда непосредственного,
силового взаимодействия между ними нет. Бозе-эйнштейновская конденсация часто
называется просто бозе-конденсацией, хотя в работе Бозе о конденсации нет ни
единого слова (он рассматривал газ равновесных фотонов, где это явление
отсутствует).
Однако
прямого экспериментального наблюдения непосредственно самой конденсации до 1995
г. не было. Это обстоятельство не случайно: чтобы ее наблюдать, необходимо
иметь газ при фантастически низких температурах. В первых экспериментах
температура была в 10 млрд раз ниже комнатной, а ведь даже при температуре
около 1 К любые вещества становятся твердыми (единственное исключение - гелий,
остающийся жидким). Рассчитывать, что при такой температуре может существовать
газ, просто невероятно. Поэтому речь могла идти только о метастабильном
состоянии, т.е. о том, чтобы искусственно приготовить газ, который “жил” бы
достаточное для эксперимента время. Но тут же возникает и вторая проблема: этот
газ не должен взаимодействовать со стенками сосуда, который его удерживает,
поскольку при таких температурах любое взаимодействие со стенками разрушит
метастабильное состояние.
Итак,
необходимо иметь, с одной стороны, рекордно низкие температуры, а с другой -
систему, в которой газ не имеет контакта со стенками. Последнее препятствие
было преодолено таким образом: роль сосуда играло магнитное поле определенной
конфигурации. В так называемой магнитной ловушке частицы с магнитным моментом
при достаточно низкой температуре испытывают фактически только отражение от
магнитной “стенки”, т.е. никакого реального физического контакта нет, и газ
существует в системе с абсолютно отражающими стенками. Получить же столь низкие
температуры (это была фундаментальная проблема) удается лишь в два этапа. На
первом используется метод лазерного охлаждения. Если поток фотонов падает на
взаимодействующие с ним атомы и рассеивается, то импульс фотонов передается
последним. При этом частицы, двигающиеся навстречу фотонам, получают импульс в
противоположном направлении, т.е. происходит их замедление. Заставить
взаимодействовать с фотонами нужную группу атомов можно, подбирая
соответствующим образом частоту лазера - так, чтобы она резонансно совпала с
частотой поглощения фотона атомом, зависящей из-за эффекта Доплера от его
движения. Работы по лазерному охлаждению получили Нобелевскую премию в 1997 году
(С.Чу, К.Коэн-Таннуджи, У.Д.Филлипс), и столь высокая оценка, была обусловлена
именно тем, что оно было использовано при охлаждении газов для достижения
бозе-конденсации. Таким образом, удается эффективно охладить до 10-4-10-5К
довольно большое число атомов, однако эти температуры все еще недостаточны для
поставленной цели.
Чтобы
до конца охладить систему, нужен второй этап, и им стало так называемое
испарительное охлаждение. Если внутри какого-нибудь сосуда с барьерами
находятся атомы, то наиболее горячие атомы или, как говорят, максвелловские
хвосты распределения преодолевают барьер, а те, которые имеют более низкую
энергию, через барьер выйти не могут. Поэтому со временем, за счет “обрезания”
этих “хвостов”, происходит понижение температуры в системе. Если уменьшить
высоту барьера, через него уйдут и другие частицы, обладающие уже меньшей
энергией. Так, постепенно понижая барьер, можно достичь исключительно низких
температур, сохраняя при этом достаточно большое количество частиц в системе.
Этот
метод был развит еще до исследований лауреатов, но они усовершенствовали его,
используя для “обрезания хвостов” парамагнитный резонанс. Поскольку в данном
случае частицы удерживаются в магнитной ловушке, можно, подавая переменное
поле, “приоткрывать” ловушку тем из них, для которых выполнено условие
парамагнитного резонанса, вызывая их ускоренный уход. Снижая по мере отсева
горячих атомов частоту электромагнитного поля, можно постепенно “срезать” слои
теплых частиц. Сочетание лазерного охлаждения и ускоренного испарения позволило
достичь температуры в 10-8К, и к 1995 г. в двух лабораториях был получен газ,
который, с одной стороны, имел такую низкую температуру, а с другой -
достаточно большое количество частиц. В лаборатории JILA, объединенного
исследовательского центра Национального института стандартов и Колорадского
университета, охлаждение было выполнено для 2000 атомов рубидия, а в
Массачусетсском технологическом институте - для еще большего числа (порядка
105) атомов натрия.
Почему
были выбраны именно натрий и рубидий? По двум причинам. Во-первых, они
представляют собой простейшую систему: щелочные металлы, как и атомарный
водород, имеют один электрон на внешней оболочке и, следовательно, имеют спин и
магнитный момент (все удержание происходит в магнитных ловушках, которые
“держат” незаряженные частицы за счет взаимодействия атома, обладающего
магнитным моментом, с магнитным полем). Необходимое качество присутствует у
всех трех упомянутых элементов. Во-вторых, щелочные элементы имеют подходящие
частоты переходов, соответствующие сравнительно стандартным лазерам.
6. Черное излучение
Важнейшим примером применения статистики Бозе является электромагнитное
излучение, находящееся в тепловом равновесии - так называемое черное излучение.
Черное
излучение можно рассматривать как газ, состоящий из фотонов. Линейность
уравнений электродинамики отражает тот факт, что фотоны не взаимодействуют друг
с другом (принцип суперпозиции 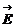 ), так
что фотонный газ можно считать идеальным. Фотоны имеют спин равный единице, и
подчиняются статистике Бозе.
), так
что фотонный газ можно считать идеальным. Фотоны имеют спин равный единице, и
подчиняются статистике Бозе.
Если
измерение находится не в вакууме, а в материальной среде, то условие
идеальности фотонного газа требует малости взаимодействия излучения с
веществом. Это условие выполнимо в газах (за исключением частот близких к
линиям поглощения). При большой плотности - только при очень больших
температурах.
Следует
иметь в виду, что наличие хотя бы небольшого количества вещества вообще
необходимо для самой возможности установления теплового равновесия в излучении,
так как фотоны практически не взаимодействуют между собой.
Число
частиц N в фотонном газе - переменная величина, т.к. они
поглощаются и излучаются атомами. Поэтому N должна сама
определяться из условия равновесия. Потребовав минимальности свободной энергии
газа (при заданных T,V) получим в качестве одного из необходимых условий ∂F/∂N =
0. Но поскольку (∂F/∂N) T,V = μ, отсюда
следует, что μ
= 0 для газа фотонов.
Распределение
фотонов по различным газовым состояниям с определенными значениями импульса 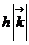 (и определенной поляризации) дается, следовательно,
формулой (с μ
= 0)
(и определенной поляризации) дается, следовательно,
формулой (с μ
= 0)
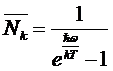 (*).
(*).
Это
так называемое распределение Планка. Считая объем достаточно большим, перейдем
от дискретного к непрерывному распределению собственных частот излучения.
Число
колебаний с компонентами волнового вектора 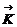 в
интервалах d3k = dkxdkydkz равно Vd3k/(2π)3, а число колебаний с абсолютной величиной волнового
вектора в интервале dk есть, соответственно 4πk3dk V/(2π)3.
в
интервалах d3k = dkxdkydkz равно Vd3k/(2π)3, а число колебаний с абсолютной величиной волнового
вектора в интервале dk есть, соответственно 4πk3dk V/(2π)3.
Вводя
частоту ω=сk и умножая на 2 (два независимых направления
поляризации колебаний), получим число квантовых состояний фотонов с частотами в
интервале {ω,
ω+d ω}
ω2d ω/(π2c3).
Умножив
распределение (*) на эту величину, найдем число фотонов в данном интервале
частот
 ,
,
а
умножив ещё на hω,
получим энергию излучения, заключенную в этом участке спектра:
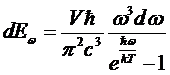 . (**)
. (**)
Эта
формула для спектрального распределения черного излучения называется формулой
Планка. При hω << kT она переходит в формулу Рэлея
-Джинса
 .
.
Это
формула не содержит постоянной Планка h. Ее смысл достаточно прост: в
классической механике на каждую колебательную степень свободы должна
приходиться энергия kT (закон равнораспределения).
В
другом предельном случае hω >> kT
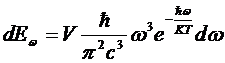
формула
Вина.
При
этом имеет место закон смещения Вина - максимум распределения при повышении
температуры смещается в сторону больших частот, пропорциональных T.
Вычислим
термодинамические величины черного излучения. При μ = 0 свободная энергия F совпадает с Ω (F = Ф
- PV = μN +Ω)
Согласно
формуле
 ,
,
где
полагаем μ
= 0 и переходим обычным образом 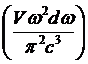 от суммирования к интегрированию, получим:
от суммирования к интегрированию, получим:
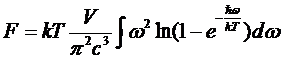 .
.
Вводя
безразмерную переменную интегрирования, и интегрируя по частям, получим:
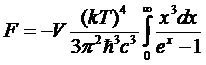 .
.
Стоящий
здесь интеграл равен π4/15.
Таким образом:
 ,
,
где
 - постоянная Стефана-Больцмана
- постоянная Стефана-Больцмана
Энтропия
черного излучения равна
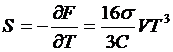 .
.
Полная
энергия излучения
идеальный газ квантовый гравитационный
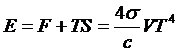 .
.
Это
выражение можно получить и интегрированием (**). Оно представляет собой
обоснование закона Больцмана - полная энергия излучения ~T4 .
Найдем
теплоемкость излучения
 .
.
Давление
черного излучения:
 .
.
Видим,
что давление не зависит от V (при изотермическом сжатии давление не меняется), что
является следствием переменности числа частиц. Из этого выражения можно
получить
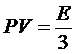 .
.
Полное
число фотонов в черном излучении
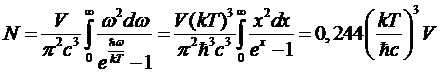 .
.
Статистический
вывод закона Стефана-Больцмана
Этот
закон был открыт Стефаном (австрия) экспериментально в 1879 году путем
измерения теплоотдачи платиновой проволоки. Теоретическое обоснование этог
закона было дано учеником Стефана Больцманом в 1884 году на основе следствий
теории электромагнитного поля Максвелла.
Рассмотрим
излучение фотонов с поверхности абсолютно черного тела. Найдем сначала
распределение вылетающих фотонов по углам. Пусть частицы вылетают из точки А
(рис.). Выделим сферу радиуса R с центром в этой точке. В равновесии все направления
полета фотонов равновероятны. Это означает, что вероятность для фотона попасть
в какую-либо часть полусферы будет равна отношению:
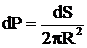 ,
,
где
dS - элементарная площадка на полусфере, а в знаменателе стоит площадь
полусферы.
Выделим
элементарную площадку для фотонов, угол отклонения которых от вертикали
находится в интервале (Θ,
Θ+dΘ):
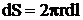 ,
,
где
dl - элемент дуги окружности.
Имея
в виду, что
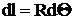 ,
,
а
так же то, что
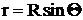 ,
,
получим:
 ,
,
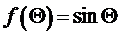 .
.
Это
и есть функция распределения вылетающих фотонов по углам. Легко убедиться в
том, что она нормирована. Таким образом, можно сделать вывод о том, что фотоны
вылетают главным образом с большими углами от вертикали.
Найдем
плотность потока энергии излучения - количество энергии, излучаемой в секунду с
единицы поверхности.
Выделим
вблизи поверхности, площадью S малый объем высотой cdt и найдем, сколько
энергии из этого объема упадет на стенку.
В
этом объеме заключена энергия:
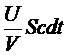 .
.
Однако
на стенку попадет только часть этой энергии. Во-первых, нас будут интересовать
только фотоны, имеющие положительную составляющую скорости по оси x (их ровно
половина). С другой стороны, на основе распределения фотонов по углам можно
записать:
 .
.
Здесь
cosΘ
появляется в результате проецирования
скорости на ось x.
Введем
плотность потока энергии:
 .
.
Таким
образом, для плотности потока энергии получим:
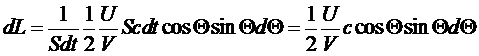 .
.
Интегрируя
по углам, получим:
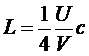 .
.
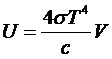 ,
,
то
окончательно получаем Закон Стефана-Больцмана:
 .
.
7. Связь квантовых и классических распределений Гиббса
Для
перехода от квантовых распределений к классическим распределениям надо заменить
суммирование 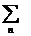 по всем возможным микросостояниям квантовой
макроскопической системы интегрированием
по всем возможным микросостояниям квантовой
макроскопической системы интегрированием 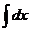 в
многомерном фазовом пространстве. Чтобы осуществить такой переход надо
определить элементарную ячейку в фазовом пространстве.
в
многомерном фазовом пространстве. Чтобы осуществить такой переход надо
определить элементарную ячейку в фазовом пространстве.
Рассмотрим
движение одной частицы в потенциальном поле. Каждое состояние в этом случае
характеризуется набором трех квантовых чисел: 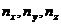 . При
этом каждому состоянию в трехмерном фазовом пространстве отвечает объем
. При
этом каждому состоянию в трехмерном фазовом пространстве отвечает объем  , т.к. ввиду соотношения неопределенностей
, т.к. ввиду соотношения неопределенностей  точнее положение точки определить нельзя. Таким
образом, на одну степень свободы приходится объем
точнее положение точки определить нельзя. Таким
образом, на одну степень свободы приходится объем 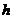 .
.
В
квантовой теории показано, что в произвольной системе с N
степенями свободы (при рассмотрении только поступательных степеней свободы) при
переходе к классическому приближению в качестве элементарной ячейки надо
использовать  .
.
Поэтому
заменим суммирование по квантовым числам интегрированием по фазовому
пространству:  (движение атома как целого).
(движение атома как целого).
Штрих
означает, что интегрирование проводится не по всему фазовому пространству, а
лишь по тем его областям, которые соответствуют физически различимым
состояниям.
В
классической системе одинаковых частиц они считаются различимыми, то есть их
можно перенумеровать и проследить за их траекториями. В квантовой механике
показано, что частицы являются тождественными (неразличимыми), а проследить за
траекториями частиц невозможно. То есть если рассмотреть возможные варианты
распределения, например, трех частиц по трем ячейкам, то в классической
механике состояния, отвечающие разным номерам частиц, считаются разными, а в
квантовой механике все они представляют собой одно состояние.


Рис.1
При вычислении статистического интеграла удобно распространить
интегрирование на всю область фазового пространства. При этом состояния,
отличающиеся лишь перестановкой частиц (неразличимых в квантовой механике)
будут учитываться N! раз. Поэтому
разделим статистический интеграл на N!. Это означает, что условием перехода к классической статистической
теории будет замена:
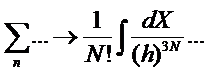 ,
,
а
статистическая сумма примет вид
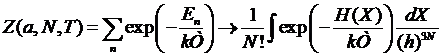 .
.
Заметим,
что это выражение безразмерно (в отличие от ранее полученного в классической
статистической физике).
Тогда
можно ввести безразмерную функцию распределения в классической теории
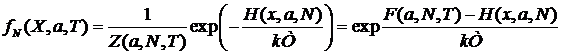 .
.
Условие
её нормировки:
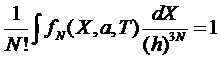 .
.
Во
многих случаях (например, для нахождения уравнений состояний) это различие на 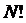 не является существенным. Однако, при расчете
энтропии оно оказывается принципиальным.
не является существенным. Однако, при расчете
энтропии оно оказывается принципиальным.
Решение
парадокса Гиббса.
Воспользуемся
формулой Стирлинга для больших величин N:
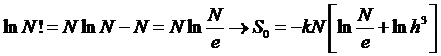 .
.
При
подстановке этого выражения в энтропии газов, получим, что парадокса Гиббса не
возникает. То есть учет тождественности частиц в квантовой теории позволяет
устранить противоречия в классических выражениях для термодинамических функций.
Таким же образом можно найти и все остальные термодинамические функции.
8. Двухатомный газ с молекулами из различных атомов. Вращение молекул
Будем рассматривать теперь идеальные газы с учетом внутренней структуры
их молекул. Наиболее простой случай представляет собой двухатомный газ.
Двухатомный газ можно рассматривать как таковой только при условии малости kТ по сравнению с энергией диссоциации
молекул. В таблице приведены характерные температуры, соответствующие
диссоциации некоторых молекул.
|
молекула
|
Eдис/k,
К
|
|
H2
|
52000
|
|
N2
|
113000
|
|
O2
|
59000
|
|
Cl2
|
29000
|
|
NO
|
61000
|
|
CO
|
98000
|
Наиболее важный практический случай - когда в своем нормальном
электронном состоянии молекула газа не имеет ни спина, ни орбитального момента
вращения относительно оси (нет тонкой структуры). Следует различать случаи
молекул, составленных из разных атомов (изотопы) и молекул, составленных из
одинаковых атомов. Будем считать, что атомы разные (не тождественные).
Уровень энергии двухатомной молекулы складывается в известном приближении
из трех независимых частей - электронной энергии (энергии кулоновского
взаимодействия ядер в их равновесном положении, отсчитываемой от суммы энергий
разведенных атомов); вращательной энергии и энергии колебания ядер внутри
молекулы. Эти уровни могут быть записаны в следующем виде:
 .
.
При
классическом вращении энергия имеет вид
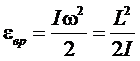 ,
,
но
из квантовой механики следует, что L2 квантуется.
Здесь
ε0-электронная энергия,  -
колебательный квант, v - колебательное квантовое число, К - вращательное
квантовое число;
-
колебательный квант, v - колебательное квантовое число, К - вращательное
квантовое число;
I = m’r02 - момент инерции молекулы, m’ - приведенная
масса обоих атомов, r0 - равновесное состояние между атомами.
При
подстановке этого выражения в статическую сумму, последняя распадается на три
независимых множителя:
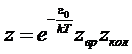 ,
,
где
вращательная и колебательная суммы определяются как
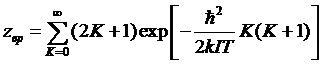 ,
,
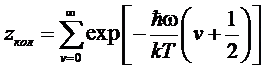 ,
,
причем
множитель 2К+1 в zвр учитывает вырождение вращательных уровней по
направлениям момента импульса L. Соответственно, свободная энергия представится как:
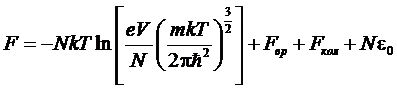
(m=m1+m2) -
масса молекулы. Первый член можно назвать поступательной частью Fпос
(поскольку он связан со степенями свободы поступательного движения молекул), а
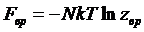 ,
,  .
.
Поступательная
теплоемкость, приходящаяся на одну молекулу, равна cпос=3/2 k.
Полная теплоемкость газа записывается в виде суммы
= cпос+ cвр + cкол; cр= cпос+
cвр + cкол + k,
каждое
слагаемое которой связано с тепловым возбуждением соответственно
поступательного, вращательного и колебательного движений.
Вычислим
вращательную свободную энергию.
Рассмотрим
случай, когда температура настолько высока, что
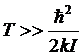 .
.
Это
означает, что вращательный квант 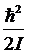 мал по
сравнению с тепловой энергией kТ. В таблице представлены величины
мал по
сравнению с тепловой энергией kТ. В таблице представлены величины 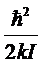 для некоторых двухатомных молекул.
для некоторых двухатомных молекул.
|
Молекула
|
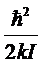 , К , К
|
|
H2
|
85,4
|
|
D2
|
43
|
|
HD
|
64
|
|
H2
|
2,9
|
|
O2
|
2,1
|
|
Cl2
|
0,36
|
|
NO
|
2,4
|
|
HCl
|
15,2
|
В этом случае в сумме Zвр
основную роль играют члены с большими числами К. Но при больших значениях К
вращение молекулы квазиклассично. Поэтому в этом случае статистическая сумма Zвр может быть замечена
соответствующим классическим интегралом по К:
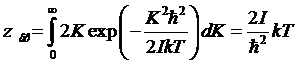 .
.
Отсюда
свободная энергия
 .
.
Таким
образом при рассматриваемых не слишком низких Т вращательная часть теплоемкости
оказывается равной k (в соответствии с общим результатом классического
рассмотрения по k/2 на каждую степень свободы):
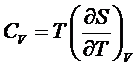 ,
, 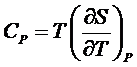 ,
, 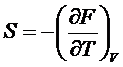 ,
,
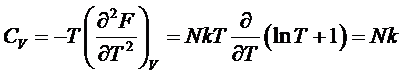 .
.
Мы
увидим ниже, что существует значительная область температур, в которой
выполнено условие 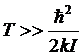 и в то же время колебательная часть свободной
энергии, а значит и колебательная часть теплоемкости отсутствуют. В этой
области теплоемкость двухатомного газа, приходящаяся на одну молекулу, равна
и в то же время колебательная часть свободной
энергии, а значит и колебательная часть теплоемкости отсутствуют. В этой
области теплоемкость двухатомного газа, приходящаяся на одну молекулу, равна
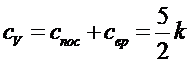 ,
, 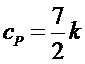 .
.
Рассмотрим
теперь обратный предельный случай низких температур, когда
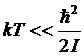 .
.
В
этом случае достаточно сохранить две первых члена суммы, поскольку именно они
будут вносить наибольший вклад.
 .
.
В
этом приближении свободная энергия будет равна
 .
.
Отсюда
энтропия:
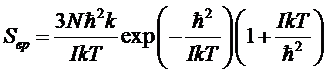
и
теплоемкость
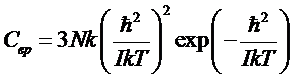 .
.
Таким
образом, вращательная энтропия и теплоемкость газа при T ® 0 обращаются в ноль в основном по экспоненциальному
закону. При низких температурах, следовательно, двухатомный газ ведет себя как
одноатомный (говорят, что в этом случае вращательные степени свободы
«заморожены»).
В
общем случае произвольных температур сумма 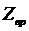 может
быть рассчитана только численно. На рис. приведен график cвр
(в единицах k) как функции безразмерной величины
может
быть рассчитана только численно. На рис. приведен график cвр
(в единицах k) как функции безразмерной величины  .
.

Рис.
2.2
Вращательная
теплоемкость имеет максимум, равный 1,1 при  , после
чего асимптотически приближается к классическому значению 1.
, после
чего асимптотически приближается к классическому значению 1.
9. Двухатомный газ. Колебания атомов
Колебательная
часть термодинамических величин газа становится существенной при значительно
более высоких температурах, чем вращательная, потому, что интервалы
колебательной структуры велики по сравнению с интервалами вращательной
структуры. В таблице приведены характерные колебательные температуры  .
.
|
Молекула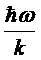 , К , К
|
|
|
H2
|
6100
|
|
N2
|
3340
|
|
O2
|
2230
|
|
NO
|
2690
|
|
HCl
|
4140
|
Мы
будем считать, однако, температуру большой лишь настолько, чтобы были
возбуждены в основном не слишком высокие колебательные уровни. Тогда колебания
можно считать малыми и гармоническими, а уровни энергии определяются обычным
выражением для гармонического осциллятора 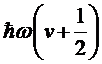 . В
случае ангармонических колебаний выражение для энергии будет значительно
сложнее.
. В
случае ангармонических колебаний выражение для энергии будет значительно
сложнее.
Вычислим
колебательную статистическую сумму
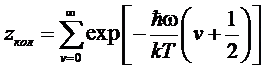 . (*)
. (*)
Хотя
при больших числах v колебания будут ангармоническими, но вследствие очень
быстрой сходимости ряда суммирование можно распространить до бесконечности.
Сумма
(*) представляет собой геометрическую прогрессию:
 ,
,
откуда
свободная энергия
 ,
,
энтропия
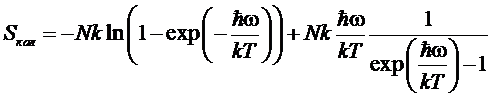 ,
,
энергия
 ,
,
и
теплоемкость 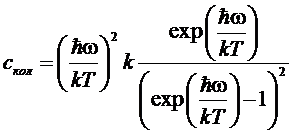 .
.
На
рисунке изображен график зависимости 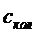 от
от 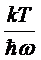 .
.

Рис.
2.3
При
низких температурах (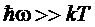 ) энтропия и теплоемкость стремятся экспоненциально к
нулю:
) энтропия и теплоемкость стремятся экспоненциально к
нулю:
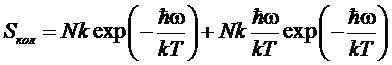 ,
,
 ,
,
а
свободная энергия и энергия стремятся к постоянной величине.
При
высоких температурах (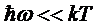 ) имеем:
) имеем:
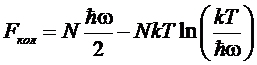 ,
,
чему
соответствует постоянная теплоемкость  .
.
Таким
образом, полная теплоемкость двухатомного газа при температурах 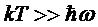 (практически уже при
(практически уже при 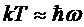 ) равна
) равна
 ,
, 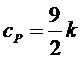 .
.
Многоатомный
газ. Свободную энергию многоатомного газа, как и двухатомного газа, можно
представить в виде суммы трех частей- поступательной, вращательной и
колебательной.
Благодаря
большой величине моментов инерции многоатомных молекул (и соответственно,
малости их вращательных квантов) их вращение можно всегда можно рассматривать
классически. Эффекты квантования вращения могли бы наблюдаться лишь у метана CH4,
где они должны появляться при температурах около 50K.
Многоатомная
молекула обладает, в общем случае, тремя вращательными степенями свободы и
большим числом колебательных степеней свободы. Если молекула обладает
какими-либо осями симметрии, то повороты вокруг этих осей совмещают молекулу
саму с собой и сводятся к перестановке одинаковых атомов. Например, если все
атомы в молекуле расположены на одной прямой (линейная молекула), то она
обладает, как и двухатомная молекула, всего двумя вращательными степенями
свободы и одним моментом инерции.
.
Флуктуации. Распределение Гаусса
Статистическое
и чисто термодинамическое описание тепловых процессов различаются тем, что из
законов статистической физики с неизбежностью вытекает существование
флуктуаций. В то же время вероятность сколько-нибудь заметных флуктуаций в
системе, содержащей большое число частиц, чрезвычайно мала.
Открытие
многочисленных примеров флуктуационных процессов явилось блестящим подтверждением
законов статистической физики и послужило одним из важнейших моментов в
окончательном утверждении молекулярной теории.
В
работах Эйнштейна и Смолуховского было показано, что целый ряд давно известных
физических процессов обусловлен явлениями флуктуаций, и была развита
комплексная теория этих вопросов, оказавшихся в прекрасном согласии с
экспериментами.
Рассмотрим
флуктуации в замкнутой системе.
Пусть
система находится в состоянии статистического равновесия и имеет энтропию S0.
Предположим теперь, что состояние системы изменяется так, что она переходит в
неравновесное состояние с энтропией S.
Будем
считать, что изменение состояния системы можно характеризовать изменением
некоторого внутреннего параметра x, значение которого зависит от состояния всей системы.
В
равновесии x = x0. Пример x - плотность ρ газа, находящегося в замкнутом теплоизолированном
сосуде. В состоянии равновесия плотность постоянна по всему объему сосуда x0=ρ0=const.
В
результате флуктуации система может самопроизвольно перейти в неравновесное
состояние с переменной плотностью x=
ρ(r).
Энтропия
системы будет некоторой функцией параметра x: S=S(x).
При этом в состоянии равновесия S0=S(x0) .
Вероятность
застать систему в интервале значений x; x+dx
должна быть пропорциональна статистическому весу (числу микросостояний) и
величине интервала dx:
 .
.
Для
изолированной системы верна формула Больцмана
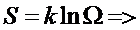
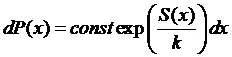
Константа
определяется из условия нормировки:
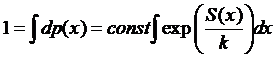
Или
для функции распределения:
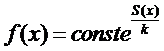 (*)
(*)
Прежде,
чем приступить к интегрированию этой функции, надо ответить на вопрос о
пределах ее применимости. Все распределения, приведенные выше, неявно
подразумевают классичность поведения x. Поэтому надо найти условие,
допускающее пренебрежение квантовыми эффектами.
Как
известно из квантовой механики, между квантовыми неопределенностями энергии и
какой-либо величины x имеет место соотношение
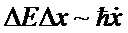
где
dx/dt - классическая скорость изменения величины x.
Пусть
τ - время, характеризующее скорость изменения нашей
величины x, которая имеет неравновесное значение. Тогда 

Ясно,
что говорить об определенном значении величины x можно лишь при
условии малости ее квантовой неопределенности 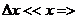

Таким
образом, квантовая неопределенность энергии должно быть велика по сравнению с  . Энтропия системы будет при этом иметь
неопределенность
. Энтропия системы будет при этом иметь
неопределенность
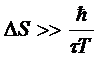
Для
того, чтобы формула (*) имела реальный смысл, необходимо, очевидно, чтобы
кавнтовая неточность энтропии была мала по сравнению с k:
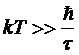 ;
; 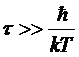
Это
и есть искомое условие. При слишком низких температурах или при слишком быстром
изменении x (слишком малом τ) флуктуации нельзя рассматривать термодинамически, т.к. на первый план
выступают чисто квантовые флуктуации.
Выберем
x так, что энтропия имеет максимум при x = x0 =
0. Поэтому
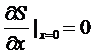 ,
, 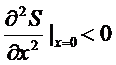
Величина
x при флуктуациях очень мала. Разлагая S(x) в
ряд по степеням x и ограничиваясь членом второго порядка, получим
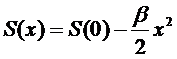
где
β>0.
Тогда получим распределение вероятностей
в виде:
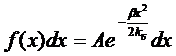
Нормирование
константы A определяется условием
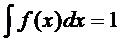
Хотя
выражение для f(x) относится к малым x, но ввиду
быстрого убывания подынтегральной функции с увеличением |x|
область интегрирования можно распространить на все значения от -∞ до +∞.
Произведя интегрирование, получим
 (интеграл
Пуассона).
(интеграл
Пуассона).
Таким
образом, имеем для величины x распределение:
 .
.
Эта
формула называется распределение Гаусса. Если обозначить
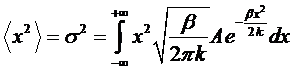 ,
,
то,
беря интеграл, распределение можно записать в виде:
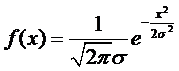 .
.
Функция f(x) имеет тем более острый максимум, чем меньше <x2>.
Отметим, что по известному <x2> можно найти аналогичную величину для любой функции j(x). Ввиду малости x имеем:
<(Dj)2> = 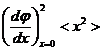
(подразумевается,
что функция j(x) мало меняется при значениях x ~ <x2> и что производная dj/dx отлична от
нуля при x = 0).
Если
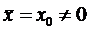 , то распределение Гаусса запишется в виде:
, то распределение Гаусса запишется в виде:
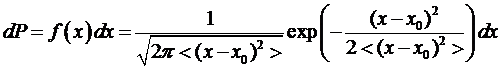 .
.
11.Флуктуации термодинамических величин
Рассчитаем теперь флуктуации конкретных термодинамических величин.
Пусть
ƒ
- любая физическая величина, испытывающая
флуктуации. Флуктуацией величины ƒ называется отклонение 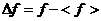 мгновенного
значения этой величины от ее среднего значения. Очевидно, что <Δƒ>
= 0. Поэтому обычно пользуются средним
квадратом флуктуации, т.е. величиной <Δƒ2>. Квадратный корень из этой величины
мгновенного
значения этой величины от ее среднего значения. Очевидно, что <Δƒ>
= 0. Поэтому обычно пользуются средним
квадратом флуктуации, т.е. величиной <Δƒ2>. Квадратный корень из этой величины 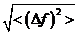 называется - среднеквадратичной флуктуацией.
называется - среднеквадратичной флуктуацией.
Усредняя
выражение  , получим
, получим
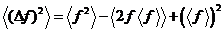
Следовательно,
 (1)
(1)
Усредним
теперь произведение двух флуктуирующих величин:

Учитывая,
что <Δƒ>=
<Δg >= 0, получим
 (2)
(2)
Формула (1) содержится здесь как частный случай,
который получается при g =f.
Величины f и g называются статистически
независимыми, если <ΔfΔg> = 0.
Для таких величин
<fg>=<f><g>. (3)
Рассмотрим теперь любую физическую систему, состоящую
из N независимых одинаковых частей. Примером такой системы может служить
идеальный газ, а составных частей - отдельные молекулы. Пусть ft - произвольная аддитивная величина,
характеризующая i-ю подсистему,
например, в приведенном примере - кинетическая энергия i-й молекулы. Тогда в силу предполагаемой аддитивности
соответствующая величина для всей системы будет F = Σƒi,. Выразим средний квадрат флуктуации
величины F через аналогичный квадрат для
величины ƒi
.Очевидно, <F> = Σ<ƒ>i = N<f>,
где индекс i опущен, так как предполагается, что
все составные части системы тождественны. Далее,
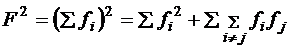
А
так как эти части независимы, то, <ƒi ƒj
>= <ƒi >< ƒj >=(<ƒ>)2. Следовательно,
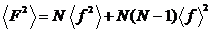
Подставляя
эти значения в формулу (1), получим
 (4)
(4)
Отсюда
на основании (1)
 (5)
(5)
Таким
образом, с увеличением N относительная флуктуация величины F
убывает обратно пропорционально 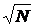 . При
больших величинах N относительные флуктуации ничтожны. Этот вывод
качественно верен и для неаддитивных величин. С ним связана достоверность
термодинамических результатов для больших макроскопических систем.
. При
больших величинах N относительные флуктуации ничтожны. Этот вывод
качественно верен и для неаддитивных величин. С ним связана достоверность
термодинамических результатов для больших макроскопических систем.
В
соответствии со сказанным видим, что в объемах с большим средним числом частиц N
относительные флуктуации малы и труднодоступны наблюдению. Наоборот, при малых N
относительные флуктуации велики. Более общий метод вычисления флуктуации
плотности, применимый также к жидкостям и твердым телам, основан на теореме о
равномерном распределении кинетической энергии по степеням свободы. Рассмотрим
малую часть жидкости или газа, окруженную такой же жидкой или газообразной
средой, температура Т которой поддерживается постоянной (термостатом). С целью
упрощения и наглядности вычислений предположим, что малая часть жидкости или
газа заключена в цилиндр с поршнем. Стенки цилиндра идеально проводят тепло, а
поршень может ходить в нем без трения. Тогда наличие стенок цилиндра и поршня
не будет препятствовать обмену энергией и выравниванию давлений между веществом
в цилиндре и термостатом. Тепловое движение молекул вещества вызовет
броуновское движение поршня. К этому движению поршня мы и применим теорему о
равномерном распределении кинетической энергии по степеням свободы. Поршень
можно рассматривать как гармонический осциллятор, совершающий беспорядочные
тепловые колебания. Среднее значение его потенциальной энергии при смещении на
х из положения равновесия х = 0 равно (1/2) кх2 = (1/2)кТ, где к - жесткость,
соответствующая такому смещению. Если S - площадь поршня, a DV -
изменение объема системы, то DV = Sx. Таким образом, <(ΔV)2 > = <S2x2>=
S2kT/K. Сила, возвращающая поршень в положение равновесия,
будет  , где Р - давление газа или жидкости. Поэтому к = - SdP/dх =S2dP/dV. В
результате получим
, где Р - давление газа или жидкости. Поэтому к = - SdP/dх =S2dP/dV. В
результате получим
 (6)
(6)
Знак
Т указывает, что в выводе предполагалось постоянство температуры окружающей
среды (термостата). Если бы вещество внутри объема V было
адиабатически изолировано, то индекс Т следовало бы заменить на S
(постоянство энтропии), т.е.
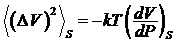 . (7)
. (7)
Формулы
(6) и (7) выражают флуктуации объема одной и той же массы вещества, находящейся
в термодинамическом равновесии с окружающей средой.
Для
идеального газа при постоянной температуре PV = const,
так что (dV/dP) т = -V/P. А так как PV = NкТ, где N -
число молекул в объеме V, то из формулы (6) получаем <Δ V 2>=V2/N.
Перейдем
теперь к вычислению флуктуации энергии. С целью лучшего уяснения метода начнем
с вычисления флуктуации кинетической энергии e молекулы
одноатомного идеального газа в отсутствие силовых полей. Согласно
максвелловскому закону распределения скоростей
 (8)
(8)
где
α
= 1/кT, dГ -
элементы объема пространства скоростей, а Z определяется
условием нормировки
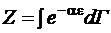 (9)
(9)
Дифференцируя
это соотношение по параметру α, получим

и
формула (8) перейдет в
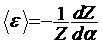 (10)
(10)
Отсюда,

Аналогично
 (11)
(11)
Сравнение
этой формулы с предыдущей дает
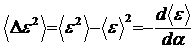
Или
после подстановки параметра α = 1/кТ
 (12)
(12)
Так
как для идеального одноатомного газа e = (3/2)кТ, то в
этом случае
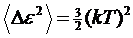 (13)
(13)
Приведенный
метод вычисления <Δε2>
может быть распространен практически без
изменений на случай величин внешнего силового поля. Надо только максвелловское
распределение заменить распределением Больцмана и производить интегрирование не
только по скоростям, но и по координатам обычного пространства. В результате
снова получится формула (12), в которой, однако, под ε следует понимать уже полную энергию молекулы,
состоящей из кинетической и потенциальной.
Важно
отметить расширение области применимости формулы (12) для флуктуации полной
энергии ε.
Выделим малую часть (подсистему)
изотропной среды (жидкости или газа), находящуюся в статистическом равновесии
со всей средой, температура Т которой поддерживается постоянной. Подсистемой
может быть и отдельная молекула. По отношению к выделенной подсистеме
окружающая среда играет роль термостата. Из-за обмена энергией между
термостатом и подсистемой энергия последней будет непрерывно флуктуировать.
Флуктуации полной энергии ε
подсистемы определяются уравнением (12). Не имеет значения, меняется ли энергия
ε непрерывно (классическая система), или принимает
дискретный ряд значений (квантовая система). Доказательство этого утверждения
дается в статистической физике. Оно основано на каноническом распределении
Гиббса, частными случаями которого являются распределения Максвелла и
Больцмана.
В
случае макроскопической подсистемы, объем которой поддерживается постоянным, e имеет смысл внутренней - энергии подсистемы, a dε/dT -ее теплоемкости Сν при постоянном объеме. Тогда из формулы (12) получается
<(Δε2)>V = kT 2Cv. (14)
Знак V
снова указывает на то, что (Δε2)V есть средний квадрат флуктуации
энергии подсистемы при сохранении ее объема V постоянным.
Рассмотрим
теперь флуктуации энтальпии H подсистемы. Для этого воспользуемся следующим
искусственным приемом. Предположим, что подсистема заключена в оболочку с
идеально проводящими подвижными стенками, так что объем подсистемы не
сохраняется постоянным. Пусть оболочка снаружи подвергается действию постоянных
внешних сил, поддерживающих внешнее давление Р постоянным. Эти силы увеличивают
потенциальную энергию подсистемы на величину PV. Если под e понимать ту же энергию, что и в предыдущем выводе, то с учетом
дополнительной потенциальной энергии PV среднее значение полной
энергии подсистемы будет 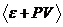 . Но это есть энтальпия подсистемы H.
Все предыдущие рассуждения можно повторить без изменений, заменив e на e + PV. В результате вместо (12) получится
. Но это есть энтальпия подсистемы H.
Все предыдущие рассуждения можно повторить без изменений, заменив e на e + PV. В результате вместо (12) получится
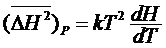 . (15)
. (15)
Но при Р = const производная dH/dT есть теплоемкость Ср подсистемы при
постоянном давлении, а потому
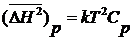 (16)
(16)
Изложенный метод вычисления флуктуаций можно
распространить на любые величины, характеризующие макроскопические свойства
подсистем.
Флуктуации в квазизамкнутой системе
Очень
часто приходится рассматривать флуктуации, происходящие не в замкнутой, а в
квазизамкнутой системе, составляющей малую часть замкнутой системы. То есть,
это подсистема, погруженная в термостат с температурой T0. При этом
флуктуации происходят только в подсистеме, а термостат при этом может совершать
квазистатический процесс, не нарушающий его равновесия. Пусть, как и раньше x -
параметр, характеризующий состояние подсистемы, а x0 - значение
этого параметра в равновесии. Будем предполагать, что изменения x
происходят достаточно медленно, так, что в каждый момент времени в подсистеме
будет существовать равновесное статистическое распределение. Процесс перехода
из равновесного состояния в неравновесное состояние у подсистемы в термостате
можно рассматривать как переход, совершающийся под действием некоторого
внешнего источника работы. При изменении x на величину 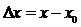 источник совершает над системой работу A(x).
источник совершает над системой работу A(x).
Напишем
теперь выражение для вероятности того, что подсистема перейдет в состояние со
значением x в интервале x+dx, в то время
как термостат останется в равновесном состоянии.
Поскольку
термостат и подсистема вместе составляют замкнутую систему, к ней применима
формула
 .
.
В
ней, однако, изменение энтропии нужно записать в виде:
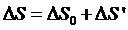 ,
,
где
второе слагаемое в правой части представляет собой изменение энтропии
подсистемы. Тогда вероятность может быть записана в виде:
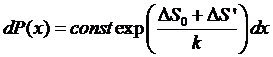 .
.
Но
в силу нашего предположения о медленности изменения макропараметров для ΔS’можно
записать:
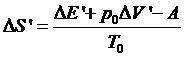 ,
,
где
T0, p0 - равновесные температуры и давление системы
(термостата), E’, V’ - энергия и объем подсистемы, А - работа внешнего
источника (не термостата, работа термостата описывается вторым слагаемым в
правой части) над системой. Для термостата можно записать:
 .
.
Но
в силу замкнутости системы (термостат + подсистема) полный ее объем остается
постоянным:
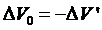 .
.
Так
же сохраняется и полная энергия:
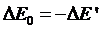 .
.
Таким
образом, имеем
 .
.
Тогда
вероятность может быть записана в виде:
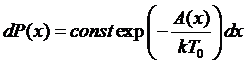 .
.
Следовательно,
мерой вероятности малых термодинамических флуктуаций в макросистеме является та
работа, которую нужно над нею совершить для изменения параметра x.
Работа может быть найдена из первого начала термодинамики.
13. Флуктуации идеальных полимерных цепей
Рассмотрим свободно-сочлененную полимерную цепь, состоящую из N сегментов. Будем предполагать, что
отдельные сегменты цепи не взаимодействуют друг с другом посредством других
сил, кроме тех, которые образуют саму цепь.
Вектор RN, соединяющий концы этой цепи,
описывается простым выражением:
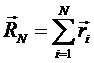 .
.
Здесь
i - порядковый номер сегмента цепи, 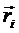 - вектор, соединяющий начало и конец сегмента с
номером i. Модули всех векторов одинаковы и равны длине одного
сегмента l. Направления всех векторов случайны и независимы друг
от друга. То есть полимерная цепь представляет собой клубок, характеризующийся
величиной величиной
- вектор, соединяющий начало и конец сегмента с
номером i. Модули всех векторов одинаковы и равны длине одного
сегмента l. Направления всех векторов случайны и независимы друг
от друга. То есть полимерная цепь представляет собой клубок, характеризующийся
величиной величиной  , равной сумме большого числа случайных слагаемых. Для
вывода формулы для характерного размера полимерного клубка введем величину
, равной сумме большого числа случайных слагаемых. Для
вывода формулы для характерного размера полимерного клубка введем величину  , т.е. вектор, соединяющий начало первого сегмента
цепи с концом сегмента с номером N-1:
, т.е. вектор, соединяющий начало первого сегмента
цепи с концом сегмента с номером N-1:
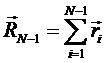 ,
, 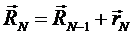 .
.
Найдем
теперь среднее расстояние между концами цепи. Учтем, что
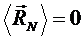 ,
,
поскольку
все направления в пространстве равновероятны. Вычислим средний квадрат
расстояния:
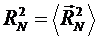 .
.
В
результате получим:
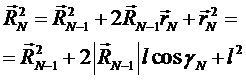 ,
,
где
γN - угол между векторами  и
и 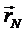 . В случае свободно-сочлененной полимерной цепи
ориентация сегмента с номером N не зависит от ориентации остальных сегментов цепи.
Следовательно, угол γN с
одинаковой вероятностью принимает любое значение, а среднее значение его
косинуса равно нулю. Таким образом, получим:
. В случае свободно-сочлененной полимерной цепи
ориентация сегмента с номером N не зависит от ориентации остальных сегментов цепи.
Следовательно, угол γN с
одинаковой вероятностью принимает любое значение, а среднее значение его
косинуса равно нулю. Таким образом, получим:
 .
.
По
индукции можно заключить, что
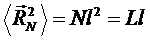 ,
,
где
L - контурная длина цепи.
Окончательно
получим:
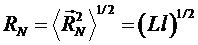 .
.
Верна
ли эта формула при других модельных представлениях о полимерной цепи?
Рассмотрим,
например, червеобразную молекулу. Если рассмотреть короткий участок такой
молекулы, то на таком участке ее гибкость не проявляется, а молекула является
жесткой. Введем понятие leff - это такая длина, участок меньше которой является
жестким, а его длина равна контурной длине. В то же время участки с контурной
длиной, больше чем leff ведут себя как последовательные сегменты
свободно-сочлененной цепи. Величина leff еще называется сегмент Куна
(по имени швейцарского ученого, впервые применившего статистическую механику к
полимерам). Если контурная длина молекулы равна L, то очевидно,
что эта молекула состоит из Neff = L/leff сегментов Куна. Тогда для определения размера цепи
можно записать:
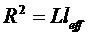 .
.
Это
равенство можно рассматривать и как определение сегмента Куна. Длина сегмента
Куна может варьировать от 1 нм до 100 нм для двойной спирали ДНК.
Распределение
Гаусса для идеальной полимерной цепи
Из-за
флуктуаций длина полимерной цепи постоянно меняется. Для доли конформаций (т.е.
разных пространственных конфигураций) с данным R среди всех
возможных конформаций можно записать выражение
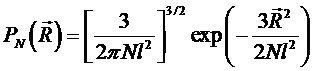 .
.
Плотность
вероятности для одной компоненты равна
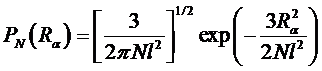 .
.
Оба
эти выражения представляют собой распределения Гаусса для R.
.
Флуктуации изгиба длинных молекул
В
обычных молекулах сильное взаимодействие атомов сводит внутримолекулярное
тепловое движение лишь к малым колебаниям атомов около положений равновесия,
практически не меняющих форму молекулы. Совсем иной характер имеет поведение
молекул, представляющих собой очень длинные цепи атомов (например, длинные
полимерные углеводородные цепи). Большая длина молекулы, а так же сравнительная
слабость сил, стремящихся удержать равновесную прямолинейную форму молекулы,
приводит к тому, что флуктуационные изгибы молекулы могут стать весьма
значительными, вплоть до скручивания молекулы. Большая длина молекулы позволяет
рассматривать ее как своеобразную макроскопическую линейную систему, и для
вычисления средних значений величин, характеризующих ее изгиб, можно применить
статистические методы.
Будем
рассматривать молекулы, имеющие вдоль своей длины однородное строение.
Интересуясь лишь их формой, мы можем рассматривать такую молекулу как
однородную сплошную нить. Форма этой нити определяется заданием в каждой ее
точке вектора кривизны 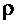 , направленного вдоль главной нормали к кривой и по
величине равного ее обратному радиусу кривизны.
, направленного вдоль главной нормали к кривой и по
величине равного ее обратному радиусу кривизны.
Испытываемые
молекулой изгибы являются, вообще говоря, слабыми в том смысле, что ее кривизна
в каждой точке мала (ввиду большой длины молекулы это, разумеется, отнюдь не
исключает того, что относительные смещения ее удаленных точек могут оказаться
весьма значительными). Для малых значений вектора 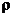 свободная энергия изогнутой молекулы (отнесенная к
единице ее длины) может быть разложена по степеням компонент вектора. Поскольку
свободная энергия минимальна в положении равновесия (прямолинейная форма,
свободная энергия изогнутой молекулы (отнесенная к
единице ее длины) может быть разложена по степеням компонент вектора. Поскольку
свободная энергия минимальна в положении равновесия (прямолинейная форма,  = 0 во всех точках), то линейные члены в разложении
отсутствуют, и мы получим
= 0 во всех точках), то линейные члены в разложении
отсутствуют, и мы получим
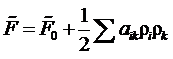 , (*)
, (*)
где
значения коэффициентов  представляют собой характеристику свойств
прямолинейной молекулы (к линии молекулы в данной ее точке) и ввиду
предполагаемой однородности молекулы постоянны вдоль ее длины.
представляют собой характеристику свойств
прямолинейной молекулы (к линии молекулы в данной ее точке) и ввиду
предполагаемой однородности молекулы постоянны вдоль ее длины.
Вектор
 расположен в нормальной (к линии молекулы в данной ее
точке) плоскости и имеет в этой плоскости две независимые компоненты.
Соответственно этому совокупность постоянных
расположен в нормальной (к линии молекулы в данной ее
точке) плоскости и имеет в этой плоскости две независимые компоненты.
Соответственно этому совокупность постоянных  составляет
двумерный симметричный тензор второго ранга в этой плоскости. Приведем его к
главным осям и обозначим через
составляет
двумерный симметричный тензор второго ранга в этой плоскости. Приведем его к
главным осям и обозначим через  и
и  главные значения этого тензора (нить, в виде которой
мы представляем себе молекулу, отнюдь не должна быть аксиально-симметричной по
своим свойствам; поэтому
главные значения этого тензора (нить, в виде которой
мы представляем себе молекулу, отнюдь не должна быть аксиально-симметричной по
своим свойствам; поэтому  и
и  не
должны быть равными). Выражение (*) примет в результате вид
не
должны быть равными). Выражение (*) примет в результате вид
 ,
,
где
 и
и 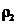 -
компоненты
-
компоненты 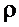 в направлении соответствующих главных осей.
в направлении соответствующих главных осей.
Наконец,
интегрируя вдоль всей длины молекулы, найдем полное изменение ее свободной
энергии в результате слабого изгиба:
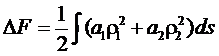 (127.2)
(127.2)
(s -
координата вдоль длины нити). Величины  и
и  , очевидно, непременно положительны.
, очевидно, непременно положительны.
Пусть
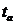 и
и  -
единичные векторы вдоль направления касательных к нити в двух ее точках (точки a и b),
разделенных участком длины s. Обозначим через
-
единичные векторы вдоль направления касательных к нити в двух ее точках (точки a и b),
разделенных участком длины s. Обозначим через  угол
между этими касательными, т.е.
угол
между этими касательными, т.е.
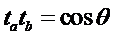 .
.
Рассмотрим
сначала случай такого слабого изгиба, при котором угол 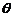 мал даже для удаленных точек. Проведем две плоскости,
проходящие через
мал даже для удаленных точек. Проведем две плоскости,
проходящие через 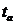 и две главные оси тензора
и две главные оси тензора  в нормальной (в точке a) плоскости.
При малых значениях
в нормальной (в точке a) плоскости.
При малых значениях 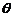 квадрат угла
квадрат угла 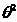 может
быть представлен в виде
может
быть представлен в виде
 , (127.3)
, (127.3)
где
 и
и  - углы
поворота вектора
- углы
поворота вектора  относительно вектора
относительно вектора 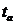 в
указанных двух плоскостях. Компоненты вектора кривизны связаны с функциями
в
указанных двух плоскостях. Компоненты вектора кривизны связаны с функциями  и
и 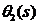 соотношениями
соотношениями
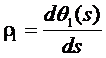 ,
, 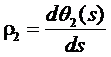 ,
,
и
изменение свободной энергии при изгибе молекулы принимает вид
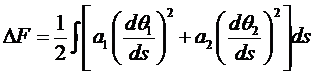 . (127.4)
. (127.4)
При
вычислении вероятности флуктуации с заданным значением 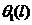 =
= и
и 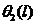 =
= при некотором определенном l надо
рассмотреть наиболее полное равновесие, возможное при этих значениях
при некотором определенном l надо
рассмотреть наиболее полное равновесие, возможное при этих значениях  и
и  . Другими
словами, надо определить наименьшее значение свободной энергии, возможное при
заданных
. Другими
словами, надо определить наименьшее значение свободной энергии, возможное при
заданных  и
и  . Но
интеграл вида
. Но
интеграл вида
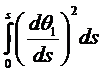
при
заданных значениях функции 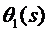 на обоих
пределах
на обоих
пределах 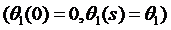 имеет минимальное значение, если
имеет минимальное значение, если  меняется по линейному закону. Покажем это. Задача
минимизации интеграла относится к классу задач вариационного счисления. Если
проводить аналогию с механикой, то выражение под интегралом есть функция
Лагранжа, а s играет роль времени. Тогда запишем уравнение:
меняется по линейному закону. Покажем это. Задача
минимизации интеграла относится к классу задач вариационного счисления. Если
проводить аналогию с механикой, то выражение под интегралом есть функция
Лагранжа, а s играет роль времени. Тогда запишем уравнение:
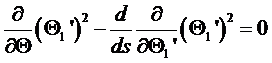 .
.
Откуда
получим:
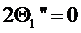 .
.
Решением
этого уравнения является линейная функция, которая при учете граничных условий
принимает вид:
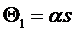 .
.
В
результате интегрирования получим
 .
.
При
изотермическом процессе способность совершать работу характеризуется свободной
энергией, следовательно, вероятность флуктуации в данном случае можно записать
в виде
 .
.
В
таком случае для средних квадратов обоих углов получаем
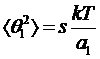 ,
, 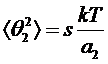
Средний
же квадрат интересующего нас угла  равен
равен
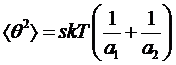 . («)
. («)
Как
и следовало ожидать, в этом приближении он оказывается пропорциональным длине
отрезка молекулы между двумя рассматриваемыми точками. В выражении («) можно
выделить величину с размерностью длины:
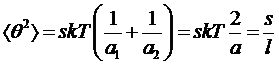 ,
,
где
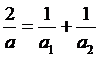 ,
,  .
.
Из
выражения для свободной энергии легко видеть, что l имеет
размерность длины.
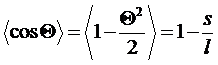 .
.
Можно
показать, что при достаточно больших величинах s среднее
значение быстро убывает с ростом s и равно
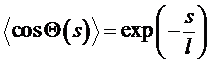 .
.
Проанализируем
это выражение. Рассмотрим короткий по сравнению с l участок цепи.
При s << l 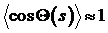 , т.е. угол флуктуирует около нуля, а концы короткого
по сравнению с l участка почти параллельны. В противоположном случае
угол принимает почти любое значение, а память о направлении цепи на длине,
намного большей l отсутствует.
, т.е. угол флуктуирует около нуля, а концы короткого
по сравнению с l участка почти параллельны. В противоположном случае
угол принимает почти любое значение, а память о направлении цепи на длине,
намного большей l отсутствует.
Величина
l называется персистентной длиной (от слова «стойкий»),
или такой минимальной длиной участка, который способен сопротивляться изгибу.
Поскольку память о направлении распространяется по обе стороны по цепи, то
легко понять, что длина сегмента Куна должны примерно в два раза превышать
персистентную длину l.
.
Высокоэластичность полимеров с точки зрения статистической физики
Как
известно, некоторые полимеры (резина, каучук) обладают свойством высокой
эластичности, т.е. способностью к большим обратимым относительным деформациям
(для резины - до 8 раз). Оказалось, что необходимым условием высоко
эластичности является наличие сшивок между полимерными цепями (вулканизация,
вкрапления атомов серы), которые приводят к формированию полимерной сетки в
веществе. Эта сетка не может течь, но может деформироваться.
Рассмотрим,
как высокоэластичность проявляется на уровне отдельных полимерных молекул.
Опишем поведение отдельной полимерной цепи, растягиваемой силой f.
Первый такой эксперимент с молекулами ДНК проведен в 1992 году. Зададимся
вопросом: как зависит координата конца вектора R от f?
Если рассмотреть идеальную полимерную цепь, состоящую из свободно-сочлененных
участков длины l, в которой отсутствуют объемные взаимодействия, то
неясно, откуда берется сила противодействия (по третьему закону Ньютона)?
Например, в случае кристалла упругость связана с наличием сил взаимодействия
(притяжения и отталкивания) между атомами (молекулами). В идеальной же
макромолекуле таких сил нет, а изменение ее длины происходит за счет
выпрямления и распутывания. Такая модель во многом сходна с идеальным газом.
При
деформации вектора R на величину ΔR совершается
работа, равная
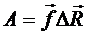 .
.
На
что идет такая работа, если растяжение происходит при постоянной температуре T?
Очевидно, что в данном случае, работа идет на изменение энтропии цепочки (здесь
проявляется аналогия со сжатием идеального газа).
Рассчитаем
энтропию полимерной цепи, исходя из распределения Гаусса. Воспользовавшись
формулой для энтропии
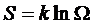 ,
,
и
считая, что величина Ω
(в данном случае - число различных
реализаций полимерной цепи при данной ее длине) пропорциональна величине PN,
получим:
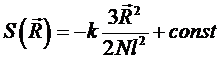 .
.
Тогда
можно записать формулу для работы:
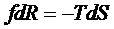
(знак
минус в данном случае возникает из-за уменьшения энтропии) и силы
 .
.
Фактически
мы получили закон Гука для данного случая. Отметим, что модуль упругости в
данном случае пропорционален 1/N, то есть очень мал для длинных полимеров.
Перейдем
теперь к рассмотрению энтропийной упругости полимерной сетки, состоящей из
идеальных субцепей (субцепь - элементарный кирпичик структуры полимерной сетки
между двумя соседними сшивками). Пусть каждая субцепь состоит из N
сегментов длины l. При растяжении сетки ее субцепи так же
растягиваются, вследствие чего их энтропия уменьшается.
Допустим,
что полимерная сетка представляет собой прямоугольный параллелепипед, который
растягивается по осям в λx, λy и λz,
соответственно. В результате получим для изменения энтропии в результате
деформации сетки:
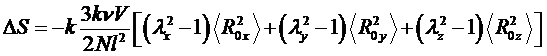 ,
,
где
ν
- число субцепей в единице объема, V -
объем сетки, R0x, R0y, R0z - координаты какой-либо субцепи. Учтем теперь, что
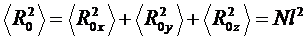 .
.
Учтем
так же, что при недеформированном образце все три координатные направления были
равноправны. Отсюда следует, что
 .
.
Окончательно
получим для энтропии:
 .
.
В
это выражение не входят параметры отдельной субцепи N и l.
Это указывает на универсальность выражения и является следствием идеальности
субцепей.
Рассмотрим
одноосное растяжение сетки вдоль оси x. При этом размеры сетки вдоль
осей y и z изменяются свободно. Оказывается, что объем полимера
при этом практически не меняется (он ведет себя как жидкость - при давлении 100
атм объем полимера изменяется лишь на 1%). Тогда имеем
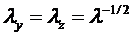 .
.
Тогда
получим для энтропии:
 .
.
Растягивающая
сила получается аналогично:
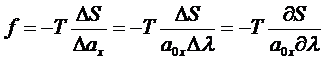 .
.
Определим
напряжение:
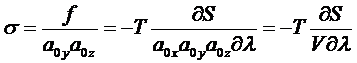 .
.
Окончательно получим:
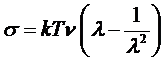 . (*)
. (*)
Формула
является одной из основных в теории высокоэластичности полимерных пленок.
Учтем, что если деформации невелики (λ близко к единице), то
 .
.
Величина
же

представляет
собой относительную деформацию. Тогда получим для модуля Юнга полимерной сетки:
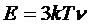 .
.
Эта
величина равна давлению идеального газа, концентрация молекул которого в три
раза больше, чем концентрация сшивок в сетке. Чем меньше степень сшивки
полимерного вещества, тем меньше его модуль Юнга. Замечательно, что выражение
(*) описывает нелинейную упругость.
Литература
1. Иродов, И.
Е. Задачи по общей физике. - СПб. : Лань, 2009. - 416 с.
. Иродов, И.
Е. Сборник задач по атомной и ядерной физике. - М. Атомиздат, 1976.
. Киттель, Ч.
Берклеевский курс физики : в 5 т. / пер. с англ. ; Ч. Кит" тель, У. Найт,
М. Рудерман [и др.] ; под ред. А. И. Шальникова, А. С. Ахматова, А. О.
Вайсенберга. - М. : Мир, 1971-1972.
. Коган, Б.
Ю. Сто задач по физике. - М. : Наука, Физматлит, 1986.
. Сивухин, Д.
В. Общий курс физики : в 5 т. - М. : Наука, Физматлит, МФТИ, 1989-2006.
. Савельев,
И. В. Курс общей физики : в 3 т. - СПб. : Лань, 2011.
. Савельев,
И. В. Сборник вопросов и задач по общей физике. - СПб. : Лань, 2007. - 288 с.
. Телеснин,
Р. В. Молекулярная физика : учеб. пособие. - СПб : Лань, 2009.
. Фейнман, Р.
Фейнмановские лекции по физике : в 9 т. / пер. с англ. ; Р. Фейнман, Р. Лейтон,
М. Сэндс ; под ред. Я. А. Смородинского. -М. : Мир, 1977.
. Фейнман, Р.
Фейнмановские лекции по физике. Задачи и упражнения с ответами и решениями /
пер. с. англ. Р. Фейнман, Р. Лейтон,
М. Сэндс ;
под общей ред. А. П. Леванюка. - М. : Мир, 1969