Теория передачи сигналов

Теория передачи сигналов

Белорусский национальный технический университет

Международный институт дистанционного образования

Кафедра "Информационные системы и технологии"

Контрольная работа

"Теория передачи сигналов"

Минск

1. Понятие количества информации

В теории информации изучаются количественные закономерности передачи, хранения ,и обработки информации.

Назначение любой системы связи - передать в течение заданного времени как можно больше достоверных сведений от одного объекта или корреспондента к другому.

Проблема достоверности при различных способах приема и передачи сообщений рассматривалась в теории помехоустойчивости. Эта теория, как мы убедились, позволяет не только найти достоверность передачи при заданных условиях, но и выяснить, при каких методах передачи и обработки сигналов эта достоверность будет наибольшей.

В теории информации основное внимание уделяется определению средней скорости передачи информации и решению задачи максимизации этой скорости путем применения соответствующего кодирования. Предельные соотношения теория информации позволяют оценить эффективность различных систем связи и установить условия согласования, в информационном отношении источника с каналом и канала с потребителем.

Для исследования этих вопросов с общих позиций необходимо прежде всего установить универсальную количественную меру информации, не зависящую от конкретной физической природы передаваемых сообщений. Когда принимается сообщение о каком-либо событии, то наши знания о нем изменяются. Мы получаем при этом некоторую информацию об этом событии. Сообщение о хорошо известном нам событии, очевидно, никакой информации не несет. Напротив, сообщение о малоизвестном событии содержит много информации. Например, сообщение бюро погоды от 20 июня о том, что в Одессе "завтра выпадет снег" несет больше информации, чем сообщение "завтра ожидается ясная погода". Первое сообщение является неожиданным, оно несет сведения о редком, маловероятном явлении и поэтому содержит много информации. Второе сообщение является весьма вероятным, оно содержит мало нового и поэтому несет мало информации.

Таким образом, количество информации в сообщении о некотором событии существенно зависит от вероятности этого события.

Вероятностный подход и положен в основу определения меры количества информации. Для количественного определения информации, в принципе, можно использовать любую монотонно убывающую функцию вероятности F[P(a)] где Р(а) - вероятность, сообщения а. Простейшей из них является функция F=1/Р(а) которая характеризует меру неожиданности (неопределенности) сообщения. Однако удобнее исчислять количество информации а логарифмических единицах, т. е. определять количество информации в отдельно взятом сообщении как

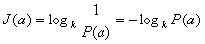
Так как 0<P(a)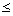l, то J(a) - величина всегда положительная и конечная. При Р(а)=1 количество информации равно нулю, т. е., сообщение об известном событии никакой информации не несет. Логарифмическая мера обладает естественным в данном случае свойством аддитивности, согласно которому количество информации, содержащееся в нескольких независимых сообщениях, равна сумме количества информации в каждом из них. Действительно, так как совместная вероятность пнезависимых сообщений 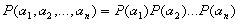, то количество информации а этих сообщениях равно: 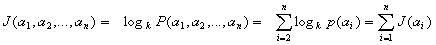, что соответствует интуитивным представлениям об увеличении информации при получении дополнительных сообщений. Основание логарифма k может быть любым. Чаще всего принимают k=2, и тогда количество информации выражается в двоичных единицах: 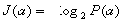дв. ед.

Двоичную единицу иногда называют бит. Слово бит произошло от сокращения выражения binary digit (двоичная цифра). В двоичных системах связи для передачи сообщения используется два символа, условно .обозначаемых 0 и 1. В таких системах при независимых и равновероятных символах, когда P(0)=P(1)=1/2, каждый из них несет одну двоичную единицу информации:

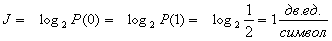
Формула (6.1) позволяет вычислять количество информация в. сообщениях, вероятность которых отлична от нуля. Это, в свою очередь, предполагает, что сообщения дискретны, а их число ограничено. В таком случае принято говорить об ансамбле сообщений, который описывается совокупностью возможных сообщений и их вероятностей:

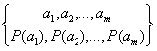
Если все сообщения равновероятны: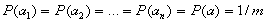, то количество информации в каждом из них определяется величиной

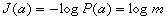
Отсюда следует, что количество информации в сообщении зависит от ансамбля, из которого, оно выбрано. До передачи сообщения имеется неопределенность относительно того, какое из mсообщений ансамбля будет передано после приема сообщения эта неопределенность снимается. Очевидно, чем больше т, тем больше неопределенность и тем большее количество информации содержится в переданном сообщении.

Рассмотрим пример. Пусть ансамбль возможных сообщений представляет собой алфавит, состоящий из m различных букв. Необходимо определить, какое количество информации содержится в передаваемом слове длиной п букв, если вероятности появления букв одинаковы, а сами буквы следуют независимо друг от друга. Количество информации при передаче одной буквы: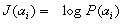. Так как все буквы равновероятны, то 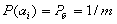 и количество информации, содержащееся в любой букве,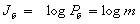. Буквы следуют независимо поэтому количество информации в слове из п букв

К определению информации можно подойти и с другой стороны. Будем рассматривать в качестве сообщения не отдельную букву, а целое слово. Если все буквы равновероятны и следуют независимо, то все слова будут также равновероятны и 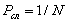 , где N=mⁿ - число возможных слов. Тогда можно записать

Для двоичного кода ансамбль элементарных сообщений состоит из двух элементов 0 и 1 (m=2). В этом случае сообщение из п элементов несет информацию,

 )

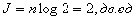В общем случае при передаче сообщений неопределенность снимается не полностью. Так, в канале с шумами возможны ошибки. По принятому сигналу v только с некоторой вероятностью 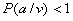 можно судить о том, что было передано сообщение а. Поэтому после получения сообщения остается некоторая неопределенность, характеризуемая величиной апостериорной вероятностиP(a/v), а количество информации, содержащееся в сигнале v, определяется степенью уменьшения неопределенности при его приеме. Если Р(а) - априорная ,вероятность, то количество информации в принятом сигнале v относительно переданного сообщения а, очевидно, будет равно:

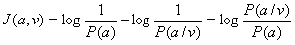
Это выражение можно рассматривать также как разность между количеством информации, поступившим от источника сообщений, и тем количеством информации, которое потеряло в канале за счет действия шумов.

Задача 1

На контролируемом пункте, аналогичном описанному в задаче 2.2.11, производится периодический контроль состояния объектов. Количество сообщений, передаваемых о состоянии каждого объекта, одинаково. Наблюдением установлено, что в среднем объект 1 включён 98%, объект 2 - 80%, а объект 3 - 0,6% всего времени. В остальное время объекты отключены. Определить количество информации, содержащееся в одном сообщении.

Решение

Так как количество сообщений, передаваемых от каждого объекта, одинаково, то 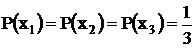. Из статистики наблюдений можно записать выражения для определения вероятности того, что объекты находятся во включенном состоянии:

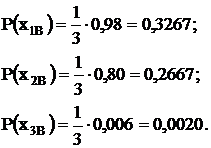
Вероятности того, что объекты находятся в отключенном состоянии:

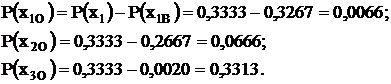
Искомая энтропия:

= 1,88 (бит / сообщение).

Ответ: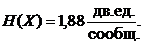

Задача 2

Закодировать блок X=x₁x₂x₂x₁x₁x₁x₂x₁ префиксным кодом при неизвестной статистике сообщений, если символы x₁ появляются с вероятностью p, а x₂ - c вероятностью q.

Решение

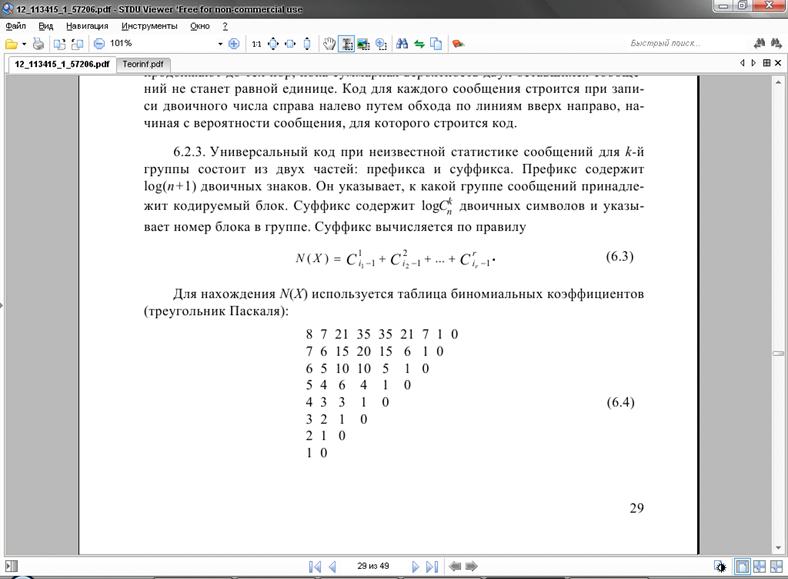
Определим число разрядов префикса: 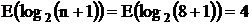, где функция Е означает округление в большую сторону.

Вероятность слова:

Тогда префикс будет 0011. Префикс указывает, к какой группе сообщений принадлежит кодируемый блок.

Число символов х₁ равно r = 5, которые размещаются на местах i₁ = 1, i₂ = 4, i₃ = 5, i₄ = 6, i₅ = 8.

Находим номер блока:

Номер блока в двоичной записи (так как 33₁₀ = 100001₂):

N(X) = 100001.

Следовательно, закодированный блок поступит в канал связи в виде:

Х = 0011100001.

Ответ: X = 0011100001

Список использованной литературы

информация сообщение кодирование префиксный

1.      Кловский Д.Д. Теория передачи сигналов.- М.,"Связь",1993.

.        Шинаков Ю.С. Теория передачи сигналов в электросвязи. - М.: Радио и связь. 1989.

4.      Мардер Н.С. Современные телекоммуникации. - М.: ИРИАС, 2006. - 384 с.

5.      Локшин Б.А. Цифровое вещание: от студии к телезрителю - М.: Компания САЙРУС СИСТЕМС, 2001. - 285 с.

.        Зубарев Ю.Б., Кривошеев И.Н., Красносельский И.Н. Цифровое телевизионное вещание. Основы, методы системы. - М.: Научно-исследовательский институт радио (НИИР), 2001.- 568 с.

.        Кривошеев М.И. Международная стандартизация цифрового телевизионного вещания.- М.: Научно-исследовательский институт радио (НИИР). 2006.-928с.

.        Красносельский И.Н. Анализ зарубежного опыта и тенденций перехода на цифровое наземное ТВ вещание // Электросвязь.- 2007.- №3.- С. 18-22.

.        Вилкова Н.Н., Зубарев Ю.Б. Состояние и перспективы развития цифрового телевизионного вещания в России// Электросвязь.- 2008.- №1.