Теория машин и механизмов
ВОПРОСЫ
К ЭКЗАМЕНУ ПО «ТММ» специальности 1705
1. Приведите классификацию
кинематических пар. Какие пары могут существовать в плоских механизмах.
2. В чем заключаются формулы образования
пространственных и плоских механизмов (Малышева. Чебышева).
3. Укажите основные характеристики
пассивных звеньев, кинематических пар и приведите примеры.
4. Каковы принципы образования
механизмов по Ассуру. Что такое группа Ассура. Приведите основные виды плоских
рычажных механизмов образованных группами 2 класса 2 порядка.
5. Структурный анализ механизмов
рассмотрите на примере. Обоснуйте основные цели и условия замены в плоских
механизмах высших кинематических пар низшими.
6. Каковы основные задачи
кинематического исследования механизмов. Понятие о геометрических и
кинематических характеристиках. Связь кинематических и передаточных функций.
7. Каковы основные задачи
кинематического анализа механизмов. Аналитический метод – способ проекций
векторного контура (рассмотреть на примере).
8. Каковы основные задачи
кинематического анализа механизмов. В чем заключается метод планов (показать на
примере).
9. Каковы основные задачи
кинематического анализа механизмов. В чем заключается метод графического
дифференцирования диаграмм.
10.Укажите основные задачи
проектирования механизмов. Приведите условие нормальной работы, кинематику и
параметры, достоинства и недостатки фрикционных передач. Что такое вариатор
скорости.
11. Объясните основную теорему
зацепления, проанализируйте её следствия.
12. Каковы геометрические элементы
зубчатых колёс.
13. Сложные зубчатые механизмы.
Приведите последовательность определения передаточного отношения зубчатых
сложных передач с промежуточными колесами и валами.
14. Укажите основные определения и виды
планетарных передач, объясните их назначение.
15. Проанализируйте на примере
аналитический метод кинематического анализа планетарных передач (метод
Виллиса).
16. В чем заключается графоаналитический
метод кинематического анализа планетарных передач (приведите последовательность
действий на примере).
17. Обоснуйте основные задачи и условия
синтеза планетарных передач.
18. Что такое волновые механизмы, их
основные преимущества, область применения, определение передаточного отношения.
19. Основные критерии синтеза зубчатых
зацеплений. Укажите основные свойства эвольвенты окружности. Что такое инволюта
угла.
20. Проанализируйте свойства
эвольвентного зацепления зубчатых колес.
21. Каковы основные методы изготовления
зубчатых колес и особенности геометрии режущего инструмента.
22. Смещение режущего инструмента при
нарезании зубчатого колеса. Заострение зуба при смещении.
23. Когда наблюдается и в чём
заключается явление подрезания зубьев. Получите минимально-допустимое
нарезаемое число зубьев, приведите и проанализируйте основные методы коррегирования
зубчатых колес.
24.Каково назначение, классификация,
геометрия и кинематика червячных передач.
25. Каково назначение, виды и
особенности геометрических параметров винтовых передач.
26. Каково назначение, основные
параметры, классификация и структура кулачковых механизмов.
27. Приведите последовательность
кинематического анализа кулачковых механизмов методом кинематических диаграмм.
28. Проанализируйте и получите основные
зависимости и условия синтеза кулачковых механизмов наименьших размеров.
29.Приведите и сопоставьте между собой
основные законы движения толкателя в кулачковых механизмах.
30. В чем заключаются основные задачи
силового анализа механизмов. Приведите классификацию сил действующих в
механизме.
31. Механические характеристики машин,
приведите примеры для машин двигателей и исполнительных машин.
32. Что такое сила инерции, объясните
особенности этих сил для тел с вращательным, поступательным и сложным
движением.
33. В чём заключается условие
кинетостатической определимости кинематических цепей.
34. Приведите последовательность
силового анализа механизмов методом планов на примере.
35. В чём заключается метод проф. Н.Е.
Жуковского для определения уравновешивающей силы, когда его целесообразнее
использовать.
36. Укажите основные режимы движения
механизмов и приведите уравнения каждого из них.
37. Прямая задача динамики. Уравнение
движения механизма в дифференциальном виде.
38. Что такое динамическая модель
машинного агрегата, для чего её используют. Приведение сил и моментов сил к
звену приведения.
39. Что такое динамическая модель
машинного агрегата, для чего её используют. Приведение масс и моментов инерции
масс звеньев в механизме.
40. Проанализируйте установившееся
движение машинного агрегата, объясните почему возникает периодическая
неравномерность движения и как решается задача её регулирования.
41. Приведите последовательность расчета
махового колеса при действии сил зависящих от положения механизма (частный
случай Jп = const).
42.Вибрации и колебания в машинах.
Понятие о неуравновешенности механизма (звена). Метод замещающих масс.
43. Полное и частичное статическое
уравновешивание кривошипно-ползунного механизма.
44. Балансировка роторов при
статической, моментной и динамической неуравновешенности.
45.Когда возникает трение скольжения,
объясните, как направлена и находится сила трение скольжения. Проанализируйте
от чего зависит коэффициент трения. Что такое угол и конус трения.
46. В чём заключается условие
самоторможения на горизонтальной плоскости, при каких случаях тело будет
двигаться ускоренно. Какое трение наблюдается при движении клинчатого ползуна.
Что такое приведенный коэффициент трения.
47. Получите основные условия для
движения тела вверх и вниз по наклонной плоскости с учетом трения.
48. Приведите последовательность расчета
момента необходимого при монтаже и демонтаже резьбового соединения.
49. Укажите особенности трения во
вращательной кинематической паре и пятах.
50. Укажите особенности трения гибких
тел. Получите формулу Эйлера.
51. Укажите особенности трения качения,
когда возможно чистое качение тела.
52. Что такое КПД, приведите основные
расчетные формулы для его определения. Как определяется КПД механизма с
последовательным соединением звеньев.
53. Что такое КПД, приведите основные
расчетные формулы для его определения. Как определяется КПД механизма с
параллельным соединением звеньев.
54. Что такое КПД. Как определяется КПД
винтовой передачи.
Лекция
1
Введение. Цель и задачи
курса ТММ. Место курса в системе подготовки инженера. Машинный агрегат и его
составные части. Классификация машин. Механизм и его элементы. Классификация
механизмов. Краткая историческая справка.
Введение. Курс «Теория машин и механизмов»
является общетехнической дисциплиной, изучается в течение одного семестра и
состоит из: курса лекций объемом 28 часов, практических занятий (включая
рубежный контроль) - 12 часов, лабораторный практикум - 12 часов. Курсовая
работа с объемом 1 лист графической части и пояснительная записка на 30-50
рукописных (машинописных) страниц. Курсовая работа защищается комиссии из двух
преподавателей, по ней проставляется дифференцированная оценка. Семестр завершается
экзаменом с учетом рубежного контроля, выполненной контрольной работы и
защищенным лабораторным работам.
Курс ТММ базируется на
знаниях полученных студентом на младших курсах при изучении физики, высшей
математики, теоретической механики, инженерной графики и вычислительной
техники. Знания, навыки и умение приобретенные студентом при изучении ТММ
служат базой для курсов детали машин, основы конструирования элементов
химического оборудования, машины и аппараты химических производств.
Рекомендуемая основная
литература
1. Теория механизмов и машин. Под
ред. К.В.Фролова. М.: Высшая школа, 1987.
2.
Артоболевкий И.И.
Теория механизмов и машин. - М.: Наука, 1988.
3.
Левитский Н.И.
Теория механизмов и машин. - М.,: Наука, 1990.
4.
Семенов М.В.
Структура и кинематика механизмов.- Л.: СЗПИ, 1967.
5.
Семенов М.В.
Динамика механизмов.- Л.: СЗПИ, 1968.
Рекомендуемая
дополнительная литература
1.
Артоболевский
И.И., Эдельштейн Б.В. Сборник задач по теории механизмов и машин. М., 1973 г.
2.
Кожевников С.Н.
Теория механизмов и машин. М., 1975 г.
3.
Кореняко А.С.
Курсовое проектирование по теории механизмов и машин. М-К.:, 1964 г.
4.
Безвесельный.
Курсовое проектирование по теории механизмов и машин в примерах. Харьков, 1960
г.
5.
Попов С.А.
Курсовое проектирование по теории механизмов и машин. М., 1986 г.
Цель и задачи курса
Теория механизмов и
машин - научная
дисциплина об общих методах исследования свойств машин и механизмов и
проектирования их новых схем. Она изучает строение (структуру), кинематику и
динамику механизмов в связи с их анализом и синтезом.
Цель ТММ - анализ и синтез типовых механизмов
и их систем.
Задачи ТММ: разработка общих методов
исследования структуры, геометрии, кинематики и динамики типовых механизмов и
их систем.
Основные разделы курса
ТММ:
· структура механизмов и машин;
· геометрия механизмов и их элементов;
· кинематика механизмов;
· динамика машин и механизмов.
Изучение курса начнем с общих
определений:
Машины
и их классификация
Машина - техническое устройство,
выполняющее преобразование энергии, материалов и информации с целью облегчения
физического и умственного труда человека, повышения его качества и производительности.
Существуют следующие виды
машин:
1.
Энергетические
машины -
преобразующие энергию одного вида в энергию другого вида. Эти машины бывают
двух разновидностей:
Двигатели (рис.1.1), которые преобразуют любой
вид энергии в механическую (например, электродвигатели преобразуют
электрическую энергию, двигатели внутреннего сгорания преобразуют энергию
расширения газов при сгорании в цилиндре).
 Pэл
(U, I) Pмех (M, )
Pэл
(U, I) Pмех (M, )

 Двигатель
Двигатель
Рис.1.1
Генераторы (рис.1.2), которые преобразуют
механическую энергию в энергию другого вида (например, электрогенератор
преобразует механическую энергию паровой или гидравлической турбины в
электрическую)


 Pмех (M,
) Pэл (U, I)
Pмех (M,
) Pэл (U, I)
Генератор
Рис.1.2
2.
Рабочие машины - машины использующие механическую
энергию для совершения работы по перемещению и преобразованию материалов. Эти
машины тоже имеют две разновидности:
Транспортные машины (рис.1.3), которые используют
механическую энергию для изменения положения объекта (его координат).


 Pмех (M, )
Pмех (M, )
Транспортная
машина
f (x0,y0)
f (xn,yn)
Рис.1.3
Технологические машины (рис.1.4), использующие механическую
энергию для преобразования формы, свойств, размеров и состояния объекта.
 Pмех (M, )
Pмех (M, )
Технологическая

 машина
машина
f (x0, y0, z0) f (xn, yn, zn)
Рис.1.4
3.
Информационные
машины - машины,
предназначенные для обработки и преобразования информации. Они подразделяются на:
Математические машины (рис.1.5), преобразующие входную
информацию в математическую модель исследуемого объекта.

Математическая

 машина
машина
I0, Кбит In, Кбит
Рис.1.5
Контрольно-управляющие
машины (рис.1.6),
преобразующие входную информацию (программу) в сигналы управления рабочей или
энергетической машиной.


 I0
I0

 Программа Контр.-упр. машина
Программа Контр.-упр. машина
Ii
Ii
Рабочая машина
Рис.1.6
4. Кибернетические
машины (рис.1.7) -
машины управляющие рабочими или энергетическими машинами, которые способны
изменять программу своих действий в зависимости от состояния окружающей среды
(т.е. машины обладающие элементами искусственного интеллекта).
Окружающая среда
Ij


 I0
I0

 Программа
Контр.-упр. машина
Программа
Контр.-упр. машина
Ii Ii
Рабочая машина
Рис.1.7
Машинный
агрегат
Машинным агрегатом (рис. 1.8) - называется техническая
система, состоящая из одной или нескольких соединенных последовательно или
параллельно машин и предназначенная для выполнения каких-либо требуемых
функций. Обычно в состав машинного агрегата входят: двигатель, передаточный
механизм и рабочая или энергетическая машина. В настоящее время в состав
машинного агрегата часто включается контрольно-управляющая или кибернетическая
машина. Передаточный механизм в машинном агрегате необходим для согласования
механических характеристик двигателя с механическими характеристиками рабочей
или энергетической машины.

 Двигатель Передаточный
механизм Рабочая машина
Двигатель Передаточный
механизм Рабочая машина
Контрольно-управляющая
машина
Рис.1.8
Типовыми механизмами будем называть простые механизмы,
имеющие при различном функциональном назначении широкое применение в машинах,
для которых разработаны типовые методы и алгоритмы синтеза и анализа.
Рассмотрим в качестве
примера кривошипно-ползунный механизм. Этот механизм широко применяется в
различных машинах: двигателях внутреннего сгорания, поршневых компрессорах и
насосах, станках, ковочных машинах и прессах. В каждом варианте функционального
назначения при проектировании необходимо учитывать специфические требования к
механизму. Однако математические зависимости, описывающие структуру, геометрию,
кинематику и динамику механизма при всех различных применениях будут
практически одинаковыми. Главное или основное отличие ТММ от учебных дисциплин
изучающих методы проектирования специальных машин в том, что ТММ основное
внимание уделяет изучению методов синтеза и анализа, общих для данного вида
механизма, независящих от его конкретного функционального назначения.
Специальные дисциплины изучают проектирование только механизмов данного
конкретного назначения, уделяя основное внимание специфическим требованиям. При
этом широко используются и общие методы синтеза и анализ, которые изучаются в
курсе ТММ.
Если при рассмотрении
структуры машины для её элементов, не принимается во внимание их форма и
внутреннее строение, а рассматривается только выполняемые ими функции, то такие
элементы называются функциональными. Для механической системы элементами могут
быть: деталь, звено, группа, узел, простой или типовой механизм.
Деталь - элемент конструкции не имеющий в
своем составе внутренних связей (состоящий из одного твердого тела).
Звено - твердое тело, или система жестко
связанных твердых тел (может состоять из одной или нескольких деталей),
входящее в состав механизма и совершающее особое относительное движение по
отношению к другим телам. Одно из звеньев механизма всегда неподвижно – это
стойка.
Стойка - звено, которое при исследовании
механизма принимается за неподвижное (корпус механизма).
Звенья механизма связаны
между собой кинематическими парами. Кинематическая пара – это подвижное
соединение двух соприкасающихся звеньев.
Группа - кинематическая цепь,
состоящая из подвижных звеньев, связанных между собой кинематическими парами
(отношениями), и удовлетворяющая некоторым заданным условиям.
Узел - несколько деталей связанных между
собой функционально, конструктивно или каким-либо другим образом.
С точки зрения системы
узлы, группы, простые или типовые механизмы рассматриваются как подсистемы.
Самым низким уровнем разбиения системы при конструировании является уровень
деталей; при проектировании - уровень звеньев. Элементы из системы можно
выделить только после определения взаимосвязей между ними, которые описываются
отношениями. Для механических систем интерес представляют отношения
определяющие структуру системы и ее функции, т. е. расположения и связи. Расположения
- такие отношения между элементами, которые описывают их геометрические относительные
положения. Связи - отношения между элементами, предназначенные для
передачи материала, энергии или информации между элементами. Связи могут осуществляться
с помощью различных физических средств: механических соединений, жидкостей,
электромагнитных или других полей, упругих элементов.
Механические соединения
могут быть подвижными (кинематические пары) и неподвижными. Неподвижные
соединения делятся на разъемные (винтовые, штифтовые) и неразъемные (сварные,
клеевые).
Механизмом называется система твердых тел,
предназначенная для передачи и преобразования заданного движения одного или
нескольких тел в требуемые движения других твердых тел.
Кинематическая цепь - система звеньев, образующих между
собой кинематические пары.
Число степеней свободы или подвижность механизма
- число независимых обобщенных координат, однозначно определяющее положение
всех его звеньев на плоскости или в пространстве.
Из теоретической
механики: Системы
материальных тел (точек), положения и движения которых подчинены некоторым
геометрическим или кинематическим ограничениям, заданным наперед и не зависящим
от начальных условий и заданных сил, называется несвободной. Эти
ограничения, наложенные на систему и делающие ее несвободной называются связями.
Положения точек системы, допускаемые наложенными на нее связями называются
возможными. Независимые друг от друга величины однозначно определяющие
возможные положения системы в произвольный момент времени называются обобщенными
координатами системы.
Входные звенья - звенья, которым сообщается
заданное движение или соответствующие силовые факторы (силы или моменты); выходные
звенья - те, на которых получают требуемое движение и силы.
Начальное звено - звено, координата которого принята
за обобщенную. Начальная кинематическая пара - пара, относительное
положение звеньев в которой принято за обобщенную координату.
Рассмотрим пример
механизма представленного на рис. 1.9: он состоит из трех подвижных звеньев,
одного неподвижного звена – стойки и четырёх кинематических пар (все они
разрешают только вращательное движение), (звенья на структурной схеме обозначаются
цифрами; кинематические пары буквами латинского алфавита, соединения со стойкой
нумерацией стойки с индексом соединяемого подвижного звена – 01, 03).
Рис. 1.9
Строение механизмов
Как отмечалось
выше, структура любой технической системы определяется функционально связанной
совокупностью элементов и отношений между ними. При этом для механизмов под
элементами понимаются звенья, группы звеньев или типовые механизмы, а под
отношениями подвижные (кинематические пары) или неподвижные соединения. Поэтому
под структурой механизма понимается совокупность его элементов и отношений
между ними, т.е. совокупность звеньев, групп или типовых механизмов и подвижных
или неподвижных соединений. Геометрическая структура механизма полностью
описывается заданием геометрической формы его элементов, их расположения,
указания вида связей между ними. Структурная схема - графическое
изображение механизма, выполненное с использованием условных обозначений
рекомендованных ГОСТ (см. например ГОСТ 2.703-68) или принятых в специальной
литературе, содержащее информацию о числе и расположении элементов (звеньев,
групп), а также о виде и классе кинематических пар, соединяющих эти элементы. В
отличие от кинематической схемы механизма, структурная схема не содержит
информации о размерах звеньев и вычерчивается без соблюдения масштабов.
(Примечание: кинематическая схема - графическая модель механизма,
предназначенная для исследования его кинематики).
Задачей структурного
анализа является
определение параметров структуры заданного механизма - числа звеньев и
структурных групп, числа и вида кинематических пар, числа подвижностей
(основных и местных), числа контуров и числа избыточных связей.
Задачей структурного
синтеза является
синтез структуры нового механизма, обладающего заданными свойствами: числом
подвижностей, отсутствием местных подвижностей и избыточных связей, минимумом
числа звеньев, с парами определенного вида (например, только вращательными,
как наиболее технологичными) и т.п.
Степень подвижности
механизма - число
независимых обобщенных координат однозначно определяющее положение звеньев
механизма на плоскости или в пространстве.
Связь - ограничение, наложенное на
перемещение тела по данной координате.
Избыточные (пассивные) - такие связи в механизме, которые
повторяют или дублируют связи, уже имеющиеся по данной координате, и поэтому не
изменяющие реальной подвижности механизма. При этом расчетная подвижность механизма
уменьшается, а степень его статической неопределимости увеличивается. Иногда
используется иное определение: Избыточные связи - это связи, число
которых в механизме определяется разностью между суммарным числом связей,
наложенных кинематическими парами, и суммой степеней подвижности всех звеньев,
местных подвижностей и заданной (требуемой) подвижностью механизма в целом.
Местные подвижности - подвижности механизма, которые не
оказывают влияния на его функцию положения (и передаточные функции), а введены
в механизм с другими целями (например, подвижность ролика в кулачковом
механизме обеспечивает замену в высшей паре трения скольжения трением качения).
Классификация
кинематических пар
Кинематические пары
определяют характер относительного движения звеньев и налагают условия связи,
т.е. ограничивают движения соединяемых звеньев.
Кинематические пары
классифицируются по следующим признакам:
1.
по числу условий
связей (согласно этой классификации класс пары равен числу условий связей, или
числу ограничений накладываемых на относительные движения звеньев).
Классификация кинематических пар по числу подвижностей и по числу связей
приведена в таблице 1.1.
Таблица 1.1 Классификация
кинематических по числу условий связей
|
Класс
пары
|
Число связей
|
Подвижность
|
Пространственная схема
(пример)
|
Условные
обозначения
|
|
I
|
1
|
5
|
z i
K5вп
y x
j
|
i
K5вп
j
|
|
II
|
2
|
4
|
z i
B4вп
y
j x
|
i
B4вп
j
|
|
Ш
|
3
|
3
|
z
i
C3сф
C
y x
j
|
i
C3сф
j
|
|
IV
|
4
|
2
|
z
j i
x
D2ц
y
|
i
D2ц
j
|
|
V
|
5
|
1
|
z
j i
x
y E1п
Поступательная КП
|
Вращательная
КП
i
E1в
j
Поступательная
КП
i
E1п
j
|
Примечание: Стрелки у
координатных осей показывают возможные угловые и линейные относительные
перемещения звеньев. Если стрелка перечеркнута, то данное движение в
кинематической паре запрещено (т.е. на данное относительное движение наложена
связь).
2.
по виду места
контакта (места связи) поверхностей звеньев:
· низшие, в которых контакт звеньев
осуществляется по плоскости или поверхности (пары скольжения);
· высшие, в которых контакт звеньев
осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием).
Два твердых тела (звена),
соприкасающиеся своими поверхностями и имеющие возможность двигаться
относительно друг друга, образуют кинематическую пару. Кинематическая пара допускает
не любое движение звеньев относительно друг друга, а только такое движение,
которое согласуется с характером соприкосновения и с формой соприкасающихся
поверхностей.
Если звенья, образующие
КП, в силу характера их соприкосновения, могут совершать только простейшие
движения относительно друг друга (вращательное, прямолинейное поступательное
или, в общем случае, винтовое), то пара является низшей. Низшая пара
- пара, в которой требуемое относительное движение звеньев обеспечивается
соприкасанием ее элементов по плоскости или поверхности. В таких парах движение
одного звена относительно другого представляет собой чистое скольжение.
Более сложные
относительные движения можно реализовать в парах, характер соприкасания звеньев
в которых допускает не только относительное скольжение, но и перекатывание.
Такие пары называются высшими. Высшая пара - пара, в которой требуемое
относительное движение звеньев может быть получено только соприкасанием звеньев
по линиям или в точках.
3.
по относительному
движению звеньев, образующих пару:
· вращательные;
· поступательные;
· винтовые;
· плоские;
· сферические.
4.
по способу
замыкания (обеспечения контакта звеньев пары):
· силовое (за счет действия сил веса
или силы упругости пружины, рис. 1.10);
· геометрическое (за счет конструкции
рабочих поверхностей пары, рис. 1.11).
|
 2 1 2 1
В,С
3 01
03
0
|
Рис.
1.10 Рис. 1.11
Кинематические пары в
плоских механизмах
Плоскими называют
механизмы, точки звеньев которых движутся в одной плоскости либо в параллельных
плоскостях.
В плоских механизмах
могут существовать только кинематические пары 4 и 5 классов (т.е. двух и одно
подвижные), причём кинематические пары 4 класса будут высшими, а 5 низшими
(табл. 1.1). Например, механизм на рис. 1.12 является плоским, имеет две низших
вращательных кинематических пары 5 класса 01 и 02 и одну
высшую 4 класса А (разрешает качение и скольжение колеса 1 по 2).
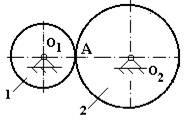
Рис. 1.12
Краткая
историческая справка
Как самостоятельная
научная дисциплина ТММ, подобно другим прикладным разделам науки, возникла в
результате промышленной революции начало которой относится к 30-м годам XVIII века. Однако машины существовали
задолго до этой даты. Поэтому в истории развития ТММ можно условно выделить
четыре периода:
1-й период до начала XIX века - период эмпирического
машиностроения в течение которого изобретается большое количество простых машин
и механизмов: подъемники, мельницы, камнедробилки, ткацкие и токарные станки,
паровые машины (Леонардо да Винчи, Вейст, Ползунов, Уатт). Одновременно
закладываются и основы теории: теорема об изменении кинетической энергии и
механической работы, «золотое правило механики», законы трения, понятие о
передаточном отношении, основы геометрической теории циклоидального и
эвольвентного зацепления (Карно, Кулон, Амонтон, Кадано Дж., Ремер, Эйлер).
2-й период от начала
до середины XIX века - период начала развития ТММ. В это
время разрабатываются такие разделы как кинематическая геометрия механизмов
(Савари, Шаль, Оливье), кинетостатика (Кариолис), расчет маховика (Понселе),
классификация механизмов по функции преобразования движения (Монж, Лану) и
другие разделы. Пишутся первые научные монографии по механике машин (Виллис,
Бориньи), читаются первые курсы лекций по ТММ и издаются первые учебники
(Бетанкур, Чижов, Вейсбах).
3-й период от второй
половины XIX века до
начала XX века - период фундаментального развития
ТММ. За этот период разработаны: основы структурной теории (Чебышев, Грюблер,
Сомов, Малышев), основы теории регулирования машин (Вышнеградский), основы
теории гидродинамической смазки (Грюблер), основы аналитической теории
зацепления (Оливье, Гохман), основы графоаналитической динамики (Виттенбауэр,
Мерцалов), структурная классификация и структурный анализ (Ассур), метод планов
скоростей и ускорений (Мор, Манке), правило проворачиваемости механизма
(Грасгоф) и многие другие разделы ТММ.
4-й период от начала XX века до настоящего времени - период интенсивного развития всех
направлений ТММ как в России, так и за рубежом. Среди русских ученых необходимо
отметить обобщающие работы Артоболевского И.И., Левитского Н.И., Фролова К.В.;
в области структуры механизмов - работы Малышева А.П., Решетова Л.Н., Озола
О.Г.; по кинематике механизмов - работы Колчина Н.И., Смирнова Л.П., Зиновьева
В.А.; по геометрии зубчатых передач - работы Литвина Ф.Л., Кетова Х.Ф.,
Гавриленко В.А., Новикова М.Л.; по динамике машин и механизмов - Горячкин В.П.,
Кожевников С.Н., Коловский М.З. и др. Данное перечисление не охватывает и малой
доли работ выдающихся ученых, внесших существенный вклад в развитие ТММ в этот
период. Из зарубежных ученых необходимо отметить работы Альта Х., Бегельзака
Г., Бейера Р., Крауса Р., Кросли Ф. и многих других.
Контрольные вопросы
1.
Что называют
машиной и как их классифицируют?
2.
из чего состоит
машинный агрегат?
3.
Что называют
механизмом?
4.
Для чего
предназначены механизмы?
5.
Что называют
звеном?
6.
В чем отличие
входного звена от выходного?
7.
Что называют
кинематической парой?
8.
Чему равен класс кинематической
пары?
9.
Какие
кинематические пары называют низшими и высшими?
10.
Для чего
предназначена структурная схема механизма?
11.
Какие
кинематические пары могут существовать в плоских механизмах?
Лекция
2
Структурные формулы механизмов.
Пассивные звенья и кинематические пары. Классификация механизмов. Образование механизмов по Л.В.
Ассуру. Структурный анализ механизмов. Замена в плоских механизмах высших пар
низшими.
Структурные формулы
механизмов
Звенья соединённые
кинематическими парами образуют кинематическую цепь. Если в замкнутой
кинематической цепи одно из звеньев сделать неподвижным, цепь образует
механизм. Итак, механизм представляет собой замкнутую кинематическую цепь с одним
неподвижным звеном (стойкой) (определение механизма согласно Рело).
Свободное тело
относительно пространственной системы координат имеет 6 степеней свободы.
Положение этого тела соответственно можно задать 6-ю независимыми параметрами,
называемыми обобщенными координатами.
Рассмотрим кинематическую
цепь, состоящую из «n»
- звеньев, образующих: «р5» - число кинематических пар 5-го
класса, «р4» - 4-го, «р3» - 3-го, «р2»
- 2-го, «р1» - 1-го. «6×n» - число степеней свободы не соединённых между собой
звеньев. Так как стойка неподвижное звено, исключаем её «6×(n-1)». Каждая кинематическая пара 5-го класса
накладывает 5 ограничений на относительные движения соединяемых звеньев, общее
число ограничений кинематических пар 5-го класса в механизме «5×р5». Рассуждая аналогично - общее число ограничений
кинематических пар 4-го класса «4×р4»,
3-го класса «3×р3», 2-го класса «2×р2»,
1-го класса «1×р1».
Следовательно, число
степеней свободы кинематической цепи относительно неподвижного звена, с которым
связана пространственная система координат, определяется по формуле Сомова
П.О., Малышева А.П.
W = 6·(n - 1) - 5·p5 - 4·p4 - 3·p3 - 2·p2- 1·p1,
где W -степень подвижности механизма (число
обобщенных координат которые нужно задать для определимости положения всех его
звеньев); n - число звеньев механизма, включая
стойку (пассивные звенья не учитываются).
Для плоского механизма
используют формулу Чебышева П.Л.
W = 3·(n - 1) - 2·p5 - 1·p4 ,
Степень подвижности
механизма определяет число ведущих звеньев его, т.е. количество звеньев,
которым необходимо задать движение, чтобы все остальные звенья двигались по
вполне определенным законам.
Звенья которым
приписывают обобщенные координаты называют начальными.
Для механизмов
определяются входные и выходные звенья: входное – звено, которому сообщается
движение, которое преобразует механизм. Выходное звено – звено совершающее
движение, для получения которого и предназначен механизм.
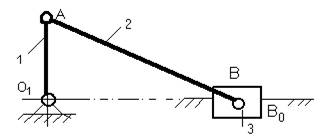
Рис. 2.1.
Решение. Кривошипно-ползунный механизм -
плоский, четырехзвенный (n =
4):
звено 0 - стойка;
звено 1 - кривошип, совершает вращательное движение; звено 2 - шатун,
совершает сложное плоскопараллельное движение (поступательное и вращательное);
звено 3 (выходное) - ползун, совершает возвратно-поступательное движение.
Стойка принята за нулевое звено.
Звенья соединены между собой четырьмя кинематическими парами 5 класса (на
структурной схеме они обозначены буквами латинского алфавита). Характеристику
кинематических пар приводим в табл. 2.1.
Определяем степень подвижности
механизма по формуле Чебышева П.Л. с учетом того, что n = 4; р5 = 4; р4
= 0
W = 3× (4 - 1) - 2 × 4 - 0
= 1
Таблица
2.1
|
Обозна-
чение
|
Наименование
|
Какими звеньями образована
|
Класс
|
Характеристика
|
|
О1
|
Вращательная
|
Кривошип 1 - стойка 0
|
5
|
Плоская, низшая
|
|
А
|
Вращательная
|
Кривошип 1 - шатун 2
|
5
|
Плоская, низшая
|
|
В
|
Вращательная
|
Шатун 2 - ползун 3
|
5
|
Плоская, низшая
|
|
ВО
|
Поступательная
|
Ползун 3 - стойка 0
|
5
|
Плоская, низшая
|
Это значит, что в данном
механизме должно быть одно начальное (ведущее) звено. В качестве начального
звена принято звено 1 - кривошип.
Пассивные звенья и кинематические пары
Пассивные звенья,
входящие в механизм не оказывают влияния на относительные движения других
звеньев, но вносят лишние степени подвижности, или накладывают избыточные
связи. При структурном исследовании механизма необходимо их выявлять.
Пример 1: Определим
степень подвижности кулачкового механизма рис. 2.2.
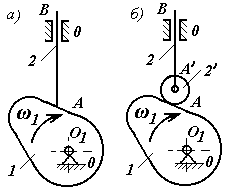
Рис. 2.2.
Решение: Кулачковый
механизм (рис. 2.2., а) – плоский, трехзвенный (n = 3): звено 0 - стойка; звено 1 - кулачок,
совершает вращательное движение; звено 2 – толкатель (выходное),
совершает возвратно-поступательное движение.
Стойка принята за нулевое звено.
Звенья соединены между собой тремя кинематическими парами (на структурной схеме
они обозначены буквами латинского алфавита). Характеристику кинематических пар
приводим в табл. 2.2.
Определяем степень
подвижности механизма по формуле Чебышева П.Л. с учетом того, что n = 3; р5 = 2; р4
= 1
W = 3× (3 - 1) - 2 × 2 - 1 × 1 = 1
С целью уменьшения сопротивления
движению на толкатель устанавливают ролик – звено 2’ (рис. 2.2, б).
Характеристику кинематических пар приводим в табл. 2.3.
Таблица
2.2.
|
Обозначение
|
Наименование
|
Какими звеньями образована
|
Класс
|
Характеристика
|
|
О1
|
Вращательная
|
Кулачок 1 - стойка 0
|
5
|
Плоская, низшая
|
А
|
Кулачковая
|
Кулачок 1 - толкатель 2
|
4
|
Плоская, высшая
|
В
|
Поступательная
|
Толкатель 3 - стойка 0
|
5
|
Плоская, низшая
|
Определяем степень
подвижности механизма по формуле Чебышева П.Л. с учетом того, что n = 4; р5 = 3; р4
= 1
W = 3× (4 - 1) - 2 × 3 - 1 × 1 = 2
Таким образом, ролик – пассивное
звено, установка которого привела к лишней степени подвижности механизма.
Таблица
2.3
|
Обозначение
|
Наименование
|
Какими звеньями образована
|
Класс
|
Характеристика
|
|
О1
|
Вращательная
|
Кулачок 1 - стойка 0
|
5
|
Плоская, низшая
|
А
|
Кулачковая
|
Кулачок 1 - ролик 2’
|
4
|
Плоская, высшая
|
|
А’
|
Вращательная
|
Ролик 2’ - толкатель 3
|
5
|
Плоская, низшая
|
В
|
Поступательная
|
Толкатель 3 - стойка 0
|
5
|
Плоская, низшая
|
Пример 2: Определим степень подвижности
механизма щёковой камнедробилки рис. 2.3.
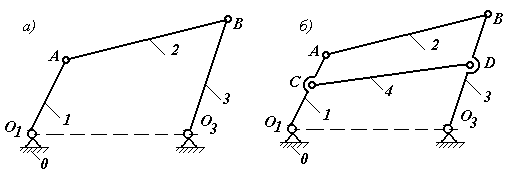
Рис. 2.3.
Решение: Шарнирный
механизм (рис. 2.3, а) – плоский, четырёхзвенный (n = 4): звено 0 - стойка; звено 1 - кривошип,
совершает вращательное движение; звено 2 – шатун, совершает сложное
плоско-параллельное движение; звено 3 – коромысло (выходное), совершает
неполно-оборотное вращательное движение.
Стойка принята за нулевое звено.
Звенья соединены между собой четырьмя кинематическими парами (на структурной
схеме они обозначены буквами латинского алфавита). Характеристику
кинематических пар приводим в табл. 2.4.
Определяем степень
подвижности механизма по формуле Чебышева П.Л. с учетом того, что n = 4; р5 = 4; р4
= 0
W = 3× (4 - 1) - 2 × 4 - 1 × 0 = 1
С целью увеличения жесткости
конструкции устанавливают дополнительное звено 4 (врезая шарниры С и D) (рис. 2.3, б).
Характеристику кинематических пар приводим в табл. 2.5.
Таблица
2.4.
|
Обозначение
|
Наименование
|
Какими звеньями образована
|
Класс
|
Характеристика
|
|
О1
|
Вращательная
|
Кривошип 1 - стойка 0
|
5
|
Плоская, низшая
|
А
|
Вращательная
|
Кривошип 1 - шатун 2
|
5
|
Плоская, низшая
|
В
|
Вращательная
|
Шатун 2 – коромысло 3
|
5
|
Плоская, низшая
|
|
О3
|
Вращательная
|
Коромысло 3 - стойка 0
|
5
|
Плоская, низшая
|
Определяем степень
подвижности механизма по формуле Чебышева П.Л. с учетом того, что n = 5; р5 = 6; р4
= 0
W = 3× (5 - 1) - 2 × 6 - 1 × 0 = 0
Таким образом, шатун 4 – пассивное
звено, установка которого привела к избыточной связи механизма.
Таблица
2.5
|
Обозначение
|
Наименование
|
Какими звеньями образована
|
Класс
|
Характеристика
|
|
О1
|
Вращательная
|
Кривошип 1 - стойка 0
|
5
|
Плоская, низшая
|
А
|
Вращательная
|
Кривошип 1 - шатун 2
|
5
|
Плоская, низшая
|
С
|
Вращательная
|
Кривошип 1 - шатун 4
|
5
|
Плоская, низшая
|
В
|
Вращательная
|
Шатун 2 – коромысло 3
|
5
|
Плоская, низшая
|
D
|
Вращательная
|
Шатун 2 – шатун 4
|
5
|
Плоская, низшая
|
|
О3
|
Вращательная
|
Коромысло 3 - стойка 0
|
5
|
Плоская, низшая
|
Классификация механизмов
Механизмы
классифицируются по следующим признакам:
1.
По области
применения и функциональному назначению:
· механизмы летательных аппаратов;
· механизмы станков;
· механизмы кузнечных машин и прессов;
· механизмы двигателей внутреннего
сгорания;
· механизмы промышленных роботов
(манипуляторы);
· механизмы компрессоров;
· механизмы насосов и т.д.
2.
по виду
передаточной функции на механизмы:
· с постоянной передаточной функцией;
· с переменной передаточной функцией:
Þ с нерегулируемой (синусные, тангенсные);
Þ с регулируемой:
à со ступенчатым регулированием
(коробки передач);
à с бесступенчатым регулированием
(вариаторы).
3.
по виду
преобразования движения на механизмы преобразующие:
· вращательное во вращательное:
Þ редукторы вх>вых;
Þ мультипликаторы вх<вых;
Þ муфты вх=вых;
· вращательное в поступательное;
· поступательное во вращательное;
· поступательное в поступательное.
4.
по движению и
расположению звеньев в пространстве:
· пространственные;
· плоские;
· сферические.
Все механизмы являются
пространственными механизмами (рис. 2.4). Часть механизмов, звенья которых
совершают движение в одной плоскости или параллельных плоскостях являются
одновременно и плоскими. Другая часть механизмов, звенья которых движутся по
сферическим поверхностям экивидистантным какой-либо одной сфере, являются
одновременно и сферическими.
Множество пространственных механизмов
Подмножество плоских Подмножество сферических
Рис. 2.4.
5.
по изменяемости
структуры механизма на механизмы:
·
с неизменяемой
структурой;
·
с изменяемой
структурой.
В процессе работы
кривошипно-ползунного механизма насоса его структурная схема все время остается
неизменной. В механизмах манипуляторов в процессе работы структурная схема
механизма может изменяться (рис. 2.5). Так если промышленный робот выполняет
сборочные операции, например, вставляет цилиндрическую деталь в отверстие, то
при транспортировке детали его манипулятор является механизмом с открытой или
разомкнутой кинематической цепью. В тот момент, когда деталь вставлена в отверстие,
кинематическая цепь замыкается, структура механизма изменяется, подвижность
уменьшается на число связей во вновь образованной кинематической паре
деталь-стойка.
С1В
 2
3 С1В
2
3 С1В
D1B
В1В
В1В
 1
D1B
1
D1B
 4
4
 0 А1В А1В
0 А1В А1В
0
W=4 W=0
Рис.2.5
Структура манипулятора
изменяется и тогда, когда в одной или нескольких кинематических парах
включается тормоз. Тогда подвижное соединение двух звеньев заменяется неподвижным,
два звена преобразуются в одно. На рис. 2.6 тормоз включен в паре С.
 2
2
 D1B
D1B

 В1В
В1В

 1
1
 3
3
 0 А1В
0 А1В
0
W=3
Рис.
2.6
6.
по числу
подвижностей механизма:
· с одной подвижностью W=1;
· с несколькими подвижностями W>1:
Þ суммирующие (интегральные, рис. 2.7, а);
Þ разделяющие (дифференциальные, рис. 2.7, б).
а)
б)


 Piвх
Pвых Pвх
Piвых
Piвх
Pвых Pвх
Piвых



 d
d
Рис.2.7
7.
по виду
кинематических пар:
· с низшими кинематическими парами (все
кинематические пары механизма низшие);
· с высшими кинематическими парами
(хотя бы одна кинематическая пара высшая);
· шарнирные (все кинематические пары
механизма вращательные - шарниры).
8.
по способу
передачи и преобразования потока энергии:
· фрикционные;
· зацеплением;
· волновые (создание волновой
деформации);
· импульсные.
9.
по форме,
конструктивному исполнению и движению звеньев:
· рычажные (рис.2.1, 2.3);
· зубчатые (рис.2.8);
· кулачковые (рис. 2.2);
· планетарные (рис. 2.9);
· манипуляторы (рис.2.5, 2.6).
|
 2 P 0 2 P 0
B
K
 A
C A
C
1 в
|
Рис.
2.8 Рис. 2.9
Механизмы с высшими кинематическими парами и их классификация
К механизмам с высшими КП
относятся любые механизмы в состав которых входит хотя бы одна высшая пара.
Простейший типовой механизм с высшей парой состоит из двух подвижных звеньев,
образующих между собой высшую кинематическую пару, а со стойкой низшие (вращательные
или поступательные) пары. К простейшим механизмам с высшей парой относятся:
· фрикционные передачи (рис. 2.10),
· зубчатые передачи (рис. 2.8),
· кулачковые механизмы (рис. 2.2),
· поводковые механизмы (в том числе и
мальтийские - рис. 2.11).
Структурные
схемы простейших механизмов с высшими кинематическими
парами
Кулачковым механизмом
называется механизм с высшей парой, ведущее звено которого выполнено в форме
замкнутой криволинейной поверхности и называется кулачком (рис. 2.2). Зубчатыми
механизмами называются механизмы звенья которых снабжены зубьями. Рабочие поверхности
зубьев должны быть выполнены так, чтобы обеспечивать передачу и преобразование
движения по заданному закону за счет их зацепления (рис. 2.8). Фрикционными
механизмами или передачами сцепления называются механизмы с высшей парой в
которых передача движения в высшей паре осуществляется за счет сил сцепления
или трения в зоне контакта (рис. 2.10). Условия, которым должны удовлетворять
рабочие поверхности высших пар, формулируются в разделе теории механизмов -
теории зацепления или теории высшей пары.
Образование
механизмов по Ассуру Л.В.
Для решения задач синтеза
и анализа сложных рычажных механизмов профессором Петербургского университета
Ассуром Л.В. была предложена оригинальная структурная классификация. По этой
классификации любой рычажный механизм не имеющий изыточных связей и местных
подвижностей может быть образован путём присоединения к начальному (первичному)
механизму групп звеньев с нулевой степенью подвижности (групп Ассура (см. рис.
2.12).
|
 Структурный синтез механизма по Ассуру Структурный синтез механизма по Ассуру
    
Механизм = Начальный
+ Начальный + .... + Структурная + Структурная + ...
с W0
механизм механизм группа
группа
W0
W=0
Структурный анализ механизма по Ассуру
|
Рис.
2.12
Под начальным
механизмом понимают механизм, состоящий из двух звеньев (одно из которых
неподвижное – стойка) образующих кинематическую пару с одной Wпм=1 или несколькими Wпм>1 подвижностями. Примеры начальных
механизмов даны на рис. 2.13.

с W=1 Начальные c W >1
  механизмы
механизмы
1 z 1
  01 01 01 01
 y
y
  x
x
0
0
1 1 z
  B1п B1п
D3пл
 y
y
0 x 0
Рис. 2.13
|
Рис.2.13
Структурной группой
Ассура (или группой
нулевой подвижности) называется кинематическая цепь, образованная только
подвижными звеньями механизма, подвижность которой (на плоскости и в пространстве)
равна нулю (Wгр = 0).
Для плоских механизмов с низшими парами структурная
формула групп Ассура имеет вид:
W = 3·n - 2·p5= 0 ,
откуда 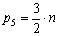
Поскольку в группе не
может быть дробное число кинематических пар, то группы Ассура должны состоять
только из четного числа звеньев (табл. 2.6).
Таблица 2.6
|
Класс и
порядок группы Ассура
|
2кл.
2 пор.
|
3кл.
3 пор.
|
и т. д.
|
|
Число звеньев
группы nгр
|
2
|
4
|
|
Число
кинематических пар p5
|
3
|
6
|
Чтобы из механизма
выделить группы Ассура, необходимо помнить их основные признаки, вытекающие из
определения:
*
число звеньев в
группе должно быть четным (n = 2, 4, 6 и т.д.);
*
степень
подвижности группы всегда равна нулю, например, группа 3-го класса 3-го порядка
(рис. 2.14, ж) содержит n = 4, p5= 6; при этом W = 3·4 - 2·6 = 0;
*
степень подвижности
оставшейся части механизма при отсоединении групп Ассура не должна изменяться.
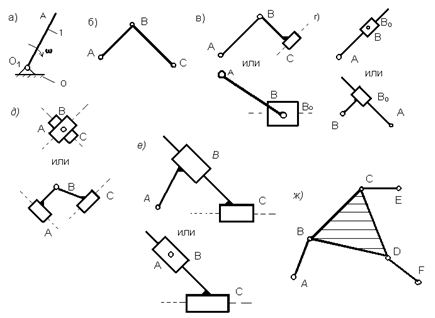
Рис.
2.14
Группа Ассура
характеризуется классом, порядком и видом.
Класс группы Ассура
определяется максимальным классом контура входящего в группу. Класс контура –
наибольшее число кинематических пар образующих в группе замкнутый контур. Если
группа Ассура образована двумя звеньями ей в качестве исключения присваивается
2 – й класс.
Порядок группы Ассура
определяется числом кинематических пар, которыми она присоединяется к основному
механизму.
Вид группы Ассура (её
характеристика) определяется соотношением входящих в неё вращательных и
поступательных кинематических пар.
Поводком называется
звено, входящее в группе в две кинематические пары, одна из которых свободная и
служит для присоединения к одному из подвижных звеньев механизма или к стойке.
Порядок структурных групп определяется числом поводков.
При структурном синтезе
механизма по Ассуру (рис.2.12) к выбранным первичным механизмам с заданной
подвижностью W0 последовательно
присоединяются структурные группы c нулевой подвижностью. Полученный таким образом механизм обладает
рациональной структурой, т.е. не содержит избыточных связей и подвижностей.
Структурный анализ механизмов
Задачи структурного
анализа:
·
определение
степени подвижности механизма;
·
выявление
пассивных звеньев (избыточных связей и местных подвижностей);
·
разбивка на
группы Ассура и начальные механизмы.
Структурному анализу по
Ассуру можно подвергать только механизмы не содержащие избыточных связей и
подвижностей. Поэтому перед проведением структурного анализа необходимо
устранить избыточные связи и выявить местные подвижности. Затем необходимо
выбрать первичные механизмы и, начиная со звеньев наиболее удаленных от
первичных, выделять из состава механизма структурные группы нулевой подвижности
(схема на рис.2.12). При этом необходимо следить, чтобы звенья, остающиеся в
механизме, не теряли связи с первичными механизмами.
Пример: Проведем
структурный анализ плоского механизма, схема которого приведена на рис. 2.15, и
представим его в виде совокупности первичного механизма и структурных групп
Ассура.
|

   6 J 3
1 6 J 3
1
  Е D Е D
5 4 02 А
01
  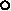 F F
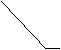 
 K 04
В 8 K 04
В 8
0
 С 08
С 08
2 7
|
Рис. 2.15

Кулачковый Движение
 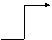   механизм подачи
механизм подачи
  Двигатель Зубчатая Двигатель Зубчатая
 передача передача
  Движение Движение
Кулисный
Коромыслово- долбяка
  механизм ползунный механизм ползунный
механизм S8
Рычажный механизм
Рис. 2.16
|
На рис.2.15 изображена структурная
схема плоского механизма долбежного станка, а на рис.2.16 его функциональная
схема на уровне типовых механизмов. Структурная схема механизма в соответствии
с принятыми условными обозначениями изображает звенья механизма, их взаимное
расположение, а также подвижные и неподвижные соединения между звеньями. На
схеме звенья обозначены цифрами, кинематические пары - заглавными латинскими
буквами. Цифры в индексах обозначения кинематических пар указывают
относительную подвижность звеньев в паре, буквы - на вид пары, который определяется
видом относительного движения звеньев ( в - вращательное, п -
поступательное, ц - цилиндрическое, вп - обозначает высшую пару в которой
возможно относительное скольжение с одновременным перекатыванием). Схема на
рис. 2.16 отражает структуру механизма в виде последовательного и параллельного
соединения простых или типовых механизмов. В этом механизме вращательное
движение вала двигателяв согласованные движения подачи и долбяка S6. При этом механическая энергия
двигателя преобразуется: скоростные составляющие энергетического потока по
величине уменьшаются, а силовые - увеличиваются. Структурные элементы (типовые
механизмы) в этой схеме связаны между собой неподвижными соединениями -
муфтами. Схема показывает из каких простых механизмов состоит исследуемый, как
эти механизмы взаимосвязаны между собой (последовательно или параллельно), как
происходит преобразование входных движений в выходные (в нашем примере в и S6).
Проведем структурный
анализ данного механизма. Число звеньев механизма, включая стойку n=9 , число кинематических пар p=12, характеристика кинематических пар
приведена в таблице 2.7.
Таблица 2.7
|
Обозначение
|
Наименование
|
Какими
звеньями образована
|
Класс
|
Характеристика
|
|
01
|
Вращательная
|
Колесо
1 - стойка 0
|
5
|
Плоская,
низшая
|
|
А
|
Зубчатая
|
Колесо
1 - колесо 2
|
4
|
Плоская,
высшая
|
|
В
|
Кулачковая
|
Кулачок
2 - ролик 7
|
4
|
Плоская,
высшая
|
|
С
|
Вращательная
|
Ролик
7 - коромысло 8
|
5
|
Плоская,
низшая
|
|
08
|
Вращательная
|
Коромысло
8 - стойка 0
|
5
|
Плоская,
низшая
|
|
02
|
Вращательная
|
Кулачок
2 - стойка 0
|
5
|
Плоская,
низшая
|
|
Е
|
Вращательная
|
Кулачок
2 - кулиса 3
|
5
|
Плоская,
низшая
|
|
D
|
Поступательная
|
Кулиса
3 - коромысло 4
|
5
|
Плоская,
низшая
|
|
04
|
Вращательная
|
Коромысло
4 - стойка 0
|
5
|
Плоская,
низшая
|
|
F
|
Вращательная
|
Коромысло
4 - шатун 5
|
5
|
Плоская,
низшая
|
|
J
|
Вращательная
|
Шатун
5 - ползун 6
|
5
|
Плоская,
низшая
|
|
К
|
Поступательная
|
Ползун
6 - стойка 0
|
5
|
Плоская,
низшая
|
Степень подвижности механизма:
W = 3·(9 - 1) - 2·10 - 1×2 = 2,
полученные две степени
свободы определяют: основную функцию механизма преобразование входного движения
в два функционально взаимосвязанных и S6. Пассивная высшая кинематическая
пара заменяет в паре кулачок - толкатель трение скольжения трением качения
Результаты структурного
анализа изображены на рис. 2.17. Звено 7 и пара С введены в
структуру механизма с целью замены трения скольжения трением качения. Механизм
имеет одну основную подвижность и, следовательно, один начальный механизм, состоящий
из звеньев 1 и 0.
|
Группа Ассура
5-6 Группа Ассура 3-4
6 J
Wгр = 3×2 - 2×3 = 0; 3 C
5
F 4 D
K Wгр = 3×2 - 2×3 = 0;
E
Начальный механизм
        1 1
 01 01
 Wпм = 3×(2-1) - 2×1 = 1; Wпм = 3×(2-1) - 2×1 = 1;
|
Рис. 2.17
Замена в плоских механизмах высших пар низшими
Плоские механизмы могут состоять из
звеньев входящих как в низшие, так и высшие пары. При изучении структуры и кинематики
плоских механизмов удобно заменять высшие кинематические пары кинематическими
цепями, или звеньями входящими только в низшие вращательные и поступательные
пары 5-го класса.
При такой замене должны выполняться
условия: чтобы механизм, полученный после такой замены, обладал прежней
степенью подвижности и чтобы сохранились относительные в рассматриваемом
положении движения всех его звеньев.
Рассмотрим плоский механизм рис.
2.18: он состоит из 3-х звеньев и 3-х кинематических пар (0-1, 2-0 – 5-го
класса, вращательные; 1-2 – 4-го класса высшая, сложная), а и в –
элементы звеньев 1 и 2 окружности радиусами 01В и 02С
соответственно
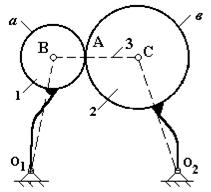
Рис. 2.18
Степень подвижности механизма:
W = 3·(3 - 1) - 2·2 - 1×1 = 1,
Рассматриваемый механизм можно
заменить эквивалентным ему шарнирным четырёхзвенным механизмом 01ВС02.
Высшая кинематическая пара 4-го класса в точке А заменяется звеном 3,
образующим в точках В и С вращательные пары 5-го класса.
Механизм 01ВС02 называют
замещающим, его степень подвижности:
W = 3·(4 - 1) - 2·4 = 1,
т.к. элементы а и в звеньев 1 и 2
являются окружностями с центрами в точках В и С, то длина ВС звена 3 является
постоянной, длины 01В и С02 являются постоянными, отсюда
относительные движения звеньев 1 и 2 сохранятся.
Контрольные вопросы
1.
Напишите формулы
для определения степени подвижности пространственного и плоского механизмов?
2.
Почему требуется
при анализе выявлять в структуре механизма пассивные звенья?
3.
Что такое группа
Ассура?
4.
Дайте определение
класса, порядка и вида группы Ассура?
5.
Приведите
последовательность структурного анализа механизмов?
6.
В чем заключаются
условия замены высших пар низшими в плоских механизмах?
Лекция
№ 3
Кинематический анализ механизмов.
Задачи кинематического анализа. Понятие о геометрических и кинематических
характеристиках механизмов (функция положения и её производные по времени и по
обобщенной координате). Графические методы кинематического анализа: метод
планов и диаграмм. Цикл и цикловые графики. Связь между кинематическими и
геометрическими параметрами. Кинематическое исследование типовых механизмов.
Основные задачи кинематического
исследования механизмов
В разделе изучается движение
отдельных звеньев механизма без учета факторов обуславливающих их движение,
какими являются силы, действующие в механизме.
Всякое движение тела характеризуется
перемещением его в пространстве, скоростью и ускорением движения его точек.
Кинематический анализ механизмов
заключается в определении параметров движения звеньев механизма по заданному
закону движения начального звена (без учета сил, обуславливающих это движение)
и предусматривает решение следующих основных задач:
1.
определение
координат и разметка траектории движения всех характерных точек механизма, что
позволяет рационально спроектировать корпусные детали механизма;
2.
определение
скоростей характерных точек механизма в различных его положениях, что позволяет
определить кинетическую энергию всех подвижных звеньев механизма;
3.
определение
ускорений характерных точек механизма, что позволяет определить силы инерции
движущихся звеньев.
Существует несколько методов
кинематического анализа:
·
Экспериментальный;
·
Графический (не
обладает большой точностью, но быстр в исполнении);
·
Графоаналитический;
·
Аналитический
(точный, но очень сложный даже для простейших схем).
Понятие о геометрических и
кинематических характеристиках механизмов
Функцией положения механизма называется зависимость
углового или линейного перемещения точки или звена механизма от времени или
обобщенной координаты (рис. 3.1).
|

 dP(q)/dq Первая
dP2(q)/dq2 Вторая dP(q)/dq Первая
dP2(q)/dq2 Вторая
переда    точная
передаточная точная
передаточная
P(q)
функция функция
 uq, q
aq, q uq, q
aq, q
  Функция Функция
положения
u, a,
  P(t) P(t)
  Скорость
Ускорение Скорость
Ускорение
dP(t)/dt dP2(t)/dt2
|
Рис. 3.1
Кинематическими
передаточными функциями механизма называются производные от функции положения по обобщенной
координате. Первая производная называется первой передаточной функцией или
аналогом скорости (обозначается uq , q), вторая - второй передаточной
функцией или аналогом ускорения (обозначается aq, q).
Кинематическими
характеристиками
механизма называются производные от функции положения по времени. Первая
производная называется скоростью (обозначается u, вторая - ускорением (обозначается a, ).
Механизм с одной подвижностью имеет
одно заданное входное движение и бесчисленное множество выходных (движение
любого звена или точки механизма). Передаточные функции тех движений, которые в
данном случае используются как выходные, называются главными, остальные -
вспомогательными.
Рассмотрим схему механической системы образованной
последовательным и параллельным соединением типовых механизмов. Схема включает
входное звено, зубчатую передачу, кулачковый и рычажный механизмы и имеет два
выходных звена (рис. 3.2).
5
 С В 2
С В 2
 6
1
6
1


 D
A P O
D
A P O
0
 K
K

 E
E
 Q
Q


 4
4
3
Рис. 3.2. Схема механической системы
 2
3
2
3

 Кулачковый
Кулачковый
механизм
- P3(2)
1 Зубчатый
 механизм P2(1)
механизм P2(1)
2
Четырехшарнирный 6

 механизм - P6(2)
механизм - P6(2)
Рис. 3.3
На рис. 3.3. представлена
функциональная схема машины. Функции положений механизмов приведены на рис.
3.4.
Функции
положения
 P3 (1)
P3 (1)


 Главные
Главные
 Входное P6 (1)
Входное P6 (1)


 перемещение
перемещение
 1
P2 (1)
1
P2 (1)


 Вспомогательные P3
(2)
Вспомогательные P3
(2)

 P6
(2)
P6
(2)
Рис. 3.4. Функции положения в механизмах
Связь кинематических и передаточных
функций
Линейные скорости и ускорения
uL = dSL/ dt = (dSL/d×d1/dt)
= uqL × 1;
aL = d(uql × 1)/dt
= (duqL/d1)×(ddt)×1 + uqL× 1 = aqL× 12 + uqL× 1;
Угловые скорости и ускорения
i = di/ dt = (di /d×d1/dt)
= qi × 1;
i = d(qi×1)/dt
= (di/d1)×(d1/dt)×1 + qi × 1 = qi× 12 + qi × i .
Так как данные формулы получены как
производные от скалярных величин, то при операциях с векторными величинами они
применимы только для проекций этих величин на оси координат.
Аналитические методы кинематического
анализа
1.1. Метод проекций векторного
контура (рычажные механизмы)
Рассмотрим простейший кулисный
механизм (рис. 3.5).
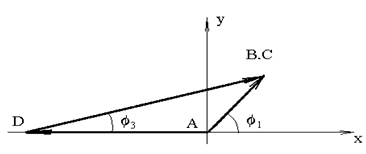
Рис. 3.5
Заменим кинематическую схему механизма
эквивалентным векторным контуром. Тогда уравнение замкнутости векторного
контура запишется
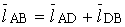
Задача о положениях звеньев механизма
Проецируем векторный контур на оси
координат и получаем координаты точки В механизма:
xB = lAB × cos (1)
= lAD× cos () + lDB × cos (3);
yB = lAB × sin ()
= lAD× sin
(lDB × sin (
из решения этой системы уравнений
определяем неизвестные величины 3 и lDB, которые определяют положение звеньев
и точек механизма
tg (3) = sin (/ cos (3) =
lAB × sin () (lAB × cos (1) - lAD× cos ());
lDB = (lAB × sin ()) / sin (
Задача о первых кинематических
передаточных функциях механизма
Продифференцируем уравнения проекций
векторного контура по обобщенной координате и получим
uqBx = - lAB × sin (uqDB × cos (3) - lDB × q3 × sin (3);
uqBy = lAB × cos (uqDB × sin (3) + lDB × q3 × cos (3).
Из этой системы уравнений определяем
первые передаточные функции uqB и q3.
Задача о вторых передаточных функциях
механизма
Вторично продифференцируем уравнения
проекций векторного контура по обобщенной координате и получим
aqBx= - lAB×cos (1) = aqDB×cos (3) -2×uqDB×q×sin () - lDB×q3×sin ( -
- lDB×q×cos (3);
aqBy = - lAB × sin (1) = aqDB × sin (3) + 2 × uqDB × q×cos () + lDB ×q3 × cos ( - lDB × q× sin (3);
Из этой системы уравнений определяем
вторые передаточные функции aqB и q3.
Для кинематического анализа
результаты целесообразнее представлять в виде кинематических диаграмм.
Цикловые кинематические
(геометрические) диаграммы для кулисного механизма (рис. 3.6).
Циклом называется период времени или
изменения обобщенной координаты по истечении, которого все параметры системы
принимают первоначальные значения. Поэтому значения величин в начале и в конце
цикла одинаковы.
1.2. Метод центроид (зубчатые
передачи) рис. 3.7
Центроидой (полоидой) называется геометрическое
место центров (полюсов) относительного вращения в системах координат связанных
со звеньями механизма. В зубчатом механизме при передаче движения центроиды
колес перекатываются друг по другу без скольжения.
Повернем ведущее колесо на малый угол
d1, тогда ведомое колесо повернется на угол dТак как центроиды или начальные
окружности колес перекатываются друг по другу без скольжения, то дуга dSw1 будет равна дуге dSw2. Тогда можно записать следующее равенство
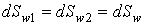 ,
,
где dSw1 = rw1 × d dSw2 = rw2 × d
Откуда
i 21 = d2/d1
= rw1/rw2 = const.
Функция положения для выходного звена
зубчатой передачи
d2= i 21
× d1 , откуда 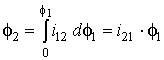 .
.
|
2
1
02
P o1
  d2 d
d2 d
rw1
  rw2 rw2
 dSw1 = dSw2 = dSw dSw1 = dSw2 = dSw
Рис. 3.7. Схема зубчатого механизма
|
Вторая передаточная функция для
выходногозвена зубчатой передачи
q2 = d i21/d
Механизм зубчатой передачи не
является цикловым механизмом, так как угловое перемещение выходного звена
увеличивается при увеличении углового перемещения входного. Поэтому
кинематические диаграммы принято строить для одного оборота входного звена (рис
3.8).
Диаграммы функции положения и
передаточных функций для зубчатой передачи.
Графические методы кинематического анализа
Метод планов (рассмотрим на примере
кривошипно-ползунного механизма):
Построение кинематических схем
(планов положений): Основная задача построения кинематических схем, заключается
в том, чтобы изобразить на бумаге схему, дающую представление о кинематических
и геометрических зависимостях отдельных звеньев механизма. Для этого нет
необходимости изображать механизм отображая сложные конструктивные формы,
достаточно изображение механизма в виде простейших линий, учитывая, что он
составлен из жестких неизменяемых звеньев.
Кинематические схемы выполняются в
масштабе (масштабном коэффициенте):
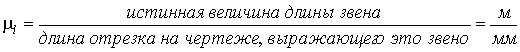
Построенный ряд
последовательных планов положений механизма позволяет получить траектории
движения точек звеньев механизма, а также их перемещения, рассмотрим последовательность
построений для кривошипно-ползунного механизма (рис. 3.9, а).
Разметка траекторий движения
всех звеньев механизма осуществляется методом засечек. С этой целью угол
поворота кривошипа разбивается 12 равных частей, и строятся текущие положения
кривошипа О1Аi (за начало отсчета удобней принять внешнее предельное
положение кривошипа и шатуна соответствующее нижней мертвой точке ползуна). Из
полученных точек Аi циркулем, расстояние, между ножками которого равно длине
шатуна АВ в масштабе построения, делаются засечки на траектории движения
ползуна (прямая ХХ), т.е. получаем текущие положения ползуна (точка Вi), соединив которые с
соответствующими точками Аi, получают промежуточные положения шатуна. На плане положений
механизма определяем текущие положения центров тяжести кривошипа и шатуна
(точки S1 и S2).
Текущие значения
перемещений ползуна можно определить из плана положений механизма, как
расстояние от крайнего нижнего положения ползуна (точка В0) до
текущего положения (точки Вi) умноженное на масштаб построений.
Построение плана
скоростей:
Построение планов
скоростей и ускорений ведется в порядке присоединения групп Ассура к начальному
механизму. Поскольку кривошипно-ползунный механизм имеет одну степень подвижности,
то заданное движение входного звена (в данном случае кривошипа О1А)
определяет движение всех остальных звеньев. Т.к. звено О1А совершает
вращательное движение, то траекторией точки А является окружность
с центром в точке О1. Вектор скорости точки А направлен по
касательной к траектории движения, т.е. перпендикулярно радиусу О1А,
в сторону вращения кривошипа. Величина скорости определяется из выражения:
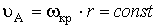 ,
,
где wкр .- угловая скорость кривошипа, рад/с; r – радиус кривошипа, м.
Известный по величине и
направлению вектор скорости `uА строят в
виде отрезка произвольной длины рuа, из выбранного полюса рu - плана скоростей (рис. 3.9, б).
В этом случае масштаб плана скоростей:
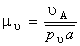 ,
, 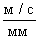 .
.
При определении скорости
точки В следует отметить, что ползун совершает возвратно-поступательное
движение, т.е. траекторией его движения является прямая линия, а вектор её
скорости направлен параллельно линии перемещения. Т.к. точка В одновременно
принадлежит и ползуну, и шатуну, то для дальнейшего построения плана скоростей
следует воспользоваться векторным уравнением, выражающим связь между скоростями
точек А и В шатуна:
 ,
,
где 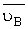 – вектор абсолютной скорости точки В;
– вектор абсолютной скорости точки В; 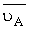 – вектор скорости переносного движения,
скорости полюса в качестве которого принята точка А;
– вектор скорости переносного движения,
скорости полюса в качестве которого принята точка А; 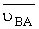 –
вектор относительной скорости точки В по отношению к точке А (вектор
вращательной скорости точки В вокруг полюса – точки А).
–
вектор относительной скорости точки В по отношению к точке А (вектор
вращательной скорости точки В вокруг полюса – точки А).
Внимание: чтобы отложить любой вектор нужно
знать его величину и направление, поэтому, здесь, и далее вектор, известный по
величине и направлению, подчеркнут двумя линиями, а вектор известный только по
направлению, подчеркнут одной линией.
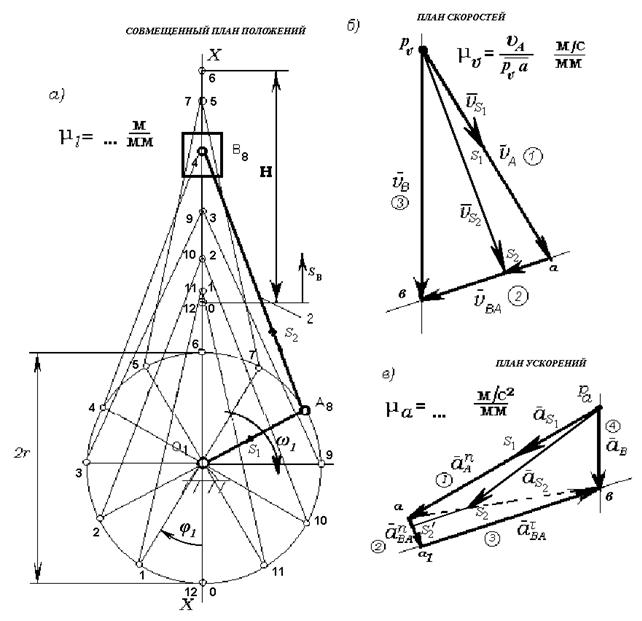
Рис. 3.9
В векторном равенстве две
неизвестные величины: скорость uВ и
относительная (вращательная) скорость uВА. Вектор абсолютной скорости 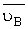 направлен параллельно
линии перемещения ползуна ХХ, а вектор относительной скорости
направлен параллельно
линии перемещения ползуна ХХ, а вектор относительной скорости 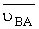 – перпендикулярно радиусу вращения, т.е.
перпендикулярно текущему положению шатуна АВ. Вектор переносной скорости
– перпендикулярно радиусу вращения, т.е.
перпендикулярно текущему положению шатуна АВ. Вектор переносной скорости 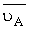 (скорости полюса) на плане скоростей
представлен отрезком рuа, поэтому данное векторное равенство можно решить графическим путем.
(скорости полюса) на плане скоростей
представлен отрезком рuа, поэтому данное векторное равенство можно решить графическим путем.
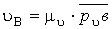 ;
; 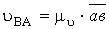 .
.
Зная относительную
скорость точки В вокруг полюса точки А, можно определить угловую скорость
шатуна, рад/с:
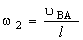 ,
,
где uВА - м/с; l
– длина шатуна, м.
Теорема подобия фигур для планов скоростей: фигуры
на плане положений и на плане скоростей образованные векторами относительных
скоростей подобны. Рассмотрим треугольники на плане положений D01АВ и на плане скоростей Dрuав, они являются подобными как имеющими две стороны
взаимно перпендикулярные друг другу и одну параллельную.
Для определения скоростей центров
тяжести звеньев следует найти положения точек S1 и S2 на плане
скоростей, воспользовавшись теоремой подобия составив соотношения:
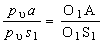 и
и 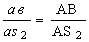 ,
,
т.е. абсолютная скорость 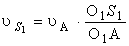 .
.
Чтобы получить абсолютную
скорость точки S2 следует соединить точку s2 с полюсом плана скоростей рu , и тогда отрезок рus2 определит в масштабе плана mu скоростей абсолютную скорость центра
тяжести шатуна. Истинное значение абсолютной скорости точки S2 определяем, м/с:
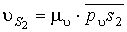 .
.
Построение плана
ускорений:
Построение плана
ускорений необходимо начать с вычисления и нанесения на план ускорения т. А
кривошипа. В общем случае полное ускорение т. А складывается из нормального
(центростремительного) 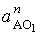 и касательного
и касательного 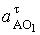 ускорений:
ускорений:
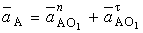 .
.
Численное значение
нормального ускорения определяют по формуле, м/с2:
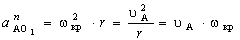 .
.
Направлено это ускорение
параллельно отрезку О1А от точки А к центру вращения О1.
Касательное ускорение
определяется по формуле, м/с2:
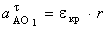 ,
,
где eкр – угловое ускорение кривошипа, с-2;
r – длина кривошипа м.
Направлено ускорение 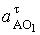 перпендикулярно отрезку О1А,
либо по направлению вектора скорости`uА
(ускоренное вращение), либо против`uА
(замедленное вращение).
перпендикулярно отрезку О1А,
либо по направлению вектора скорости`uА
(ускоренное вращение), либо против`uА
(замедленное вращение).
Складывая геометрически
нормальное и касательное ускорения, найдем полное ускорение точки А:

При равномерном вращении
кривошипа (wкр=const) его угловое ускорение 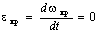 , следовательно, полное ускорение точки А
будет определяться только нормальной составляющей
, следовательно, полное ускорение точки А
будет определяться только нормальной составляющей 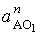 ,
имеющей численное значение:
,
имеющей численное значение:
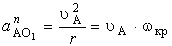 ,
,
Вычисленное нормальное
ускорение изображаем на плане ускорений в виде отрезка раа произвольной
длины, из выбранного полюса ра плана ускорений так, чтобы он
был параллелен текущему положению кривошипа О1А и направлен от точки
А к точке О1 (рис. 3.9, в). Тогда масштаб плана ускорений:
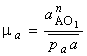 ,
,
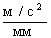 .
.
Далее переходят к
определению ускорения точки В. В векторном виде:
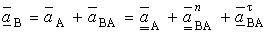 ,
,
где`аВ – вектор полного ускорения точки В ползуна и шатуна;`аА - вектор полного ускорения точки А кривошипа;`аВА - вектор относительного ускорения
движения точки В шатуна по отношению к точке А кривошипа, которое можно
разложить на нормальную (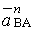 ) и касательную (
) и касательную (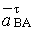 ) составляющие, направления которых
известны (вектор
) составляющие, направления которых
известны (вектор 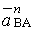 направлен параллельно положению
шатуна АВ от точки В к точке А, вектор
направлен параллельно положению
шатуна АВ от точки В к точке А, вектор 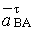 направлен
перпендикулярно вектору нормального ускорения). При известной вращательной
скорости точки В вокруг полюса А (uВА), численное значение нормального ускорения определяют по формуле, м/с2:
направлен
перпендикулярно вектору нормального ускорения). При известной вращательной
скорости точки В вокруг полюса А (uВА), численное значение нормального ускорения определяют по формуле, м/с2:
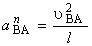 ,
,
здесь uВА - в м/с; l
– длина шатуна в м.
Чертежное значение длины
вектора 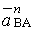 равно
равно 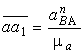 , мм.
, мм.
Следовательно, векторное
уравнение может быть решено графическим путём.
Через точку а проводят
прямую, параллельную текущему положению шатуна АiВi , и откладываем на ней вектор 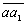 в направлении от точки Вi к точке Аi. Затем через точку а1
проводят линию действия касательного ускорения, перпендикулярную данному положению
шатуна. Из полюса плана ускорений ра проводят линию действия
полного ускорения точки В, параллельную линии ХХ перемещения ползуна.
Расстояние от точки в, пересечения линий действия двух последних
ускорений до полюса и точки а1 определяет в масштабе значения
ускорений, м/с2:
в направлении от точки Вi к точке Аi. Затем через точку а1
проводят линию действия касательного ускорения, перпендикулярную данному положению
шатуна. Из полюса плана ускорений ра проводят линию действия
полного ускорения точки В, параллельную линии ХХ перемещения ползуна.
Расстояние от точки в, пересечения линий действия двух последних
ускорений до полюса и точки а1 определяет в масштабе значения
ускорений, м/с2:
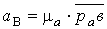 ;
;  .
.
Соединив точки а и
в вектором  , получаем полное
ускорение точки В в относительном движении по отношению к полюсу точке А, т.е.:
, получаем полное
ускорение точки В в относительном движении по отношению к полюсу точке А, т.е.:
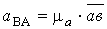 , м/с2.
, м/с2.
Для определения ускорений
центров тяжести звеньев следует найти положения точек S1 и S2 на плане
ускорений, воспользовавшись соотношениями:
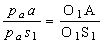 и
и 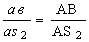 ,
,
Абсолютные значения ускорений центров
тяжести звеньев, м/с2:
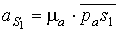 и
и 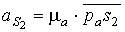 .
.
Зная величину
касательного ускорения 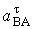 , можно определить угловое
ускорение шатуна, с-2:
, можно определить угловое
ускорение шатуна, с-2:
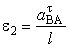 .
.
Чтобы определить, какое
движение совершает шатун (ускоренное или замедленное), необходимо знать
направление угловой скорости w2 и углового
ускорения e2 в данный момент времени. Для этого
векторы вращательной скорости `uВА с плана
скоростей и касательного ускорения 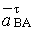 с плана ускорений
переносятся параллельно в соответствующую точку В плана положений механизма. Их
направление относительно точки А и определит направление угловых скорости и
ускорения. Если направление угловой скорости совпадает с направлением углового
ускорения, то движение шатуна будет ускоренным и наоборот.
с плана ускорений
переносятся параллельно в соответствующую точку В плана положений механизма. Их
направление относительно точки А и определит направление угловых скорости и
ускорения. Если направление угловой скорости совпадает с направлением углового
ускорения, то движение шатуна будет ускоренным и наоборот.
Планы скоростей и ускорений
построенные для данного положения механизма, дают возможность установить лишь
значения мгновенных скоростей и ускорений различных точек звеньев механизма, в
соответствующее время. Построение последовательных планов положений, скоростей
и ускорений механизма позволяет получить кинематические диаграммы S = S(t), u = u(t), a = a(t)
соответственно. Кинематические диаграммы строятся в прямоугольной системе
координат: по оси абсцисс откладываем отрезок l – длина которого в масштабе mt, принимается равным времени одного
оборота (периода) начального звена.
Контрольные
вопросы
1.
Что такое
кинематические характеристики механизма?
2.
В чем заключается
метод проекций кинематического анализа рычажного механизма?
3.
Для чего строится
кинематическая схема механизма?
4.
На чем основано
определение скоростей точек звеньев, совершающих сложное (плоскопараллельное)
движение?
5.
В чем заключается
используемый при построении планов скоростей и ускорений метод подобия?
Лекция
4
Графическое дифференцирование. Задачи
проектирования механизмов. Механические передачи: классификация, параметры.
Метод кинематических диаграмм
Графический способ кинематического
анализа методом построения диаграмм отличается простотой выполнения и
наглядностью представления результатов. Итогом метода являются графики
перемещений, скоростей и ускорений в зависимости от времени или угла поворота
начального звена, данные графики получили название кинематических диаграмм.
При кинематическом анализе используют
способ графического дифференцирования (существует способ хорд и способ
касательных, рассмотрим первый: делается допущение, что хорда дуги окружности
адекватна касательной).
Пусть задан график S = S(t),
требуется построить u = u(t) и a
= a(t). Для точки А кривой (рис. 4.1) можно записать:
S = у ×mS ,
t = x ×mt
Тогда:
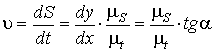 ,
,
где a - угол наклона касательной к рассматриваемой точке А
(предполагаем, что касательная параллельна хорде дуги окружности около
рассматриваемой точки).
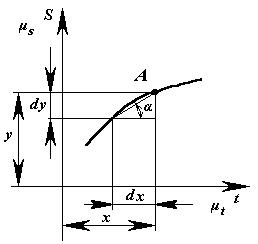
Рис.
4.1
Методика графического
дифференцирования (рис. 4.2):
Диаграмма скоростей. Её строят графическим
дифференцированием диаграммы перемещений по методу хорд:
·
разделяют ось
абсцисс диаграммы перемещений на произвольное число одинаковых частей;
·
через точки
деления 1, 2, 3… проводят координатную сетку;
·
точки пересечения
ординат с графиком перемещений соединяют отрезками (хордами) 0¢-1¢, 0¢-2¢, 0¢-3¢, ¼ (чем больше точек деления, тем хорды будут ближе к истинной кривой);
·
строят систему
координат u = ¦(t), справа от начала координат
откладываем отрезок 0рu., называемый полюсным расстоянием, длиной Н1
и отмечают полюс диаграммы скоростей рu;
Примечание: Величина Н1
выбирается в зависимости от желаемого размаха диаграммы u = ¦(t).
· из полюса рu проводят лучи, параллельные
соответствующим хордам на диаграмме перемещений до пересечения с осью ординат,
получают точки 1¢¢, 2¢, ¼
· из полученных точек проводят
горизонтальные лучи до пересечения с вертикальными прямыми, опущенными из
середин соответствующих отрезков на диаграмме перемещений. Полученные точки 1², 2²,¼ соединяют плавной кривой и получают диаграмму
изменения скорости (первое приближение), в масштабе
 ,
,
где mS - масштаб диаграммы перемещений,
м/мм; mj - масштаб угла поворота начального
звена, рад/мм; w1- угловая
скорость начального звена, рад/с; mt - масштаб времени, с/мм; Н1-
полюсное расстояние, взятое с чертежа, мм.
· Проделав аналогичные операции с
диаграммой u = ¦(t), предварительно восстановив точки 1, 2, 3, и
т.д., получаем зависимость ускорения а = ¦(t) в масштабе
 ,
,
где Н2 - полюсное расстояние для
диаграммы а = ¦(t),
мм.
Рис. 4.2
Экспериментальный метод кинематического исследования
При экспериментальном исследовании
кинематики механизмов кинематические характеристики звеньев и точек механизма
определяются и регистрируются с помощью чувствительных элементов - датчиков,
которые используя различные физические эффекты преобразуют кинематические
параметры в пропорциональные электрические сигналы. Эти сигналы регистрируются
измерительными самопишущими приборами (самописцами, осциллографами и др.).
В последнее время для регистрации и
обработки экспериментальных данных все более широко используются специальные
или универсальные компьютеры. Для примера рассмотрим экспериментальную
установку для исследования кинематических характеристик синусного механизма
(рис. 4.3):
 Датчик перемещения
Датчик перемещения


 1
2
1
2





 B, C R
B, C R

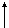

 SD = f(t)
SD = f(t)



 A D
A D


 Датчик Датчик
Датчик Датчик
 0 скорости N S ускорения
0 скорости N S ускорения

 3
Тензометрический
3
Тензометрический
uD= f(t)
усилитель
Рис.
4.3 aD = f(t)
В этой экспериментальной установке:
· для измерения перемещения выходного
звена используется потенциометрический датчик перемещения, в котором
пропорционально положению движка потенциометра изменяется его сопротивление;
· для измерения скорости выходного
звена используется индукционный датчик скорости, в котором напряжение на концах
катушки движущейся в поле постоянного магнита пропорционально скорости катушки;
· для измерения ускорения выходного
звена используется тензометрическиий акселерометр. Он состоит из пластинчатой
пружины, один конец которой закреплен на выходном звене механизма, а на втором
закреплена масса. На пластину наклеены проволочные тензопреобразователи. При
движении выходного звена с ускорением инерционность массы вызывает изгиб
пластины, деформацию тензопреобразователей и изменение их сопротивления
пропорциональное ускорению выходного звена.
Проектирование типовых плоских и пространственных
механизмов
Задачи
проектирования
При проектировании
механизмов различают три этапа:
1.
первым этапом
является установление кинематической схемы механизма, которая обеспечила бы
требуемый вид и закон движения;
2.
второй этап –
разработка конструктивных форм механизма, обеспечивающих прочность,
долговечность, высокий к.п.д. и т.д.;
3.
третий этап –
разработка технологических и технико-экономических показателей проектируемого
механизма, определяемых эксплуатацией в производстве, ремонтами и т.д.
Теория механизмов и машин занимается первым этапом.
Раздел ТММ, посвященный методам проектирования по заданным кинематическим
условиям схем механизмов, получил название – синтеза механизмов.
Основные задачи синтеза механизмов:
-
преобразование
вращательного движения вокруг одной оси во вращательное движение вокруг другой
оси;
-
преобразование
вращательного движения вокруг одной оси в поступательное движение вдоль
некоторой заданной прямой и наоборот;
-
преобразование
поступательного движения вдоль одной заданной прямой в поступательное движение
вдоль другой заданной прямой;
-
воспроизведение
одной из точек звеньев рычажного механизма требуемой траектории,
воспроизведение заданных углов поворота выходного звена, движение выходного
звена с остановами.
Механизмы передачи
Предназначены для передачи вращательного движения
между звеньями.
Передача вращательного движения может производиться с
изменением угловой скорости вращения, с сохранением или изменением направления
вращения. Параметр, характеризующий при передаче движения изменение скорости и
направления, называют передаточным отношением:
 , или
, или
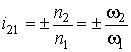 ,
,
где знак (+) если вращение звеньев в
одном направлении; знак (-)
если вращение звеньев в противоположных направлениях; n1,
w1 - соответственно частота, об/мин. и скорость вращения, рад/с, вала 1; n2,
w2 - соответственно частота, об/мин. и скорость вращения, рад/с, вала 2.
Примечание: Знак передаточного отношения имеет
смысл при передачи движения между звеньями с параллельными осями.
Механизмы передачи (механические передачи)
классифицируются в зависимости от названия основных звеньев: фрикционные,
ременные, цепные, зубчатые, червячные, волновые.
Все передачи характеризуются количеством ступеней.
Одноступенчатая – это передача образованная двумя подвижными звеньями,
образуемыми низшие пары со стойкой и высшую пару между собой (рис. 4.4).
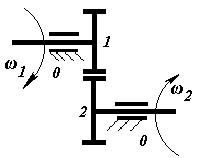
Рис. 4.4
Многоступенчатая –
несколько ступеней соединенных последовательно (рис. 4.5).
Общее
передаточное отношение любого типа сложного
зубчатого механизма i1n, включающего несколько последовательно соединенных друг с
другом простых (одноступенчатых) механизмов, равно произведению передаточных отношений отдельных простых механизмов
(ступеней), входящих в его состав, т.е.:
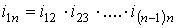
Так, для механизма, представленного
на рис. 4.5 общее передаточное отношение равно:
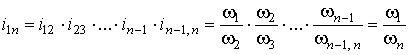 .
.
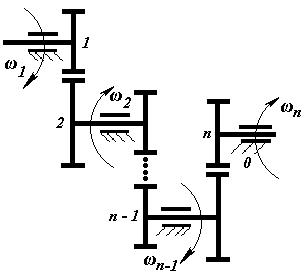
Рис. 4.5
Кроме одноступенчатых и
многоступенчатых применяются планетарные и волновые передачи.
Контрольные вопросы
6.
На чем основано
графическое дифференцирование по методу хорд?
7.
Сформулируйте
основные задачи, решаемые ТММ при проектировании механизма?
8.
Что такое
передаточное отношение?
9.
Что означает знак
передаточного отношения?
10.
Что такое ступень
в зубчатом механизме?
11.
Как определяется
передаточное отношение сложного зубчатого механизма?
Лекция
5
Фрикционные передачи.
Вариатор скорости. Зубчатые механизмы. Основная теорема зацепления.
Геометрические параметры зубчатых колес.
Фрикционные передачи
Фрикционные передачи предназначены
для передачи вращательного движения за счет сил трения (рис. 5.1).
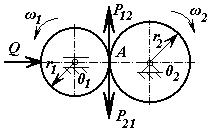
Рис. 5.1
Условием передачи
движения во фрикционном механизме является:
 ,
,
где Р21, Р12 – передаваемое усилие; Fтр – сила
трения в месте контакта валков 1 и 2, определяемая по формуле:
 ,
,
где Q – нормальное усилие прижима валков; f – коэффициент трения скольжения.
Так как чаще всего f » 0,2…0,3, то для передачи движения во
фрикционной передаче усилие прижима должно быть приблизительно в 5 раз больше,
чем передаваемое усилие.
Рассмотрим общую для
валков точку контакта валков А, её окружная скорость равна: для
первого валка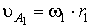 , для второго валка
, для второго валка 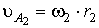 .
.
При отсутствии
проскальзывания валков 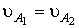 , тогда:
, тогда:
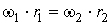 ®
® 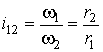 .
.
Цилиндры перекатывающиеся
один относительно другого без проскальзывания называются начальными.
Окружности, получающиеся в пересечении этих цилиндров плоскостью
перпендикулярной их осям называются начальными (радиусы r1 и r2).
Передаточное отношение
имеет знак: «-» когда направления движения не совпадают (т.е. когда касание
внешнее, рис. 5.2, а); «+» когда направления движения
совпадают (т.е. когда касание внутреннее, рис. 5.2, б).
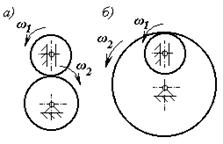
Рис. 5.2
Лобовая
фрикционная передача (вариатор скорости)
Лобовая фрикционная передача
позволяет плавное изменение скорости выходного звена за счет изменения радиуса
начальной окружности (рис. 5.3).
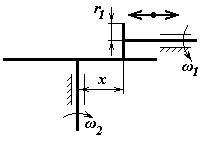
Рис. 5.3
Передаточное отношение его можно
найти из полученной формулы:
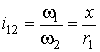
Так как расстояние х можно изменять, то и передаточное отношение
пропорционально будет меняться.
Достоинства фрикционных передач:
1.
Простота
конструкции и изготовления;
2.
Бесшумность
работы;
3.
Не передача от
одного звена другому случайных перегрузок за счет проскальзывания;
4.
Возможность
бесступенчатого регулирования скорости при некотором конструктивном исполнении.
Недостатки
фрикционных передач:
1.
Большая нагрузка
на валы и опоры от усилия прижатия;
2.
Возможность
нарушения кинематической связи, вследствие проскальзывания;
3.
Невысокая
нагрузочная способность.
Зубчатые механизмы (передачи)
Общие положения
Зубчатый механизм - механизм,
высшая пара которого образована зубчатыми звеньями (колесами). Зубчатые
механизмы служат главным образом для передачи вращательного движения между
двумя какими-либо осями с изменением угловой скорости ведомого вала. Вал, от
которого передается движение, называется ведущим; вал, которому
передается движение, называется ведомым.
Простой зубчатый механизм, или простая зубчатая передача,
представляет собой трехзвенный механизм, оба подвижных звена которого являются
зубчатыми колесами. Зубчатые колеса образуют со стойкой две низшие вращательные
пары, а между собой высшую (зубчатое зацепление). В зависимости от расположения
осей зубчатых колес различают зубчатые передачи с параллельными осями или
цилиндрические (рис. 5.4), с пересекающимися осями, или конические (рис. 5.5),
и с перекрещивающимися осями, или гиперболоидные, вариантами которых являются
винтовые (рис. 5.6, а), червячные (рис. 5.6, б) и гипоидные (рис. 5.6, в)
передачи. Помимо этого все передачи делятся на передачи с внешним, внутренним и
реечным зацеплениями. Признаком передачи с внешним зацеплением (рис. 5.4, а)
является вращение её зубчатых колес в противоположные стороны, а передачи с
внутренним зацеплением (рис. 5.4, 6) - в одном направлении. Передача с реечным зацеплением (рис.
5.4, в) состоит из колеса и рейки.
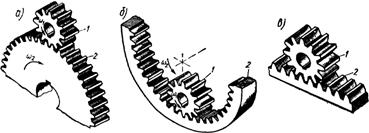
Рис. 5.4
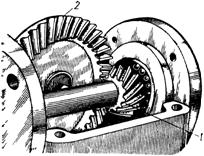
Рис. 5.5
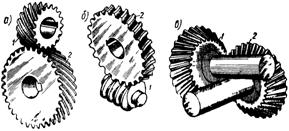
Рис. 5.6
В зависимости от того,
требуется ли обеспечить постоянное отношение угловых скоростей ведущего и
ведомого зубчатых колес или, наоборот, переменное по заданному закону, зубчатые
передачи выполняют соответственно из «круглых»
(рис. 5.4, а, б) и «некруглых» (рис. 5.7) колес.
Рис. 5.7
Сложные зубчатые
механизмы делятся на
зубчатые передачи с промежуточными колесами и валами (многократные или
многоступенчатые) и планетарные механизмы. Многократной зубчатой передачей
называется механизм, представляющий собой соединение нескольких простых
зубчатых передач (ступеней) с неподвижными (по отношению к стойке) осями колес
(рис. 5.8, а). Звено 2 механизма состоит из двух зубчатых колес 2"
и 2', насаженных жестко на один общий вал. На рис. 5.8 зубчатые колеса условно
показаны в виде цилиндров, механизм обладает одной степенью свободы и носит
название редуктора. Промежуточное колесо получает движение от
предыдущего колеса и передает следующему. Промежуточный вал получает
движение через одну пару колес и передает через другую (на рис. 5.8, а
это средний вал).
Рис. 5.8
Передаточным
отношением зубчатого
механизма называется отношение частот вращения зубчатых колес:
Передаточное отношение
трехзвенного зубчатого механизма можно выразить не только через отношение
частот вращения зубчатых колес (n1 и n2),
но и через отношение: угловых скоростей (w1
и w2); чисел зубьев колес (Z1 и Z2);
отношение диаметров начальных окружностей (dw1 и dw2,
кроме червячных):

где знак (+) для внутреннего
зацепления (вращение звеньев в одном направлении); знак (-) для внешнего
зацепления (вращение звеньев в противоположных направлениях).
Передаточное отношение в направлении силового потока, т.е.
отношение угловой скорости ведущего вала к угловой скорости ведомого,
называется передаточным числом.
Передаточное число всегда больше или равно единице.
Основная теорема зацепления
Рассмотрим тела 1
и 2, совершающие вращательные движения, соответственно вокруг центров 01
и 02 с угловыми скоростями w1 и w2 , и образующих между собой высшую кинематическую
пару А (рис. 5.9).
Общая нормаль n-n профилей в точке контакта А
пересекает линию межцентрового расстояния 0102
точке Р, называемой полюсом зацепления, и в кинематическом
отношении, являющейся центром мгновенного вращения в относительном движении
звеньев высшей кинематической пары.
В плоском механизме
обеспечении передачи заданного движения зависит от геометрии сопряженных
профилей (I и II на рис. 5.9). Часто на практике геометрию сопряженных
профилей подбирают так, чтобы она обеспечивала закон движения, характеризуемый
постоянством передаточного отношения между звеньями 1 и 2 высшей пары, т.е. i12 = const.
В рассматриваемый момент
времени скорости точки А равны:
- в системе колеса 1: 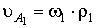 ,
,
- в системе колеса 2: 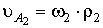 ,
,
где r1 и r1 – радиус
векторы (расстояния соответственно от центов вращения 01 и 02
до точки А).
Рис. 5.9
Проекции 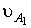 и
и  на
нормаль n-n должны быть равны:
на
нормаль n-n должны быть равны:
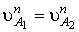 ®
® (1)
(1)
Иначе, или зубья будут
внедряться один в другой, или колеса выйдут из зацепления.
Проекции  и
и 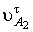 на
касательную t-t не равны между собой, поэтому в
высшей кинематической паре возникает проскальзывание профилей.
на
касательную t-t не равны между собой, поэтому в
высшей кинематической паре возникает проскальзывание профилей.
Проецируем центры
вращения 01 и 02 на нормаль n-n получаем точки N1 и N2.
Из треугольника D01N1А: 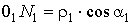 . Из
треугольника D02N2А:
. Из
треугольника D02N2А: 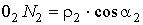 .
.
Следовательно, с учетом
выражения 1:  ,
,
или 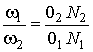 .
.
Рассматривая треугольники
D01РN1 и D02РN2,
устанавливаем, что они подобные (имеют три стороны взаимно параллельные друг
другу), составляем пропорцию:
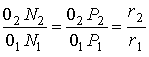 ,
,
где r1 и r2 – радиусы
начальных окружностей. Если они используются в качестве производственных
окружностей в процессе нарезания колес, то они получают ещё название делительных
окружностей.
Следовательно
передаточное отношение в общем виде может быть записано:
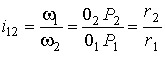 ® основная теорема зацепления.
® основная теорема зацепления.
Т.е. общая нормаль n-n к соприкасающимся (сопряженным)
профилям зубьев делить межосевое расстояние 0102
на части обратно пропорциональные угловым скоростям (передаточному
отношению). Следовательно, для обеспечения постоянства передаточного отношения
контактирующие участки профилей должны быть очерчены по таким кривым, чтобы в
любой момент соприкосновения их общая нормаль в точке контакта проходила через
одну и ту же точку Р (полюс зацепления), на линии центров, т.е.
полюс зацепления в процессе перекатывания зубьев не меняет своего положения.
Межосевое расстояние
можно определить:
 ,
или
,
или 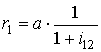 ;
; 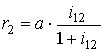 .
.
Угол aW, составленный общей нормалью n-n к профилям зубьев (линией
зацепления) и общей касательной к начальным окружностям, называют углом зацепления.
Для рассмотрения
относительного движения тел используем метод обращения движения (метод
мысленной остановки), т.е. сообщим всем звеньям системы вращательное движение
вокруг оси 01 с угловой скоростью w1 в направлении, противоположном
первоначальному. Тогда 1-е звено остановится, второе будет совершать сложное
плоскопараллельное движение, состоящее из вращения вокруг осей 01
и 02 одновременно, а его движение по отношению к неподвижному
первому телу можно рассматривать, применяя метод мгновенных центров скоростей
(известный из теоретической механики).
Окружные скорости точек,
лежащих на начальных окружностях r1 и r2, всегда равны, следовательно, если
первая окружность остановлена, то вторая будет катиться по первой без
скольжения, а точка Р станет мгновенным центром скоростей второго
тела. Для определения мгновенной скорости w запишем скорость оси 02 в виде равенства:
 .
.
Так как  , а
, а 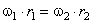 , то:
, то:
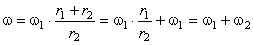 .
.
Итак, после остановки первого тела
второе будет вращаться вокруг полюса с мгновенной угловой скоростью  . Отсюда следует, что точка А
контакта второго тела будет скользить по поверхности первого тела со скоростью,
. Отсюда следует, что точка А
контакта второго тела будет скользить по поверхности первого тела со скоростью,
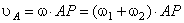 ,
,
которую называют скоростью скольжения
контактных точек. Скольжение контактных точек сопровождается трением.
Требованиям основной теоремы
зацепления удовлетворяют различные кривые, но наибольшее распространение
получили: эвольвентное, круговое (зацепление М.Л. Новикова) и циклоидальное.
Геометрические параметры зубчатых колёс
При проектировании
зубчатого колеса вначале нужно определить его число зубьев Z, а затем определить параметры
зубьев.
Основным параметром
зацепления является шаг р – расстояние между двумя одноименными точками
двух соседних профилей зубьев измеренное по делительной окружности (рис. 5.10):
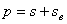 ,
,
где s – толщина зуба; sв – ширина впадины.
Величина 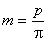 , мм называется модулем зацепления.
, мм называется модулем зацепления.
Получим формулу для
определения радиуса делительной окружности rw. Длина делительной окружности колеса равна:
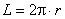 ,
или в шагах
,
или в шагах 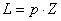 .
.
Отсюда: 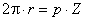 ®
® 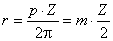 .
.
Делительная окружность –
это окружность для которой шаг дает в пересчете стандартное значение модуля.
Для нормальных колес
находящихся в зацеплении делительные окружности совпадают с начальными r = rw.
Делительная окружность делит зуб на
головку и ножку. Высота зуба равна:
h = h¢ + h²,
где h¢ – высота головки зуба, h¢ = m; h² - высота ножки зуба, h² = 1,25× m.
Полная высота зуба h =2,25× m.
Отсюда радиус окружности
выступов:
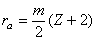 .
.
Радиус окружности впадин:
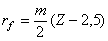 .
.
Передаточное отношение
зубчатой передачи можно определить используя основную теорему зацепления:
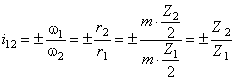 ,
,
Для зубчатых механизмов
существует еще одна характеристика – передаточное число: отношение зубьев
большего колеса к числу зубьев меньшего колеса:
 ,
(т.е. всегда положительное).
,
(т.е. всегда положительное).
Межосевое расстояние при
внешнем зацеплении колес:

На колесе можно провести
бесчисленное число окружностей на каждой из которых будет свой модуль. Для
ограничения этого числа ГОСТом введен стандартный ряд модулей. Стандартной
модуль определяется по окружности называемой делительной. Точнее делительной
называется такая окружность зубчатого колеса, на которой модуль и шаг принимают
стандартное значение. Окружным шагом или шагом называется расстояние по дуге
окружности между одноименными точками профилей соседних зубьев (под одноименными
понимаются правые или левые профили зуба). Угловой шаг t - центральный угол соответствующий
дуге p - окружному шагу по делительной окружности.
Примечание: Согласно ГОСТ основные элементы
зубчатого колеса обозначаются по следующим правилам: линейные величины -
строчными буквами латинского алфавита, угловые - греческими буками;
установлены индексы для величин:
· по окружностям: делительной - без
индекса, вершин - a , впадин - f , основная - b , начальная - w ;
· по сечениям: нормальное сечение - n , торцевое сечение - t , осевое сечение - x;
· относящихся к зуборезному инструменту
- 0 .
Радиус основной
окружности для эвольвенты:
rb = r× cos a.
где a - угол профиля на делительной
окружности,
Углом профиля называется острый угол
между касательной к профилю в данной точки и радиусом - вектором, проведенным в
данную точку из центра колеса.
Контрольные
вопросы
12.
Проанализируйте
достоинства и недостатки фрикционной передачи?
13.
Что такое
фрикционный вариатор скорости?
14.
Назовите основные
виды зубчатых механизмов?
15.
Сформулируйте и
докажите основную теорему зацепления?
16.
Что называется
шагом зацепления?
17.
Что называется
модулем зацепления, зачем его гостируют?
18.
Чему равен
диаметр делительной окружности?
19.
Чему в долях
модуля равна высота ножки и головки зуба нормального колеса?
Лекция
6
Сложные зубчатые
передачи. Передаточное отношение передач с промежуточными колесами и валами.
Планетарные механизмы. Формула Виллиса. Кинематическое исследование типовых
планетарных механизмов аналитическим методам.
Сложные
зубчатые механизмы
В большинстве современных
машин и приборов возникает необходимость осуществлять передачу вращения от
ведущего вала к ведомому с большим передаточным отношением (при значительных
межосевых расстояниях) и строгом согласовании скоростей вращения отдельных
валов. В этом случае применяют зубчатые механизмы либо замедляющие (wведущего > wведомого), так называемые редукторы, либо ускоряющие (wведущего < wведомого) - мультипликаторы. Такие механизмы
обладают одной степенью свободы (лекция 5, рис 5.4, а, б). Так
как в машиностроении чаще возникает необходимость в уменьшении скоростей
вращения, то замедляющие механизмы (или редукторы) нашли более широкое
применение на практике. Использование их в машиностроении позволяет применять
быстроходные, а следовательно, малогабаритные и более дешевые двигатели
(электро-, турбо и прочие двигатели) при тихоходных рабочих машинах, малые
скорости движения которых обусловливается требованиями технологического или
рабочего процессов. В приборостроении применение понижающих передач
обеспечивает малые перемещения измеряющих или регулирующих элементов (получение
более точной настройки прибора или установки вводимой в него величины - индикаторы, тахометры и др.), повышающие
передачи применяют для расширения шкалы и более точного отсчета замеряемой
величины. Однако ускоряющие механизмы (мультипликаторы) применяют значительно
реже и главным образом там, где передаточное отношение изменяется в пределах от
-1 до +1. У редукторов передаточное отношение может изменяться
в очень широком диапазоне (до сотен и даже нескольких тысяч). Но осуществлять
большие передаточные отношения с помощью простейшего зубчатого механизма
(одноступенчатого, два колеса и стойка), нецелесообразно, так как в этом случае
получаются большие размеры механизма. Кроме того, при высоких значениях
передаточного отношения в одной паре колес зубья малого колеса входят в контакт
значительно большее число раз, чем зубья большого колеса, вследствие чего они
изнашиваются быстрее. Поэтому с точки зрения уменьшения габаритов, повышения
долговечности и улучшения условий не принудительной смазки делать в одной паре
зубчатых колес передаточное отношение больше 6¼8 конструктивно нерационально.
В тех случаях, когда
заданное передаточное отношение превышает целесообразное для одной пары колес
или когда требуется обеспечить большое межосевое расстояние, используют сложные
зубчатые механизмы, состоящие из нескольких параллельно или последовательно
соединенных друг с другом зубчатых передач. Различают два вида таких
механизмов: сложные зубчатые механизмы с неподвижными осями (многократные
зубчатые передачи лекция 5, рис 5.8, а) и планетарные (эпициклические)
зубчатые механизмы (оси отдельных колес могут перемещаться относительно стойки,
как на рис 5.8, б, в лекции 5). Каждый из этих видов сложных
зубчатых механизмов может быть составлен не только из однородных колес
(цилиндрических или конических) и передач (с неподвижными осями или
планетарных), но и из их сочетания (рис. 6.1). Наибольшее распространение
получили сложные зубчатые механизмы, составленные из цилиндрических колес с
прямыми зубьями (реже косыми) с равноделенным шагом. Если у зубчатых механизмов
оси ведущего и ведомого звеньев располагаются по одной прямой (рис 5.8, б,
в), то они называются соосными.
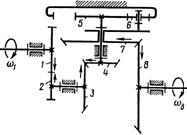
Рис. 6.1
Общее
передаточное отношение любого типа сложного
зубчатого механизма i1n, включающего несколько последовательно соединенных друг с
другом простых механизмов (не планетарных ступеней, планетарных или их
комбинаций) из n колес, равно произведению передаточных отношений отдельных простых механизмов
(ступеней), входящих в его состав, т.е.:
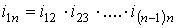 ,
,
Так, для механизма,
представленного на рис. 6.1, состоящего из ступени цилиндрической передачи с
колесами 1-2 с неподвижными осями, конической
передачи 3-4, планетарной ступени 5-6-7,
конической передачи с неподвижными осями 7-8,
общее передаточное отношение равно:

так как w2 = w3;
w4 = w5.
Степень подвижности механизмов
с неподвижными осями колес равна единице, благодаря чему соотношение между
угловыми скоростями ведущего и ведомого звеньев остается постоянным. Поэтому в
задачу исследования этих механизмов входит определение передаточного отношения
по заданной схеме и размерам колес. При этом колеса на схемах сложных зубчатых
механизмов изображаются полоидными или совпадающими с ними начальными
окружностями. Планетарные механизмы могут иметь две и более степени свободы. В
этом случае соотношения между угловыми скоростями выходных валов будут
неоднозначными. Определение угловых скоростей колес таких механизмов при
различных режимах работы является основной задачей их исследования.
Проектирование любых зубчатых механизмов обязательно
состоит из двух этапов: выбора структурной и кинематической схем механизма и
определение чисел зубьев для обеспечения требуемого передаточного отношения.
Кинематическое
исследование механизмов
Исследование
рядовых зубчатых механизмов
Рядовые зубчатые
механизмы (передачи с промежуточными или паразитными колесами), представляют
собой последовательное соединение нескольких пар зубчатых колес, на каждой из
неподвижных осей которых помещено по одному колесу (рис. 6.2). Имея схему
передачи и зная числа зубьев или радиусы полоидных окружностей колес, можно
определить общее передаточное отношение редуктора аналитически или графически.
Для механизма, состоящего
из четырех последовательно соединенных цилиндрических колес внешнего зацепления
(рис. 6.2), общее передаточное отношение:
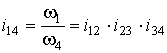
где i12 - передаточное отношение первой пары сцепляющихся зубчатых
колес внешнего зацепления:
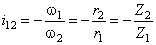

Рис. 6.2
Знак минус поставлен
потому, что колеса 1 и 2 вращаются в противоположных направлениях. Для второй
пары:
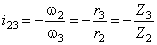
Для третьей пары:
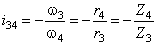 ,
,
Тогда искомое передаточное
отношение:
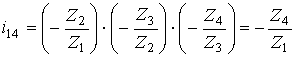
В общем случае при n колесах в механизме:
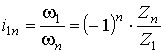
Общее передаточное
отношение рядового зубчатого механизма равно обратному отношению чисел зубьев
или радиусов крайних колес. Знак передаточного отношения определяется множителем (-1)n, где n -
число передач внешнего зацепления. При n четном i >
0, т.е. ведомое и ведущее звенья редуктора или мультипликатора вращаются в
одном направлении; при нечетном n - в
разных направлениях.
Анализируя приведенные
примеры устанавливаем,
что число зубьев промежуточных колес 2 и 3, находящихся одновременно в
зацеплении с двумя другими колесами, не влияет на величину общего передаточного
отношения механизма. Но установка таких промежуточных колес позволяет изменять
направление вращения ведомого звена. При четном числе промежуточных колес
направление вращения ведущего и ведомого звеньев противоположны, при нечетном - одинаковы. Применяют эти колеса
главным образом там, где необходимо изменить направление вращения ведомого вала
при неизменном направлении вращения ведущего (механизм трензеля токарного
станка, механизм заднего хода автомобильной коробки передач и др.), либо там,
где необходимо обеспечить передачу движения при больших межосевых расстояниях
(когда нельзя увеличивать размеры ведущих и ведомых колес из-за их больших габаритов).
Исследование
зубчатых механизмов с промежуточными валами
Сложные зубчатые механизмы с промежуточными валами
представляют собой последовательное соединение нескольких пар колес, на каждый
из валов которого помещено более одного колеса (кроме валов ведущего и ведомого
колес). На рис. 6.3 представлен такой трёхступенчатый механизм для
преобразования движения между параллельными валами, который состоит из двух
ступеней внешнего зацепления с цилиндрическими колесами (1-2 и 3-4) и одной ступени
внутреннего о зацепления (колеса 5-6). Колеса 2-3 и 4-5 соединены вместе,
образуя звенья.
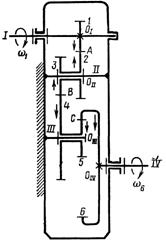
Рис. 6.3
Передаточное отношение первой ступени
равно:
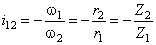 ,
,
второй:
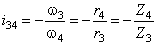
третьей:
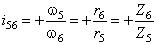
Перемножая эти значения передаточных
отношений, получаем
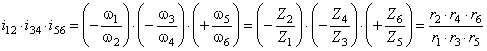
Учитывая, что , w2 = w3;
w4 = w5,
после сокращения получаем
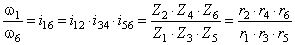
Общее передаточное отношение
ступенчатой передачи равно произведению передаточных отношений ступеней,
входящих в состав механизма, или равно отношению произведения чисел зубьев
(полоидных радиусов) ведомых колес к произведению чисел зубьев (радиусов)
ведущих колее, взятых со своими знаками. Так как передаточное отношение этого
механизма (в отличие от рядового) зависит от числа зубьев всех входящих в его
состав колес, то путем соответствующего подбора чисел зубьев колес можно
получить большие передаточные отношения.
В общем случае при n колесах q внешних зацеплений, общее передаточное отношение равно:

В случае соосного
механизма, составленного из нулевых колес (рис. 6.4) должно удовлетворяться
условие соосности (равенство межосевых расстояний):
 ,
,
или
 ,
,
где m12 и m34 - соответственно модули зацеплений первой и второй ступеней.
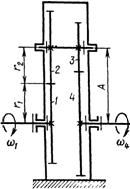
Рис. 6.4
Планетарные механизмы
Сложные зубчатые механизмы, в которых
ось хотя бы одного колеса подвижна, называются планетарными механизмами.
К типовым планетарным механизмам относятся:
· однорядный планетарный механизм;
· двухрядный планетарный механизм с
одним внешним и одним внутренним зацеплением;
· двухрядный планетарный механизм с
двумя внешними зацеплениями;
· двухрядный планетарный механизм с
двумя внутренними зацеплениями.
Элементы планетарного механизма имеют
специальные названия:
· зубчатые колеса оси которых
неподвижны называются центральными. Колесо с внешними зубьями, расположенное в
центре механизма называется солнечным, колесо с внутренними зубьями называют
короной или эпициклом;
· колеса, оси которых подвижны,
называют планетными или сателлитами;
· подвижное звено, соединяющее оси
центральных колес и сателлитов называют водилом. Водило принято обозначать не
цифрой, а латинской буквой h, или русской в.
В таблице 6.1 приведены структурные
схемы типовых планетарных механизмов, а также диапазоны рекомендуемых
передаточных отношений и ориентировочные значения КПД при этих передаточных
отношениях.
Таблица 6.1 Типовые схемы
планетарных механизмов
Если степень подвижности планетарного
механизма 2 и более, то его называют дифференциальным. Для механизма
выполненного по схеме 1 табл. 6.1 степень подвижности при закреплённом колесе 3
равна:
W = 3× (4 – 1) - 2×3 – 1× 2 = 1.
При свободном колесе 3:
W = 3× (5 – 1) - 2×4 – 1× 2 = 2.
Достоинства планетарных механизмов:
большие передаточные отношения при малых габаритных размерах; можно применять
для сложения, или разделения движения.
Метод
Виллиса (аналитический метод кинематического анализа)
Метод Виллиса основан на способе
обращения движения (способ мысленной остановки водила): всем звеньям механизма
мысленно придаем вращение с угловой скоростью равной угловой скорости водила,
только в обратном направлении. Относительные движения звеньев при этом не
изменяются, абсолютные будут следующими (для схемы 1, табл. 6.1):
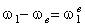 ,
,
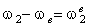 ,
,
 ,
,
 .
.
Расшифруем принятые обозначения: w1, w2, w3, wв –
истинные значения угловых скоростей звеньев;  -
угловая скорость центрального колеса 1 при остановленном водиле;
-
угловая скорость центрального колеса 1 при остановленном водиле;  - угловая скорость сателлита 2 при
остановленном водиле;
- угловая скорость сателлита 2 при
остановленном водиле;  - угловая скорость центрального
колеса 3 при остановленном водиле (равна - wв);
- угловая скорость центрального
колеса 3 при остановленном водиле (равна - wв);  - угловая скорость водила при
остановленном водиле (равна нулю).
- угловая скорость водила при
остановленном водиле (равна нулю).
Тогда получаем, что все колеса
совершают вращательные движения вокруг неподвижных осей и общее передаточное
отношение можно найти по формуле:
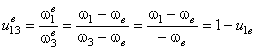 ® формула Виллиса.
® формула Виллиса.
После применения метода обращения
движения, рассматриваемый механизм можно рассматривать как сложный
двухступенчатый с промежуточным колесом:
 ,
,
тогда:
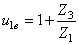 .
.
Контрольные
вопросы
20.
Почему при
определении передаточного отношения зубчатого сложного механизма с
промежуточными колесами можно не учитывать количество зубьев промежуточных
колес?
21.
Что такое
промежуточный вал?
22.
Дайте
характеристику звеньев входящих в планетарный механизм?
23.
Выведите формулу
Виллиса для анализа планетарного механизма?
Лекция
7
Проектирование
планетарных зубчатых механизмов. Постановка задачи синтеза. Условия подбора
чисел зубьев. Вывод расчетных формул для условий соосности, соседства и сборки.
Задачи синтеза зацеплений. Эвольвента. Эвольвентное зацепление.
Проектирование
планетарных механизмов.
Постановка
задачи синтеза
При проектировании многопоточных
планетарных механизмов необходимо, кроме требований технического задания,
выполнять ряд условий связанных с особенностями планетарных механизмов. Задачей
синтеза, является получение требуемого передаточного отношения, выбор схемы
отвечающей требованиям наиболее высокого КПД и габаритными размерами и т.д.
После выбора схемы механизма
необходимо определить сочетание чисел зубьев его колес, которые обеспечат
выполнение условий технического задания – для редуктора это передаточное
отношение и величина момента сопротивления на выходном валу. Передаточное
отношение задает условия выбора относительных размеров зубчатых колес – чисел
зубьев колес, крутящий момент задает условия выбора абсолютных размеров – модулей
зубчатых зацеплений. Так как для определения модуля необходимо выбрать материал
зубчатой пары и вид его термообработки, то на первых этапах проектирования принимают
модуль зубчатых колес равным единице, то есть решают задачу кинематического
синтеза механизма в относительных величинах.
Обычно при определении размеров
звеньев механизмов, т.е. при подборе чисел зубьев колес выполняют условие 3-х
«с»: соосности, соседства и сборки.
Условия
подбора чисел зубьев.
Вывод
расчетных формул для условий соосности, соседства и сборки.
Условия, которые необходимо выполнить
при подборе чисел зубьев колес типового планетарного механизма:
1.
заданное
передаточное отношение с требуемой точностью;
2.
соосность
входного и выходного валов механизма;
3.
свободное
размещение (соседство) сателлитов;
4.
сборку механизма
при выбранных числах зубьев колес;
5.
минимальные
относительные габариты механизма.
Рассмотрим эти условия подробнее на
примере двухрядного планетарного механизма с одним внешним и одним внутренним
зацеплением (рис. 7.1).
1.
Обеспечение
заданного передаточного отношения с требуемой точностью.
Принимаем требуемую точность ± 5%, тогда для рассматриваемой схемы
механизма
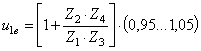
2.
Обеспечение условия
соосности входного и выходного валов.
Для этого необходимо чтобы межосевое
расстояние в передаче внешнего зацепления (первый ряд) равнялось межосевому
расстоянию в передаче внутреннего зацепления (второй ряд), то есть:
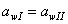 ;
;
 ;
;
 .
.
Обычно в планетарных механизмах
применяются зубчатые колеса без смещения, для которых xi = 0 и
rwi = ri = Zi × m / 2. Тогда
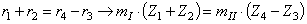
Принимаем, что mI =
mII = m, и получаем условие соосности для данной
схемы механизма
 .
.
 3
3


 С1
С1






 2 C
2 C










 B В1
B В1











 awI A
awII
awI A
awII







 A1
A1

















 0
0



 w1
wв B2 А2 А3
B3
w1
wв B2 А2 А3
B3



 1 C2
C3
1 C2
C3
 в
в
jв
Рис. 7.1
3.
Обеспечение условия
соседства сателлитов заключается в том, чтобы сателлиты поставленные
для повышения жесткости, прочности, а также уравновешивания масс не задевали
друг друга (при числе сателлитов k > 1).
Сателлиты размещаются на окружности
радиуса aw. Вершины зубьев сателлитов не будут мешать
движению друг друга, если выполняется условие:
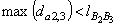
Для зубчатых колес без смещения
максимальный из диаметров сателлитов равен:
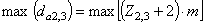 .
.
Расстояние между осями сателлитов
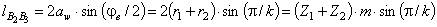 ,
,
где jв – угол между двумя соседними сателлитами.
Подставим полученные выражения в
неравенство и получим условие соседства:
 ,
,
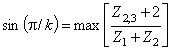 .
.
4. Условие сборки –
условие равных углов между сателлитами, заключается в том, что при постановке
1-го сателлита центральные колеса займут вполне определённое взаимное
расположение и остальные сателлиты могут быть введены в зацепление только при
определённом соотношении между числом их зубьев.
Найдем длины дуг между двумя
сателлитами колеса 3 и 1:
- в шагах: 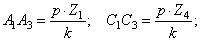
- через количество зубьев на дуге: 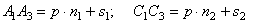 , (целое число зубьев плюс кусочек зуба).
, (целое число зубьев плюс кусочек зуба).
Сложим левые и правые части
выражений:
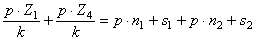 ,
,
группируем: 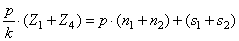 ,
,
после деления получаем:  .
.
Видим, что в левой половине целое
число, следовательно и сумма в правой половине выражения должна дать целое
число, т.к. первое слагаемое тоже дает всегда целое число, то:
Это выполняется когда:  .
.
Следовательно, получаем:
 ,
,
где 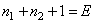 , Е
– любое целое число.
, Е
– любое целое число.
Отсюда условие сборки
принимает вид:
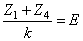 .
.
Сумма зубьев центральных
колес должна быть кратной числу сателлитов.
Оптимальный
синтез планетарных механизмов
при
автоматизированном проектировании
При
автоматизированном проектировании с помощью компьютера можно за относительно
небольшой промежуток времени получить большое количество возможных решений задачи.
Сопоставляя эти решения между собой находят то, которое удовлетворяет всем
требованиям наилучшим образом. При этом перебор вариантов осуществляется в
пределах заданных ограничений на параметры (в данном случае на числа зубьев
колес) по какой-либо стратегии или чаще случайным образом. Программы
оптимального синтеза могут использовать рассмотренные выше методы (например,
метод сомножителей), а могут просто перебирать допустимые сочетания параметров
и проверять их на соответствие заданным условиям. Использование компьютерных
программ для синтеза планетарных механизмов позволяет существенно сократить
время проектирования и существенно улучшить качественные показатели
спроектированных механизмов.
Синтез зубчатых зацеплений
Зубчатым зацеплением
называется высшая кинематическая пара образуемая последовательно
взаимодействующими поверхностями зубьев.
Синтез зубчатого
зацепления состоит в том, чтобы отыскать такие взаимодействующие поверхности,
которые обеспечивали заданный закон их относительного движения.
Синтез основан на
использовании основной теоремы зацепления:
 .
.
Следствия теоремы: для
получения постоянного передаточного отношения необходимо чтобы отношение
радиусов начальных окружностей было постоянно, т.е. точка Р – полюс
зацепления не менял своего положения.
При выборе кривых
очерчивающих профиль зуба руководствуются соображениями кинематического,
динамического, технологического и эксплуатационного характера:
-
кинематические –
состоят в том, чтобы проектируемые профили очерчивались простыми
геометрическими приёмами, и удовлетворялось требуемое передаточное отношение;
-
динамические –
чтобы при постоянной передаваемой мощности, усилие действующее на зубья и опоры
было постоянным по величине и направлению и чтобы форма зуба обеспечивала
наибольшую прочность;
-
технологические и
эксплуатационные – простота изготовления, бесшумная и безударная работа,
допустимость некоторых погрешностей в изготовлении и монтаже.
В современном машиностроении наибольшее
распространение получили колеса с эвольвентным и круговым (зацепление Новикова)
профилями зубьев. В точном машиностроении и приборостроении разновидности
циклоидального зацепления.
Эвольвента окружности и её свойства
Эвольвентой называется
кривая, очерчиваемая точкой прямой, при перекатывании этой прямой по окружности
без проскальзывания (рис. 7.3). В теории зацепления прямую называют
производящей (образующей), а окружность – основной окружностью (радиус rb).
Рассмотрим построение
эвольвенты Е (рис. 7.3). В произвольной точке эвольвенты М
проведем нормаль, которая касается основной окружности в точке В,
получаем радиус кривизны эвольвенты r.
Рис. 7.3
Из прямоугольного треугольника DОВМ найдем катет МВ:
 .
.
Из условия образования эвольвенты
радиус кривизны МВ должен быть равен длине развертываемой дуги АВ
основной окружности:
ÈАВ = rb×(q+a),
 ,
,
где q - полярный угол наклона радиус
вектора; - угол между
направлением радиус вектора и направлением радиуса основной окружности
проведенного в точке касания нормали.
Отсюда:
 .
.
Разность тангенса и угла
представляет собой эвольвентную функцию называемую инволютой. Инволюта является
параметром для геометрических расчетов зубчатых механизмов.
Свойства эвольвенты:
-
эвольвента не
имеет точек внутри основной окружности;
-
нормаль к любой
точке эвольвенты направлена по касательной к основной окружности;
-
центр кривизны
эвольвенты лежит в точке касания нормали с основной окружностью.
Эвольвентное зацепление и его
свойства
Из свойств эвольвенты
вытекают свойства эвольвентного зацепления. Пусть профиль зуба колеса 1 (рис.
7.4) очерчен по эольвенте основной окружности с радиусом rb1, а профиль зуба колеса 2 – по эвольвенте основной
окружности радиуса rb2. Поместим центры этих окружностей в
центры вращения О1 и О2. Нормаль к эвольвенте первого колеса
должна быть касательной к основной окружности первого колеса, а нормаль к
эвольвенте второго колеса должна быть касательной к основной окружности второго
колеса. В точке касания эвольвент нормаль должна быть общей к обоим профилям,
и, следовательно, точка контакта лежит на общей касательной к основным
окружностям. При вращении ведущего колеса 1 против часовой стрелки, а ведомого
колеса 2 – по часовой (рис. 7.4, а) точка касания эвольвент перемещается
по отрезку В1В2 этой касательной, т.к. вне отрезка В1В2
эвольвенты не могут касаться, т.е. иметь общую нормаль; В1В2
является линией зацепления.
Точка пересечения общей
нормали к эвольвентам с линией межосевого расстояния О1О2
является полюсом зацепления Р и занимает неизменное положение.
Если направление вращение
ведущего колеса 1 и ведомого колеса 2 изменится, то линия зацепления В1В2,
по которой перемещается точка контакта, займет новой положение (рис. 7.4, б).
Угол между линией
зацепления В1В2 и прямой, перпендикулярной линии межосевого
расстояния, называется углом зацепления и обозначается через aw. Углы РВ1О1 и
РВ2О2 равны углу зацепления aw как углы с соответственно
перпендикулярными сторонами. Поскольку РО1 = rw1, а РО2 = rw2, то
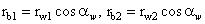 .
.
Следовательно, при эвольвентном зацеплении
передаточное отношение может быть выражено через отношение радиусов основных
окружностей:
 ,
,
причем знак плюс относится к внутреннему зацеплению, а
знак минус – к внешнему.
Из формулы видно, что при
эвольвентном зацеплении изменение межосевого расстояния не влияет на значение
передаточного отношения вследствие неизменности радиусов основных окружностей.
При изменении межосевого расстояния изменяются лишь радиусы начальных
окружностей и угол зацепления.
Контрольные вопросы
1.
Сформулируйте
основные задачи синтеза планетарных механизмов?
2.
В чем заключаются
условия соосности, соседства и сборки при синтезе планерных механизмов?
3.
Сформулируйте
основные требования предъявляемые к геометрическим кривым очерчивающим профили
зубьев?
4.
Назовите свойства
эвольвенты?
5.
Что такое
инволюта (эвольвентная функция) угла?
6.
Назовите основные
свойства эвольвентного зацепления?
Лекция
8
Изготовление зубчатых
колес. Смещение режущего инструмента. Коэффициент перекрытия. Явление
подрезания. Коррегирование эвольвентного зацепления. Качественные
характеристики зубчатой передачи.
Методы
изготовления эвольвентных зубчатых колес
Существует множество
вариантов изготовления зубчатых колес. В их основу положены два принципиально
отличных метода:
· метод копирования, при котором
рабочие кромки инструмента по форме соответствуют обрабатываемой поверхности
(конгруэнтны ей, т.е. заполняют эту поверхность как отливка заполняет форму).
Строится копия, по этой копии изготавливается фреза.
· метод обкатки, при котором инструмент
и заготовка за счет кинематической цепи станка выполняют два движения - резания
и огибания (под огибанием понимается такое относительное движение заготовки и
инструмента, которое соответствует станочному зацеплению, т.е.
зацеплению инструмента и заготовки с требуемым законом изменения передаточного
отношения).
Из вариантов
изготовления по способу копирования можно отметить:
· нарезание зубчатого колеса
профилированной дисковой или пальцевой фрезой (проекция режущих кромок которой
соответствует конфигурации впадин, рис. 8.1). При этом методе резание
производится в следующем прядке: прорезается впадина первого зуба, затем
заготовка с помощью делительного устройства (делительной головки) поворачивается
на угловой шаг и прорезается следующая впадина. Операции повторяются пока не
будут прорезаны все впадины. Недостатки метода: производительность низкая,
сложность изготовления инструмента, по мере износа инструмента ухудшение точности
и качества поверхности нарезаемого колеса, для изготовления колес с различными
модулями необходим набор фрез.
Рис. 8.1
· отливка зубчатого колеса в форму. При
этом внутренняя поверхность литейной формы конгруэнтна наружной поверхности
зубчатого колеса. Производительность и точность метода высокая, однако при этом
нельзя получить высокой прочности и твердости зубьев.
Из вариантов изготовления
по методу обкатки наибольшее распространение получили:
·
обработка на
зубофрезерных или зубодолбежных станках червячными фрезами (рис. 8.2, а),
долбяками (рис. 8.2, б), инструментальной рейкой – гребёнкой (рис. 8.2, в).
Производительность достаточно высокая, точность изготовления и чистота поверхностей
средняя. Можно обрабатывать колеса из материалов с невысокой твердостью
поверхности. Долбяк позволяет нарезать колеса с внутренним зацеплением.
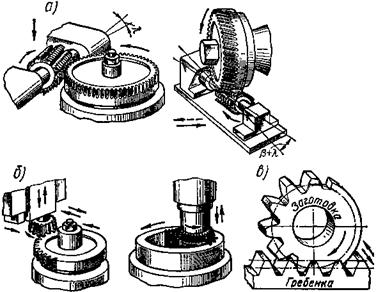
Рис. 8.2
· накатка зубьев с помощью специального
профилированного инструмента. Обеспечивает высокую производительность и хорошую
чистоту поверхности. Применяется для пластичных материалов, обычно на этапах
черновой обработки. Недостаток метода образование наклепанного поверхностного
слоя, который после окончания обработки изменяет свои размеры.
· обработка на зубошлифовальных станках
дисковыми кругами. Применяется как окончательная операция после зубонарезания
(или накатки зубьев) и термической обработки. Обеспечивает высокую точность и
чистоту поверхности. Применяется для материалов с высокой поверхностной прочностью.
На
рис. 8.3 показан контур зубьев рейки, который называется исходным, так как он
служит основой для определения форм и расположения режущих кромок. Отличие размеров
инструментов от нарезаемого колеса состоит в том, что их высота увеличена на
радиальный зазор (0,25 m).
Необходимость зазора обусловлена технологическими требованиями (охлаждение
заготовки рабочей жидкостью, сход стружки). Головка зуба режущего инструмента
вырезает ножку зуба в заготовке. Этот контур называется производящим, так как
при движении режущих кромок он образует производящую поверхность. Прямая СС,
проходящая по середине прямолинейной части зуба называется делительной прямой.
По делительной прямой толщина зуба равна ширине впадины.
Для сокращения
номенклатуры режущего инструмента стандарт устанавливает нормативный ряд
модулей и определенные соотношения между размерами элементов зуба.
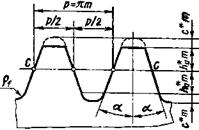
Рис. 8.3
По ГОСТ 13755-81 значения
параметров исходного контура должны быть следующими:
· угол главного профиля a = 20°;
· коэффициент высоты зуба 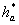 = 1;
= 1;
· коэффициент радиального зазора в паре
исходных контуров 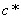 = 0,25;
= 0,25;
· радиус закругления  = 0,4 m.
= 0,4 m.
Исходный производящий
контур отличается от исходного высотой зуба h0 = 2,5m.
Исходный и исходный
производящий контуры образуют между собой конгруэнтную пару (рис. 8.3), т.е.
один заполняет другой как отливка заполняет заготовку (с радиальным зазором с*× m в зоне прямой вершин зуба исходной
рейки).
Достоинства метода: простота изготовления
инструмента, по мере износа легко заточить, обеспечение прямолинейности режущих
кромок.
Смещение
режущего инструмента
Если при нарезании колеса
средняя линия инструментальной рейки касается делительной окружности
нарезаемого колеса, то нарезаемое колесо называют нормальным или нулевым.
Если при нарезании
среднюю линию инструментальной рейки сс сместить относительно
делительной окружности нарезаемого колеса, то получим колеса нарезанные со
смещением режущего инструмента.
Величина смещения:
в = x×m,
где x – коэффициент смещения, если x > 0 – нарезается положительное колесо, если x < 0 – нарезается отрицательное колесо (рис. 8.4).
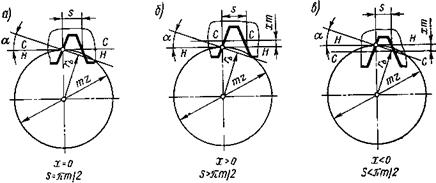
Рис. 8.4
В зависимости от
положения рейки зуб колеса очерчивается разными участками эвольвенты, и форма
зуба при этом меняется. На рис. 8.5 приведена картина форм зубьев для различных
вариантов смещения. Как видно из рисунка, при положительном смещении толщина
зуба по делительной окружности увеличивается, а при отрицательном –
уменьшается. Изменение геометрических параметров влечет за собой изменение
прочностных характеристик зубьев нарезаемого колеса. Таким образом,
соответствующим выбором коэффициента смещения можно влиять на геометрические и
эксплуатационные характеристики колеса и зацепления в целом (изменяется форма
зуба, изгибная и контактная прочность, коэффициент перекрытия).
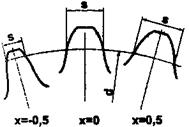
Рис. 8.5
Введя в зацепление колеса
нарезанные по всем трём вариантам, получают 3 варианта зацепления: нулевое,
положительное и отрицательное.
Заострение
зубчатого колеса
Если при нарезании
зубчатого колеса увеличивать смещение, то основная и делительная окружность не
изменяют своего размера, а окружности вершин и впадин увеличиваются. При этом
участок эвольвенты, который используется для профиля зуба, увеличивает свой
радиус кривизны и профильный угол. Толщина зуба по делительной окружности
увеличивается, а по окружности вершин уменьшается.
На рис. 8.6
изображены два эвольвентных зуба для которых:
x2
> x1 Þ ra2 > ra1
;
s2
> s1 Þ sa2 < sa1.
Для термообработанных
зубчатых колес с высокой поверхностной прочностью зуба заострение вершины зуба
является нежелательным. Термообработка зубьев (азотирование, цементация,
цианирование), обеспечивающая высокую поверхностную прочность и твердость
зубьев при сохранении вязкой сердцевины, осуществляется за счет насыщения
поверхностных слоев углеродом. Вершины зубьев, как выступающие элементы колеса,
насыщаются углеродом больше. Поэтому после закалки они становятся более
твердыми и хрупкими. У заостренных зубьев появляется склонность к скалыванию
зубьев на вершинах. Поэтому рекомендуется при изготовлении не допускать толщин
зубьев меньших некоторых допустимых значений. То есть заостренным
считается зуб у которого sa < [sa].
При этом удобнее
пользоваться относительными величинами [sa /m]. Обычно принимают следующие допустимые
значения:
улучшение,
нормализация [sa /m] = 0,2;
цианирование, азотирование
[sa /m] = 0,25...0,3;
цементация
[sa /m] = 0,35...0,4.
Подрезание
эвольвентных зубьев
Явление подрезания
наблюдается, когда рабочий участок выходит за пределы теоретического.
Рассмотрим критический случай, когда они совпадают. Участок линии зацепления,
соответствующий эвольвентному зацеплению определяется отрезком зацепления.
Текущая точка контакта Bl определяется пересечением линии станочного зацепления и
прямой граничных точек инструмента. Если точка Bl располагается ниже (рис. 8.7) точки N, то возникает подрезание зуба.
Условие при котором нет подрезания можно записать так:
P0N ³ P0Bl .
Из D P0N0
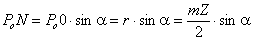 , а из D P0BlF
, а из D P0BlF
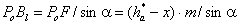 .
.
|
 линия станочного зацепления линия станочного зацепления
делит. прямая

h*a× m x× m P0 ст.-нач. прямая
  пр.гран.точек Bl пр.гран.точек Bl
   F N F N
  a a
 r rb r rb
  0 0
Рис. 8.5
|
Тогда:
 ,
,
при x= 0
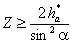 ,
,
откуда:
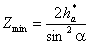 ,
,
где Zmin - минимальное число зубьев нулевого
колеса нарезаемое без подрезания, при стандартном угле a = 20° и при коэффициенте высоты головки зуба  , равно 17.
, равно 17.
Если средняя прямая рейки
сдвигается на величину  , то предельное число зубьев
будет равняться:
, то предельное число зубьев
будет равняться:
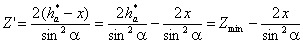 ,
,
При a = 20° и 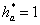 , имеем:
, имеем:
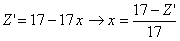 .
.
Величина х –
коэффициент смещения, показывает на какое число модулей нужно отодвинуть среднюю
прямую от касательной к делительной окружности, чтобы при числе зубьев меньшем
17, не возникло явление подрезания (рис. 8.6, а).
Установив критическое
условие подрезания эвольвентных колес, рассмотрим меры которые применяют для
устранения явления подрезания.
Все эти меры называют
методами коррегирования, или исправления эвольвентного зацепления.
Коррегирование
На практике применяются
три способа коррегирования: высотное, угловое и смешанное.
Рассмотрим все виды
коррегирования:
1.
Высотное
коррегирование (рис. 8.6, б).
При высотном
коррегировании два сопряженных колеса нарезаются инструментом, который получает
одинаковое по величине смещение относительно оси заготовки.
У коррегированных колес
диаметры окружности выступов отличаются от нормальных: у малого колеса диаметр
окружности выступов увеличен, а у большого колеса на такую же величину
уменьшен. Высота головок зубьев коррегированной пары неодинакова: у малого
колеса больше, у большого – меньше. Общая высота не изменяется и остается такой
же, как у некоррегируемых колес.
Высотное коррегирование с
постоянным межосевым расстоянием рекомендуется для передач, у которых Z1 + Z2 ³ 25, а число зубьев малого колеса Z1 ³ 7.
2.
Угловое
коррегирование (рис. 8.6, в).
Угловое коррегирование
применяют, когда необходимо уменьшить число зубьев на малом колесе.
Поскольку выше нами
установлено, что 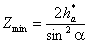 , то число зубьев уменьшается при
увеличении угла зацепления. В таких случаях угол зацепления доводят до 32°. Зуб при этом утолщается у ножки.
Одновременно возрастает радиус кривизны профиля.
, то число зубьев уменьшается при
увеличении угла зацепления. В таких случаях угол зацепления доводят до 32°. Зуб при этом утолщается у ножки.
Одновременно возрастает радиус кривизны профиля.
Однако при увеличении
угла зацепления уменьшается действительная длина зацепления и соответственно
коэффициент перекрытия. Отсюда уменьшается плавность работы передачи и
появляются удары. На рис 8.6 в, сплошной линией показан профиль при a = 20°, а пунктиром – при большем угле. Во втором случае
профиль более пологий и рабочая часть линии зацепления М¢N¢ меньше по величине.
Рис. 8.6
3.
Смешанное
коррегирование (рис. 8.6 г).
Этот вид коррегирования
получил наибольшее распространение. При нарезании заготовки режущий инструмент
смещается на зуборезном станке.
На рис. 8.6 г,
пунктиром показано стандартное зацепление колеса с рейкой, а смещенное на
величину в – контурными линиями. При положительном смещении толщина зуба
рейки по линии сс, проходящей через полюс зацепления Р, будет
меньше, чем на линии с¢с¢, поэтому ширину впадины шестерни во избежание ударов уменьшают, т.е. при
каждом таком шаге толщину её зуба увеличивают. Толщина нарезаемого зуба у основания
увеличивается, что упрочняет зуб.
Коэффициент
торцевого перекрытия.
Если в зубчатой передаче
требуется обеспечить только непрерывность в передаче вращения, то достаточно,
чтобы в зацеплении постоянно находились не менее одной пары зубьев. Однако в
передачах состоящих из зубчатых колес с малым числом зубьев при работе на
больших скоростях возникает шум и удары в зацеплении, теряется равномерность
передачи окружной силы.
Если в зацеплении
находится несколько пар зубьев одновременно, то указанные факторы уменьшаются.
Полный
коэффициент перекрытия eg является суммой торцового коэффициента
перекрытия ea и осевого коэффициента перекрытия eb, т.е.
eg = ea + eb.
Значение торцового
коэффициента перекрытия может быть вычислено как отношение длины активной линии
зацепления ga к шагу эвольвентного зацепления рa:
 .
.
Активная линия зацепления – участок линии зацепления, в точках
которого последовательно соприкасаются взаимодействующие профили зубьев. При
отсутствии подрезания этот участок заключен между точками
Н1
и
Н2 (рис. 8.7).
Шагом зацепления рa называется расстояние по
контактной
нормали (нормаль к главным профилям в точке их касания) между двумя
контактными точками одноименных главных профилей соседних зубьев:
рa = m p cosa .
Длина активной линии
зацепления ga:
Здесь радиус основной окружности rb
получен из прямоугольного треугольника (рис. 8.8), где гипотенуза – радиус
делительной окружности (r = mZ/2), а прилежащий катет – радиус основной окружности:
 .
.
Окончательно
 .
.
 .
.
Для прямозубых зубчатых
колес обычно ea <
1,7. Для увеличения коэффициента перекрытия используют косозубые колеса, тогда
добавляется коэффициент осевого перекрытия eb, который может быть вычислен как отношение рабочей ширины
венца передачи bw к осевому
шагу рх (рис. 8.9):
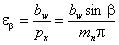 ,
,
где mn – расчетный или нормальный модуль,
т.е. модуль в нормальном сечении nn.
Качественные
характеристики передачи
Рассмотрим геометрические и кинематические
характеристики зубчатой передачи, зависящие от исходных параметров передачи Z1, Z2, m, x1, x2 и влияющие
на эксплуатационные качества передачи.
1.
Приведенный
радиус кривизны.
Усталостное выкрашивание является основным видом разрушения активной поверхности
зубьев закрытых и хорошо смазанных зубчатых передач. Выкрашивание заключается в
том, что вследствие многократного возникновения контактных напряжений на
поверхности зубьев вблизи полюса появляются микроскопические трещины, которые,
развиваясь и объединяясь, приводят к отделению мелких частиц металла и
образованию ямок. Для предотвращения выкрашивания необходимо, чтобы контактные
напряжения на активных поверхностях не превышали допустимых.
Если эвольвенты в полюсе зацепления заменить дугами
окружности с радиусами r1 и r2, равным радиусам кривизны эвольвент в полюсе, то
контактные напряжения можно приближенно определить по формуле Герца-Беляева для
двух контактирующих цилиндров (рис. 8.10).
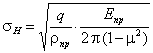 ,
,
где q
– удельная нагрузка; rпр –
приведённый радиус кривизны; Eпр –
приведенный модуль упругости; m - коэффициент Пуассона.
Из этой формулы, в частности, следует, что контактные
напряжения обратно пропорциональны 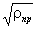 . Приведенный радиус кривизны
rпр равен:
. Приведенный радиус кривизны
rпр равен:
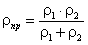 .
.
Следовательно, контактные напряжения уменьшаются с
увеличением rпр, который, в свою очередь, растет с
увеличением r1 и r2 . Можно показать, что радиус кривизны растет с
увеличением угла зацепления. Следовательно, максимальная контактная прочность
достигается максимальной суммой коэффициентов смещения хS = х1 + х2.
Необходимо отметить, что в зубчатой передаче внутреннего зацепления (рис. 8.11)
приведенный радиус кривизны значительно больше, чем в передаче внешнего зацепления:
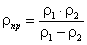 .
.
В соответствии с ранее сказанным контактные напряжения
в передаче внутреннего зацепления значительно меньше, чем в передаче внешнего
зацепления.
Эвольвентное зацепление – не единственное, хотя и
самое распространенное. Существует, например, зацепление Новикова (рис.
8.12), в котором приведенный радиус кривизны, также значительно больше, чем в
эвольвентных колесах внешнего зацепления. Вследствие этого значительно меньше
контактные напряжения и выше нагрузочная способность. Особенность зацепления
Новикова – торцовый коэффициент перекрытия ea = 0, поэтому eg = eb, т.е. зацепление работоспособно только в косозубом
исполнении. Недостаток зацепления Новикова – чувствительность к точности
изготовления, которое является достаточно сложным.
2. Коэффициент, учитывающий форму зуба. Под
действием приложенных нагрузок может произойти поломка зубьев. Для
предотвращения этого зубья должны быть рассчитаны на изгибную прочность.
На рис. 8.13 представлено поперечное сечение зуба прямозубого
колеса, схема действия сил и эпюры напряжений. Здесь сила R – реакция со стороны сопряженного
колеса, разложенная на две составляющие: окружную силу Р, создающую
крутящий момент на колесе и вызывающую появление в сечении изгибных напряжений,
и радиальную силу F, сжимающую зуб. Зададимся вопросом, в какой области
наиболее вероятно разрушение зуба?
Сравнивая суммарные напряжения s
S зоны «А» и «В», приходим к выводу,
что наиболее опасной является зона «А», т.к. именно в ней наибольшие
положительные напряжения. В зоне «В» суммарные напряжения по модулю больше, но
они – отрицательные, т.е. соответствуют деформации сжатия. Из сопротивления
материалов известно, что чрезвычайно трудно разрушить образец, подвергаемый
сжатию.
Максимальное значение нормальных напряжений в опасном
сечении зуба обратно пропорционально коэффициенту YF, учитывающему форму зуба. С
увеличением этого коэффициента напряжения от изгиба уменьшаются. Коэффициент YF зависит в числе прочего от
коэффициента смещения и от того, является ли зубчатое колесо в передаче ведущим
или ведомым.
Повышение изгибной прочности достигается подбором
таких коэффициентов смещения, которое обеспечивает получение максимальных
коэффициентов YF
при условии равнопрочности зубьев обоих зубчатых колес передачи. Отметим, что
это повышение наблюдается при увеличении до определенных значений суммы
коэффициентов смещения.
2.
Удельное
скольжение. Износ
зубьев происходит вследствие относительного скольжения их активных поверхностей
и наличия абразивных частиц между ними. Он приводит к искажению поверхностей и,
следовательно, к появлению дополнительных динамических нагрузок и шума. Износ
поверхностей зубьев получается, как показывает практика, неодинаковым по высоте
зуба и в первом приближении может характеризоваться удельным скольжением.
Пусть при повороте зубчатых колес на углы dji и djj общая точка контакта профилей
переместилась по одному профилю на длину дуги dsi, а по другому – на длину дуги dsj. Разность dsi - dsj представляет собой абсолютное
скольжение профилей. Величину
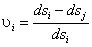 ,
,
называют удельным скольжением, отнесенным к
профилю зуба i-го зубчатого
колеса.
Пусть задана текущая точка
К
эвольвентного профиля с радиусом кривизны в ней r
К = ВК (рис. 8.14). Возьмем две бесконечно
близкие точки С и D. Бесконечно малая
дуга
ds:
 ,
,
где dn -
бесконечно малый угол развернутости, равный бесконечно малому углу dj поворота зубчатого колеса. В
результате получим:
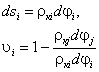 .
.
Отношение djj / dji выражает передаточное отношение
зубчатой передачи, следовательно,
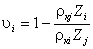 .
.
Анализируя полученное выражение, устанавливаем, что в
полюсе Р удельные скольжения равны 0, т.е. профили не скользят, а
перекатываются друг по другу; на начальных головках, которые
располагаются между окружностью вершин и начальной окружностью, удельные
скольжения невелики; на начальных ножках (между начальной окружностью и
окружностью впадин) удельные скольжения заметно больше, чем на начальных
головках. Соответствующим выбором коэффициентов смещения можно уменьшить и
сделать одинаковыми максимальные удельные скольжения на начальных ножках зубьев
первого и второго зубчатых колес.
3.
Коэффициент
перекрытия зубчатой
передачи. Он характеризует среднее число пар зубьев, находящихся одновременно в
зацеплении. Для более плавной и спокойной работы он должен быть возможно
большим – обычно не менее 1,2. Его вычисляют по формулам, рассмотренным в
лекции 8.
Зная коэффициент
смещения, можно полностью рассчитать геометрические параметры и размеры
передачи. Остается вопрос: как выбрать коэффициенты смещения?
Выбор
коэффициентов смещения. Блокирующий контур
Выбор коэффициентов
смещения во многом определяет геометрию и качественные характеристики зубчатой
передачи. Возможность назначать смещения по своему усмотрению, не усложняя
производства зубчатых колес, дает конструктору удобное средство управления
геометрией и качественными показателями зубчатой передачи с сохранением ее
габаритов. Однако коэффициенты смещения, выгодные, например, по изгибной
прочности или по удельному скольжению, вовсе не являются таковыми с точки
зрения достижения максимальной контактной прочности или максимального
коэффициента перекрытия. Кроме того, выбранные коэффициенты смещения должны задавать
передачу из области ее существования, т.е. в передаче должны отсутствовать
подрезание, заострение, интерференция и обеспечиваться плавность ее работы.
Противоречивость влияния
смещений на геометрию и качественные показатели передачи приводит к заключению,
что универсальных рекомендаций для их определения не может быть. В каждом
конкретном случае коэффициенты смещения следует назначать с учетом условий
работы зубчатой передачи. Один из наиболее распространенных методов выбора
коэффициентов смещения – метод «блокирующих контуров».
Достоинства
и недостатки эвольвентного зацепления
К основным достоинствам эвольвентного
зацепления относят: простоту образования профилей при нарезании; допущение
регулирования межосевого расстояния без изменения передаточного отношения;
взаимозаменяемость колес.
К основным недостаткам эвольвентного
зацепления относят: сравнительно невысокую нагрузочную способность; повышенный
износ профилей вследствие большого относительного скольжения.
Контрольные
вопросы
1.
Какие существуют
основные методы для изготовления зубчатых колес.
2.
Назовите основные
параметры исходного контура инструментальной рейки.
3.
Что называют
смещением режущего инструмента, как оно отражается на профиле нарезаемого зуба.
4.
Чему равняется
минимально допускаемое число зубьев при нарезании колес без появления явления
подрезания зубьев, как оно получается.
5.
Дайте
характеристику основным способам коррегирования.
6.
В чем заключается
физический смысл коэффициента перекрытия.
7.
Проанализируйте
качественные характеристики зубчатых передач.
8.
Что такое
блокирующий контур, используемый при выборе смещения режущего инструмента.
Лекция
9
Циклоидальное зацепление.
Червячные и винтовые механизмы.
Циклоидальное
зацепление
Циклоидальное зацепление
появилось значительно раньше эвольвентного, но в настоящее время вытеснено
эвольвентным. Циклоидальное зацепление применяется в точных механизмах
(особенно в часовых).
Циклоидальное зацепление
– это зацепление в котором профили зубьев очерчиваются по эпициклоиде и
гипоциклоиде.
Примечание: Циклоидой
называется кривая, очерчиваемая точкой окружности при перекатывании её по
другой окружности без проскальзывания. Гипоциклоида получается при внутреннем
перекатывании, эпициклоида при внешнем перекатывании.
Зацепление
характеризуется переменным углом зацепления и криволинейной линией зацепления
по дугам двух производящих окружностей  и
и 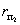 , размеры которых принимают в зависимости
от радиусов начальных окружностей
, размеры которых принимают в зависимости
от радиусов начальных окружностей 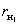 и
и 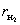 :
:
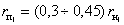 ;
;
 .
.
Рассмотрим принципиальную
схему образования внешнего циклоидального зацепления (рис. 9.1).
Рис. 9.1
Перекатыванием
производящей окружности радиусом 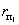 по начальной окружности
радиусом
по начальной окружности
радиусом 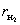 , точка Р образует головку
зуба колеса 2 очерченную по эпициклоиде. Перекатыванием производящей окружности
радиусом
, точка Р образует головку
зуба колеса 2 очерченную по эпициклоиде. Перекатыванием производящей окружности
радиусом 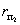 по начальной окружности радиусом
по начальной окружности радиусом  , точка Р образует ножку
зуба колеса 2 очерченную по гипоциклоиде. Перекатыванием производящей
окружности радиусом
, точка Р образует ножку
зуба колеса 2 очерченную по гипоциклоиде. Перекатыванием производящей
окружности радиусом  по начальной окружности радиусом
по начальной окружности радиусом , точка Р образует головку
зуба колеса 1 очерченную по эпициклоиде. Перекатыванием производящей окружности
радиусом
, точка Р образует головку
зуба колеса 1 очерченную по эпициклоиде. Перекатыванием производящей окружности
радиусом  по начальной окружности радиусом
по начальной окружности радиусом , точка Р образует ножку
зуба колеса 1 очерченную по гипоциклоиде.
, точка Р образует ножку
зуба колеса 1 очерченную по гипоциклоиде.
Основными достоинствами
циклоидального зацепления являются: высокая нагрузочная способность, малый
износ (вследствие малого относительного скольжения).
Основными недостатками
циклоидального зацепления являются: сложность изготовления, чувствительность к
изменению межосевого расстояния, невзаимозаменяемость колес.
Если радиус производящей
окружности равен половине радиуса начальной окружности, то гипоциклоиды
очерчивающие ножки зубьев вырождаются в радиальные прямые. Получается более
простой профиль зуба, упрощается изготовление колёс, такое зацепление называют часовым.
Особенностями часового зацепления являются: высокие передаточные отношения;
малый износ; коэффициент перекрытия равен 1 (e = 1) и между зубьями всегда имеется зазор, что
ограничивает применение их в передачах с односторонним вращением в этом случае
боковые зазоры зубьев не влияют на точность работы механизма.
Частным случаем
циклоидального зацепления является цевочное зацепление – оно
имеет место когда радиус производящей окружности равен радиусу начальной (на
рис. 9.2, а  ).
).
Рис. 9.2
В данном случае профиль
зуба колеса 1 превращается в точку, а у зуба колеса 2 присутствует только
головка, очерченная только по эпициклоиде (перекатывание производящей
окружности радиусом  по начальной окружности радиусом
по начальной окружности радиусом
 ). В итоге получается точечное
циклоидальное зацепление, т.к. на практике зубья невозможно выполнить в виде
точки, то точечный зуб заменяется цевкой (валиком, или пальцем) (рис. 9.2, б).
Цевочное зацепление применяется в поворотных механизмах кранов и экскаваторов.
). В итоге получается точечное
циклоидальное зацепление, т.к. на практике зубья невозможно выполнить в виде
точки, то точечный зуб заменяется цевкой (валиком, или пальцем) (рис. 9.2, б).
Цевочное зацепление применяется в поворотных механизмах кранов и экскаваторов.
Зубчатые передачи со
скрещивающимися и параллельными осями
(червячные и винтовые)
Червячные
передачи
Червячной называется зубчатая передача,
состоящая из двух подвижных звеньев – червяка и зубчатого колеса и
предназначенная для передачи и преобразования вращательного движения между
звеньями оси которых скрещиваются. Угол скрещивания может быть любым, но чаще
он равен 90°. Червяком
называют звено, наружная поверхность которого имеет форму винта. Червячным
колесом называется зубчатое колесо, которое зацепляется с червяком.
Основные достоинства
червячных передач:
·
благодаря малому
числу заходов червяка (Z1= 1…4)
червячная передача позволяет реализовывать в одной ступени большие передаточные
отношения;
·
обладает высокой
плавностью, низким уровнем вибраций и шума;
·
позволяет
обеспечить самоторможение червячного колеса (при малых углах подъема витка
передача движения от вала червячного колеса к червяку становится невозможной).
Основные недостатки
червячных передач: высокая скорость скольжения вдоль линии зуба, что ведет к
повышенной склонности к заеданию (необходимы специальные смазки и материалы для
зубчатого венца червячного колеса), снижению КПД и более высокому тепловыделению.
Червячные передачи
подразделяются:
1.
по виду
делительной поверхности червяка
·
цилиндрические
червячные передачи (рис. 9.3, а) – червяк и колесо в передаче имеют
цилиндрические делительные и начальные поверхности;
·
глобоидные
червячные передачи (рис. 9.3, б) – делительная и начальная поверхности
червяка образованы вращением отрезка дуги делительной или начальной поверхности
парного червячного колеса вокруг оси червяка;
2.
по виду
теоретического торцового профиля витка червяка
·
архимедов червяк
– профиль выполнен по архимедовой спирали;
·
эвольвентный
червяк – профиль выполнен по эвольвенте окружности;
·

























 конволютный червяк – профиль выполнен по удлиненной эвольвенте.
конволютный червяк – профиль выполнен по удлиненной эвольвенте.
a) б)
2
2
02 02
w2 w2
P P
 01 01
01 01
w1 w1
1
1
Цилиндрическая
червячная передача Глобоидная червячная передача
Рис. 9.3
Геометрия
зацепления цилиндрической червячной передачи
Основными геометрическими параметрами
червяка являются (рис. 9.4):
·
диаметр
начального цилиндра dw1;
·
диаметр
делительного цилиндра d1 (если червячное зацепление
выполнено без смещения режущего инструмента совпадает с начальным);
·
диаметр цилиндра
выступов dа1;
·
диаметр цилиндра
впадин df1;
·
длина нарезанной
части червяка b1;
da2
02
 n
db2
n
db2
an
df2 N
aw
P
da1 d1 df1
b1 n
Рис. 9.4
Наиболее часто
встречаются червяки у которых сечение винта трапецеидальное с углом при вершине
40°. В плоскости перпендикулярной оси
колеса червячное зацепление представляет собой эвольвентное реечное зацепление,
поэтому геометрические размеры зубьев червяка и червячного колеса совпадают с
размерами зубьев цилиндрического прямозубого колеса. Единственное отличие, то,
что величина радиального зазора равна 0,2×m.
Поверхность червяка
представляет собой совокупность винтовых линий. В зависимости от направления
винтовой линии различают правые и левые винтовые поверхности червяков.
Перемещая винтовую линию вдоль образующей цилиндра на некоторую долю шага,
получаем параллельно расположенную винтовую линию, которую называют заходом.
Червяки бывают одно-, двух-, трех- и четырёх- заходные. Число заходов удобнее
определять по торцевому сечению (рис. 9.5) и обозначают Z1.
Рис. 9.5
Установим связь между
диаметром делительного цилиндра и числом заходов червяка. Так как червяк
представляет собой винт, то его развертка захода представляет собой наклонную
линию под углом l
(угол подъема винтовой линии) (рис. 9.6).

 d1
S = p×Z1
d1
S = p×Z1

 S
S
l
l


 p× d1
p× d1
Рис. 9.6
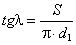 ,®
,®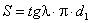 ,
,
где S – ход червяка, это путь который
проходит точка делительного цилиндра за время одного оборота червяка:
 ,
,
здесь р – шаг
нарезки червяка.
Отсюда:
 ®
®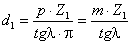 .
.
В целях создания
определенной номенклатуры инструмента, применяемого для изготовления червяков
(червячных фрез) в полученную формулу вводится коэффициент червяка 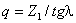 , тогда:
, тогда:
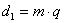 .
.
Наряду с осевым шагом у
многозаходных червяков различают и торцевой шаг pt равный длине дуги окружности
делительного цилиндра между двумя соседними заходами, исходя из рис. 9.6
получаем:
 .
.
Кинематика
червячной передачи
Получим формулу для
передаточного отношения червячной передачи. В точке контакта окружные скорости
червяка и червячного колеса совпадают:

где u1 - скорость на червяке:
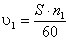 ,
,
где n1 – частота вращения червяка, об/мин; S – ход червяка, м.
u2 - скорость на червячном колесе:
 .
.
Отсюда приравнивая правые
части полученных выражений имеем:
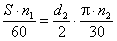 ,
,
так как  и
и 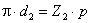 (длина делительной окружности червячного
колеса в радиусах и в шагах), окончательно получаем:
(длина делительной окружности червячного
колеса в радиусах и в шагах), окончательно получаем:
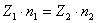 ®
®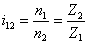 ,
,
или 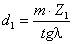 и
и 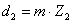 , отсюда:
, отсюда:
 .
.
Винтовые
передачи
Винтовые передачи предназначены для
преобразования вращательного движения в поступательное, при этом гайка и винт
могут иметь либо одно из указанных движений, либо оба движения вместе.
Имеют степень подвижности равную
единице, т.к. при повороте подвижного звена вокруг оси оно перемещается на
определённую величину вдоль той же оси. Звенья передачи образуют кинематическую
пару 5 класса.
Основные достоинства передачи:
простота конструкции и изготовления; компактность при высоких передаваемых
нагрузках; плавность и бесшумность работы; возможность обеспечения медленных
перемещений с большой точностью.
Основные недостатки передачи:
повышенный износ резьбы вследствие большого трения скольжения; низкий к.п.д.
Винтовые передачи классифицируются по
функциональному назначению на:
- грузовые, предназначенные для
создания больших сил (прессы, домкраты, тиски и т.п.);
- ходовые, предназначенные для точных
перемещений (механизмы подачи станков, измерительные приборы, установочные и
регулировочные устройства).
Основные типы резьб:
1.
Прямоугольная
(рис. 9.7). Профиль резьбы – квадрат. Из всех резьб имеют самый высокий к.п.д.,
так как угол профиля резьбы a = 0°. Обладают
пониженной прочностью. При износе образуются осевые зазоры, которые трудно
устранить. В настоящее время не стандартизированы. Имеют ограниченное
применение.
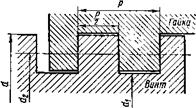
Рис. 9.7
Основные параметры резьбы: d, d1, d2 - соответственно наружный, средний и
внутренний диаметр резьбы; р – шаг резьбы, расстояние между двумя
одноимёнными сторонами двух соседних витков в осевом направлении; S – ход резьбы, расстояние между двумя
одноимёнными сторонами одного и того же витка в осевом направлении (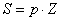 , где Z – число заходов резьбы); a -
угол профиля резьбы; g - угол подъёма резьбы.
, где Z – число заходов резьбы); a -
угол профиля резьбы; g - угол подъёма резьбы.
2.
Трапецеидальная
симметричная (рис. 9.8). Профиль резьбы – равнобочная трапеция с углом a = 30°. Характеризуются небольшими потерями на трение,
технологичны. Применяется для передачи реверсивного движения под нагрузкой.
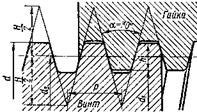
Рис. 9.8
3.
Трапецеидальная
несимметричная, или упорная (рис. 9.9). Профиль резьбы – неравнобочная трапеция
с углом a = 27°. Для возможности изготовления резьбы фрезерованием
рабочая сторона профиля имеет угол наклона 3°. К.п.д. выше, чем у трапецеидальной симметричной. Закругление
впадин повышает прочность. Применяются преимущественно при высоких
односторонних нагрузках.
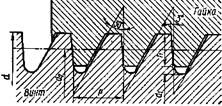
Рис. 9.9
Контрольные
вопросы
9.
Как формируется
профиль зуба циклоидального зацепления.
10.
Дайте
характеристику часового и цевочного циклоидальных зацеплений.
11.
Назовите основные
геометрические параметры червяка и червячного колеса.
12.
Проанализируйте
кинематику червячных передач.
13.
Проанализируйте и
сопоставьте между собой основные виды винтовых передач.
Лекция
10
Кулачковые механизмы:
общие сведения, классификация, кинематический анализ и синтез, определение
минимально-допустимых размеров кулачка. Выбор закона движения толкателя.
Кулачковые механизмы
Кулачковым называется трехзвенный механизм с
высшей кинематической парой, входное звено которого называется кулачком, а
выходное - толкателем
(или коромыслом). Кулачок – звено, элемент высшей пары, имеющий профиль
переменной кривизны. Толкатель может совершать поступательное или вращательное
движение, во втором случае его называют коромысло.
Часто для замены в высшей паре трения
скольжения трением качения и уменьшения износа, как кулачка, так и толкателя, в
схему механизма включают пассивное дополнительное звено – ролик и вращательную
кинематическую пару.
Назначение и область применения
Кулачковые механизмы предназначены
для преобразования вращательного или поступательного движения кулачка в
возвратно-вращательное или возвратно-поступательное движение толкателя. При
этом в механизме с двумя подвижными звеньями можно реализовать преобразование
движения по сложному закону. Важным преимуществом кулачковых механизмов
является возможность обеспечения точных выстоев выходного звена. Это
преимущество определило их широкое применение в простейших устройствах цикловой
автоматики и в механических счетно-решающих устройствах (арифмометры,
календарные механизмы). Кулачковые механизмы можно разделить на две группы.
Механизмы первой обеспечивают перемещение толкателя по заданному закону
движения. Механизмы второй группы обеспечивают только заданное максимальное
перемещение выходного звена – ход толкателя. При этом закон, по которому
осуществляется это перемещение, выбирается из набора типовых законов движения в
зависимости от условий эксплуатации и технологии изготовления.
Основные
параметры кулачкового механизма (рис. 10.1)
Большинство кулачковых механизмов
относится к цикловым механизмам с периодом цикла равным 2p . В цикле движения толкателя в общем случае можно
выделить четыре фазы: удаления, верхнего стояния (или выстоя), приближения и
нижнего стояния (или выстоя). В соответствии с этим, углы поворота кулачка или
фазовые углы делятся на: угол удаления jу ; угол верхнего выстоя jвв ; угол приближения jп ; угол нижнего выстоя jнв .
Сумма трех углов образует угол jраб, который называется рабочим углом.
jраб = jу + jвв + jп.
Кулачок механизма характеризуется
двумя профилями: центровым (или теоретическим) и конструктивным (или
действительным). Под конструктивным понимается наружный рабочий профиль
кулачка. Теоретическим или центровым называется профиль, который в системе
координат кулачка описывает центр ролика при движении ролика по конструктивному
профилю кулачка. На рис. 10.1 изображена схема плоского кулачкового механизма с
двумя видами выходного звена: с толкателем 2, совершающим
возвратно-поступательное движение и коромыслом 4, совершающим качающееся
(возвратно-вращательное) движение. На этой схеме указаны основные параметры
плоских кулачковых механизмов.
 5 aI n 4
5 aI n 4

 uBi
uBi 

SAi
SBi j4










 2 0 3 B
2 0 3 B








 C
C






 ai
ai





 uAi K2
j40
uAi K2
j40


 n n
n n



 A K1
jраб jу
A K1
jраб jу





 rр
jвв aw
rр
jвв aw

 SAi
SAi
 jп
jп






 01
01


 е
е

 r
r
 1 jнв
1 jнв
r0
Рис. 10.1
На рисунке 10.1:
SAi и SВi –
текущие значения перемещения центров роликов;
j40 - начальная угловая координата коромысла;
j4 - текущее угловое перемещение
коромысла;
SAmax - максимальное перемещение центра
ролика (ход толкателя);
r0 - радиус начальной
шайбы теоретического профиля кулачка;
r - радиус начальной шайбы
конструктивного профиля кулачка;
r p - радиус ролика
(скругления рабочего участка толкателя);
ai - текущее значение угла давления;
aw - межосевое (межцентровое) расстояние;
e - эксцентриситет (смещение);
Теоретический профиль кулачка обычно
представляется в полярных координатах зависимостью:
ri = f (di),
где ri - радиус-вектор текущей точки
теоретического или центрового профиля кулачка.
Классификация
кулачковых механизмов.
Кулачковые механизмы классифицируются
по следующим признакам:
·
по расположению
звеньев в пространстве:
¨
пространственные;
¨
плоские;
·
по движению
кулачка:
¨
вращательное
(рис. 10.2, б, в, г, д, е);
¨
поступательное
(рис. 10.2, а);
¨
сложное;

Рис. 10.2
·
по движению
выходного звена:
¨
возвратно-поступательное
(с толкателем рис. 10.2, а, б, в, г, ж);
¨
возвратно-вращательное
(с коромыслом рис. 10.2, д, е);
·
по наличию
ролика:
¨
с роликом;
¨
без ролика;
·
по виду кулачка:
¨
дисковый
(плоский);
¨
цилиндрический;
¨
коноид (сложный
пространственный);
·
по форме рабочей
поверхности выходного звена:
¨
плоская (рис.
10.2, е);
¨
заостренная (рис.
10.2, б);
¨
цилиндрическая;
¨
сферическая;
¨
эвольвентная;
·
по способу
замыкания элементов высшей пары:
¨
силовое (рис.
10.3, а);
¨
геометрическое
(рис. 10.3, б).
 а) 3 2 б)
2
а) 3 2 б)
2





 А C K2
А C K2







 А
А
 1 K
K1 3
1 K
K1 3



 01 01
01 01
1
Рис. 10.3
При силовом
замыкании удаление толкателя осуществляется воздействием контактной поверхности
кулачка на толкатель (ведущее звено – кулачок, ведомое – толкатель). Движение
толкателя при сближении осуществляется за счет силы упругости пружины или силы
веса толкателя, при этом кулачок не является ведущим звеном. При геометрическом
замыкании движение толкателя при удалении осуществляется воздействием наружной
рабочей поверхности кулачка на толкатель, при сближении – воздействием
внутренней рабочей поверхности кулачка на толкатель. На обеих фазах движения
кулачок ведущее звено, толкатель – ведомое.
Структура
кулачковых механизмов
Степень подвижности плоского
кулачкового механизма определяется по формуле Чебышева:
W = 3×(n-1) - 2× p5 - 1× p4,
Для механизма рис. 10.4, а,
имеем n = 4; p5 = 3; p4
= 1:
W = 3×(4 - 1) - 2× 3 - 1× 1 = 2,
В кулачковом механизме с роликом
имеется излишняя степень подвижности, которая введена в механизм для замены в
высшей паре трения скольжения трением качения, т.е. ролик является пассивным
звеном.
Для механизма рис. 10.4, б,
имеем n = 3; p5 = 2; p4 =
1:
W = 3×(3 - 1) - 2× 2 - 1× 1 = 1.
 а) 3 2 б) 2
а) 3 2 б) 2

 D
C
D
C






 А
А

 1
1
 01
01
 01
01




 0
0
1
0
Рис. 10.4
Кинематический
анализ кулачкового механизма
Кинематический анализ кулачкового
механизма может быть проведен любым из описанных выше методов. При исследовании
кулачковых механизмов с типовым законом движения выходного звена наиболее часто
применяется метод кинематических диаграмм. Для применения этого метода
необходимо определить одну из кинематических диаграмм. Так как при
кинематическом анализе кулачковый механизм задан, то известна его кинематическая
схема и форма конструктивного профиля кулачка. Построение диаграммы перемещений
проводится в следующей последовательности:
·
строится
кинематическая схема кулачкового механизма;
·
в полученный
центровой профиль вписываются окружности радиусов r0 и
r0 + SАmax , определяется величина эксцентриситета е;
·
по величине
участков, не совпадающих с дугами окружностей радиусов r0 и
r0 + SАmax, определяются фазовые углы jраб , jу , jвв и jп ;
·
дуга окружности r,
соответствующая рабочему фазовому углу, разбивается на несколько равных
участков; через точки разбиения проводятся касательно к окружности радиуса
эксцентриситета прямые линии, (эти линии соответствуют положениям оси толкателя
в его движении относительно кулачка);
·
на этих прямых
измеряются отрезки расположенные между центровым профилем и окружностью радиуса
r0 ; эти отрезки соответствуют перемещениям центра
ролика толкателя SАi ;
·
по полученным
перемещениям SАi строится диаграмма функции положения
центра ролика толкателя SАi = f (j1 );
·
методом
графического дифференцирования диаграммы перемещений получают диаграммы uАi = f(j1)и аАi = f(j1).


 C SАi , м ; mS , мм/м
C SАi , м ; mS , мм/м




 А
А
SАi 









 ySаi SАmax
ySаi SАmax
 K
K










 А0 0 j1
А0 0 j1
j1i
mj , мм/рад




 j1i 01 j1у j1п
j1i 01 j1у j1п
jраб
Рис.10.5
На рис. 10.5 показана схема
построения функции положения для кулачкового механизма с центральным (е
= 0) поступательно движущимся роликовым толкателем.
Синтез
кулачкового механизма. Этапы синтеза
При синтезе кулачкового механизма,
как и при синтезе любого механизма, решается ряд задач из которых в курсе ТММ
рассматриваются две: выбор структурной схемы и определение основных размеров
звеньев механизма (включая профиль кулачка).
Первый этап синтеза – структурный.
Структурная схема определяет число звеньев механизма; число, вид и подвижность
кинематических пар; число избыточных связей и местных подвижностей. При
структурном синтезе необходимо обосновать введение в схему механизма каждой
избыточной связи и местной подвижности. Определяющими условиями при выборе
структурной схемы являются: заданный вид преобразования движения, расположение
осей входного и выходного звеньев. Входное движение в механизме преобразуется в
выходное, например, вращательное во вращательное, вращательное в поступательное
и т.п. Если оси параллельны, то выбирается плоская схема механизма. При пересекающихся
или перекрещивающихся осях необходимо использовать пространственную схему. В
кинематических механизмах нагрузки малы, поэтому можно использовать толкатели с
заостренным наконечником. В силовых механизмах для повышения долговечности и
уменьшения износа в схему механизма вводят ролик или увеличивают приведенный
радиус кривизны контактирующих поверхностей высшей пары.
Второй этап синтеза – метрический. На
этом этапе определяются основные размеры звеньев механизма, которые
обеспечивают заданный закон преобразования движения в механизме или заданную
передаточную функцию. Как отмечалось выше, передаточная функция является чисто
геометрической характеристикой механизма, а, следовательно, задача метрического
синтеза чисто геометрическая задача, независящая от времени или скоростей.
Основные критерии, которыми руководствуется проектировщик, при решении задач
метрического синтеза: минимизация габаритов, а, следовательно, и массы; минимизация
угла давления в вышей паре; получение технологичной формы профиля кулачка.
Размеры кулачкового механизма
определяются минимальным радиусом кулачка. Один и тот же закон движения
толкателя может быть воспроизведён кулачком с различными минимальными радиусами.
Как правило, желательно получить механизм наименьших размеров, но уменьшение
размеров кулачка приводит к увеличению сопротивления в кулачковой паре и в
крайнем случае к возможности заклинивания толкателя.
Минимально-допустимые размеры кулачка
определяются из условия обеспечения допускаемых углов давления. В качестве
примера рассмотрим кулачковый механизм со смещением толкателя (рис. 10.6, а).
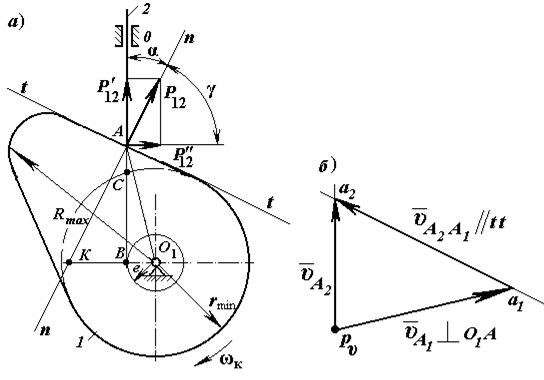
Рис. 10.6
В месте контакта толкателя и кулачка
точка А, возникает реакция Р12 кулачка на толкатель,
направленная по нормали n-n проведённой к профилю кулачка.
Разложим полную реакцию на проекции  и
и  , угол между Р12 и
линией движения толкателя является углом давления a. Чем больше угол давления, тем
больше сопротивление движению, тем меньше к.п.д.
, угол между Р12 и
линией движения толкателя является углом давления a. Чем больше угол давления, тем
больше сопротивление движению, тем меньше к.п.д.
Для нормальной работы кулачкового
механизма необходимо, чтобы максимальный угол давления не превосходил угла
передачи движения g.
Установим зависимость угла давления
от геометрических и кинематических параметров кулачкового механизма, для чего
рассмотрим треугольник ВАК:
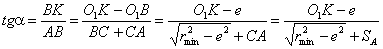 .
.
Для окончательного выражения выразим
отрезок О1К, для чего построим план скоростей
кулачкового механизма (рис. 10.6, б).
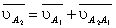 ,
,
где  –
вектор скорости переносного движения (окружная скорость кулачка) направлен
перпендикулярно радиус вектору
–
вектор скорости переносного движения (окружная скорость кулачка) направлен
перпендикулярно радиус вектору 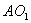 по направлению
вращения кулачка w1.
по направлению
вращения кулачка w1.
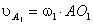 .
.
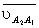 –
вектор скорости относительного движения (скорость скольжения толкателя по
кулачку) направлена по направлению скольжения т.е. параллельно касательной t-t проведенной в точке контакта А к профилю
кулачка;
–
вектор скорости относительного движения (скорость скольжения толкателя по
кулачку) направлена по направлению скольжения т.е. параллельно касательной t-t проведенной в точке контакта А к профилю
кулачка;
 –
вектор абсолютной скорости толкателя направлен по направлению движения толкателя.
–
вектор абсолютной скорости толкателя направлен по направлению движения толкателя.
Рассмотрим треугольники DО1КА и Dрuа1а2 , устанавливаем, что они подобны, т.к. соответственно
имеют две стороны перпендикулярные друг другу и одну параллельную. Составим
пропорцию:
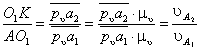 ,
,
откуда
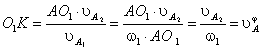 .
.
Установили, что отрезок О1К
является аналогом скорости толкателя кулачкового механизма, следовательно:
 .
.
Анализируя полученное выражение
устанавливаем, что с уменьшением минимального радиуса кулачка угол давления
возрастает, введение смещения толкателя позволяет уменьшить размеры кулачка при
одном и том же угле давления.
Выбор
закона движения толкателя
Если в задании на проектирование не
дан закон движения, то конструктор должен выбрать его из набора типовых законов
движения, необходимо, чтобы ускорения толкателя не приводили к большим
инерционным нагрузкам, а имеющаяся на предприятии технология позволила бы
изготовить профиль с достаточной точностью.
Типовые законы движения делятся на
законы с жесткими, мягкими ударами и безударные. С точки зрения динамических
нагрузок, желательны безударные законы. Однако кулачки с такими законами
движения технологически более сложны, так как требуют более точного и сложного
оборудования, поэтому их изготовление существенно дороже. Законы с жесткими
ударами имеют весьма ограниченное применение и используются в неответственных
механизмах при низких скоростях движения и невысокой долговечности. Кулачки с
безударными законами целесообразно применять в механизмах высокими скоростями
движения при жестких требованиях к точности и долговечности. Наибольшее
распространение получили законы движения с мягкими ударами, с помощью которых
можно обеспечить рациональное сочетание стоимости изготовления и
эксплуатационных характеристик механизма.
Рассмотрим четыре закона движения
толкателя (рис. 10.8):
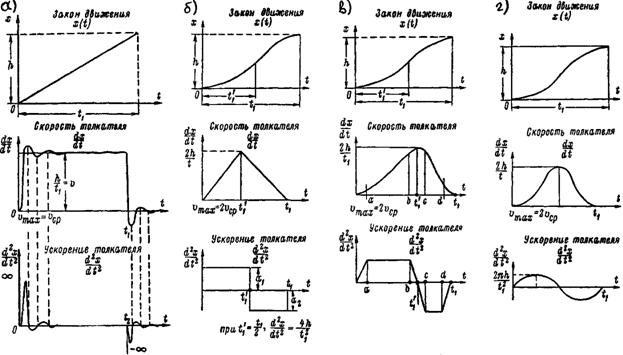
Рис. 10.8
1. Равномерное движение толкателя
(рис. 10.8, а) это наиболее простой закон движения. Кулачок имеет
несложный профиль. Однако для быстроходных кулачковых механизмов он не
пригоден, так как он связан со скачками скорости в начале и в конце хода
толкателя, которые приводят к возникновению ускорений не ограниченных по
величине (+¥; - ¥):
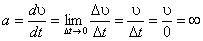 .
.
В начале и в конце хода толкателя,
следовательно, силы инерции достигли бы бесконечно большой величины, имеют место
«жесткие» удары.
Исходя из указанных соображений,
равномерное движение толкателя можно применять лишь для кулачковых механизмов
при малых скоростях и малых мощностях.
2. Равноускоренное движение толкателя
(рис. 10.8, б) скорость на первой части хода  равномерно
возрастает, а затем на втором участке хода равномерно убывает до нуля. На
протяжении участков хода ускорение одинаковое. Участки разгона и замедления
часто делают неодинаковыми, чтобы уменьшить ускорение и силы инерции на одном
из них.
равномерно
возрастает, а затем на втором участке хода равномерно убывает до нуля. На
протяжении участков хода ускорение одинаковое. Участки разгона и замедления
часто делают неодинаковыми, чтобы уменьшить ускорение и силы инерции на одном
из них.
Равноускоренное движение,
характеризуемое прямоугольной диаграммой ускорений, не сопровождается ударами,
скачков скорости нет, ускорения и, следовательно, силы инерции остаются
ограниченными. Однако в быстроходных кулачковых механизмах этот закон движения
вызывает повышенную вибрацию и износ. Причиной этого является изменение
ускорения толкателя скачком, вызывающее «мгновенное» (за очень короткий
промежуток времени) приложение к толкателю больших сил. Это явление называют
«мягким» ударом.
3. Сглаженное равноускоренное
движение толкателя (рис. 10.8, в). Достоинство – наименьшая величина
максимального ускорения толкателя. Диаграмма ускорений имеет форму трапеции,
что позволяет избежать скачков ускорения и «мягких» ударов. Такой закон
движения может применяться и для быстроходных кулачковых механизмов.
4. Синусоидальный закон движения
толкателя (рис. 10.8, г) позволяет получить наибольшую плавность
движения, отсутствуют удары. Этот закон движения наиболее предпочтительно
применять в быстроходных механизмах. Главным недостатком синусоидального (и
трапецеидального) является высокая точность профиля кулачка.
Контрольные
вопросы
14.
Классификация и
назначение кулачковых механизмов.
15.
Основные
параметры кулачковых механизмов.
16.
Как производится
кинематический анализ кулачковых механизмов.
17.
Определение
минимально-допустимых размеров кулачковых механизмов.
18.
Как выбирается на
стадии проектирования закон движения толкателя. Проанализируйте основные виды.
Лекция
11
Динамика механизмов и
машин. Задачи силового анализа механизмов. Силы и их классификация. Условие
кинетостатической определимости кинематических цепей. Графо-аналитический
способ силового анализа (метод планов).
Динамика
механизмов и машин
Динамика изучает
закономерности движения звеньев механизма под действием приложенных сил, при
этом рассматривают две задачи:
Прямая задача динамики - определение закона движения
системы при заданном силовом воздействии.
Обратная задача
динамики -
определение требуемого силового воздействия, обеспечивающего заданный закон
движения системы.
В общей постановке
динамика - изучение каких-либо процессов или явлений в функции времени. Динамическая
модель - модель системы, предназначенная для исследования ее свойств в
функции времени (или модель системы, предназначенная для исследования в ней
динамических явлений).
Методы составления
уравнений (динамической модели системы):
· энергетический (уравнения
энергетического равновесия - закон сохранения энергия);
· кинетостатический (уравнения силового
равновесия с учетом сил инерции по принципу Д’Аламбера).
Классификация
сил, действующих в механизмах
Все силы, действующие в
механизмах, условно делятся на:
· внешние, действующие на исследуемую
систему со стороны внешних систем и совершающие работу над системой. Эти силы в
свою очередь подразделяются на:
Þ движущие – это силы которые ускоряют движение звеньев
и совершают положительную работу (увеличивает энергию системы);
Þ сопротивления, работа которых отрицательна (уменьшает
энергию системы). Силы сопротивления делятся на:
* силы полезного (производственного)
сопротивления - возникающие при выполнении механической системой ее основных
функций (выполнение требуемой работы по изменению координат, формы или свойств
изделия и т.п., совершают отрицательную работу);
* силы вредного сопротивления – это силы
трения возникающие в месте связи в КП и определяемые условиями
физико-механического взаимодействия между звеньями и силы сопротивления среды
(работа всегда отрицательна);
Þ взаимодействия с потенциальными полями (позиционные) -
возникают при размещении объекта в потенциальном поле, величина зависит от
потенциала точки, в которой размещается тело (работа при перемещении из точки с
низким потенциалом в точку с более высоким - положительна; за цикл, т.е. при
возврате в исходное положение, работа равна нулю). Потенциальное поле - силы
тяжести или веса. Существуют электромагнитные, электростатические и другие
поля.
· внутренние, действующие между
звеньями механической системы. Работа этих сил не изменяет энергии системы. В
механических системах эти силы называются реакциями в кинематических парах.
· расчетные (теоретические) - силы,
которые не существуют в реальности, а только используются в различных расчетах
с целью их упрощения:
Þ силы инерции - предложены Д’Аламбером для силового
расчета подвижных механических систем. При добавлении этих сил к внешним силам,
действующим на систему, устанавливается квазистатическое равновесие системы и
ее можно рассчитывать, используя уравнения статики (метод кинетостатики).
Þ приведенные (обобщенные) силы - силы совершающие
работу по обобщенной координате равную работе соответствующей реальной силы на
эквивалентном перемещении точки ее приложения.
Необходимо отметить, что
под силами понимаются равнодействующие соответствующих распределенных в месте
контакта кинематических пар нагрузок. Все вышесказанное относительно сил
распространяется и на моменты сил.
Движущие и силы полезных
сопротивлений чаще всего задают в виде механических характеристик машины.
Механические
характеристики машин
Механической
характеристикой машины называется зависимость силы или момента на выходном валу или рабочем
органе машины от скорости или перемещения точки или звена ее приложения.
Рассмотрим примеры
механических характеристик различных машин.
1.
Четырёхтактный
двигатель внутреннего сгорания (ДВС) в качестве движущей силы выступает сила
давления сгораемых газов в цилиндре.
Индикаторная диаграмма - графическое изображение зависимости давления в цилиндре
поршневой машины от хода поршня (рис. 11.1).










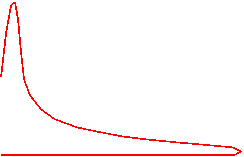

 р, МПа
р, МПа
ab - расширение
(рабочий ход);
bc - выхлоп;
a
pmax
cd - всасывание;
b da - сжатие.

 c
c
0
d S, м
H

Рис. 11.1
2.
Электродвигатели:
· асинхронный электродвигатель
переменного тока (механическая характеристика приведена на рис. 11.2):
На диаграмме: Мдп
- пусковой момент; Мдн - номинальный крутящий момент; Мдк
или Мдmax - критический или максимальный момент;
wдн - номинальная круговая частота вращения
вала двигателя; wдхх или wдс - частота вращения вала двигателя холостого хода или
синхронная.
Уравнение статической
характеристики асинхронного электродвигателя на линеаризованном участке устойчивой
части:
Мд = b1 + k1×wд ,
где Мд
- движущий момент на валу двигателя, wд - круговая частота вала двигателя: b1 и k1 – коэффициенты определяемые
соответственно по формулам:
b1 = Мдн × wд /(wдс - wдн ) , k1 = - Мдн / (wдс - wдн ).


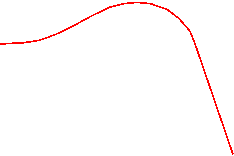 Мд ,Н× м
Мд ,Н× м 
 b ab - неустойчивый
b ab - неустойчивый
 a участок характеристики;
a участок характеристики;
 с bd -устойчивый
с bd -устойчивый
Мдн


 Мдmax участок характеристики.
Мдmax участок характеристики.
Мдп




 d
d
0 wдк wдн wдс wд , рад/с
Рис. 11.2
Статическая характеристика
асинхронного двигателя, выражающая зависимость нагрузки от скольжения,
определяется формулой Клосса:
Мд = 2× Мдк × (S/Sк + Sк/S ),
где S = 1 - wд /wдс; Sк = 1 - wдк /wдс , wд ³ wдс .
· двигатель постоянного тока с
независимым возбуждением (механическая характеристика приведена на рис. 11.3):
 Мд ,Н× м
Мд ,Н× м

 a ac - внешняя характеристика
a ac - внешняя характеристика
 регулировочные
регулировочные
характеристики



 Мдп Мдн b
Мдп Мдн b




 c
c
0
wдн wдхх wд , рад/с
Рис. 11.3
Уравнение статической
характеристики для двигателя постоянного тока с независимым возбуждением:
Мд = Mдн + k× (wдн - wд ),
где k = Мдн /(wдхх - wдн ).
В электрических
параметрах характеристика записывается в следующем виде
Мд = kM × (Uя - kw ×wд)/ Rя ,
где kM - коэффициент момента:
kM = Mдн/Iян ,
kw - коэффициент противоэлектродвижущей
силы:
kw = (Uян - Rя× Iян ) / wдн
Uя – номинальное напряжение в цепи
якоря;
Rя - сопротивление цепи якоря.
Jя - номинальная сила тока в цепи якоря.
3.
Рабочие
(исполнительные) машины
· поршневой насос (индикаторная
диаграмма приведена на рис. 11.4):
р, МПа

 ab - нагнетание;
ab - нагнетание;



 a
b
a
b
cd - всасывание.
pmax
линия
атмосферного давления

 pmin
pmin
 0
0



 d
c S, м
d
c S, м
H

Рис. 11.4
· поршневой компрессор (индикаторная
диаграмма приведена на рис. 11.5):
 р, МПа
р, МПа
a ba – нагнетание;





 b cb - сжатие;
b cb - сжатие;
dc - всасывание;
ad – расширение остаточного воздуха.
pmax
линия атмосферного
давления

 pmin
pmin



 0 d
c S, м
0 d
c S, м
H

Рис. 11.5
Линии bc и ad - линии сжатия и расширения газа
(воздуха) определяются параметрами газа (объемом, давлением и температурой) и в
общем виде описываются уравнением политропы p× Vn = const , где n - показатель политропы (1< n < 0).
Механические характеристики
определяют внешние силы и моменты, действующие на входные и выходные звенья,
рассматриваемой механической системы со стороны взаимодействующих с ней внешних
систем и окружающей среды. Характеристики определяются экспериментально, по
результатам экспериментов получают регрессионные эмпирические модели, которые в
дальнейшем используются при проведении динамических расчетов машин и механизмов.
Силы
инерции звеньев
Силы инерции звеньев
рассматриваются как реакции звена на изменение его скорости по величине и
направлению. Существование сил инерции обусловлено двумя обстоятельствами:
фактом наличия у звеньев массы и фактом движения звеньев, сопровождающегося в
общем случае ускорениями отдельных точек и всего звена в целом, так как
известно из теоретической механики, что мерой сил инерции является произведение
массы на ускорение.
Из курса теоретической
механики известно, что систему сил инерции в общем случае можно привести к силе
– главному вектору сил инерции  приложенного в центре
масс s звена (рис. 11.6) и к паре сил,
момент которой называется главным моментом сил инерции
приложенного в центре
масс s звена (рис. 11.6) и к паре сил,
момент которой называется главным моментом сил инерции  .
.
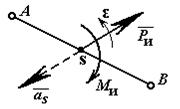
Рис. 11.6
Главный вектор сил
инерции определяют по формуле:
 .
.
Главный момент сил
инерции определяют по формуле:
 ,
,
где m – масса звена, кг; аs – ускорение цента масс, м/с2;
Js – момент инерции звена относительно
оси проходящей через центр масс перпендикулярной плоскости движения, кг/м2;
e - угловое ускорение звена, с-2.
Знак «-» указывает на то, что векторы и
и соответственно
направлены противоположно аs и e.
соответственно
направлены противоположно аs и e.
Силы
инерции звеньев совершающих вращательное движение
При равномерном
вращательном движении звеньев имеющих цилиндрическую форму (рис. 11.7, а)
имеем:  и
и  , так
как соответственно аs = 0 и e =
0.
, так
как соответственно аs = 0 и e =
0.
При неравномерном
вращении звеньев имеющих цилиндрическую форму имеем:  так
как аs = 0 и
так
как аs = 0 и  , т.к. e ¹ 0.
, т.к. e ¹ 0.
Рис. 11.7
При равномерном вращении
кривошипа (рис. 11.7, б) имеем: 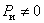 так
как аs ¹ 0 и
так
как аs ¹ 0 и 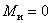 , т.к.
e = 0.
, т.к.
e = 0.
При неравномерном
вращении кривошипа (рис. 11.7, в) имеем: 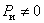 так
как аs ¹ 0 и
так
как аs ¹ 0 и 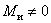 , т.к.
e ¹ 0. Для удобства расчетов данную систему принято заменять
одной результирующей силой инерции
, т.к.
e ¹ 0. Для удобства расчетов данную систему принято заменять
одной результирующей силой инерции  приложенной в центре
качания К, расположение которой определяют из выражения:
приложенной в центре
качания К, расположение которой определяют из выражения:
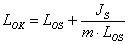 .
.
Силы
инерции звеньев совершающих поступательное движение
Если звено совершает
только поступательное движение (рис. 11.8) то:  и
и  , так как e = 0.
, так как e = 0.
Рис. 11.8
Силы
инерции звеньев совершающих плоско-параллельное движение
При сложном
плоско-параллельном движении звена, например шатуна в кривошипно-ползунном
механизме (рис. 11.9), возникают главный вектор сил инерции 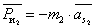 и главный момент сил инерции
и главный момент сил инерции 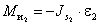 .
.
Для удобства расчетов
данную систему принято заменять одной результирующей силой инерции  приложенной в центре качания К,
имеющей плечо относительно центра масс равное
приложенной в центре качания К,
имеющей плечо относительно центра масс равное  и
создающей момент в направлении обратном угловому ускорению шатуна e2.
и
создающей момент в направлении обратном угловому ускорению шатуна e2.
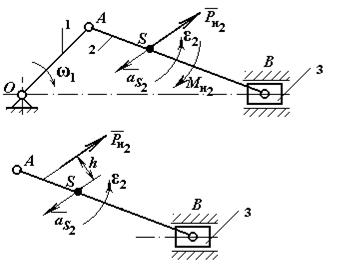
Рис. 11.9
Условие
кинетостатической определимости кинематических цепей
Сила, как векторная
величина характеризуется относительно звеньев механизма тремя параметрами:
координатами точки приложения, величиной и направлением. Рассмотрим с этих
позиций реакции в кинематических парах плоских механизмов.
1. Поступательная
кинематическая пара.
В поступательной
кинематической паре связи, наложенные на относительное движение звеньев
запрещают относительное поступательное движение по оси y и относительное вращение. Заменяя
эти связи реакциями, получим реакцию R12 (рис. 11.10).
|
 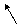  y (n) y (n)
  R12 x R12 x

   Pj
Pj Pj
Pj
   A A
1
2
R12
n
Рис. 11.10
|
При силовом расчете
поступательной кинематической пары определяют величину реакции R12 и точку её приложения, при этом
известно направление - нормаль к контактирующим поверхностям звеньев.
Число связей (ограничений
движений) в кинематической паре 2, число разрешаемых движений - 1, число неизвестных при силовом
расчете - 2.
2. Вращательная кинематическая
пара.
Во вращательной
кинематической паре связи, наложенные на относительное движение звеньев
запрещают относительные поступательные движения по осям y и x. Заменяя эти связи реакциями, получим реакцию R12 (рис. 11.11).
   y x y x
  Рi w Рi w
  Рj
Рj
 1 B 2 1 B 2
R12
Рис. 11.11
|
При силовом расчете
вращательной кинематической пары определяется направление и величина реакции R12, при известной точке приложения силы
- геометрическому центру кинематической пары B.
Число связей (ограничений
движений) в кинематической паре 2, число разрешаемых движений - 1, число неизвестных при силовом
расчете 2.
3. Высшая кинематическая
пара.
В высшей паре связи,
наложенные на относительное движение звеньев, запрещают движение в направлении
нормали (nn) к контактирующим поверхностям (ось y). Заменяя эту связь реакцией,
получим реакцию R12 (рис. 11.12).
|
    y (n) y (n)
  Рi w x
t Рi w x
t
    Рj Рj
1 С
t R12
2
n
Рис. 11.12
|
При силовом расчете в
высшей кинематической паре определяют величину реакции R12 по известным точке приложения силы
(точка контакта рабочих профилей кинематической пары С) и
направлению вектора силы - нормаль
к профилям.
Число связей (ограничений
движений) в кинематической паре 1, число разрешаемых движений - 2, число неизвестных при силовом
расчете 1.
Рассмотрим плоский
механизм состоящий из n звеньев, соединённых в кинематические пары: 5 класса в количестве р5
и 4 класса в количестве р4. Число уравнений статики которые
мы можем составить – 3, общее число уравнений - 3×n. Каждая кинематическая пара 5 класса содержит 2
неизвестные о реакции, 4 класса 1 неизвестное, тогда общее число неизвестных 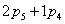 . Тогда условие кинетостатической определимости
плоского механизма можно записать как:
. Тогда условие кинетостатической определимости
плоского механизма можно записать как:
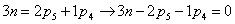 .
.
Т.е. для статически
определимых механизмов степень подвижности равна нулю. Для рычажных механизмов 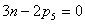 , то есть группы Ассура являются
статически определимыми.
, то есть группы Ассура являются
статически определимыми.
Силовой
расчет типовых механизмов
Постановка задачи
силового расчета:
для исследуемого механизма при известных кинематических характеристиках и
внешних силах определить уравновешивающую силу или момент (управляющее силовое
воздействие) и реакции в кинематических парах механизма.
Виды силового расчета:
· статический - для механизмов
находящихся в покое или движущихся с малыми скоростями, когда инерционные силы
пренебрежимо малы, или в случаях, когда неизвестны массы и моменты инерции
звеньев механизма (на этапах, предшествующих эскизному проектированию);
Уравнения статического
равновесия:
f m
å Рi = 0; å Mi = 0;
i=1 i=1
где Рi - внешние силы, приложенные к
механизму или его звеньям; Mi- внешние моменты сил, приложенные к
механизму или его звеньям.
· кинетостатический - для движущихся механизмов при
известных массах и моментах инерции звеньев, когда пренебрежение инерционными
силами приводит к существенным погрешностям;
Уравнения
кинетостатического равновесия:
f n m k
å Рi + å Риi = 0; å Mi + å Mиi = 0;
i=1 i=1 i=1
i=1
где Риi - инерционные силы, приложенные к
звеньям; Mиi- моменты сил инерции, приложенные к звеньям.
· кинетостатический с учетом трения -
может быть проведен когда определены характеристики трения в кинематических
парах и размеры элементов пар.
Определение числа
неизвестных при силовом расчете. Для определения числа неизвестных, а, следовательно, и числа
независимых уравнений, при силовых расчетах необходимо провести структурный
анализ механизма и определить число и классы кинематических пар, число основных
подвижностей механизма, число избыточных связей. Чтобы силовой расчет можно
было провести, используя только уравнения кинетостатики, необходимо устранить в
нем избыточные связи. Так как каждая связь в кинематической паре механизма
соответствует одной компоненте реакции, то число неизвестных компонент реакций
равно суммарному числу связей накладываемых кинематическими парами механизма.
Контрольные
вопросы
19.
Классификация сил
действующих на механизм.
20.
Приведите примеры
механических характеристик машин.
21.
Силы инерции
звеньев совершающих вращательное, поступательное и плоско-параллельное
движение.
22.
Условие
кинетостатической определимости кинематических цепей.
Лекция
12
Силовой анализ рычажных
механизмов. Режимы движения механизмов. Уравнение движения механизмов.
Динамическая модель механизма. Приведение сил и масс в механизмах. Динамическая
модель.
Силовой
анализ рычажного механизма методом планов сил
(без учета
трения в кинематических парах)
Кинетостатический метод
расчета позволяет находить реакции в кинематических парах, а также определить
уравновешивающую силу (или уравновешивающий момент пары сил). Под
уравновешивающими силами понимают силы, приложенные к ведущим звеньям, которые
уравновешивают систему всех внешних сил и пар сил и всех сил инерции и пар сил
инерции.
Если механизм имеет
несколько степеней свободы, то для его равновесия необходимо столько
уравновешивающих сил или пар сил, сколько имеется степеней свободы.
Графическое определение
реакций в кинематических парах плоских механизмов с помощью планов сил
применяется не только вследствие наглядности, но и потому, что внешние силы,
действующие на звенья механизма, обычно известны лишь приближённо, и точность
простейших графических построений оказывается вполне достаточной.
Силовой анализ механизмов
методом построения планов сил рассмотрим на примере шарнирного четырёхзвенного
механизма (рис. 12.1). Считаем, что по заданному закону движения начального
звена 1 выполнен кинематический анализ и определены силы и пары сил
инерции: кривошипа 1 Ри1; шатуна 2 Ри2,
Ми2; коромысла 3 Ри3, Ми3.
Решение задачи начинают с
построения кинематической схемы механизма (рис. 12.1, а) с приложенными
силами. Силовой анализ проводят в порядке отсоединения групп Асура.
Силовой
анализ группы Ассура (рис. 12.1, б)
Анализ начинаем с
рассмотрения группы Ассура (включающей шатун 2 и коромысло 3), на
которую действуют силы: веса шатуна G2; веса коромысла G3; силы и моменты сил инерции шатуна и
коромысла, соответственно Ри2, Ми2, и Ри3, Ми3; реакции в шарнирах (опорах) R03, R12(соответственно: стойки 0 на
коромысло 3; кривошипа 1 на шатун 2).
Строим в масштабе ml (м/мм) группу Ассура. В
соответствующие точки прикладываем внешние силы параллельно их действию, при
этом суммарное действие на звено силы и момента силы инерции заменяем одной
результирующей силой инерции, создающей момент, действующий в обратном
направлении угловому ускорению, и приложенной в центре качания:
· точке К для
коромысла 3, лежащей на расстоянии lО3К от оси вращения О3
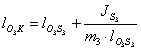 ,
,
где lО3S3 - расстояние от оси вращения коромысла
3 до его центра тяжести, м.
· для шатуна 2, отстоящей от
линии действия силы инерции Ри2 на расстоянии
 .
.
В шарнирах А
и О3 прикладываем реакции R12 и R 03, раскладывая их на нормальные и
касательные составляющие. Нормальные составляющие 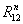 и
и 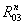 направляем параллельно соответственно
звеньям 3 и 2, касательные
направляем параллельно соответственно
звеньям 3 и 2, касательные 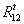 и
и 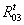 - перпендикулярно звеньям.
- перпендикулярно звеньям.
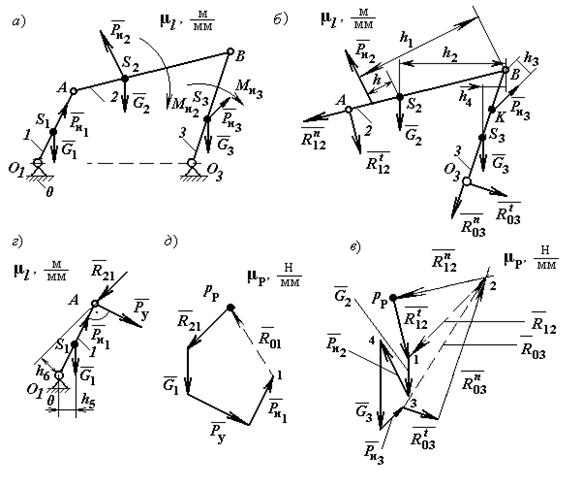
Рис. 12.1
Составляем уравнение
моментов сил относительно точки В для второго звена (на рис.
12.1, б отмечаем плечи сил):
å М2В(Рi) = 0;
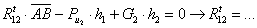
Полученное отрицательное
значение силы говорит о том, что направление силы следует изменить на
противоположное, перечеркнув крестом на схеме исходный вектор.
Значения плеч
взятых с чертежа, в уравнение моментов, можно подставлять в миллиметрах, т.к.
уравнение не содержит моментов сил в чистом виде (Мi).
Составляем уравнение моментов
сил относительно точки В для третьего звена
å М3В
(Рi) = 0;
Составляем векторное
уравнение сил, действующих на группу Ассура, где неизвестные записываем в конце
(нормальные составляющие реакций  и
и 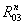 ):
):
å`Рi = 0;
`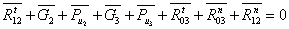 .
.
Производим графическое
сложение векторов в масштабе mР (рис. 12.1, в). Последний вектор
 откладываем из полюса плана сил.
откладываем из полюса плана сил.
На плане получаем
направления и значения сил в масштабе  и
и 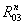 . Векторно складывая касательные и
нормальные составляющие, получаем абсолютные значения реакций (на рис. 12.1, в
представлены пунктиром):
. Векторно складывая касательные и
нормальные составляющие, получаем абсолютные значения реакций (на рис. 12.1, в
представлены пунктиром):
· соединяя точки 1 и 2 получаем
`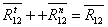 ,
, 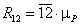 ,
Н;
,
Н;
· соединяя точки 3 и 2 получаем ` ,
, 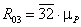 ,
Н.
,
Н.
Для определения реакции в
шарнире В следует векторно сложить все силы, действующие на звено
2 или 3, например, для звена 2
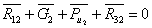
На рис. 12.1, в
соединив точки 4 и 2, получаем направление действия реакции R32 коромысла 3 на шатун 2.
После рассмотрения
условий равновесия группы Асура переходим к определению сил, действующих на
начальный механизм.
Силовой
анализ начального механизма
Строим кинематическую
схему начального механизма в масштабе (рис. 12.1, г), в соответствующие
точки прикладываем силы: инерции кривошипа 1 Ри1; веса кривошипа 1 G1; реакции в шарнирах (опорах) R21 - шатуна 2 на кривошип 1;
R01 - стойки 0 на кривошип 1;
уравновешивающую силу Ру.
Реакция шатуна 2
на коромысло 1, R21 определена при рассмотрении силового анализа группы Ассура (но там
определена реакция кривошипа 1 на шатун 2, поэтому при приложении
её необходимо изменить направление на противоположное);
Уравновешивающая сила Ру.
(реакция двигателя на механизм), неизвестная величина, прикладывается в
шарнире А перпендикулярно О1А.
Указываем плечи действия
сил относительно шарнира О1 и составляем уравнение
моментов всех сил относительно О1:
å МО1(Рi)= 0;
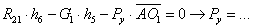 .
.
Момент уравновешивающей
силы 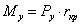 (здесь rкр – радиус кривошипа, м).
(здесь rкр – радиус кривошипа, м).
Реакцию в шарнире О1,
R01, определяем из векторного уравнения
равновесия всех сил, действующих на звено 1:
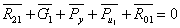 .
.
Строим план сил (рис.
12.1, д) в масштабе сил mр, Н/мм, где замыкающий вектор определяет направление и
величину опорной реакции R01, её значение 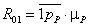 .
.
Определение
уравновешивающей силы методом Н.Е. Жуковского
При определении мощности
двигателя и установлении его типа, расчете махового колеса, составлении
характеристики регуляторов и в ряде других случаев необходимо знать только
уравновешивающий момент или уравновешивающую силу, реакции в кинематических
парах исследуемого механизма при этом могут остаться неизвестными. В этом
случае удобнее использовать теорему Жуковского: если какой-либо механизм под
действием системы сил, находится в состоянии равновесия, то повёрнутый на 90° в какую-либо сторону план скоростей,
рассматриваемый как твёрдое тело, вращающееся вокруг полюса плана и нагруженное
теми же силами, приложенными в соответствующие точки плана, также находится в
равновесии.
Теорему Жуковского можно
применить и к системе, не находящейся в равновесии. Для этого достаточно, кроме
действующих сил приложить и силы инерции.
Для доказательства
теоремы воспользуемся принципом возможных перемещений: если система находится в
равновесии, то сумма элементарных работ на возможных перемещениях равна нулю
(возможные перемещения – это перемещения допускаемые связями):
 ,
,
или разделив на dt,
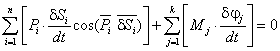 ,
,
Получаем:
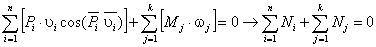 ,
,
где Рi – задаваемые силы; ui – скорости точек приложения Рi; wj – скорости вращения звеньев к
которым приложены моменты сил Мj; Ni, Nj – мощности соответственно сил Рi и моментов сил Мj.
Предположим, что в какой
то точке звена приложена сила Рi перенесённая параллельно самой себе
в соответствующую точку повёрнутого на 90° плана скоростей. Мощность этой силы можно выразить следующим
образом:
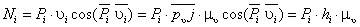 ,
,
где hi – перпендикуляр, опущенный из полюса
плана скоростей на линию действия силы Рi.
Так как полученное выше
уравнение, определяющее величину Ni, имеет место для всех сил Рi, действующих на другие звенья
механизма, то получаем:
 .
.
Поскольку  , то:
, то:
 ,
,
что и является доказательством
теоремы.
Применим метод Жуковского
к нахождению приведенной, или уравновешивающей силы Ру. Рассмотрим
шарнирный четырёхзвенный механизм (рис. 12.2, а) находящийся в состоянии
равновесия под действием сил: веса кривошипа 1 G1, шатуна 2 G2 и коромысла 3 G3; инерции: кривошипа 1 Ри1;
шатуна 2 Ри2, Ми2;
коромысла 3 Ри3, Ми3.
Суммарное действие на звено силы и момента силы инерции заменяем одной
результирующей силой инерции, создающей момент, действующий в обратном
направлении угловому ускорению, и приложенной в центре качания (для
шатуна 2 – K2, коромысла 3 – K3).
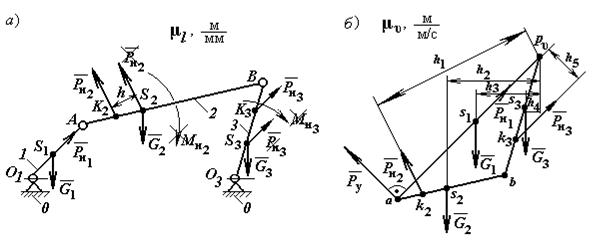
Рис. 12.2
Для приведения механизма
в равновесное состояние необходимо, в какой либо точке механизма приложить
уравновешивающую силу Ру. За точку приложения уравновешивающей
силы чаще всего принимают точку А начального звена, направляя её перпендикулярно
к О1А. Строим в произвольном масштабе повернутый на 90° план скоростей механизма (рис. 12.2,
б) и переносим в соответствующие точки вектора внешних сил, а также
уравновешивающую силу параллельно их действию. Принимая план скоростей за рычаг,
нагруженный силами G1, G2, G3, Ри1, Ри2,
Ри3 и Ру, составляем
уравнение моментов этих сил относительно полюса плана скоростей рu:
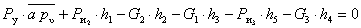 .
.
Из этого уравнения
определяют величину уравновешивающей силы, если она получилась положительной,
то направление её действия выбрано правильно. При отрицательном значении Ру
необходимо изменить её направление на противоположное.
Уравновешивающая сила
является условной, и её используют лишь для вопросов, связанных с определением
мощности или работы машины.
Режимы
движения механизмов
В зависимости от того
какую работу совершают внешние силы машины различают три режима движения:
разгон (разбег, пуск), торможение (выбег, останов) и установившееся движение
(рис. 12.3).
 w1, рад/с Tц
w1, рад/с Tц
w1ср = const
w10
0 t, c.
Разгон
Установившееся движение Выбег
Рис. 12.3
Для идеальной
механической системы, в которой нет потерь энергии и звенья абсолютно жесткие
при получении уравнений движения механизма можно воспользоваться теоремой об
изменении кинетический энергии: разность энергии за какой либо промежуток времени
равна работе сил за тот же промежуток времени.
 ,
,
где Ад.с.
– работа движущих сил; Ап.с. – работа сил производственных
сопротивлений; Ав.с. – работа сил вредных сопротивлений
(трения и внешней среды); АG – работа сил веса.
Для режима разгона: wi0 = 0, Ап.с. = 0, тогда:
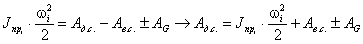 .
.
Работа движущих сил при
разгоне расходуется кинетическую энергию, работу сил вредных сопротивлений и
веса.
При установившемся
движении за каждый цикл движения работа всех внешних сил равна нулю .
.
Для режима выбега: wi = 0, Ад.с. = 0, Ап.с.
= 0 тогда:
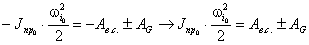 .
.
Запасённая кинетическая
энергия при выбеге тратится на преодоление работ сил вредных сопротивлений и
веса.
Режимы разгона и выбега
называют режимами неустановившегося движения.
Основные
формы уравнения движения механизма
(прямая
задача динамики)
Прямая задача динамики
машины решает вопросы анализа - определение закона движения механической
системы под действием заданных внешних сил. При решении этой задачи параметры
машинного агрегата и действующие на него внешние силы известны, необходимо
определить закон движения: скорости и ускорения в функции времени или
обобщенной координаты. Иначе эту задачу можно сформулировать так: заданы
управляющие силы и силы внешнего сопротивления, определить обеспечиваемый ими
закон движения машины.
Уравнение движения
машины, или механизма даёт возможность оценить их динамические качества в
несколько упрощенном виде и свести это исследование к рассмотрению движения
какого либо одного звена (в большинстве случаев начального), т.е.
воспринимающего непосредственно мощность двигателя. Для этого к этому звену (в
дальнейшем будем называть его звеном приведения), приводят все внешние силы,
действующие на механизм и массы звеньев.
Уравнение
движения механизма в дифференциальном виде
Содержит вторые
производные от координат по времени. Изменение кинетической энергии механизма
равно приращению работ сил действующих на механизм:
 .
.
В случае если начальное
звено совершает вращательное движение:
 .
.
Тогда:
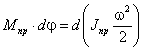 ,
,
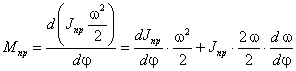 ,
,
Преобразуем второе
слагаемое с учетом:
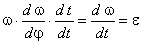 .
.
Подставляя получаем:
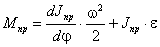 .
.
В случае если Jпр = const (маховое колесо, ротор двигателя и т.п.) 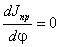 получаем
получаем  (второй
закон Ньютона для вращательного движения).
(второй
закон Ньютона для вращательного движения).
Если начальное звено
совершает поступательное движение получаем:
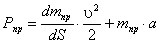 .
.
В случае если mпр = const получаем  .
.
Динамическая
модель механизма
Динамическая модель
механизма, или машины представляет собой уравнение движения звена приведения, к
которому приведены все силы и массы звеньев.
В случае если звено
приведения совершает вращательное движение (например кривошип, рис. 12. 3, а)
то уравнение движения принимает вид:
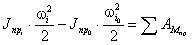 ,
,
где Jпр – приведенный момент инерции звена
приведения; Мпр – приведенный момент сил звена приведения.
Рис. 12.3
В случае если звено
приведения совершает поступательное движение (ползун, рис. 12.3, б)
уравнение движения имеет вид:
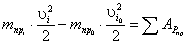 .
.
где mпр – приведенная масса звена
приведения; Рпр – приведенная сила звена приведения.
Приведение
сил и моментов сил к звену приведения
(определение
параметров динамической модели)
На звенья механизма действуют силы и моменты сил,
развивающие соответствующие мощности. Таким образом, мощность всех задаваемых
сил состоит из двух частей:
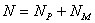 ,
,
где NР - мощность, развиваемая силами, приложенными в различных
точках звеньев, совершающих поступательное или сложное плоское движение; NМ - мощность, развиваемая моментами сил,
приложенными к вращающимся звеньям.
Мощность NР может быть вычислена по формуле:
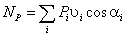 ,
,
где Рi - силы, приложенные к i-м
звеньям механизма; ui -
скорости точек приложения сил; ai- углы,
образованные направлением сил и скоростей их точек приложения.
Мощность NМ вычисляется по формуле:
 ,
,
где Mk - момент, действующий на k-e вращающиеся звенья; wk - угловые скорости этих звеньев.
Подставляя значения NР и NМ получим:
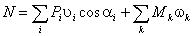 .
.
Эту мощность, развиваемую силами и моментами сил,
приложенными ко всем подвижным звеньям механизма, можно приложить к любому
выбранному звену приведения. Если звено приведения совершает вращательное
движение, то его мощность будет представлена следующим выражением:
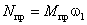 ,
,
где w1 - угловая скорость звена приведения.
Так как левые части
уравнений равны, то:
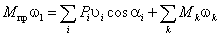 .
.
Таким образом, приведенным
моментом сил называется момент (Мпр),
приложенный к звену приведения и развивающий мощность, равную сумме мощностей
всех сил и моментов сил, приложенных к звеньям механизма.
На основании уравнения имеем:
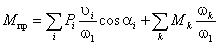 .
.
Полученное уравнение чаще
применяют к шарнирным и кулачковым механизмам, видно, что Мпр
зависит от отношений скоростей, числовые значения которых меняются в
зависимости от величины -
угла поворота звена приведения j.
Таким образом, Mnp = f(j). Для определения отношений скоростей необходимо построить планы
скоростей для нескольких положений механизма. Так как отношение скоростей не
будет зависеть от масштаба, то при построении их можно принять w1 = 1 рад/сек.
Для механизмов, преобразующих только вращательное
движение с постоянным отношением угловых скоростей, приведенный момент сил:
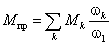 .
.
Отношения 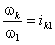 , представляют собой передаточные отношения.
Тогда:
, представляют собой передаточные отношения.
Тогда:
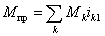 .
.
Если Mk = const, то приведенный момент сил также является постоянной
величиной, не зависящей от угла поворота звена приведения.
Приведенный момент движущих сил направлен в сторону
вращения звена приведения, приведенный момент сил сопротивления направлен в
сторону, противоположную направлению вращения звена приведения.
Если приводить к звену
приведения все задаваемые силы, то приведенный момент сил представляет собою
разность между приведенными моментами сил движущих (Мд.с.) и
сил сопротивления (Мс.с.), т. е. 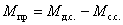 .
.
Если звено приведения совершает поступательное
движение, то его мощность будет представлена следующим выражением:
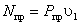 ,
,
где u1 - скорость звена приведения.
Приведённой силой
называется сила (Рпр), приложенная к звену приведения и создающая
мощность, равную сумме мощностей всех сил и моментов сил, приложенных к звеньям
механизма, т.е.:
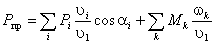 .
.
Приведение масс и моментов инерции
звеньев
Для приведения масс и моментов инерции используется
понятие о кинетической энергии звеньев. Отметим, как вычисляется кинетическая
энергия звеньев при различных видах их движения.
Для звена, совершающего поступательное движение,
кинетическая энергия определяется по следующей формуле:
 ,
,
где m -масса звена; u - скорость любой точки звена, м/сек.
Если звено совершает вращательное движение, то
кинетическая энергия:
 ,
,
где J - момент инерции звена относительно
оси его вращения, кг×м2; w - угловая скорость звена, рад/сек.
Для звена, совершающего сложное плоское движение,
кинетическая энергия состоит из кинетической энергии в поступательном движении
вместе с центром тяжести и кинетической энергии во вращательном движении вокруг
оси, проходящей через центр тяжести:
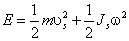 ,
,
где us - скорость центра тяжести звена; Js - момент инерции звена относительно
оси, проходящей через его центр тяжести.
Обозначим число звеньев
механизма, совершающих поступательное, вращательное и сложно-плоское движения,
соответственно через р, k и q. Тогда уравнение кинетической
энергии примет следующий вид:
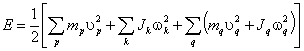 .
.
Кинетическую энергию
механизма можно представить как кинетическую энергию вращающегося звена 1
приведения, т. е.  .
.
Отсюда
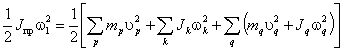
Следовательно:
 .
.
Таким образом, приведенный
момент инерции Jnp представляет собой момент инерции звена
приведения, обладающий кинетической энергией, равной сумме кинетических энергий
всех движущихся звеньев механизма.
Формула применяется
главным образом для плоских шарнирных механизмов. В этом случае Jnp зависит от положения механизма, так
как для каждого его положения отношения скоростей  будут
меняться. Отношение скоростей следует определять из плана скоростей.
будут
меняться. Отношение скоростей следует определять из плана скоростей.
Если механизм состоит
только из вращающихся звеньев (например, различные виды передач), то уравнение принимает
следующий вид:
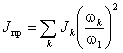 .
.
Заменяя отношение угловых скоростей соответствующим
передаточным отношением, получим:
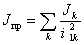 .
.
Так как для передаточных
механизмов значения i1k постоянны, то приведенный момент инерции в этом случае также является
постоянным.
Отметим, что в ряде случаев, например в следящих
устройствах, нужно выбрать двигатель, который обеспечил бы механизму
необходимое по условиям эксплуатации время срабатывания. Необходимая пусковая
мощность может быть определена по пусковому моменту, который равен произведению
приведенного момента инерции на угловое ускорение.
Контрольные
вопросы
23.
Силовой анализ
рычажного механизма методом планов сил.
24.
В чем заключается
метод Н.Е. Жуковского для определения уравновешивающей силы.
25.
Основные режимы и
уравнения движения механизма.
26.
Уравнение
движения механизма в дифференциальном виде.
27.
Динамическая
модель машинного агрегата.
28.
Приведение сил в
механизмах.
29.
Приведение масс в
механизмах.
Лекция
13
Установившееся движении
механизма. Неравномерность движения. Расчет махового колеса.
Установившееся
движение машинного агрегата
Неравномерность
движения
Установившимся режимом
движения называют режим, у которого обобщенная скорость звена приведения есть
периодическая функция во времени (рис. 13.1).
w1, рад/с tпериода
Dw1
w1min w1ср = const w1max
0
t, сек
Рис. 13.1
За время одного периода wi0 = wi, и как следствие DЕ
= 0, АG = 0. Тогда из закона изменения кинетической энергии получаем:
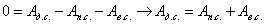 .
.
Если рассматривать
установившееся движение внутри периода следует использовать уравнение:
 .
.
В пределах периода
текущее значение суммарной работы не равно нулю. Работа может быть то
положительной, то отрицательной. При положительной величине работы машина
увеличивает свою кинетическую энергию за счет увеличения скорости, то есть
разгоняется. На участках, где суммарная работа отрицательна, кинетическая
энергия и скорость машины уменьшается, машина притормаживается. В
установившемся режиме величины увеличения скорости на участках разгона и
снижения на участках торможения за цикл равны, поэтому средняя скорость
движения w1ср
= const постоянна. В машинах приведенный
момент инерции которых зависит от обобщенной координаты, на неравномерность
движения оказывает влияние величина изменения приведенного момента инерции. Колебания
скорости изменения обобщенной координаты машины не оказывают прямого влияния на
фундамент машины. Поэтому эти колебания и вызывающие их причины определяют, так
называемую, внутреннюю виброактивность машины.
Величина амплитуды
колебаний скорости Dw1 определяется разностью между максимальной
w1max и минимальной w1min скоростями. За меру измерения
колебаний скорости в установившемся режиме принята относительная величина,
называемая коэффициентом неравномерности движения (неравномерности хода):
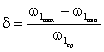 ,
,
где  .
.
Явление периодической
неравномерности в машинах нежелательно с точки зрения прочности и технологии
производственного процесса. Чем выше требования к машинам тем должна быть
меньше неравномерность.
Для различных машин в
зависимости от требований нормального функционирования (снижение чистоты
поверхности в металлорежущих станках, нагрев обмоток и снижение КПД в
электрогенераторах и т.д.) допускаются различные максимальные значения
коэффициента неравномерности движения. Существующая нормативная документация
устанавливает следующие допустимые значения коэффициента неравномерности [d]:
· дробилки [d] = 0,2 ... 0,1;
· прессы, ковочные машины [d] = 0,15 ... 0,1;
· насосы [d] = 0,05 ... 0,03;
· металлорежущие станки нормальной
точности [d] = 0,05 ... 0,01;
· металлорежущие станки прецизионные [d] = 0,005 ... 0,001;
· двигатели внутреннего сгорания [d] = 0,015 ... 0,005;
· электрогенераторы [d] = 0,01 ... 0,005;
Чтобы снизить
внутреннюю виброактивность и неравномерность движения применяются различные
методы:
1.
уменьшение
влияния неравномерности внешних сил (например, применение многоцилиндровых ДВС,
насосов и компрессоров с рациональным сдвигом рабочих процессов в цилиндрах);
2.
уменьшение
влияния переменности приведенного момента инерции (тоже обеспечивается
увеличением числа цилиндров в поршневых машинах, а также уменьшением масс и
моментов инерции деталей, приведенный момент инерции которых зависит от
обобщенной координаты);
3.
установка на
валах машины центробежных регуляторов или аккумуляторов кинетической энергии -
маховиков;
4.
активное
регулирование скорости с использованием систем автоматического управления,
включая и компьютерное управление.
Определение
момента инерции махового колеса
Рассмотрим подробно
наиболее простой способ регулирования неравномерности вращения - установку дополнительной маховой
массы или маховика. Маховик в машине выполняет роль аккумулятора кинетической
энергии. При разгоне часть положительной работы внешних сил расходуется на
увеличение кинетической энергии маховика и скорость до которой разгоняется
система становится меньше, при торможении маховик отдает запасенную энергию
обратно в систему и величина снижения скорости машины уменьшается. Сказанное
иллюстрируется графиками, изображенными на рис. 13.2. На этом рисунке: Dw1 - изменение угловой скорости до
установки маховика, Dw1* - после установки маховика. Отсюда
можно сделать вывод: чем больше дополнительная маховая масса, тем меньше
изменение Dw1* и коэффициент неравномерности d.
Произведём расчет
махового колеса по заданному коэффициенту неравномерности d для двух случаев:
1. Частный случай: для
машин с постоянным приведённым моментом инерции  .
.
Пусть за время периода
работа движущих сил не равна работе сил сопротивления тогда максимальные и
минимальные угловые скорости будут соответствовать максимальным и минимальным
энергиям:
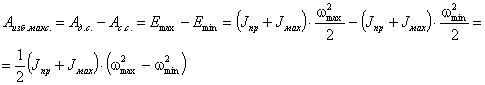 ,
,
где Аизб.макс.
– максимальная избыточная работа; Ад.с. – работа движущих
сил; Ас.с. – работа сил сопротивлений; Emax – максимальная кинетическая энергия
механизма; Emin – минимальная кинетическая энергия
механизма; Jпр – приведённый момент инерции масс; Jмах – момент инерции махового колеса.
Тогда преобразуя:
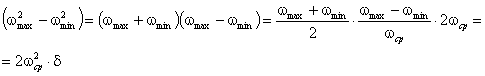 .
.
Окончательно получаем:
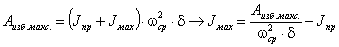 .
.
 w1, рад/с без маховика w1, рад/с без маховика
     Dw1 Dw1

Dw1*
w1ср = const с маховиком
 0 t, сек 0 t, сек
Рис. 13.2
|
2. Общий случай (для
машин с переменным приведённым моментом инерции 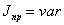 ),
положения с максимальными и минимальными значениями скорости не совпадают с
положениями при которых максимальные и минимальные значения энергии. Рассмотрим
графический способ по методу Виттенбауэра (метод построения диаграммы
энерго-масс).
),
положения с максимальными и минимальными значениями скорости не совпадают с
положениями при которых максимальные и минимальные значения энергии. Рассмотрим
графический способ по методу Виттенбауэра (метод построения диаграммы
энерго-масс).
Контрольные
вопросы
30.
Установившийся
режим движения машинного агрегата.
31.
Причины
вызывающие неравномерность движения.
32.
Как оценивается и
регулируется неравномерность движения.
33.
Определение
момента инерции махового колеса для машин с постоянным приведенным моментом инерции.
Лекция
14
Вибрации и колебания в
машинах и механизмах, виброактивность и виброзащита. Понятие о
неуравновешенности звена и механизма. Статическое уравновешивание рычажных
механизмов. Метод замещающих масс. Полное и частичное уравновешивание механизма.
Ротор и виды его уравновешивания: статическое, динамическое. Балансировка.
Вибрации и
колебания в машинах и механизмах
При движении механической
системы под действием внешних сил в ней могут возникать механические колебания
или вибрации. Причинами возникновения вибраций могут быть периодические
изменения сил (силовое возмущение), перемещений (кинематическое возмущение) или
инерционных характеристик (параметрическое возмущение). Вибрацией (от
лат. vibratio - колебание) называют механические
колебания в машинах или механизмах. Колебание - движение или изменение состояния,
обладающие той или иной степенью повторяемости или периодичностью. Если
источник возникновения вибраций определяется внутренними свойствами машины или
механизма, то говорят об его виброактивности. Чтобы вибрации механизма не
распространялись на окружающие его системы или чтобы защитить механизм от
вибраций, воздействующих на него со стороны внешних систем, применяются
различные методы виброзащиты. Различают внешнюю и внутреннюю виброактивность.
Под внутренней виброактивностью понимают колебания возникающие внутри механизма
или машины, которые происходят по его подвижностям или обобщенным координатам.
Эти колебания не оказывают непосредственного влияния на окружающую среду. При
внешней виброактивности изменение положения механизма приводит к изменению
реакций в опорах (т.е. связях механизма с окружающей средой) и
непосредственному вибрационному воздействию на связанные с ним системы. Одна и
основных причин внешней виброактивности - неуравновешенность его звеньев и
механизма в целом.
Понятие о
неуравновешенности механизма (звена)
Неуравновешенным будем
называть такой механизм (или его звено), в котором при движении центр масс
механизма (или звена) движется с ускорением. Так как ускоренное движение
системы возникает только в случае, если равнодействующая внешних силовых
воздействий не равна нулю. Согласно принципу Д’Аламбера, для уравновешивания
внешних сил к системе добавляются расчетные силы - силы и моменты сил инерции.
Поэтому уравновешенным будем считать механизм, в котором главные вектора и
моменты сил инерции равны нулю, а неуравновешенным механизм, в котором эти силы
неравны нулю. Для примера рассмотрим четырехшарнирный механизм (рис. 14.1).
Механизм будет находится
в состоянии кинетостатического равновесия, если сумма действующих на него
внешних сил и моментов сил (включая силы и моменты сил инерции) будет равна
нулю.
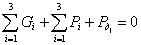 ;
;
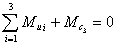 .
.
Уравновешенность является
свойством или характеристикой механизма и не должна зависеть от действующих на
него внешних сил. Если исключить из рассмотрения все внешние силы, то в
уравнении равновесия останутся только инерционные составляющие, которые
определяются инерционными параметрами механизма - массами и моментами инерции и законом движения
(например, центра масс системы Sм), поэтому уравновешенным считается механизм для которого главный вектор
и главный момент сил инерции равны нулю:
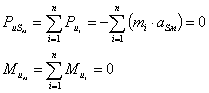 .
.
Неуравновешенность - такое состояние механизма, при котором главный вектор или
главный момент сил инерции не равны нулю. Различают:
· статическую неуравновешенность 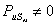 ;
;
· моментную неуравновешенность  ;
;
· динамическую неуравновешенность  .
.
При статическом
уравновешивании механизма необходимо обеспечить:
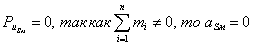
Это условие выполняется
если скорость центра масс механизма равна нулю 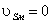 , или
она постоянна по величине и направлению
, или
она постоянна по величине и направлению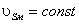 .
Обеспечить выполнение условия
.
Обеспечить выполнение условия 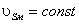 в
механизме практически невозможно, поэтому при статическом уравновешивании
обеспечивают выполнение условия
в
механизме практически невозможно, поэтому при статическом уравновешивании
обеспечивают выполнение условия 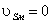 . Это возможно, когда
центр масс механизма лежит на оси вращения звена 1 - rSм= 0 или когда он неподвижен rSм= const, тогда:
. Это возможно, когда
центр масс механизма лежит на оси вращения звена 1 - rSм= 0 или когда он неподвижен rSм= const, тогда:
 .
.
На практике наиболее
часто статическое уравновешивание проводят следующими методами:
· выбирая симметричные схемы механизма
(рис. 14.2);
· устанавливая на звеньях механизма
противовесы (или корректирующие массы);
· размещая противовесы на
дополнительных звеньях или кинематических цепях.
3 2
B 1
D,C A,S1,Sм E,Q

0 K
4 5
Рис. 14.2
|
Метод
замещающих масс
При использовании метода
замещающих масс, звено механизма с распределенной массой заменяется расчетной
моделью, которая состоит из точечных масс.
Условиями перехода от
звена с распределенной массой к модели с точечными массами являются:
1.
Сохранение массы
звена: miA + miB = mi;
2.
Сохранение
положения центра масс: lASi = const;
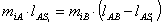 .
.
3.
Сохранение
момента инерции:
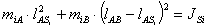 .
.
Одновремённое выполнение
всех трёх условий системой с двумя массами невозможно, поэтому при статическом
уравновешивании механизмов ограничиваются выполнением только двух первых
условий. Чтобы обеспечить выполнение всех трех условий необходимо ввести третью
массу miSi. Рассмотрим применение метода
замещающих масс при полном и частичном статическом уравновешивании
кривошипно-ползунного механизма.
Полное
статическое уравновешивание
кривошипно-
ползунного механизма (рис. 14.4)
Дано: lAB, lBC,
lAS1, lBS2, lCS3=0, m1,
m2, m3.
Определить: mk1, mk2.
Для определения величины
сосредоточенных масс распределим массы звеньев по методу замещающих масс,
сосредоточив их в центрах шарниров A,B,C.
Тогда
 m1 = mA1 + mB1 - масса первого звена, распределенная
между массами, сосредоточенными в точках В;
m1 = mA1 + mB1 - масса первого звена, распределенная
между массами, сосредоточенными в точках В;
m2 = mВ2 + mС2 - масса второго звена, распределенная
между массами, сосредоточенными в точках В и С .
Вначале проведем
уравновешивание массы mC корректирующей массой mk2. Составим уравнение статических
моментов относительно точки В для звеньев 2 и 3:
 .
.
Задаемся величиной lk2 и получаем корректирующую
массу:
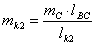 .
.
Затем уравновешиваем
массы центра, который после установки корректирующей массы расположился в точке
В:
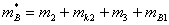 .
.
Составляем уравнение
статических моментов относительно точки А:
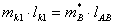 .
.
Задаемся величиной lk1 и получаем корректирующую массу:
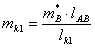 .
.
Частичное
статическое уравновешивание
кривошипно-ползунного
механизма
1. Уравновешивание
вертикальной составляющей главного вектора сил инерции (рис. 14.5).
Дано: lAB, lBC,
lAS1, lBS2, lCS3=0, m1,
m2, m3.
Определить: mk1
В этом случае необходимо
добиться, чтобы центр масс механизма Sм при движении перемещался вдоль направляющей
ползуна (для схемы на рис. 14.5 по горизонтали). Для этого достаточно
уравновесить только массу mB. Составляем уравнение статических моментов
относительно точки А:
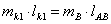 .
.
Задаемся величиной lk1 и получаем корректирующую массу:
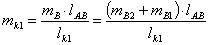 .
.
2. Уравновешивание
горизонтальной составляющей главного вектора сил инерции.
Дано: lAB, lBC, lAS1, lBS2, lCS3=0, m1,
m2, m3.
Определить: mk1
В этом случае необходимо
добиться, чтобы центр масс механизма при движении перемещался по дуге
окружности радиуса  (рис.
14.6). Расчет корректирующей массы ведется в два этапа. В начале первой
составляющей корректирующей массы
(рис.
14.6). Расчет корректирующей массы ведется в два этапа. В начале первой
составляющей корректирующей массы  уравновешивается масса mB. Составляется, как и в
предыдущем примере, уравнение статических моментов относительно точки А:
уравновешивается масса mB. Составляется, как и в
предыдущем примере, уравнение статических моментов относительно точки А:
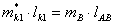 .
.
Задается величина lk1 и рассчитывается корректирующая
масса:
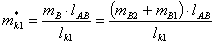 .
.
Затем с помощью второй
составляющей корректирующей массы  центр массы mС. перемещается в точку
центр массы mС. перемещается в точку  . Величина
. Величина 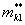 определяется следующим образом:
центр шарнира С соединяется прямой с концом отрезка lk1 точкой Sk. Радиус
определяется следующим образом:
центр шарнира С соединяется прямой с концом отрезка lk1 точкой Sk. Радиус 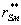 проводится параллельно отрезку BС. Тогда,
проводится параллельно отрезку BС. Тогда, 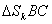 подобен
подобен
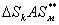 и
и 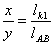 .
.
Статический момент относительно
точки  :
:
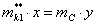 ,
,
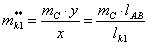 .
.
Радиус-вектор 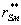 определяется из пропорций
соответствующих сторон треугольников:
определяется из пропорций
соответствующих сторон треугольников:
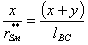 ,
,
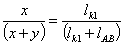 ,
,
откуда
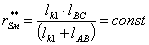 .
.
Корректирующая масса,
обеспечивающая уравновешивание горизонтальной составляющей главного вектора сил
инерции кривошипно-ползунного механизма, размещается на первом звене механизма
и равна сумме составляющих:
 .
.
Центр массы механизма при
таком уравновешивании расположен в точке Sм, которая движется по дуге радиуса rSм:
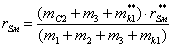 .
.
Схема распределения масс
в механизме после уравновешивания дана на рис. 14.7.
Балансировка
роторов
Общие сведения о
балансировке. Ротор, неуравновешенность ротора и ее виды. Задачи балансировки
Ротором называют звенья механизмов,
совершающие вращательное движение и удерживаемые при этом своими несущими
поверхностями в опорах. Если масса ротора распределена относительно оси
вращения равномерно, то главная центральная ось инерции x-x совпадает с осью вращения и ротор
является уравновешенным или идеальным. При несовпадении оси вращения с осью x-x, ротор будет неуравновешенным и в
его опорах при вращении возникнут переменные реакции, вызванные действием
инерционных сил и моментов сил (точнее, движением центра масс с ускорением).
В зависимости от
взаимного расположения оси вращения и главной центральной оси инерции x-x , различают следующие виды
неуравновешенности роторов (рис. 14.8):
- статическую, когда эти оси
параллельны (рис. 14. 8, а);
- моментную, когда оси пересекаются в
центре масс ротора S (рис. 14. 8, б);
- динамическую, когда оси либо
пересекаются вне центра масс, либо не пересекаются, а перекрещиваются в
пространстве (рис. 14. 8, в).
Неуравновешенность
определяется конструктивными характеристиками ротора или механизма и не зависит
от параметров движения. Поэтому при балансировке оперируют не инерционными
силами, а дисбалансами. Дисбаланс - мера статической неуравновешенности ротора, векторная
величина, равная произведению неуравновешенной массы m на ее эксцентриситет e, где эксцентриситет e - радиус-вектор центра этой массы
относительно оси ротора. Направление главного вектора дисбаланса D совпадает с направлением главного
вектора сил инерции Ри, действующих на ротор при вращении:
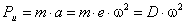 .
.
Моментная
неуравновешенность характеризуется главным моментом дисбалансов ротора MD , который пропорционален главному
моменту сил инерции (рис. 14.9):
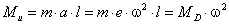 .
.
Главный момент
дисбалансов ротора полностью определяется моментом пары равных по величине и
противоположных по направлению дисбалансов DM1 + DM2 = DM, расположенных в двух произвольных
плоскостях (I и II), перпендикулярных оси вращения ротора. Дисбаланс и момент
дисбалансов не зависят от частоты вращения, они полностью определяются
конструкцией ротора и точностью его изготовления.
Балансировкой называют
процесс определения значений и угловых координат дисбалансов ротора и их
уменьшения с помощью корректировки размещения его масс. Балансировка
эквивалентна уравновешиванию системы инерционных сил, прикладываемых к
подвижному ротору для его равновесия.
|
b D2
x
 MD S MD S
Dc1 Dc2
   D1 ek1 0 y
DM2 D1 ek1 0 y
DM2

DM1 mk1 e
II
x
x Dk1 ek2
l
I mk2
Dk2
Рис. 14.9
|
Данную систему, как и
любую произвольную систему сил, можно заменить равнодействующими - главным вектором и главным моментом
или двумя векторами, расположенными в произвольных параллельных плоскостях. Для
уравновешивания системы сил достаточно уравновесить эти равнодействующие. При
балансировке операции над силами заменяют действиями над дисбалансами. Поэтому
для жестких роторов вышесказанное можно сформулировать так: жесткий ротор можно
уравновесить двумя корректирующими массами, расположенными в двух произвольно
выбранных плоскостях, перпендикулярных оси его вращения. Эти плоскости называют
плоскостями коррекции.
Задача балансировки ротора заключается в определении, в
выбранных плоскостях коррекции, значений и углов дисбалансов и размещении в
этих плоскостях корректирующих масс, дисбалансы которых равны по величине и
противоположны по направлению найденным дисбалансам ротора. На практике
балансировку проводят: при конструировании - расчетными методами, в процессе изготовления деталей и узлов
- экспериментально на специальных
балансировочных станках. Балансировка на станках является более точным и
надежным методом, по сравнению с расчетными. Поэтому она применяется для
ответственных деталей с высокими рабочими частотами вращения. Корректировка
масс ротора осуществляется либо присоединением к нему дополнительных
корректирующих масс (наплавлением, наваркой или привинчиванием противовесов),
либо удалением части массы ротора с «тяжелой» стороны (фрезерованием или
высверливанием). Точность балансировки характеризуется величиной остаточного
дисбаланса D0
ротора в
каждой из плоскостей коррекции. Величина D0 не должна превышать допустимых для
данного класса точности значений, регламентируемых ГОСТ.
Балансировка роторов при различных видах неуравновешенности
Статическая неуравновешенность
При статической
неуравновешенности (рис. 14.10) главная центральная ось инерции параллельна оси
вращения ротора, главный вектор дисбалансов больше нуля, а главный момент
дисбалансов равен нулю (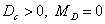 ), т.е. необходимо
уравновесить только вектор Dс = m × e. Для этого достаточно
установить на роторе только одну корректирующую массу mk, величина которой определяется из
равенства:
), т.е. необходимо
уравновесить только вектор Dс = m × e. Для этого достаточно
установить на роторе только одну корректирующую массу mk, величина которой определяется из
равенства:
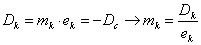 ,
,
где величиной ek задаются из соображений удобства
размещения противовесов. Направление вектора Dk противоположно направлению Dc.
Таким образом, условие
статической уравновешенности ротора заключается в  .
.
Моментная
неуравновешенность
|
 Dk MDk Dk MDk
   m m
  mk mk
   ek
x ek
x
   МD МD
   S S
 x ek x ek

lk
lk mk
 l Dk l Dk

Рис. 14.11
|
При моментной
неуравновешенности (рис. 14.11) главная центральная ось инерции пересекает ось
вращения в центре масс ротора точке S, главный вектор дисбалансов Dс равен нулю, главный момент
дисбалансов МD не равен нулю (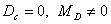 ), т.е. необходимо
уравновесить только момент дисбалансов МD. Для этого достаточно
разместить на роторе две одинаковых корректирующих массы mk на равных расстояниях от оси
вращения ek и от центра масс S - lk. Массы выбираются и размещаются так, чтобы момент их
дисбалансов MDk был по величине равен, а по направлению противоположен моменту
дисбалансов ротора МD:
), т.е. необходимо
уравновесить только момент дисбалансов МD. Для этого достаточно
разместить на роторе две одинаковых корректирующих массы mk на равных расстояниях от оси
вращения ek и от центра масс S - lk. Массы выбираются и размещаются так, чтобы момент их
дисбалансов MDk был по величине равен, а по направлению противоположен моменту
дисбалансов ротора МD:
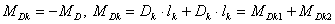 ,
,
где Dk – дисбаланс корректирующей массы, 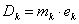 .
.
В этих зависимостях
величинами lk и ek задаются по условиям удобства размещения
противовесов на роторе, а величину mk рассчитывают. Необходимо отметить,
что величины Dk в плоскостях коррекции необязательно должны быть равными, необходимо выполнять
только неизменность положения центра масс - он должен оставаться на оси вращения.
Таким образом, условие
моментной уравновешенности ротора заключается в 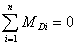 .
.
Динамическая
неуравновешенность
При динамической
неуравновешенности (рис. 14.12) главная центральная ось инерции пересекает ось
вращения не в центре масс ротора точке S, либо перекрещивается с ней; и
главный вектор дисбалансов Dс, и главный момент дисбалансов МD не равны нулю (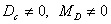 ), т.е. необходимо уравновесить вектор
Dс и момент дисбалансов МD . Для этого достаточно разместить на
роторе две корректирующих массы mk1 и mk2 на расстояниях от оси вращения ek1 и ek2, а от ценра масс S, соответственно на lk1 и lk2. Массы выбираются и размещаются так,
чтобы момент их дисбалансов MDk был по величине равен, а по направлению
противоположен моменту дисбалансов ротора МD:
), т.е. необходимо уравновесить вектор
Dс и момент дисбалансов МD . Для этого достаточно разместить на
роторе две корректирующих массы mk1 и mk2 на расстояниях от оси вращения ek1 и ek2, а от ценра масс S, соответственно на lk1 и lk2. Массы выбираются и размещаются так,
чтобы момент их дисбалансов MDk был по величине равен, а по направлению
противоположен моменту дисбалансов ротора МD:
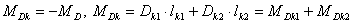 ,
,
где Dk1 и Dk2
– дисбалансы корректирующих масс, 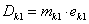 и
и  .
.
Векторная сумма
дисбалансов при этом должна быть равна и противоположно направлена вектору Dс:
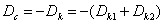 .
.
В этих зависимостях
величинами lki и eki задаются по условиям удобства размещения
противовесов на роторе, а величины mki рассчитывают.
Таким образом, условие
динамической уравновешенности ротора заключается в 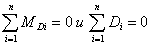 .
.
Контрольные
вопросы
34.
Вибрации и
колебания в машинах и механизмах.
35.
Что такое
неуравновешенность механизма, её разновидности.
36.
Метод замещающих
масс.
37.
Полное
статическое уравновешивание кривошипно-ползунного механизма методом замещающих
масс.
38.
Частичное
статическое уравновешивание кривошипно-ползунного механизма методом замещающих
масс.
39.
Балансировка
роторов. Как решаются задачи уравновешивания при статической, моментной и
динамической неуравновешенности.
Лекция
15
Уравновешивание роторов
при проектировании. Виброзащита машин и механизмов. Методы виброзащиты.
Подрессоривание и виброизоляция. Динамическое гашение колебаний.
Уравновешивание
роторов при проектировании
Статическое уравновешивание при проектировании
При проектировании статически
уравновешивают детали, имеющие небольшие осевые размеры и конструктивно
неуравновешенные, например, дисковые кулачки (рис. 15.1).
Когда кулачок неподвижен w1 = 0, реакция в опоре R10 = - G. При вращении кулачка w1 ¹ 0,
реакция в опоре равна векторной сумме сил тяжести и центробежной силы инерции R10 = - (G + Pи), где Pи = - m1× e1 ×w12. При проектировании детали типа
кулачка уравновешивание производится так: в деталь с центром на оси вращения
вписывается окружность, подсчитываются площади ограниченные контуром кулачка и
расположенные вне или внутри окружности, определяется массы и центры масс Sn неуравновешенных частей кулачка,
находится эксцентриситет e1 центра масс S1 кулачка по величине и направлению и определяется его дисбаланс D1 = m1× e1, с помощью корректирующей массы mk, размещаемой на эксцентриситете ek, создается дисбаланс Dk равный по величине и противоположный
по направлению D1.
|
 
  1 1 Ри 1 1 Ри
 w1 Sn R w1 Sn R
e S
 A
ek A A
ek A
  R10
G R10
G
0
0
mk
Pиk
Рис. 15.1
|
Динамическое уравновешивание при проектировании
Динамическое
уравновешивание при проектировании проводят с деталями и узлами, в которых
массы распределены относительно оси вращения неравномерно, например, детали
типа коленчатого вала. Эти детали делят на несколько дисков и в каждом диске,
также как при статическом уравновешивании, определяют величину и направление дисбаланса
Di. На детали выбирают две плоскости
коррекции и каждый вектор дисбаланса раскладывают на две составляющие,
расположенные в плоскостях коррекции. Затем составляющие векторы дисбалансов в
плоскостях коррекции суммируются и их равнодействующий дисбаланс, например, DI, уравновешивается соответствующей
корректирующей массой mIk. Пример такого уравновешивания изображен на
рис. 15.2.
Схема размещения
корректирующих масс в плоскостях коррекции приведена на рис. 15.3.


I II
 DII
DII
DI eII







 0I
0II
0I
0II

 eI DkI
mkII
eI DkI
mkII
mkI
DkII
Рис. 15.3
Виброзащита
машин и механизмов
При движении механической
системы под действием внешних сил в ней возникают механические колебания или
вибрации. Эти вибрации оказывают влияние на функционирование механизма и часто
ухудшают его эксплуатационные характеристики: снижают точность, уменьшают КПД и
долговечность машины, увеличивают нагрев деталей, снижают их прочность,
оказывают вредное воздействие на человека-оператора. Для снижения влияния
вибраций используют различные методы борьбы с вибрацией. С одной стороны при
проектировании машины принимают меры для снижения ее виброактивности
(уравновешивание и балансировка механизмов), с другой - предусматриваются средства защиты
как машины от вибраций, исходящих от других машин (для рассматриваемой машины
от среды), так среды и операторов от вибраций данной машины.
Существует два способа
виброзащиты: виброгашение и виброизоляция. Виброгашение основано на
присоединении к колеблющимся звеньям машины дополнительных колебательных систем
(динамических виброгасителей). Виброизоляция основана на разделении исходной
системы на две части и соединения этих частей посредством виброизоляторов или
амортизаторов.
Динамические гасители или
антивибраторы, основаны на изменении соотношения между собственными частотами
системы и частотами возмущающих сил для устранения резонансных колебаний.
Виброизоляторы, в которых
за счет их упругих и демпфирующих свойств уменьшается амплитуда колебаний как на
резонансных и нерезонансных режимах.
Взаимодействие
двух подвижных звеньев
Рассмотрим механическую
систему (рис. 15.4), состоящую из двух подвижных звеньев, образующих между
собой кинематическую пару. Для упрощения предположим, что движение звеньев возможно
только по одной координате x. Масса первого звена m1, второго - m2. На звено 2 действует периодическая
внешняя сила Р2 = R20× sin wt , действием сил веса пренебрегаем.
Уравнения движения звеньев имеют вид:
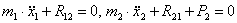 .
.
Если считать, что контакт
между звеньями в процессе движения не нарушается и тела абсолютно жесткие, то
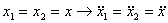 .
.
С учетом R21 = - R12, определим реакцию в точке контакта
между звеньями:
  1
m1 1
m1
K x1
  2 m2 2 m2
 x2 x2

Р2 = R20× sin wt
Рис. 15.4
|
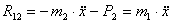 .
.
Откуда
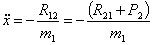 ,
,
и после преобразований
получаем:
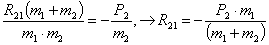 .
.
Проанализируем эту
зависимость:
если m1 Þ 0, то R21 Þ 0;
если m2 Þ 0, то R21 Þ - P2;
если m2 = m1 = m, то R21 Þ - 0,5 × Р2 ;
если m2 Þ ¥, то R21 Þ 0;
если m1 Þ ¥, то R21 Þ - P2.
Анализ показывает, что
реакция взаимодействия между звеньями зависит от соотношения их масс и величины
внешней силы. При этом кинетическая энергия системы составляет:
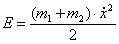 ,
,
а потенциальная равна
нулю.
Подрессоривание
или виброизоляция
При виброизоляции между
рассматриваемыми звеньями устанавливают линейный или нелинейный виброизолятор,
который обычно состоит из упругого и демпфирующего элементов (рис. 15.5).
|
 1 m1 1 m1
x1
  
    c k c k
 2
m2 2
m2 
  x2 x2
Р2 = R20× sin wt
Рис. 15.5
|
В этой механической
системе x2 ¹ x1 (предположим, что x2 > x1) и Dx = x2 - x1, тогда кинетическая энергия системы
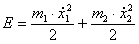 ,
,
а потенциальная
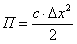 .
.
То есть в системе с
виброизолятором только часть работы внешней силы расходуется на изменение
кинетической энергии. Часть этой работы переходит в потенциальную энергию
упругого элемента, и часть рассеивается демпфером (переходит в тепло и рассеивается
в окружающей среде).
Уравнения движения:
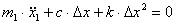 ,
,
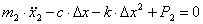 .
.
Решение этой системы
уравнений подробно рассматривается в курсе теории колебаний, поэтому
ограничимся только анализом амплитудно-частотной характеристики (рис. 15.6).
Характеристику построим в относительных координатах Dxотн = x/xст , где xст - статическая деформация упругого
элемента.
Динамическое
гашение колебаний
Динамические гасители или
антивибраторы широко применяются в машинах работающих в установившихся режимах
для отстройки от резонансных частот (например, в судовых двигателях внутреннего
сгорания). Динамические гасители могут быть выполнены в виде упругого или
физического маятника. Рассмотрим простейший линейный упругий динамический
гаситель (рис. 15.7). Принцип действия динамического гасителя заключается в
создании гасителем силы направленной противоположно возмущающей силе. Настройка
динамического гасителя заключается в подборе его собственной частоты:
собственная частота гасителя должна быть равна частоте тех колебаний, амплитуду
которых необходимо уменьшить («погасить»):
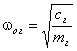 ,
,
где 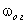 - собственная частота гасителя, mг - масса гасителя, сг - жесткость пружины гасителя.
- собственная частота гасителя, mг - масса гасителя, сг - жесткость пружины гасителя.
Уравнения движения
системы с динамическим гасителем, схема которого изображена на рис. 15.7 имеют
вид:
|
0 с
Р2 = R20× sin wt
   1 1

x1
   m1 m1
    cг kг cг kг
 г mг г mг 
 xг xг
Рис. 15. 7
|
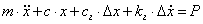 ,
,
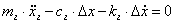 ,
,
где Dx = x - xг - деформация пружины гасителя.
На рис. 15.8 приведены
амплитудно-частотные характеристики этой системы без динамического гасителя и с
динамическим гасителем. Как видно из этих характеристик, при установке
динамического гасителя амплитуда на частоте настройки резко снижается, однако в
системе вместо одной собственной частоты возникает две. Поэтому динамические
гасители эффективны только в узком диапазоне частот вблизи частоты настройки
гасителя. Изображенные на рисунке кривые 1 и 2 относятся
к динамическому гасителю без демпфирования. При наличии в системе демпферов
форма кривой изменяется (кривая 3): амплитуды в зонах гашения
увеличиваются, а зонах резонанса - уменьшаются.
Контрольные
вопросы
40.
Статическое и
динамическое уравновешивание при проектировании деталей.
41.
В чем различие
между виброгашением и виброизоляцией.
42.
Сущность
подрессоривания, или виброизоляции.
43.
Динамическое
гашение колебаний.
Лекция
16
Трение в кинематических
парах. Трение скольжения: сила трения, угол и конус трения, движение на
горизонтальной плоскости, трение на наклонной плоскости, трение клинчатого
ползуна, трение во вращательных парах, трение в пятах.
Трение в кинематических парах
Явление трения имеет
место всегда, когда любые тела – твёрдые, жидкие или газообразные, находящиеся
в соприкосновении одно с другим, движутся относительно друг друга, или
подвергаются воздействию сил, стремящихся вызвать их относительное движение.
Трение в машинах играет весьма существенную роль. В
передаточных механизмах – фрикционных, ременных и др. за счет силы трения
осуществляется передача движения от ведущего звена к ведомому. В других случаях
трение нежелательно, так как оно препятствует движению и на преодоление сил
трения затрачивается значительная часть работы движущих сил – так называется
работа сил вредных сопротивлений.
Трение вызывает износ
трущихся частей машины, что существенно препятствует повышению скоростей
движения, а следовательно и производительности машин.
В дальнейшем мы будем
иметь в виду трение только на поверхностях соприкасающихся твёрдых тел.
Способность контактирующих поверхностей звеньев сопротивляться их относительному
движению называется внешним трением.
Трение обусловлено
неидеальным состоянием контактирующих поверхностей (микронеровности, загрязнения,
окисные пленки и т.п.) и силами межмолекулярного сцепления.
Опыт показывает, что при
относительном движении двух соприкасающихся твёрдых тел, прижатых одно к
другому некоторой силой, на поверхности соприкосновения действует сила,
сопротивляющаяся относительному движению – сила трения.
Различают следующие виды
трения:
· трение покоя проявляется в момент,
когда два тела находящиеся в состоянии относительного покоя начинают
относительное движение (касательную составляющую, возникающую в зоне контакта
до возникновения относительного движения, в условиях когда она меньше силы
трения покоя, будем называть силой сцепления; максимальная величина силы
сцепления равна силе трения покоя);
· трение скольжения появляется в
кинематической паре при наличии относительного движения звеньев;
· трение качения появляется в высших
кинематических парах при наличии относительного вращательного движения звеньев
вокруг оси или точки контакта;
· трение верчения возникает при
взаимодействии торцевых поверхностей звеньев вращательных кинематических пар
(подпятники).
Опыт показывает также,
что сила трения уменьшается, если соприкасающиеся поверхности твёрдых тел
смазаны жидкостью. По наличию и виду применяемых смазочных материалов различают
сухое, граничное, жидкостное трение и с газовой смазкой.
Снижение трения в
подвижных соединениях машин требует дополнительных решений, эффективность
которых в большой степени зависит от роддержания условий эксплуатации (рис.
16.1).

Рис. 16.1.
Пути снижения трения
Трение
скольжения несмазанных тел
Сила трения скольжения F возникает в плоскости касания (скольжения) двух соприкасающихся
прижатых силой Fn
друг к другу тел при их относительном перемещении. Для преодоления силы трения
необходимо приложить сдвигающую силу Ft, расположенную в плоскости скольжения.
Силу трения скольжения можно выразить следующей
приближенной формулой (закон Кулона-Амонтона):
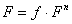 ,
,
где F – сила трения скольжения, т.е. сила,
препятствующая относительному движению двух соприкасающихся тел; f – коэффициент пропорциональности для
конкретных условий трения, называемый коэффициентом трения скольжения
(коэффициент трения 1-рода); Fn – результирующая сила нормальных давлений, направленная по
общей нормали к поверхности соприкасающихся тел, соответственно нормальная реакция
Rn равна Fn. Тогда
 .
.
Трение появляется не только во время движения тел, но
и тогда, когда тела находятся в покое. Трущиеся тела 1 и 2 (рис. 16.2) с
большей или меньшей силой сцеплены одно с другим. Пусть к телу 1
приложена сила, стремящаяся сдвинуть его слева направо. При увеличении силы
будет иметь место невидимый глазом, но обнаруживаемый точными приборами упругий
сдвиг одной трущейся поверхности относительно другой. При увеличении силы
деформация сдвига будет увеличиваться и при некотором предельном значении
сдвигающей силы начнется видимое движение тела 1 относительно тела 2.
Опыты показывают, что для приведения в движение тела 1 требуется сила,
несколько большая той, которую приходится преодолевать при последующем
равномерном движении. Предельная сила, сопротивляющаяся в начальный момент
движения трущегося тела, называется силой трения покоя или силой сцепления, а
сила сопротивления, возникающая во время движения, получила название силы
трения движения.
Для того, чтобы тело 1 (рис. 16.2) вывести из
состояния покоя, к нему нужно приложить движущую силу 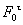 ,
равную
,
равную
 .
.
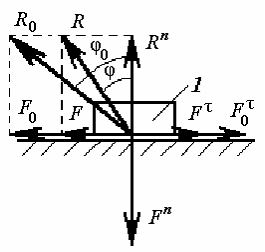
Рис. 16.2
Установлено, что трение
представляет сложный комплекс механических, химических и др. явлений. Однако
количественный учет этих явлений в настоящее время произвести не представляется
возможным. Опыты показывают, что величина силы трения чрезвычайно изменчива.
Помимо материала, чистоты обработки поверхности, смазки, удельного давления и
относительной скорости передвижения трущихся тел на величину силы трения
оказывают влияние такие, казалось бы, малозначимые факторы, как наличие или
отсутствие оксидной плёнки, влажность, температура и т.п. Всё это приводит к
тому, что наука до сих пор еще не имеет до конца разработанной теории трения и
износа. Поэтому в инженерных расчетах приходится пользоваться некоторыми
приблизительными (усредненными) величинами коэффициентов трения, значения
которых получены как результат обобщения большого экспериментального материала.
В большинстве справочников значения коэффициентов трения скольжения приводят в
зависимости от материала соприкасающихся тел, чистоты обработки поверхности и
для случая сухого трения.
Коэффициент f0 называется коэффициентом трения покоя. Угол j0, образованный направлениями полной реакции R0 и нормальной реакции 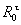 , называется углом трения покоя.
, называется углом трения покоя.
Для того, чтобы тело
продолжало движение с постоянной скоростью, необходимо приложить силу 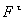 , несколько меньшую силы
, несколько меньшую силы 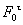 и равную
и равную
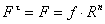 .
.
Из рис. 16.2 получим
 ;
;  ;
;
так как  >
> , то F0 >
, то F0 > , f0 > f, j0 > j, т.е. коэффициент трения покоя больше коэффициента трения движения.
, f0 > f, j0 > j, т.е. коэффициент трения покоя больше коэффициента трения движения.
При движении тела 1 в
разных направлениях по плоскости 2 равнодействующая R21 будет отклоняться от нормальной реакции Rn на угол j в сторону противоположную относительному
движению, образуя конус с углом 2j при вершине – называемый конусом трения (рис. 16.3).
Конус трения –
поверхность описываемая равнодействующей (силы трения и нормальной реакции) при
вращении её вокруг нормальной реакции, или конус с углом при вершине равным
двойному углу трения.
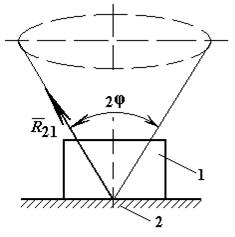
Рис. 16.3
Трение на
горизонтальной плоскости
Движение тела на
плоскости можно рассматривать под действием только одной силы, т.к. несколько
действующих сил на тело можно привести к одной - равнодействующей.
Предположим, что на тело
действует сила Р (рис. 16.4) под углом l к нормали. Перенесём силу Р в точку
пересечения её вектора с перпендикуляром к плоскости соприкосновения и разложим
её по двум взаимно перпендикулярным направлениям. Нормальная составляющая Рn, прижимая тело к плоскости, создает
противодействующую движению тела силу F0 трения покоя; тангенциальная составляющая Рt стремится сдвинуть тело.
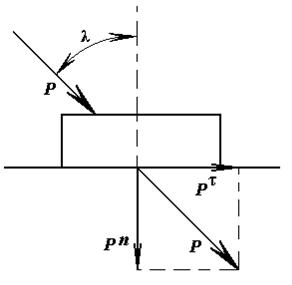
Рис. 16.4
Для возможности движения
необходимо выполнение условия:
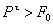 .
.
Так как
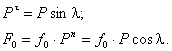
То
 ,
,
откуда
 ,
,
где j0 - угол трения покоя.
Из этого следует, что
сила, действующая внутри конуса трения, независимо от её величины, привести в
движение тело не может.
Подставив в приведённые
выше неравенства F вместо F0, f
и j вместо f0 и j0 и заменив
во всех неравенствах знак > знаками ³, придём к заключению, что движение тела на плоскости
возможно лишь при соблюдении условия  .
.
При  получаем
получаем  и
движение с постоянной скоростью, при
и
движение с постоянной скоростью, при  получаем
получаем  и движение с ускорением.
и движение с ускорением.
При  возникновение движения невозможно, при
возникновение движения невозможно, при  вызванное какими-либо силами и
продолжающееся по инерции движение тела при действии на него силы Р
будет происходить с замедлением, так как в этом случае создаваемая силой Рn противодействующая движению сила
трения будет больше силы Рt, поддерживающей движение.
вызванное какими-либо силами и
продолжающееся по инерции движение тела при действии на него силы Р
будет происходить с замедлением, так как в этом случае создаваемая силой Рn противодействующая движению сила
трения будет больше силы Рt, поддерживающей движение.
Трение на
наклонной плоскости
Рассмотрим случай, когда
на тело, находящееся на наклонной плоскости с углом l к горизонту, действует одна сила,
перпендикулярная основанию плоскости (рис 16.5), например сила веса.

Рис. 16.5
В этом случае возможно
движение только вниз при соблюдении условия  . При
. При 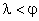 под действием силы, перпендикулярной
основанию плоскости, движение, независимо от величины силы, не может ни
возникнуть, ни продолжаться без замедления.
под действием силы, перпендикулярной
основанию плоскости, движение, независимо от величины силы, не может ни
возникнуть, ни продолжаться без замедления.
Плоскость с углом
наклона, меньшим угла трения, называется самотормозящей.
Рассмотрим случай, когда на
тело, находящееся на плоскости, наклоненной под углом l к горизонту, действуют две силы,
одна из которых перпендикулярна основанию плоскости, а другая параллельна. В
этом случае возможно движение тела вверх, или вниз по наклонной плоскости.
1.
Движение тела
вверх по наклонной плоскости (рис. 16.6).
Рис. 16.6
В этом случае
параллельная основанию плоскости сила Р должна быть направлена вправо.
Для возможности движения вверх по плоскости необходимо, чтобы равнодействующая R сил P и Q
составляла угол b с
перпендикуляром к плоскости не меньше угла трения j, т.е. необходимо выполнение условия
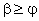 .
.
Из построения следует
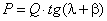 .
.
Из приведенных выше
неравенства и равенства вытекает следующее условие для возможности движения тела
вверх по наклонной плоскости:
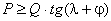 .
.
2.
Движение тела
вниз по наклонной плоскости (рис. 16.7).
В этом случае из
построения следует
и, следовательно,
движения тела вниз по наклонной плоскости оказывается при  возможным при соблюдении условия
возможным при соблюдении условия
 .
.
Рис. 16.7
На рис. 16.7 сила Р
направлена вправо и является силой, противодействующей движению. Необходимость
в силе Р, направленной влево (рис. 16.8), для движения тела вниз будет
только в том случае, если под действием только одной силы Q движение не будет происходить
(самотормозящая плоскость).
Из построения (рис. 16.8)
получаем
При  необходимая для движения сила Р должна
удовлетворять условию
необходимая для движения сила Р должна
удовлетворять условию
 .
.
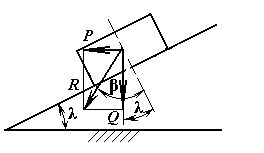
Рис. 16.8
Трение
клинчатого ползуна
На рис. 16.9 изображён
клинчатый ползун, имеющий в поперечном сечении форму трапеции, который
прижимается силой Q
к двум поверхностям трения, наклоненным каждая к линии действия силы Q под углом g. При движении клинчатого ползуна в
направлении, перпендикулярном к плоскости чертежа, величина силы трения:
 .
.
Приняв во внимание, что
сумма проекций сил на вертикаль равна нулю, получаем
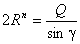 .
.
Введя обозначение 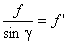 , получаем
, получаем
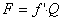 ,
,
где величина f¢ называется фиктивным или приведённым
коэффициентом трения.
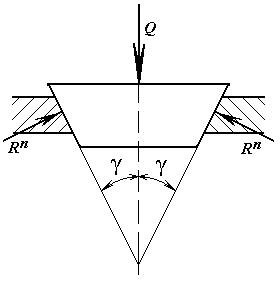
Рис. 16.9
Трение во
вращательных парах
Вращательная
кинематическая пара образуется цапфой (опорной частью вала) и охватывающим её
подшипником.
Для того чтобы цапфа,
находящаяся под действием нескольких приложенных к ней сил, могла вращаться,
необходимо, чтобы равнодействующая Р этих сил (рис. 16.10) создавала
момент не меньший момента силы трения.
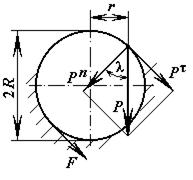
Рис. 16.10
Разложив силу Р на
нормальную Рn и тангенциальную Рt составляющие и обозначив через: r плечо действия силы Р относительно оси
вращения цапфы; R – радиус
цапфы; l - угол между линией действия силы Р
и радиусом, проведённым в точку приложения силы P, получим:
момент, вращающий цапфу,
равен
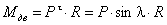 ;
;
момент силы F трения равен
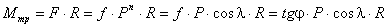 .
.
Для возможности движения
необходимо соблюдение условия
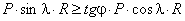 ,
,
откуда
 ,
,
и поэтому
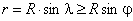 .
.
Следовательно, момент
силы Р не может вращать цапфы, если линия действия силы Р
проходит внутри круга с радиусом 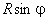 .
.
Такой круг получил
название – круга трения.
Трение в
пятах (трение верчения)
Трение в пятах имеет
место на поверхности соприкосновения двух прижатых одно к другому тел,
вращающихся одно относительно другого вокруг нормали к поверхности
соприкосновения (рис. 16.11, а).
Рис. 16.11
При учете сопротивления,
оказываемого силами трения моменту, вращающему одно тело относительно другого,
приходится определять равнодействующий момент сил трения, заменяя элементарные
силы трения на всей поверхности трения равнодействующей силой, приложенной на
окружности с радиусом R.
Определим величину радиуса R,
предположив, что поверхность трения представляет собой кольцевую площадь с
внешним радиусом r1 и внутренним радиусом r2 и что вращение происходит вокруг общего центра
окружностей (рис. 16.11, б).
Полная сила трения
скольжения равна:
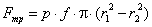 ,
,
где р – давление на
поверхности трения, т.е. сила, приходящаяся на единицу поверхности трения; 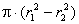 - площадь поверхности соприкосновения.
- площадь поверхности соприкосновения.
Момент полной силы трения
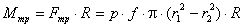 ,
,
где R – радиус окружности, на которой
приложена равнодействующая элементарных сил трения.
Элементарная сила трения,
распределённая по кольцу с площадью  , равна
, равна
 .
.
Момент элементарной силы
трения равен
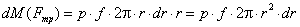 .
.
Суммарный момент
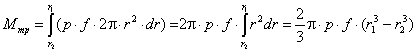 .
.
Тогда приравнивая правые
половины уравнений, получаем равенство
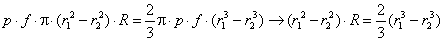 ,
,
откуда
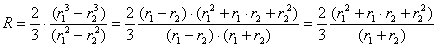 .
.
При r2 = 0, получаем 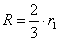 .
.
Контрольные
вопросы
44.
Что такое трение,
и от чего оно зависит.
45.
Трение
скольжения: сила, угол и конус трения.
46.
Трение на
горизонтальной плоскости.
47.
Трение на
наклонной плоскости.
48.
Трение клинчатого
ползуна, приведенный коэффициент трения.
49.
Трение во
вращательных парах.
50.
Трение в пятах.
Лекция
17
Трение гибких тел. Трение
качения. Коэффициент полезного действия механизмов: общие сведения, КПД при
последовательном и параллельном соединении звеньев, КПД винтовой передачи.
Трение
гибких тел
Рассмотрим идеально
гибкое и нерастяжимое тело, т.е. тело, совершенно не деформирующееся под
действием растягивающей силы и не оказывающее никакого сопротивления при его
перегибе, которое огибает неподвижный цилиндр. Охват цилиндра происходит по
дуге ab с центральным углом a (рис. 17.1). На тело действуют силы S1 и S2, для
движения его по цилиндру с равномерной скоростью необходимо соблюдение условия
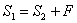 ,
,
где F – сила трения между гибким телом и цилиндром.
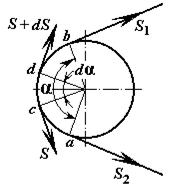
Рис. 17.1
Так как сила трения
распределена на дуге ab
соприкосновения гибкого тела с цилиндром, то натяжение гибкого тела от точки a набегания его на цилиндр до точки b сбегания его с цилиндра возрастает
по некоторому закону от S2 до S1. В точке с бесконечно малой дуги cd натяжение достигает некоторой
величины S, в точке d натяжение увеличивается до S + dS.
Бесконечно малая сила
трения на дуге cd,
обуславливающая увеличение натяжения на величину dS и поэтому равная dS, может быть выражена следующим образом:
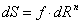 ,
,
где f – коэффициент трения; dRn – бесконечно малая сила, нормальная
к поверхности трения.
Величина силы dRn создается проекциями натяжений S и S + dS
на радиус, проведенный в середину дуги cd:
 .
.
Так как  и
и  , как
член высшего порядка малости, то
, как
член высшего порядка малости, то
 ;
;
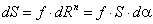 .
.
Разделив, получаем
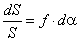 .
.
Интегрируя, а затем,
дифференцируя, получаем
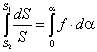 ;
;
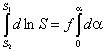 ;
;
 ;
;
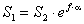 .
.
Зависимость между силой S1, движущей идеально гибкое и нерастяжимое тело, охватывающее
цилиндр, и силой S2, сопротивляющейся движению была
получена Л. Эйлером.
На основании формулы
Эйлера сила трения на поверхности соприкосновения гибкого тела и охватываемого
им цилиндра равна
 .
.
Анализируя формулу,
видим, что величина силы трения в значительной степени зависит и от
коэффициента трения и от угла охвата: при f = 0,35 обмотав гибкое тело вокруг цилиндра на два
полных оборота (a =
4p), силой 10 Н, можно уравновесить
силу 800 Н.
Трение
качения
При перекатывании одного тела,
имеющего криволинейную поверхность, по другому телу с плоской или криволинейной
поверхностью возникает сопротивление, которое называется трением второго рода
или трением качения. Сопротивление перекатыванию зависит от упругих свойств
материалов соприкасающихся тел, кривизны их поверхностей и величины нормальной
силы, действующей между телами.
Пусть на плоскости лежит цилиндр, вес
которого G (рис. 17.2, а). Так как цилиндр
и плоскость не являются абсолютно твёрдыми телами, то в зоне их соприкосновения
под действием силы G
образуется некоторая площадка смятия АВ. Согласно теории упругости
Герца, в зоне площадки смятия напряжения распределяются по эллиптическому
закону. Равнодействующая этих напряжений Rn будет равна по величине и
противоположна по направлению силе G и действует по одной линии с нею.
Рис. 17.2
Если цилиндр не будет находиться в
статическом состоянии, то закон распределения напряжений изменится: на участке СВ
контактной площадки напряжения будут больше, нежели на участке АС (рис.
17.2, б). Участок СВ называется зоной нарастающих деформаций, а
участок АС – зоной исчезающих деформаций. Зона исчезающих деформаций является
результатом гистерезиса, т.е. сохранения части деформаций и после того, как
исчезла причина, вызвавшая эту деформацию.
Равнодействующая напряжений всей
контактной площадки, равная внешней нагрузке G, будет смещена за вертикальную ось симметрии цилиндра
на некоторую величину k.
Эту величину называют коэффициентом трения качения.
Для перекатывания тела необходимо
преодолеть момент трения равный:
 .
.
Если на цилиндр действует внешняя
сдвигающая горизонтальная сила Р, приложенная по центру цилиндра, то для
преодоления момента трения необходимо приложить момент
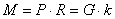 ,
,
откуда внешняя сдвигающая
сила
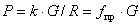 .
.
Отношение k/R можно рассматривать как приведенный коэффициент трения
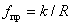 .
.
Если между телами
сцепление недостаточно, то возможно появление скольжения
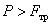 .,
т.е.
.,
т.е. 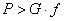 или
или 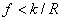 .
.
Таким образом, при 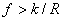 тело будет катиться без скольжения, в
противном случае тело будет скользить без качения. При
тело будет катиться без скольжения, в
противном случае тело будет скользить без качения. При 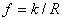 будет
одинаковая возможность и качения и скольжения.
будет
одинаковая возможность и качения и скольжения.
Коэффициент
полезного действия механизмов
Коэффициентом
полезного действия или КПД механической системы называют отношение работы сил полезного
сопротивления к работе движущих сил.
КПД механизма
характеризует его эффективность при преобразовании энергии, определяет
соотношение полученной на выходе полезной энергии и энергетических потерь в
механизме на трение, перемешивание масла, вентиляцию, деформацию звеньев и др.
Величину КПД можно рассчитать по следующей зависимости:
|
Апот
Ý

Мд    .с. Механическая Мп.с. .с. Механическая Мп.с.
  Ai система Aj Ai система Aj
с КПД < 1
wI iij w j
Рис. 17.3
|
 ,
,
где Ai - работа движущих сил; Aj - работа сил полезного сопротивления;
Aj - работа сил вредных сопротивлений
(потерянная); h - коэффициент полезного действия, y - коэффициент потерь.
Если при установившемся
движении силы или моменты сил приложены к одному и тому же звену, или звену
приведения (многозвенные механизмы), то КПД можно вычислять как:
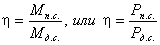 ,
,
где Мд.с.
и Мп.с. – соответственно моменты движущих сил и
сил полезных сопротивлений; Рд.с. и Рп.с.
– соответственно силы движущие и силы полезных сопротивлений.
Если вычисляется КПД за
бесконечно малый промежуток времени (мгновенный КПД) берётся соотношение
мощностей:
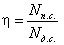 .
.
При обследовании машины
состоящей из нескольких механизмов, в которых происходит потеря энергии,
является целесообразным определение КПД как всей машины, так и отдельных
механизмов.
КПД
механической системы с последовательным соединением механизмов
Рассмотрим машину,
состоящую из n
последовательно соединенных механизмов (рис. 17.4), при этом поток мощности
проходит последовательно через каждый механизм. Пусть КПД отдельных механизмов h1, h2 и hn.
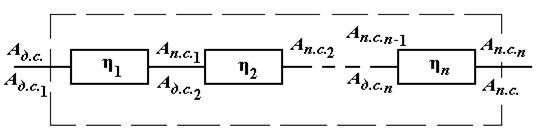
Рис. 17.4
Обозначив соответственно
работы сил движущих и полезных сопротивлений отдельных механизмов получим:
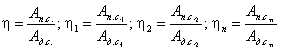 .
.
При этом 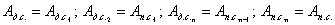 .
.
Перемножая, левые и
правые части и произведя сокращения, получим
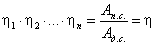 .
.
Анализируя формулу
устанавливаем, что КПД всей машины меньше меньшего из значений КПД входящих
механизмов.
КПД
механической системы с параллельным соединением механизмов
При параллельном
соединении механизмов поток мощности делится на несколько частей проходящих
через отдельные механизмы. Рассмотрим КПД роликового конвейера (рольганга) рис.
17.5.
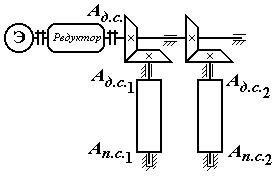
Рис. 17.5
Пусть КПД приводных
роликов h1 и h2, работа
движущих сил на приводном валу с учетом потерь в редукторе Ад.с..
Часть работы Ад.с.1 идет на преодоление Ап.с.1,
а другая часть Ад.с.2 на преодоление Ап.с.2.
Очевидно, что
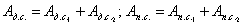 .
.
Тогда
 .
.
Выразим
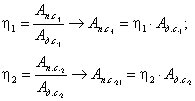
Подставляя в выражение для общего
КПД, получаем
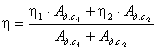 .
.
Рассмотрим частные случаи:
1.
При h1 = h2:
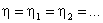
2.
При 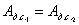 :
:
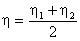 ,
,
т.е. общий КПД равен
среднему арифметическому частных КПД.
3.
При 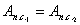 :
:
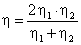 .
.
Параллельное соединение
позволяет получить более высокие значения КПД чем последовательное.
КПД
винтовой передачи
При определении величины
КПД винтовой передачи предполагается, что развернутая винтовая поверхность
гайки представляет собой наклонную плоскость (l - угол подъёма винтовой линии резьбы) с винтом в виде
груза на наклонной плоскости или, наоборот (рис. 17.6).
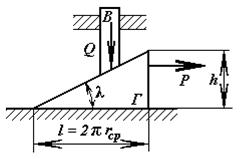
Рис. 17.6
Тело совершает
поступательное движение. Полезную работу совершает сила Q. За один полный оборот винта
перемещение составит h,
тогда работа:
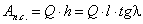 .
.
Работа движущей силы 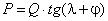 составит
составит
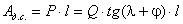 .
.
Тогда КПД можно
определить как
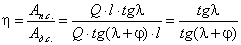 .
.
По данной формуле
определяется КПД винтовой передачи с прямоугольной резьбой, в случае
остроугольной резьбы вместо j следует подставлять приведенный угол трения j¢.
Контрольные
вопросы
51.
Трение гибких
тел. Формула Эйлера.
52.
Трение качения.
53.
КПД механизмов.
54.
КПД механической
системы с последовательным соединением механизмов.
55.
КПД механической
системы с параллельным соединением механизмов.
56.
КПД винтовой
передачи.