Расчет выборочного коэффициента корреляции
Министерство
образования и науки Российской Федерации
Федеральное
государственное бюджетное образовательное учреждение
Высшего
профессионального образования
"Уфимский
государственный нефтяной технический университет"
Кафедра
математики
Лабораторная
работа №2
По
дисциплине "Корреляционный и регрессионный анализ"
Выполнил:
студент гр. БЭГ-12-01 Зиннатуллина
Г.Ф.
Проверил:
старший преподаватель кафедры
Янтудин М.Н.
Уфа 2014
Цель работы: Используя уравнение регрессии, оценить среднее количество окиси
железа (X) в руде, содержащей 25% закиси железа (Y). Выявить силу корреляции У на Х.
Ход работы:
В таблице дано распределение 100
проб руды, добытой на руднике, по содержанию окиси X (%) и закиси железа Y (%)
Таблица 1 - Исходная таблица
|
x
|
y
|
|
65
|
95
|
125
|
155
|
185
|
215
|
mx
|
|
45
|
|
|
1
|
6
|
4
|
6
|
17
|
|
55
|
|
|
2
|
18
|
10
|
2
|
32
|
|
65
|
|
6
|
14
|
2
|
2
|
|
24
|
|
75
|
4
|
8
|
|
|
|
|
12
|
|
95
|
6
|
|
|
|
|
|
6
|
|
my
|
10
|
14
|
17
|
26
|
16
|
8
|
91
|
В случае параболической корреляции
второго порядка выборочное уравнение регрессии У на Х имеет вид:
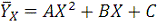
Неизвестные параметры А, В и С
находятся из системы уравнений:
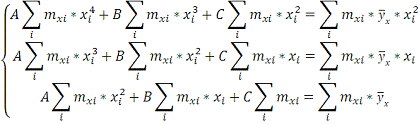
Для решения этой системы, составим
таблицу вспомогательных данных:
Таблица 2 - Вспомогательные данные
|
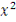
|
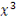
|
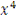
|
mx*x
|
mx*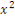 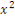 mx* mx*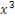 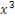 mx* mx*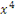 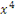 mx* mx*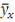 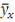 mx*x* mx*x*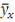 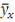 mx* mx*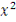 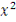 * *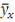 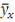
|
|
|
|
|
|
|
2025
|
4100625
|
765
|
34425
|
1549125
|
69710625
|
3085
|
138825
|
6247125
|
|
3025
|
166375
|
9150625
|
1760
|
96800
|
5324000
|
292820000
|
5320
|
292600
|
16093000
|
|
4225
|
274625
|
17850625
|
1560
|
101400
|
6591000
|
428415000
|
3000
|
195000
|
12675000
|
|
5625
|
421875
|
31640625
|
900
|
67500
|
5062500
|
379687500
|
1020
|
76500
|
5737500
|
|
9025
|
857375
|
81450625
|
570
|
54150
|
5144250
|
488703750
|
390
|
37050
|
3519750
|
|
∑23925
|
1811375
|
144193125
|
5555
|
354275
|
23670875
|
1659336875
|
12815
|
739975
|
44272375
|
выборочный коэффициент корреляция
регрессия
Подставив найденные коэффициенты в
уравнение регрессии найдем f (x)
Таблица 3 - вспомогательные данные
|
x
|
45
|
55
|
65
|
75
|
85
|
95
|
|
f (x)
|
190,660
|
126,292
|
99,336
|
75,866
|
55,882
|
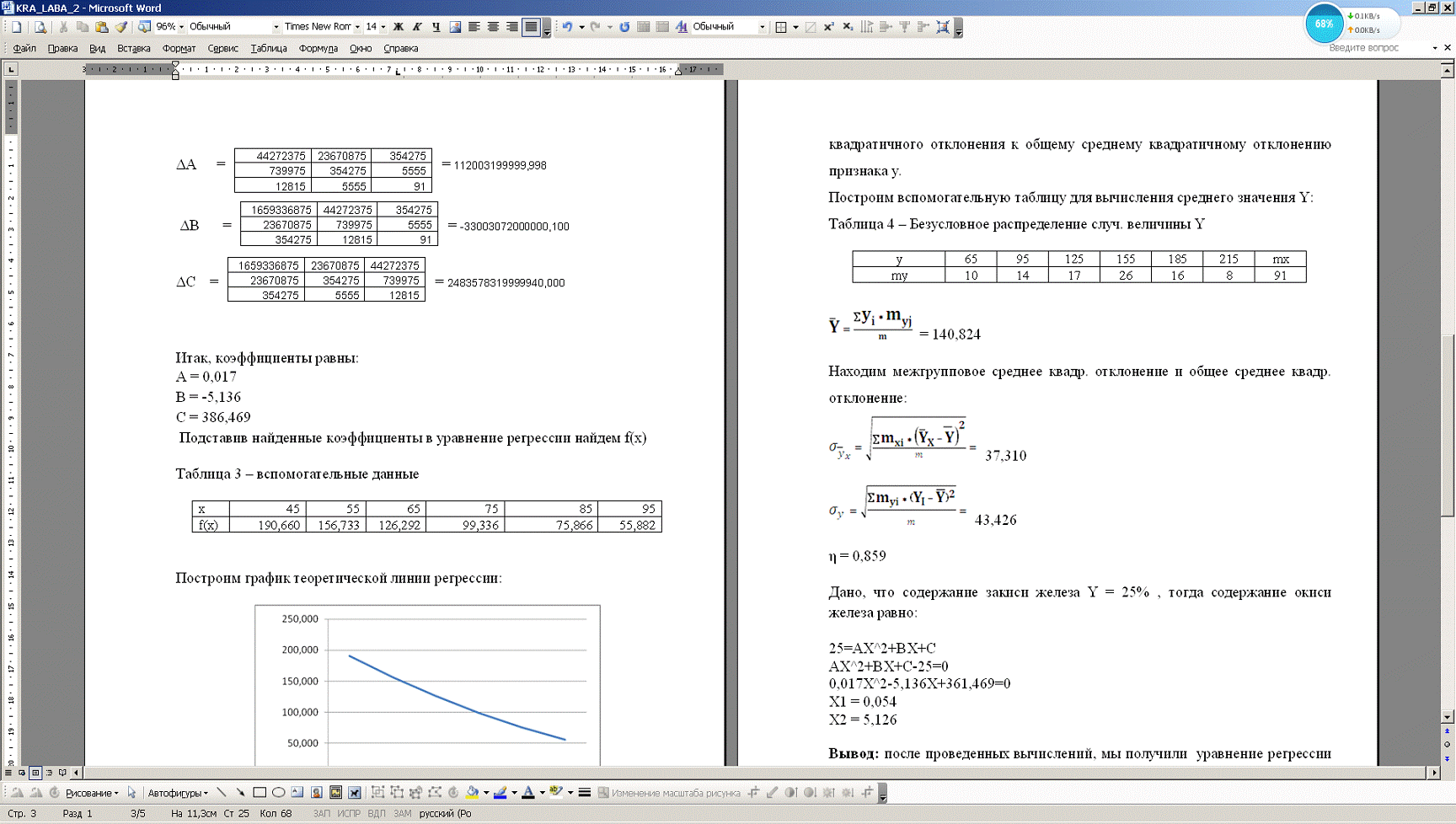
Построим график теоретической линии
регрессии:
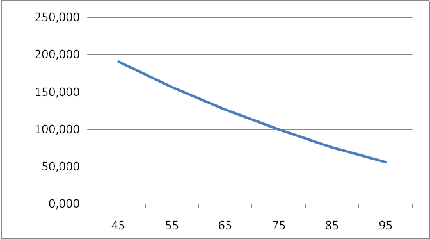
График 1 - Теоретическая линия
регрессии
Для определения силы корреляции У на
Х служат выборочное корреляционное отношение, то есть отношение межгруппового
среднего квадратичного отклонения к общему среднему квадратичному отклонению
признака у.
Построим вспомогательную таблицу для
вычисления среднего значения Y:
Таблица 4 - Безусловное
распределение случ. величины Y
|
y
|
65
|
95
|
125
|
155
|
185
|
215
|
mx
|
|
my
|
10
|
14
|
17
|
26
|
16
|
8
|
91
|
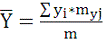
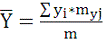 = 140,824
= 140,824
Находим межгрупповое среднее квадр.
отклонение и общее среднее квадр. отклонение:
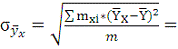
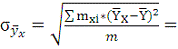 37,310,
37,310, 
 43,426 η
= 0,859
43,426 η
= 0,859
Дано, что содержание
закиси железа Y = 25%, тогда содержание окиси железа равно:
25=AX^2+BX+C^2+BX+C-25=0
0,017X^2-5,136X+361,469=0
X1 = 0,054 X2
= 5,126
Вывод: после
проведенных вычислений, мы получили уравнение регрессии на основе данных
таблицы распределения 100 проб руды, добытой на руднике, по содержанию окиси X (%) железа и закиси железа Y
(%). Выборочное корреляционное отношение равно 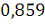
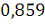 , а значит между
величинами прямая криволинейная зависимость с высокой теснотой связи. После
вычислений выборочного коэффициента корреляции мы подставили заданное значение
количества закиси железа в руде и получили среднее количество окиси железа.
, а значит между
величинами прямая криволинейная зависимость с высокой теснотой связи. После
вычислений выборочного коэффициента корреляции мы подставили заданное значение
количества закиси железа в руде и получили среднее количество окиси железа.