Построение многофакторной модели. Прогнозирование по однофакторной модели

Построение многофакторной модели. Прогнозирование по однофакторной модели

Содержание

1. Построение многофакторной модели

2. Проверка на адекватность однофакторной модели

3. Прогнозирование по однофакторной модели

1. Построение многофакторной модели

 

1.      Построим эконометрическую модель, описывающую линейную зависимость результативного признака факторов, входящих в модель, методом матрицы для х=5:

Таблица 1

№	y	x1	х2	х3	х4	х5
1	36,4	140	96,5	210	393,31	239,57
2	8,7	180	53,8	175	233,21	170,38
3	50,6	122	99,9	199	403,39	290,18
4	29,2	110	130,9	198	429,05	223,86
5	45	159	108,3	273	456,17	217,07
6	64,2	79	179,7	172	531,96	327,12
7	25,6	194	72,5	196	316,63	200,74
8	57,3	86	132,1	204	591,22	282,19
9	47,2	111	121,6	200	499,58	302,78
10	31,2	112	126	205	594,5	289,73
11	68,1	159	201,8	153	311,38	211,81
12	33,9	54	109	317	1019,06	367,02
13	46,6	136	243,6	204	399,6	233,87
14	38,1	85	80,9	190	466,38	280,67
15	40,2	228	103,3	246	349,97	265,82
16	40,6	129	53,9	256	404	230,92
17	3,1	131	104,9	345	663,76	240,78
18	40,8	202	128,8	145	204,32	176,1
19	41,2	119	129,3	175	647,66	234,75
20	58,9	166	137,5	173	379,98	232,79
Сумма	806,9	2702	2414,3	4236	9295,13	5018,15

Таблица 2

	1	140	96,5	210	393,31	239,57
	1	180	53,8	175	233,21	170,38
	1	122	99,9	199	403,39	290,18
	1	110	130,9	198	429,05	223,86
	1	159	108,3	273	456,17	217,07
	1	79	179,7	172	531,96	327,12
	1	194	72,5	196	316,63	200,74
	1	86	132,1	204	591,22	282,19
	1	111	121,6	200	499,58	302,78
х=	1	112	126	205	594,5	289,73
	1	159	201,8	153	311,38	211,81
	1	54	109	317	1019,06	367,02
	1	136	243,6	204	399,6	233,87
	1	85	80,9	190	466,38	280,67
	1	228	103,3	246	349,97	265,82
	1	129	53,9	256	404	230,92
	1	131	104,9	345	663,76	240,78
	1	202	128,8	145	204,32	176,1
	1	119	129,3	175	647,66	234,75
	1	166	137,5	173	379,98	232,79

1) С помощью встроенной функции ТРАНСП в Excel поменяем ориентацию матрицы  с вертикальной на горизонтальную и получим:

Таблица 3

	1	1	1 …	1	1	1
	140	180	122 …	202	119	166
xtransp=	96,5	53,8	99,9 …	128,8	129,3	137,5
	210	175	199 …	145	175	173
	393,31	233,21	403,39 …	204,32	647,66	379,98
	239,57	170,38	290,18 …	176,1	234,75	232,79

2) С помощью встроенной функции МУМНОЖ в Excel перемножим матрицы  и  и получим:

Таблица 4

	20	2702	2414,3	4236	9295,13	5018,15
	2702	402628	320687	563160	1141123,81	647110,16
xtransp*x=	2414,3	320687	331996,01	498246,5	1127519,362	610656,796
	4236	563160	498246,5	947970	2077152,77	1078837,31	1141123,81	1127519,362	2077152,77	4944264,166	2460939,457
	5018,15	647110,16	610656,796	1078837,31	2460939,457	1305721,952

3) С помощью встроенной функции МОБР в Excel рассчитаем обратную матрицу для произведения  и получим:

Таблица 5

	7,760865706	-0,01929076	-0,004519555	-0,002478441	-0,000812058	-0,014574148
	-0,01929076	8,67776E-05	-1,32303E-06	-2,52389E-05	1,55151E-05	2,33619E-05
mobr=	-0,004519555	-1,32303E-06	2,9194E-05	1,29169E-05	-2,35996E-06	-1,8527E-06
	-0,002478441	-2,52389E-05	1,29169E-05	4,61355E-05	-1,34117E-05	3,15113E-06
	-0,000812058	1,55151E-05	-2,35996E-06	-1,34117E-05	8,55586E-06	-8,50884E-06
	-0,014574148	2,33619E-05	-1,8527E-06	3,15113E-06	-8,50884E-06	5,94989E-05

4) С помощью встроенной функции МУМНОЖ в Excel перемножим  и матрицу  и получим:

Таблица 6

	806,9
	106867,3
	105583,04
xtransp*y	163466,7
	370146,967
	206664,704

5) С помощью встроенной функции МУМНОЖ в Excel перемножим матрицы и () и получим:

Таблица 7

	5,817485316
	0,01350837
0,149241371
	-0,104726657
	-0,030290777
	0,203046155

Отсюда =, =, =, =, = =.

;

;

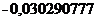
806,9=806,9.

6)      Определим дисперсионно-ковариационную матрицу:

Найдем оценку дисперсии случайной величины при =6:

Рассчитаем дисперсионно-ковариационную матрицу:

Таблица 8

	764,1763868	-1,899471543	-0,445019604	-0,244040522	-0,079959565	-1,435048622
	-1,899471543	0,008544583	-0,000130272	-0,002485158	0,001527698	0,002300342
	-0,445019604	-0,000130272	0,002874593	0,001271871	-0,000232374	-0,000182426
Varcov(b)=	-0,244040522	-0,002485158	0,001271871	0,004542748	-0,001320591	0,000310277
	-0,079959565	0,001527698	-0,000232374	-0,001320591	0,000842456	-0,000837826
	-1,435048622	0,002300342	-0,000182426	0,000310277	-0,000837826	0,005858583

) Проверим достоверность эконометрической модели и статистическую значимость её параметров:

ytransp=

36,4

8,7

50,6

29,2

45

… 40,6

3,1

40,8

41,2

58,9

Коэффициент корреляции принимает значение: 0£r_xy£1 и r_xy ®+1 (r_xy), следовательно, корреляционная связь между переменными прямая и сильная.

8)      Проверим достоверность эконометрической модели по критерию Фишера:

В Excel вычисление  осуществляется функцией FРАСПОБР. Ее первым аргументом нужно задать значение a, в нашем случае a=1% (этот аргумент называется «Вероятность»), другим аргументом задается единица (=1), а третьим значением = n- k =14:

.

Так как выполняется условие >, то Н₀ - гипотеза о случайной природе оцениваемых характеристик не отклоняется и признается статистическая незначимость и ненадёжность уравнения регрессии.

) Проверим значимость коэффициента корреляции с помощью t-критерия Стьюдента:

В Excel  вычисляем функцией СТЬЮДРАСПОБР. Ее первым аргументом нужно задать значение a, в нашем случае a=1% (этот аргумент называется «Вероятность»), вторым аргументом задается n- k =14, получим:

.

Так как выполняется условие <, можно сказать, что эконометрическая модель адекватна и достоверна.

10)    Определим t-статику для каждого параметра модели:

 

- min

.

2.      Построим эконометрическую модель, описывающую линейную зависимость результативного признака факторов, входящих в модель, методом матрицы для х=4:

эконометрический матрица дисперсия корреляция

Таблица 9

№	y	x1	x2	x3	x4
1	36,4	140	96,5	393,31	239,57
2	8,7	180	53,8	233,21	170,38
3	50,6	122	99,9	403,39	290,18
4	29,2	110	130,9	429,05	223,86
5	45	159	108,3	456,17	217,07
6	64,2	79	179,7	531,96	327,12
7	25,6	194	72,5	316,63	200,74
8	57,3	86	132,1	591,22	282,19
9	47,2	111	121,6	499,58	302,78
10	31,2	112	126	594,5	289,73
11	68,1	159	201,8	311,38	211,81
12	33,9	54	109	1019,06	367,02
13	46,6	136	243,6	399,6	233,87
14	38,1	85	80,9	466,38	280,67
15	40,2	228	103,3	349,97	265,82
16	40,6	129	53,9	404	230,92
17	3,1	131	104,9	663,76	240,78
18	40,8	202	128,8	204,32	176,1
19	41,2	119	129,3	647,66	234,75
20	58,9	166	137,5	379,98	232,79
Сумма	806,9	2702	2414,3	9295,13	5018,15

Таблица 10

	1	140	96,5	393,31	239,57
	1	180	53,8	233,21	170,38
	1	122	99,9	403,39	290,18
	1	110	130,9	429,05	223,86
	1	159	108,3	456,17	217,07
	1	79	179,7	531,96	327,12
	1	194	72,5	316,63	200,74
	1	86	132,1	591,22	282,19
	1	111	121,6	499,58	302,78
x=	1	112	126	594,5	289,73
	1	159	201,8	311,38	211,81
	1	54	109	1019,06	367,02
	1	136	243,6	399,6	233,87	85	80,9	466,38	280,67
	1	228	103,3	349,97	265,82
	1	129	53,9	404	230,92
	1	131	104,9	663,76	240,78
	1	202	128,8	204,32	176,1
	1	119	129,3	647,66	234,75
	1	166	137,5	379,98	232,79

1) С помощью встроенной функции ТРАНСП в Excel поменяем ориентацию матрицы  с вертикальной на горизонтальную и получим:

Таблица 11

	1	1	1	… 1	1	1
	140	180	122	… 202	119	166
xtransp=	96,5	53,8	99,9	… 128,8	129,3	137,5
	393,31	233,21	403,39	… 204,32	647,66	379,98
	239,57	170,38	290,18	… 176,1	234,75	232,79

2) С помощью встроенной функции МУМНОЖ в Excel перемножим матрицы  и  и получим:

Таблица 12

	20	2702	2414,3	9295,13	5018,15
	2702	402628	320687	1141123,81	647110,16
xtransp*x=	2414,3	320687	331996,01	1127519,362	610656,796
	9295,13	1141123,81	1127519,362	4944264,166	2460939,457
	5018,15	647110,16	610656,796	2460939,457	1305721,952

3) С помощью встроенной функции МОБР в Excel рассчитаем обратную матрицу для произведения  и получим:

Таблица 13

	7,627721633	-0,020646617	-0,003825645	-0,001532549	-0,014404866
	-0,020646617	7,29703E-05	5,74332E-06	8,17805E-06	2,50858E-05
mobr=	-0,003825645	5,74332E-06	2,55775E-05	1,39504E-06	-2,73495E-06
	-0,001532549	8,17805E-06	1,39504E-06	4,65702E-06	-7,5928E-06
	-0,014404866	2,50858E-05	-2,73495E-06	-7,5928E-06	5,92837E-05

4) С помощью встроенной функции МУМНОЖ в Excel перемножим  и матрицу  и получим:

Таблица 14

	806,9
	106867,3
xtransp*y=	105583,04
	370146,967
	206664,704

5) С помощью встроенной функции МУМНОЖ в Excel перемножим матрицы и () и получим:

Таблица 15

	0,191474306
	-0,043783448
0,178562573
	-0,060735154
	0,210199161

Отсюда =, =, =, =, =.

;

;

806,9=806,9.

6)      Определим дисперсионно-ковариационную матрицу:

Найдем оценку дисперсии случайной величины при =5:

Рассчитаем дисперсионно-ковариационную матрицу:

Таблица 16

	1183,331435	-3,203026075	-0,593493928	-0,237752887	-2,234708055
	-3,203026075	0,011320301	0,000890994	0,001268707	0,003891702
Varcov(b)=	-0,593493928	0,000890994	0,00396798	0,000216421	-0,000424288
	-0,237752887	0,001268707	0,000216421	0,00072247	-0,001177914
	-2,234708055	0,003891702	-0,000424288	-0,001177914	0,009197015

7) Проверим достоверность эконометрической модели и статистическую значимость её параметров:

ytransp=

36,4

8,7

50,6

29,2

45

… 40,6

3,1

40,8

41,2

58,9

Коэффициент корреляции принимает значение: 0£r_xy£1 и r_xy ®+1 (r_xy), следовательно, корреляционная связь между переменными прямая и сильная.

8) Проверим достоверность эконометрической модели по критерию Фишера:

В Excel вычисление  осуществляется функцией FРАСПОБР. Ее первым аргументом нужно задать значение a, в нашем случае a=1% (этот аргумент называется «Вероятность»), другим аргументом задается единица (=1), а третьим значением = n- k =15:

.

Так как выполняется условие >, то Н₀ - гипотеза о случайной природе оцениваемых характеристик не отклоняется и признается статистическая незначимость и ненадёжность уравнения регрессии.

) Проверим значимость коэффициента корреляции с помощью t-критерия Стьюдента:

В Excel  вычисляем функцией СТЬЮДРАСПОБР. Ее первым аргументом нужно задать значение a, в нашем случае a=1% (этот аргумент называется «Вероятность»), вторым аргументом задается n- k =15, получим:

.

Так как выполняется условие <, можно сказать, что эконометрическая модель адекватна и достоверна.

10)    Определим t-статику для каждого параметра модели:

 

- min

.

3.      Построим эконометрическую модель, описывающую линейную зависимость результативного признака факторов, входящих в модель, методом матрицы для х=3:

Таблица 17

№	y	x1	x2	x3
1	36,4	140	96,5	239,57
2	8,7	180	53,8	170,38
3	50,6	122	99,9	290,18
4	29,2	110	130,9	223,86
5	45	159	108,3	217,07
6	64,2	79	179,7	327,12
7	25,6	194	72,5	200,74
8	57,3	86	132,1	282,19
9	47,2	111	121,6	302,78
10	31,2	112	126	289,73
11	68,1	159	201,8	211,81
12	33,9	54	109	367,02
13	46,6	136	243,6	233,87
14	38,1	85	80,9	280,67
15	40,2	228	103,3	265,82
16	40,6	129	53,9	230,92
17	3,1	131	104,9	240,78
18	40,8	202	128,8	176,1
19	41,2	119	129,3	234,75
20	58,9	166	137,5	232,79
Сумма	806,9	2702	2414,3	5018,15

Таблица 18

	1	140	96,5	239,57
	1	180	53,8	170,38
	1	122	99,9	290,18
	1	110	130,9	223,86
	1	159	108,3	217,07
	1	79	179,7	327,12
	1	194	72,5	200,74
	1	86	282,19
	1	111	121,6	302,78
x=	1	112	126	289,73
	1	159	201,8	211,81
	1	54	109	367,02
	1	136	243,6	233,87
	1	85	80,9	280,67
	1	228	103,3	265,82
	1	129	53,9	230,92
	1	131	104,9	240,78
	1	202	128,8	176,1
	1	119	129,3	234,75
	1	166	137,5	232,79

1) С помощью встроенной функции ТРАНСП в Excel поменяем ориентацию матрицы  с вертикальной на горизонтальную и получим:

Таблица 19

	1	1	1	… 1	1	1	1
xtransp=	140	180	122	… 131	202	119	166
	96,5	53,8	99,9	… 104,9	128,8	129,3	137,5
	239,57	170,38	290,18	… 240,78	176,1	234,75	232,79

2) С помощью встроенной функции МУМНОЖ в Excel перемножим матрицы  и  и получим:

Таблица 20

	20	2702	2414,3	5018,15
xtransp*x=	2702	402628	320687	647110,16
	2414,3	320687	331996,01	610656,796
	5018,15	647110,16	610656,796	1305721,952

3) С помощью встроенной функции МОБР в Excel рассчитаем обратную матрицу для произведения  и получим:

Таблица 21

	7,123385552	-0,017955358	-0,003366561	-0,016903529
mobr=	-0,017955358	5,86091E-05	3,29353E-06	3,84193E-05
	-0,003366561	3,29353E-06	2,51596E-05	-4,60475E-07
	-0,016903529	3,84193E-05	-4,60475E-07	4,69044E-05

4) С помощью встроенной функции МУМНОЖ в Excel перемножим  и матрицу  и получим:

Таблица 22

	806,9
xtransp*y=	106867,3
	105583,04
	206664,704

5) С помощью встроенной функции МУМНОЖ в Excel перемножим матрицы и () и получим:

Таблица 23

	-19,79544885
0,062871613
	0,196756175
	0,111176718

Отсюда =, =, =, =.

;

;

806,9=806,9.

6)      Определим дисперсионно-ковариационную матрицу:

Найдем оценку дисперсии случайной величины при =4:

Рассчитаем дисперсионно-ковариационную матрицу:

Таблица 24

	1388,668227	-3,500306814	-0,656294103	-3,295258154
	-3,500306814	0,011425557	0,000642058	0,007489645
Varcov(b)=	-0,656294103	0,000642058	0,004904737	-8,97672E-05
	-3,295258154	0,007489645	-8,97672E-05	0,009143782

7) Проверим достоверность эконометрической модели и статистическую значимость её параметров:

ytransp=

36,4

8,7

50,6

29,2

45

… 40,6

3,1

40,8

41,2

58,9

Коэффициент корреляции принимает значение: 0£r_xy£1 и r_xy ®+1 (r_xy), следовательно, корреляционная связь между переменными прямая и сильная.

8) Проверим достоверность эконометрической модели по критерию Фишера:

В Excel вычисление  осуществляется функцией FРАСПОБР. Ее первым аргументом нужно задать значение a, в нашем случае a=1% (этот аргумент называется «Вероятность»), другим аргументом задается единица (=1), а третьим значением = n- k =16:

.

Так как выполняется условие >, то Н₀ - гипотеза о случайной природе оцениваемых характеристик не отклоняется и признается статистическая незначимость и ненадёжность уравнения регрессии.

) Проверим значимость коэффициента корреляции с помощью t-критерия Стьюдента:

В Excel  вычисляем функцией СТЬЮДРАСПОБР. Ее первым аргументом нужно задать значение a, в нашем случае a=1% (этот аргумент называется «Вероятность»), вторым аргументом задается n- k =16, получим:

.

Так как выполняется условие <, можно сказать, что эконометрическая модель адекватна и достоверна.

10)    Определим t-статику для каждого параметра модели:

 - min

.

4.      Построим эконометрическую модель, описывающую линейную зависимость результативного признака факторов, входящих в модель, методом матрицы для х=2:

Таблица 25

№	y	x1	x2
1	36,4	96,5	239,57
2	8,7	53,8	170,38
3	50,6	99,9	290,18
4	29,2	130,9	223,86
5	45	108,3	217,07
6	64,2	179,7	327,12
7	25,6	72,5	200,74
8	57,3	132,1	282,19
9	47,2	121,6	302,78
10	31,2	126	289,73
11	68,1	201,8	211,81
12	33,9	109	367,02
13	46,6	243,6	233,87
14	38,1	80,9	280,67
15	40,2	103,3	265,82
16	40,6	53,9	230,92
17	3,1	104,9	240,78
18	40,8	128,8	176,1
19	41,2	129,3	234,75
20	58,9	137,5	232,79
Сумма	806,9	2414,3	5018,15

Таблица 26

	1	96,5	239,57
	1	53,8	170,38
	1	99,9	290,18
	1	130,9	223,86
	1	108,3	217,07
	1	179,7	327,12
	1	72,5	200,74
	1	132,1	282,19
x=	1	121,6	302,78
	1	126	289,73
	1	201,8	211,81
	1	109	367,02
	1	243,6	233,87
	1	80,9	280,67
	1	103,3	265,82
	1	53,9	230,92
	1	104,9	240,78
	1	128,8	176,1
	1	129,3	234,75
	1	137,5	232,79

1) С помощью встроенной функции ТРАНСП в Excel поменяем ориентацию матрицы  с вертикальной на горизонтальную и получим:

Таблица 27

	1	1	1	… 1	1
xtransp=	96,5	53,8	99,9	… 128,8	129,3	137,5
	239,57	170,38	290,18	… 176,1	234,75	232,79

2) С помощью встроенной функции МУМНОЖ в Excel перемножим матрицы  и  и получим:

Таблица 28

	20	2414,3	5018,15
xtransp*x=	2414,3	331996,01	610656,796
	5018,15	610656,796	1305721,952

3) С помощью встроенной функции МОБР в Excel рассчитаем обратную матрицу для произведения  и получим:

Таблица 29

	1,622624089	-0,002357561	-0,00513349
mobr=	-0,002357561	2,49745E-05	-2,61944E-06
	-0,00513349	-2,61944E-06	2,17199E-05

4) С помощью встроенной функции МУМНОЖ в Excel перемножим  и матрицу  и получим:

Таблица 30

	806,9
xtransp*y=	105583,04
	206664,704

5) С помощью встроенной функции МУМНОЖ в Excel перемножим матрицы и () и получим:

Таблица 31

	-0,534248505
0,193223111
	0,069963316

Отсюда =, =, =.

;

;

806,9=806,9.

7)      Определим дисперсионно-ковариационную матрицу:

Найдем оценку дисперсии случайной величины при =3:

Рассчитаем дисперсионно-ковариационную матрицу:

Таблица 32

	304,1526491	-0,441912883	-0,962246601
Varcov(b)=	-0,441912883	0,004681346	-0,000491001
	-0,962246601	-0,000491001	0,004071292

7) Проверим достоверность эконометрической модели и статистическую значимость её параметров:

Таблица 33

ytransp=

36,4

8,7

50,6

29,2

45

… 40,6

3,1

40,8

41,2

58,9

Коэффициент корреляции принимает значение: 0£r_xy£1 и r_xy ®+1 (r_xy), следовательно, корреляционная связь между переменными прямая и сильная.

8) Проверим достоверность эконометрической модели по критерию Фишера:

В Excel вычисление  осуществляется функцией FРАСПОБР. Ее первым аргументом нужно задать значение a, в нашем случае a=1% (этот аргумент называется «Вероятность»), другим аргументом задается единица (=1), а третьим значением = n- k =17:

.

Так как выполняется условие >, то Н₀ - гипотеза о случайной природе оцениваемых характеристик не отклоняется и признается статистическая незначимость и ненадёжность уравнения регрессии.

) Проверим значимость коэффициента корреляции с помощью t-критерия Стьюдента:

В Excel  вычисляем функцией СТЬЮДРАСПОБР. Ее первым аргументом нужно задать значение a, в нашем случае a=1% (этот аргумент называется «Вероятность»), вторым аргументом задается n- k =17, получим:

.

Так как выполняется условие <, можно сказать, что эконометрическая модель адекватна и достоверна.

11)    Определим t-статику для каждого параметра модели:

 

 - min.

Далее определим интервальные оценки для каждого параметра и сделаем прогноз эконометрических показателей по однофакторной модели.

2. Проверка на адекватность однофакторной модели

1.      Используя данные, вычислим для линейной регрессионной модели:

1)  Дисперсию с помощью встроенной функции ДИСП в Excel:

s²_х⁼var(x)=, s²_у=var(y)=.

2)  Ковариацию с помощью встроенной функции КОВАР в Excel:

cov(x,y)=.

3)  Коэффициент корреляции с помощью встроенной функции КОРРЕЛ в Excel:

r_xy==.

Коэффициент корреляции принимает значение: 0£r_xy£1 и r_xy ®+1 (r_xy), следовательно, корреляционная связь между переменными прямая и сильная.

4)  Коэффициент детерминации по формуле:

.

Так как  стремиться больше к 0, чем к 1, то это означает, что регрессия имеет плохую подгонку, т.е. чем ближе  к 0, тем больше количество ошибок.

. Проверим адекватность эконометрической модели по критерию Фишера:

Для этого проведем сравнение фактического  и табличного значений F-критерия Фишера.  определяется по формуле:

,

где n - число единиц совокупности,

m - число параметров при переменных х.

В Excel вычисление  осуществляется функцией FРАСПОБР. Ее первым аргументом нужно задать значение a, в нашем случае a=1 (этот аргумент называется «Вероятность»), другим аргументом задается единица, а третьим значение =n- 2=18.

Так как выполняется условие <, то Н₀ - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается статистическая незначимость и ненадёжность уравнения регрессии.

. Применим тест Стьюдента для проверки на значимость параметров выборочной регрессионной модели (b₀ и b₁):

T_{факт b0}=t₀=;

T_{факт b1}=t₁=.

В Excel  вычисляем функцией СТЬЮДРАСПОБР. Ее первым аргументом нужно задать значение a, в нашем случае a=1% (этот аргумент называется «Вероятность»), вторым аргументом задается n- 2 =18, получим:

.

. Построим интервалы доверия для параметров классической регрессионной модели (b₀ и b₁) применив тест Стьюдента.

Определим интервалы доверия для параметров обобщенной регрессионной модели  и :

;

∆ .

Для расчета доверительного интервала для каждого показателя определим предельную ошибку :

;

.

Тогда доверительные интервалы примут вид:

0 41,35611191;

,0048697880,398451697.

3. Прогнозирование по однофакторной модели

1.      Построим по модели простой линейной регрессии точечный прогноз и предсказание:

;

;

.

2.      Определим интервалы доверия для прогнозного и среднего значения зависимой переменной:

;

; ;

;

; .

.        Определим интервалы доверия для математического ожидания зависимой переменной:

;

;
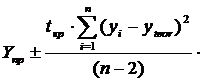