Построение межотраслевого баланса

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

"Забайкальский государственный университет"

Факультет дополнительного профессионального образования

Кафедра экономики и бухгалтерского учета

Контрольная работа

По предмету: "Методы оптимальных решений"

Выполнил: студент гр. ЭКБ - 12-1 Лескова А.С.

Проверил: Мурзина Н.В.

Чита 2014

Задача 1

Заданы таблица межотраслевых потоков и таблица конечных продуктов. Постройте межотраслевой баланс в отчетном периоде и, увеличив конечный продукт на 10 процентов, постройте межотраслевой баланс в плановом периоде.

Таблицы межотраслевых потоков

	1	2	3	4	5
1	46,05	3,52	17,61	4,26	6,59
2	4,26	35,56	0,86	2,86	0,58
3	0	0	0	0	0
4	0,53	24,26	1,02	16,15	0
5	15,26	4,53	0,5	4,89	0,58

Таблица конечных продуктов

1

35,33

66,54

32,14

20,56

2,23

Решение.

. Построим межотраслевой баланс в отчетном периоде и занесем в таблицу:

Отрасли	1	2	3	4	5	Итого	Конечный продукт	Валовой продукт
1	46,05	3,52	17,61	4,26	6,59	78,03	35,33	113,36
2	4,26	35,56	0,86	2,86	0,58	44,12	66,54	110,66
3	0	0	0	0	0	0	32,14	32,14
4	0,53	24,26	1,02	16,15	0	41,96	20,56	62,52
5	15,26	4,53	0,5	4,89	0,58	25,76	2,23	27,99
Итого	66,1	67,87	19,99	28,16	7,75	189,87	156,8	346,67
Чистая продукция	47,26	42,79	12,15	34,36	20,24	156,8
Всего	113,36	110,66	32,14	62,52	27,99	346,67

. Построим межотраслевой баланс в плановом периоде.

Найдем матрицу А прямых затрат, элементы которой рассчитаем по формуле

: \

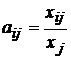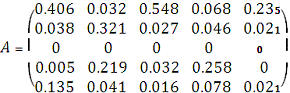Она имеет неотрицательные значения и удовлетворяет критерию продуктивности:

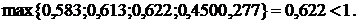
Поэтому для любого вектора конечного продукта 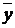 можно найти необходимый объем валового выпуска по формуле:

.

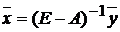Матрица .

Обратная к ней матрица имеет вид:

.

Посчитаем величину конечного продукта в плановом периоде, увеличив его на 10 %:

.

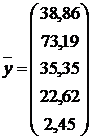Определим величину валовой продукции в плановом периоде:

=.

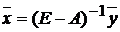Посчитаем межотраслевые потоки в плановом периоде по формуле

межотраслевой баланс в плановом периоде

Отрасли	1	2	3	4	5	Итого	Конечный продукт	Валовой продукт
1	50,66	3,87	19,37	4,69	7,25	85,83	38,86	124,70
2	4,69	39,12	0,95	3,15	0,64	48,53	73, 19	121,73
3	0,00	0,00	0,00	0,00	0,00	0,00	35,35	35,35
4	0,58	26,69	1,12	17,77	0,00	46,16	22,62	68,77
5	16,79	4,98	0,55	5,38	0,64	28,34	2,45	30,79
Итого	72,71	74,66	21,99	30,98	8,53	208,86	172,48	381,34
Чистая продукция	51,99	47,07	13,37	37,80	22,26	172,48
Всего	124,70	121,73	35,35	68,77	30,79	381,34

Задача 2

Построить на плоскости область решений линейных неравенств и геометрически найти максимальное и минимальное значения целевой функции в этой области.

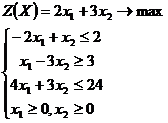
Решение.

Определим сначала многоугольник решений, для чего систему ограничений-неравенств запишем в виде уравнений и пронумеруем их:

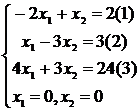
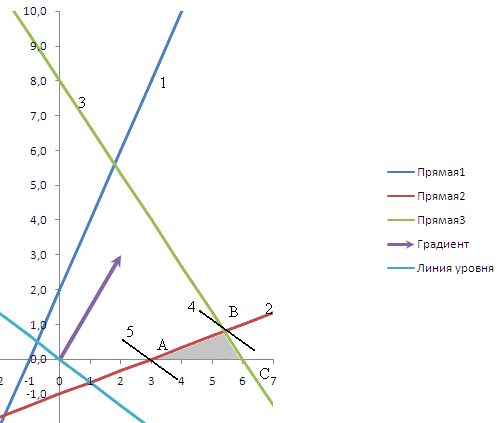
Построим область допустимых значений: на координатной плоскости нанесем прямые, соответствующие неравенствам системы ограничений, и отметим соответствующие полуплоскости.

Прямая (1) - х₂ = 2 + 2х₁ - проходит через точки:

х1	0	-1
х2	2	0

Прямая (2) - х₂ = - 1+ 1/3 х₁ - проходит через точки:

х1	0	3
х2	-1	0

Прямая (3) - х₂ = 8 - 4/3 х₁ - проходит через точки:

х106
х2	8	0

Построим область допустимых значений - треугольник ABC.

Координаты вектор-градиента равны коэффициентам целевой функции:

.

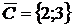Проведём через область ABCD произвольную линию уровня перпендикулярно направлению градиента - прямая, линия уровня.

Поскольку задача решается на максимум, перемещаем линию уровня в направлении возрастания целевой функции, т.е. в направлении градиента.

Предельное положение - линия (4). Следовательно, точка В является оптимальным решением, обеспечивающим максимальное значение целевой функции.

Если задачу решать на минимум, перемещаем линию уровня в направлении убывания целевой функции, т.е. в направлении антиградиента.

Предельное положение - линия (5). Следовательно, точка А является оптимальным решением, обеспечивающим минимальное значение целевой функции.

Определим координаты точки В как пересечение прямых (2) и (3):

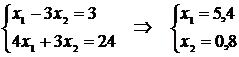
Следовательно, максимальное значение целевая функция достигает в точке  и равно .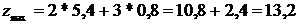

Определим координаты точки А как пересечение прямых (2) и оси Ох₁:

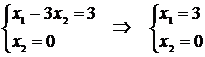
Следовательно, минимальное значение целевая функция достигает в точке 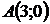 и равно .

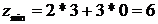Задача 3

Решить симплексным методом задачи:

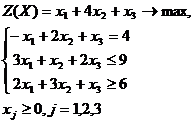
Решение.

Запишем эту задачу в форме основной задачи линейного программирования. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений

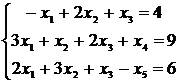
Введем искусственные переменные x:

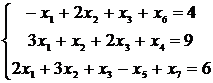
Для постановки задачи на максимум целевую функцию запишем так:

Z (X) = x₁ + 4x₂ + x₃ - Mx₆ - Mx₇ → max

Из уравнений выражаем искусственные переменные и подставим в целевую функцию:

x₆ = 4 + x_{1 -} 2x_{2 -} x₃₇ = 6 - 2x_{1 -} 3x₂ - x₃+x₅(X) = x₁ + 4x₂ + x₃ - M (4 + x₁ - 2x₂ - x₃) - M (6 - 2x₁ - 3x₂ - x₃ + x₅) → max(X) = (1 + M) x₁ + (4 + 5M) x₂ + (1 + 2M) x₃ + ( - M) x₅ + ( - 10M) → max

Решим систему уравнений относительно базисных переменных: x₆, x₄, x₇.

Полагая, что свободные переменные равны 0, получим первый опорный план: X₁ = (0,0,0,9,0,4,6)

азис	B	x1	x2	x3	x4	x5	x6	x7
x6	4	- 1	2	1	0	0	1	0
x4	9	3	1	2	1	0	0	0
x7	6	2	3	1	0	- 1	0	1
Z (X0)	- 10M	- 1 - M	- 4 - 5M	- 1 - 2M	0	M	0	0

Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i2

и из них выберем наименьшее: min (4: 2, 9: 1, 6: 3) = 2

Следовательно, 1-ая строка является ведущей.

Получаем новую симплекс - таблицу:

Базис	B	x1	x2	x3	x4	x5	x6	x7
x2	2	- 0.5	1	0.5	0	0	0.5	0	7	3.5	0	1.5	1	0	- 0.5	0
x7	0	3.5	0	- 0.5	0	- 1	- 1.5	1
Z (X1)	8	- 3 - 3.5M	0	1 + M	0	M	2 + 2.5M	0

Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₁, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i1

и из них выберем наименьшее:

(-, 7: 3.5, 0: 3.5) = 0

Следовательно, 3-ая строка является ведущей.

Получаем новую симплекс - таблицу:

Базис	B	x1	x2	x3	x4	x5	x6	x7	min
x2	2	0	1	3/7	0	- 1/7	2/7	1/7	-
x4	7	0	0	2	1	1	1	- 1	7
x1	0	1	0	- 1/7	0	- 2/7	- 3/7	2/7	-
Z (X3)	8	0	0	4/7	0	- 6/7	5/7 + M	6/7 + M	0

Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₅, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i5

и из них выберем наименьшее:

(-, 7: 1, - ) = 7

Следовательно, 2-ая строка является ведущей.

Получаем новую симплекс - таблицу:

Базис	B	x1	x2	x3	x4	x5	x6	x7
x2	3	0	1	5/7	1/7	0	3/7	0
x5	7	0	0	2	1	1	1	- 1
x1	2	1	0	3/7	2/7	0	- 1/7	0
Z (X3)	14	0	0	22/7	6/7	0	14/7 + M	M

Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.

Так как в оптимальном решении отсутствуют искусственные переменные (равны нулю), то данное решение является допустимым.

Оптимальный план можно записать так: x₂ = 3, x₁ = 2.

Тогда Z_max = 4*3 + 1*2 = 14.

Задача 4

Решить методом потенциалов транспортные задачи:

	1	2	3	4	5	Всего
1	1	5	7	9	3	10
2	4	6	4	7	13	20
3	1	5	3	4	9	10
4	2	4	2	10	3	30
5	3	2	5	6	4	10
всего	10	10	25	25	30

Решение.

Проверим равенство запасов и потребностей:

;

.

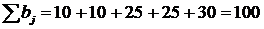Равенство не выполняется (), следовательно, транспортная задача является открытой. Сведём её к закрытой модели путем введения фиктивного поставщика. Положим его запас равным дефициту ресурса (100 - 80 = 20), а тарифы на перевозки - равными 0.

Построим новую транспортную таблицу и определим начальное распределение методом северо-западного угла:

		10		10		25		25		30
10		1		5		7		9		3
	10
20		4		6		4		7		13
			10		10
10		1		5		3		4		9
					10
30		2		4		2		10		3
					5		25
10		3		2		5		6	10	4
20		0		0		0		0	20	0

При этом стоимость перевозок составит:

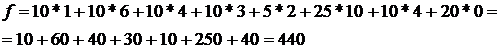
Проверяем количество заполненных клеток - 8, а должно быть  Следовательно, опорный план является вырожденным.

межотраслевое баланс симплексный

Строим новый план методом минимальной стоимости, порядок заполнения клеток указан.

	vj	1		5		7		2		8
ui			10		10		25		25		30
0	10		1		5		7		9		3
		10	(1)	0		0
5	20		4		6		4		7		13
								15	(6)	5	(7)
2	10		1		5		3		4		9
								10	(5)
-5	30		2		4		2		10		3
						25	(3)			5	(4)
-3	10		3		2		5		6		4
				10	(2)
-8	20		0		0		0		0		0
										20	(8)

При этом стоимость перевозок составит:

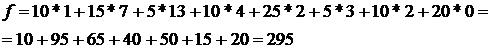
Проверяем количество заполненных клеток - 8, а должно быть  Следовательно, опорный план является вырожденным. Для получения невырожденного плана принудительно добавляем нуль (0) в клетку (1,2) и (1,3).

Определим потенциалы и оценки свободных клеток:

u₁ + v₁ = 1₁ + v₂ = 5₁ + v₃ = 7₂ + v₄ = 7₂ + v₅ = 13₃ + v₄ = 4₄ + v₃ = 2₄ + v₅ = 3₅ + v₂ = 2₆ + v₅ = 0

Пусть u₁ = 0, тогда v₁ = 1, v₂ = 5, v₃ = 7, u₄ = - 5, v₅ = 8, u₂ = 5, v₄ = 2, u₃ = 2, u₅ = - 3, u₆ = - 8

Найдём оценки свободных клеток :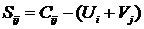

S₁₄ = 9 - (0 + 2) = 7

S₁₅ = 3 - (0 + 8) = - 5₂₁ = 4 - (5 + 1) = - 2₂₂ = 6 - (5 + 5) = - 4₂₃ = 4 - (5 + 7) = - 8₃₁ = 1 - (2 + 1) = - 2₃₂ = 5 - (2 + 5) = - 2₃₃ = 3 - (2 + 7) = - 6₄₁ = 2 - (-5 + 1) = 6₄₂ = 4 - (-5 + 5) = 4₄₄ = 10 - (-5 + 2) = 13₅₁ = 3 - (-3 + 1) = 5

S₅₃ = 5 - (-3 + 7) = 1

S₅₄ = 6 - (-3 + 2) = 7

S₅₅ = 4 - (-3 + 8) = - 1

S₆₁ = 0 - (-8 + 1) = 7

S₆₂ = 0 - (-8 + 5) = 3

S₆₃ = 0 - (-8 + 7) = 1

S₆₄ = 0 - (-8 + 2) = 6

S₆₅ = 0 - (-8 + 8) = 0

Поскольку среди оценок свободных клеток есть отрицательные, то найденный план оптимальным не является.

Для перераспределения поставок выбираем клетку с наибольшей по модулю отрицательной оценкой - клетка (2;3) - и строим цикл, первая вершина которого находится в выбранной клетке, а остальные - в заполненных клетках. В вершинах цикла поочередно расставляем знаки "+" и "-", начиная со свободной клетки.

	vj	1		5		7		2		8
ui			10		10		25		25		30	10		1		5		7		9		3
		10		0		0
5	20		4		6	+	4		7	-	13
								15		5
2	10		1		5		3		4		9
								10
-5	30		2		4	-	2		10	+	3
						25				5
-3	10		3		2		5		6		4
				10
-8	20		0		0		0		0		0
										20

Определяем размер перераспределяемой поставки (минимальное из значений в клетках со знаком "-"): min (25;5) = 5. Перераспределяем 5 единиц ресурса и получаем новый план поставок:

	vj	1		5		7		9		8
ui			10		10		25		25		30
0	10		1		5		7		9		3
		10		0		0
-2	20		4		6		4		7		13
						5		15
1	10		1		5		3		4		9
								10
-5	30		2		4		2		10		3
						20				10
-3	10		3		2		5		6		4
				10
-8	20		0		0		0		0		0
										20

При этом стоимость перевозок составит:

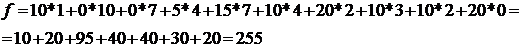
Определим потенциалы и оценки свободных клеток:

u₁ + v₁ = 1₁ + v₂ = 5₁ + v₃ = 7₂ + v₃ = 4₂ + v₄ = 7₃ + v₄ = 4₄ + v₃ = 2₄ + v₅ = 3₅ + v₂ = 2₆ + v₅ = 0

Пусть u₁ = 0, тогда v₁ = 1, v₂ = 5, v₃ = 7, u₄ = - 5, v₅ = 8, u₂ = - 2, v₄ = 9, u₃ = 1, u₅ = - 3, u₆ = - 8. Найдём оценки свободных клеток :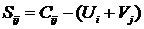

S₁₄ = 9 - (0 + 9) = 0

S₁₅ = 3 - (0 + 8) = - 5₂₁ = 4 - (-2 + 1) = 5₂₂ = 6 - (-2 + 5) = 3₂₅ = 13 - (-2 + 8) = 7₃₁ = 1 - (1 + 1) = - 1₃₂ = 5 - (1 + 5) = - 1₃₃ = 3 - (1 + 7) = - 5₄₁ = 2 - (-5 + 1) = 6₄₂ = 4 - (-5 + 5) = 4₄₄ = 10 - (-5 + 9) = 6₅₁ = 3 - (-3 + 1) = 5

S₅₃ = 5 - (-3 + 7) = 1

S₅₄ = 6 - (-3 + 9) = 0

S₅₅ = 4 - (-3 + 8) = - 1

S₆₁ = 0 - (-8 + 1) = 7

S₆₂ = 0 - (-8 + 5) = 3

S₆₃ = 0 - (-8 + 7) = 1

S₆₄ = 0 - (-8 + 9) = 1

Поскольку среди оценок свободных клеток есть отрицательные, то найденный план оптимальным не является.

Для перераспределения поставок выбираем клетку с наибольшей по модулю отрицательной оценкой - клетка (3;3) - и строим цикл, первая вершина которого находится в выбранной клетке, а остальные - в заполненных клетках. В вершинах цикла поочередно расставляем знаки "+" и "-", начиная со свободной клетки.

	vj	1		5		7		9		8
ui			10		10		25		25		30
0	10		1		5		7		9		3
		10		0		0
-2	20		4		6	-	4	+	7		13
						5		15
1	10		1		5	+	3	-	4		9
								10
-5	30		2		4		2		10		3
						20				10
-3	10		3		2		5		6		4
				10
-8	20		0		0		0		0		0
										20

Определяем размер перераспределяемой поставки (минимальное из значений в клетках со знаком "-"):min (10;5) = 5. Перераспределяем 5 единиц ресурса и получаем новый план поставок:

	vj	1		5		7		8		8
ui			10		10		25		25		30
0	10		1		5		7		9		3
		10		0		0
-1	20		4		6		4		7		13
								20
-4	10		1		5		3		4		9
						5		5
-5	30		2		4		2		10		3
						20				10
-3	10		3		2		5		6		4
				10
-8	20		0		0		0		0		0
										20

При этом стоимость перевозок составит:

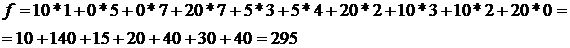
Определим потенциалы и оценки свободных клеток:

u₁ + v₁ = 1₁ + v₂ = 5₁ + v₃ = 7₂ + v₄ = 7₃ + v₃ = 3₃ + v₄ = 4₄ + v₃ = 2₄ + v₅ = 3₅ + v₂ = 2₆ + v₅ = 0

Пусть u₁ = 0, тогда₁ = 1, v₂ = 5, v₃ = 7, u₄ = - 5, v₅ = 8, u₂ = - 1, v₄ = 8, u₃ = - 4, u₅ = - 3, u₆ = - 8. Найдём оценки свободных клеток :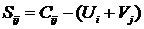

S₁₄ = 9 - (0 + 8) = 1

S₁₅ = 3 - (0 + 8) = - 5₂₁ = 4 - (-1 + 1) = 4₂₂ = 6 - (-1 + 5) = 2₂₃ = 4 - (-1 + 7) = - 2₂₅ = 13 - (-1 + 8) = 6₃₁ = 1 - (-4 + 1) = 4₃₂ = 5 - (-4 + 5) = 6₄₁ = 2 - (-5 + 1) = 6₄₂ = 4 - (-5 + 5) = 4₄₄ = 10 - (-5 + 8) = 7₅₁ = 3 - (-3 + 1) = 5

S₅₃ = 5 - (-3 + 7) = 1

S₅₄ = 6 - (-3 + 8) = 1

S₅₅ = 4 - (-3 + 8) = - 1

S₆₁ = 0 - (-8 + 1) = 7

S₆₂ = 0 - (-8 + 5) = 3

S₆₃ = 0 - (-8 + 7) = 1

S₆₄ = 0 - (-8 + 8) = 0

Поскольку среди оценок свободных клеток есть отрицательные, то найденный план оптимальным не является.

Для перераспределения поставок выбираем клетку с наибольшей по модулю отрицательной оценкой - клетка (1;

) - и строим цикл, первая вершина которого находится в выбранной клетке, а остальные - в заполненных клетках. В вершинах цикла поочередно расставляем знаки "+" и "-", начиная со свободной клетки.

	vj	1		5		7		8		8
ui			10		10		25		25		30
0	10		1		5	-	7		9	+	3
		10		0		0
-1	20		4		6		4		7		13
								20
-4	10		1		5		3		4		9
						5		5
-5	30		2		4	+	2		10	-	3
						20				10
-3	10		3		2		5		6		4
				10
-8	20		0		0		0		0
										20

Определяем размер перераспределяемой поставки (минимальное из значений в клетках со знаком "-"): min (0;10) = 0. Перераспределяем 0 единиц ресурса и получаем новый план поставок:

	vj	1		5		2		3		3
ui			10		10		25		25		30
0	10		1		5		7		9		3
		10		0						0
4	20		4		6		4		7		13
								20
1	10		1		5		3		4		9
						5		5
0	30		2		4		2		10		3
						20				10
-3	10		3		2		5		6		4
				10
-3	20		0		0		0		0		0
										20

При этом стоимость перевозок составит:

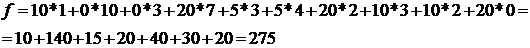
Определим потенциалы и оценки свободных клеток:

u₁ + v₁ = 1₁ + v₂ = 5₁ + v₅ = 3₂ + v₄ = 7₃ + v₃ = 3₃ + v₄ = 4₄ + v₃ = 2₄ + v₅ = 3₅ + v₂ = 2₆ + v₅ = 0

Пусть u₁ = 0, тогдаv₁ = 1, v₂ = 5, v₃ = 2, u₄ = 0, v₅ = 3, u₂ = 4, v₄ = 3, u₃ = 1, u₅ = - 3, u₆ = - 3

Найдём оценки свободных клеток :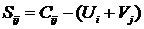

S₁₃ = 7 - (0 + 2) = 5

S₁₄ = 9 - (0 + 3) = 6₂₁ = 4 - (4 + 1) = - 1₂₂ = 6 - (4 + 5) = - 3₂₃ = 4 - (4 + 2) = - 2₂₅ = 13 - (4 + 3) = 6₃₁ = 1 - (1 + 1) = - 1₃₂ = 5 - (1 + 5) = - 1₄₁ = 2 - (0 + 1) = 1₄₂ = 4 - (0 + 5) = - 1₄₄ = 10 - (0 + 3) = 7₅₁ = 3 - (-3 + 1) = 5

S₅₃ = 5 - (-3 + 2) = 6

S₅₄ = 6 - (-3 + 3) = 6

S₅₅ = 4 - (-3 + 3) = 4

S₆₁ = 0 - (-3 + 1) = 2

S₆₂ = 0 - (-3 + 5) = - 2

S₆₃ = 0 - (-3 + 2) = 1

S₆₄ = 0 - (-3 + 3) = 0

Поскольку среди оценок свободных клеток есть отрицательные, то найденный план оптимальным не является.

Для перераспределения поставок выбираем клетку с наибольшей по модулю отрицательной оценкой - клетка (2;

) - и строим цикл, первая вершина которого находится в выбранной клетке, а остальные - в заполненных клетках. В вершинах цикла поочередно расставляем знаки "+" и "-", начиная со свободной клетки.

	vj	1		5		2		3		3
uiъ			10		10		25		25		30
0	10		1	-	5		7		9	+	3
		10		0						0
4	20		4	+	6		4	-	7		13
								20
1	10		1		5	-	3	+	4		9
						5		5
0	30		2		4	+	2		10	-	3
						20				10
-3	10		3		2		5		6		4
				10
-3	20		0		0		0		0		0
										20

Определяем размер перераспределяемой поставки (минимальное из значений в клетках со знаком "-"): min (0; 5; 20;10) = 0. Перераспределяем 0 единиц ресурса и получаем новый план поставок:

	vj	1		4		4		5		3
ui			10		10		25		25		30
0	10		1		5		7		9		3
		10								0
2	20		4		6		4		7		13
				0				20
-1	10		1		5		3		4		9
						5		5
0	30		2		4		2		10		3
						20				10
2	10		3		2		5		6		4
				10
-3	20		0		0		0		0		0
										20

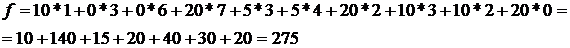
Определим потенциалы и оценки свободных клеток:

u₁ + v₁ = 1₁ + v₅ = 3₂ + v₂ = 6₂ + v₄ = 7₃ + v₃ = 3₃ + v₄ = 4₄ + v₃ = 2₄ + v₅ = 3₅ + v₂ = 2₆ + v₅ = 0

Пусть u₁ = 0, тогда v₁ = 1, v₂ = 4, v₃ = 4, u₄ = 0, v₅ = 3, u₂ = 2, v₄ = 5, u₃ = - 1, u₅ = 2, u₆ = - 3. Найдём оценки свободных клеток :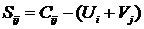

S₁₂ = 5 - (0 + 4) = 1

S₁₃ = 7 - (0 + 4) =3₁₄ = 9 - (0 + 3) = 6₂₁ = 4 - (2 + 1) = 1₂₃ = 4 - (2 + 4) = - 2₂₅ = 13 - (2 + 3) = 8₃₁ = 1 - (-1 + 1) = 1₃₂ = 5 - (-1 + 4) = 2₄₁ = 2 - (0 + 1) = 1₄₂ = 4 - (0 + 4) = 0₄₄ = 10 - (0 + 3) = 7₅₁ = 3 - (2 + 1) = 0

S₅₃ = 5 - (2 + 4) = - 1

S₅₄ = 6 - (2 + 3) = 1

S₅₅ = 4 - (2 + 3) = - 1

S₆₁ = 0 - (-3 + 1) = 2

S₆₂ = 0 - (-3 + 4) = - 1

S₆₃ = 0 - (-3 + 4) = 1

S₆₄ = 0 - (-3 + 3) = 0

Поскольку среди оценок свободных клеток есть отрицательные, то найденный план оптимальным не является.

Для перераспределения поставок выбираем клетку с наибольшей по модулю отрицательной оценкой - клетка (2;

) - и строим цикл, первая вершина которого находится в выбранной клетке, а остальные - в заполненных клетках. В вершинах цикла поочередно расставляем знаки "+" и "-", начиная со свободной клетки.

	vj	1		4		4		5		3
ui			10		10		25		25		30
0	10		1		5		7		9		3
		10								0
2	20		4		6	+	4	-	7		13
				0				20
-1	10		1		5	-	3	+	4		9
						5		5
0	30		2		4		2		10		3
						20				10
2	10		3		2		5		6		4
				10
-3	20		0		0		0		0		0
										20

Определяем размер перераспределяемой поставки (минимальное из значений в клетках со знаком "-"): min (5; 20) = 5. Перераспределяем 5 единиц ресурса и получаем новый план поставок:

	vj	1		4		2		5		3
ui			10		10		25		25		30
0	10		1		5		7		9		3
		10								0
2	20		4		6		4		7		13
				0		5		15
-1	10		1		5		3		4		9
								10
0	30		2		2		10		3
						20				10
-2	10		3		2		5		6		4
				10
-3	20		0		0		0		0		0
										20

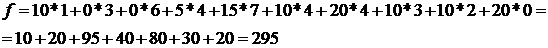
Определим потенциалы и оценки свободных клеток:

u₁ + v₁ = 1₁ + v₅ = 3₂ + v₂ = 6₂ + v₃ = 4₂ + v₄ = 7₃ + v₄ = 4₄ + v₃ = 2₄ + v₅ = 3₅ + v₂ = 2₆ + v₅ = 0

Пусть u₁ = 0, тогда v₁ = 1, v₂ = 4, v₃ = 2, u₄ = 0, v₅ = 3, u₂ = 2, v₄ = 5, u₃ = - 1, u₅ = - 2, u₆ = - 3

Найдём оценки свободных клеток :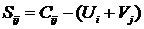

S₁₂ = 5 - (0 + 4) = 1

S₁₃ = 7 - (0 + 2) =5₁₄ = 9 - (0 + 5) = 4₂₁ = 4 - (2 + 1) = 1₂₅ = 13 - (2 + 3) = 8₃₁ = 1 - (-1 + 1) = 1₃₂ = 5 - (-1 + 4) = 2₃₃ = 3 - (-1 + 2) = 2₄₁ = 2 - (0 + 1) = 1₄₂ = 4 - (0 + 4) = 0₄₄ = 10 - (0 + 5) = 5₅₁ = 3 - (-2 + 1) = 4

S₅₃ = 5 - (-2 + 2) = 5

S₅₄ = 6 - (-2 + 5) = 3

S₅₅ = 4 - (-2 + 3) = 3

S₆₁ = 0 - (-3 + 1) = 2

S₆₂ = 0 - (-3 + 4) = - 1

S₆₃ = 0 - (-3 + 2) = 1

S₆₄ = 0 - (-3 + 5) = - 2

Поскольку среди оценок свободных клеток есть отрицательные, то найденный план оптимальным не является.

Для перераспределения поставок выбираем клетку с наибольшей по модулю отрицательной оценкой - клетка (6;

) - и строим цикл, первая вершина которого находится в выбранной клетке, а остальные - в заполненных клетках. В вершинах цикла поочередно расставляем знаки "+" и "-", начиная со свободной клетки.

	vj	1		4		2		5		3
ui			10		10		25		25		30
0	10		1		5		7		9		3
		10								0
2	20		4		6	+	4	-	7		13
				0		5		15
-1	10		1		5		3		4		9
								10
0	30		2		4	-	2		10	+	3
						20				10
-2	10		3		2		5		6		4
				10
-3	20		0		0		0	+	0	-	0
										20

Определяем размер перераспределяемой поставки (минимальное из значений в клетках со знаком "-"): min (20; 20; 15) = 15. Перераспределяем 0 единиц ресурса и получаем новый план поставок:

¢

	vj	1		4		2		3		3
ui			10		10		25		25		30
0	10		1		5		7		9		3
		10								0
2	20		4		6		4		7		13
				0		20
1	10		1		5		3		4		9
								10
0	30		2		4		2		10		3
						5				25
-2	10		3		2		5		6		4
				10
-3	20		0		0		0		0		0
								15		5

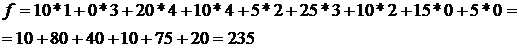
Определим потенциалы и оценки свободных клеток:

u₁ + v₁ = 1₁ + v₅ = 3₂ + v₂ = 6₂ + v₃ = 4₃ + v₄ = 4₄ + v₃ = 2₄ + v₅ = 3₅ + v₂ = 2₆ + v₄ = 0₆ + v₅ = 0

Пусть u₁ = 0, тогда v₁ = 1, v₂ = 4, v₃ = 2, u₄ = 0, v₅ = 3, u₂ = 2, v₄ = 3, u₃ = 1, u₅ = - 2, u₆ = - 3

Найдём оценки свободных клеток :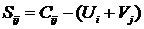

S₁₂ = 5 - (0 + 4) = 1

S₁₃ = 7 - (0 + 2) =5₁₄ = 9 - (0 + 4) = 5₂₁ = 4 - (2 + 1) = 1₂₄ = 7 - (2 + 4) = 1₂₅ = 13 - (2 + 3) = 8₃₁ = 1 - (1 + 1) = - 1₃₂ = 5 - (1 + 4) = 0₃₃ = 3 - (1 + 2) = 0₄₁ = 2 - (0 + 1) = 1₄₂ = 4 - (0 + 4) = 0₄₄ = 10 - (0 + 4) = 6

S₅₁ = 3 - (-2 + 1) = 4

S₅₃ = 5 - (-2 + 2) = 5

S₅₄ = 6 - (-2 + 4) = 4

S₅₅ = 4 - (-2 + 3) = 3

S₆₁ = 0 - (-3 + 1) = 2

S₆₂ = 0 - (-3 + 4) = - 1

S₆₃ = 0 - (-3 + 2) = 1

Поскольку среди оценок свободных клеток есть отрицательные, то найденный план оптимальным не является.

Для перераспределения поставок выбираем клетку с наибольшей по модулю отрицательной оценкой - клетка (6;

) - и строим цикл, первая вершина которого находится в выбранной клетке, а остальные - в заполненных клетках. В вершинах цикла поочередно расставляем знаки "+" и "-", начиная со свободной клетки.

	vj	1		4		2		3		3
ui			10		10		25		25		30
0	10		1		5		7		9		3
		10								0
2	20		4	-	6	+	4		7		13
				0		20
1	10		1		5		3		4		9
								10
0	30		2		4	-	2		10	+	3
						5				25
-2	10		3		2		5		6		4
				10
-3	20		0	+	0		0		0	-	0
								15		5

Определяем размер перераспределяемой поставки (минимальное из значений в клетках со знаком "-"): min (0; 5;5) = 0. Перераспределяем 0 единиц ресурса и получаем новый план поставок:

	vj	1		3		2		3		3
ui			10		10		25		25		30
0	10		1		5		7		9		3
		10								0
2	20		4		6		4		7		13
						20
1	10		1		5		3		4		9
								10
0	30		2		4		2		10		3
						5				25
1	10		3		2		5		6		4
				10
-3	20		0		0		0		0		0
				0				15		5

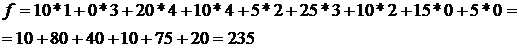
Определим потенциалы и оценки свободных клеток:

u₁ + v₁ = 1₁ + v₅ = 3₂ + v₃ = 4₃ + v₄ = 4₄ + v₃ = 2₄ + v₅ = 3₅ + v₂ = 2₆ + v₂ = 0₆ + v₄ = 0₆ + v₅ = 0

Пусть u₁ = 0, тогда v₁ = 1, v₂ = 3, v₃ = 2, u₄ = 0, v₅ = 3, u₂ = 2, v₄ = 3, u₃ = 1, u₅ = 1, u₆ = - 3

Найдём оценки свободных клеток :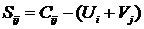

S₁₂ = 5 - (0 + 3) = 2

S₁₃ = 7 - (0 + 2) =5₁₄ = 9 - (0 + 3) = 6₂₁ = 4 - (2 + 1) = 1₂₂ = 6 - (2 + 3) = 1₂₄ = 7 - (2 + 3) = 2₂₅ = 13 - (2 + 3) = 8₃₁ = 1 - (1 + 1) = - 1₃₂ = 5 - (1 + 3) = 2₃₃ = 3 - (1 + 2) = 0₄₁ = 2 - (0 + 1) = 1₄₂ = 4 - (0 + 3) = 1

S₄₄ = 10 - (0 + 3) = 7

S₅₁ = 3 - (1 + 1) = 1

S₅₃ = 5 - (1 + 2) = 3

S₅₄ = 6 - (1 + 3) = 4

S₅₅ = 4 - (1 + 3) = 0

S₆₁ = 0 - (-3 + 1) = 2

S₆₃ = 0 - (-3 + 2) = 1

Поскольку среди оценок свободных клеток есть отрицательные, то найденный план оптимальным не является.

Для перераспределения поставок выбираем клетку с наибольшей по модулю отрицательной оценкой - клетка (3;

) - и строим цикл, первая вершина которого находится в выбранной клетке, а остальные - в заполненных клетках. В вершинах цикла поочередно расставляем знаки "+" и "-", начиная со свободной клетки.

	vj	1		3		2		3		3
ui		10		25		25		30
0	10	-	1		5		7		9	+	3
		10								0
2	20		4		6		4		7		13
						20
1	10	+	1		5		3	-	4		9
								10
0	30		2		4		2		10		3
						5				25
1	10		3		2		5		6		4
				10
-3	20		0		0		0	+	0	-	0
				0				15		5

Определяем размер перераспределяемой поставки (минимальное из значений в клетках со знаком "-"): min (10; 10; 5) = 5. Перераспределяем 5 единиц ресурса и получаем новый план поставок:

	vj	1		4		2		4		3
ui			10		10		25		25		30
0	10		1		5		7		9		3
		5								5
2	20		4		6		4		7		13
						20
0	10		1		5		3		4		9
		5						5
0	30		2		4		2		10		3
						5				25
-2	10		3		2		5		6		4
				10
-4	20		0		0		0		0		0
				0				20

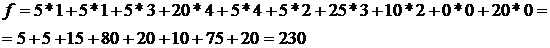
Определим потенциалы и оценки свободных клеток:

u₁ + v₁ = 1₁ + v₅ = 3₂ + v₃ = 4₃ + v₁ = 1₃ + v₄ = 4₄ + v₃ = 2₄ + v₅ = 3₅ + v₂ = 2₆ + v₂ = 0₆ + v₄ = 0

Пусть u₁ = 0, тогда v₁ = 1, v₂ = 4, v₃ = 2, u₄ = 0, v₅ = 3, u₂ = 2, v₄ = 4, u₃ = 0, u₅ = - 2, u₆ = - 4

Найдём оценки свободных клеток :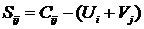

S₁₂ = 5 - (0 + 2) = 3

S₁₄ = 9 - (0 + 4) = 5₂₁ = 4 - (2 + 1) = 1₂₂ = 6 - (2 + 2) = 2₂₄ = 7 - (2 + 4) = 1₂₅ = 13 - (2 + 3) = 8₃₁ = 1 - (0 + 1) = 0₃₂ = 5 - (0 + 2) = 3₃₃ = 3 - (0 + 2) = 1₄₁ = 2 - (0 + 1) = 1₄₂ = 4 - (0 + 2) = 2₄₄ = 10 - (0 + 4) = 6

S₅₁ = 3 - (-2 + 1) = 4

S₅₃ = 5 - (-2 + 2) = 5

S₅₄ = 6 - (-2 + 4) = 4

S₅₅ = 4 - (-2 + 3) = 3

S₆₁ = 0 - (-4 + 1) = 3

S₆₃ = 0 - (-4 + 2) = 2

S₆₅ = 0 - (-4 + 3) = 1

Поскольку все оценки неотрицательны, найденный план является оптимальным. Однако оптимальное решение не единственно, поскольку среди оценок свободных клеток есть нулевые.

Список использованных источников

1.      Акулич И.Л. Математическое программирование в примерах и задачах: учеб. пособие/ И. Л Акулич. - Москва: Высшая школа, 2009. - 347 с.

2.      Балдин К.В. Математическое программирование: учебник / под ред. К.В. Балдин, Н.А. Брызгалов, А.В. Рукосуев. - Москва: Дашков и К, 2009. - 218 с.

.        Красс М.С. Математические методы и модели для магистрантов экономики: учеб. пособие для студентов/ М.С. Красс, Б.П. Чупрынов. - Москва: Высшая школа, 2010. - 496 с.

.        Математика для экономистов. Задачник: учеб. практ. пособие для студентов вузов / под ред.С.И. Макарова, М.В. Мищенко. - Москва: КноРус, 2008. - 358 с.