Статистические методы управление качеством

Введение

технологический брак управление

Любая продукция или услуга есть результат некоторого процесса. Под процессом подразумевают совокупность взаимосвязанных ресурсов и деятельности, которая преобразует входящие элементы в выходящие.

Причем к ресурсам относятся персонал, оборудование, материалы, технология (методы и средства), окружающая среда, информация. По существу, процесс представляет собой взаимодействие людей, оборудования, материалов, методов и среды, в результате которого производится продукция или оказываются услуги.

Все процессы и их результаты подвержены изменчивости - вариабельности. Поэтому при решении задач статистического управления процессами исходят из того, что как в производственных, так и в любых других процессах, всегда имеют место изменения или вариации, проявляющиеся в отклонении от целевых значений каких-либо параметров, характеризующих процесс.

При естественном ходе процесса его изменчивость обычно обусловлена влиянием множества разнообразных случайных (обычных) неконтролируемых причин. Каждая из таких постоянно присущих причин составляет незначительную долю общей изменчивости, и ни одна из них не значима сама по себе. Тем не менее, сумма всех этих случайных причин изменчивости процесса измерима, и предполагается, что она внутренне присуща процессу. Исключение или уменьшение влияния обычных причин требует управленческих решений и выделения ресурсов на улучшение процесса и в ряде случаев оказывается экономически нецелесообразным или технически невозможным.

Основными задачами статистического управления процессами являются:

обеспечение и поддержание процессов на приемлемом и стабильном уровне, гарантирующем соответствие продукции и услуг установленным требованиям;

своевременное распознавание перехода процесса в статистически неуправляемое состояние;

обнаружение неслучайных (особых) причин изменчивости процесса и принятие надлежащих мер для исключения или ослабления их влияния на ход процесса;

исключение излишнего управления процессом, находящимся в статистически управляемом состоянии, и случаев непринятия необходимых действий при переходе процесса в статистически неуправляемое состояние.

Простым и эффективным средством статистического управления процессами являются контрольные карты, которые отражают текущее состояние процесса, дают возможность производить оценку степени изменчивости процесса, определять наличие статистической управляемости процесса и оказывают помощь в достижении такой управляемости.

1. Статистическое регулирование технологических процессов

Статистическое регулирование технологических процессов - корректирование значений параметров технологического процесса по результатам выборочного контроля контролируемых параметров, осуществляемое для технологического обеспечения требуемого уровня качества. При этом технологический процесс должен быть статистически управляемым и стабильным.

Принято считать, что процесс находится в «статистически управляемом состоянии» или «статистически управляем или контролируемым», если источником его изменчивости являются только случайные (обычные) причины, которые имеют стабильное и повторяемое распределение во времени. Такую изменчивость процесса называют собственной.

Любой процесс, находящийся в статистически управляемом состоянии, стабилен и характеризуется тем, что ход процесса предсказуем, его параметры со временем не отклоняются от целевых значений, а разброс параметров находится в прогнозируемых пределах.

Однако естественный ход процесса может нарушаться из-за изменений, обусловленных неслучайными (особыми) причинами, внутренне не присущими процессу. Применительно к производственному процессу такими непредсказуемыми и нестабильными причинами могут быть поломка инструмента, неправильная настройка станка, его износ, недостаточная однородность обрабатываемого материала, нарушение рабочим требований документации из-за усталости или недомогания, ошибки контрольно-измерительного оборудования, колебания источников энергии, изменения окружающей среды и т.д.

При воздействии на процесс неслучайных (особых) причин изменчивости он выходит из статистически управляемого состоянии, ход процесса становится непредсказуемым, его параметры могут существенно отклониться от целевых значений, разброс параметров может оказаться неприемлемым, а выход процесса нестабильным во времени. Когда процесс оказывается в «статистически неуправляемом состоянии», необходимо возможно быстрее обнаружить неслучайные изменения процесса с тем, чтобы выявить их причину и своевременно внести необходимые корректировки в процесс. Тем самым предотвращаются существенные отклонения характеристик процесса от целевых значений, и обеспечивается поддержание процесса на приемлемом и стабильном уровне, гарантируя соответствие продукции и услуг установленным требованиям.

Статистическое регулирование технологических процессов заключается в том, что в определенные моменты времени или через определенное количество изготовленных единиц продукции отбирается мгновенная выборка установленного объема и производится измерение контролируемого параметра.

По результатам измерений определяют статистическую характеристику контролируемого параметра, значение которой наносят на контрольную карту и, в зависимости от этого значения принимают решение о корректировке технологического процесса или о продолжении процесса баз корректировки, т.е. на основании данных о состоянии технологического процесса в предшествующие моменты времени прогнозируется его состояние в последующие моменты времени.

Значение статистической характеристики контролируемого параметра качества продукции, при котором наступает разладка операции или процесса, должно определяться, исходя из выборочной характеристики.

Главным направлением деятельности ООО «Ростовтехсервис» является постоянное и целенаправленное совершенствование технологических процессов, надежность и эффективность поставки, услуг предоставления в аренду помещений. Именно это диктуется современными условиями рынка и конкуренции. В этих условиях потребителя необходимо обеспечить разнообразным ассортиментом продукции, услуг, ее высоким качеством и приемлемым уровнем цен.

2. Виды статистического регулирования технологических процессов

Задача статистического регулирования технологического процесса состоит в том, чтобы на основании результатов периодического контроля выборок малого объема приходить к заключению: «процесс налажен» или «процесс разлажен».

Выявление разладки технологического процесса основано на результатах периодического контроля малых выборок, осуществляемого по количественному или альтернативному признакам. Для каждого из этих способов контроля используются свои статистические методы регулирования.

Контроль по количественному признаку заключается в определении с требуемой точностью фактических значений контролируемого параметра у единиц продукции из выборки. Фактические значения контролируемого параметра необходимы для последующего вычисления статистических характеристик, по которым принимается решение о состоянии технологического процесса. Такими характеристиками являются медиана и выборочное среднее; квадратическое отклонение и размах. Первые две характеристики - характеристики положения, а последние две - характеристики рассеивания случайной величины Х.

Контроль по альтернативному признаку заключается в определении соответствия контролируемого параметра или единицы продукции установленным требованиям. При этом каждое отдельное несоответствие установленным требованиям считается дефектом, а единица продукции, имеющая хотя бы один дефект, считается дефектной.

При контроле по альтернативному признаку не требуется знать фактическое значение контролируемого параметра - достаточно установить факт соответствия или несоответствия его установленным требованиям.

Поэтому можно использовать простейшие средства контроля: шаблоны, калибры, контроль по образцу и др.

Решение о состоянии технологического процесса принимается в зависимости от числа дефектов или числа дефектных единиц продукции, обнаруженных в выборке.

Каждый из перечисленных способов контроля имеет свои преимущества и свои недостатки. Преимущество контроля по количественному признаку состоит в том, что он более информативен (по сравнению с контролем по альтернативному признаку) и поэтому требует меньшего объема выборки. Однако такой контроль более дорогой, поскольку для него необходимы такие технические средства контроля, которые позволяют получать фактические значения контролируемого параметра.

Кроме того, для статистического регулирования при контроле по количественному признаку необходимы вычисления, связанные с определением статистических характеристик.

Преимущество контроля по альтернативному признаку заключается в его простоте и относительной дешевизне, поскольку можно использовать простейшие средства контроля или визуальный контроль. К недостаткам такого контроля относится его меньшая информативность, что требует значительно большего объема выборки при равных исходных данных.

3. Теоретические основы статистических методов регулирования технологических процессов

Контроль по количественному признаку

Контроль по количественному признаку заключается в определении с требуемой точностью фактических значений контролируемого параметра у единиц продукции из выборки. Фактические значения контролируемого параметра необходимы для последующего вычисления статистических характеристик, по которым принимается решение о состоянии технологического процесса. Такими характеристиками являются медиана и выборочное среднее; квадратическое отклонение и размах.

При контроле по количественному признаку об отклонениях в процессе судят как по среднему значению контролируемого параметра, так и по рассеиванию значений контролируемого параметра относительно этого среднего. Смещение среднего значения в любую сторону относительно середины поля допуска и увеличение поля рассеяния приводят к увеличению доли дефектной продукции.

В качестве характеристики рассеяния при статистическом регулировании используют либо выборочное среднее квадратическое отклонение S, либо размах R и соответственно строят либо S - карту, либо R - карту. При выборе карты можно учесть, что вычисление размаха гораздо проще, чем среднего квадратического отклонения, хотя S - более точная оценка, чем R.

На практике часто используют двойные контрольные карты, на одной из которых отмечают среднее значение, а на другой - характеристику рассеивания, например, карта X - R.

Для определения границ регулирования необходимо знать параметры нормального распределения µ и σ. Как правило, эти параметры неизвестны, поэтому должно быть проведено предварительное исследование состояния технологического процесса, в результате которого получают оценки параметров µ и σ.

Таким образом, в результате предварительного исследования состояния

техпроцесса решаются следующие задачи:

получают оценки параметров нормального распределения µ и σ,

определяют вероятную долю дефектной продукции,

определяют индекс воспроизводимости Ср.

Контроль по альтернативному признаку

Контроль по альтернативному признаку заключается в определении соответствия контролируемого параметра или единицы продукции установленным требованиям. При этом каждое отдельное несоответствие установленным требованиям считается дефектом, а единица продукции, имеющая хотя бы один дефект, считается дефектной.

При контроле по альтернативному признаку не требуется знать фактическое значение контролируемого параметра - достаточно установить факт соответствия или несоответствия его установленным требованиям. Поэтому можно использовать простейшие средства контроля: шаблоны, калибры, контроль по образцу и др.

Решение о состоянии технологического процесса принимается в зависимости от числа дефектов или числа дефектных единиц продукции, обнаруженных в выборке.

Каждый из перечисленных способов контроля имеет свои преимущества и свои недостатки. Преимущество контроля по количественному признаку состоит в том, что он более информативен (по сравнению с контролем по альтернативному признаку) и поэтому требует меньшего объема выборки. Однако такой контроль более дорогой, поскольку для него необходимы такие технические средства контроля, которые позволяют получать фактические значения контролируемого параметра. Кроме того, для статистического регулирования при контроле по количественному признаку необходимы вычисления, связанные с определением статистических характеристик.

Преимущество контроля по альтернативному признаку заключается в его простоте и относительной дешевизне, поскольку можно использовать простейшие средства контроля или визуальный контроль. К недостаткам такого контроля относится его меньшая информативность, что требует значительно большего объема выборки при равных исходных данных.

С учетом изложенных фактов выбирают тот или иной способ контроля для статистического регулирования. Рассмотрим суть статистических методов регулирования технологических процессов.

Любой контролируемый параметр по своей природе является случайной величиной, поскольку он может принять то или иное значение, причем заранее нам неизвестное.

Случайная величина (показатель качества - масса, диаметр отверстия, вала и пр.) может быть, в частности, непрерывной или дискретной. Например, диаметр вала представляет собой непрерывную случайную величину, которая теоретически может принимать все значения в интервале, ограниченном допуском, скажем, между 34,5 и 35,5 мм. Непрерывную величину мы получаем при контроле качества продукции по количественному признаку с помощью измерительных средств, позволяющих получить значение контролируемого параметра с большой точностью.

Дискретную величину мы получаем, например, при контроле качества продукции по альтернативному признаку «годен» или «не годен». В результате такого контроля мы подсчитываем число дефектных единиц или число дефектов. При этом нас не интересует истинное значение параметра Х, достаточно лишь установить соответствует ли оно установленному требованию или нет.

Наиболее часто применяемым при решении задач статистического контроля качества распределением непрерывной случайной величины Х является нормальное распределение.

4. Анализ причин несоответствий (брака) показателей качества процесса

Диаграмма (блок-схема) потока процессов (ДПП). Для повышения качества технологических процессов необходимо выявлять и устранять причины несоответствий показателей процесса установленным требованиям. Во многих случаях эти несоответствия заложены в нарушении последовательности операций (или переходов) или подмене звеньев процесса. Очевидно, что оценка несоответствий возможна только в случае анализа реального (а не проектного) процесса. Обычно для построения и дальнейшего анализа блоксхемы процесса привлекаются лица, в нем задействованные, т.е. исполнители процесса. В то же время причины несоответствий могут быть заложены и в проектной схеме процесса, и возможное изменение его последовательности или замена отдельных звеньев может стабилизировать процесс.

Желательно в диаграмме воспроизвести все элементы процесса, в том числе места, в которых принимаются решения, а также порядок документирования той или иной операции, наличие базы данных или появление допол-нительной информации о процессе. Таким образом, диаграмма потока процесса - не просто перечень и последовательность технологических звеньев, но и сопровождающая их технологическая и контрольная информация. Анализируя ДПП, желательно ответить на ряд следующих вопросов:

можно ли изменить ту или другую операцию за счет применения другой технологии, оборудования или изменения методов работы,

можно ли сократить время процесса,

можно ли сократить затрачиваемые ресурсы,

можно ли уменьшить число транспортировок,

можно ли совместить операции и т.д.

Для снижения затрат при отладке процесса важно не дожидаться появления несоответствий в реальном процессе, а провести анализ блок-схемы процесса еще в проектном варианте.

Анализ Парето

Особенно важно выявить причины несоответствий, приводящие к большим экономическим потерям. Для этого сначала целесообразно провести ранжирование несоответствий (дефектов) по их потенциальному ущербу производству.

Одним из наиболее распространенных на практике методов выявления наиболее значимых (по затратам) дефектов является анализ Парето.

Сущность анализа Парето заключается в выявлении таких дефектов, на поиске причин которых необходимо сосредоточить особое внимание. При этом действует правило Парето, что 80% всех дефектов вызвано небольшим числом причин.

Очевидно также, что для производственников важно прояснить картину распределения дефектов и потерь, вызванных отбраковкой продукции, где эти дефекты проявятся. Конечно, важно устранить причины наиболее многочисленных дефектов. Но в отдельных ситуациях еще важнее выявить причины появления пусть немногочисленных, но приводящих к большим производственным издержкам дефектов. Для этого применяется одна из разновидностей анализа Парето - метод АВС (кривая Лоренца).

Рассмотрим применение анализа Парето и метода АВС на конкретном примере.

Допустим, что в цехе на операции штамповки заготовок коленчатого вала работники контроля отбраковали 200 заготовок. При этом были выявлены следующие виды дефектов и их количество: трещины - 10, царапины - 42, пятна - 6, деформации -104, разрывы - 4, раковины - 20, прочие - 14.

Требуется выделить наиболее значимые дефекты для поиска причин их возникновения.

Для проведения анализа Парето необходимо таким образом сгруппировать виды причин, чтобы ранжирование видов дефектов шло по их количеству. Отразить данные группирования дефектов в таблицу 1.

Таблица 1

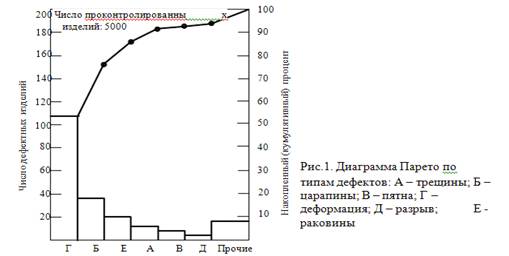
По результатам таблицы 1 построить столбчатую диаграмму (рисунок 1) распределения дефектов и на этом же графике начертить кумулятивную кривую числа дефектов (или процентов), соединив отрезками прямых линий точки, соответствующие накопленному числу дефектов (или процентов).

Полученная кумулятивная кривая носит название кривой Парето. Из диаграммы видно, что накопленные 80% соответствуют трем видам дефектов: деформации, царапины, трещины. Именно причины этих дефектов в первую очередь необходимо определить.

Допустим, что в цехе изготавливают одни и те же детали на разном технологическом оборудовании (станках) в разном количестве. Мы также располагаем информацией о числе дефектных деталей.

Данные о числе изготовленных деталей, числе и доли дефектных деталей и их стоимости, необходимые для построения кривой Лоренца, приведены в таблице 1.1. Требуется выяснить, не какие станки являются главными источниками брака при изготовлении продукции, а на каких станках требуется в первую очередь искать причины брака.

Решение поставленной задачи не лежит на поверхности. На первый взгляд, анализируя данные таблицы 1.1., можно рекомендовать искать причины брака на станке Г, потому что именно на нем самая большая доля брака. Однако, если подсчитать издержки от брака по каждому станку и отнести их к общему количеству изготовленных деталей на этих же станках, то получим приведенные затраты на одну деталь (последняя графа таблицы 1.1.), которые показывают, что в первую очередь необходимо искать причину брака на станке Д.

Диаграмма Исикавы

Выявить основные источники брака, еще не значит определить его причины. А причин может быть много, так же как и множество факторов, вызывающих эти причины. Прежде, чем искать причины, необходимо обозначить наиболее вероятные факторы, которые эти причины инициируют. Японский ученый К. Исикава первым предложил методику поиска причин, которая называется диаграммой Исикавы. Эта диаграмма имеет еще несколько названий: диаграмма причин и результатов, диаграмма «речных притоков», диаграмма «рыбий скелет». Последние два названия связаны с графической интерпретацией диаграммы.

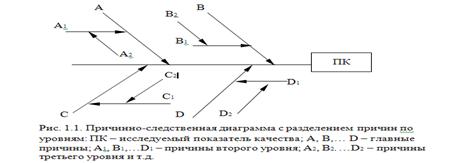
Рассмотрим построение диаграммы Исикавы. На первом этапе необходимо выделить (сформулировать) проблему. Например, выход за пределы допуска размера параметра качества. График диаграммы действительно похож на скелет рыбы, на котором центральный хребет представляет собой анализируемый показатель качества, а большие кости скелета, направленные к хребту почти вертикально (но с небольшим наклоном назад, от головы, где сформулирована проблема), представляют собой главные причины, которые могут привести к отклонению показателя качества. К главным причинам (костям) под прямым углом проводятся горизонтальные отрезки причин второго порядка и т.д. (рисунок 1.1.).

Количество второстепенных костей, соответствующих причинам низшего порядка значимости, зависит от глубины дальнейшего анализа.

На втором этапе команда специалистов методом «мозгового штурма» выделяет наиболее вероятные (главные и второстепенные) причины отклонений показателя качества. Создание команды не исключает привлечения к обсуждению проблемы других специалистов функциональных подразделений или работников подразделения, в котором сформировалась проблема.

На третьем этапе производится сортировка причин по их предполагае мой значимости (вероятности). При сортировке можно использовать диаграмму Парето с целью экспериментальной проверки в первую очередь тех вероятных причин, суммарная значимость которых превышает 75-80%.

На четвертом этапе разрабатываются мероприятия по экспериментальной проверке этих причин. При планировании экспериментов необходимо подбирать контрольные партии образцов с учетом расслоения вероятных факторов. Анализ и проверка продолжаются, пока не будут выяснены истинные причины отклонения показателя. При длительных безуспешных поисках выделенных причин целесообразно вернуться к диаграмме и определить новые направления поиска. Процесс поиска можно считать законченным, если издержки производства по данному показателю качества снизились в 2-5 раз.

Управление процессом с помощью контрольных карт

Для управления процессом с помощью контрольных карт надо проверить, приемлема ли его воспроизводимость, т.е. определить, стабилен ли процесс и указывает ли диапазон варьирования показателя качества на карте на удовлетворительное согласование с требованиями документации. Если оказывается, что процесс неадекватен, и показатель качества находится в неконтролируемом состоянии, надо проработать план проведения экспериментов, позволяющих выявить причины отклонений и преодолеть ненормальность в рамках действующих контрольных границ, одновременно улучшая процесс.

Если контрольная карта показывает, что процесс после улучшения находится в желаемом состоянии, то принятые новые контрольные границы и вводятся для управления процессом.

Когда в состоянии процесса обнаруживаются технические недостатки, контрольные линии (границы) надо пересматривать. Такой пересмотр необходимо осуществлять как можно быстрее. Даже если и не обнаруживаются заметные изменения, все равно надо делать регулярные перепроверки контрольных линий. Их пересмотр должен основываться на размахе вариаций, которые могут встретиться при хорошо управляемом процессе.

Для введения процесса в целом в контролируемое состояние, прежде всего, следует представить себе вклад различных факторов в возмущение процесса и избегать ненормальных изменений этих факторов. А чтобы этого достигнуть, нужна стандартизация (разработка СТП) технологических приемов и методов. Способность удовлетворять главными факторами процесса обязательна при планировании стандарта. Стандарты надо непрерывно пересматривать для улучшения ведения процесса с использованием контрольных карт.

При разработке стандартов необходимо пересмотреть все связанные с этим процедуры, их документальное оформление, пересмотр, подготовку кадров и внедрение.

5. Управление качеством продукции и регулирование технологических процессов на ООО «Ростовтехсервис»

Управление качеством (англ. qualitycontrol) - деятельность оперативного характера, осуществляемая руководителями и персоналом предприятия, воздействующими на процесс создания продукции с целью обеспечения её качества путём выполнения функций планирования и контроля качества, коммуникации (информации), разработки и внедрения мероприятий и принятия решений по качеству.

ООО «Ростовтехсервис» расположен по адресу: г. Ростов-на Дону ул. Доватора 150. Оказывает посреднические услуги по предоставлению в субаренду складских помещений, открытых площадок, предоставляет места для погрузки, выгрузки автомобилей и производство продукции.

Операции с недвижимым имуществом, предоставление посреднических услуг, связанных с недвижимым имуществом, деятельность агентств по операциям с недвижимым имуществом. Предоставление посреднических услуг при покупке, продаже и аренде недвижимого имущества, предоставление посреднических услуг при покупке, продаже и аренде нежилого недвижимого имущества. Эксплуатация гаражей, стоянок для автотранспортных средств, велосипедов, предоставление различных услуг клиентам.

С ООО «Ростовтехсервис» сотрудничает компания по производству «Ростовский воздухозавод» производитель воздухораспределителей, вентиляционного оборудования, систем дымоудаления и т.д.

Главная задача фирмы - это сохранять высокое качество, доступность продукции и услуг широким слоям населения. Только грамотная политика предприятия в области качества может привести к успеху. Основой обеспечения качества продукции и услуг ООО «Ростовтехсервис» являются согласованные и отрегулированные технологические производственные процессы. К этому относится также консультации и обслуживание клиентов на профессиональном уровне, взвешенный подход к процессу производства продукции с учетом пожеланий потребителей и арендатора.

6. Использование статистических моделей для прогнозирования состояния складских помещений и цены услуг аренды на ООО «Ростовтехсервис»

Постановка задачи

Руководство компании ООО «Ростехсервис» поручило службе качества определить зависимость между состоянием складских помещений (%) и стоимости арендной платы (тыс. руб.).

Задания:

)        Исследовать зависимость между признаками по выборочным данным с использованием поля корреляции.

)        Исследовать зависимость между признаками с использованием коэффициента корреляции и оценить наличие связи для генеральной совокупности с вероятностью 0,95.

)        Построить уравнение линейной регрессии, устанавливающее функциональную зависимость между состоянием складских помещений (%) от стоимости арендной платы (тыс. руб.).

)        С вероятностью 0,95 определить прогноз стоимости арендной платы (тыс. руб.), если состояние складских помещений равно 50 (%).

Задание 1

Исследовать зависимость между признаками по выборочным данным с использованием поля корреляции.

Решение: Обозначим переменные:

Х - независимая переменная - состояние складских помещений, %;

У - зависимая переменная - стоимость арендной платы (тыс.).

Построим поле корреляции, для чего можно использовать мастер диаграмм в табличном процессоре MSExcel

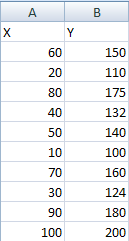
Занесем данные выборочных наблюдений в таблицу MSExcel (рис 1).

Отсортируем данные по убыванию переменной Х и визуально убедимся в том, что с убыванием значений независимой переменной Х значения зависимой переменной У возрастают, что свидетельствует об обратной связи между признаками.

Рисунок 1

Построим поле корреляции, чтобы визуально определить наличие связи между Х иY, используя точечную диаграмму.

По направлению точек поля корреляции видим, что с возрастанием значений независимой переменной Х значения зависимой переменной У также возрастает, что подтверждает наличие прямой связи между признаками. (Рис. 2)

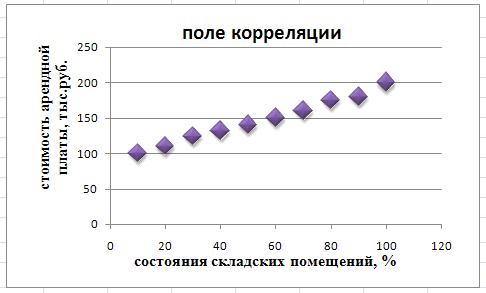
Рисунок 2 Точечная диаграмма

Для более точной числовой оценки наличия и тесноты связи между признаками используются разные критерии: коэффициент Фехнера, критерий Пирсона, коэффициент корреляции. Наиболее точный вывод о наличии или отсутствии корреляционной связи позволяет сделать линейный коэффициент корреляции, вычисленный и оцененный в соответствии со специальным алгоритмом.

Расчет коэффициента корреляции производится по формуле:

,

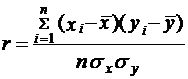n - объем выборки,

x_i,y_i выборочные значения соответствующих признаков,

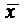и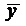- средние арифметические выборочных значений соответствующих признаков,

σ_xи σ_y - средние квадратические отклонения выборочных значений соответствующих признаков.

Близость расчетного коэффициента к -1 свидетельствует о наличии тесной обратной связи между исследуемыми признаками.

Коэффициент корреляции, приближающийся по своему значению к +1, свидетельствует о прямой зависимости одного признака от другого.

Незначительное отклонение коэффициента корреляции его от нуля означает отсутствие связи.

Как же оценить близость или удаленность коэффициента корреляции, рассчитанного по выборочным данным к |1| во всей генеральной совокупности? Ведь вывод ос связи зависит и от размера выборочной совокупности, и от точности, с которой мы хотим получить результат, и от величины самого выборочного коэффициента корреляции.

Коэффициент корреляции оценивают с помощью t - критерия (критерия Стьюдента) для оценки значимости коэффициента корреляции.

Проверка критерия осуществляется по следующему алгоритму:

Выдвигается гипотеза Но:

коэффициент корреляцииr=0, т.е. между переменными х и у не существует линейной связи, иначе говоря, независимая переменная х не помогает в предсказании значений зависимой переменной у.

Альтернативная гипотеза H₁:

коэффициент корреляцииr близок к ±1 между переменными х и у существует некая линейная связь, х помогает в прогнозировании у.

Для оценки этих двух альтернативных гипотез используем критерий Стьюдента, имеющий для оценки коэффициента корреляции такой вид:

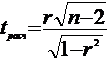
Расчетное значение критерия сравниваем с табличным значением t-распределения Стьюдента для уровня значимости α=1-γ (где γ - вероятность, с которой мы хотим получить оценку) и числа степеней свободы k=n-2 для двух переменных (где n - объем выборочной совокупности - число пар значений выборки).

Если 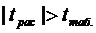, то с вероятностью γ=1-α можно утверждать, что гипотеза Н₀ отклоняется в пользу альтернативной, а это означает значимость коэффициента корреляции для генеральной совокупности, значит между переменными х и у существует некая линейная связь и переменная х помогает в прогнозировании переменной у.

Если 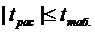, значит, с вероятностью γ, нулевая гипотеза принимается, и между переменными х и у не существует линейной связи, а отличие коэффициента корреляции от нуля произошло благодаря случайным колебаниям выборки.

Для расчета коэффициента корреляции можно построить дополнительную таблицу, позволяющую упростить вычисления.

Задание 2

Исследовать зависимость между признаками с использованием коэффициента корреляции и оценить наличие связи для генеральной совокупности с вероятностью 0,95.

Решение: Обозначим переменные:

Х - независимая переменная - состояние складских помещений (%);

У - зависимая переменная-стоимость арендной платы (тыс. руб.).

Вычислим коэффициент корреляции по формуле (.1)

γ - заданная вероятность оценки зависимости.

Построим вспомогательную таблицу для удобства вычислений (Таблица 1).

Таблица 1

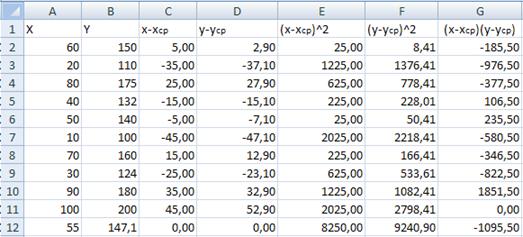
Используя табличные данные вычислим:

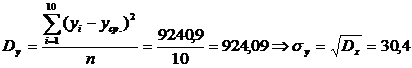
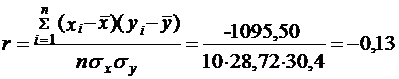
По данным выборки получен коэффициент корреляции r= -0,13. Отрицательное значение коэффициента корреляции и его близость к -1 по абсолютной величине свидетельствуют о наличии обратной связи между Х и У.

Оценим коэффициент корреляции, используя t - критерий Стьюдента

Выдвигаем гипотезу Но:

коэффициент корреляцииr=0, т.е. между переменными х и у не существует линейной связи.

Альтернативная гипотеза H₁:

коэффициент корреляцииr близок к -1 между переменными х и у существует обратная линейная связь.

Для оценки этих двух альтернативных гипотез используем критерий Стьюдента (2.)

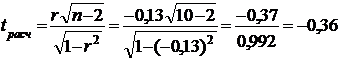
Расчетное значение критерия сравниваем с табличным значением t-распределения Стьюдента для уровня значимости α=1-0,95=0,05 (где γ - вероятность, с которой мы хотим получить оценку) и числа степеней свободы k=n-2=8. Значение получаем из таблицы t_таб.= 2,31.

Ответ: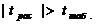, значит с вероятностью γ=0,95 можно утверждать, что гипотеза Н₀ отклоняется в пользу альтернативной, а это означает значимость коэффициента корреляции для генеральной совокупности, значит между переменными х и у существует обратная линейная связь.

Значение коэффициента корреляции можно получить проще, если использовать мастер функций табличного процессора MSEXCEL. Для этого, можно воспользоваться статистической функцией КОРРЕЛ в мастере функций, используемая для расчета коэффициента корреляции между данными двух рядов наблюдений.

Необходимо сделать активной ячейку, куда будет заноситься полученный результат, выбрать «Мастер функций», категория «Статистические», в открывшемся списке выбрать функцию КОРРЕЛ и ОК.

Затем в режиме диалога указываем диапазоны ячеек, в которых находятся выборочные данные X и Y

Для расчета коэффициента корреляции необходимо указать адреса массивов с данными на листе EXCEL, выделив мышью соответствующие диапазоны ячеек.

Для расчета значения t_расч можно записать в ячейке таблицы EXCEL формулу, используя математическую функцию КОРЕНЬ.

Определить табличное значение t-критерия Стьюдента для уровня значимости a=0.05 и числа степеней свободы n-2=10-2=8 можно используя статистическую функцию СТЬЮДРАСПОБР (0.05; 8).

Задание 3

Построить уравнение линейной регрессии, устанавливающее функциональную зависимость между состоянием складских помещений (%) от стоимости арендной платы (тыс. руб.).

Решение:

У - зависимая переменная - состояние складских помещений (%).

Х - независимая переменная - стоимость арендной платы (тыс. руб.);

Используя данные в таблице 1, определим:

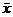=55; σ_x = 28,72

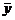=147,1; σ_y = 30,4

По данным выборки при выполнении задания 2 был получен коэффициент корреляции r=-0,13.

Построим уравнение линейной регрессии вида ŷ(x)=a₀+a₁x, для этого определим значения a₀ и a₁, используя коэффициент корреляции по формулам.

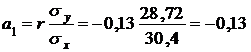
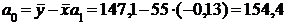
Ответ: Уравнение регрессии У по Х имеет вид: y=154,4+(-0,13) x.

Прогноз по регрессии

Знание функциональной зависимости между двумя переменными имеет существенное практическое значение, так как дает возможность составить прогноз значения результативного признака в предположении, что признак-фактор примет определенное значение. Определение величины результативного признака для определенного уровня признака-фактора является первым этапом при практическом использовании уравнений регрессионной зависимости.

Функциональная зависимость позволяет с определенной вероятностью по отдельному значению факторного признака x₀ установить значение результативного признака y₀. Получить точечную оценку прогноза можно из уравнения регрессии ŷ(x)=a₀+a₁x, если подставить в него значение x₀.

Полученное после подстановки значение y(x₀) называется точечным прогнозом зависимого или результативного признака при заданном значении факторного признака x_0.

Однако на практике не используются точечные прогнозы, так как уравнение, построенное по эмпирическим данным, не может давать точного результата. Уравнение регрессии дает характеристику связи лишь в среднем. Однако средняя величина должна быть дополнена показателями рассеяния, которые дадут возможность выяснить, насколько показательна средняя.

Обычно точечное значение используется для построения доверительного интервала прогноза, который строится вокруг точечной оценки. Доверительный интервал прогноза рассчитывается для заданного уровня значимости.

Под доверительным интервалом прогноза понимают интервал, в который с заданным уровнем значимости α=1-γ, где γ - надежность прогноза, попадают значения результативного признака при конкретном (точечном) значении признака (x₀).

Для оценки степени пригодности рассчитанного уравнения функциональной зависимости в тех или иных практических целях нужно знать меру рассеяния эмпирических точек относительно линии.

Иногда рассеяние эмпирических точек настолько велико, что нет смысла для прогнозов пользоваться рассчитанными уравнениями корреляционной связи, так как погрешность такого прогноза будет чрезвычайно велика.

В качестве меры достоверности уравнения регрессии используют среднюю квадратичную ошибку уравнения, представляющую собой среднее квадратическое отклонение эмпирических значений относительно значений, рассчитанных по уравнению регрессии:

,

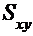-средняя квадратическая ошибка вычисленных значений;

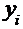-фактические значения результативного признака, полученные по данным наблюдения;

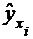- значения результативного признака, рассчитанные по уравнению корреляционной связи и полученные подстановкой значений факторного признака x_i в уравнение ŷ= a₀+a₁x.

Величину

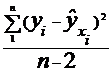
называют остаточной дисперсией, она характеризует ту часть общей дисперсии результативного показателя, которая обусловлена действием прочих факторов.

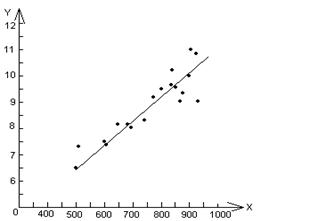
Рис. 3. Колеблемость фактических значений признака Y относительно линии регрессии

Чем меньше рассеяние эмпирических точек вокруг прямой (см. рис.), тем меньше средняя квадратическая ошибка уравнения. Таким образом, величина 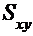 служит показателем значимости и полезности прямой, выражающей соотношение между двумя признаками.

Средняя квадратическая ошибка уравнения дает нам возможность в каждом отдельном случае с определенной вероятностью указать, что величина результативного признака окажется в определенном интервале относительно значения, вычисленного по уравнению связи.

Поскольку в основном для построения регрессионных моделей используются данные выборок, то зачастую интерпретация взаимоотношений между переменными в генеральной совокупности базируется на выборочных результатах. Для оценки истинного значения прогноза исследуемого параметра обычно используется доверительный интервал.

Доверительный интервал прогнозаимеет вид:

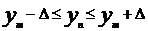
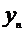- прогнозное значение результативного признака;

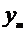- предсказанное значение y (точечное значение прогноза), которое получено подстановкой в ŷ= a₀+a₁x точечного значения факторного признака x₀;

∆ - интервальная оценка.

Оценка интервала прогноза ∆ находится по следующей формуле:

,

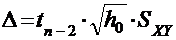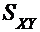 - средняя квадратичная ошибка уравнения (10);

t_n-2 - значение t-распределения Стьюдента для заданного уровня значимости и числа степеней свободы n-2,

h₀ - рассчитывается по формуле (13):

;

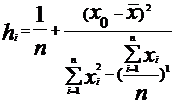n - объем выборки;

x₀ - заданное значение факторного признака x (точка прогноза)

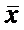- среднее значение факторного признака в выборке.

Очевидно, что увеличение объема выборки n уменьшит длину интервала. Более того, ширина интервала также варьирует с различными значениями X. Когда оценивается 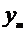 по значениям X, близким к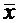; то интервал тем уже, чем меньше абсолютное отклонение x_i от 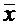(см. рис.).

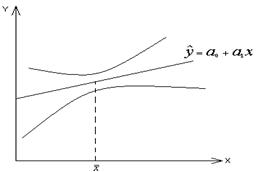
Когда оценка осуществляется по значениям X, удаленным от среднего 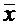, то величина интервала возрастает.

Если прогноз по уравнению регрессии строится нахождения неизвестных значений, находящихся внутри интервала экспериментальных значений факторного признака, то мы имеем дело с интерполяцией результирующего признака, если искомые значения выходят за этот интервал, то речь идет об экстраполяции.

При практическом использовании уравнений регрессии следует помнить, что экстраполяция допускается только тогда, когда существенно не изменяются условия формирования уровней признаков, которые лежали в основе определения функции регрессии. В противном случае использование уравнений для составления прогнозов должно быть отвергнуто. Необходим новый эмпирический материал, который отразит взаимосвязь между признаками в новых условиях с определенными качественными сдвигами.

Задание 4

С вероятностью 0,95 определить прогноз стоимости арендной платы (тыс. руб.), если состояние складских помещений равно 50 (%).

Решение:

У - зависимая переменная - стоимость арендной платы (тыс. руб.);

Х - независимая переменная - состояние складских помещений (%);

x₀=50 - точка, в которой рассчитывается прогноз

y=154,4+(-0,13) x - прогнозное уравнение регрессии.

Чтобы вычислить точечный прогноз, подставим в уравнение регрессии значениеx₀=50, получим y(x₀)=154,4+(-0,13)* 50=147,76

Построим доверительный интервал прогноза, для этого используем дополнительную таблицу (Таблица 2), в которой рассчитаем _I=154,4 - (-0,13) x_i

Таблица 2

Найдем интервальную оценку ∆, используя формулы 3-6.

Определим среднюю квадратичную ошибку уравнения, используя данные таблицы:

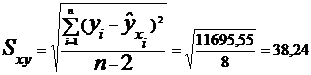
Найдем значение:

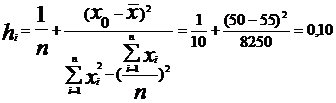
Определим t_n-2 табличное значение t-распределения Стьюдента для заданного уровня значимости α =0,05 и числа степеней свободы n-2=8.

Из таблицы получим t_n-2 =-0,36

Найдем ∆:

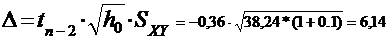
Построим доверительный интервал прогноза:

,76 - 6,14<Y_прогн.< 147,76 + 6,14

,63<Y_прогн.< 153,90 (%)

Ответ: с вероятностью 0,95 можно утверждать, что прогнозное значение стоимости арендной платы (тыс. руб.), если состояние складских помещений равно 50 (%) находится в доверительном интервале 141,63<Y_прогн.< 153,9 (%).

Заключение

Статистическое регулирование качества - это текущий контроль за производством и предупреждение брака путем своевременного вмешательства в технологический процесс. Техническим вспомогательным средством статистического регулирования является контрольная карта, позволяющая наглядно отразить ход производственного процесса на диаграмме и таким образом выявить нарушения технологии.

При построении контрольных карт важен выбор контролируемого параметра. Предпочтение целесообразно отдавать тем параметрам, которые непосредственно влияют на эксплуатационные характеристики продукции, легко поддаются измерению и на которые можно воздействовать путем регулирования технологического процесса.

Услуги ООО «Ростехсервис» отличаются своим широким набором услуг, небольшим количеством выпускаемой продукции, неизменно высоким качеством предоставления, и в то же время приемлемым уровнем цен. Это не только традиционные складские помещения с местами для хранения продукции, но и целый ряд удобных для арендаторов мест погрузки, выгрузки продукции, холодильные камеры, жд дороги, автокраны и т.д., способных заинтересовать даже самого искушенного клиента. Все услуги предоставляются по нормативной документации, стандартам. Проводятся экспертизы на предприятии и контроль документов. Все процессы на предприятие контролируют уполномоченные органы, в том числе и технологические процессы. Им уделяется огромное внимание.

Решение о виде контрольных карт для статистического управления технологическим процессом принимает разработчик технологии контрольных операций с учетом конкретных условий производства.

Список используемой литературы

1)  Мхитарян В.С. Статистические методы в управлении качеством продукции. М.: Финансы и статистика, 1982 г.

2)      ГОСТ Р 50 779.40-96. Статистические методы. Контрольные карты. Общее руководство и введение. М.: Изд-во стандартов, 1996 г.

3)  Статистические методы управления качеством // www.lenobl.ru, 2005 г.

4)      Максимова О.В., Махоткина А.М. Теория вероятностей и математическая статистика, г. Ростов-на-Дону, издательство Феникс 2008 г.

)        Максимова О.В. Теория вероятностей и математическая статистика. г. Москва, Дашков и К°, 2006 г.

)        Ефимов В.В. Статистические методы в управлении качеством. Ульяновск: УлГТУ, 2003 г.

)        Клячкин В.Н. Статистические методы в управлении качеством: компьютерные технологии, г. Москва, финансы и статистика 2008 г.

8)  http://www.list-org.com/company/7438562

9)      http://www.coolreferat.com/Статистические_методы_управления_качеством

)        http://ru.wikipedia.org/wiki/Технологический_процесс

) http://stud24.ru/sociology/statisticheskie-metody-kontrolya-kachestva-produkcii/70858-226363-page4.html