Основные статистические расчеты
Федеральное государственное бюджетное
образовательное учреждение
Высшего профессионального образования
Пермский национальный
исследовательский политехнический университет
Кафедра Маркетинга и Менеджмента
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Статистика»
Выполнила
студентка
Гуманитарного
факультета
Заочного
отделения
Направление:
«Управление персоналом»
Группы УП-
13Б
Нургалиева
Алёна Андреевна
Проверил
преподаватель:
Ламанова
Надежда Геннадьевна
Пермь 2014
ВАРИАНТ II
Тема 1.
Абсолютные и относительные величины
Решение задачи №1
Таблица 1
|
Год
|
Инвестировано (млн. руб.)
|
|
Запланировано
|
Фактически
|
|
1999
|
120 (упл)
|
130 (y0)
|
|
2000
|
140 (упл)
|
125 (y1)
|
90 35

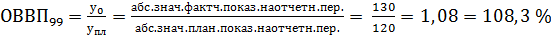
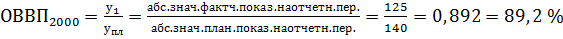


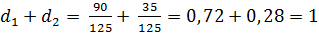
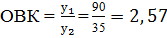
Тема 2. Средние величины
Решение задачи №2
Пусть хi - дневная
выработка i - го продавца; n - количество продавцов.
Таблица 2
|
Группы продавцов универмага по дневной выработке одного
продавца, тыс. руб.
|
10
|
12
|
15
|
0
|
|
Количество продавцов
|
5
|
7
|
4
|
|
Тогда ФЗП = 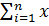 i= x1 + x2…+ x3 = 7000 руб. Средняя заработная плата
определяется по формуле простой средней,
i= x1 + x2…+ x3 = 7000 руб. Средняя заработная плата
определяется по формуле простой средней,
х = 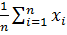 ,
,
Значения хi
, i = 1, n называется вариантами, тогда n - число вариант; fi , i = 1, k - частоты (определяют как часто встречается i - я варианта). В нашем примере
каждая варианта встречается один раз. Число вариант n = 3.
Тогда определим среднюю выработку одного продавца:
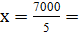 1400 руб.
1400 руб.
Из формулы простой средней следует, что
 = nx.
= nx.
Определение медианы и моды:
 Медиана по не сгруппированным данным (первичным)
определяется: совокупность значений ранжируется (упорядочивается),
Медиана по не сгруппированным данным (первичным)
определяется: совокупность значений ранжируется (упорядочивается),
Ме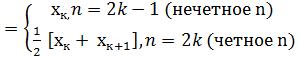 ,
,
в первом случае:
где k - номер элемента упорядоченного
ряда,
k =  ,
, 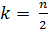 ;=
;= 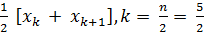 = 2, 5
= 2, 5
)Мода = М - значение признака, которому соответствует мах частота:
= 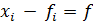 max
max
где 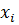 - частота,
- частота,
fi - количество продавцов.
M = 5
- 2 = 3
Решение задачи № 3
Пусть хi - зарплата
i - го работника; n - число групп работников предприятия.
Таблица 3
1
|
2
|
3
|
Всего
|
|
зарплата, тыс. руб.
|
2000
|
4 000
|
5000
|
11000
|
Тогда ФЗП = 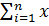 i= x1 + x2…+ x3 = 11000 руб. Средняя заработная
плата определяется по формуле простой средней,
i= x1 + x2…+ x3 = 11000 руб. Средняя заработная
плата определяется по формуле простой средней,
х = 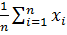 ,
,
Значения хi
, i = 1, n называется вариантами, тогда n - число вариант; fi , i = 1, k - частоты (определяют как часто встречается i - я варианта). В нашем примере
каждая варианта встречается один раз. Число вариант n = 3.
Тогда определим среднюю зарплату работников предприятия:
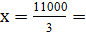 3667 руб.
3667 руб.
Из формулы простой средней следует, что
 = nx.
= nx.
Тема 3.
Статистические распределения и их основные характеристики
Решение задачи № 4
,1; 8,7; 8,5; 9,2; 5,8; 6,1; 5,2; 4,5; 6,4; 6,9; 8,1; 8,0; 7,2; 9,8;
10,2; 7,5; 7,7; 10,4; 10,5; 7,9.
Заметим, варианты признака не повторяются. Количество групп интервального
вариационного ряда определим по формуле Стэрджесса:
К = 1 + 3, 322  lgn,
где n - объем изучаемой совокупности;
lgn,
где n - объем изучаемой совокупности;
+ 3, 322 lg20 = 1 + 3, 322  1, 301 = 5, 32
1, 301 = 5, 32 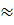 5.
5.
Размах вариации - R = (Х
мах - Х мin) = (10, 5 - 4, 5) = 6.
Величина интервала - h = R/К,
где К - число групп; h= 6/5
= 1,2.
Тогда интервальный ряд фирм по величине прибыли:
(4,5 - 5,7) (5,7 - 6,9) (6,9 -8,1) (8,1 - 9,3) (9,3 - 10, 5).
Для облегчения подсчётов расположим данные в порядке возрастания:
,5; 5,2; 5,8; 6,1; 6,4; 6,9; 7,2; 7,5; 7,7; 7,9; 8,0; 8,1; 8,5; 8,7; 9,1;
9,2; 9,8; 10,2; 10.4; 10,5.
Подсчитаем количество фирм в каждой группе fi, накопленные частоты Si, центральные значения для каждого
интервала хi0 fiи поместим в таблицу. Знак (-) рядом
с интервалом означает, что величина признака, совпадающая с верхней границей
интервала в этот интервал не включается, а попадает в следующий интервал. Знак
(+) означает, что верхняя граница включается в интервал.
fiи поместим в таблицу. Знак (-) рядом
с интервалом означает, что величина признака, совпадающая с верхней границей
интервала в этот интервал не включается, а попадает в следующий интервал. Знак
(+) означает, что верхняя граница включается в интервал.
Таблица 4
|
Первичные данные о затратах (усл. ден. ед.)
|
Число фирм или частота, fi
|
Накопленная частота, Si
|
Хi-центральное
значение интервалов
|
Хi0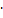 fi fi
|
|
(-)4,5 - 5,7
|
2
|
2
|
5,1
|
10, 20
|
|
5,7 - 6,9
|
3
|
5
|
6,3
|
18, 90
|
|
6,9 - 8,1
|
6
|
11
|
7, 5
|
45, 00
|
|
8,1 - 9,3
|
5
|
16
|
8, 7
|
43, 50
|
|
9,3 - 10,5
|
4
|
20
|
9, 9
|
39, 60
|
|
Итого
|
20
|
-
|
-
|
157, 20
|
 ;
;
Хi0 = 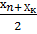 ;
;
Среднюю арифметическую вычислим по формуле:
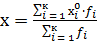 ,
,
где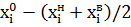 - центральное значение i-го интервала;
- центральное значение i-го интервала;
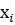 - варианты значения признака;
- варианты значения признака;
fi - частота повторения данного варианта.
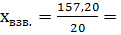 7, 860 млн. руб.
7, 860 млн. руб.
Определение моды и медианы интервального ряда распределения:
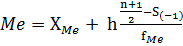 ,
,
где 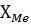 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
h -
величина интервала;
S(-1) - накопленная частота интервала,
предшествующего медианному;
FMe - частота медианного интервала.
К = (20 +1)/2 или К = n/2 ,
где n-число единиц совокупности;
К - номер (позиция) того значения признака, которое равно медиане;
Хi - значение признака i= 1, n.
К = (20 + 1)/2 = 10,5.
Сравнивая К с накопленными частотами, находим интервал соответствующий S3=11, FMe= 6, в котором находится медиана: (6, 9 - 8,1).
S(-1) = 5. Тогда:
Мe
Таким образом, 50 % фирм имеют прибыль 8 млн. руб., а 50 %- больше 8 млн.
руб.
М =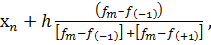
где хm- начало
модального интервала;
fm- частота соответствующая модальному интервалу;
f(-1)
- предмодальная
частота;
f(+1)
- постмодальная
частота.
Наибольшая частотаf3 = 6, соответствует интервалу (6, 9 -
8, 1). Значит мода находится в том же интервале что и медиана. Тогда:
M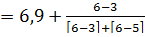 = 6, 9 + 0,75 = 7, 650 млн. руб.
= 6, 9 + 0,75 = 7, 650 млн. руб.
Таким образом, в данной совокупности фирм наиболее часто встречается
прибыль - 7, 650 млн. руб.
Таблица 5
|
Размер прибыли, млн. руб.
|
Число фирм, Fi
|
Расчетные показатели
|
|
|

|
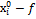 i i
|
xi - x
|
 fi fi
|
 fi fi
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
|
4,5 - 5,7(-)
|
2
|
5,1
|
10,20
|
-2,760
|
5,520
|
15,236
|
|
|
5,7 - 6,9
|
3
|
6,3
|
18,90
|
-1,560
|
4,680
|
7,309
|
|
|
6,9 - 8,1
|
6
|
7,5
|
45,00
|
-0,360
|
2,160
|
0,778
|
|
|
8,1 - 9,3
|
5
|
8,7
|
43,50
|
0,840
|
4,200
|
3,528
|
4
|
9,9
|
39,60
|
2,040
|
8,160
|
16,647
|
|
|
Итого
|
20
|
-
|
157,20
|
-
|
24,720
|
43,498
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение среднего линейного отклонения, дисперсии, среднего
квадратичного отклонения:
Размер вариации:
1) R = Хmax - Хmin ,
где Хmax -
максимальное значение;
Хmin - минимальное значение.
R =
(10, 5 - 4, 5) = 6.
Определение среднего линейного отклонения:
2) 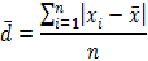 ,
,
где d - среднее линейное отклонение;
| | - абсолютное значение отклонения
варианта от средней арифметической;
| - абсолютное значение отклонения
варианта от средней арифметической;
n -
число фирм.
d = 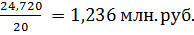
Определение дисперсии:
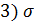 2 =
2 = 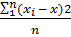 ,
,
где,  дисперсия;
дисперсия;
| | - абсолютное значение (модуль)
отклонения варианта от средней арифметической;
| - абсолютное значение (модуль)
отклонения варианта от средней арифметической;
n -
число фирм.
 = 2, 175 (млн. руб.)2
= 2, 175 (млн. руб.)2
Определение СКО:
 ,
,
где, 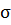 - дисперсия;
- дисперсия;
 =
=  =
= 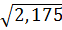 =1.088 млн. руб.
=1.088 млн. руб.
Тема 5. Ряды
динамики
Решение задачи № 4
) Абсолютный прирост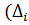 ) показывает, на сколько данный
уровень базисный:
) показывает, на сколько данный
уровень базисный:
 =
= 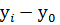 ,
,
где yi - уровень сравниваемого периода,
y0 - уровень базисного периода.
Абсолютный прирост при сравнении с переменной базой называют скоростью
роста:
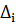 =
= 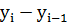 ,
,
где 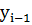 - уровень предшествующего периода.
- уровень предшествующего периода.
 =
=  =
=  n/1 ,
n/1 ,
где n - число уровней динамического ряда.
Сумма цепных абсолютных приростов:
 = 1, 0 + 0, 2 - 0, 6 - 0, 2 = 0, 4 =
= 1, 0 + 0, 2 - 0, 6 - 0, 2 = 0, 4 = 
) Коэффициент роста (Кi) показывает во сколько раз данный уровень превышает
уровень базисного периода.
При сравнении с постоянной базой Кi =  /y0
/y0
Коэффициенты выраженные в %, называют темпами роста:
Тpi = Кi 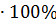
Если известны базисные коэффициенты роста, то частные от их
последовательного деления равно соответствующим цепным коэффициентам роста:
К5/4 = 1,1819/1,2728 = 0,9286
К4/3 = 1,2728/1,5455 = 0,8236
К3/2 = 1,5455/1,4546 = 1.0625
К2/1 = 1,4546/1 = 1,4546
Если известны цепные коэффициенты роста, то соответствующий базисный
коэффициент роста находится перемножением цепных коэффициентов роста.
величина интервал отклонение динамический
Кi/1
= 
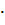 К3/2 … К(i-1)(i-2)
К3/2 … К(i-1)(i-2) Кi/(i-1).
Кi/(i-1).
К5/1 = 1, 4546 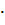 1, 0625
1, 0625 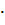 0, 8236
0, 8236 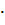 0, 9286 = 1, 1819
0, 9286 = 1, 1819
) Темп прироста (Тп) показывает, на сколько % уровень
данного периода больше (или меньше) базисного.
Этот показатель можно рассчитать двумя способами:
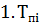 =
= 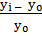 =
= 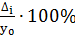 или
или 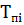 =
= 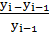 =
= 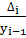 ,
,
. Тп = Тpi -
100%
) Абсолютное значение 1% прироста (Аi) сопоставляет темп прироста с абсолютным приростом за
тот же период времени:
Аi = 
где 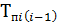 - темп прироста i - го уровня по сравнению с
- темп прироста i - го уровня по сравнению с - м уровнем.
- м уровнем.
Абсолютные значения 1% прироста Аi = 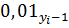 .
.
А2 = 2, 2 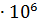
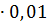 = 2, 2
= 2, 2  = 22000м2
= 22000м2
А3 = 3, 2 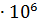
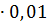 = 3, 2
= 3, 2 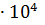 = 32000м2
= 32000м2
А5 = 2, 8 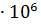
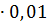 = 2, 8
= 2, 8 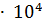 = 28000м2
= 28000м2
Таблица 6
|
Годы
|
Всего уровень безработицы по офиц. методике, %
|
Абсолютный прирост по сравнению, млн. 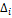
|
Коэффициенты роста по сравнению, Кi
|
Темпы прироста по сравнению, % 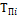
|
Абсолют-ное значение 1 % прироста, тыс.
|
|
|
С 1994г
|
С пред- шест- вую-щим годом
|
С 1994
г
|
С пред- шест- вую-щим годом
|
С 1994
г
|
С пред- шест- вую- щим годом
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
1994
|
2, 2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
1995
|
3, 2
|
1, 0
|
1, 0
|
1, 4546
|
1, 4546
|
45, 46
|
45, 46
|
22
|
|
1996
|
3, 4
|
1, 2
|
0, 2
|
1, 5455
|
1, 0625
|
54, 55
|
6, 25
|
32
|
|
1997
|
2, 8
|
0, 6
|
-0, 6
|
1, 2728
|
0, 8236
|
27, 28
|
-11,76
|
34
|
|
1998
|
2, 6
|
0, 4
|
-0, 2
|
1, 1819
|
0, 9286
|
18, 19
|
-7, 14
|
28
|
) Средний уровень ряда динамики высчитывается по формуле:
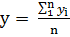 - интервал,
- интервал,
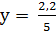 = 0, 44
= 0, 44
) Средний абсолютный прирост ряда динамики высчитывается по
формуле:
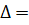
 ,
,
где n - число уровней ряда.
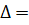
 =
= 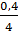 = 0,1
= 0,1
) Средний коэффициент роста ряда динамики высчитывается по
формуле:
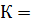
 …
… ,
,
где К1,..., Кn-1 - ценные коэффициенты роста;
n -
число уровней ряда.
Эту формулу можно записать иначе, если учесть взаимосвязь цепных и
базисных коэффициентов роста, т.е. что:
К1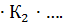
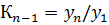
К = 
) Средний темп роста ряда динамики, представляет собой средний
коэффициент роста, выраженный в процентах, и вычисляется он по формуле:
Тр = К 
где К - среднегодовой коэффициент роста
Тр = 0, 82 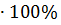 = 82%
= 82%
Таким образом, Т = 82%, а это значит, что в среднем ежегодно уровень
безработицы составлял 82% к уровню предыдущего года, т.е. в среднем уровень
безработицы снижался на 8%.
Тема 6.
Экономические индексы
Решение задачи № 6
) Индекс физического объема продукции определяется по формуле:
iqi =  ,
,
где  и
и  - количество единиц продукции в отчетном и базисном
периодах.
- количество единиц продукции в отчетном и базисном
периодах.
) Индекс цен продукции определяется по формуле:
рi
= 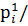
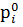 ,
,
где  - цена единицы продукции в отчетном и базисном периодах.
- цена единицы продукции в отчетном и базисном периодах.
Таблица 7
|
Вид про- дук- ции
|
Продано товара, кг
|
Цена 1 кг товара, руб.
|
Индивидуальные индексы физического объема iqi
|
Индивидуальные индексы цен iрi
|
|
Базисный период 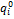
|
Отчетный период 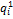
|
Базисный период 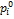
|
Отчетный период 
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
I
|
40
|
50
|
2,0
|
1,7
|
1,25
|
0,85
|
|
II
|
50
|
30
|
1,4
|
1,5
|
0,6
|
1,0715
|
Представление об изменении объема продукции дает индекс объема
(количества) продукции, предложенный в 1864г. Э. Ласпейресом.
) Агрегатный индекс динамики физического объема по Ласпейресу
определяется по формуле:
Iq =  ,
,
где 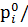
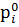 - коэффициент соизмерения или вес;
- коэффициент соизмерения или вес;
 - индексируемая часть.
- индексируемая часть.
IqI =  =
= 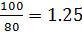
IqII = 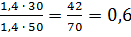
4) Индекс цен дает информацию об изменении цены и определяется по
формуле предложенной в 1874г. Г. Пааше:
p =  ,
,
где 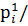
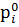 - индексируемая часть;
- индексируемая часть;
 - коэффициент соизмерения или вес.
- коэффициент соизмерения или вес.
IpI = 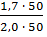 =
= 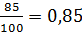 IpII =
IpII =