|
№
|
Назва визначників (чим
задана площина)
|
Визначник площини
|
Зображення площини
|
|
1
|
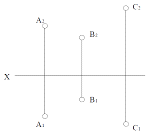
Трьома точками, які не належать
одній прямій.
Точки
А, В, С.
|
Σ (А, В, С)
|
|
|
2
|
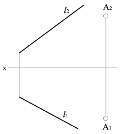
Прямою і точкою, яка не належить прямій. l ⊅
•А.
|
Σ (l, А)
|
|
|
3
|
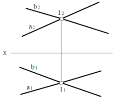
Двома перетинаючими прямими,
наприклад,
а
∩ b
|
Σ (а ∩ b)
|
|
|
№
|
Назва визначників (чим
задана площина)
|
Визначник площини
|
Зображення площини
|
|
4
|
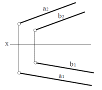
Двома паралельними прямими,
а || b
|
Σ (а || b)
|
|
|
5
|
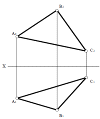
Плоскою фігурою (наприклад, трикутником
АВС)
|
Σ (ΔАВС)
|
|
|
6
|
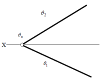
Слідами або лініями нульового
рівня
|
θ ( θ 1 ,
θ 2
), або θ
(f ̊∩ h ̊)
|
|
.3 Взаємне положення площин
Відрізняють три взаємних положення
площин (або їх відсіків):
· які збігаються;
· паралельні (не
співпадаючі);
· які перетинаються.
Методика визначення взаємного
розташування відсіків двох площин:
Дві прямі, які перетинаються, однієї
площини (її відсіку) перевіряються на належність їх до другої площини (до
другого відсіку) і далі аналізують взаємне розташування прямих однієї площини і
побудованих прямих другої площини і:
o Якщо дві прямі, які
перетинаються належать одному відсіку і другому відсіку (в своєму продовженні),
то один та другий відсік належать одній площині. Такі відсіки називаються
збігаючими (компланарними).
o Якщо дві прямі, які
перетинаються, однієї площини паралельні двом прямим, які перетинаються другої
площини, то ці дві площини паралельні між собою.
o Якщо дві прямі, які
перетинаються, однієї площини мимобіжні (або перетинаючі) відносно двох прямих,
які перетинаються другої площини, то такі дві площини перетинаються між собою.
2. Паралельність площин
Розглянемо взаємне положення площин
Р і θ, на рис. 8:
П2 ∩ Р ⇒
Р2; П2 ∩ θ ⇒
θ
2;
Якщо: Р1 ||
θ 1,
а Р2 || θ
2, то Р || θ.
Тобто, якщо дві паралельні площини Р
і θ перетинаються
площиною П1 або П2, то лінії їх перетину будуть
паралельні між собою.
В площині Р: Р1 і Р2
- дві прямі, що перетинаються, належні цій площині Р.
В площині θ:
θ
1 і θ
2 - дві прямі, що перетинаються,
належні цій площині θ.
Звідси витікає ознака паралельності двох площин: дві площини паралельні, якщо
дві прямі, що перетинаються однієї площини паралельні двом прямим, що
перетинаються другої площини. Такими прямими, що перетинаються можуть бути і
сліди площин, і їх прямі рівня, або довільні дві прямі цієї площини. Якщо дві
площини Р і θ
задані, наприклад, двома прямими, що перетинаються, то може бути, що: площина Р
задана: Р (Р1, Р2) або Р (f ∩h) або Р (а ∩
в), а площина задана θ
(θ 1,
θ
2) або θ
(f’ ∩h’) або θ(с
|| d) і Р || θ
, то на епюрі:
Якщо: Р(Р1, Р2)
|| θ (θ1,
θ2),
то Р2
|| θ2,
а Р1 || θ1
(рис. 9).
Якщо: Р(f ∩ h)
|| θ (f′ ∩ h′),
то f2 || f′2,
h1 || h′1 (рис. 10).
Якщо: Р(а ∩ b)
|| θ(c ∩ d),
то (а2 ∩ b2
) || (c2 ∩ d2),
(а1 ∩ b1)
|| (c1 ∩ d1).
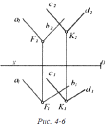
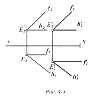
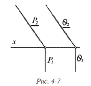
Рисунок 10 Рисунок 11
Якщо площини Р і θ
- паралельні між собою, то вони паралельні, коли
паралельні дві будь-які однойменні пари слідів, а якщо Р і θ
проектуючі,
то їх паралельність достатньо підкреслюється, коли одна з цих паралельних
однойменних пар є сліди на площині проекцій, до якої Р і θ
перпендикулярні
(рис. 11) (коли сліди - проекції паралельні).
3. Взаємно перпендикулярні площини
Дві площини взаємно перпендикулярні,
якщо одній із них належить пряма, яка перпендикулярна до іншої площини.
Побудову площини Р, яка перпендикулярна до площини θ
, можна виконати двома шляхами:
. Площину Р будуємо через пряму m,
яка перпендикулярна до площини θ
: ( m ⊥ θ
) ∧ ( m ∈
P) ⇒ P ⊥
θ
.
. Площину Р будуємо перпендикулярно
до прямої n, яка лежить у площині Q або паралельна цій площині: (n || θ
) ^ ( n ⊥
P) ⇒ P ⊥
θ
, оскільки через пряму m можливо провести безліч площин (перший шлях), а також
у площині або паралельно до неї можливо провести безліч прямих кож у площині
або паралельно до неї можливо провести безліч прямих n (другий шлях), то задача
має безліч розв’язків. Для отримання одного розв’язку необхідно накласти
додаткові умови. На рис.12 наведено приклад побудови на комплексному кресленні
для заданої площини P( Δ
ABC) із точки D перпендикулярної площини θ
.
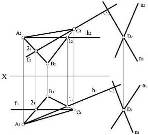
a ∈θ,
∈
a⊥ f2⊥
h1∈ n
θ( n
∩ a)⊥θ
Рисунок 12
Алгоритм розв ’язання задачі
складається з таких операцій:
1. Будуємо головні лінії площини
АВС: h - горизонталь, f - фронталь.
. З точки D будуємо пряму n, яка
перпендикулярна до площини
АВС: n2 ⊥
f2 , n1 ⊥
h1
3. Через точку D будуємо пряму а
загального положення:
P(ABC) ⊥
θ(
n ∩ a).
На рис. 13 наведено приклад побудови
на комплексному кресленні
двох взаємно перпендикулярних
площин, які задані слідами, одна з яких - площина загального положення Р, а
інша - горизонтально проекціювальна площина S.
Якщо площина S перпендикулярна до
площини П1 та до площини Р,
то S ⊥
P1 , як до лінії перетину площини Р та горизонтальної площини проекцій П1, тому
P1 ⊥ S1 , як до однієї
з прямих у площині S.
Проте, якщо однойменні сліди двох
площин загального положення взаємно перпендикулярні, то самі площини не
перпендикулярні між собою, оскільки при цьому не дотримується умова
перпендикулярності площин.
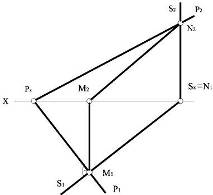
( S ⊥
П1 ) ∧ ( S ⊥
P ) ⇒ S ⊥
P1
Рисунок 13
4. Приклади розвязання задач
Приклад 1
Дано: площина Δ
(
Δ2,
Δ1
) і точка А, яка не належить цій площині (рис. 14). Необхідно через точку А
провести площину Σ паралельно
заданій площині Δ.
Через точку А проводимо горизонталь
Рисунок 14 шуканої площини, на епюрі (рис. 15).
На полі П2: •А2 ⊂
h2 ‖ Ox; На полі П1: •А1⊂
h1 ‖ Δ1
; h1 ∩ Ох → •N1, побудувавши •N2, отримуємо точку, яка належить
фронтальному сліду Σ2
, який пройде через • N2 і розташується ‖ Δ2.
Σ2
∩ Ох → Σx
⊂
Σ1
‖ Δ1
; Σ ‖ Δ
,
так як Σ2
‖
Δ2
, а Σ1 ‖ Δ1
.
Рисунок 15
Приклад 2
Для побудови Σ
‖
Δ
,
коли Δ ⊥
П1, і точка А ⊂
Σ
,
достатньо побудувати Σ1
⊃
•А1 і розташується Σ1
‖ Δ1
, що показано на рис. 16.
Коли задано площину Δ
⊥
П3, то площина Σ пройде
через точку А і розташується || Δ ,
при цьому на епюрі (рис. 4-21) •А3 ⊂
Σ3
‖ Δ3
, а Σ2 і Σ1
‖ Ох відповідно з точок сходу слідів Σz
i Σy .
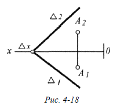
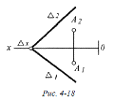
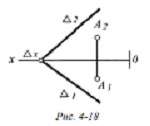
Рисунок 16
Висновок
Усі задачі на побудову двох
паралельних площин ґрунтуються на такій теоремі: дві площини паралельні, якщо
дві пересічні прямі однієї площини паралельні двом пересічним прямим іншої
площини.
Під час розв’язання позиційних задач
на перпендикулярність площин потрібно використовувати таку теорему: дві площини
взаємно перпендикулярні, якщо в одній з них існує пряма, перпендикулярна до
іншої площини. На підставі умови перпендикулярності площин, задачу про побудову
площини Ω, перпендикулярної
до площини Σ, необхідно
розв’язувати у такій послідовності:
) будується пряма l, перпендикулярна
до площини Σ;
2) через пряму l проводиться площина
Ω.
Оскільки через пряму l можна
провести безліч площин, то вказана задача на перпендикулярність двох площин у
загальному випадку має множину розв’язків. У зв’язку з цим, з метою
конкретизації відповіді, необхідно вказувати додаткові умови задачі.
Список використаної літератури
1. Курс нарисної геометрії
(О.М. Джеджула, C.І. Кормановський, А.В. Спірін, М.М. Пятак, А.Й. Островський)
2. Нарисна
геометрія (О.С. Хмеленко)
. Методичні вказівки для
самостійної роботи з виконання графічних завдань з дисципліни нарисна
геометрія, інженерна та машинна графіка
4. Інженерна
та компютерна графіка (В.Є. Михайленко, В.В. Ванін, С.М. Ковальов)
5. Курс
начертательной геометрии под редакцией В. Гордон