Схемные функции и частотные характеристики линейных электрических цепей
Контрольная
работа
по дисциплине
«Основы теории цепей»
СХЕМНЫЕ
ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Аннотация
В данной работе необходимо исследовать входные и передаточные операторные
функции.
Произвести расчет частотных характеристик по выражениям
амплитудно-частотных и фазово-частотных характеристик на основе карты нулей и
полюсов и с использованием автоматизированных методов анализа цепей.
Содержание
Введение
1. Исходные данные
2. Анализ исходных данных
3. Исследование нагрузки
4. Исследование транзистора с обобщенной
нагрузкой
5. Исследование транзистора с
избирательной нагрузкой
Заключение
Список
использованных источников
Введение
Основой метода анализа цепей в данной работе служат схемные функции этих цепей.
Схемная функция - это реакция цепи на входное воздействие. Любая цепь,
содержащая R, L, C элементы, может
быть описана системой дифференциальных уравнений, а для одной переменной
дифференциальным уравнением n-го
порядка:
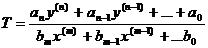
где
: x - воздействие; y - отклик;
ai и bi - коэффициенты, определяемы параметрами элементов и топологией схемы.
Если
данную функцию представить в комплексном виде, то она упрощается и в
топологическом виде выглядит:
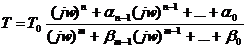 , где
, где
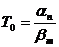 -
нормировочный коэффициент.
-
нормировочный коэффициент.
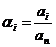 и
и 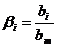 - коэффициенты при степенях.
- коэффициенты при степенях.
Комплексный метод не применим, если хоть один элемент нелинейный.
Комплексные функции определяются аналитическим способом - применение
методов контурных токов, узловых напряжений. Полученные функции используются
для исследования частотных характеристик цепи. По полученным комплексным
функциям можно построить карту нулей и полюсов, которая дает полную
характеристику цепи. На основе кары нулей и полюсов можно рассчитать
приближенные значения сопротивления и фазы по формулам:
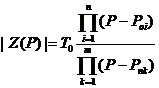
где
(P-Poi) - расстояние от текущей частоты до i-го
нуля.
(P-Pok) - расстояние то текущей частоты до k-го
полюса
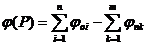
где
joi
- угол между вещественной осью и прямой, соединяющей текущую частоту и нуль.
jпk
- угол между вещественной осью и прямой, соединяющей текущую частоту и полюс.
1.
Исходные данные
Дана
эквивалентная схема замещения биполярного транзистора с общей базой (рисунок
2.1) и его параметры.
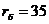 Ом
Ом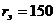 Ом
Ом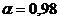
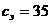 пФ
пФ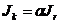
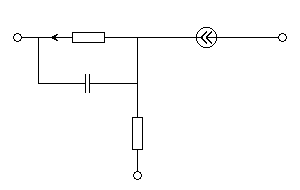
Рисунок
2.1 - Эквивалентная схема замещения биполярного транзистора.
где
: Cэ -
емкость эмиттерной цепи
rэ - сопротивление эмиттерной цепи
rб - сопротивление базы
Jк = a Jr - ток, зависящий от тока на сопротивлении эмиттера
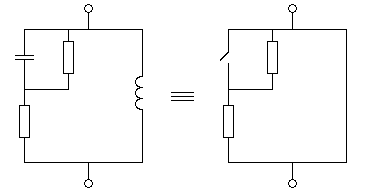
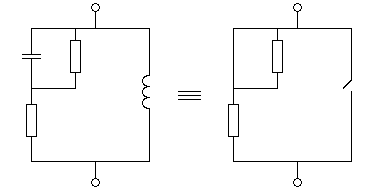
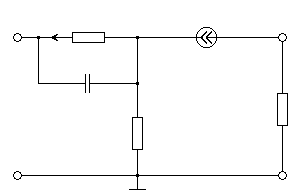
Схема
нагрузки изображена на рисунке 2.2
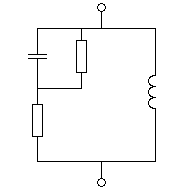
Рисунок
2.2 - Схема нагрузки.
где
: 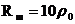 - шунтирующее сопротивление
- шунтирующее сопротивление
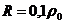 -
сопротивление
-
сопротивление
C - емкость
L -
индуктивность
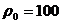 Ом
Ом
.
Анализ исходных данных
Расчет
резонансной частоты
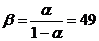 ;
; 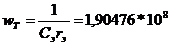 ;
; 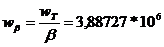 ;
;
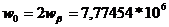
Нормировка
значений производится по формулам:
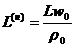 ;
; 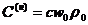 ;
; 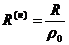 ;
;
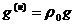 ;
;
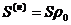 ;
;
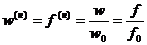 ;
; 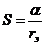 ;
;
Таблица
3.1 - Нормированные значения элементов.
|
Элементы
|
Параметры элементов
|
Нормированные значения
|
|
rэ
|
150 Ом
|
1.5
|
|
rб
|
35
|
0.35
|
|
Сэ
|
35 пФ
|
0.027211
|
|
R
|
10 Ом
|
|
Rш
|
1000 Ом
|
10
|
|
gэ
|
0.006667
|
0.6667
|
|
gб
|
0.028571
|
2.8571
|
|
g
|
0.1
|
10
|
|
gш
|
0.001
|
0.1
|
|
a
|
0.98
|
|
|
S
|
0.006533
|
0.6533
|
|
L
|
|
1
|
|
C
|
|
1
|
|
w
|
7774540
|
1
|
3. Исследование нагрузки
Рассчитаем параметры нагрузки на резонансной частоте

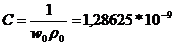 ;
; 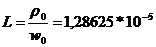 ;
;
для вычисления добротности, нужно схему преобразовать в эквивалентную
схему, где сопротивление шунта и емкость соединены последовательно.
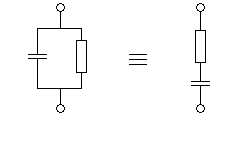
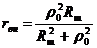 r0=100; Rш=1000; rвн=9,901;
r0=100; Rш=1000; rвн=9,901;
добротность
(R=10):
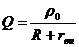 =5,025
=5,025
Вывод
операторных выражений входной и передаточной функций.
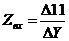 ;
; 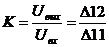 ;
;
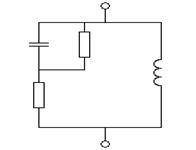
составим
матрицу проводимости нагрузки:
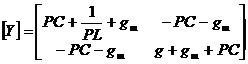 ;
;
вычислим
определитель матрицы проводимости нагрузки:
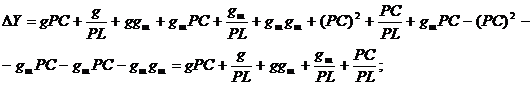
вычислим
алгебраическое дополнение:
D11=(g+gш+PC)
Входная
функция
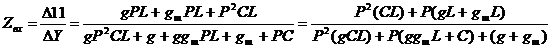
проверка
на размерность:
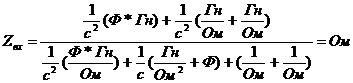
Исследование модели на крайних частотах
При w®0 :
(0)=j0; j(0)=90°;
При w®¥ :
z(¥)=0,1; j(¥)=-0°;
Нормировка
входной функции.
Подставив
нормированные значения в операторную функцию C=1; L=1; g=10;
g=0,1; получим:
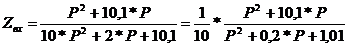 ;
;
Решив
нормированное уравнение входной функции, получим нули и полюсы операторной
функции:
P01=0; P02=-10,1;
- нули
Pп1=-0,1-j; Pп2=-0,1+j; -
полюсы
Карта
нулей и полюсов для нагрузки:
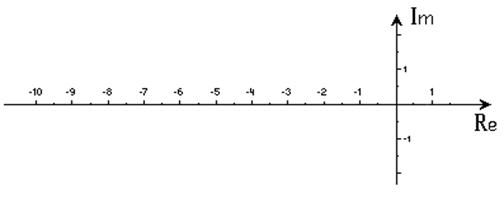
z(0)=0
z(1)=5,068
z(¥)=0,1
j(0)=90°
j(1)=8,52°
j(¥)=-0°
Амплитудно-частотная характеристика нагрузки.
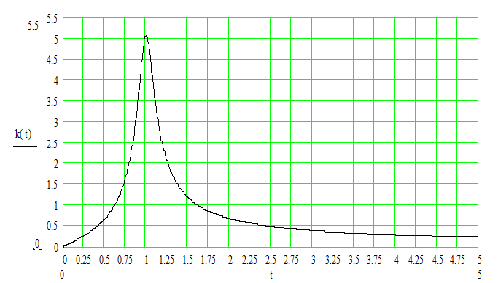
Фазово-частотная характеристика нагрузки.
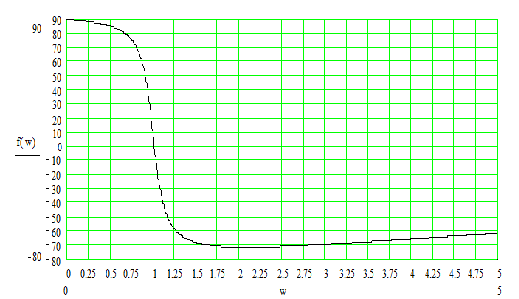

Расчет резонансных сопротивлений.
P=j - в нормированном, С=1; L=1; g=10; gш=0,1
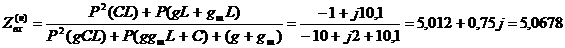
В
разнормированном виде:
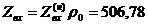 Ом
Ом
Определение полосы пропускания цепи (в нормированных единицах).
транзистор
биполярный нагрузка резонансный
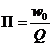 =0,199
=0,199
Определение
полосы пропускания цепи по карте нулей и полюсов.
Нужно
вычислить частоты при:
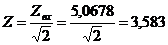 .
.
Составим
уравнение на основании карты нулей и полюсов
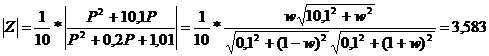
Найдем из последнего равенства w
w1=0,9098; w2=-0,9098; w3=1,1105; w4=-1,1105; т.к. w2 и w4 отрицательны и не имеют смысла, их можно отбросить, то
получается что граничные частоты это w1 и w3 . И следовательно полоса пропускания цепи равна (w3 - w1) . в нормированных частотах:
П=0,2007 в ненормированных частотах: П=1 560 350 (рад/с)
. Исследование транзистора с обобщенной нагрузкой
Операторное выражение передаточной функции.
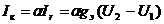 ;
;
Передаточная
функция:
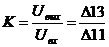 ;
;
Матрица
проводимости для транзистора с обобщенной нагрузкой.
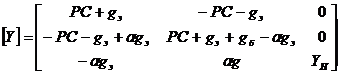 ;
;
алгебраические дополнения:
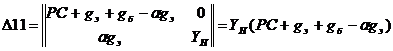 ;
;
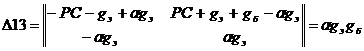 ;
;
подставив
алгебраические дополнения в передаточную функцию, получим:
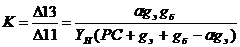 , т.к.
, т.к. 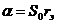 , то
, то
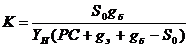 ;
;
Нормировка
передаточной функции: S0=0,6533; gб=2,8571; gэ=0,6667;
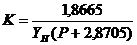
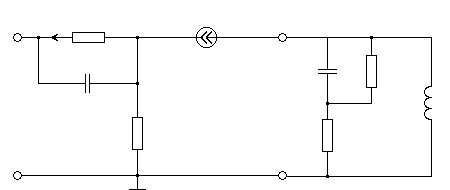
5. Исследование транзистора с избирательной нагрузкой
Схема транзистора с избирательной нагрузкой.
Выражение
передаточной функции
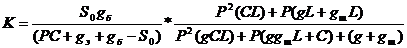
проверка
по размерности
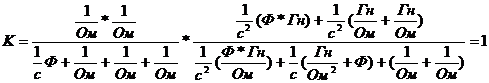
Нормированное
выражение передаточной функции транзистора
Подставив
нормированные значения в операторную функцию C=1; L=1; g=10; g=0,1; S0=0,6533;
gб=2,8571; gэ=0,6667; получим:
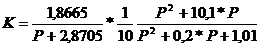
Решив
нормированное уравнение передаточной функции транзистора, получим нули и полюсы
операторной функции:
P01=0; P02=-10,1;
- нули
Pп1=-0,1-j; Pп2=-0,1+j; Pп3=-2,8705; - полюсы
Карта
нулей и полюсов для транзистора с избирательной нагрузкой:
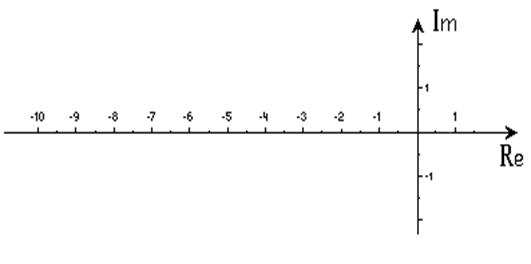
z(0)=¥
z(1)=3,1124
z(¥)=0
j(0)=90°
j(1)=-10,7°
j(¥)=-90°
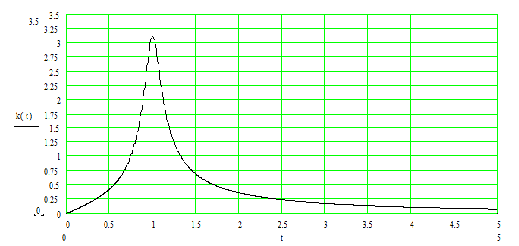
Амплитудно-частотная характеристика.

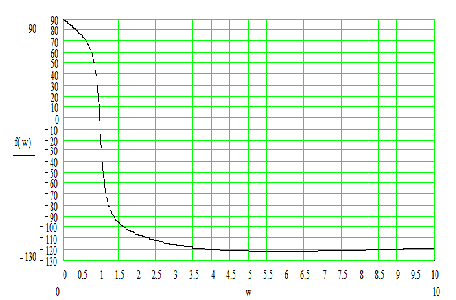
Фазово-частотная характеристика.

Заключение
В результате проделанной работы, исследовал нагрузку, транзистор с
обобщенной нагрузкой, полную цепь и получил для них входные и передаточные
функции.
Построил карты нулей и полюсов для нагрузки и полной цепи, а на основе
карт нулей и полюсов исследовал частотные характеристики, построил АЧХ и ФЧХ с
использованием автоматизированных методов.
Список использованных источников
1. Лосев А.К. Теория линейных
электрических цепей. - М.: Высшая школа 2007. - 511с.
2. Попов В.П. Основы теории цепей. - М.:
Высшая школа 2010. - 496с.
3. Основы теории цепей: Учебник для
вузов/ Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. - М.:Энергоатомиздат,
2009. - 528с.