Основные формулы теоретической механики
Задача С1
Для заданной схемы балки требуется найти опорные
реакции, если l=14 м, а=3,8 м, b=5 м, М=11 кН∙м, F=10 кН.
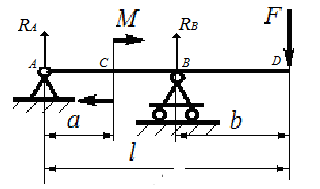
Рис.1
Решение. Так как горизонтальная нагрузка отсутствует,
то опора А имеет только вертикальную реакцию RA. Составляем уравнения равновесия в виде моментов всех сил
относительно точек А и В.
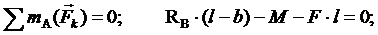
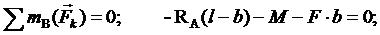
откуда
находим
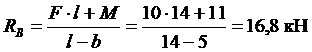 ,
,
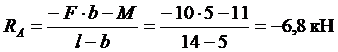 .
.
Для
проверки составим уравнение равновесия на вертикальную ось:
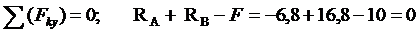
Контрольные
вопросы
балка шарнир сила точка
1. Как находится проекция силы на ось?
Проекция силы на ось - это алгебраическая величина,
равная произведению модуля силы на косинус угла между положительным
направлением оси и вектором силы (т.е. это отрезок, откладываемый силой на
соответствующие оси).
= F∙cosα;= P∙cosβ= P cos90o=0;= R∙cosγ = -R cos(180o-γ).
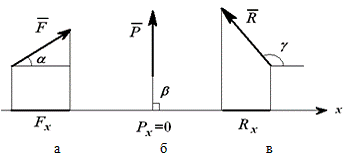
Рис. 2
Проекция силы на ось положительна, рис. 2 а), если 0 ≤
α < π/2.
2. В каком случае проекция силы на ось равна нулю?
Проекция силы на ось может быть равной нулю, рис. 2
б), если β = π/2.)
3.
В каком случае проекция силы на ось равна модулю силы?
Проекция силы на ось равна модулю силы, если α =0º.
4. В каком случае проекция силы на ось
отрицательна?
Проекция силы на ось может быть отрицательной, рис. 2
в), если π/2 < γ ≤ π.
5. Сколько уравнений равновесия составляется для
плоской сходящейся системы сил?
Силы называют сходящимися, если их линии действия
пересекаются в одной точке. Различают плоскую систему сходящихся сил, когда
линии действия всех данных сил лежат в одной плоскости.
Равновесие системы сходящихся сил.
Из законов механики следует, что твердое тело, на
которое действуют взаимно уравновешенные внешние силы, может не только
находиться в покое, но и совершать движение, которое мы назовем движением «по
инерции». Таким движением будет, например, поступательное равномерное и
прямолинейное движение тела.
Отсюда получаем два важных вывода:
) Условиям равновесия статики удовлетворяют силы,
действующие как на покоящееся тело, так и на тело, движущееся «по инерции».
) Уравновешенность сил, приложенных к свободному
твердому телу, является необходимым, но не достаточным условием равновесия
(покоя) самого тела; в покое тело будет при этом находиться лишь в том случае,
если оно было в покое и до момента приложения к нему уравновешенных сил.
Для равновесия приложенной к твердому телу системы
сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил была
равна нулю. Условия, которым при этом должны удовлетворять сами силы, можно
выразить в геометрической или аналитической форме.
1.
Геометрическое условие равновесия. Так как равнодействующая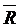 сходящихся сил определяется как замыкающая сторона
силового многоугольника, построенного из этих сил, то
сходящихся сил определяется как замыкающая сторона
силового многоугольника, построенного из этих сил, то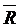 может обратиться в нуль тогда и только тогда, когда
конец последней силы в многоугольнике совпадает с началом первой, т. е. когда
многоугольник замкнется.
может обратиться в нуль тогда и только тогда, когда
конец последней силы в многоугольнике совпадает с началом первой, т. е. когда
многоугольник замкнется.
Следовательно,
для равновесия системы, сходящихся сил необходимо и достаточно, чтобы силовой
многоугольник, построенный из этих сил, был замкнут.
.
Аналитические условия равновесия. Аналитически равнодействующая системы
сходящихся сил определяется формулой
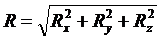
Так
как под корнем стоит сумма положительных слагаемых, то R обратится в
нуль только тогда, когда одновременно
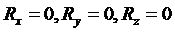
т.
е. когда действующие на тело силы будут удовлетворять равенствам:
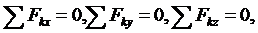
Равенства
выражают условия равновесия в аналитической форме: для равновесия
пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы
проекций этих сил на каждую из трех координатных осей были равны нулю.
Если
все действующие на тело сходящиеся силы лежат в одной плоскости, то они
образуют плоскую систему сходящихся сил. В случае плоской системы сходящихся
сил получим, очевидно, только два условия равновесия
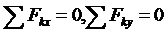
Равенства
выражают также необходимые условия (или уравнения) равновесия свободного
твердого тела, находящегося под действием сходящихся сил.
6. В какую сторону направлена реакция стержня с
шарнирным крепление концов?
Пусть в какой-нибудь конструкции связью является
стержень АВ, закрепленный на концах шарнирами (рис.3). Примем, что весом
стержня по сравнению с воспринимаемой им нагрузкой можно пренебречь. Тогда на
стержень будут действовать только две силы приложенные в шарнирах А и В. Но
если стержень АВ находится в равновесии, то приложенные в точках А и В силы
должны быть направлены вдоль одной прямой, т. е. вдоль оси стержня.
Следовательно, нагруженный на концах стержень, весом которого по сравнению с
этими нагрузками можно пренебречь, работает только на растяжение или на сжатие.
Если такой стержень является связью, то реакция стержня будет направлена вдоль
оси стержня.
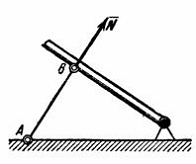
Рис.3
7. Как находится момент силы относительно точки?
Момент
силы относительно точки определяется произведением модуля силы на длину
перпендикуляра, опущенного из точки на линию действия силы (рис. 4, а). При
закреплении тела в точке О сила 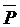 стремится
вращать его вокруг этой точки. Точка О, относительно которой берется момент,
называется центром момента, а длина перпендикуляра а называется плечом силы
относительно центра момента.
стремится
вращать его вокруг этой точки. Точка О, относительно которой берется момент,
называется центром момента, а длина перпендикуляра а называется плечом силы
относительно центра момента.
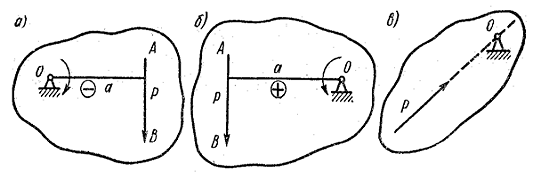
Рис.
4
Измеряются
моменты сил в ньютонометрах (Н∙м) или килограммометрах (кгс∙м) или
в соответствующих кратных и дольных единицах, как и моменты пар.
Момент
принято считать положительным, если сила стремится вращать тело против часовой
стрелки (рис.4, б), и отрицательным - в противоположном случае (рис. 4, а).
8. В каком случае момент силы относительно точки
равен нулю?
Когда линия действия силы проходит через данную точку,
ее момент относительно этой точки равен нулю, так как в рассматриваемом случае
плечо равно нулю: а = 0 (рис. 4, в).
9. Сколько уравнений равновесия составляется для
плоской произвольной системы сил?
Для плоской произвольной системы сил можно составить
три уравнения равновесия:
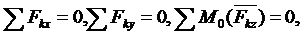
10. Как направлены реакции в неподвижном шарнире?
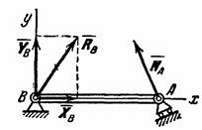
Рис.5
Неподвижная
шарнирная опора (рис.5, опора В). Реакция  такой
опоры проходит через ось шарнира и может иметь любое направление в плоскости
чертежа. При решении задач будем реакцию
такой
опоры проходит через ось шарнира и может иметь любое направление в плоскости
чертежа. При решении задач будем реакцию  изображать
ее составляющими
изображать
ее составляющими 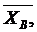 и
и 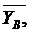 по
направлениям осей координат. Если мы, решив задачу, найдем
по
направлениям осей координат. Если мы, решив задачу, найдем 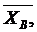 и
и 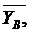 , то тем
самым будет определена и реакция
, то тем
самым будет определена и реакция  ; по
модулю
; по
модулю
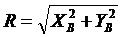
11. Как направлена реакция в подвижном шарнире?
Подвижная
шарнирная опора (рис.6, опора А) препятствует движению тела только в
направлении перпендикулярном плоскости скольжения опоры. Реакция такой опоры 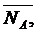 направлена по нормали к поверхности, на которую
опираются катки подвижной опоры.
направлена по нормали к поверхности, на которую
опираются катки подвижной опоры.
Задача
К1
Даны
уравнения движения точки в плоскости ху :
(х,
у - в сантиметрах, t - в секундах).
Определить
уравнение траектории точки; для момента времени t1 = 1c найти скорость и
ускорение точки.
Решение.
Для определения уравнения траектории точки исключим из заданных уравнений
движения время t.
Отсюда
находим следующее уравнение траектории точки (парабола, рис. 3):
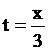 (2)
(2)
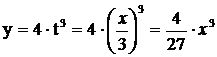
Скорость
точки найдем по ее проекциям на координатные оси:
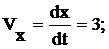
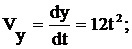
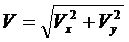
и
при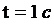 :
: 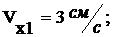
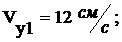
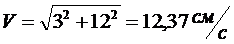 (3)
(3)
Аналогично
найдем ускорение точки :
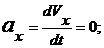
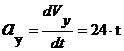
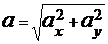
и
при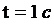 :
: 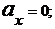
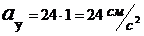
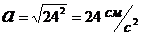
Касательное
ускорение

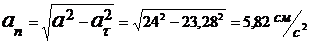
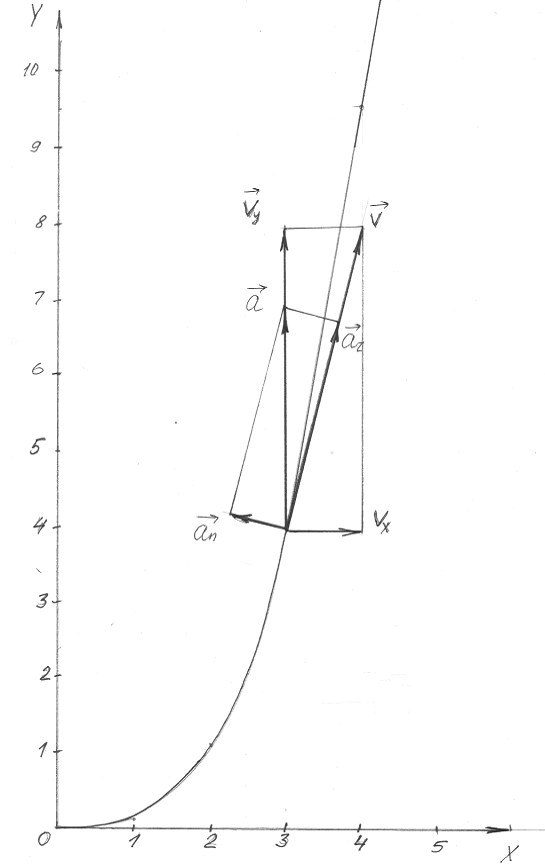
Рис. 7
Контрольные вопросы
1. Какими способами может быть задано движение
точки?
Движение точки может быть задано тремя способами:
естественным, векторным и координатным.
2. Что задается при векторном способе задания
движения?
При
векторном способе задания движения точки положение точки M
определяется величиной и направлением радиуса-вектора 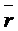 , проведенного из неподвижного центра O в
данную точку (рис. 8). При движении точки ее радиус-вектор
, проведенного из неподвижного центра O в
данную точку (рис. 8). При движении точки ее радиус-вектор 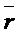 изменяется по величине и направлению. Поэтому, чтобы
определить положение точки в любой момент времени, достаточно задать ее
радиус-вектор
изменяется по величине и направлению. Поэтому, чтобы
определить положение точки в любой момент времени, достаточно задать ее
радиус-вектор 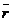 как функцию времени:
как функцию времени:
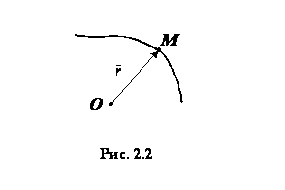
Рис.8
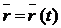 -это
равенство называется векторным уравнением движения точки.
-это
равенство называется векторным уравнением движения точки.
3. Что задается при координатном способе задания
движения?
При
координатном способе задания движения положение точки по отношению к выбранной
системе отсчета определяется при помощи прямоугольной системы декартовых
координат (рис. 9). При движении точки ее координаты изменяются с течением
времени. Поэтому, чтобы определить положение точки в любой момент времени,
достаточно задать координаты 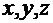 как
функции времени:
как
функции времени:
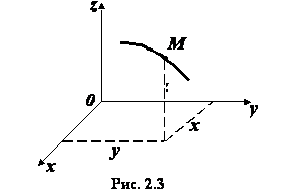
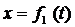 ,
, 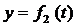 ,
,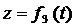
Эти
равенства называются уравнениями движения точки в прямоугольных декартовых
координатах. Движение точки в плоскости определяется двумя уравнениями системы,
прямолинейное движение - одним.
4. Что задается при естественном способе задания
движения?

Рис. 10
При естественном способе задания движения дается
траектория, т. е. линия, по которой движется точка (рис.10). На этой траектории
выбирается некоторая точка О, принимаемая за начало отсчета. Выбираются
положительное и отрицательное направления отсчета дуговой координаты S, определяющей положение точки на
траектории. При движении точки расстояние S будет изменяться. Поэтому, чтобы определить положение точки
в любой момент времени, достаточно задать дуговую координату S как функцию времени:
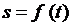
Это
равенство называется уравнением движения точки по данной траектории.
Итак,
движение точки в рассматриваемом случае определяется совокупностью следующих данных:
траектории точки, положения начала отсчета дуговой координаты, положительного и
отрицательного направлений отсчета и функции
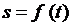
5. Как находится траектория точки координатном
способе задания движения?
Уравнения
движения точки в координатной форме - то параметрические уравнения траектории
движущейся точки, в которых роль параметра играет время 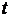 . Чтобы записать ее уравнение в явной форме, надо
исключить из них
. Чтобы записать ее уравнение в явной форме, надо
исключить из них 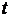 . В случае пространственной траектории, исключив
. В случае пространственной траектории, исключив 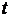 , получим:
, получим:
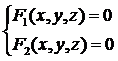
В
случае плоской траектории
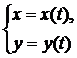
исключив
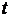 , получим
, получим
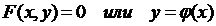
6. Как находится скорость и ускорение точки
векторном способе задания движения?
Пусть
точка за время 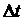 переходит из положения М в положение М1 , двигаясь
вдоль траектории (Рис. 11)
переходит из положения М в положение М1 , двигаясь
вдоль траектории (Рис. 11)
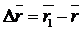
называется
вектором перемещения
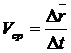 -
средняя скорость.
-
средняя скорость.
Например,
вектор 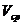 по хорде М М1 .
по хорде М М1 .
Если
уменьшать промежуток времени 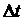 , то
хорда будет приближаться к касательной, а средняя скорость к мгновенной.
, то
хорда будет приближаться к касательной, а средняя скорость к мгновенной.
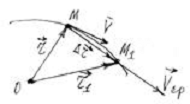
Рис.
11
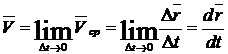
Направлен
вектор скорости по касательной к траектории.
Определение
ускорения:
Пусть
в положении М скорость 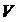 , а в положении М1 (через время
, а в положении М1 (через время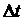 ) скорость
) скорость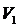 .
Приращение скорости
.
Приращение скорости
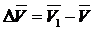
Среднее
ускорение:
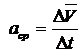
Ускорение
в данный момент
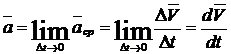

Лежит
вектор ускорения в плоскости, проведенных через касательной к траектории в двух
бесконечно близких точках. Эта плоскость называется соприкасающейся или
плоскостью главной кривизны.
7. Как находится скорость и ускорение точки
координатном способе задания движения?
При координатном способе задания движения:
с
другой стороны:
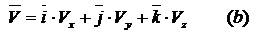
Сравнивая
(а) и (б) находим
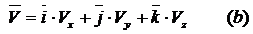
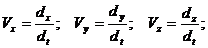
т.е.
проекция вектора скорости на оси координат равны первым производным по времени
от соответствующих координат.
Величина
скорости

Направление
вектора скорости определяется с помощью направляющих косинусов, т.е. косинусов
углов между вектором скорости и осями координат (рис. 12).

Рис.
12
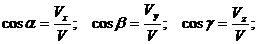
Аналогично
ищем ускорения:
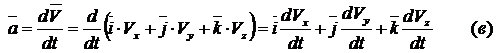
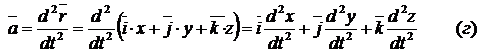
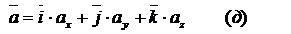
Сравнивая
(в), (г), (д) находим:
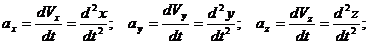
Проекция
ускорения равны первым производным по времени от соответствующих проекций
скорости или вторым производным по времени от соответствующих координат.
Величина
ускорения:
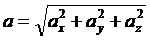
8. Как находится скорость и ускорение точки естественном
способе задания движения?
Пусть
за время 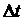 точка переместилась из положения М в положение М1 ,
совершив перемещение
точка переместилась из положения М в положение М1 ,
совершив перемещение 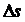 (рис. 13)
(рис. 13)
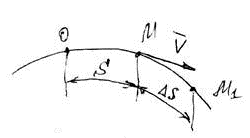
Рис.13
Величина
скорости точки:
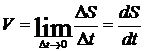
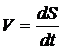
Направлена
скорость по касательной к траектории:
Найдем
ускорение точки.
Пусть
в положении М точка имеет скорость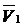 (рис.
14).
(рис.
14).
Полное
ускорение точки будет:
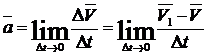
Обозначим
угол между касательными через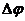 (угол
смежности). Спроецируем вектор ускорения
(угол
смежности). Спроецируем вектор ускорения 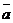 на
касательную τ и нормаль п .
на
касательную τ и нормаль п .
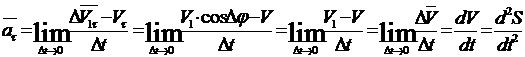
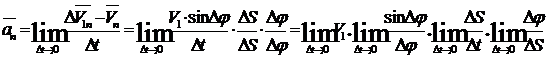

Рис.
14
Найдем
эти пределы, учитывая, что при 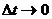 одновременно
и
одновременно
и 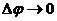 и
и 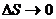 .
.
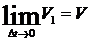
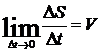
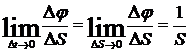
Подставив
эти значения в ап получим
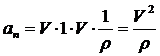
где
ρ - радиус кривизны траектории в данной точке.
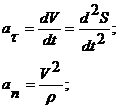
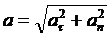
Касательное
ускорение направлено по касательной к траектории (в сторону скорости при
ускоренном движении и противоположно скорости - при замедленном) и
характеризует изменение величины скорости.
Нормальное
ускорение направлено по нормам к траектории к центру кривизны и характеризует
изменение направления скорости.
Задача Д1
Груз D массой m, получив в точке А начальную скорость
v0, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости;
участки трубы или оба наклонные, или один горизонтальный, а другой наклонный.
На участке АВ на груз кроме силы тяжести действуют
постоянная сила Q (ее направление показано на рисунках).
В точке В груз, не изменяя своей скорости, переходит
на участок ВС трубы, где на него кроме силы тяжести действует переменная сила
F, проекция которой Fx на ось х задана в таблице.
Считая груз материальной точкой и зная время t1
движения груза от точки А до точки В, найти скорость груза на участке ВС через t2= 2 сек после выхода из точки В.
Трением груза о трубу пренебречь.

Рис. 15
Дано : m = 3 кг, Q = 9 Н v0 = 22 м/с, t1= 3 с, Fx = 2t2-1.
Определить: V2 -скорость движения груза на участке ВС через t2= 2 с после выхода из точки В.
Решение.
Рассмотрим
движение груза на участке АВ, считая груз материальной точкой. Изображаем груз
(в произвольном положении) и действующие на него силы 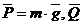 и
и 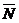 .
Проводим ось АZ и составляем дифференциальное уравнение движения груза в
проекции на эту ось :
.
Проводим ось АZ и составляем дифференциальное уравнение движения груза в
проекции на эту ось :
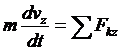 (1)
(1)
или
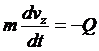 (2)
(2)
Разделим
в уравнении (2) переменные
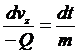 (3)
(3)
а
затем, берем от обеих частей интегралы
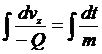
Получим
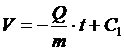 (4)
(4)
Постоянную
С1 найдем по начальным условиям:
при , тогда С1 = 22м/с.
, тогда С1 = 22м/с.
В
результате находим
Полагая
в равенстве (5) t = 3 с , определим скорость 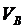 груза в точке В :
груза в точке В :
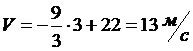
Теперь
рассмотрим движение груза на участке ВС; найденная скорость 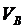 будет для движения на этом участке начальной
скоростью (
будет для движения на этом участке начальной
скоростью (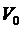 =
= 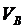 ).
).
Изображаем
груз (в произвольном положении) и действующие на него силы 
Проведем
из точки В ось ВХ и составим дифференциальное уравнение движения груза в
проекции на эту ось :
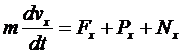 (6)
(6)
Так
как 
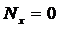 ,
,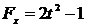 , то уравнение (6) примет вид
, то уравнение (6) примет вид
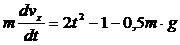 (7)
(7)
Разделим
обе части равенства (7) на m = 3 кг
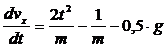
и
полагая g @ 10 м/с2 ,
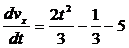
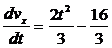 (8)
(8)
Умножая
обе части равенства (8) на dt
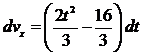 (9)
(9)
и
интегрируя, найдем
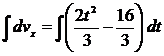 (10)
(10)
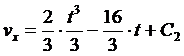 (11)
(11)
Постоянную
С2 найдем по начальным условиям.
Будем
теперь отсчитывать время от момента, когда груз находится в точке В, считая в
этот момент t = 0.
Тогда
при
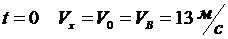 ,
,
Подставляя
эти величины в (11), получим
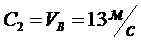
Тогда
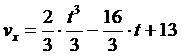
Подставляя
время движения на участке ВС t2=2c находим
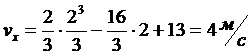
Контрольные
вопросы
1. Как формулируется первый закон динамики?
Любая изолированная материальная точка, то есть такая
точка, которая не подвержена влиянию других материальных тел, может совершать
по отношению к какой-либо неподвижной системе отсчета только равномерное
прямолинейное движение (скорость в данном случае величина постоянная) или
находиться в состоянии покоя (скорость равна нулю).
2. Как формулируется второй закон динамики?
Второй закон динамики (Ньютона) утверждает, что
причина ускорения тела − взаимодействие тел, характеристикой которого
является сила. Этот закон дает основное уравнение динамики, позволяющее, в
принципе, находить закон движения тела, если известны силы, действующие на
него. Этот закон может быть сформулирован следующим образом (рис. 16):
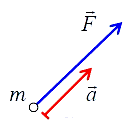
Рис. 16
ускорение точечного тела (материальной точки) прямо
пропорционально сумме сил, действующих на тело, и обратно пропорционально массе
тела:

здесь F − результирующая сила, то есть векторная
сумма всех сил, действующих на тело.
3. Как формулируется третий закон динамики?
Третий закон динамики (Ньютона) подчеркивает, что
причиной ускорения является взаимное действие тел друг на друга. Поэтому силы,
действующие на взаимодействующие тела, являются характеристиками одного и того
же взаимодействия. С этой точки зрения нет ничего удивительного в третьем
законе Ньютона (рис. 17):
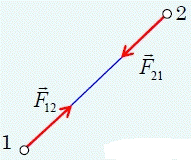
Рис. 17
Точечные тела (материальные точки) взаимодействуют с
силами, равными по величине и противоположными по направлению и направленными
вдоль прямой, соединяющей эти тела:

где F12 − сила, действующая на первое тело со
стороны второго, a F21 − сила, действующая на второе тело со стороны
первого. Очевидно, что эти силы имеют одинаковую природу. Этот закон также
является обобщением многочисленных экспериментальных фактов.
4.
Как записываются дифференциальные уравнения движения точки в декартовой системе
координат?
Из второго закона Ньютона динамики материальной точки
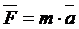
получаются
две наиболее распространенные формы дифференциальных уравнений движения:
дифференциальные
уравнения движения точки в координатной форме
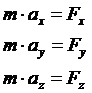 или
или 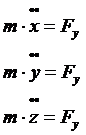
Где
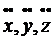 - проекции ускорения
- проекции ускорения 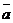 на оси
декартовых координат,
на оси
декартовых координат, 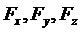 - проекции силы
- проекции силы 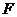 на те же
оси декартовых координат;
на те же
оси декартовых координат;
дифференциальные
уравнения движения точки в естественной форме
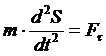
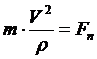
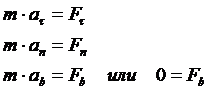
Где
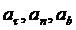 - проекции ускорения
- проекции ускорения 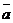 на
естественные оси координат;
на
естественные оси координат;
S - дуговая
координата точки;
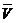 -
скорость точки;
-
скорость точки;
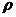 - радиус
кривизны траектории;
- радиус
кривизны траектории;
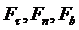 -
проекции силы
-
проекции силы 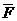 на естественные оси координат.
на естественные оси координат.
5. Как формулируются задачи динамики?
Для свободной материальной точки задачами динамики
являются следующие:
) зная закон движения точки, определить действующую на
нее силу (первая задача динамики);
) зная действующие на точку силы, определить закон
движения точки (вторая или основная задача динамики).
Решаются обе эти задачи с помощью уравнений,
выражающих основной закон динамики, так как эти уравнения связывают ускорение
т.е. величину, характеризующую движение точки, и действующие на нее силы.
6. Для чего нужны начальные условия?
При решении обратной задачи вводятся понятия
“начальное условие”. К начальному условию в механике относятся две величины
“положение материальной точки и скорость”, в момент рассмотрения задачи, т.е. в
момент рассмотрения задачи, т.е. в момент, когда время отсчёта равно 0, т.е.
при
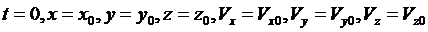
начальное
условие.
7. Как связаны вес и масса тела?
Вес и масса - разные понятия. Вес - сила, с которой
тело действует на горизонтальную опору или вертикальный подвес. Масса же - мера
инертности тела. Масса измеряется в килограммах, а вес в ньютонах. Вес - это
произведение массы на ускорение свободного падения (P = m∙g). Значение
веса (при неизменной массе тела) пропорционально ускорению свободного падения,
которое зависит от высоты над земной (или другой планеты) поверхностью. А если,
еще точнее, то вес - это частное определение 2-го закона Ньютона - сила равна
произведению массы на ускорение (F=m∙a). Поэтому его и вычисляют в
Ньютонах, как все силы.
Основные единицы: килограмм, метр, секунда, ампер,
кельвин, моль и кандела. В рамках СИ считается, что эти единицы имеют
независимую размерность, т. е. ни одна из основных единиц не может быть
получена из других.
9. В каких единицах выражается сила в системе СИ?
Сила в системе СИ измеряется в ньютонах (русское
обозначение: Н; международное: N)
Ньютон - производная единица. Исходя из второго закона
Ньютона она определяется как сила, изменяющая за 1 секунду скорость тела массой
1 кг на 1 м/с в направлении действия силы. Таким образом, 1 Н = 1 кг∙м/с2.
10. Что такое ускорение свободного падения?
Ускорение свободного падения (ускорение силы тяжести)
- ускорение, придаваемое телу силой тяжести, при исключении из рассмотрения
других сил. В соответствии с уравнением движения тел в неинерциальных системах
отсчёта ускорение свободного падения численно равно силе тяжести,
воздействующей на объект единичной массы.
Ускорение свободного падения на поверхности Земли g
(обычно произносится как «Же») варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах. Стандартное
(«нормальное») значение, принятое при построении систем единиц, составляет g =
9,80665 м/с². Стандартное значение g было определено как «среднее» в
каком-то смысле на всей Земле, оно примерно равно ускорению свободного падения
на широте 45,5° на уровне моря. В приблизительных расчётах его обычно принимают
равным 9,81; 9,8 или 10 м/с².
Список литературы
1. Тарг С.М. Краткий курс теоретической механики. М., 2009 - 416 с.
2. Мещерский И.В. Задачи по теоретической механике. М., 2005- 448 с.
. Пирогов С.П. Конспект лекций по теоретической механике. Тюмень,
ТюмГНГУ, 2005-108 с.
. Митягин Н.П., Пирогов С.П. Понятия, формулы, уравнения
теоретической механики (справочник). Тюмень, ТюмГНГУ, 2005-108 с.