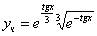Дифференциальные уравнения
Задания
Задание 1
Найти общий интеграл дифференциального уравнения
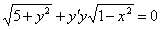
Решение:
Сделаем чертеж:
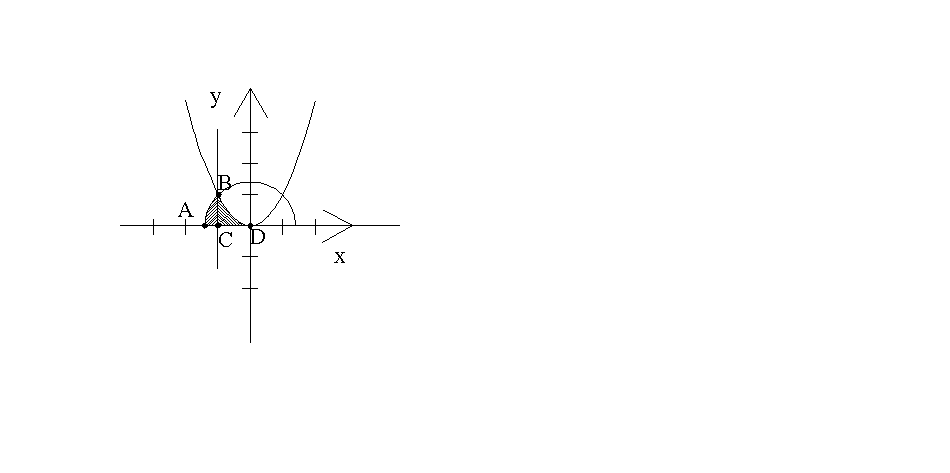
Из чертежа видим, что предел интегрирования по у [0; 1], покажем
это:
Найдем предел интегрирования по х:
Также можно найти сумму:
предел интегрирования по у [0; 1], покажем это:
Найдем предел интегрирования по х:
Задание 2
Найти общий интеграл дифференциального уравнения
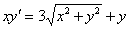
Решение:
Сделаем чертеж области D:
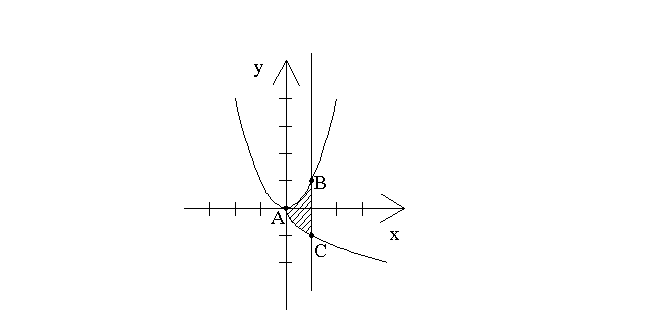
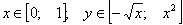
Расставим пределы интегрирования:
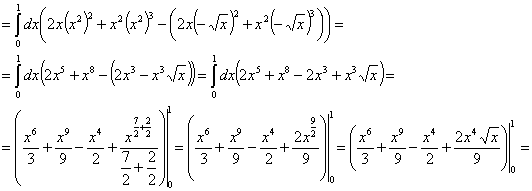
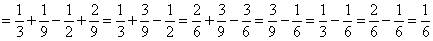
Задание 3
Найти общий интеграл дифференциального уравнения
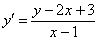
Решение:
Сделаем чертеж:
- графиком функции является парабола, ветви которой направлены
вверх.
Найдем координаты вершины параболы
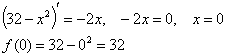
(0; 32) - координаты вершины параболы.
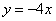- графиком функции является прямая.
Найдем точки пересечения прямой и параболы:
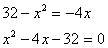
(8; - 32) и (-4; 16) - координаты точек пересечения графиков функций.
На промежутке [-4; 8]
Вычислим площадь фигуры с пределами интегрирования а=8 и b=-4.
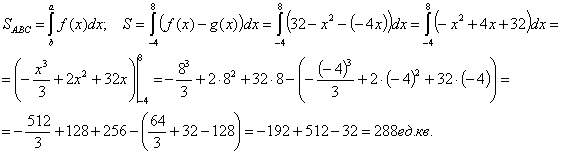
Ответ: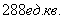 
Задание 4
Вычислить:
Решение:
Сделаем чертеж области D:
Расставим пределы интегрирования:
Задание 5
Найти объем тела, ограниченного поверхностями:
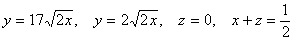
Решение:
Сделаем чертеж:
Из чертежа видим, что предел интегрирования по у:
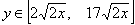
Из чертежа видим, что предел интегрирования по х:
предел интегрирования по z:
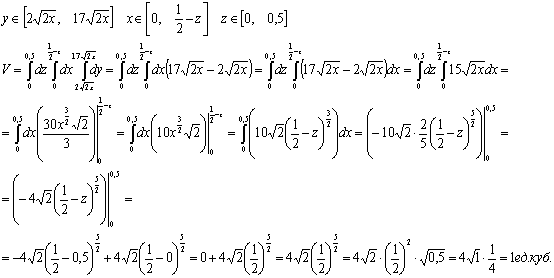
Ответ: 
Задание 6
Вычислить криволинейный интеграл
,
где L - путь, соединяющий точки А (0; 0) и В (2;
) по
Решение: х=у, dx=dy
Задание 7
Вычислить криволинейный интеграл
,
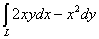где L - ломаная, соединяющий точки О (0; 0) А
(2;
) и В (2; 0) по
Решение:
ОВ, ВА
На участке ОВ принимаем за параметр ординату, при этом х=2, dx=0, на участке ВА, абсциссу, при этом у=1,
dy=0.
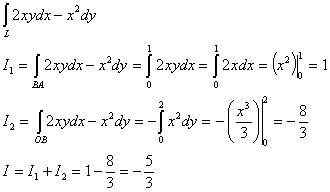
Задание 8
Показать, что данное выражение является полным дифференциалом
функции
. Найти функцию
Решение:
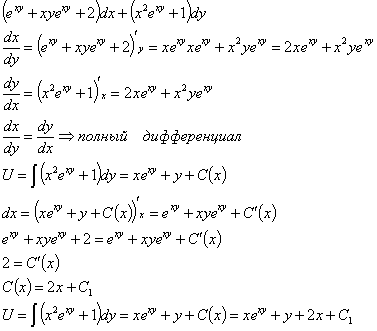
Задание 9
Вычислить криволинейный интеграл
,
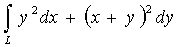где L - ломаная, соединяющий точки А (2; 0) В
(2;
) и В (0;2)
Решение:
Разбиваем замкнутый путь СВАС на три участка СВ, ВА, АС
На участке СВ принимаем за параметр ординату, при этом у=2, dу=0, на участке ВА, абсциссу, при этом х=2, dх=0, на участке АС ординату, при чем - ---х+2=у, х=2-у, - dx=dy
Задание 10
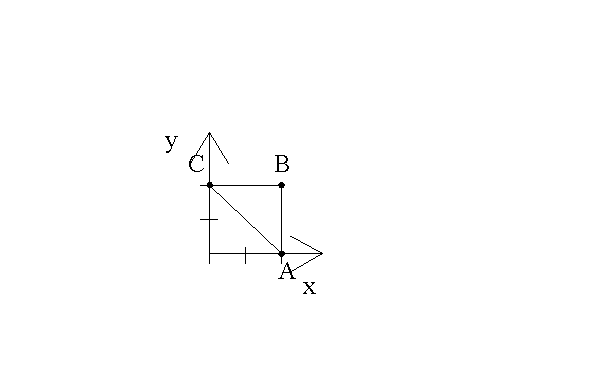
Вычислить длину дуги одной арки циклойды
Решение:
Задание 11
. Вычислить длину дуги цепной линии
Решение:
Сделаем чертеж:
Вычислим длину дуги кривой по формуле:
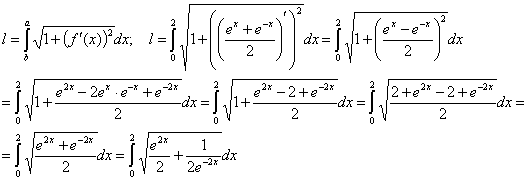
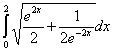- такой интеграл я не умею считать
Задание 12
Найти общее решение дифференциального уравнения
Решение:
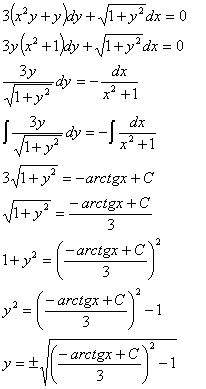
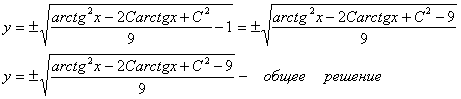
Ответ:
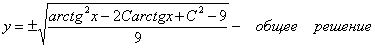
Задание 13
Решить задачу Коши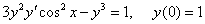 
Решение:
дифференциальное уравнение функция координата
Для отыскания частного решения найдем С
Ответ: 