Базисная система уравнений

Базисная система уравнений

Задание 1

Решить систему методом Гаусса и указать одно из базисных решений:

Решение

а) Найдем общее решение данной системы уравнений методом Гаусса. Для этого сначала выпишем ее расширенную матрицу:

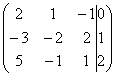
Далее с помощью элементарных преобразований полученной матрицы мы приведем ее к ступенчатому виду:

 ~  ~

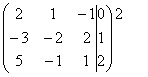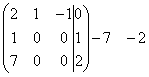Система несовместна, т.к. ранг матрицы равен 2, а ранг расширенной матрицы равен 3. Следовательно решений нет.

Задание №4

Решить систему методом Гаусса и указать одно из базисных решений:

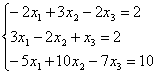
Решение

а) Найдем общее решение данной системы уравнений методом Гаусса. Для этого сначала выпишем ее расширенную матрицу:

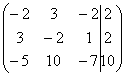
Далее с помощью элементарных преобразований полученной матрицы мы приведем ее к ступенчатому виду:

 ~  ~

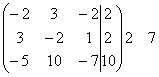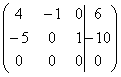
матрица уже имеет ступенчатый вид, поэтому можно перейти к системе эквивалентной данной. Выпишем соответствующую этой матрице систему:

.

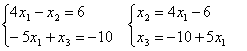Получили трапециевидную матрицу, в которой только две ненулевые строки. Значит ранг r = 2. Число неизвестных в системе n = 3. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 3 - 2 = 1 параметров.

Получаем, что х₂, х₃ - базисные неизвестные, а х₁ - параметры.

Обозначим для удобства х₁ =С₁ и выразим базисные неизвестные через параметры.

Мы нашли общее решение исходной системы: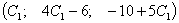

б) Найдем базисное решение исходной системы. Напомним вначале, что базисным называется такое решение системы, в котором все свободные неизвестные равны нулю. Такое решение мы получим, если в найденном нами общем решении положим :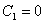

.

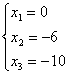
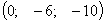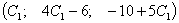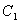Ответ: а) общее решение: , где  и 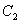 - произвольные числа б) базисное решение: .

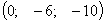Задание №3

Найти общее решение системы

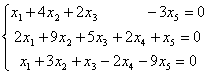
Решение

С помощью элементарных преобразований найдем ранг матрицы системы. Для этого приведем матрицу к трапециевидному виду, число ненулевых строк в трапециевидной матрице и будет равно рангу матрицы.

Помножим первую строку на (-2) и сложим со второй, затем помножим первую строку на (-1) и сложим с третьей.

 Сложим вторую строку с третьей.

Получили трапециевидную матрицу, в которой три ненулевые строки. Значит ранг r = 3. Число неизвестных в системе n = 5. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 5 - 3 = 2 параметров. Базисный минор это отличный от нуля минор, порядок которого равен рангу матрицы. Пусть 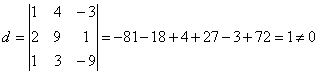- базисный минор. Тогда х₁ и х₂ , х₅ - базисные неизвестные, т. к. коэффициенты перед ними образуют базисный минор, х₃, х₄ - параметры. Обозначим для удобства х₃ =С₁, х₄ =С₂ и выразим базисные неизвестные через параметры. Так как r = 3, то достаточно взять три уравнения, соответствующие базисному минору:

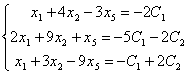
Решим эту систему с помощью формул Крамера.

Тогда:

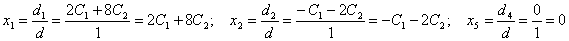
Общее решение исходной системы имеет вид:

Частные решения системы линейных уравнений получаем, придавая параметрам конкретные числовые значения. Множество решений однородной системы линейных уравнений образует линейное пространство размерности - r = 5 - 3 = 2, т. е. базис в этом пространстве состоит из одного линейно независимого решения. Придадим параметру С₁, С₂, С₃, поочередно следующее значение: С₁ = 1, С₂ = 0 и С₁ = 1, С₂ = 0, тогда получим два частных решения системы, линейно-независимых между собой,

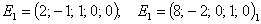
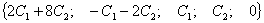Решения Е₁ и Е₂ образуют один из базисов пространства решений данной системы, которое можно записать, как  оно состоит из бесчисленного множества четверок вида , где С₁ и С₂ принимают произвольные значения. Размерность этого пространства равна двум.

Задание №2

Построить пространство решений однородной системы трех линейных уравнений с четырьмя неизвестными и указать какой-либо базис:

Решение

С помощью элементарных преобразований найдем ранг матрицы системы. Для этого приведем матрицу к трапециевидному виду, число ненулевых строк в трапециевидной матрице и будет равно рангу матрицы.

 первую строку домножим на (-1) и сложим с третьей и четвертой.

 Сложим вторую строку с третьей домножив на (-1), и сложим вторую строку с четвертой.

Получили трапециевидную матрицу, в которой только две ненулевые строки. Значит ранг r = 2. Число неизвестных в системе n = 4. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 4 - 2 = 2 параметров. Базисный минор это отличный от нуля минор, порядок которого равен рангу матрицы. Пусть 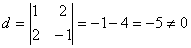- базисный минор. Тогда х₁ и х₂ - базисные неизвестные, т. к. коэффициенты перед ними образуют базисный минор, х₃ и х₄ - параметры. Обозначим для удобства х₃ =С₁ и х₄ = С₂ и выразим базисные неизвестные через параметры. Так как r = 2, то достаточно взять два уравнения, соответствующие базисному минору:

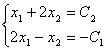
Решим эту систему с помощью формул Крамера.

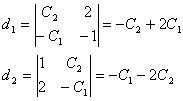
Тогда:

Общее решение исходной системы имеет вид:

Частные решения системы линейных уравнений получаем, придавая параметрам конкретные числовые значения. Множество решений однородной системы линейных уравнений образует линейное пространство размерности

n - r = 4 - 2 = 2, т. е. базис в этом пространстве состоит из двух линейно независимых решений. Придадим параметрам С₁ и С₂ поочередно следующие значения: С₁ = 1 и С₂ = 0 и С₁ = 0 и С₂ = 1, тогда получим два частных решения системы, линейно-независимых между собой,

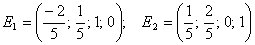
Решения Е₁ и Е₂ образуют один из базисов пространства решений данной системы, которое можно записать, как  оно состоит из бесчисленного множества четверок вида , где С₁ и С₂ принимают произвольные значения. Размерность этого пространства равна двум.

Задание 3

Решить систему методом Гаусса и указать одно из базисных решений:

Решение.

а) Найдем общее решение данной системы уравнений методом Гаусса. Для этого сначала выпишем ее расширенную матрицу:

Далее с помощью элементарных преобразований полученной матрицы мы приведем ее к ступенчатому виду:

 ~  ~

~  ~  

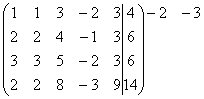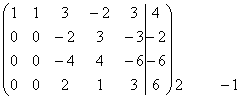Эта матрица уже имеет ступенчатый вид, поэтому можно перейти к системе эквивалентной данной. Выпишем соответствующую этой матрице систему:

.

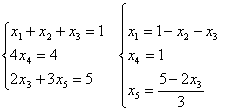Получили трапециевидную матрицу, в которой только три ненулевые строки. Значит ранг r = 3. Число неизвестных в системе n = 5. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 5 - 3 = 2 параметров.

Получаем, что х₁, х₄, х₅ - базисные неизвестные, а х₂, х₃ - параметры.

Обозначим для удобства х₂ =С₁, х₃ =С₂ и выразим базисные неизвестные через параметры.

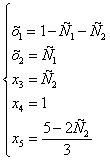
Мы нашли общее решение исходной системы:

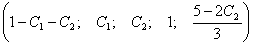
б) Найдем базисное решение исходной системы. Напомним вначале, что базисным называется такое решение системы, в котором все свободные неизвестные равны нулю. Такое решение мы получим, если в найденном нами общем решении положим :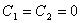

.

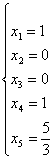
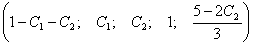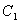Ответ: а) общее решение: , где  и 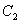 - произвольные числа б) базисное решение: .

Задание 4

Построить пространство решений однородной системы трех линейных уравнений с четырьмя неизвестными и указать какой-либо базис:

Решение

С помощью элементарных преобразований найдем ранг матрицы системы. Для этого приведем матрицу к трапециевидному виду, число ненулевых строк в трапециевидной матрице и будет равно рангу матрицы.

 первую строку домножим на 3 и сложим со второй, затем помножим первую строку на (5) и сложим с третьей.

 Сложим вторую строку с третьей домножив на (-1).

Получили трапециевидную матрицу, в которой только две ненулевые строки. Значит ранг r = 2. Число неизвестных в системе n = 4. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 4 - 2 = 2 параметров. Базисный минор это отличный от нуля минор, порядок которого равен рангу матрицы. Пусть 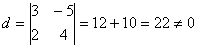- базисный минор. Тогда х₁ и х₂ - базисные неизвестные, т. к. коэффициенты перед ними образуют базисный минор, х₃ и х₄ - параметры. Обозначим для удобства х₃ =С₁ и х₄ = С₂ и выразим базисные неизвестные через параметры. Так как r = 2, то достаточно взять два уравнения, соответствующие базисному минору:

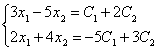
Решим эту систему с помощью формул Крамера.

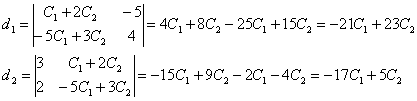
Тогда:

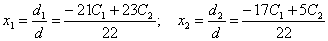
Общее решение исходной системы имеет вид:

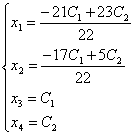
Частные решения системы линейных уравнений получаем, придавая параметрам конкретные числовые значения. Множество решений однородной системы линейных уравнений образует линейное пространство размерности

n - r = 4 - 2 = 2, т. е. базис в этом пространстве состоит из двух линейно независимых решений. Придадим параметрам С₁ и С₂ поочередно следующие значения: С₁ = 1 и С₂ = 0 и С₁ = 0 и С₂ = 1, тогда получим два частных решения системы, линейно-независимых между собой,

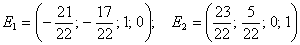
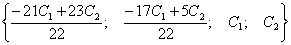Решения Е₁ и Е₂ образуют один из базисов пространства решений данной системы, которое можно записать, как  оно состоит из бесчисленного множества четверок вида , где С₁ и С₂ принимают произвольные значения. Размерность этого пространства равна двум.

Задание 5

Построить пространство решений однородной системы трех линейных уравнений с четырьмя неизвестными и указать какой-либо базис:

Решение

С помощью элементарных преобразований найдем ранг матрицы системы. Для этого приведем матрицу к трапециевидному виду, число ненулевых строк в трапециевидной матрице и будет равно рангу матрицы.

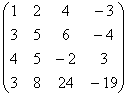 первую строку домножим на 3 и сложим со второй, помножим первую строку на (-4) и сложим с третьей.

затем помножим первую строку на (-3) и сложим с четвертой.

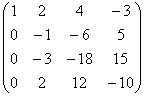 Сложим вторую строку с третьей домножив на (-3), и с чеивертой домножив на (2).

Получили трапециевидную матрицу, в которой только две ненулевые строки. Значит ранг r = 2. Число неизвестных в системе n = 4. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 4 - 2 = 2 параметров. Базисный минор это отличный от нуля минор, порядок которого равен рангу матрицы. Пусть 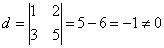- базисный минор. Тогда х₁ и х₂ - базисные неизвестные, т. к. коэффициенты перед ними образуют базисный минор, х₃ и х₄ - параметры. Обозначим для удобства х₃ =С₁ и х₄ = С₂ и выразим базисные неизвестные через параметры. Так как r = 2, то достаточно взять два уравнения, соответствующие базисному минору:

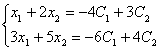
Решим эту систему с помощью формул Крамера.

Тогда:

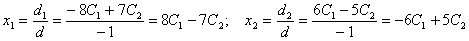
Общее решение исходной системы имеет вид:

Частные решения системы линейных уравнений получаем, придавая параметрам конкретные числовые значения. Множество решений однородной системы линейных уравнений образует линейное пространство размерности

n - r = 4 - 2 = 2, т. е. базис в этом пространстве состоит из двух линейно независимых решений. Придадим параметрам С₁ и С₂ поочередно следующие значения: С₁ = 1 и С₂ = 0 и С₁ = 0 и С₂ = 1, тогда получим два частных решения системы, линейно-независимых между собой,

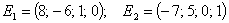
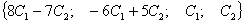Решения Е₁ и Е₂ образуют один из базисов пространства решений данной системы, которое можно записать, как  оно состоит из бесчисленного множества четверок вида , где С₁ и С₂ принимают произвольные значения. Размерность этого пространства равна двум.

Задание №6

Решить систему методом Гаусса и указать одно из базисных решений:

Решение

а) Найдем общее решение данной системы уравнений методом Гаусса. Для этого сначала выпишем ее расширенную матрицу:

Далее с помощью элементарных преобразований полученной матрицы мы приведем ее к ступенчатому виду:

 ~  ~

~~

~

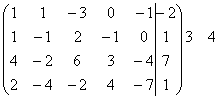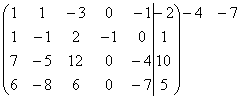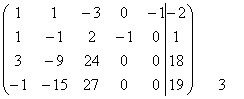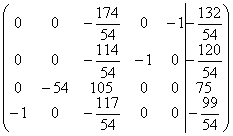
Эта матрица уже имеет ступенчатый вид, поэтому можно перейти к системе эквивалентной данной. Выпишем соответствующую этой матрице систему:

.

Получили трапециевидную матрицу, в которой четыре ненулевые строки. Значит ранг r = 4. Число неизвестных в системе n = 5. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 5 - 4 = 1 параметров.

Получаем, что х₁, х₂, х₄, х₅, - базисные неизвестные, а х₃ - параметры.

Обозначим для удобства х3 =С1 и выразим базисные неизвестные через параметры.

Мы нашли общее решение исходной системы:

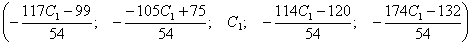
б) Найдем базисное решение исходной системы. Напомним вначале, что базисным называется такое решение системы, в котором все свободные неизвестные равны нулю. Такое решение мы получим, если в найденном нами общем решении положим :

.

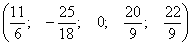Ответ: а) общее решение:

,

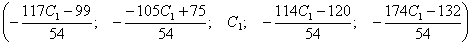где 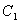 - произвольные числа

б) базисное решение: .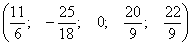

Задание №7

Построить пространство решений однородной системы трех линейных уравнений с четырьмя неизвестными и указать какой-либо базис:

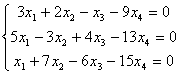
Решение

С помощью элементарных преобразований найдем ранг матрицы системы. Для этого приведем матрицу к трапециевидному виду, число ненулевых строк в трапециевидной матрице и будет равно рангу матрицы.

Помножим первую строку на (4) и сложим со второй, затем помножим первую строку на (-6) и сложим с третьей.

 Сложим вторую строку с третьей.

Получили трапециевидную матрицу, в которой только три ненулевые строки. Значит ранг r = 3. Число неизвестных в системе n = 4. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 4 - 3 = 1 параметров. Базисный минор это отличный от нуля минор, порядок которого равен рангу матрицы. Пусть 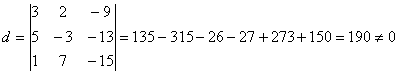- базисный минор. Тогда х₁ и х₂ , х₄ - базисные неизвестные, т. к. коэффициенты перед ними образуют базисный минор, х₃ - параметры. Обозначим для удобства х₃ =С₁ и выразим базисные неизвестные через параметры. Так как r = 3, то достаточно взять три уравнения, соответствующие базисному минору:

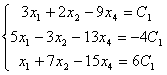
Решим эту систему с помощью формул Крамера.

Тогда:

Общее решение исходной системы имеет вид:

Частные решения системы линейных уравнений получаем, придавая параметрам конкретные числовые значения. Множество решений однородной системы линейных уравнений образует линейное пространство размерности

n - r = 4 - 3 = 1, т. е. базис в этом пространстве состоит из одного линейно независимого решения. Придадим параметру С₁ следующее значение: С₁ = 1, тогда получим одно частное решение системы.

Решения Е₁ образует один из базисов пространства решений данной системы, которое можно записать, как  оно состоит из бесчисленного множества четверок вида 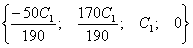, где С₁ принимает произвольные значения. Размерность этого пространства равна одному.

Задание №8

Определите размерность пространства решений неоднородной системы уравнений, и указать какой-нибудь базис этого пространства.

Решение.

а) Найдем общее решение данной системы уравнений методом Гаусса. Для этого сначала выпишем ее расширенную матрицу:

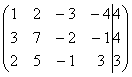
Далее с помощью элементарных преобразований полученной матрицы мы приведем ее к ступенчатому виду:

 ~  ~

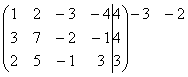Эта матрица уже имеет ступенчатый вид, поэтому можно перейти к системе эквивалентной данной. Выпишем соответствующую этой матрице систему:

.

Получаем, что х₁, х₂ - базисные неизвестные, а х₃, х₄ - параметры.

Обозначим для удобства х₄ =С₁ и выразим базисные неизвестные через параметры.

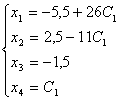
Мы нашли общее решение исходной системы: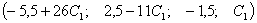

б) Найдем базисное решение исходной системы. Напомним вначале, что базисным называется такое решение системы, в котором все свободные неизвестные равны нулю. Такое решение мы получим, если в найденном нами общем решении положим :

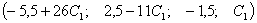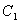Ответ: а) общее решение: , где  и 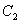 - произвольные числа б) базисное решение: .

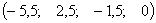уравнение крамер линейный базис

Задание №9

Решить систему методом Гаусса и указать одно из базисных решений:

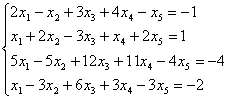
Решение

а) Найдем общее решение данной системы уравнений методом Гаусса. Для этого сначала выпишем ее расширенную матрицу:

Далее с помощью элементарных преобразований полученной матрицы мы приведем ее к ступенчатому виду:

 ~

 ~

~  ~  

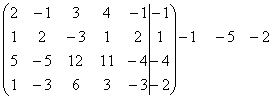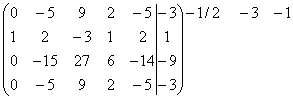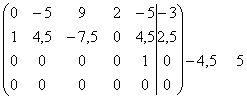Эта матрица уже имеет ступенчатый вид, поэтому можно перейти к системе эквивалентной данной. Выпишем соответствующую этой матрице систему:

.

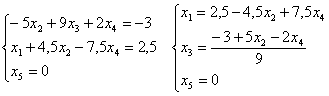Получили трапециевидную матрицу, в которой только три ненулевые строки. Значит ранг r = 3. Число неизвестных в системе n = 5. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 5 - 3 = 2 параметров.

Получаем, что х₁, х₃, х₅ - базисные неизвестные, а х₂, х₄ - параметры.

Обозначим для удобства х₂ =С₁, х₄ =С₂ и выразим базисные неизвестные через параметры.

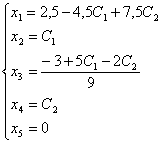
Мы нашли общее решение исходной системы:

б) Найдем базисное решение исходной системы. Напомним вначале, что базисным называется такое решение системы, в котором все свободные неизвестные равны нулю. Такое решение мы получим, если в найденном нами общем решении положим :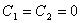

.

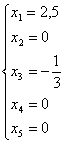
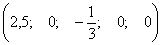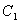Ответ: а) общее решение: , где  и 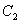 - произвольные числа б) базисное решение: .

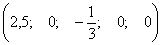Задание №10

Построить пространство решений однородной системы трех линейных уравнений с четырьмя неизвестными и указать какой-либо базис:

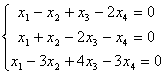
Решение

С помощью элементарных преобразований найдем ранг матрицы системы. Для этого приведем матрицу к трапециевидному виду, число ненулевых строк в трапециевидной матрице и будет равно рангу матрицы.

Сложим вторую строку с третьей.

Получили трапециевидную матрицу, в которой только две ненулевые строки. Значит ранг r = 2. Число неизвестных в системе n = 4. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 4 - 2 = 2 параметров. Базисный минор это отличный от нуля минор, порядок которого равен рангу матрицы. Пусть 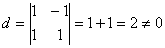- базисный минор. Тогда х₁ и х₂ - базисные неизвестные, т. к. коэффициенты перед ними образуют базисный минор, х₃ и х₄ - параметры. Обозначим для удобства х₃ =С₁ и х₄ = С₂ и выразим базисные неизвестные через параметры. Так как r = 2, то достаточно взять два уравнения, соответствующие базисному минору:

Решим эту систему с помощью формул Крамера.

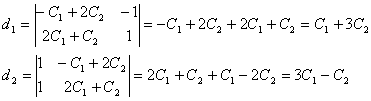
Тогда:

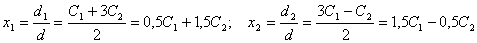
Общее решение исходной системы имеет вид:

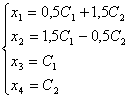
Частные решения системы линейных уравнений получаем, придавая параметрам конкретные числовые значения. Множество решений однородной системы линейных уравнений образует линейное пространство размерности

n - r = 4 - 2 = 2, т. е. базис в этом пространстве состоит из двух линейно независимых решений. Придадим параметрам С₁ и С₂ поочередно следующие значения: С₁ = 1 и С₂ = 0 и С₁ = 0 и С₂ = 1, тогда получим два частных решения системы, линейно-независимых между собой,

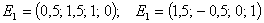
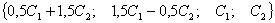Решения Е₁ и Е₂ образуют один из базисов пространства решений данной системы, которое можно записать, как  оно состоит из бесчисленного множества четверок вида , где С₁ и С₂ принимают произвольные значения. Размерность этого пространства равна двум.

Задание №11

Решить систему методом Гаусса и указать одно из базисных решений:

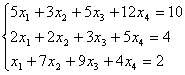
Решение

а) Найдем общее решение данной системы уравнений методом Гаусса. Для этого сначала выпишем ее расширенную матрицу:

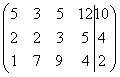
Далее с помощью элементарных преобразований полученной матрицы мы приведем ее к ступенчатому виду:

~~

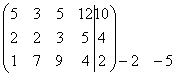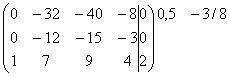Эта матрица уже имеет ступенчатый вид, поэтому можно перейти к системе эквивалентной данной. Выпишем соответствующую этой матрице систему:

.

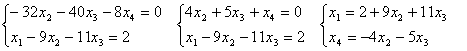Получили трапециевидную матрицу, в которой только две ненулевые строки. Значит ранг r = 2. Число неизвестных в системе n = 4. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 4 - 2 = 2 параметров.

Получаем, что х₁, х₄ - базисные неизвестные, а х₂, х₃ - параметры.

Обозначим для удобства х₂ =С₁, х₃ =С₂ и выразим базисные неизвестные через параметры.

Мы нашли общее решение исходной системы: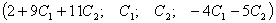

б) Найдем базисное решение исходной системы. Напомним вначале, что базисным называется такое решение системы, в котором все свободные неизвестные равны нулю. Такое решение мы получим, если в найденном нами общем решении положим :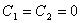

.

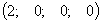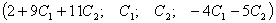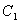Ответ: а) общее решение: , где  и 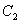 - произвольные числа б) базисное решение: .

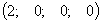Задание №12

Определите размерность пространства решений неоднородной системы уравнений, и указать какой-нибудь базис этого пространства.

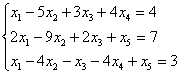
Решение

а) Найдем общее решение данной системы уравнений методом Гаусса. Для этого сначала выпишем ее расширенную матрицу:

Далее с помощью элементарных преобразований полученной матрицы мы приведем ее к ступенчатому виду:

 ~ ~

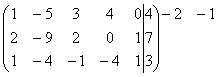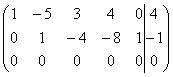
Эта матрица имеет ступенчатый вид, поэтому можно перейти к системе эквивалентной данной. Выпишем соответствующую этой матрице систему:

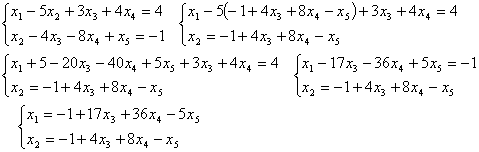
Получили трапециевидную матрицу, в которой только две ненулевые строки. Значит ранг r = 2. Число неизвестных в системе n = 5. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 5 - 2 = 3 параметров. Получаем, что х₁, х₂ - базисные неизвестные, а х₃, х₄, х₅ - параметры.

Обозначим для удобства х₃ =С₁, х₄ =С₂ х₅ =С₃ и выразим базисные неизвестные через параметры.

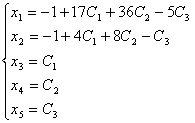
Мы нашли общее решение исходной системы:

б) Найдем базисное решение исходной системы. Напомним вначале, что базисным называется такое решение системы, в котором все свободные неизвестные равны нулю. Такое решение мы получим, если в найденном нами общем решении положим :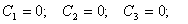

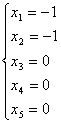
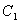Ответ: а) общее решение: , где  и 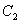 - произвольные числа б) базисное решение: .

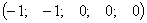Задание №13

Построить пространство решений однородной системы трех линейных уравнений с четырьмя неизвестными и указать какой-либо базис:

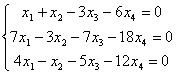
Решение

С помощью элементарных преобразований найдем ранг матрицы системы. Для этого приведем матрицу к трапециевидному виду, число ненулевых строк в трапециевидной матрице и будет равно рангу матрицы.

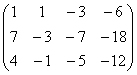 первую строку домножим на 3 и сложим со второй, затем сложим первую строку с третьей.

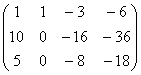 третью строку домножим на (-2) и сложим со второй.

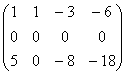
Получили трапециевидную матрицу, в которой только две ненулевые строки. Значит ранг r = 2. Число неизвестных в системе n = 4. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 4 - 2 = 2 параметров. Базисный минор это отличный от нуля минор, порядок которого равен рангу матрицы. Пусть 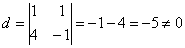- базисный минор. Тогда х₁ и х₂ - базисные неизвестные, т. к. коэффициенты перед ними образуют базисный минор, х₃ и х₄ - параметры. Обозначим для удобства х₃ =С₁ и х₄ = С₂ и выразим базисные неизвестные через параметры. Так как r = 2, то достаточно взять два уравнения, соответствующие базисному минору:

Решим эту систему с помощью формул Крамера.

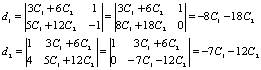
Тогда:

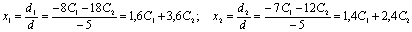
Общее решение исходной системы имеет вид:

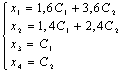
Частные решения системы линейных уравнений получаем, придавая параметрам конкретные числовые значения. Множество решений однородной системы линейных уравнений образует линейное пространство размерности

n - r = 4 - 2 = 2, т. е. базис в этом пространстве состоит из двух линейно независимых решений. Придадим параметрам С₁ и С₂ поочередно следующие значения: С₁ = 1 и С₂ = 0 и С₁ = 0 и С₂ = 1, тогда получим два частных решения системы, линейно-независимых между собой,

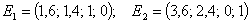
Задание №14

Построить пространство решений однородной системы трех линейных уравнений с четырьмя неизвестными и указать какой-либо базис:

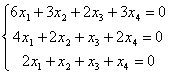
Решение

С помощью элементарных преобразований найдем ранг матрицы системы. Для этого приведем матрицу к трапециевидному виду, число ненулевых строк в трапециевидной матрице и будет равно рангу матрицы.

 третью строку домножим на -2 и сложим со второй, затем помножим третью строку на -3 и сложим с первой.

 Сложим первую строку со второй домножив на (-1), первую строку сложим с третьей.

Получили трапециевидную матрицу, в которой только две ненулевые строки. Значит ранг r = 2. Число неизвестных в системе n = 4. Так как r < n, то система имеет бесчисленное множество решений, зависящих от n - r = 4 - 2 = 2 параметров.

Получаем, что х₁, х₃, - базисные неизвестные, а х₂, х₄ - параметры.

Обозначим для удобства х₂ =С₁ , х₄ =С₂ и выразим базисные неизвестные через параметры.

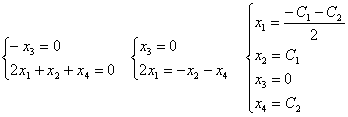
Мы нашли общее решение исходной системы:

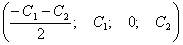
б) Найдем базисное решение исходной системы. Напомним вначале, что базисным называется такое решение системы, в котором все свободные неизвестные равны нулю. Такое решение мы получим, если в найденном нами общем решении положим :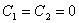

.

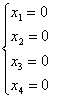
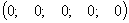Ответ: а) общее решение:

,

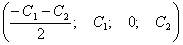где 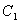 - произвольные числа

б) базисное решение: 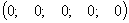.