Поляризация света
Реферат
тема:
«Поляризация света»
Содержание
Введение
.
Характеристики поляризованного света
.
Поляризация света при отражении и преломлении
.
Двойное лучепреломление
.
Вращение плоскости поляризации
.
Основные формулы поляризации света
Список
использованной литературы и источников
Введение
Световые волны являются поперечными, т.е. в них
колебания векторов напряженности электрического и магнитного полей совершаются
в направлениях, перпендикулярных линии распространения световой волны. Нас в
первую очередь интересуют колебания вектора напряженности электрического поля.
Следовательно, для полного описания движения светового луча надо указать
направление распространения света и направление колебаний вектора Е - его
называют световым вектором.
Свет называют поляризованным, если колебания
светового вектора являются упорядоченными. Характер упорядоченности колебаний
светового вектора рассмотрим ниже.
Естественный свет представляет смесь различных
световых волн (цугов) и обычно является неполяризованным. Каждый цуг можно
считать волновым пакетом длиной около 3 м, колебания световых векторов в каждом
пакете являются хаотическими, поэтому в естественном свете никакой
упорядоченности колебаний нет.
1. Характеристики поляризованного света
Естественный свет состоит из многих корпускул, в
которых направления колебаний различные. Рассмотрим одну световую волну.
Плоскость, в которой происходят колебания светового вектора (Е) называют
плоскостью колебаний. Плоскость, проходящая через световой луч, перпендикулярно
плоскости колебаний называется плоскостью поляризации (плоскость колебаний
вектора Н).

Разложим световой вектор на два взаимно
перпендикулярных колебания.

Колебания векторов Ех и Еу могут отличаться по
фазе и описываются уравнениями
 ,
, 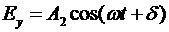 ,
,
где δ - угол сдвига
фаз. Эти уравнения описывают эллипс, т.е. конец вектора Е движется по эллипсу.
Для естественного света величина δ испытывает хаотические
изменения, т.к. свет состоит из огромного количества неупорядоченных корпускул.
Поэтому для естественного света векторы Ех и Еу можно считать некогерентными.
Свет называют частично
поляризованным, если существует выделенное направление колебаний вектора Е.
Свет называется плоскополяризованным
(линейно поляризованным), если все колебания вектора Е совершаются в одной
плоскости. Схематически направления колебаний светового вектора  показаны
ниже.
показаны
ниже.

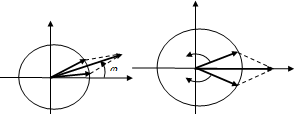
Неполяризованный луч

Частично поляризованный
луч

Линейно поляризованный луч
Свет называется эллиптически поляризованным,
если для него вектор Е со временем меняется так, что его конец описывает
эллипс. Если эллипс вырождается в окружность, то свет называется циркулярно
поляризованным (поляризованным по кругу). Такое явление называют круговой поляризацией.
Степенью поляризации называется величина
 ,
,
где Imax и Imin - максимальная и
минимальная интенсивности света, соответствующие двум взаимно перпендикулярным
компонентам вектора Е.
Для преобразования естественного
света в поляризованный существуют специальные поляризаторы, пропускающие только
колебания определенного направления. Это могут быть анизотропные кристаллы,
например, турмалин. Если на пути распространения неполяризованного света
поставить поляризатор, то свет выходит плоскополяризованным.

Интенсивность света, прошедшего через
поляризатор, составляет половину интенсивности исходного света и определяется
формулой
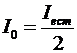 .
.
Изменение поляризации света можно
наблюдать с помощью двух пластинок турмалина

При этом первую пластинку называют
поляризатором, а вторую - анализатором. Поворачивая вторую пластинку
относительно первой, можно исследовать зависимость интенсивности прошедшего
света как функцию угла поворота.

Интенсивность света, прошедшего через обе
пластинки, определяется законом Малюса:
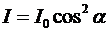 ,
,
где I0 и I интенсивности света, падающего
на второй кристалл и выходящего из него. Здесь первая пластинка турмалина
преобразует естественный свет в плоскополяризованный, а вторая пластинка
пропускает часть этого света с амплитудой
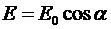 .
.
Учитывая тот факт, что интенсивность
света пропорциональна квадрату амплитуды, отсюда получим формулу Малюса.
Существуют различные механизмы
поляризации света. Поляризация происходит при рассеянии света, отражении и
преломлении, при прохождении света через анизотропные среды. Но во всех случаях
поляризация возникает в процессе излучении света электронами атома при
вынужденных колебаниях электрона в поле проходящей световой волны. Поляризацию
света при отражении и преломлении рассмотрим в следующем параграфе, а сейчас
сделаем несколько замечаний об устройстве поляризаторов.
В качестве поляризаторов часто
используют анизотропные кристаллы, обладающие свойством двойного
лучепреломления. В них показатель преломления зависит от направления колебаний
светового вектора. Это приводит к разделению падающего неполяризованного луча
на два поляризованных луча со взаимно перпендикулярными плоскостями
поляризации. Пропуская один из этих лучей, получим плоскополяризованный свет.
Примером такого поляризатора является призма НИколя (нИколь), получаемая из
кристаллов исландского шпата (СаСО3).
Иногда в качестве поляризаторов
используют кристаллы с сильно выраженной анизотропией поглощения. В таких
кристаллах лучи с некоторым направлением колебаний вектора  проходят
почти свободно, а лучи со взаимно перпендикулярным колебанием вектора
проходят
почти свободно, а лучи со взаимно перпендикулярным колебанием вектора  почти
полностью поглощаются. В результате на выходе получается плоскополяризованный
луч. Таким поляризатором является, например, тонкая пленка из целлулоида. К
вопросу о поляризаторах мы вернемся в параграфе о двулучепреломлении.
почти
полностью поглощаются. В результате на выходе получается плоскополяризованный
луч. Таким поляризатором является, например, тонкая пленка из целлулоида. К
вопросу о поляризаторах мы вернемся в параграфе о двулучепреломлении.
. Поляризация света при отражении и
преломлении
На границе двух диэлектриков, когда
свет испытывает отражение и преломление, он также поляризуется. Это можно
наблюдать с помощью анализатора (пластинки турмалина).
Условно поляризация света при
отражении и преломлении схематически показана на рисунке. Здесь показаны
поляризованные лучи, падающие на границу раздела двух сред. В первом случае
колебания вектора  перпендикулярны
плоскости рисунка, во втором - происходят в плоскости рисунка. Из уравнений
Максвелла следует, что направления колебаний вектора
перпендикулярны
плоскости рисунка, во втором - происходят в плоскости рисунка. Из уравнений
Максвелла следует, что направления колебаний вектора  не
изменятся. Произойдет разделение падающего луча на отраженный и преломленный.
не
изменятся. Произойдет разделение падающего луча на отраженный и преломленный.

При отражении и преломлении
неполяризованного света происходит частичная поляризация. Для определения
степени поляризации можно использовать уравнения Максвелла. Соответствующие
формулы получены Френелем. Они определяют интенсивности отраженных и
преломленных лучей различной поляризации. На рисунке показано разделение
неполяризованного света на частично поляризованные лучи. Степень поляризации
зависит от угла падения i и показателей преломления обоих сред.
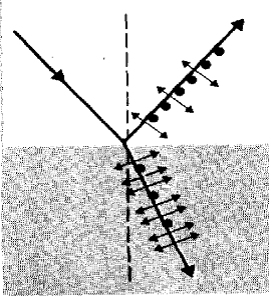
Закон Брюстера: При угле падения iB
, определяемом соотношением
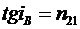
отраженный луч является
плоскополяризованным.
При этом в отраженном луче
происходят колебания, перпендикулярные плоскости падения, а в преломленном
преобладают лучи параллельные плоскости падения. Сам угол iB называется углом
Брюстера.
Если свет падает на границу раздела
под углом Брюстера, то отраженный и преломленный лучи взаимно перпендикулярны.
Докажем это утверждение.


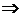
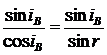
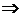
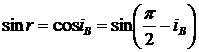
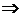
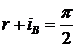 .
.
Степень поляризации преломленного
света можно повысить, накладывая друг на друга несколько стеклянных пластинок.
После преломления и поляризации на каждой из пластинок преломленный луч
становится практически полностью поляризованным. Такая совокупность пластинок
называется стопой.
. Двойное лучепреломление
Большинство прозрачных кристаллов
обладает двойным лучепреломлением. Впервые это явление было обнаружено в 17
веке в кристаллах исландского шпата (СаСО3). Если смотреть через этот кристалл
на некоторый предмет, то видим двойное изображение предмета.
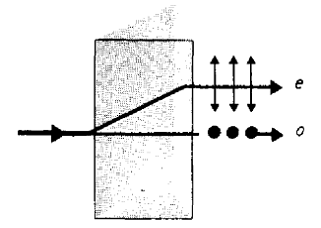
Если на толстый кристалл исландского
шпата направить тонкий луч, то из кристалла выходят два пространственно
разделенных луча, каждый из которых является плоскополяризованным. Даже, если
лучи падают на кристалл нормально, один из лучей отклоняется от первоначального
распространения. Луч, который не отклоняется при нормальном падении, называется
обыкновенным и обозначается о, второй луч называется необыкновенным и
обозначается е. Для необыкновенных лучей не выполняются обычные законы
преломления. Более того, показатель преломления для них зависит от выбора
направления распространения луча.
В кристалле исландского шпата
существует одно направление, вдоль которого луч не испытывает двойного
лучепреломления. Это направление называется оптической осью кристалла. В других
кристаллах могут быть две оптических оси.
Неодинаковое преломление оптических
лучей указывает на то, что для обыкновенного и необыкновенного лучей существуют
различные показатели преломления по и пе , а, следовательно, эти лучи
распространяются в кристалле с различными скоростями vo и ve. Причиной появления
двойного лучепреломления является анизотропия кристаллов. Для необыкновенного
луча показатель преломления зависит от направления распространения луча, для
обыкновенного луча он является величиной постоянной и одинаков во всех
направлениях (поэтому луч называется обыкновенным).
Свойство двойного лучепреломления
используется для получения поляризованного света и создания различных
поляризационных приборов (призмы и поляроиды, нИколи, поляроидные пленки и
пр.). Более детально эти приборы описаны в учебнике Трофимовой.
Среды, не являющиеся
двулучепреломляющими, можно сделать оптически анизотропными с помощью различных
силовых полей.
Сжатие или растяжение кристаллов.
Разность показателей преломления
по - пе = k1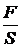 .
.
Действие электрического поля (эффект
Керра)
по - пе = k2Е2.
Действие магнитного поля
по - пе = k3 Н2.
Деформационная анизотропия
используется для изучения напряжений в прозрачных кристаллических конструкциях.
Эффект Керра используется для изучения быстропротекающих процессов (10 - 10 с)
и создания приборов для управления такими процессами.
. Вращение плоскости поляризации
Некоторые вещества, называемые оптически
активными, обладают способностью вращать плоскость поляризации. К таким
веществам относится кварц, водный раствор сахара, скипидар.

Опыт показывает, что угол поворота
плоскости поляризации для оптически активных кристаллов и чистых жидкостей
определяется формулой
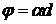
где α - удельное
вращение, d - расстояние, пройденное светом в оптически активной среде. Для
оптически активных растворов
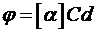 ,
,
где С - массовая концентрация
оптически активного вещества в растворе, [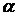 ] - удельное вращение на единицу
концентрации.
] - удельное вращение на единицу
концентрации.
Рассмотрим физический механизм
вращения плоскости поляризации. Предварительно покажем, что
плоскополяризованный луч можно представить в виде суммы двух лучей с круговой
поляризацией противоположных направлений. Пусть плоскополяризованный луч,
двигающийся на нас, совершает колебания вдоль направления  .
.

Представим этот луч в виде суммы
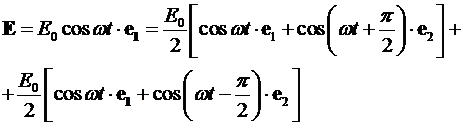
Выражения в квадратных скобках
представляют собой лучи, поляризованные по кругу, - лучи с правой и левой
круговыми поляризациями. Следовательно, плоскополяризованный луч можно
разложить на два луча с противоположно направленными круговыми поляризациями.
В средах, обладающих спиральной
структурой или винтовой анизотропией, скорости лучей с различными круговыми
поляризациями могут различаться. Это приведет к тому, что направление линейной
поляризации изменяется - плоскость поляризации поворачивается.
Оптически активные вещества
разделяются на право- и левовращающие. Явление вращения плоскости поляризации
используется для определения концентрации растворов. Этот метод определения
концентрации называется поляриметрией (сахариметрией).
. Основные формулы поляризации света
Закон Малюса
 .
.
Закон Брюстера
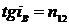 .
.
При падении света под углом Брюстера
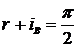 .
.
Сжатие или растяжение кристаллов
по - пе = k1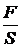 .
.
Эффект Керра
по - пе = k1Е2.
Действие магнитного поля
по - пе = k1 Н2.
Угол поворота плоскости поляризации
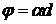 ,
,
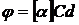 .
.
поляризация свет
преломление
Список использованной литературы и
источников
1.
Трофимова Т.И. Курс физики, М.: Высшая школа, 1998, 478 с.
.
Трофимова Т.И. Сборник задач по курсу физики, М.: Высшая школа, 1996, 304 с.
.
Волькенштейн В.С. Сборник задач по общему курсу физики, СПб.: «Специальная
литература», 1999, 328 с.
.
Трофимова Т.И., Павлова З.Г. Сборник задач по курсу физики с решениями, М.:
Высшая школа, 1999, 592 с.
.
Все решения к «Сборнику задач по общему курсу физики» В.С. Волькенштейн, М.:
Аст, 1999, книга 1, 430 с., книга 2, 588 с.
.
Красильников О.М. Физика. Методическое руководство по обработке результатов
наблюдений. М.: МИСиС, 2002, 29 с.
.
Супрун И.Т., Абрамова С.С. Физика. Методические указания по выполнению
лабораторных работ, Электросталь: ЭПИ МИСиС, 2004, 54 с.