Основы линейной алгебры
1. Найти произведение
заданных матриц А и В

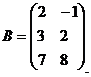
Решение:
Матрицы: А - размерность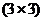 ,
В-размерность
,
В-размерность  .
.
Так как количество
столбцов матрицы: А равно количеству строк матрицы В, то произведение А на В
существует.
Итоговая матрица 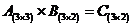 имеет
размерность
имеет
размерность 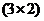 :
:
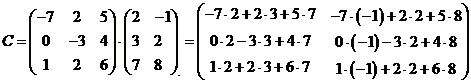
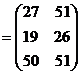
Ответ:
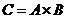
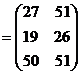
2. Решить систему
линейных алгебраических уравнений по формулам Крамера, матричным методом и
методом Гаусса
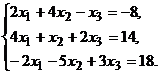
Решение:
а)
Решим систему по формулам Крамера
Для системы 3-х линейных
алгебраических уравнений

если  ¹
0, можно найти единственное решение по формулам Крамера:
¹
0, можно найти единственное решение по формулам Крамера:
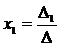 ,
, 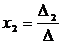 ,
,
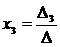 .
.
∆ =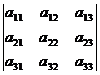 ;
D1=
;
D1=
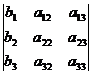 ;
D2=
;
D2=
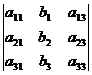 ;
D3=
;
D3=
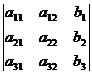 ;
;
Найдем значение
определителя ∆ по формуле:
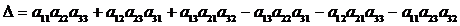
Аналогично вычислим
значения определителей D1,
D2,
D3
∆ = 2·1·3
+4·2·(-2)+4·(-5)·(-1) - (-2)·1·(-1) - 4∙4·3-2·2·(-5)= -20 ¹
0
2·1·3
+4·2·(-2)+4·(-5)·(-1) - (-2)·1·(-1) - 4∙4·3-2·2·(-5)= -20 ¹
0
D1= -8·1·3
+4·2·18+14·(-5)·(-1) - 18·1·(-1) - 14∙4·3 - (-8)·2·(-5)=-40
-8·1·3
+4·2·18+14·(-5)·(-1) - 18·1·(-1) - 14∙4·3 - (-8)·2·(-5)=-40
D2
=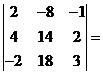 2·14·3
+(-8)·2·(-2)+4·18·(-1) - (-2)·14·(-1) - 4∙(-8)·3-2·2·18=40
2·14·3
+(-8)·2·(-2)+4·18·(-1) - (-2)·14·(-1) - 4∙(-8)·3-2·2·18=40
D3=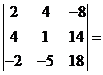 2·1·18
+4·14·(-2)+4·(-5)·(-8) - (-2)·1·(-8) - 4∙4·18-2·14·(-5)=-80
2·1·18
+4·14·(-2)+4·(-5)·(-8) - (-2)·1·(-8) - 4∙4·18-2·14·(-5)=-80
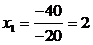
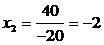
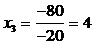
Сделаем проверку: 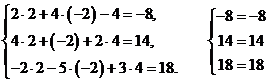
Получили равенства.
Ответ: 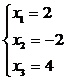

б)
Решим систему матричным методом
Систему линейных
алгебраических уравнений можно представить в матричном виде: А ∙ X = В, где А - матрица системы из коэффициентов при неизвестных,
Х и В-матрицы - столбцы
из неизвестных 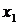 ,
,
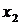 ,
,
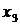 и
свободных членов соответственно:
и
свободных членов соответственно:
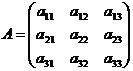 .
. 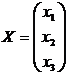 ;
; 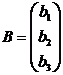 .
.
Для нахождения
неизвестных используется формула Х = А-1 ∙ В, где А-1
- обратная матрица к квадратной матрице А
Обратная матрица
вычисляется по формуле:
А-1=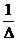 ∙АТ,
где АТ =
∙АТ,
где АТ = 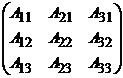 - транспонированная
матрица к
- транспонированная
матрица к 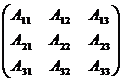
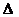 - главный определитель
матрицы А,
- главный определитель
матрицы А,
Аij - это алгебраическое дополнение равное Aij
= (-1)i+jМ
Минор 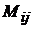 -
это определитель, полученный из главного определителя вычеркиванием i-ой строки и j-гo столбца
-
это определитель, полученный из главного определителя вычеркиванием i-ой строки и j-гo столбца
Для исходной системы:

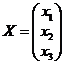

Найдем обратную матрицу.
Значение главного определителя известно:
∆ = -20
¹
0
-20
¹
0
Найдем
алгебраические дополнения Аij:
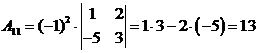
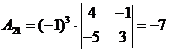
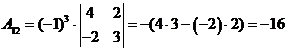
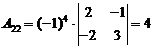
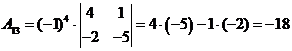
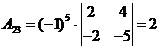
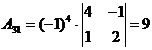
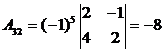

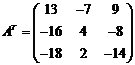 ;
; 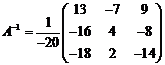
Умножая обратную матрицу
А-1 на 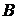 , получаем матрицу
, получаем матрицу  .
.
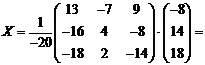

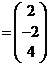
Ответ: 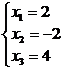
в)
Решим систему методом Гаусса
Это метод
последовательного исключения неизвестных из уравнений системы.
В первом уравнении
выбираем коэффициент, отличный от нуля. Затем 1-ое уравнение делим на этот
коэффициент, и далее с помощью первого уравнения исключаем первое неизвестное
из всех уравнений, кроме первого (вычитанием).
Применим метод Гаусса,
составив таблицу:
|
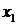 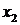  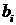 Комментарий Комментарий
|
|
|
|
|
|
2 4 -2
|
4 1 -5
|
-1 2 3
|
-8 14 18
|
|
|
1 4 -2
|
2 1 -5
|
-1/2 2 3
|
-4 14 18
|
1-ю строку разделили на 2
|
|
1 шаг
|
1 0 0
|
2 -7 -1
|
-1/2 4 2
|
-4 30 10
|
|
2 шаг
|
1 0 0
|
2 1 -1
|
-1/2 -4/7 2
|
-4 -30/7 10
|
2-ю строку разделили на (-7)
|
|
3 шаг
|
1 0 0
|
2 1 0
|
-1/2 -4/7 10/7
|
-4 -30/7 40/7
|
2-ю строку слож. с 3-й
|
|
4 шаг
|
1 0 0
|
2 1 0
|
-1/2 -4/7 1
|
-4 -30/7 4
|
3-ю строку делим на 10/7
|
После проделанных операций система
привелась к треугольному виду

Начинаем обратный ход
метода Гаусса.
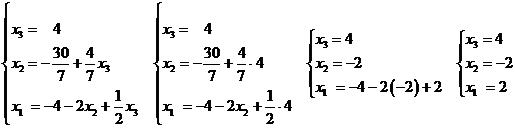
Ответ: 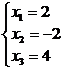
3. Показать, что векторы
а1, а2, а3 образуют базис в пространстве R3,
и найти координаты вектора а в этом базисе. 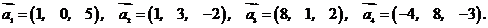
Решение
Вычислим определитель,
столбцами которого служат координаты векторов а1, а2,
а3:
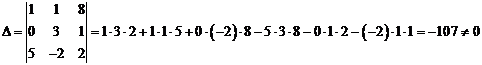
Так как Δ
≠ 0, то система векторов а1, а2, а3
образует базис в R3. Вектор а4 разлагается
по векторам этого базиса, т.е. справедливо равенство вида

Последнее равенство в
координатной форме имеет следующий вид:
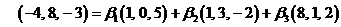
Согласно определению
равенства векторов и действиям над векторами получим систему линейных
алгебраических уравнений с неизвестными :
:
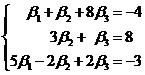
Решим эту систему
методом Крамера:
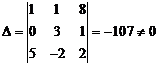
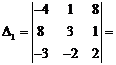

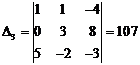
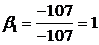

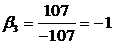
Ответ: 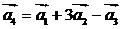
4. Определить ранг
заданной матрицы

Решение
Методом окаймляющих
миноров найдем ранг матрицы.
Высший порядок миноров
матрицы А - третий. Вычислим эти миноры.
Вычислим сначала угловой
минор второго порядка:
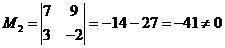
Он отличен от нуля.
Составим и вычислим два
минора третьего порядка, которые окаймляют этот минор. Один из таких миноров -
угловой минор:
 ,
,
Следующий минор: 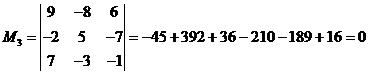
Все миноры третьего
порядка равны нулю.
Следовательно, ранг
матрицы А равен двум.
Ответ: 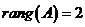
5. Привести систему к
системе с базисом методом Жордана-Гаусса и найти одно
базисное решение
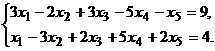
Решение
Матрица А и расширенная
матрица Ā данной системы имеют одним из миноров высшего порядка минор
второго порядка: 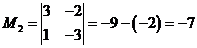 ,
который отличен от нуля. Следовательно, r(А) = r(Ā)
= 2. Система совместна, и так как r < n (n = 5), то она имеет бесчисленное
множество решений. Число ее базисных решений не превосходит числа
,
который отличен от нуля. Следовательно, r(А) = r(Ā)
= 2. Система совместна, и так как r < n (n = 5), то она имеет бесчисленное
множество решений. Число ее базисных решений не превосходит числа  .
.
Так как ранг системы
равен двум, то и число базисных переменных равно двум. Так как n - r = 5 - 2 =
3, то свободными будут три переменные.
Представим коэффициенты
при неизвестных в виде таблицы и решим систему методом Жордана-Гаусса:
|
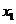 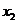  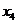 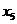 b b
|
|
|
|
|
|
|
3 1
|
-2 -3
|
3 2
|
-5 5
|
-1 2
|
9 4
|
|
1 3
|
-3 -2
|
2 3
|
5 -5
|
2 -1
|
|
1 0
|
-3 7
|
2 -3
|
5 -20
|
2 -7
|
4 -3
|
|
1 0
|
0 1
|
5/7 -3/7
|
25/7 -20/7
|
-1 -1
|
19/7 -3/7
|
В результате трех итераций система
преобразовалась к виду:
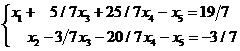
Следовательно, исходная
система имеет бесчисленное множество решений.
Последняя система
уравнений есть система с базисом и разрешается относительно базисных
неизвестных х1, х2, (х3, х4, х5
- свободные неизвестные):
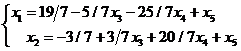
Методом Жордана-Гаусса
получено общее решение исходной системы.
Найдем одно базисное
решение:
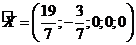
Сделаем проверку:
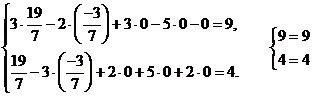
Ответ: 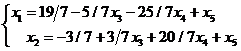 - общее
решение исходной системы
- общее
решение исходной системы
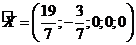 - базисное
решение системы
- базисное
решение системы
матрица уравнение крамер
гаусс
Библиографический список
1. Бугров Я.С., Никольский С.М. Высшая математика. Элементы
линейной алгебры и аналитической геометрии. - М: Наука. Главная редакция
физико-математической литературы, 1998
2. Бутузов В.Ф., Крутицкая Н.Ч., Шишкин А.А, Линейная алгебра
в вопросах и задачах: Учеб. пособие / Под ред. В.Ф. Бутузова. - ФИЗМАТЛИТ,
2002. -248 с.
3. Высшая математика для экономистов: Учебник для вузов / Н.Ш.
Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера -
М.: ЮНИТИ, 2003. - 471 с.
4. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей
математики для экономических вузов. Ч. 1, ч. 2.-М.: Высшая школа, 1982. - 320
с.
. Тиунчик М.Ф. Математика, часть 1. Линейная алгебра и
аналитическая геометрия: Учебное пособие. Хабаровск: ХГАЭП, 2002, - 104 с.