где R>0 - радиус окружности. Это уравнение называется каноническим
уравнением окружности, а система координат, в которой окружность описывается
каноническим уравнением, называется канонической. В канонической системе начало
координат является центром окружности (рис. 1).
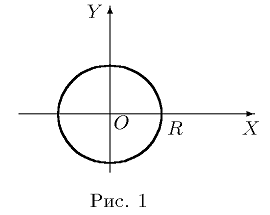
Уравнение
(x − a)2 + (y − b)2 = R2
определяет окружность радиуса R с центром в точке O'(a, b).
Эллипс
Эллипсом называется кривая второго порядка, которая в некоторой
декартовой системе координат описывается уравнением:
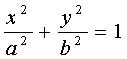
где a>0 , b>0 - параметры эллипса. Это уравнение называется
каноническим уравнением эллипса, а система координат, в которой эллипс
описывается каноническим уравнением, называется канонической.
В канонической системе оси координат являются осями симметрии эллипса, а
начало координат - его центром симметрии. Следовательно, мы можем ограничиться
исследованием функции
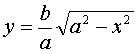 (1)
(1)
при x ≥ 0 , y ≥ 0 , т.е. рассматривать часть эллипса, лежащую
в первой четверти, а затем полученную кривую отразить симметрично относительно
осей координат.
Область определения функции (1): 0 ≤ x ≤ a , область значений
функции(1): 0 ≤ y ≤ b , т.е. весь эллипс лежит внутри
прямоугольника |x| ≤ a , |y| ≤ b . Вычислив производные y' и y'',
легко убедиться в том, что функция (1) в интервале x Î (0, a) убывает от b до нуля и ее
график является выпуклым вверх (рис.1).
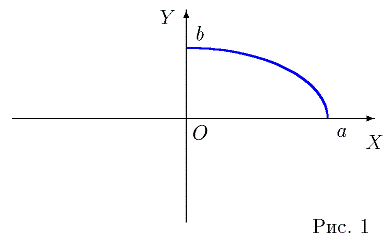
Отразив полученный график функции (1) симметрично, относительно осей
координат, получаем искомый эллипс (рис. 2):
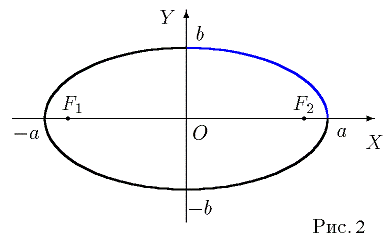
Точки пересечения эллипса с осями координат ( ± a, 0) и (0, ± b)
называются вершинами эллипса, а соответствующие отрезки a и b -полуосями
эллипса. Пусть a>b . Положим:
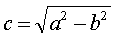 .
.
Точки
F1( −c, 0) и F2(c, 0) называются фокусами эллипса (если a<b , то 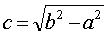 и фокусы эллипса расположены на оси OY ).
и фокусы эллипса расположены на оси OY ).
Эксцентриситетом
e эллипса называется отношение расстояния между
фокусами 2с к большой оси 2а:
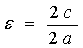 (e<1, т.к. с<а ).
(e<1, т.к. с<а ).
В частном случае a = b = R (e=0) эллипс является окружностью с уравнением
+ y2 = R2.
Гипербола
Гиперболой называется кривая второго порядка, которая в некоторой
декартовой системе координат описывается уравнением:
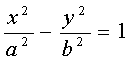 ,
,
где a>0 , b>0 - параметры гиперболы. Это уравнение называется
каноническим уравнением гиперболы, а система координат, в которой гипербола
описывается каноническим уравнением, называется канонической.
Заметим, что в канонической системе оси координат являются осями
симметрии гиперболы, а начало координат - ее центром симметрии. Следовательно,
мы можем ограничиться исследованием функции:
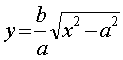 (2)
(2)
при a ≤ x< + ∞, y ≥ 0, т.е. рассматривать часть
гиперболы, лежащую в первой четверти, а затем полученную кривую отразить
симметрично относительно осей координат.
Область определения функции (2): a ≤ x< + ∞, область
значений функции (2): 0 ≤ y< + ∞. Вычислив производные y' и y''
, легко убедиться в том, что функция (2) в интервале x Î (a, + ∞) возрастает от нуля до
+ ∞ и ее график является выпуклым вверх. Прямая y = bx/a является
асимптотой гиперболы при x → + ∞ (рис.1).
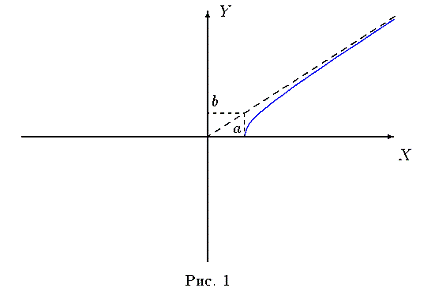
Отразив полученный график функции (2) симметрично, относительно осей
координат, получаем искомую гиперболу (рис. 2)
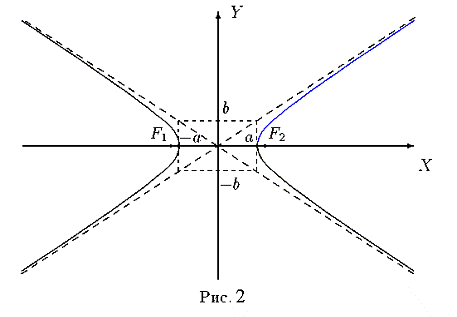
Точки
пересечения гиперболы с осью OX ( ± a, 0) называются вершинами гиперболы (с
осью OY гипербола не пересекается), отрезки a и b -полуосями гиперболы
(а-действительная, 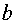 -мнимая). Положим
-мнимая). Положим
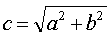 .
.
Точки
F1( −c, 0) и F2(c, 0) называются фокусами гиперболы. e=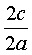 (e>1)-эксцентриситет гиперболы.
(e>1)-эксцентриситет гиперболы.
Замечания.
1) Если а=в, то гипербола называется равносторонней. Ее уравнение принимает
вид:
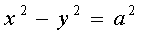 .
.
)
если фокусы гиперболы лежат на оси Оу, то уравнение гиперболы имеет вид
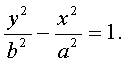
)
уравнение гиперболы с осями, параллельными координатным, имеет вид:
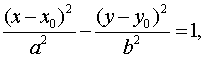
где
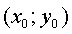 -координаты центра гиперболы.
-координаты центра гиперболы.
Парабола
Параболой называется кривая второго порядка, которая в некоторой
декартовой системе координат описывается уравнением:
= 2px, (1)
где p>0 - параметр параболы. Это уравнение называется каноническим
уравнением параболы, а система координат, в которой парабола описывается
каноническим уравнением, называется канонической.
Заметим, что в канонической системе ось OX является осью симметрии
параболы. Следовательно, мы можем ограничиться исследованием функции
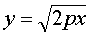 (2)
(2)
при 0 ≤ x< + ∞ , т.е. рассматривать часть параболы,
лежащую в первой четверти, а затем полученную кривую отразить симметрично
относительно оси OX .
Область определения функции (2): 0 ≤ x< + ∞ , область
значений функции(2): 0 ≤ y< + ∞ . Вычислив y' и y'' , легко
убедиться в том, что функция (2) в интервале x Î (0, + ∞) возрастает от нуля до
+ ∞ и ее график является выпуклым вверх. Асимптот у параболы нет. Начало
координат (0, 0) -вершина параболы (рис. 1).
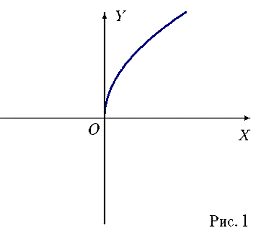
Отражая график функции (2) относительно оси OX, получаем искомую параболу
(рис. 2).
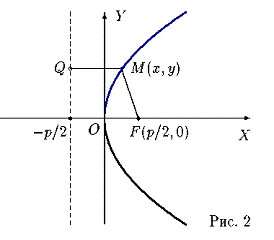
Прямая x = −p/2 называется директрисой параболы, а точка (p/2, 0) -
ее фокусом.
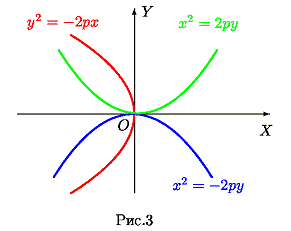
Уравнения y2 = −2px , x2 = 2py и x2 = −2py (p>0) также
описывают параболы, ветви которых направлены влево, вверх и вниз,
соответственно (рис. 3).
ТЕМА 13. Плоскость
Уравнение плоскости, проходящей через данную точку перпендикулярно
данному вектору
Пусть в трехмерном пространстве задана прямоугольная декартова система
координат. Сформулируем следующую задачу:
Составить
уравнение плоскости, проходящей через данную точку M(x0, y0, z0)
перпендикулярно данному вектору 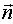 = {A, B,
C} .
= {A, B,
C} .
Решение.
Пусть P(x, y, z) - произвольная точка пространства. Точка P принадлежит
плоскости тогда и только тогда, когда вектор MP = {x − x0, y − y0,
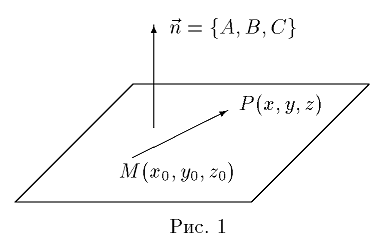
z − z0} ортогонален вектору 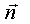 = {A, B,
C} (рис.1).
= {A, B,
C} (рис.1).
Написав
условие ортогональности этих векторов (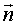 , MP) = 0
в координатной форме, получим:
, MP) = 0
в координатной форме, получим:
(x − x0) + B(y − y0) +
C(z − z0) = 0 (1)
Это
и есть искомое уравнение. Вектор 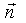 = {A, B,
C} называется нормальным вектором плоскости.
= {A, B,
C} называется нормальным вектором плоскости.
Таким
образом, чтобы написать уравнение плоскости, нужно знать нормальный вектор
плоскости и какую-нибудь точку, принадлежащую плоскости.
Общее
уравнение плоскости
Если
теперь в уравнении (1) раскрыть скобки и привести подобные члены, получим общее
уравнение плоскости:
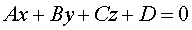
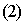
где D =
−Ax0 − By0 − Cz-
В трехмерном пространстве в декартовой системе координат любая плоскость
описывается уравнением 1-ой степени (линейным уравнением). И обратно, любое
линейное уравнение определяет плоскость.
Частные случаи общего уравнения плоскости:
Ах+Ву+Сz=0 (D=0) - плоскость проходит через начало координат;
Ах+Ву+D=0 (C=0) - плоскость параллельна оси Oz (аналогичный смысл имеют уравнения Ах+Сz+D=0, By+Cz+D=0);
Ах+Ву=0 (D=C=0) - плоскость проходит чрез ось Oz (Ax+Cz=0, By+Cz=0 - через оси Oy и Ox, соответственно);
Ax+D=0 (B=D=0) -плоскость
параллельна плоскости Oyz (Cz+D=0, By+D=0- параллельно плоскости Oxy и Oxz, соответственно);
Ax=0,
т.е. х=0 (В=С=D =0) - плоскость совпадает с
плоскостью Oyz (y=0, z=0 -
уравнения плоскостей Oxz и Oxy, соответственно).
Уравнение плоскости в отрезках: x/a+y/b+z/c=1,
где а, b,c - абсцисса, ордината и аппликата точек пересечения с
плоскостью координатных осей Ox, Oy, Oz, соответственно.
Уравнение плоскости, проходящей через три данные точки М1(x1;y1;z1), M2(x2;y2;z2) и M3(x3;y3;z3):

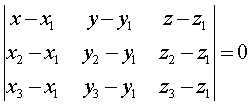
Расстояние
от точки до плоскости
Поставим следующую задачу:
Найти расстояние d от точки P(x0, y0, z0) до плоскости Ax + By + Cz + D =
0 .
Решение: фиксируем некоторую точку M(x1, y1, z1), , принадлежащую
плоскости, и построим вектор MP (рис. 1).
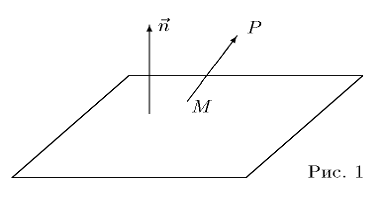
Искомое расстояние d равно абсолютной величине проекции вектора MP на
нормальный вектор плоскости. Получаем:
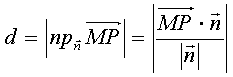
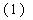
В нашем случае:
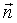 = {A, B,
C} и
= {A, B,
C} и 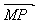 = {x0 − x1, y0 − y1, z0 − z1} .
= {x0 − x1, y0 − y1, z0 − z1} .
По формуле (1) имеем:
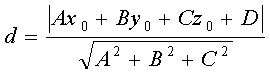
ТЕМА 14. Прямая линия в пространстве
Общие
уравнения прямой в пространстве
Линия в трехмерном пространстве определяется, вообще говоря, пересечением
двух поверхностей, т.е. описывается системой двух уравнений.
Прямую в пространстве можно рассматривать как линию пересечения двух
плоскостей и, следовательно, описывать системой двух линейных уравнений
A1x+B1y+C1z+D2=0 (1)x+B2y+C2z+D2=0,
при
условии, что эти плоскости непараллельны, т.е. их нормальные векторы 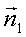 = {A1, B1, C1} и
= {A1, B1, C1} и 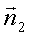 = {A2,
B2, C2} неколлинеарны. Эта система уравнений (1) называется общими уравнениями
прямой в пространстве.
= {A2,
B2, C2} неколлинеарны. Эта система уравнений (1) называется общими уравнениями
прямой в пространстве.
Канонические
и параметрические уравнения прямой
Поставим следующую задачу:
Составить
уравнения прямой, проходящей через данную точку M(x0, y0, z0) параллельно
данному вектору 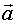 = {l, m, n} (вектор
= {l, m, n} (вектор 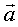 называется
направляющим вектором прямой).
называется
направляющим вектором прямой).
Решение. Пусть N(x, y, z) - произвольная точка пространства. Построим
вектор MN = {x − x0, y − y0, z − z0} (рис.1).
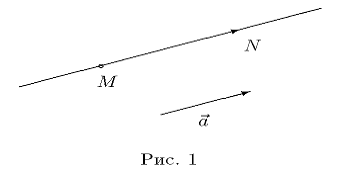
Очевидно,
что точка N принадлежит прямой тогда и только тогда, когда вектор MN
коллинеарен вектору 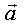 = {l, m, n} , т.е. когда их координаты
пропорциональны:
= {l, m, n} , т.е. когда их координаты
пропорциональны:
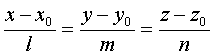 (2)
(2)
Эти
уравнения называются каноническими уравнениями прямой в пространстве.
Если
в (2) ввести параметр t
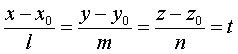 ,
,
то
уравнения прямой можно записать в виде:
x = x0+lt= y0+mt (3)= z0+nt.
Уравнения (3) называются параметрическими уравнениями прямой.
ТЕМА 15. Прямая и плоскость в аффинном
пространстве
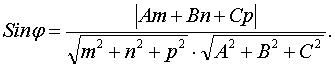
Условие параллельности прямой (L) и плоскости (Q) имеет вид:
+Bn + Cp =0;
условие их перпендикулярности:
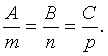
Для нахождения точки пересечения прямой и плоскости удобно
воспользоваться параметрическими уравнениями прямой:
x = x0+mt= y0+nt= z0+pt
Координаты точки пересечения находятся из системы уравнений:
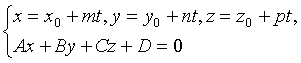
Условие, при котором прямая (L) лежит в плоскости (Q):
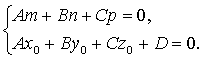
Если
Am +Bn +Cp ¹0, то
прямая пересекает плоскость; если Am +Bn + Cp =
0 и Ax0 +By0 +Cz0 +D ¹ 0 - прямая параллельна плоскости.
ТЕМА 16. Цилиндрические и конические
поверхности. Поверхности вращения
Системы координат в пространстве: декартовы, цилиндрические и сферические
координаты
Декартова система координат в пространстве определяется точкой и базисом
из трех векторов. Точка O называется началом координат. Прямые, проведенные
через начало координат в направлении базисных векторов, называются осями
координат. В трехмерном пространстве они называются осями абсцисс, ординат и
аппликат. Оси координат являются числовыми осями с началом в точке O ,
положительным направлением, совпадающим с направлением соответствующего
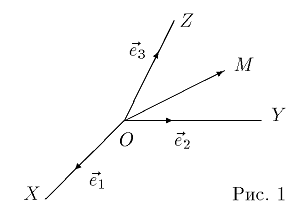
базисного вектора, и единицей длины, равной длине этого вектора. Координатами
точки M называются координаты вектора OM (радиус-вектора) (см. рис. 1). Если
базис ортонормированный, то связанная с ним декартова система координат
называется прямоугольной.
Поверхностью 2-го порядка называется поверхность, которая в некоторой
прямоугольной декартовой системе координат определяется уравнением
Ax2 + By2 + Cz2 + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Kz + L =
0
где A2 + B2 + C2 ≠ 0 .
Цилиндрические
и сферические координаты определяются точкой O, исходящим из нее лучом l и
единичным вектором 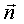 , перпендикулярным l (рис. 2).
, перпендикулярным l (рис. 2).
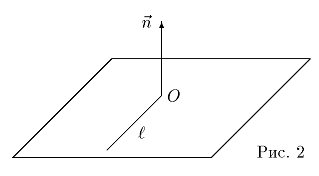
Проведем
через точку O перпендикулярно вектору  плоскость
P и обозначим проекцию точки M на эту плоскость M' .
плоскость
P и обозначим проекцию точки M на эту плоскость M' .
В
цилиндрических координатах положение точки M определяется числами ρ, j и z , где ρ
и j - полярные
координаты точки M' , а z - проекция вектора OM на вектор  . Пусть точка O совпадает с началом прямоугольной
декартовой системы координат, луч l - с положительной частью оси
абсцисс, а вектор
. Пусть точка O совпадает с началом прямоугольной
декартовой системы координат, луч l - с положительной частью оси
абсцисс, а вектор  - с положительной частью оси аппликат (рис. 3).
- с положительной частью оси аппликат (рис. 3).
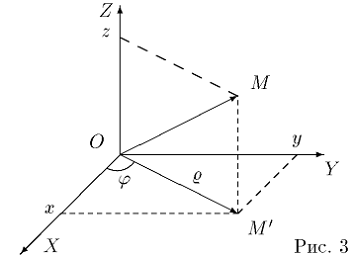
Декартовы координаты x , y и z точки M выражаются через ее цилиндрические
координаты ρ , j и z по формулам
x = ρcosj, y = ρsinj, z = z.
В
сферических координатах положение точки M определяется числами ρ, j и θ,
где ρ = |OM| , j - полярный угол точки M' , а θ - угол между векторами 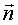 и OM. Мы
будем отсчитывать угол θ
от вектора
и OM. Мы
будем отсчитывать угол θ
от вектора 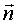 по
направлению к вектору OM . Угол θ принимает значения от 0 до π .
по
направлению к вектору OM . Угол θ принимает значения от 0 до π .
Пусть
точка O совпадает с началом прямоугольной декартовой системы координат, луч l - с
положительной частью оси абсцисс, а вектор 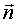 - с
положительной частью оси аппликат (рис. 4), то
- с
положительной частью оси аппликат (рис. 4), то
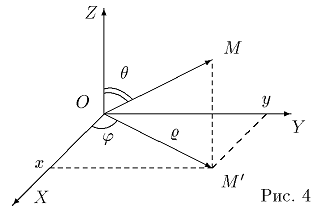
Декартовы координаты x , y и z точки M выражаются через ее сферические
координаты ρ , j и θ по формулам
= ρcosjsinθ, y = ρsinjsinθ, z = ρcosθ
Эллипсоид,
сфера
Эллипсоидом называется поверхность, которая в некоторой декартовой
системе координат определяется уравнением
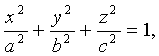
где a, b, c>0 - параметры эллипсоида. Это уравнение называется
каноническим уравнением эллипсоида, а система координат, в которой эллипсоид
описывается каноническим уравнением, называется канонической.
Из уравнения эллипсоида следует, что поверхность симметрична относительно
координатных плоскостей, начало координат является центром эллипсоида (рис.1).
В частном случае a = b = c = R имеем уравнение сферы:
+ y2 + z2 = R2 .
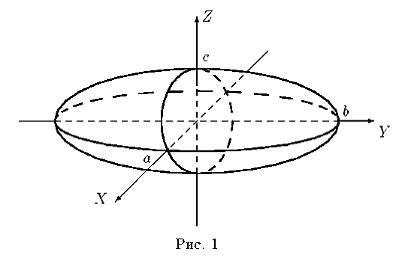
Однополостный гиперболоид.
Однополостным гиперболоидом называется поверхность, которая в некоторой
декартовой системе координат определяется уравнением
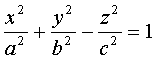 ,
,
где a, b, c>0 - параметры гиперболоида (его полуоси см. рис.1). Это
уравнение называется каноническим уравнением однополостного гиперболоида, а
система координат, в которой гиперболоид описывается каноническим уравнением,
называется канонической.
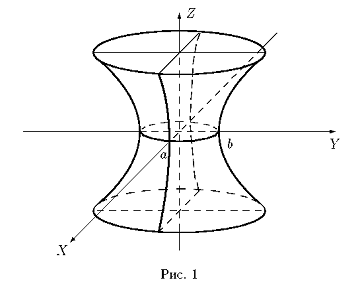
Сечения
гиперболоида горизонтальными плоскостями z=h
являются эллипсами:
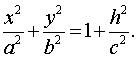
Сечения гиперболоида вертикальными плоскостями x=h или y=h являются гиперболами:
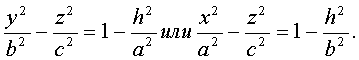
Цилиндрические
поверхности
Цилиндрической поверхностью называется поверхность, которая в некоторой
декартовой системе координат определяется уравнением, в котором не фигурирует
одна из переменных:
(x, y) = 0, F(x, z) = 0 или F(y, z) = 0.
Свойство цилиндрических поверхностей
Если некоторая точка M0(x0, y0, z0) принадлежит цилиндрической
поверхности, описываемой уравнением F(x, y) = 0 , то все точки прямой,
проходящей через эту точку параллельно оси OZ , также принадлежат
цилиндрической поверхности. Такие прямые называются образующими цилиндрической
поверхности, а кривая, описываемая уравнением F(x, y) = 0 и получающаяся в
сечении любой плоскостью z = h , называется направляющей.
Примеры цилиндрических поверхностей 2-го порядка
Эллиптический цилиндр (рис.1).
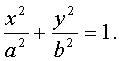
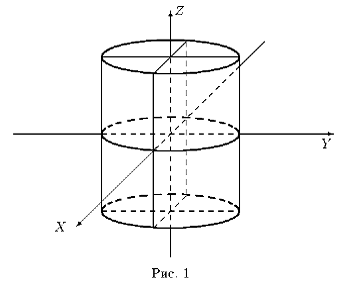
Если
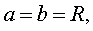 то уравнение x2 + y2 = R2 в трехмерном пространстве
определяет круглый цилиндр.
то уравнение x2 + y2 = R2 в трехмерном пространстве
определяет круглый цилиндр.
Гиперболический
цилиндр.
Уравнение
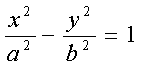
в трехмерном пространстве определяет цилиндрическую поверхность с
образующими, параллельными оси OZ . Направляющей является гипербола с полуосями
a и b (рис. 2).
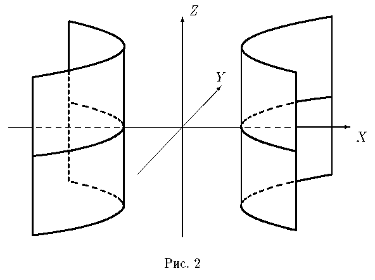
Параболический цилиндр.
Уравнение
= 2px ( p>0 )
в трехмерном пространстве определяет цилиндрическую поверхность с
образующими, параллельными оси OZ . Направляющей является парабола (рис. 3).
ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Второй семестр
ТЕМА 1. Множества. Действительные числа.
Множества, подмножества. Основные понятия
Под множеством понимается совокупность некоторых объектов. Объекты,
которые образуют множество, называются элементами или точками этого множества.
Множества обозначаются прописными буквами, а их элементы - строчными.
Если а есть элемент множества А, то используется запись а Î А. Если в не является элементом
множества А, то пишут в Ï А.
Множество, не содержащее ни одного элемента, называется пустым и
обозначается символом Æ.
Если множество В состоит из части элементов множества А или совпадает с
ним, то множество В называется подмножеством множества А и обозначается В Ì А.
Два множества называются равными, если они состоят из одних и тех же
элементов.
Объединением двух множеств А и В называется множество С, состоящее из
всех элементов, принадлежащих хотя бы одному из данных множеств, т.е. С = А È В.
Пересечением двух множеств А и В называется множество D, состоящее из всех элементов,
одновременно принадлежащих каждому из данных множеств А и В, т. е. D = A Ç B.
Разностью множеств А и В называется множество Е, состоящее из всех
элементов множества А, которые не принадлежат множеству В, т. е. Е =А \ B.
Очевидно, что А È Æ = А, А Ç Æ =Æ, А \ Æ = A.
Элементы логической символики
Для сокращения записей используются некоторые простейшие логические
символы:
a Þ b -
означает «из предложения a
следует предложение b»;
a Û b -
«предложения a и b равносильны», т.е. из a следует b и из b следует a;
" - означает « для любого», «для
всякого»;
$ - «существует», «найдется»;
: - «имеет место», «такое что»;
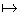 - «соответствие».
- «соответствие».
Например, запись "х Ï А. a означает: «для всякого элемента х из множества А
имеет место предложение a».
Числовые множества. Множества действительных чисел
Множества, элементами которых являются числа, называются числовыми.
Примерами числовых множеств являются:
N = {1; 2; 3;…; n;…} -множество натуральных чисел;
Z0 = {0; 1; 2;…;n;…} - множество целых неотрицательных
чисел;
Z = {0; ±1; ±2; …;±n;…} - множество целых чисел;
Q = 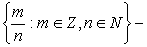 множество рациональных чисел;
множество рациональных чисел;
R - множество действительных чисел.
Между этими множествами существует соотношение:
N Ì Z0 Ì Z Ì Q ÌR.
Множество R содержит
рациональные и иррациональные числа. Всякое рациональное число выражается или
конечной десятичной дробью или бесконечной периодической дробью. Действительные
числа, не являющиеся рациональными, называются иррациональными.
Числовые промежутки. Окрестность точки
Пусть а и в -
действительные числа, причем а < в.
Числовыми промежутками (интервалами) называют подмножества всех
действительных чисел, имеющих следующий вид:
[а;в] ={х : а£ х £ в} -
отрезок (сегмент, замкнутый прмежуток);
( а; в ) ={х :
а< х < в} - интервал (открытый промежуток);
[а; в) = {х : а£ х < в} ;
(а;в] ={х : а< х£ в} - полуоткрытые интервалы (или
полуоткрытые отрезки);
(-¥;в] = {х :
х £ в}; [а;+¥) = {х : х ³ а};
(-¥;в) = {х : х < в}; (а;+¥) = {х : х > а};
(-¥; ¥) = {х :
-¥ < х <
+¥ } = R - бесконечные интервалы (промежутки).
Пусть х0 -
любое действительное число (точка на числовой прямой). Окрестностью точки х0
называется любой интервал (а;в), содержащий точку х0. В частности, интервал (х0
- e, х0 + e),
где e > 0, называется e -
окрестностью точки х0. Число х0 называется центром, а число e - радиусом.
Если х Î (х0 - e; х0 +e),
то выполняется неравенство х0 - e < х <
х0 + e.
Абсолютная величина (модуль) действительного числа
Абсолютной величиной действительного числа х называется само число х,
если х неотрицательно, и противоположное число - х, если х отрицательно:
÷х÷ = 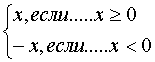 .
.

Очевидно, по определению, что ÷ х÷ ³0.
Свойства абсолютных величин:
1.
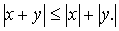 3.
3. 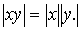
. 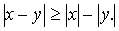 4.
4. 
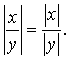
Абсолютная величина разности двух чисел ÷х - а÷ означает расстояние между точками х и а числовой прямой как для случая х
<a, так и для х > a.
Поэтому, например, решениями неравенства ÷х -а÷< e
(где e > 0) будут точки х интервала (а - e, а + e),
удовлетворяющие неравенству а - e <x <a + e.
ТЕМА 2. Числовые последовательности. Предел
числовой последовательности
Понятие о числовой последовательности
Если
по некоторому закону каждому натуральному числу n поставлено в
соответствие вполне определенное число xn, то говорят,
что задана числовая последовательность 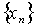 :
:
x1,x2, …,xn,…. .
Иными словами, числовая последовательность - это функция натурального аргумента: xn=f(n).
Числа
x1, x2,…,xn в последовательности 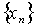 называются
членами последовательности. При этом число xn называется n-м
(энным) или общим членом последовательности. Формулы, позволяющие выразить n-член
последовательности через предыдущие члены, называются рекуррентными.
называются
членами последовательности. При этом число xn называется n-м
(энным) или общим членом последовательности. Формулы, позволяющие выразить n-член
последовательности через предыдущие члены, называются рекуррентными.
Свойства последовательностей
Последовательность, все члены которой равны одному и тому же числу,
называется постоянной.
Последовательность {xn} называется неубывающей (невозрастающей), если "n: xn £ xn+1 (соответственно, "n: xn ³ xn+1). Невозрастающие и неубывающие последовательности
объединяют общим термином - монотонные последовательности.
Последовательность {xn} называется возрастающей (убывающей), если "n: xn<xn+1,
(соответственно, "n: xn>xn+1). Возрастающие и убывающие
последовательности объединяют общим названием - строго монотонные последовательности.
Последовательность {xn} называется ограниченной сверху (ограниченной снизу), если существует
такое число М, что все члены последовательности меньше (соответственно,
больше), чем М. Последовательность, ограниченная сверху и снизу одновременно,
называется ограниченной.
Последовательность {xn} называется неограниченной, если для любого М>0 найдется такой ее член xn, что çxnç>М.
Предел последовательности
Число а называется пределом последовательности {xn}, если для любого положительного
числа e можно подобрать такой номер N (как правило, зависящий от e), что, начиная с этого номера (т.е.
для всех n³N), будет выполнено неравенство
çxn - aç < e.
В случае, если последовательность имеет пределом число а, говорят также,
что последовательность {xn} сходится к числу а, и обозначается этот факт так:
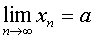 или xn® a при
(n®¥).
или xn® a при
(n®¥).
Если последовательность не имеет предела, то говорят, что она расходится.
Геометрический смысл предела последовательности состоит в следующем:
число а называется пределом последовательности {xn}, если в любом интервале с центром в
точке а находятся почти все (т.е. все, кроме конечного числа) члены этой
последовательности.
Операции над пределами последовательностей
Предел суммы (разности) двух сходящихся последовательностей равен сумме
(разности) их пределов:
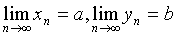 Þ
Þ 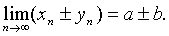
Предел произведения двух сходящихся последовательностей равен
произведению их пределов:
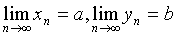 Þ
Þ 
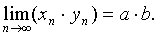
В частности:
- постоянный множитель можно выносить за знак предела:
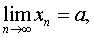 сÎR Þ
сÎR Þ 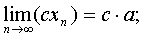
- предел натуральной степени от сходящейся последовательности равен этой
степени от ее предела:
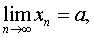 Þ
Þ 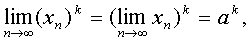 к = 1,2,3,…
к = 1,2,3,…
Предел корня к-ой степени от сходящейся последовательности равен корню
этой же степени от предела последовательности:
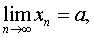 к =
2,3,4,… Þ
к =
2,3,4,… Þ 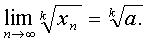

Пределы
и неравенства
Пусть все члены данной сходящейся последовательности неотрицательны.
Тогда ее предел также неотрицателен:
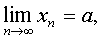 xn ³ 0 "n Þ a ³ 0.
xn ³ 0 "n Þ a ³ 0.
Пусть каждый член одной сходящейся последовательности больше или равен
соответствующему члену другой сходящейся последовательности. Тогда и предел
первой последовательности больше или равен пределу второй последовательности:
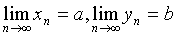 , xn ³ yn "n Þ a ³ b.
, xn ³ yn "n Þ a ³ b.
Пусть соответствующие члены трех данных последовательностей {xn}, {yn} и {zn} удовлетворяют условию xn £yn £zn.
Тогда если последовательности {xn} и {zn} сходятся к одному и тому же пределу, то последовательность {yn} также сходится к этому пределу:
xn £yn £zn, "n, 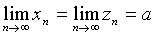 Þ
Þ 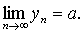
Число
е
Последовательность
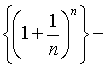 возрастает и ограничена сверху, а поэтому сходится. Ее
пределом является замечательное иррациональное число е=2,71828182845…, служащее
основанием натуральных логарифмов.
возрастает и ограничена сверху, а поэтому сходится. Ее
пределом является замечательное иррациональное число е=2,71828182845…, служащее
основанием натуральных логарифмов.
Таким
образом,
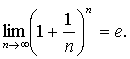
ТЕМА 3. Функция одной переменной. Графики
элементарных функций
Понятие функции
Если каждому элементу (значению) х множества Х поставить в соответствие
определенный элемент (значение) у множества У, то говорят, что на множестве Х
задана функция y=f(x); при этом множество Х называется областью определения
функции y, а множество У - областью значений функции у.
Основные характеристики функции
Функция y=f(x) называется
четной, если для любых значений х из области определения функции f(-x) = f(x), и нечетной, если f(-x) = -f(x). В противном случае f(x) - функция
общего вида.
Функция f(x) называется возрастающей (убывающей) на некотором промежутке
Х, если большему значению аргумента соответствует большее (меньшее) значение
функции f(x). Возрастающие и убывающие функции называются монотонными.
Функция f(x) называется ограниченной на промежутке Х, если существует
такое число М>0, что ½f(x)½<М, для всех хÎХ. В противном случае функция называется неограниченной.
Функция f(x), определенная на множестве Х, называется периодической на
этом множестве, если существует такое число Т>0, что при любом хÎХ значение (х+Т)ÎХ и f(x+T) = f(x).
При этом число Т называется периодом функции.
Обратная функция
Пусть задана функция y=f(x) с областью определения Х и множеством значений У. Если
каждому значению уÎУ соответствует единственное значение хÎХ, то определена функция х=j(у) с областью определения У и множеством
значений Х. Такая функция j(у) называется обратной к функции f(x) и записывается
в следующем виде:
x=j(у)=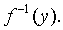
Про функции y=f(x) и x=j(y) говорят, что они являются взаимно обратными.
Сложная функция
Если функция y = f(u) есть функция переменной u (определенной на множестве U с областью значений У), а переменная u, в свою очередь, также является
функцией u = j(x)
(определенной на множестве Х с областью значений U), то заданная на множестве Х функция y=f(j(x)) называется сложной функцией.
Основные элементарные функции
1)
степенная функция 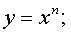
)
показательная функция 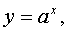
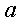 > 0,
> 0, 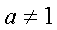 (Х=(-¥;+¥); У=(0;+¥));
(Х=(-¥;+¥); У=(0;+¥));
)
логарифмическая функция 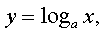
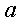 > 0,
> 0, 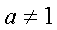 (Х=(0;+¥); У=(-¥;+¥));
(Х=(0;+¥); У=(-¥;+¥));
)
тригонометрические функции y=sin x, y=cos x, y=tg x, y=ctg x;
)
обратные тригонометрические функции y=arcsin
x, y=arccos x, y= arctg x, y= arcctg x.
Функции, построенные из основных элементарных функций при помощи
конечного числа алгебраических действий и конечного числа операций образования
сложной функции, называются элементарными.
Преобразование графиков
1) y=f(x+a) - сдвигает график y=f(x) параллельно оси
Ох на çа ç единиц, (а>0-влево,
а<0-вправо);
2) у=f(x)+b - cдвигает график y=f(x) параллельно оси Оу на çb çединиц, (b>0 - вверх, b<0 - вниз);
3) y=cf(x) (c¹0) -
растягивает в с раз (с>1)
или сжимает (0<с<1) график y=f(x) относительно оси Оу; при с<0 симметрично отображает график
относительно оси Ох;
4) y=f(kx) (k¹0) -
сжимает в к раз (к>1)
или растягивает (0<к<1) график y=f(x) относительно оси Ох; при к<0 симметрично отображает график
относительно оси Оу.
ТЕМА 4. Предел функции одой переменной
Определение предела
Окрестностью точки x0
называется любой интервал с центром в точке x0. Пусть функция f(x) определена в некоторой окрестности
точки x0 кроме самой точки x0.
Число
А называется пределом функции f(x) в точке x0, если для любого сколь угодно
малого числа e>0 найдется такое число d>0 (вообще
говоря, зависящее от e), что для всех x таких, что 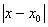 <d, x
<d, x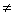 x0, выполняется
неравенство
x0, выполняется
неравенство 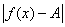 <e.
<e.
Обозначается
это так: 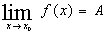 или f(x)®A (при х®х0).
или f(x)®A (при х®х0).
Операции над пределами
Пусть
функции f(x) и g(x) определены в некоторой окрестности точки x0 и,
кроме того, 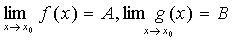 . Тогда:
. Тогда:
. 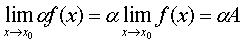 (
( 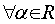 )
)
. 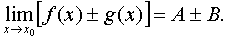
. 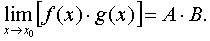
. 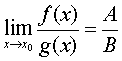 (В¹0).
(В¹0).
Предел
функции на бесконечности
Число
А называется пределом функции f(x) при x®+¥, если при любом значении e>0 найдется такое число М>0, что для всех
значений х>М выполняется неравенство 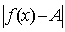 <e.
<e.
Обозначение:
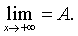
Аналогично
определяется предел функции f(x) при х®- ¥.
Обозначение:
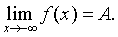
Односторонние пределы
Число
А называется пределом функции f(x) слева в точке х0, если для любого числа e>0 существует число d>0 такое, что при хÎ(х0-d;х0), выполняется неравенство 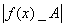 <e. Предел слева записывается так:
<e. Предел слева записывается так: 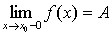 или
коротко: f(x0-0)=A.
или
коротко: f(x0-0)=A.
Аналогично
определяется предел функции справа, обозначаемый 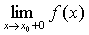 или f(x0+0).
Пределы функции слева и справа называются односторонними пределами.
или f(x0+0).
Пределы функции слева и справа называются односторонними пределами.
Замечательные пределы
Первый замечательный предел
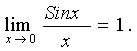
Второй замечательный предел
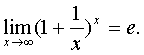
Часто используются следующие следствия из обоих замечательных пределов:
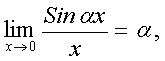 aÎR;
aÎR;
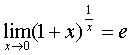 ,
, 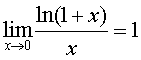 ,
, 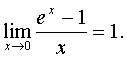
Бесконечно
малые функции
Функция
a(x) называется бесконечно малой при х®х0, если 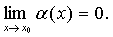
Если
функция f(x) имеет предел, равный А, то ее можно представить как
сумму числа А и бесконечно малой функции a(х), т.е. если 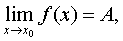 то
то
f(x) = A+a(x).
Пусть
a(х) и b(х) -бесконечно малые функции при х®х0. Тогда, если 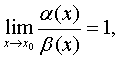 то a(х) и b(х) называются эквивалентными бесконечно малыми, что обозначается так: a(х) ~ b(х), х®х0.
то a(х) и b(х) называются эквивалентными бесконечно малыми, что обозначается так: a(х) ~ b(х), х®х0.
При
решении многих задач используются следующие эквивалентности, верные при х®0:
Sinx ~ x, 1-Cosx ~ 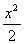 , tgx ~ x,
arcsinx ~ x, ln(1+x) ~ x,
, tgx ~ x,
arcsinx ~ x, ln(1+x) ~ x, 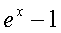 ~ x.
~ x.
Бесконечно большие функции
Функция
f(x) называется бесконечно большой при х®х0, если для любого числа М>0 существует
число d = d(М) >0, что для всех х, удовлетворяющих неравенству 0<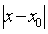 <d, выполняется
неравенство
<d, выполняется
неравенство 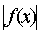 >М. Записывают
>М. Записывают 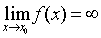 или f(x) ®¥ при х®х0.
или f(x) ®¥ при х®х0.
ТЕМА 5. Непрерывность функции одной переменной
Непрерывность функции в точке
Функция f(x) называется непрерывной в точке х0, если она определена в
некоторой окрестности этой точки и
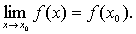
Если обозначить х-х0=Dх (приращение аргумента), f(x)-f(x0)=Dy (приращение функции, соответствующее приращению аргумента Dх), то это определение можно записать
в эквивалентной форме.
Функция f(x) называется непрерывной в точке х0, если она определена в
некоторой окрестности этой точки и

Таким образом, если функция f(x) непрерывна в точке х0, то бесконечно
малому приращению аргумента в этой точке соответствует бесконечно малое
приращение функции.
Непрерывность функции на промежутке
Функция f(x) называется непрерывной на данном промежутке (интервале,
полуинтервале, отрезке), если она непрерывна в каждой точке этого промежутка.
Односторонняя непрерывность
Функция f(x) называется непрерывной слева в точке х0, если она
определена на некотором полуинтервале (а;х0] и
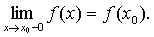
Функция f(x) называется непрерывной справа в точке х0, если она
определена на некотором полуинтервале [х0;в) и
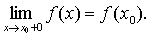
Функция f(x) непрерывна в точке х0 тогда и только тогда, когда она
непрерывна слева и справа в этой точке, т.е. когда
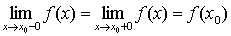
Точки
разрыва функции
Точка х0 называется точкой разрыва функции f(x), если f(x) не является непрерывной в этой точке, причем:
а)
если оба односторонних предела 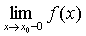 и
и 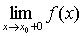 конечны, но не равны между собой, то х0- точка разрыва первого рода;
конечны, но не равны между собой, то х0- точка разрыва первого рода;
б)
если оба односторонних предела 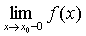 и
и 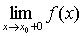 конечны, равны между собой, но не равны f(x0),
то х0 - точка устранимого разрыва первого рода;
конечны, равны между собой, но не равны f(x0),
то х0 - точка устранимого разрыва первого рода;
в)
если хотя бы один из односторонних пределов 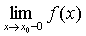 или
или 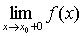 бесконечен, или не существует то х0 - точка разрыва второго рода.
бесконечен, или не существует то х0 - точка разрыва второго рода.
Свойства функций, непрерывных в точке
1. Если f(x) и g(x) непрерывны в
точке х0, то функции f(x)±g(x); f(x).g(x); и f(x)/g(x) (если g(x)¹0) также непрерывны в точке х0.
2. Если функция u(x) непрерывна в точке х0, а функция f(u) непрерывна в точке u0=u(x0), то сложная функция f(u(x)) непрерывна в
точке х0.
Все элементарные функции непрерывны в каждой точке своих областей
определения.
Свойства функций, непрерывных на отрезке
Теорема (Вейерштрасса). Если функция непрерывна на отрезке, то она
достигает на этом отрезке своего наибольшего и наименьшего значений.
Следствие. Если функция непрерывна на отрезке, то она ограничена на этом
отрезке.
Теорема (Больцано - Коши). Если функция y=f(x) непрерывна на отрезке [а;в] и принимает на его концах неравные значения f(a) = A и f(в) = В, то на этом отрезке она
принимает и все промежуточные значения между А и В.
Следствие. Если функция y =f(x) непрерывна на отрезке [а;в] и
на его концах принимает значения разных знаков, то внутри отрезка [а;в] найдется хотя бы одна точка c, в которой данная функция f(x) обращается в
ноль: f(c)= 0.
ТЕМА 6. Производная и дифференциал функции одной
переменной
Определение производной
Производной функции y=f(x) называется конечный предел приращения функции к приращению
аргумента при стремлении последнего к нулю (при условии, что этот предел
существует):
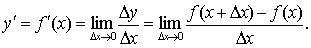
Если функция в точке х0 (или на промежутке Х) имеет конечную производную,
то функция называется дифференцируемой в этой точке (или на промежутке Х).
Таблица производных
1. (с)¢=0, c=const;
2. 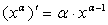 (где aÎR);
(где aÎR);
. 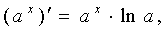
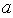 > 0,
> 0, 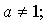 в частности
в частности 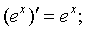
. 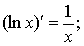
. 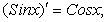
. 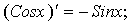
. 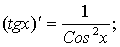
8. 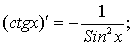
9. 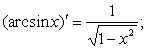
. 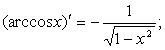
. 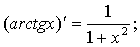
. 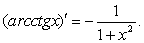
Основные правила дифференцирования
с-постоянная, u(x) и v(x)-дифференцируемые
функции:
с¢=0; х¢=1; (uvw)¢=u¢vw+uv¢w+uvw¢;
(u ±v)¢=u¢±v¢; 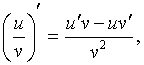
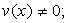
(u×v)¢=u¢v
+ uv¢; 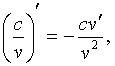
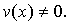 ;
;
(cu)¢=cu¢;
Пусть
функция u = j(x)
имеет производную в точке х0, а функция y=f(u) - в точке u0=j(x0). Тогда
сложная функция y=f(j(x)) также
имеет производную в точке х0, причем
y¢(x0)=y¢(u0)×u¢(x0).
Если
y=f(x) - дифференцируемая и
строго монотонная функция на промежутке Х, то функция обратная к данной х=j(у), также дифференцируема и ее производная определяется соотношением:
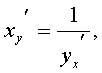 y¢x ¹ 0.
y¢x ¹ 0.
Геометрический
смысл производной
Пусть функция y=f(x) имеет производную в точке х0. Тогда существует касательная
к графику этой функции в точке М0(х0;у0), уравнение которой имеет вид
у-у0=f¢(x0)(x-x0).
При этом f¢(x0)=tga, где a-угол наклона этой касательной к оси Ох.
Прямая, проходящая через точку касания, перпендикулярно касательной,
называется нормалью к кривой и имеет уравнение
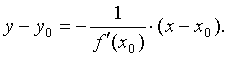
Производная
неявной функции
Пусть функция y=y(x), обладающая производной в точке х, задана неявно уравнением
F(x,y)=0.
Тогда производную y¢(x) этой функции можно найти,
продифференцировав это уравнение (при этом у считается функцией от х), и разрешая
затем полученное уравнение относительно у¢.
Производные высших порядков
Производная
от функции f¢(x) называется производной второго порядка от функции f(x)
(или второй производной) и обозначается 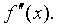
Аналогично
определяются производная третьего порядка (или производная), обозначаемая 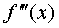 и т.д.
и т.д.
Производная
n-го порядка обозначается 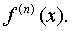
Дифференциал функции
Приращение
Dу дифференцируемой функции y=f(x)
можно представить в виде 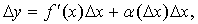 где f¢(x) -производная функции f(x); Dx-приращение
независимой переменной; a(Dх)-бесконечно
малая величина.
где f¢(x) -производная функции f(x); Dx-приращение
независимой переменной; a(Dх)-бесконечно
малая величина.
Дифференциалом
(первого порядка) функции y=f(x) называется главная, линейная относительно Dх часть приращения функции, равная произведению производной на
приращение независимой переменной:
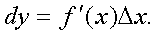
Дифференциал независимой переменной равен приращению этой переменной:
dx=Dx.
Поэтому дифференциал функции:
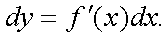
Геометрический
смысл дифференциала
Геометрически приращение Dу функции f(x) в точке х - есть приращение ординаты точки на
кривой, а дифференциал dy
функции в этой точке -
приращение ординаты соответствующей на касательной.
Применение дифференциала в приближенных вычислениях
При достаточно малых значениях Dх приращение функции Dу»dy,
т.е.
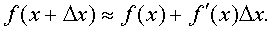
Чем меньше значение Dх, тем точнее эта формула.
Дифференциалы высших порядков
Дифференциалом
второго порядка (или вторым дифференциалом)  функции y=f(x)
называется дифференциал от дифференциала первого порядка этой функции. Т.е.
функции y=f(x)
называется дифференциал от дифференциала первого порядка этой функции. Т.е. 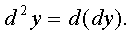
Дифференциалом
n-го порядка 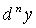 называется
дифференциал от дифференциала (n-1)-го порядка этой функции, т.е
называется
дифференциал от дифференциала (n-1)-го порядка этой функции, т.е 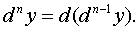
ТЕМА 7. Свойства дифференцируемых функций
Теоремы о среднем
Теорема (Ролля). Пусть функция f(x) непрерывна на отрезке [а;в], дифференцируема на интервале (а;в) и принимает на
концах отрезка равные значения (т.е. f(a)=f(b)). Тогда
существует по крайней мере одна точка с на интервале (а;в), для которой f¢(c)=0.
Теорема Лагранжа. Пусть функция f(x) непрерывна на отрезке [а;в] и дифференцируема на интервале (а;в). Тогда на
интервале (а;в) найдется такая точка с, что
f(b)-f(a)=f¢(c)(b-a).
Теорема (Коши). Пусть функции f(x) и g(x) непрерывны на
отрезке [а;в] и дифференцируемы на интервале (а;в), причем g(x)¹0 для всех хÎ(а;в). Тогда найдется такая точка с на этом интервале, что
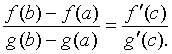
Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно
больших функций равен пределу отношения их производных (конечному или
бесконечному), если последний существует в указанном смысле:
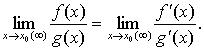
Таким
образом, правило Лопиталя используется для раскрытия неопределенностей вида 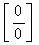 или
или 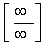 .
.
Правило
Лопиталя можно применять также и для раскрытия неопределенностей вида [0×¥]. Для этого произведение f(x)g(x)
следует записать в виде 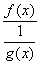 (или
(или 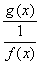 ),
получить неопределенность вида
),
получить неопределенность вида 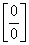 или
или 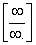 .
.
Если
имеется неопределенность вида 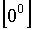 или
или 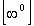 , при вычислении предела функции
, при вычислении предела функции 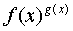 , то логарифм этой функции представляет собой
неопределенность вида [0×¥]. При этом
используется соотношение:
, то логарифм этой функции представляет собой
неопределенность вида [0×¥]. При этом
используется соотношение:
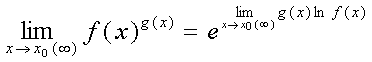 .
.
Формула
Тейлора. Пусть функция f(x) имеет в некоторой окрестности точки х0 производные 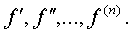 Тогда для любой точки х из этой окрестности имеет
место равенство
Тогда для любой точки х из этой окрестности имеет
место равенство
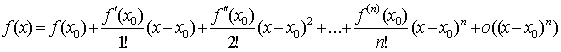
при
х®х0.
Эта формула называется формулой Тейлора с остаточным членом в форме
Пеано. Последнее слагаемое (т.е. остаточный член) в формуле Тейлора иногда
записывают в виде:
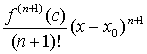 .
.
Соответствующая
формула тогда называется формулой Тейлора с остаточным членом в форме Лагранжа.
В
случае х0=0 формула Тейлора принимает вид:
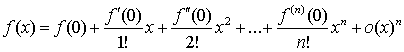 ,
,
при
х®0 и называется формулой Маклорена.
Полезно помнить разложения по формуле Маклорена некоторых важнейших
элементарных функций:
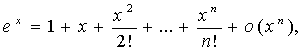
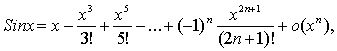
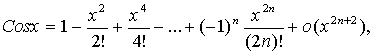
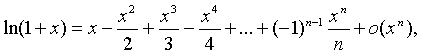
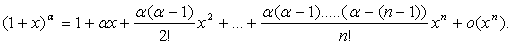
ТЕМА 8. Исследование функций
Условия
монотонности функции
Если
функция f(x) дифференцируема на интервале (a;b) и f¢(x) > 0 (f¢(x) < 0) 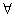 x Î (a;b), то f(x) возрастает (соответственно убывает) на этом
интервале.
x Î (a;b), то f(x) возрастает (соответственно убывает) на этом
интервале.
Если
же f¢(x) ³ 0 (f¢(x) £ 0) 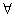 x Î (a;b),
то функция f(x) не убывает (соответственно, не возрастает) на
интервале (a;b), т.е.
x Î (a;b),
то функция f(x) не убывает (соответственно, не возрастает) на
интервале (a;b), т.е. 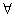 x1, x2 Î (a;b) из
х1<х2 следует f(x1) £ f(x2)
(соответственно, f(x1) ³f(x2)).
x1, x2 Î (a;b) из
х1<х2 следует f(x1) £ f(x2)
(соответственно, f(x1) ³f(x2)).
Экстремум функции
Точка х0 называется точкой максимума (минимума) функции f(x), если существует интервал, содержащий точку х0, такой, что
для всех х из этого интервала имеет место неравенство f(x0) ³ f(x), (f(x0) £ f(x)). Точки максимума и минимума называются точками экстремума.
Необходимое условие экстремума: в точке экстремума функции ее производная
либо равна нулю (f¢(x)=0), либо не существует.
Первое достаточное условие экстремума: если в точке х0 функция y=f(x) непрерывна, а
производная f¢(x) при переходе через точку х0 меняет знак, то точка х0 - точка экстремума: максимума, если
знак меняется с «+» на «-»,
и минимума, если с «-»
на «+».
Если при переходе через точку х0 производная не меняет знак, то в точке
х0 экстремума нет.
Выпуклость графика функции. Точки перегиба
Функция y = f(x) называется
выпуклой вверх (вниз) на промежутке, если для любых двух значений х1, х2 из
этого промежутка выполняется неравенство:
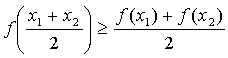
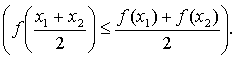
Точки, разделяющие интервалы выпуклости, называются точками перегиба.
Если вторая производная f¢¢(x) функции y = f(x) положительна
(отрицательна) на промежутке, то функция является выпуклой вниз (вверх) на этом
промежутке.
Если х0 - точка перегиба
функции y = f(x) и f¢¢(x0) существует, то f¢¢(x0) =
0.
Если 2-ая производная f¢¢(x) меняет знак при
переходе через точку х0, то точка х0 является точкой перегиба функции y = f(x).
Асимптоты
1.
Прямая 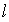
 называется
асимптотой графика функции y = f(x), если расстояние от точки (x,f(x))
до этой прямой стремится к нулю при неограниченном удалении точки графика от
начала координат.
называется
асимптотой графика функции y = f(x), если расстояние от точки (x,f(x))
до этой прямой стремится к нулю при неограниченном удалении точки графика от
начала координат.
Асимптоты
бывают вертикальными, горизонтальными и наклонными.
.
Прямая х =х0 является вертикальной асимптотой графика функции y=(x),
если хотя бы один из пределов 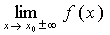 (правосторонний
или левосторонний) равен ±¥.
(правосторонний
или левосторонний) равен ±¥.
.
Прямая y = b является горизонтальной асимптотой, если 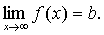

.
Если 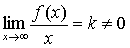 и
и 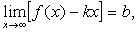 то
прямая y = kx+b является наклонной асимптотой графика функции y = f(x).
то
прямая y = kx+b является наклонной асимптотой графика функции y = f(x).
Общая
схема исследования функций и построения графиков
1) найти область определения функции;
2) исследовать функцию на четность - нечетность;
) найти вертикальные асимптоты;
4) исследовать поведение функции в бесконечности; найти
горизонтальные и наклонные асимптоты;
5) найти экстремумы и интервалы монотонности функции;
6) найти интервалы выпуклости функции и точки перегиба;
7) найти точки пересечения графика функции с осями координат и,
возможно, некоторые дополнительные точки, уточняющие график.
ТЕМА 9. Комплексные числа
Основные понятия
Комплексным
числом называется выражение вида z=x+iy, где х и у- действительные
числа, i-мнимая единица (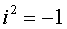 ). Число x=Re(z)
называется действительной частью числа z, а число y=Im(z) - мнимой частью числа z.
). Число x=Re(z)
называется действительной частью числа z, а число y=Im(z) - мнимой частью числа z.
Два
комплексных числа z1=x1+iy1 и z2=x2+iy2, равны, если х1=х2; у1=у2.
z=0,
если х=0, у=0.
Числа
z=x+iy и 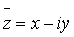 называются
сопряженными.
называются
сопряженными.
Арифметические операции над комплексными числами
1. Сложение (вычитание):
±z2=(x1±x2)+i(y1±y2).
2. Умножение:
z1z2= (x1x2-y1y2) + i(x1y2+x2y1).
В
частности, 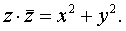
3. Деление:
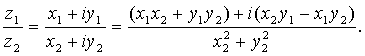
Все
арифметические операции над комплексными числами проводятся по правилам
действий над многочленами х1+iy1 и x2+iy2, считая 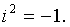
Тригонометрическая форма комплексного числа
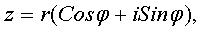
где
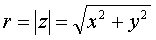
- модуль комплексного числа; j -
аргумент комплексного числа (Arg z)
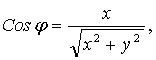
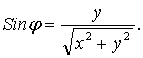
Из
значений j =Arg z выделяется главное значение arg z, удовлетворяющее условию 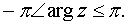
Арифметические операции над комплексными числами в тригонометрической
форме
1. Умножение:
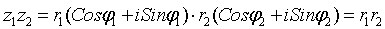 [Cos(j1+j2)
+ iSin(j1+j2)].
[Cos(j1+j2)
+ iSin(j1+j2)].
2. Деление:
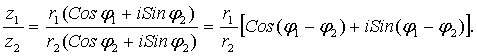
3. Возведение в степень. Формула Муавра:
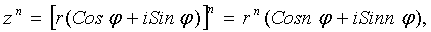 n-целое число.
n-целое число.
4.
Извлечение корня:
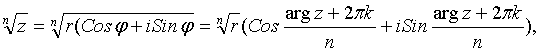
где к=0,1, 2,…,n-1.
Показательная форма комплексного числа
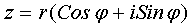
Воспользуемся формулой Эйлера:
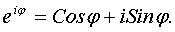
Тогда
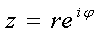 - показательная форма комплексного числа.
- показательная форма комплексного числа.
ТЕМА 10. Неопределенный интеграл
Понятие неопределенного интеграла
Функция F(x) называется первообразной для функции f(x) на промежутке Х, если в каждой точке х этого промежутка
справедливо равенство F¢(x) = f(x).
Совокупность
всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом
от функции f(x) и обозначается 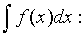
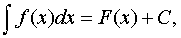
где С - произвольная
постоянная.
В
записи 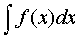 f(x) называется подынтегральной функцией, а f(x)dx-подынтегральным
выражением.
f(x) называется подынтегральной функцией, а f(x)dx-подынтегральным
выражением.
Нахождение
неопределенного интеграла от некоторой функции называется интегрированием этой
функции. Операции интегрирования и дифференцирования взаимно обратны.
Основные свойства неопределенного интеграла
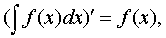
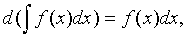
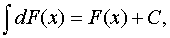
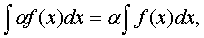
где a-некоторое
число;
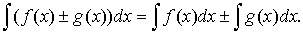
Табличные
интегралы
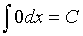 ,
,
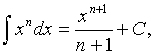 где n¹-1
где n¹-1
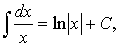
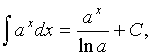 где a>0,
a¹1;
где a>0,
a¹1;
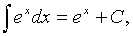
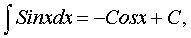
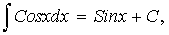
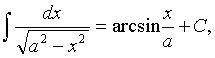 где -а<х<а, а>0;
где -а<х<а, а>0;
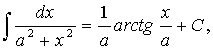 а¹0;
а¹0;
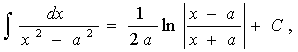 а¹0;
а¹0;
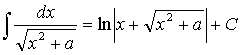 , а¹0;
, а¹0;
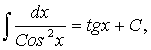

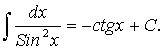
Основные
методы интегрирования
а) метод непосредственного интегрирования:
данный интеграл путем тождественных преобразований подынтегральной
функции (или подынтегрального выражения) и применения свойств неопределенного
интеграла приводится к одному или нескольким табличным интегралам.
б) метод замены переменной:
пусть x=j(t) - функция дифференцируемая на рассматриваемом промежутке. Тогда
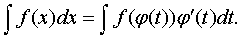
Эта формула называется формулой замены переменной в неопределенном
интеграле.
в) метод интегрирования по частям:
пусть u=u(x) и v(x) -
непрерывно дифференцируемые функции. Тогда справедлива формула:
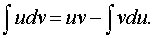
Эта формула называется формулой интегрирования по частям.
Интегрирование рациональных дробей
Рациональной
дробью называется выражение вида 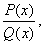 где Р(х)
и Q(x)-многочлены.
где Р(х)
и Q(x)-многочлены.
Рациональная
дробь 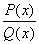 называется правильной, если степень многочлена Р(х) в
ее числителе меньше степени многочлена Q(x) в
знаменателе. В противном случае дробь называется неправильной.
называется правильной, если степень многочлена Р(х) в
ее числителе меньше степени многочлена Q(x) в
знаменателе. В противном случае дробь называется неправильной.
Всякая
неправильная рациональная дробь с помощью деления числителя на знаменатель
приводится к виду:
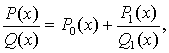 где
где
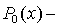
 многочлен
(целая часть при делении), а
многочлен
(целая часть при делении), а 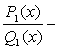 правильная
рациональная дробь (остаток).
правильная
рациональная дробь (остаток).
Поэтому
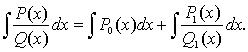
Так
как интеграл 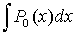 вычисляется элементарно (сводится к сумме табличных),
то интегрирование неправильной дроби сводится к интегрированию правильной
дроби. Интегрирование правильной рациональной дроби сводится, в свою очередь, к
интегрированию простейших дробей.
вычисляется элементарно (сводится к сумме табличных),
то интегрирование неправильной дроби сводится к интегрированию правильной
дроби. Интегрирование правильной рациональной дроби сводится, в свою очередь, к
интегрированию простейших дробей.
ТЕМА 11. Определенный интеграл
Определенный интеграл как предел интегральной суммы
Пусть
функция y = f(x) задана на отрезке [а,в]. Разобьем отрезок [а,в] на n элементарных отрезков точками х0 = а<х1<х2<…<хn=b. В каждом из отрезков разбиения 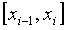 выберем произвольную точку xi и положим Dxi = xi -xi-1, где i=1,2,…,n.
Тогда сумма вида:
выберем произвольную точку xi и положим Dxi = xi -xi-1, где i=1,2,…,n.
Тогда сумма вида:
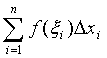 (1)
называется интегральной суммой для функции y=f(x) на
отрезке [а,в].
(1)
называется интегральной суммой для функции y=f(x) на
отрезке [а,в].
Пусть
существует и конечен предел S интегральной суммы (1) при стремлении к нулю длины
максимального элементарного отрезка Dxi, не зависящий от способа разбиения отрезка [а,в] на части и способа выбора точек xi на отрезках
разбиения. Тогда функция y=f(x) называется интегрируемой на [а,в], а число S - определенным интегралом от f(x) на [а,в] и обозначается 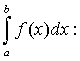
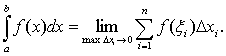 (2)
(2)
Достаточным условием интегрируемости функции является ее непрерывность на
рассматриваемом отрезке.
Свойства определенного интеграла
1)
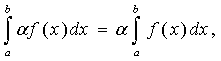 где a - некоторое
число.
где a - некоторое
число.
) 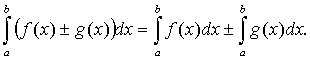
) 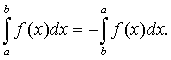
) 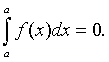
) 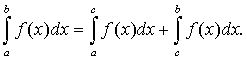
)
Теорема о среднем. Если функция y=f(x) непрерывна на отрезке [а,в], то найдется такое значение xÎ[а,в], что
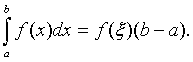
)
Если функция y=f(x) - четная, то
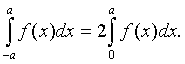
Если
функция y=f(x) - нечетная, то
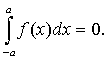
Формула
Ньютона-Лейбница
Определенный интеграл от непрерывной на отрезке [а,в] функции f(x) равен приращению любой ее
первообразной F(x) на этом отрезке:
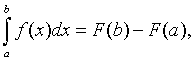 или (в
иной записи)
или (в
иной записи)
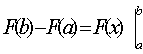 .
.
Замена
переменной в определенном интеграле
Если
функция j(t) имеет непрерывную производную на отрезке [a;b], 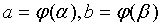 и
функция f(x) непрерывна в каждой точке х=j(t), где tÎ[a;b], то
и
функция f(x) непрерывна в каждой точке х=j(t), где tÎ[a;b], то
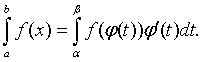
Интегрирование
по частям определенного интеграла
Если функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [а,в], то
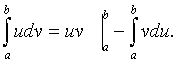
Геометрическое
приложение определенного интеграла
Площади
плоских фигур
1. Если функция f(x) неотрицательна на отрезке [а,в], то площадь S под кривой y=f(x) на [а,в] (площадь криволинейной трапеции,
ограниченной кривой y=f(x) и прямыми x=a, x=b, y=0) численно равна определенному
интегралу от f(x) на данном отрезке:
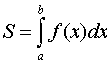 (3)
(геометрический смысл определенного интеграла).
(3)
(геометрический смысл определенного интеграла).
2. Если функция y=f(x) неположительна на отрезке [а,в], то площадь S над кривой y=f(x) на [а,в] равна определенному интегралу от f(x) на [а,в], взятому со знаком «минус»:
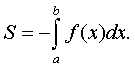 (4)
(4)
Формулы (3) и (4) можно объединить в одну
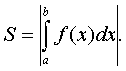
. Если
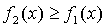 на отрезке [а,в], то площадь S фигуры, заключенной между кривыми y=f2(x) и y=f1(x) на
этом отрезке, определяется формулой
на отрезке [а,в], то площадь S фигуры, заключенной между кривыми y=f2(x) и y=f1(x) на
этом отрезке, определяется формулой
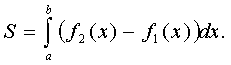
Объемы
тел вращения
Если функция y=y(x) знакопостоянна на отрезке [а,в], то объем Vx тела,
образованного вращением вокруг оси Ох фигуры, ограниченной линиями y=y(x), x=a, x=b, y=0, вычисляется по формуле
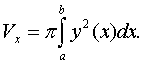
Приближенное
вычисление определенного интеграла
Пусть функция y=f(x) задана на отрезке [а,в] и
этот отрезок разбит на n
равных частей точками а=х0<х1<…<хn=в,
xi=xi-1+ih,
где h=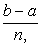 , i=1,2,…,n.
, i=1,2,…,n.
Тогда
приближенное значение определенного интеграла от функции y=f(x) на
[а,в] может быть найдена по формуле
трапеций:
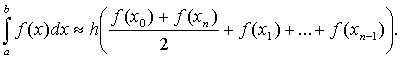
Погрешность
Dот применения формулы трапеций оценивается по формуле:
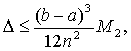
где
М2-максимальное значение модуля второй производной
функции y=f(x) на отрезке [а,в], т.е.
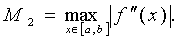
ТЕМА 12. Несобственные интегралы
Несобственные
интегралы с бесконечными пределами интегрирования (I рода)
Несобственные интегралы с бесконечными пределами интегрирования
определяются следующим образом:
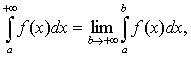
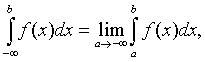 (1)
(1)
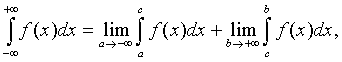
где
с-произвольное число (обычно с=0).
Несобственные интегралы I рода
называются сходящимися, если существуют конечные пределы, стоящие в правых
частях равенств (1). Если же указанные пределы не существуют или бесконечны, то
несобственные интегралы называются расходящимися.
Признаки сходимости и расходимости несобственных интегралов I-го рода
1. Если
на промежутке [а;+¥) непрерывные функции f(x) и j(x) удовлетворяют условию 0 £ f(x) £ j(x), то из сходимости интеграла 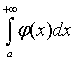 следует сходимость интеграла
следует сходимость интеграла 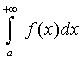 , а из расходимости интеграла
, а из расходимости интеграла 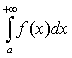 следует расходимость интеграла
следует расходимость интеграла 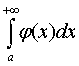 («признак сравнения»).
(«признак сравнения»).
. Если
при х Î [а; +¥), f(x) >0, j(x) > 0 и существует конечный
предел 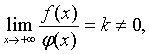 то интегралы
то интегралы 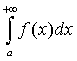 и
и 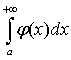 сходятся или расходятся одновременно («предельный
признак сравнения»).
сходятся или расходятся одновременно («предельный
признак сравнения»).
. Если
сходится интеграл 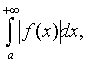 то сходится и интеграл
то сходится и интеграл 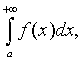 который
в этом случае называется абсолютно сходящимся.
который
в этом случае называется абсолютно сходящимся.
Несобственные интегралы от неограниченных функций (II рода)
Пусть
функция y = f(x) - непрерывна, но не ограничена на полуинтервале [а,в). В этом случае интеграл 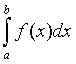 называется
несобственным интегралом второго рода и, по определению,
называется
несобственным интегралом второго рода и, по определению,
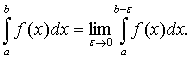
Если предел, стоящий в правой части последнего равенства, существует и
конечен, то этот интеграл называется сходящимся; в противном случае - расходящимся.
Аналогично, если функция y=f(x) непрерывная, но неограниченная на полуинтервале (а;в], то , по определению,
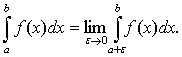
Если функция y=f(x) терпит разрыв II-го рода во внутренней точке сÎ[а;в], то несобственный интеграл второго рода определяется формулой:
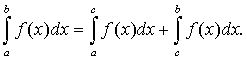
В этом случае интеграл называется сходящимся, если оба несобственных
интеграла, стоящих справа, сходятся.
Признаки сходимости и расходимости несобственных интегралов II-го рода:
1.
Если на промежутке [а;в) функции f(x) и j(x) непрерывны, при х=в терпят разрыв II-го
рода и удовлетворяют условию 0 £ f(x) £ j(x),
то из сходимости интеграла 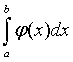 следует
сходимость интеграла
следует
сходимость интеграла 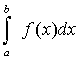 , а из расходимости интеграла
, а из расходимости интеграла 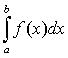 следует расходимость интеграла
следует расходимость интеграла 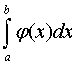 («признак сравнения»).
(«признак сравнения»).
.
Пусть функции f(x) и j(x) непрерывны на
промежутке [а;в) и в точке х=в терпят разрыв II-го
рода. Если существует предел 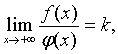 0 < к <¥,то интегралы
0 < к <¥,то интегралы 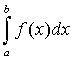 и
и 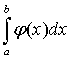 сходятся или расходятся одновременно («предельный
признак сравнения»).
сходятся или расходятся одновременно («предельный
признак сравнения»).
.
Если функция f(x), знакопеременная на отрезке [а;в], имеет разрыв в точке х=в и несобственный интеграл 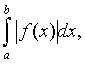 сходится, то сходится и интеграл
сходится, то сходится и интеграл 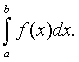
ТЕМА 13. Дифференциальные уравнения
Основные
понятия
Дифференциальным уравнением называется уравнение, связывающее искомую
функцию некоторой переменной, эту переменную и производные различных порядков
данной функции:
G(x, y, y¢,…,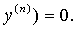
Порядок n старшей производной, входящей в
уравнение, называется порядком этого дифференциального уравнения.
Любая функция y=y(x), которая при подстановке в уравнение обращает его в
тождество, называется решением этого дифференциального уравнения. Решение,
заданное в неявном виде f(x,y) = 0, называется интегралом дифференциального уравнения.
График решения (интеграла) дифференциального уравнения называется
интегральной кривой этого уравнения.
Решение (интеграл) дифференциального уравнения n-го порядка, зависящее от n произвольных независимых постоянных, называется общим
решением (интегралом) этого уравнения. Решение (интеграл), полученное при
конкретных числовых значениях этих постоянных, называется частным решением
(частным интегралом) дифференциального уравнения.
Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение первого порядка называется уравнением с
разделяющимися переменными, если оно может быть представлено в виде:
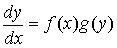 (1) или
в виде
(1) или
в виде
M(x)N(y)dx + P(x)Q(y)dy =
0,
где f(x), M(x), P(x) - некоторые функции переменной х, g(y), N(y), Q(y) - функции переменной у.
Для решения такого уравнения его следует преобразовать к виду, в котором
дифференциал и функции переменной х окажутся в одной части равенства, а
переменной у - в другой.
Затем проинтегрировать обе части полученного равенства. Например, из (1)
следует, что
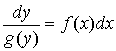 и
и 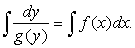
Выполняя интегрирование, приходим к решению уравнения (1).
Однородные дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка называется однородным, если
оно может быть представлено в виде:
y¢ =g(y/x),
где g -некоторая функция (одной переменной).
Понятие однородного дифференциального уравнения связано с однородными
функциями. Функция y=f(x,y) называется
однородной степени к (по переменным х и у), если для произвольного числа a выполняется равенство:
f(ax,ay) = 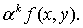
Если
функция f(x,y) однородная степени 0, то уравнение y¢ = f(x,y)
может быть сведено к однородному.
Замена
переменной z = y/x, где z = z(x), сводит однородные дифференциальные уравнения к
уравнениям с разделяющимися переменными.
Линейные дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка называется линейным, если оно
имеет вид:
y¢ + f(x)y = g(x), (2)
где f(x) и g(x) - некоторые непрерывные функции
переменной х. В случае, когда функция g(x) тождественно равна нулю, уравнение
называется однородным, в противном случае - неоднородным.
Будем искать решение в виде:
y = u(x)v(x).
Так как y¢ = u¢v + uv¢, то из (2) следует u¢v + uv¢ + f(x)uv = g(x) или vu¢ + u(v¢ + f(x)v) = g(x). (3)
Найдем сначала какое-либо частное решение v = v(x) уравнения:
v¢ + f(x)v = 0.
Тогда (см. (3)) функция u = u(x) -
решение уравнения vu¢ = g(x).
Тем самым решение исходного уравнения (2) сводится к решению двух
уравнений с разделяющимися переменными.
Линейные дифференциальные уравнения второго порядка с постоянными
коэффициентами
Линейное дифференциальное уравнение второго порядка с постоянными
коэффициентами имеет вид:
y² + py¢ +qy = r(x), (4)
где p и q - некоторые действительные числа, r(x) -
некоторая функция.
Если функция r(x) тождественно равна нулю, то
соответствующее уравнение называется однородным, в противном случае - неоднородным.
Рассмотрим решение однородного дифференциального уравнения:
y² + py¢ +qy = 0. (5)
Дифференциальному уравнению (5) ставится в соответствие
характеристическое уравнение:
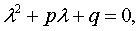 где l - переменная.
где l - переменная.
1. Если характеристическое уравнение имеет действительные корни l1 и l2, причем l1¹l2, то общее решение уравнения (4) имеет вид:
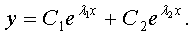
2. Если характеристическое уравнение имеет один корень l (кратности), то общее решение
уравнения (4) имеет вид:
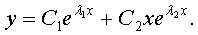
. Если
характеристическое уравнение имеет комплексные корни 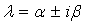 , где a = - p/2, b =
, где a = - p/2, b = 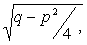 то общее решение уравнения (4) имеет вид:
то общее решение уравнения (4) имеет вид:
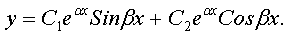
Использование
дифференциальных уравнений в экономической динамике
Рассмотрим примеры применения дифференциальных уравнений для описания
процессов микроэкономической динамики.
Пусть y = y(t) - объем производства некоторого
производителя, реализованный к моменту времени t. Предположим, что цена на данный товар остается постоянной
(в пределах рассматриваемого промежутка времени). Тогда функция y = y(t) удовлетворяет
уравнению:
y¢ =ky, (6)
где k = mpl, m -
норма инвестиций, p - продажная
цена, l - коэффициент пропорциональности
между величиной инвестиций и скоростью выпуска продукции.
Уравнение (6) является уравнением с разделяющимися переменными. Его
решение имеет вид:
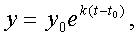
где
у0 = y(t0).
Уравнение
(6) описывает также рост народонаселения, динамику роста цен при постоянной
инфляции и т.д.
ТЕМА 14. Ряды
Понятие числового ряда
Числовым рядом называется бесконечная последовательность чисел, соединенных
знаком сложения:
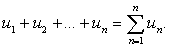
Числа
u1, u2,… называются членами ряда, член un - общим или n-м членом ряда, сумма n
первых членов ряда 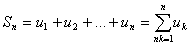 называется n-ой частичной суммой ряда.
называется n-ой частичной суммой ряда.
Ряд
называется сходящимся, если существует конечный предел последовательности его
частичных сумм:
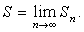
Число
S называется суммой ряда. Если конечного предела
последовательности частичных сумм не существует, то ряд называется
расходящимся.
Если
ряд 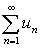 сходится, то предел его общего члена при n®¥ равен
нулю (необходимое условие сходимости ряда).
сходится, то предел его общего члена при n®¥ равен
нулю (необходимое условие сходимости ряда).
При
нарушении необходимого условия сходимости ряда, т.е. если предел общего члена
ряда при n®¥ не существует или если он не равен нулю, ряд
расходится. Заметим, что если предел общего члена ряда равен нулю, то вывод о
сходимости или расходимости ряда можно сделать только после дополнительного
исследования.
Признаки сходимости рядов с положительными членами
1.
Признак сравнения. Пусть 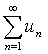 и
и 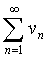 - два ряда с
положительными членами, и члены первого ряда не превосходят членов второго,
т.е. un £ vn при любом n. Тогда
- два ряда с
положительными членами, и члены первого ряда не превосходят членов второго,
т.е. un £ vn при любом n. Тогда
а)
если сходится ряд 
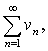 то
сходится и ряд
то
сходится и ряд 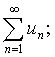
в)
если расходится ряд 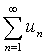 , то расходится и ряд
, то расходится и ряд 
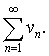
.
Предельный признак сравнения. Если 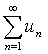 и
и 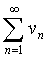 - ряды с положительными членами и существует конечный предел отношения
их общих членов:
- ряды с положительными членами и существует конечный предел отношения
их общих членов:
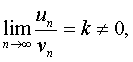
то
ряды либо одновременно сходятся, либо одновременно расходятся.
.
Признак Даламбера. Пусть для ряда 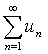 с
положительными членами существует предел отношения (n+1)-го члена к n-ому:
с
положительными членами существует предел отношения (n+1)-го члена к n-ому:
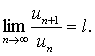
Тогда при l<1
ряд сходится, при l>1
и при l=¥ ряд расходится. При l = 1 для ответа на вопрос о
сходимости ряда требуется дополнительное исследование.
4.
Интегральный признак сходимости. Пусть дан положительный ряд 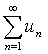 и пусть функция f(x)
такая, что f(1)=u1, f(2) = u2,…, f(n) =un,… непрерывна и не возрастает при х³1. Тогда для сходимости ряда
и пусть функция f(x)
такая, что f(1)=u1, f(2) = u2,…, f(n) =un,… непрерывна и не возрастает при х³1. Тогда для сходимости ряда 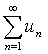 необходимо и достаточно, чтобы сходился несобственный
интеграл
необходимо и достаточно, чтобы сходился несобственный
интеграл 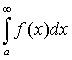 при некотором а ³ 1.
при некотором а ³ 1.
Сходимость рядов с членами произвольного знака
1. Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и
ряд, составленный из абсолютных величин его членов.
Ряд называется условно сходящимся, если сам ряд сходится, а ряд,
составленный из абсолютных величин его членов, расходится.
. Достаточный признак сходимости знакопеременного ряда. Если ряд,
составленный из абсолютных величин членов данного ряда, сходится, то сходится и
данный ряд.
. Ряд называется знакочередующимся, если его члены попеременно то
положительны, то отрицательны.
4.
Признак Лейбница. Если члены знакочередующегося ряда убывают по абсолютной
величине т.е. u1>u2>…>un>…>0, и предел модуля его общего члена равен нулю, т.е. 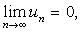 то ряд сходится, а его сумма не превосходит первого
члена: S £ u1.
то ряд сходится, а его сумма не превосходит первого
члена: S £ u1.
Определение и свойства степенного ряда
. Степенным рядом называется ряд
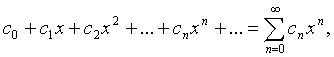 (1)
(1)
где
с0, с1,…,сn - коэффициенты
степенного ряда.
2. Областью сходимости степенного ряда называется совокупность тех
значений х, при которых степенной ряд (1) сходится.
. Число R - такое, что при çхç< R ряд
(1) сходится, а при çхç>R - расходится, называется радиусом сходимости степенного ряда.
Интервал (-R;R) называется интервалом сходимости степенного ряда. При х=-R, x=R ряд может как
сходится, так и расходится.
. Радиус сходимости степенного ряда может быть найден по формуле:
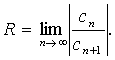 (2)
(2)
Формула
(2) применима, если, начиная с некоторого номера n, все сn ¹0.
ТЕМА 15. Функции нескольких переменных. Основные
понятия
Область
определения
Если каждому набору n
переменных х1,…, хn из некоторого
множества Х соответствует одно вполне определенное значение переменной z, то говорят, что задана функция
нескольких переменных z = f(x1,…,xn).
Множество Х называется областью определения функции.
Предел функции
Число А называется пределом функции z =f(x,y) при х®х0,
у®у0, если для любого числа e > 0 найдется число d >
0, зависящее от e,
такое что для всех точек (х,у), отстоящих от точки (х0,у0) не более, чем на d, выполняется неравенство ÷f(x,y) - A÷ < e.
Частные производные
Частными производными z = f(x,y) по х и у
называются пределы вида:
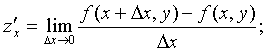
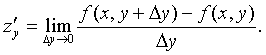
Дифференциал функции
Дифференциалом функции z =f(x,y) называется
сумма произведений частных производных этой функции на приращение независимых
переменных
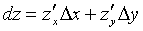
или
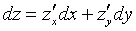 ,
,
учитывая,
что 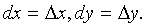
Экстремум
функции нескольких переменных. Условный экстремум
1. Точка М(х0,у0) называется точкой максимума (минимума) функции z = f(x,y), если существует окрестность точки
М, такая, что для всех точек (х,у) из этой окрестности выполняется неравенство:
f(x0,y0) ³ f(x,y) (f(x0,y0) £ f(x,y).
2. Если в точке максимума или минимума обе частные производные
существуют и непрерывны, то они равны нулю в этой точке (необходимое условие
экстремума).
3. Если
в точке (х0,у0) обе частные производные обращаются в ноль, то характер этой
точки определяется величиной 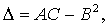 где А = z²xx, B = z²xy, C = z²yy.
где А = z²xx, B = z²xy, C = z²yy.
При D > 0 имеется экстремум (максимум при А < 0 и минимум при А > 0).
При D < 0 функция в данной точке не имеет
экстремума.
При D = 0 вопрос о
наличии экстремума остается открытым (достаточное условие экстремума).
. Наибольшее (наименьшее) значение функции z = f(x,y) определяется как наибольшее (наименьшее) значение функции в
замкнутой области из ее значений в критических точках внутри области и на ее
границе.
. Точка М(х0,у0) называется точкой условного максимума (минимума) функции
z = f(x,y), при условии g(x,y) = C, если существует такая окрестность
этой точки, что во всех точках (х,у) из этой окрестности, удовлетворяющих
условию g(x,y) = C, выполняется неравенство:
f(x0,y0) ³ f(x,y) (f(x0,y0) £ f(x,y)).
Уравнение g(x,y) = C называется
уравнением связи.
Точка условного экстремума является точкой экстремума функции
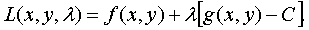 ,
,
функция
L называется функцией Лагранжа, а l - множителем Лагранжа.
ТЕМАТИЧЕСКИЙ
ПЛАН ЗАНЯТИЙ
изучения
дисциплины «Математика I»
Дневная форма
обучения
Первый семестр
(Линейная алгебра и аналитическая геометрия)
|
Лекции
|
Число часов
|
Семинарские (практические)
|
Задачи, решаемые на
практических занятиях
|
Число часов
|
Самостоятельная работа
|
|
Матрицы. Действия над
матрицами.
|
4
|
Сложение, вычитание матриц,
умножение матрицы на число. Умножение матриц. Возведение матриц в степень.
|
[1] с. 36 № 1.15 - 1.18 [10] с.14 - 17 № 1.1.42 - 1.1.44, № 1.1.53 -1.1.55, № 1.172 - 1.1.74, № 1.1.78 -1.1.80
|
4
|
[1] с.9 - 16 теория Задачи: [2] с.10 №1.6- 1.16.
|
|
Определители.
|
2
|
Определители 2-го и 3-го
порядков. Разложение определителей по элементам ряда.
|
[11] с. 126 - 127 №№ 22,
25, 28 - 31, 35. [2] с. 18 № 1.44.
|
2
|
[1] с. 16 - 26 теория
Задачи: [2] с. 17 №1.29 - 1.35 с.18 № 1.37 - 1.41. Выдача дом. контр. раб. №1
по [2] и [10]
|
|
Ранг матрицы.
|
2
|
Вычисление ранга матриц.
|
[10] с. 38 № 1.3.9 -
1.3.14.
|
2
|
[1] с. 29 - 35 теория
Задачи: [2] с.22 №1.54 - 1.61.
|
|
Обратная матрица
|
2
|
Нахождение обратных матриц
методом присоединенной матрицы.
|
[10] с. 43 № 1.4.2 - 1.4.8.
|
2
|
[1] с. 26-29 теория Задачи:
[2] с. 18-19 №1.45-1.49 [1] с.36 №1.22.
|
|
Система n
линейных уравнений с n неизвестными (СЛУ)
|
2
|
Матричный способ решения
СЛУ. Решение СЛУ по формулам Крамера.
|
[11] с.129 № 38 -43.
|
2
|
[1] с. 38 - 44 теория
Задачи: [2] с. 39 №2.6 - 2.13. [10] с.75 №2.2.20 -2.2.26.
|
|
Теорема Кронекера-Капелли.
Решение систем по методу Гаусса.
|
2
|
Решение систем методом
Гаусса.
|
[1] с.61 № 2.15 - 2.18 [2] с. 40 № 2.21.
|
2
|
[1] с. 44-53 теория Задачи:
[2] с. 40 №2.14 - 2.20.
|
|
n - мерное векторное пространство
|
Векторы. Действия над
векторами.
|
[2] с.76 № 3.32 - 3.37
|
2
|
Прием домашней контрольной
работы №1 [1] с. 68 - 74 теория Задачи: [2]
с.77 №3.43 - 3.49
|
|
Линейные операторы.
|
2
|
Собственные векторы и
собственные значения линейного оператора.
|
[1] с. 94 № 3.24, 3.25, 3.26, 3.27
|
2
|
[1] с.78 - 86 теория Задачи: [2]
с. 86 №3.74 -3.78.
|
|
Квадратичные формы
|
2
|
Приведение квадратичной
формы к каноническому виду.
|
[1] с.94 № 3.31 - 3.36
|
2
|
[1] с.86-91 теория Задачи:
[2] с.91 №3.103 - 3.110. Выдача дом. контр раб. №2 по [2] и
[10].
|
|
Векторы на плоскости и в
пространстве.
|
4
|
Действия над векторами. Скалярное,
векторное и смешанное произведения.
|
[11] c.160
№ 41 - 48. с.163 № 63 - 65, 70 - 73. с. 165 № 84 - 88.
|
4
|
[4]с.31 - 47 теория Задачи:
[2] с.67 №3.5 - 3.10. с.68 №3.14 - 3.18. [10] с.103 №3.2.6 -3.2.9. с.108
№3.3.2 - 3.3.8. с. 113 №3.4.5 -3.4.7.
|
|
Прямая линия на плоскости.
|
2
|
Метод координат. Уравнения
прямой на плоскости.
|
[11] с.29 № 86 - 96.
|
2
|
[4] с.56 - 62 теория
Задачи: [2] с.107 №4.8 - 4.11 с.108 №4.23 - 4.27 с.109 №4.32 - 4.38.
|
|
Кривые 2 -го порядка.
|
4
|
Окружность, эллипс,
гипербола, парабола.
|
[11] с.33 №126 - 132. с.35
- 36 №142 -147, 150 - 155.
|
2
|
[1]с.104 - 115 теория
Задачи: [2)]с. 116 №4.55 - 4.60 с.117 №4.63 -4.73. с.118 №4.80 -4.84.
|
|
Плоскость.
|
2
|
Уравнения плоскости в
пространстве.
|
[11] с.169 №108 - 112, 119 - 122.
|
2
|
[4]с. 78 - 82 теория Задачи: [2]
с.126-127 №4.93 - 4.102.
|
|
Прямая линия в
пространстве.
|
2
|
Уравнения прямой в
пространстве.
|
[11] c.172 №131 - 134, 142 - 145.
|
2
|
[4] с.82 - 86 теория
Задачи: [2] с.127 №4.103 - 4.106. с.129 №4.130, 4.131.
|
|
Прямая линия и плоскость в
аффинном пространстве.
|
2
|
Прямая и плоскость в
пространстве. Основные задачи.
|
[11] с.174 - 175 №151 - 153, 155 - 159.
|
2
|
[4] с.86 - 88 теория
Задачи: [10] с.205 №5.4.5 -5.4.8. с.206 № 5.4.14 -5.4.17. Прием домашней
контрольной работы №2.
|
|
Цилиндрические и конические
поверхности. Поверхности вращения.
|
2
|
Канонический вид уравнений
поверхностей 2- порядка. Геометрическое изображение.
|
[11] с.176 №165 - 168.
|
2
|
[4] с.88 - 95 теория
Задачи: [10] с.215 №5.5.7 - 5.5.10. с.220 №5.5.16.
|
|
Итого
|
38
|
|
|
36
|
|
Второй семестр
(Основы математического анализа)
|
Лекции
|
Число часов
|
Семинарские (практические)
|
Задачи, решаемые на
практических занятиях
|
Число часов
|
Самостоятельная работа
|
|
Множества. Действительные
числа.
|
2
|
Действия над множествами.
|
[8] с.7 №12- 17.
|
2
|
Теория: [4] с.97 - 100, [1]
с.123 -125. Задачи: [8] с.7 №18-22.
|
|
Числовая
последовательность. Предел числовой последовательности.
|
2
|
Нахождение пределов
последовательности
|
[8] с.14 №21- 28.
|
2
|
Теория по любому из
указанных пособий: [1] с.141-143, [4] с.107 - 111. Задачи: [8] с.13 №12,13,14(1,2)
с.14 №29-39
|
|
Функция одной переменной.
Графики элементарных функций.
|
2
|
Область определения,
область значений функции. Основные характеристики функций. Построение
графиков элементарных функций.
|
[8] с.38 №15 - 20. с.40 - 41 №45, 50 - 52, 62 - 65.
|
2
|
Теория по любому из
указанных пособий: [1] с.125 - 134, [9] с.108 - 117 Задачи: [2] с.151 №5.12,
5.15, 5.17 с.152 №5.40 - 5.47
|
|
Предел функции одной
переменной.
|
4
|
Вычисление пределов
функций.
|
[8] с. 45 №214 - 216. с.49
№282 - 291.
|
2
|
Теория по любому из
указанных пособий: [1] с.143-154 [4] с.112-129 [9] с.117- 133 Задачи: [2]
с.166 №6.50 - 6.60 с.168 №6.70 - 6.80 с.172 №6.115 - 6.118 с.173 №6.124 -
6.126
|
|
Непрерывность функции одной
переменной.
|
2
|
Непрерывность функций и
точки разрыва. Классификация точек разрыва. Выдача дом. работы №3 по (2) и
(10).
|
[10] с.282 -283 № 6.5.15, 6.5.16, 6.5.18 - 6.5.20.
|
2
|
Теория по любому из
указанных пособий: [4] с.130-136 [9] с.139-144 Задачи: [1] c.174
№6.38-6.41 [8] с.47 №225 - 227.
|
|
Производная и дифференциал
функции одной переменной.
|
4
|
Вычисление производных и
дифференциалов функций
|
[11] с.71 № 1 - 5. [1] с.207 №
7.22 - 7.31. [8] с.60 № 151 - 155. с.63 № 206 - 208.
|
4
|
Теория: [1] с.176 - 198 [4]
с.157 - 163 Задачи: [2]с.191№7.40 - 7.50 с.192 №7.71, 7.76 -7.78 с.245 №9.15
- 9.20 с.246 №9.41 - 9.43
|
|
Свойства дифференцируемых
функций
|
2
|
Раскрытие неопределенностей
по правилу Лопиталя
|
[8] с. 67 - 68 № 225 - 230,
243 - 246, 251 - 253.
|
2
|
Теория: [4] с.164 - 169 [9]
с.178 - 183 Задачи: [2] с.215 №8.15 - 8.18 с.216 №8.24 - 8.30
|
|
Исследование функций
|
2
|
Исследование функций при
помощи производных. Построение графиков.
|
[8] с. 74 - 75 №293 -295,
296. с.81 № 297, 312, 326.
|
2
|
Теория: [1] с.216 - 232 [2]
с. 171 - 180 [9] с.191 - 198 Задачи: [8] с.81 №297 - 303
|
|
Комплексные числа
|
2
|
Действия над комплексными
числами. Прием домашней контрольной работы №3
|
[8] с. 148 № 1 - 6, 14 -
20, 35 - 38.
|
2
|
Теория: [9] с.144-149
Задачи: [10] с.438 №10.2.3 - 10.2.6 с.442 №10.2.23, 10.2.25(а,в), 10.2.26
|
|
Неопределенный интеграл
|
4
|
Методы вычисления неопределенного
интеграла
|
[8] с. 86 № 2 - 7, 12 - 17.
с. 90 - 91 № 50 - 53, 67,79, 90,92,95. с.93 - 94 №102 - 107, 115 - 117, 130 -
133.
|
4
|
Теория: [1] с.251 - 270 [9]
с.213 - 224 Задачи: [2] с.270 №10.28 - 10.40 с.274 №10.75 - 10.85 с.277
№10.107 - 10.112
|
|
Определенный интеграл
|
4
|
Вычисление определенных
интегралов. Формула Ньютона - Лейбница.
|
[8] с. 104 - 105 № 254 -
261, 270 - 273, 285 - 289. с. 108 №290 - 295.
|
4
|
Теория: [1] с.295 - 307 [4]
с.221 - 233 Задачи: [2]с.292 №11.2 - 11.12 с.300 №11.36 - 11.40
|
|
Несобственные интегралы
|
2
|
Вычисление несобственных
интегралов Выдача домашней контр. раб. №4 по (2) и (10)
|
[8] с. 120-121 № 355-358,
365-369.
|
2
|
Теория: [1] с.307 - 312 [4]
с.233 - 237 Задачи: [2] с.305 №11.75 - 11.77; 11.83 - 11.85
|
|
Дифференциальные уравнения
|
2
|
Дифференциальные уравнения
1 -го порядка. Линейные дифференциальные уравнения 2-го порядка с постоянными
коэффициентами.
|
[2] с.320 №12.17 - 12.20.
[8] с.232 №84 - 89
|
2
|
Теория: [1] с.325 -330,
с.337 - 344 [5] с.11 - 17, с.36 - 38 Задачи: с.236 №98 - 103
|
|
Ряды
|
2
|
Числовые ряды. Признаки их
сходимости. Степенные ряды. Разложение функций в степенные ряды.
|
[8] с.139 №103 - 107
|
2
|
Теория: [1] с.356 - 369 [5]
с.114 - 137 Задачи: [2] с.356 №13.29 ; 13.30. с.357 №13.56 - 13.61
|
|
Функции нескольких
переменных. Основные понятия
|
2
|
Частные производные. Полный
дифференциал функции. Экстремум функции нескольких переменных.
|
[8] с.185-187 № 1 - 5, 23 -
25. с.190 №34 - 39.
|
2
|
Прием домашней контр. Раб.
№4[1] с.402 - 420 Задачи: [2] с.397 15.31;15.32;15.42; с.400 №15.62 - 15.65
|
|
Итого
|
38
|
|
|
36
|
|
ТЕМАТИЧЕСКИЙ
ПЛАН
изучения
дисциплины «Математика I»
Заочная форма
обучения
1-й семестр
(Линейная алгебра и аналитическая геометрия)
|
Лекции
|
Число часов
|
Самостоятельная работа
|
|
Определители, их свойства.
Способы вычисления.
|
2
|
[1] с. 16 - 26 теория
Задачи: [2] с. 17 №1.29 - 1.35 с.18 № 1.37 - 1.41.
|
|
Матрицы. Действия над
матрицами. Обратная матрица .
|
2
|
[1] с.9 - 16 теория Задачи: [2] с.10 №1.6- 1.16. [1] с. 26-29 теория Задачи: [2] с.
18-19 №1.45-1.49 [1] с.36 №1.22.
|
|
Решение систем линейных
алгебраических уравнений матричным способом, по формулам Крамера и методом
Гаусса.
|
2
|
[1] с. 38 - 44 теория
Задачи: [2] с. 39 №2.6 - 2.13. [10] с.75 №2.2.20 -2.2.26. [1]
с. 44-53 теория Задачи: [2] с. 40 №2.14 - 2.20.
|
|
Действия над векторами.
Скалярное, векторное и смешанное произведения.
|
2
|
[4]с.31 - 47 теория Задачи:
[2] с.67 №3.5 - 3.10. с.68 №3.14 - 3.18. [10]
с.103 №3.2.6 -3.2.9. с.108 №3.3.2 - 3.3.8. с. 113 №3.4.5 -3.4.7.
|
|
Прямая линия на плоскости.
Кривые 2-го порядка.
|
2
|
[4] с.56 - 62 теория Задачи:
[2] с.107 №4.8 - 4.11 с.108 №4.23 - 4.27 с.109 №4.32 - 4.38. [1]с.104 - 115
теория Задачи: [2)]с. 116 №4.55 - 4.60 с.117 №4.63 -4.73. с.118 №4.80 -4.84.
|
|
Прямая линия и плоскость в
аффинном пространстве.
|
2
|
[4] с.78 - 88 теория Задачи: [2] с.126-127 №4.93 - 4.102. [2] с.127 №4.103 -
4.106. с.129 №4.130, 4.131. [10] с.205 №5.4.5 -5.4.8. с.206 № 5.4.14 -5.4.17.
|
|
Цилиндрические и конические
поверхности. Поверхности вращения.
|
2
|
[4] с.88 - 95 теория
Задачи: [10] с.215 №5.5.7 - 5.5.10. с.220 №5.5.16.
|
|
Итого
|
14
|
|
Заочная форма
обучения
2-й семестр
(Основы математического анализа)
|
Лекции
|
Число часов
|
Самостоятельная работа
|
|
Функция одной переменной.
Предел функции одной переменной.
|
2
|
Теория по любому из
указанных пособий: [1] с.125 - 134, 143 - 154 [9] с.108 - 133 [4] с.112-129 Задачи: [2] с.151 №5.12, 5.15,
5.17 с.152 №5.40 - 5.47 [2] с.166 №6.50 - 6.60 с.168 №6.70 - 6.80 с.172 №6.115
- 6.118 с.173 №6.124 - 6.126
|
|
Непрерывность функции.
Производная и дифференциал функции одной переменной.
|
2
|
Теория:[1] с.176 - 198 [4]
с.157 - 163 Задачи: [2]с.191№7.40 - 7.50 с.192 №7.71, 7.76 -7.78 с.245 №9.15
- 9.20 с.246 №9.41 - 9.43
|
|
Правило Лопиталя.
Исследование функций при помощи производных.
|
2
|
Теория:[1] с.216 - 232 [2]
с. 171 - 180 [4] с.164 - 169 [9] с.178 - 183, с.191 - 198 Задачи: [2] с.215
№8.15 - 8.18 с.216 №8.24 - 8.30
[8] с.81 №297 -
303
|
|
Неопределенный интеграл.
Методы его вычисления.
|
2
|
Теория:1] с.251 - 270 [9]
с.213 - 224 Задачи: [2] с.270 №10.28 - 10.40 с.274 №10.75 - 10.85 с.277
№10.107 - 10.112
|
|
Определенный интеграл.
Методы его вычисления. Некоторые приложения определенного интеграла.
|
2
|
Теория:[1] с.295 - 307[4]
с.221 - 233 Задачи:[2]с.292 №11.2 - 11.12 с.300 №11.36 - 11.40
|
|
Дифференциальные уравнения
1 -го порядка. Линейные дифференциальные уравнения 2-го порядка с постоянными
коэффициентами.
|
2
|
Теория: [1] с.325 -330,
с.337 - 344 [5] с.11 - 17, с.36 - 38 Задачи: [2] с.320 №12.17 - 12.20 [8]
с.232 №84 - 89 с.236 №98 - 103
|
|
Числовые ряды. Признаки их
сходимости. Степенные ряды.
|
2
|
Теория:[1] с.356 - 369 Задачи:[2]
с.356 №13.29 ; 13.30.с.357 №13.56 - 13.61
|
|
Итого
|
14
|
|
САМОСТОЯТЕЛЬНАЯ
РАБОТА
Методические
указания
Организация самостоятельной работы студентов имеет цель:
– систематизировать и расширить их теоретические знания;
– закрепить практические навыки;
– научить работать с учебной и научной литературой, проводить её анализ
и делать выводы;
– стимулировать профессиональный рост студентов, воспитывать творческую
активность и инициативу.
Домашняя самостоятельная работа студентов организуется преподавателем в
соответствии с календарным планом изучения дисциплины и предполагает:
– изучение лекционного материала, чтение рекомендуемых литературных
источников, решение задач, ответы на контрольные вопросы или тесты и т.д.;
– самостоятельное изучение материала по заданным преподавателем темам.
По курсу «Математика I» (линейная алгебра с элементами аналитической
геометрии и основы математического анализа) проводятся 5 контрольных работ.
Контрольные работы за 1 семестр
Домашняя контрольная работа 1.
Выдается по задачникам [2] и [10].
Содержит 6 заданий.
Тема: «Вычисление определителей. Действия с матрицами. Решение систем
линейных алгебраических уравнений».
Вариант контрольной работы 1.
1.
Вычислить определитель.
.
Найти матрицу 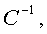 обратную к матрице
обратную к матрице 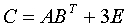
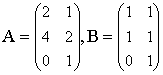 .
.
.
Решить матричное уравнение
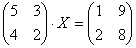 .
.
.
Решить систему уравнений с помощью обратной матрицы
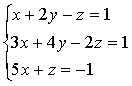
.
Решить систему уравнений по формулам Крамера.
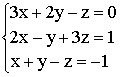
.
Решить систему уравнений методом Гаусса.
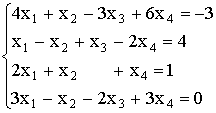
Домашняя
контрольная работа 2.
Тема:
«Векторная алгебра. Прямая и плоскость в пространстве».
Вариант
контрольной работы 2.
.
Даны векторы 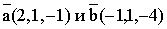 .
.
Найти:
1)
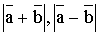 ,
,
) 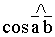 ,
,
)
найти вектор 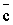 , коллинеарный вектору
, коллинеарный вектору 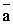 и
удовлетворяющий условию
и
удовлетворяющий условию 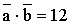 .
.
.
Даны векторы 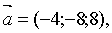
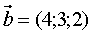 . Найти векторное произведение, синус угла между ними,
площадь параллелограмма, построенного на этих векторах.
. Найти векторное произведение, синус угла между ними,
площадь параллелограмма, построенного на этих векторах.
.
Вычислить произведение 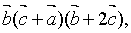 если
если 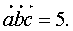
.
Найти точку пересечения прямой 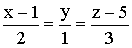 и
плоскости 2x-y+z+1=0.
и
плоскости 2x-y+z+1=0.
.
Составить уравнение плоскости, проходящей через точки М1(2;3;-1) и М2(1;5;3),
перпендикулярно плоскости 3х - у +3z + 15 = 0.
.
При каких значениях C и D прямая 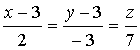 лежит в
плоскости 2x - y + Cz + D = 0?
лежит в
плоскости 2x - y + Cz + D = 0?
Контрольные работы за 2 семестр
Контрольная работа 3
Тема: «Пределы и непрерывность»
Вариант контрольной работы 3
Найти пределы:
1.
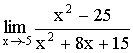
. 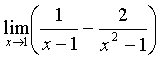
. 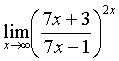
. 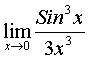
. 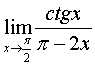
.
Найти точку разрыва функции (указать характер):
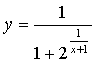
Контрольная
работа 4
Тема:
«Производная и дифференциал функции»
Вариант
контрольной работы 4
.
Найти производную функции:
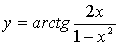
.
Найти предел, используя правило Лопиталя:
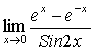
.
Найти интервалы выпуклости и точки перегиба функции:
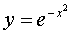
.
Найти dy и 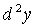 функции:
y = Sin x ×ln x
функции:
y = Sin x ×ln x
.
Найти Dу и dy функции: 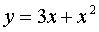 при х =
2, Dх = 0,001
при х =
2, Dх = 0,001
.
Вычислить приближенно с помощью дифференциала:
Sin (p + 0,01)
Контрольная
работа 5
Тема:
«Вычисление неопределенных и определенных интегралов»
Вариант
контрольной работы №5
Вычислить интегралы:
1.
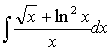
. 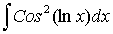
. 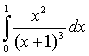
. 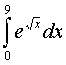
.
Найти площадь фигуры, ограниченной линиями:
y = ln x, 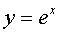 , x =
2, x = 0, y = 0
, x =
2, x = 0, y = 0
.
Вычислить по формуле трапеций для n = 10 интеграл 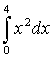 . Найти значение погрешности полученного результата.
. Найти значение погрешности полученного результата.
Контрольная работа для студентов заочной формы обучения
Методические указания
На первом курсе обучения по разделу «Математика I» выполняются две контрольные работы: №1 - по аналитической геометрии
и линейной алгебре и №2 по основам математического анализа. К выполнению каждой
контрольной работы следует приступать только после изучения соответствующего
материала курса по учебникам, предложенным в списке литературы, и решения
задач, указанных к каждой теме данного УМК. При выполнении работ следует
руководствоваться следующими указаниями.
1. Каждую работу следует выполнять в отдельной тетради, на внешней
обложке которой должны быть указаны фамилия и инициалы студентов, полный шифр,
номер контрольной работы и дата ее отправки в институт.
Условия задач следует переписывать полностью, без сокращений. Решения
всех задач и пояснения к ним должны быть достаточно подробными. При
необходимости следует делать ссылки на вопросы теории с указанием формул,
теорем, выводов, которые используются при решении данной задачи. Все вычисления
(в том числе и вспомогательные) необходимо делать полностью. Чертежи и графики
должны быть выполнены (желательно на миллиметровой бумаге) аккуратно и четко с
указанием единиц масштаба, координатных осей и других элементов чертежа. В
конце работы следует указать, какие учебники и учебные пособия (включая
методические указания) были использованы при выполнении работы.
Для замечаний преподавателя необходимо на каждой странице оставлять поля
шириной 3 - 4 см.
. После получения работы (как зачтенной, так и не зачтенной) студент
должен исправить в ней все отмеченные рецензентом недостатки. В случае незачета
студент обязан в кратчайший срок выполнить все требования рецензента и представить
работу на повторную рецензию, приложив при этом первоначально выполненную
работу.
. Контрольные работы должны выполняться самостоятельно. Если будет
установлено, что та или иная контрольная работа выполнена несамостоятельно, то
она не будет зачтена, даже если в этой работе все задачи решены верно.
. При необходимости (по требованию преподавателя) студент должен давать
на экзамене устные пояснения ко всем или некоторым задачам, содержащимся в этих
работах.
. Студент выполняет тот вариант контрольных работ, который совпадает с
последней цифрой его учебного шифра (номер студенческого билета). При этом
последняя цифра ноль (0) соответствует варианту №10.
Варианты контрольной работы 1 для студентов заочной формы обучения
(Аналитическая геометрия и линейная алгебра)
Вариант №1
1. В треугольнике с вершинами А(3;-2), В(5;2), С(-1;4) найдите длины всех сторон, длину медианы BD и точку М пересечения медиан.
2. Составьте
уравнение гиперболы, вершины которой находятся в фокусах эллипса 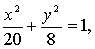 а фокусы в вершинах эллипса.
а фокусы в вершинах эллипса.
. Из
точки Р(2;3;-5) на координатные плоскости опущены перпендикуляры.
Составить уравнение плоскости, проходящей через их основания.
. Решить
матричное уравнение:
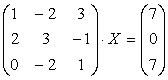
5. Определить при каких значениях m и n
система
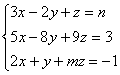
а)
имеет единственное решение; б) не имеет решений.
.
Методом Гаусса решить систему уравнений
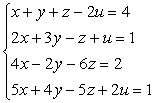
Вариант
2.
1. Треугольник задан вершинами: А(-5;-2), В(7;6) и С(5;-4).
Найдите: 1) уравнение стороны АВ; 2) уравнение медианы, проведенной из вершины
А; 3) уравнение высоты, проведенной из вершины С; 4) центр тяжести этого
треугольника.
2. Эллипс проходит через точку М(1;1) и имеет эксцентриситет e = 3/5. Составить уравнение эллипса.
3. Составить уравнение плоскости, проходящей через точку М(3;-1;-5) и перпендикулярной плоскостям 3x - 2y + 2z + 7 = 0 и 5х - 4у + 3z + 1= 0.
4. Решить
уравнение 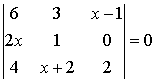 .
.
. По
формулам Крамера решить систему
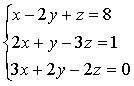
6. Методом Гаусса решить систему уравнений:
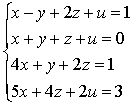
Вариант
3
.
Найти уравнение множества точек, равноудаленных от точек А(2;0) и В(0;1).
.
Составьте уравнение эллипса с фокусами на оси Ох, если сумма полуосей равна 25,
а фокусы имеют координаты (-5;0) и (5;0).
.
Написать канонические уравнения прямой L , заданной
уравнениями,
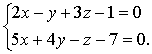
.
Вычислить произведения 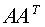 и
и 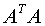 , при
заданной матрице А:
, при
заданной матрице А:
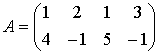 .
.
.
Определить при каких значениях m и n система
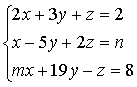
а)
имеет единственное решение; б) не имеет решений.
.
Методом Гаусса решить систему уравнений:
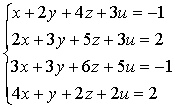 .
.
Вариант
4
1. Даны три стороны треугольника: х + у - 6 = 0, 3х - 5у + 14 = 0 и
5х - 3у - 14 = 0. Составить уравнения его высот.
2. Составьте уравнение эллипса с фокусами на оси Ох, если сумма
полуосей равна 25, а фокусы имеют координаты (-5;0) и (5;0).
. Составить уравнение плоскости, проходящей через прямую,
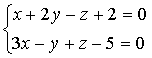
параллельно
прямой 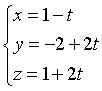 .
.
. Представить
вектор 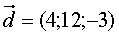 как линейную комбинацию векторов
как линейную комбинацию векторов 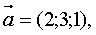
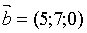 ,
, 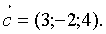
. Вычислить
определитель:
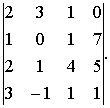
6. Решить систему методом обратной матрицы:
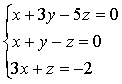 .
.
Вариант
5
.
Составить уравнения трех сторон квадрата, если известно, что четвертой стороной
является отрезок прямой 4х + 3у - 12 = 0, концы которого лежат на осях
координат.
.
Составить уравнение плоскости, проходящей через точку М(3;-1;-5) и перпендикулярной плоскостям 3х - 2у + 2z + 7
= 0 и 5х - 4у + 3z +1 = 0.
.
Найти значение матричного многочлена
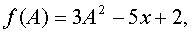
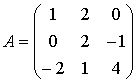
5. Решить систему уравнений с помощью обратной матрицы:
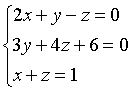
. Решить систему уравнений методом Гаусса:
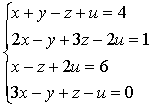
Вариант
6
.
Даны три стороны треугольника: х + у - 6 = 0, 3х - 5у + 14 = 0 и 5х - 3у -14 =
0. Составить уравнения его высот.
.
Дана гипербола 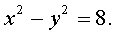 Найти софокусный эллипс, проходящий через точку
М(4;6).
Найти софокусный эллипс, проходящий через точку
М(4;6).
.
Написать канонические уравнения прямой L , заданной
уравнениями: 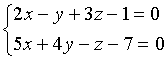
.
Представить вектор 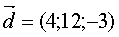 как линейную комбинацию векторов
как линейную комбинацию векторов 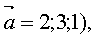
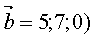 и
и 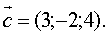
.
Определить при каких значениях m и n система
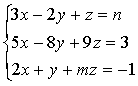
а)
имеет единственное решение; б) не имеет решений.
.
Решить систему уравнений с помощью обратной матрицы
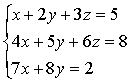 .
.
Вариант
7
1. Треугольник задан вершинами: А(-5;-2), В(7;6) и С(5;-4).
Найдите: 1) уравнение стороны АВ; 2) уравнение медианы, проведенной из
вершины А; 3) уравнение высоты, проведенной из вершины С; 4) центр тяжести
этого треугольника.
2. Дан
эллипс 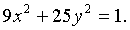 Написать уравнение софокусной равнобочной гиперболы.
Написать уравнение софокусной равнобочной гиперболы.
. Составить
уравнение плоскости, проходящей через прямую,
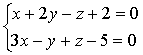
параллельно
прямой 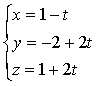 .
.
. Доказать,
что векторы 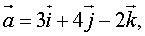
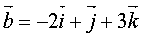 и
и 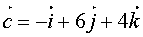 компланарны.
компланарны.
. Определить
при каких значениях m система уравнений
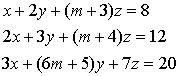
а) имеет единственное решение; б) не имеет решений.
6. Решить систему методом Гаусса:
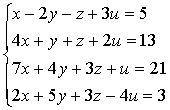 .
.
Вариант
8
1. Найти уравнение множества точек, равноудаленных от точек А(2;0)
и В(0;1).
2. Центр окружности находится в точке О(-3:1). Составить уравнение
окружности, если она касается прямой 4х + 3у - 16 = 0.
3. Вычислить объем пирамиды, ограниченной плоскостью Р: 2х - 3у + 6z- 12 = 0 и координатными плоскостями.
4. Даны
векторы: 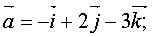
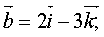
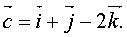
Найти
{(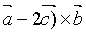 }
}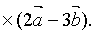

5. Решить систему уравнений с помощью обратной матрицы:
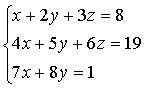 .
.
6. Решить систему уравнений методом Гаусса:
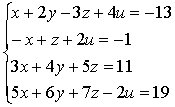
Вариант
9
1. В треугольнике с вершинами А(3;-2), В(5;2), С(-1;4) найдите длины всех сторон, длину медианы BD и точку М пересечения медиан.
2. Найти
уравнение прямой, проходящей через центры окружностей, 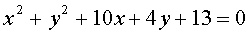 и
и 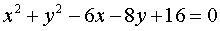 .
.
. В
уравнениях прямой 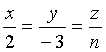 определить параметр n так, чтобы эта
прямая пересекалась с прямой
определить параметр n так, чтобы эта
прямая пересекалась с прямой 
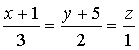 , и найти
точку их пересечения.
, и найти
точку их пересечения.
. Даны
векторы 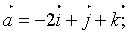
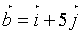 и
и 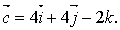
Вычислить
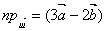 .
.
. Вычислить
определитель 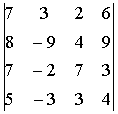 .
.
. Методом
Гаусса решить систему уравнений:
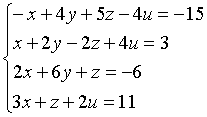 .
.
Вариант
10.
.
Даны три стороны треугольника: х + у - 6 = 0, 3х - 5у + 14 = 0 и 5х - 3у -14 =
0. Составить уравнения его высот.
.
Составить уравнение параболы с вершиной в начале координат, симметричной
относительно оси Оу и отсекающей на биссектрисе I и III
координатных углов хорду длиной 8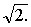
.
Найти уравнение проекции прямой 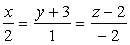 на
плоскость 2х + 3у - z - 5 = 0.
на
плоскость 2х + 3у - z - 5 = 0.
.
Найти объем треугольной пирамиды с вершинами А(2;2;2), В(4;3;3), С(4;5;4) и D(5;5;6).
.
Решить систему уравнений по формулам Крамера:
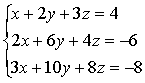
. Решить систему уравнений методом Гаусса:
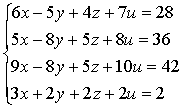 .
.
Варианты
контрольной работы 2 для студентов заочной формы обучения (Основы
математического анализа)
Вариант 1
1. Найти область определения функции:
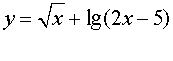
. Вычислить
предел 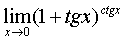
. Найти
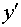
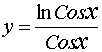
. Вычислить
интеграл 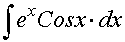
. Вычислить
интеграл 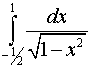
. Вычислить
площадь фигуры, ограниченной линиями,
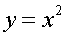 и
и 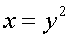
Вариант 2
1.
Найти область определения функции 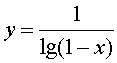
.
Вычислить предел 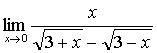
.
Найти 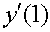
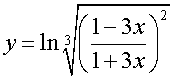
.
Вычислить интеграл 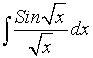
.
Вычислить интеграл 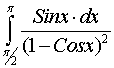
.
Вычислить площадь фигуры, ограниченной линиями,
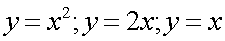
Вариант 3
1.
Найти область определения функции 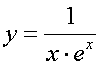
.
Вычислить предел 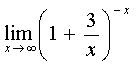
.
Найдите 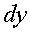
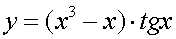
.
Вычислить интеграл 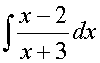
.
Вычислить интеграл 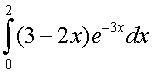
.
Вычислить площадь фигуры, ограниченной линиями,
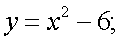
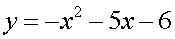
Вариант 4
1.
Найти область определения функции 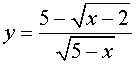
.
Вычислить предел 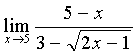
.
Найдите 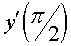
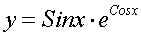
4.
Вычислить интеграл 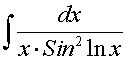
.
Вычислить интеграл 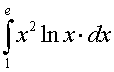
7. Вычислить площадь фигуры, ограниченной линиями,
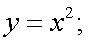
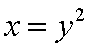
Вариант 5
1.
Найти множество значений функции 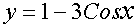
.
Вычислить предел 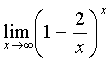
.
Найдите 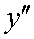
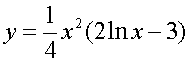
.
Вычислить интеграл 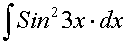
.
Вычислить интеграл 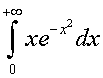
.
Вычислить площадь фигуры, ограниченной линиями,
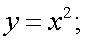
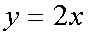
Вариант 6
1.
Найти область определения функции 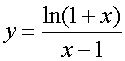
.
Вычислить предел по правилу Лопиталя 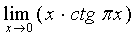
.
Найдите 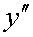
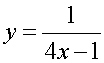
.
Вычислить интеграл 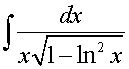
.
Вычислить интеграл 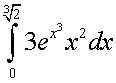
.
Вычислить площадь фигуры, ограниченной линиями,
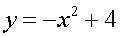 ;
; 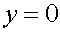
Вариант 7
1.
Установить четность или нечетность функции 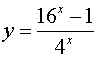
.
Вычислить предел по правилу Лопиталя 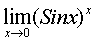
.
Найдите 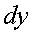
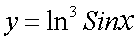
.
Вычислить интеграл 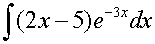
.
Вычислить интеграл 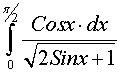
.
Вычислить площадь фигуры, ограниченной линиями,
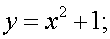
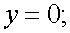
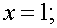
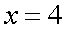
Вариант 8
1.
Установить четность или нечетность функции 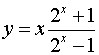
.
Вычислить предел по правилу Лопиталя 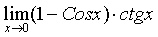
.
Найдите 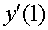
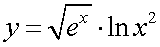
.
Вычислить интеграл 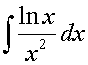
.
Вычислить интеграл 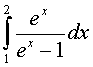
.
Вычислить площадь фигуры, ограниченной линиями, 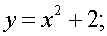
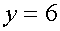
Вариант
9
.
Найти область определения функции 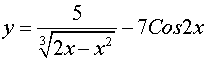
.
Вычислить предел по правилу Лопиталя 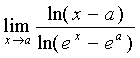
.
Найдите 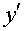
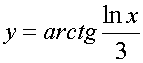
4.
Вычислить интеграл 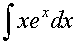
.
Вычислить интеграл 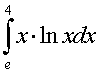
.
Вычислить площадь фигуры, ограниченной линиями
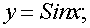
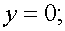
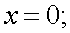
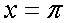
Вариант 10
1.
Найти множество значений функции 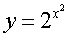
.
Вычислить предел по правилу Лопиталя 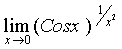
.
Найдите 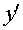
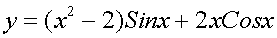
.
Вычислить интеграл 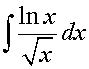
.
Вычислить интеграл 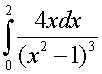
.
Вычислить площадь фигуры, ограниченной линиями,
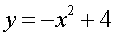 ;
; 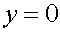
КОНТРОЛЬ
Тестовые задания для промежуточного контроля студентов
«Линейная алгебра с элементами аналитической геометрии»
Вопрос 1. Найти C=2A - 3BТ, если
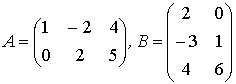
Ответы:
а) 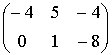 ; б)
; б) 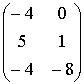 ; в)
; в) 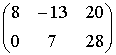 ; г)
; г) 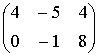
Варианты
ответов
.
а
.
б
.
в
.
г
Вопрос
2. Найти AB, если
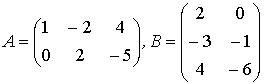
Ответы:
а)
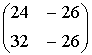 ; б)
; б) 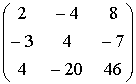 ; в)
; в) 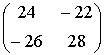 ; г)
; г) 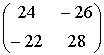
Варианты
ответов
.
а
.
б
.
в
.
г
Вопрос
3. Чему равно данное выражение (AB)Т?
Ответы:
а)
АТВТ; б) (ВА)Т; в) ВТАТ
Варианты
ответов
.
а
.
б
.
в
Вопрос
4. Вычислить определитель 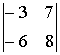
Варианты
ответов
.
18
.
68
.
- 68
.
- 18
Вопрос
5. Дана матрица 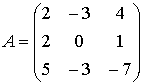 . Найти алгебраическое дополнение для элемента a23
ее определителя.
. Найти алгебраическое дополнение для элемента a23
ее определителя.
Варианты
ответов
.
9
.
-21
.
-6
.
другой ответ
Вопрос
6. Вычислить определитель данной матрицы:
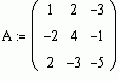
Варианты
ответов 1. 41; 2. 52; 3. другой ответ
Вопрос
7. Вычислить определитель данной матрицы
дифференциал функция вектор множество
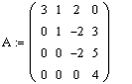
Варианты
ответов
.
-24
.
24
.
другой ответ
Вопрос
8. Даны матрицы А и В.
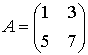 и
и 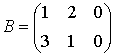
Выяснить,
какие из следующих операций можно выполнить:
а)
А+В; b) АТ+В; c) A+ BT; d) AB; e) BA; f) ATB; g) BTAT
Варианты
ответов
.
a)
. b)
. c)
. d)
. e)
. f)
. g)
Вопрос
9. Как возвести матрицу в третью степень?
Варианты
ответов
1. Умножить матрицу на матрицу, а затем полученную матрицу умножить на
исходную матрицу
2. возвести в третью степень каждый элемент матрицы
3. Умножить матрицу на матрицу, а затем исходную матрицу умножить на
полученную матрицу
Вопрос
10. Для матрицы 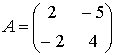 найти обратную матрицу
найти обратную матрицу 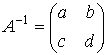 .
Соответствующие числа a, b, c, d найдите в вариантах ответов.
.
Соответствующие числа a, b, c, d найдите в вариантах ответов.
Варианты
ответов
. 4,
5, 2, 2
. 4,
2, 5, 2
.
-4, -5, -2, -2
.
-4, -2, -5, -2
Вопрос
11. Матрица-строка размером:
Варианты
ответов
. 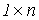
. 
. 
Вопрос
12. Каким свойством не обладает произведение матриц?
Варианты
ответов
. АВ=ВА
.
(АВ)С=А(ВС)
3. λ(А+В)= λА+ λВ
Вопрос
13. При умножении матрицы на обратную ей получаем:
Варианты
ответов
.
нулевую
.
транспонированную
.
единичную
Вопрос
14. Какая система называется однородной?
Варианты
ответов
.
содержащая одинаковые уравнения
.
у которой свободные члены равны 0
.
у которой количество уравнений совпадает с числом переменных
Вопрос
15. Метод исключения переменных это:
Варианты
ответов
.
метод Гаусса
.
метод Крамера
.
матричный метод.
Вопрос
16. По формулам Крамера решить систему уравнений

В
ответе указать значение суммы переменных x1, x2 и
определителя 
Варианты
ответов
. 7
. 9
. 5
Вопрос
17. Каким методом можно решить система уравнений, если определитель системы=0?
Варианты
ответов
1. методом Гаусса
. методом Крамера
. матричным методом.
Вопрос 18. Назовите вид системы векторов, если третий вектор равен сумме
двух других векторов.
Варианты ответов
. линейно зависимая
. линейно независимая
. линейно независимая при условии
. может быть любого вида
Вопрос 19. Установить соответствие между рисунками и векторным равенством
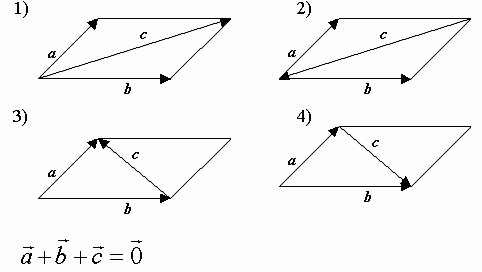
Варианты ответов
. 1)
. 2)
. 3)
. 4)
Вопрос
20. Определить длину вектора 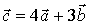 , если
, если 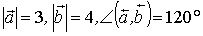
Варианты
ответов
.
12
. 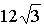
.
24
Вопрос 21. Даны векторы
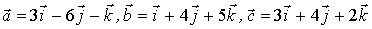
Найти
с точностью до 0,1 проекцию вектора 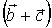 на
направление вектора
на
направление вектора 
Варианты ответов
. 4,7
. 2,5
. другой ответ
Вопрос 22. Выяснить, какие из приведенных троек векторов образуют базис в
трехмерном пространстве
. (0; 0; 1), (0; 1; 0), (0; 1; 1),
. (0; 0; 1), (1; 0; 0), (0; 1; 0),
. (1; 1; 1), (0; 1; 0), (2; 2; 2),
Варианты ответов
. 1
. 2
. 3
Вопрос 23. Установить соответствие между рисунками и векторным равенством
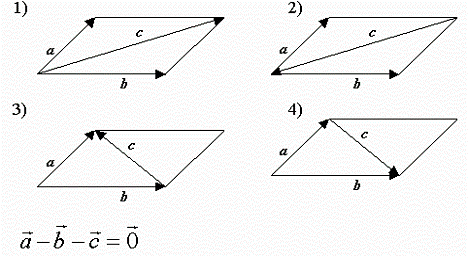
Варианты ответов
. 1)
. 2)
. 3)
. 4)
Вопрос 24. Два вектора коллинеарны, если:
Варианты ответов
. Их векторное произведение равно 0
. Их скалярное произведение равно 0
Вопрос 25. Найти координаты точки (x0; y0)
пересечения медиан треугольника АВС, где
А(2; 4), В(-3; 0), С(7; -1)
Варианты ответов
. (2; 1)
. (3; 4)
. (1; 2)
Вопрос
26. Найти в градусах острый угол между прямыми 4x-2y-7=0
и 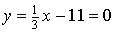
Варианты
ответов
.
45
.
60
.
30
Вопрос
27. Какие из данных прямых перпендикулярны прямой 2x - y+3=0
)
4x+8y+17=0; 2) 4x-8y-11=0, 3) 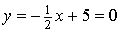 ; 4) y=-2x - 7; 5)
; 4) y=-2x - 7; 5) 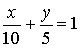
Варианты
ответов
. 1),
3), 5)
. 2),
4)
. 1),
3)
Вопрос
28. А(-4; 3), В(2; 5), С(6; -2). - вершины треугольника АВС. Составить
уравнение высоты 4x+by+c=0, проведенной из вершины А
Варианты
ответов
. b=
-7, c=37
. b= 7,
c=37
. b=
-7, c=-5
Вопрос
29. Найти расстояние между параллельными прямыми
y = - 0,75x - 6
и 3x + 4y - 12 =0
Варианты
ответов
. 7,2
. 2,4
. другой
ответ
Вопрос
30. Выяснить, в каком случае плоскости A1x+B1y+C1z+D1=0,
A2x+B2y+C2z+D2=0 параллельны.
Варианты
ответов
. 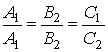
. 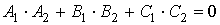
Вопрос
31. Выяснить, в каком случае плоскости A1x+B1y+C1z+D1=0,
A2x+B2y+C2z+D2=0 перпендикулярны.
Варианты
ответов
. 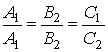
. 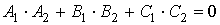
Вопрос
32. Выяснить, в каком случае плоскость Ax+By+Cz+D=0 и
прямая 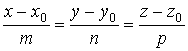 параллельны?
параллельны?
Варианты
ответов
. 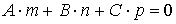
. 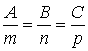
Вопрос
33. Выяснить, в каком случае плоскость Ax+By+Cz+D=0 и
прямая 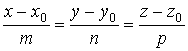 перпендикулярны?
перпендикулярны?
Варианты
ответов
. 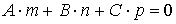
. 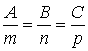
Вопрос
34. Найдите длину АВ, если А(2; 0) и В(5; 4)
Варианты
ответов
. 5
. 33
. 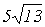
Вопрос
35. Найдите координаты середины отрезка АВ, если А(5; 3) и В(-1; 5)
Варианты
ответов
. (2;
4)
. (3;
-1)
. (-3;
1)
Вопрос
36. Лежит ли точка А(2; -4) на линии х2-y = 0
Варианты
ответов
. Да
. Нет
Вопрос
37. Найдите координаты точки делящей отрезок, заданный точками А(-1; -3) и В(5;
3) в отношении 2 : 1
Варианты
ответов
. (3;
1)
. (1;
3)
. (2;
0)
Вопрос
38. Условие параллельности прямых:
Варианты
ответов
. 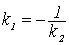
. 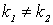
Вопрос 39. Написать уравнение окружности, касающейся оси Ox в начале координат и проходящей через
точку А(0; -8)
Варианты ответов
. x2+ (y+4)2=16
. x2+y2=64
. (x+4)2+ y2=16
Вопрос 40. Какую кривую второго определяет уравнение
x2 -
10x + y2 - 8y + 32
= 40
Варианты ответов
. окружность
. гиперболу
параболу
. эллипс
Вопрос 41. Указать каноническое уравнение эллипса, если даны его полуоси a = 3, b = 4
Варианты ответов
1. 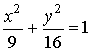
. 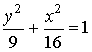
. 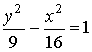
Вопрос
42. Какую кривую второго определяет уравнение
x2 - 10x + y2 -
8y + 32 = 0
Варианты
ответов
.
окружность
.
гиперболу
параболу
.
эллипс
Вопрос
43. Найти расстояние между фокусами эллипса 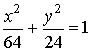
Варианты
ответов
. 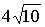
. 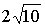
. 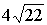
. 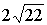
Вопрос
44. Найти расстояние между фокусами гиперболы 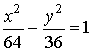
Варианты
ответов
. 20
. 10
. 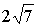
. 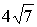
Вопрос
45. Множество всех точек плоскости, для которых сумма расстояний от двух данных
точек, называемых фокусами, есть величина постоянная, меньшая расстояния между
фокусами, есть:
)
прямая линия, 2) окружность, 3) гипербола. 4) парабола, 5) эллипс.
Варианты
ответов
. 1)
. 2)
. 3)
. 4)
. 5)
Вопрос
46. Множество всех точек плоскости, каждая из которых находится на одинаковом
расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой
директрисой и не проходящей через фокус, есть:
)
прямая линия, 2) окружность, 3) гипербола. 4) парабола, 5) эллипс.
Варианты
ответов
. 1)
. 2)
. 3)
. 4)
. 5)
Вопрос
47. Множество всех точек плоскости, для которых сумма расстояний от двух данных
точек, называемых фокусами, есть величина постоянная, большая расстояния между
фокусами, есть:
)
прямая линия, 2) окружность, 3) гипербола. 4) парабола, 5) эллипс.
Варианты
ответов
. 1)
. 2)
. 3)
. 4)
. 5)
Вопрос
48. Какое уравнение не определяет эллипс?
Варианты
ответов
. 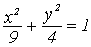
. 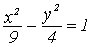
. 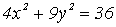
Вопрос
49. Парабола 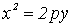 симметрична относительно:
симметрична относительно:
Варианты
ответов
.
оси ординат
.
оси абсцисс
.
начала координат
Вопрос
50. Найти радиус окружности 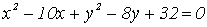
Варианты
ответов
. 3
. 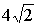
. 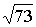
Тестовые
задания для промежуточного контроля студентов
«Основы
математического анализа»
Вопрос
1. Выяснить, какие из данных функций являются сложными:
1) 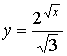 ,
2)
,
2) 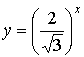 , 3) y = arcsin x, 4) y = arcsin (3x)
, 3) y = arcsin x, 4) y = arcsin (3x)
Варианты
ответов
. 1)
. 2)
. 3)
. 4)
Вопрос
2. График нечетной функции симметричен относительно:
Варианты
ответов
. начала
координат
. оси
абсцисс
. оси
ординат
Вопрос
3. Область определения функции 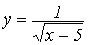 :
:
Варианты
ответов
. (5;
+∞)
. (-∞;
5) U (5; +∞)
. [5;
+∞)
Вопрос
4. Выяснить, какие из функций являются монотонным при 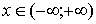
Варианты
ответов
. 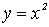
. 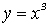
. 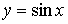
Вопрос
5. Выяснить какая из функций является четной:
Варианты
ответов
. 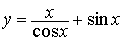
. 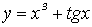
. 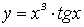
Вопрос
6. Укажите верное утверждение для функции 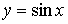 :
:
Варианты
ответов
. монотонная
. четная
. нечетная
. общего
вида
Вопрос
7. График четной функции симметричен относительно:
Варианты
ответов
. начала
координат
. оси
абсцисс
. оси
ординат
Вопрос
8. Выяснить, чему равен 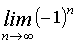
Варианты
ответов
. -1
. не
существует
. 1
.
бесконечность
Вопрос
9. Выяснить, какие из перечисленных функций бесконечно малые при 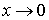
) 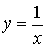 , 2) y=x10, 3)
, 2) y=x10, 3) 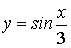 , 4) y=cos2x, 5)
, 4) y=cos2x, 5)
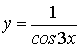 .
.
Варианты
ответов
. 1)
. 2)
. 3)
. 4)
. 5)
Вопрос
10. Выяснить, какая из перечисленных функций не является бесконечно большой при
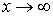
) 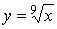 ; 2) y=tgx; 3) y=log0,5 x; 4)
; 2) y=tgx; 3) y=log0,5 x; 4)
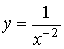 ;
;
Варианты
ответов
. 1)
. 2)
. 3)
. 4)
Вопрос
11. Произведение двух бесконечно малых и бесконечно большой величин являются
Варианты
ответов
.
Бесконечно малой величиной
.
Бесконечно большой величиной
.
Неопределенностью.
Вопрос
12. Выяснить, какие из перечисленных функций непрерывны в точке х = 0
) 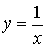 ; 2)
; 2) 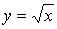 ; 3)
; 3) 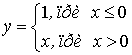 ; 4)
; 4) 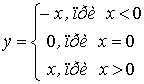 ; 5) y=tg x
; 5) y=tg x
Варианты
ответов
. 1)
. 2)
. 3)
. 4)
. 5)
Вопрос
13. Какого рода точка разрыва функции
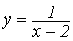
. второго
рода
. первого
рода
Вопрос
14. Найти
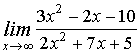
Варианты
ответов
. 1,5
. ∞
. 0
Вопрос
15. Найти
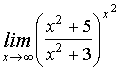
Варианты
ответов
e2
. e-2
. ∞
. 0
Вопрос
16. Найти
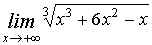
Варианты
ответов
. +
∞
. -
∞
. 0
Вопрос
17. Найти α,
если
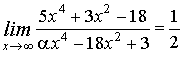
Варианты
ответов
. 1
. 10
. 25
Вопрос
18. Найти α,
если
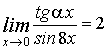
Варианты
ответов
. 16
. 4
. 2
Вопрос
19. Вычислить предел:
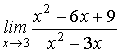
Варианты
ответов
. 6
. 0
. ∞
Вопрос
20. Вычислить
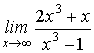
Варианты
ответов
. 2
. 0
.
-2
Вопрос
21. Чему равен
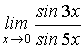
Варианты
ответов
. 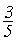
. 1
. 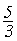
Вопрос
22. Какая формула не является вторым замечательным пределом?
1.
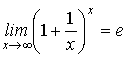 ,2.
,2. 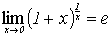 , 3.
, 3. 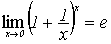
Вопрос
23. 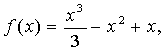 найти f¢(0), f¢(1), f¢(-1)
найти f¢(0), f¢(1), f¢(-1)
Варианты
ответов
1. 0, 0, 0
2. 1, 4, 0
. 1, 0, 4
. 4, 1, 0
Вопрос
24. Найти производную функции 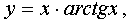 в точке
х0 = 0
в точке
х0 = 0
Варианты
ответов
1. 0
2. 1
. -1
4. 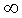
Вопрос
25. Найти уравнение касательной к кривой 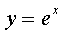 в точке
х0 = 0
в точке
х0 = 0
Варианты
ответов
1. у = х
2. у = х - 1
. у = -х +
1
. у = х + 1
Вопрос
26. Найти уравнение нормали к кривой 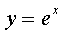 в точке
х0 = 0
в точке
х0 = 0
Варианты
ответов
1.
у = х
2. у = х - 1
. у = -х +
1
. у = х + 1
Вопрос
27. 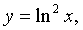 найти у²
найти у²
Варианты
ответов
. 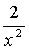
. 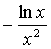
. 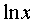
. 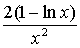
Вопрос
28. 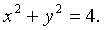 Найти у¢ в точке
Найти у¢ в точке 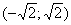
Варианты
ответов
1. 1
2. -1
. 0
. µ
Вопрос
29. Дифференциал функции 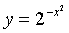 равен
равен
Варианты
ответов
. 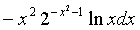
. 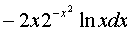
. 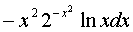
Вопрос
30. Найти приращение и дифференциал функции 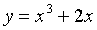 в точке
х0=1, если известно Dх = 0,01.
в точке
х0=1, если известно Dх = 0,01.
Варианты
ответов
. Dу = 0,050301 dy = 0,05
. Dy =
0,05 dy = 0,05
. Dу = 0,055 dy = 0,04
. Dy =
0,06 dy = 0,04
Вопрос
31. Вычислить приближенно tg 44°
Варианты
ответов
1. 0,995
2. 0,985
. 0,975
. 0,965
Вопрос
32. 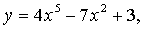 найти
найти 
Варианты
ответов
. 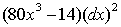
. 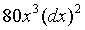
. 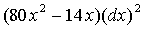
Вопрос
33. Вычислить предел по правилу Лопиталя
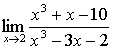
Варианты
ответов
1. 1
2. 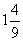
. 2
. 1,6
Вопрос
34. Вычислить предел по правилу Лопиталя 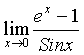
Варианты
ответов
1. 1
2. 0
. -1
. µ
Вопрос
35. Вычислить предел по правилу Лопиталя 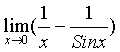
Варианты
ответов
1. 1
2. 0
. -1
. µ
Вопрос 36. Выяснить какое из приведенных утверждений является неверным:
1) в точке экстремума производная функции равна нулю или не
существует;
2) в точке экстремума функция меняет знак;
) в точке экстремума производная меняет знак;
) в точке, в которой производная равна нулю или не существует,
может не быть экстремума.
Варианты ответов
1. 1
2. 2
. 3
. 4
Вопрос
37. Среди перечисленных функций горизонтальную асимптоту имеет функция: 1) 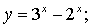 2)
2) 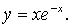
Варианты
ответов
1. 1
2. обе функции имеют
. 2
. обе функции не имеют
Вопрос
38. Найти наибольшее и наименьшее значения функции 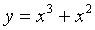 на отрезке [-1;2].
на отрезке [-1;2].
Варианты
ответов
1. fнаиб.(2) = 12; fнаим.(-1)
= fнаим.(0) = 0
2. fнаиб.(1) = 4; fнаим.(0) = 0
3. fнаиб.(0) = 5; fнаим.(-1) = -5
Вопрос
39. Найти интервалы возрастания и убывания функции 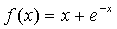
Варианты
ответов
1. возрастает при х>0, убывает при х<0
2. функция только возрастает
. функция только убывает
. возрастает при х < 0, убывает при х > 0
Вопрос 40. Следующее утверждение из перечисленных является всегда верным:
1) в точке перегиба всегда существует конечная 1-я производная;
2) в точке перегиба всегда существует конечная 2-я производная;
3) точка перегиба является точкой экстремума 1-й производной дважды
дифференцируемой функции;
4) точка перегиба является точкой экстремума 2-й производной
функции.
Варианты ответов
1. 1
2. 2
. 3
. 4
Вопрос
41. При каких а и в функция 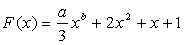 является
первообразной для
является
первообразной для 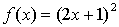 ?
?
Варианты ответов
. а = 3 в = 4
. а = 4 в = 3
. а = 3 в = 3
. а = 4 в = 4
Вопрос
42. Найти интеграл 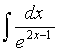
Варианты
ответов
. 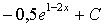
. 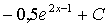
. 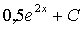
. 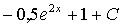
Вопрос
43. Найти интеграл 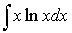
Варианты
ответов
. 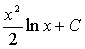
. 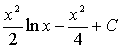
. 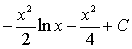
. 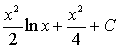
Вопрос
44. При каких значениях параметров а и в справедливо равенство
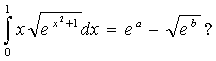
Варианты
ответов
.
а = 0 в = 0
.
а = 1 в = 1
.
а = 2 в = 2
.
а = 0 в = 1
Вопрос
45. Вычислить определенный интеграл 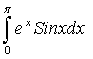
Варианты
ответов
. 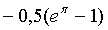
. 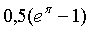
. 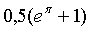
. 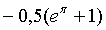
Варианты
ответов
1. 2ln2 - 1
2. 1 - 2ln2
. 2
. ln2 + 1
Вопрос
47. Площадь фигуры, ограниченная линиями 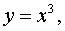
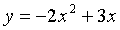 (фигура
расположена в 1-ой четверти)
(фигура
расположена в 1-ой четверти)
Варианты
ответов
1. 1; 2. 0,5 ; 37/12; 4.5/8
Вопрос
48. При каком минимальном значении n формула трапеций обеспечивает
вычисление интеграла 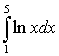 с точностью до 0,001?
с точностью до 0,001?
Варианты
ответов: 1.74; 2.65; 3. 86; 4.48
Вопрос
49. Вычислить несобственный интеграл 1-го рода 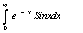
Варианты
ответов
1. 1
2. 2
. 0,25
. 0,5
Вопрос
50. Вычислить несобственный интеграл 2-го рода 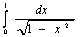
Варианты
ответов
1. p/4
2. p/2
. p; 4.3p/2
КОНТРОЛЬ
Вопросы для
подготовки к экзамену за первый семестр
«Линейная алгебра с элементами аналитической геометрии»
1. Метод координат на плоскости. Основные задачи, решаемые методом
координат.
2. Уравнение прямой с угловым коэффициентом. Общее уравнение
прямой.
3. Уравнение прямой в отрезках. Условия параллельности и
перпендикулярности прямых на плоскости.
. Уравнение прямой, проходящей через данную точку; через две
данные точки.
5. Расстояние от точки до прямой.
6. Окружность. Уравнение окружности.
. Эллипс. Каноническое уравнение эллипса.
8. Гипербола. Каноническое уравнение гиперболы. Асимптоты и
эксцентриситет гиперболы.
9. Парабола. Каноническое уравнение параболы.
10. Линейные операции над векторами и их свойства.
. Линейная зависимость векторов на плоскости.
. Проекция вектора на ось и ее свойства.
13. Декартова прямоугольная система координат в пространстве.
Разложение вектора по ортам координатных осей.
14. Действия над векторами, заданными проекциями. Координаты точки.
Координаты вектора.
15. Скалярное произведение векторов и его свойства.
16. Векторное произведение векторов и его свойства.
. Смешанное произведение векторов и его свойства.
. Действия над матрицами.
. Элементарные преобразования матриц, эквивалентные матрицы.
. Ранг матрицы.
. Матричные уравнения.
. Определители второго и третьего порядка. Свойства
определителей.
23. Понятие минора и алгебраического дополнения. Разложение
определителя по элементам ряда.
24. Выражение векторного и смешанного произведений векторов через
координаты сомножителей.
. Невырожденные матрицы. Обратная матрица. Алгоритм ее
нахождения.
. Система линейных уравнений (СЛУ). Основные понятия. Решение СЛУ
матричным способом.
27. Формулы Крамера.
28. Метод Гаусса решения СЛУ.
. Теорема Кронекера - Капели.
. Понятие n - мерного векторного пространства.
31. Линейные операторы. Собственные векторы и собственные значения
линейного оператора.
32. Квадратичные формы. Приведение канонической формы к каноническому
виду.
. Уравнение плоскости, проходящей через данную точку
перпендикулярно данному вектору.
34. Уравнение плоскости, проходящей через три данные точки.
35. Уравнение плоскости в отрезках.
. Общее уравнение плоскости и его частные случаи.
37. Угол между плоскостями. Условие параллельности и
перпендикулярности плоскостей.
38. Расстояние от точки до плоскости.
39. Векторное и параметрическое уравнение прямой в пространстве.
40. Канонические уравнения прямой.
41. Общее уравнение прямой. Переход к каноническим уравнениям.
42. Угол между прямыми. Условия параллельности и перпендикулярности
прямой в пространстве.
43. Условие, при котором две прямые лежат в одной плоскости.
44. Угол между прямой и плоскостью. Условия параллельности и
перпендикулярности прямой и плоскости.
45. Пересечение прямой с плоскостью.
46. Условие принадлежности прямой плоскости.
. Цилиндрические поверхности.
. Поверхности вращения. Конические поверхности.
Вопросы для подготовки к экзамену за второй семестр.
«Основы математического анализа»
1. Понятие множества. Множества конечные и бесконечные. Действия с
множествами.
2. Выпуклые множества и их свойства.
. Абсолютная величина действительного числа. Свойства абсолютных
величин.
. Числовая ось. Числовые промежутки. Окрестность точки.
5. Определение функции. Область существования функции. Способы
задания функции. Классификация функций.
6. Числовая последовательность. Ограниченные, неограниченные,
монотонные последовательности. Предел последовательности.
7. Предел функции. Бесконечно малые функции, их свойства.
8. Теорема о единственности предела функции.
. Признак существования предела функции.
. Вывод 1-го замечательного предела.
11. Второй замечательный предел, разные формы второго замечательного
предела.
12. Определение непрерывности функции в точке на языке ²e-d². Определение непрерывности функции в
точке на языке приращений.
13. Точки разрыва функции. Их классификация.
14. Сравнение бесконечно малых функций.
. Производная. Геометрический смысл производной.
. Теорема о связи дифференцируемости и непрерывности функции.
. Правила дифференцирования функции.
. Производная сложной и обратной функций.
. Производные основных элементарных функций.
. Дифференцирование неявных функций.
. Производные высших порядков.
. Уравнение касательной и нормали к кривой
. Понятие дифференциала функции.
. Геометрический смысл дифференциала функции.
. Основные теоремы о дифференциалах.
. Дифференциалы высших порядков.
. Применения дифференциалов к приближенным вычислениям.
28. Теоремы о дифференцируемых функциях (теоремы Роля, Лагранжа и их
геометрический смысл)
29. Правила Лопиталя.
30. Возрастание и убывание функций.
. Максимум и минимум функций.
. Наибольшее и наименьшее значения функции на отрезке.
. Выпуклость и вогнутость кривой; точки перегиба.
. Асимптоты графика функции.
. Правила построения графика функции.
. Формула Тейлора.
37. Понятие неопределенного интеграла. Свойства неопределенных
интегралов.
38. Основные методы интегрирования (неопределенный интеграл).
39. Интегрирование рациональных дробей.
. Определенный интеграл как предел интегральной суммы.
. Геометрический смысл определенного интеграла.
. Формула Ньютона - Лейбница.
. Основные свойства определенных интегралов.
. Методы вычисления определенных интегралов.
45. Приложение определенного интеграла. Вычисление площадей плоских
фигур.
46. Приближенное вычисление определенного интеграла.
47. Несобственные интегралы 1-го рода.
. Несобственные интегралы 2-го рода.
. Числовые ряды. Основные понятия.
. Определение и свойства степенного ряда.
. Дифференциальные уравнения 1-го порядка.
. Дифференциальные уравнения с разделяющимися переменными.
. Однородные дифференциальные уравнения 1-го порядка.
. Линейные дифференциальные уравнения 1-го порядка.
55. Линейные дифференциальные уравнения 2-го порядка с постоянными
коэффициентами.
56. Дифференцируемость и полный дифференциал функции нескольких
переменных.
57. Частные производные.
58. Экстремум функции нескольких переменных.
59. Определение комплексных чисел, их геометрическое изображение и
формы записи.
ЛИТЕРАТУРА
Основная:
1. Высшая математика для экономистов.
Под. редакцией проф. Н.Ш. Кремера. - М.: ЮНИТИ, 2002.
2. Высшая математика для экономистов.
Практикум. 2-е издание. Под. редакцией проф. Н.Ш. Кремера. - М.: ЮНИТИ, 2007
3. Курс высшей математики. В.С.
Шипачев.- М.: Изд - во Оникс, 2007.
4. Конспект лекций по высшей математике.
Части 1. Письменный Д.Т. -
М.: Айрис пресс, 2002.
5. Конспект лекций по высшей математике.
Части 2. Письменный Д.Т. -
М.: Айрис пресс, 2002.
6. Практикум по высшей математике.
Каплан И.А., Пустынников В.И. - М:2006.
7. Математика. Для экономических
специальностей ВУЗов, часть I. Под редакцией Р.Ш. Марданова. Казань: Изд-во
КЭФИ, 2000.
8. Сборник задач по высшей математике.
В.С. Щипачев. - М.: "Высшая школа", 2006.
9. Высшая математика. - Баврин И.И. - М.: 2007.
10. Сборник задач по высшей математике (с
контрольными работами). Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. - М.: Айрис пресс, 2003.
11. Математический анализ. Шипачев В.С. - М.: Высшая школа, 2002.
12. Высшая математика. Гусак А.А. - Минск: 2007.
13. Аналитическая геометрия и линейная
алгебра (справочное пособие к решению задач). Гусак А.А. - Минск: 2001.
14. Математический анализ и
дифференциальные уравнения (справочное пособие к решению задач). Гусак А.А. - Минск: 2003.
15. Математика. Для экономических
специальностей Вузов. Часть 2. Под. ред. Р.Ш. Марданова. Издательство КФЭИ.
2001.
16. Высшая математика. Виленкин И.В.,
Гробер В.М. -
Ростов-на-Дону: Изд - во «Феникс», 2002.
17. Практикум по высшей математике.
Соболь Б.В., Мишняков Н.Т., Поркшеян В.М. - Ростов-на-Дону: Изд - во «Феникс», 2004.
18. Высшая математика в упражнениях и
задачах. Часть 1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. - М.: Оникс. 2002.
19. Высшая математика в упражнениях и
задачах. Часть 2..Данко П.Е., Попов А.Г., Кожевникова Т.Я. - М.: Оникс. 2002.
Дополнительная:
1
Математика для
экономических специальностей. Красс М.С. - М.: Дело,
2003.
2
Высшая
математика. Ильин В.А., Куркина А.В. - М.: Проспект, 2002.
3
Математика.
Высшее образование. Барашков А.С. - М.: Филол. о-во СЛОВО, Изд - во Эксмо, 2005.
4
Краткий курс
высшей математики. Демидович Б.П., Кудрявцев В.А. - М.: Изд - во Астрель, 2001.
5
Линейная алгебра
и аналитическая геометрия. Ильин В.А., Ким Т.Д. - М.: Изд -во МГУ, 2008.
6
Колесников А.Н.
Краткий курс математики для экономистов. - М.: ИНФРА-М, 1997.
7
Высшая математика
для экономистов (курс лекций). Луканкин Г.Л., Луканкин А.Г. - М.: Экзамен, 2006.
8
Руководство к
решению задач с экономическим содержанием по курсу высшей математики. Под ред.
А.И. Карасева, Н.Ш. Кремера. - М.: Экономическое образование,1989.
9
Сборник задач и
упражнений по высшей математике. Булдык Г.М. - Минск: ООО Юнипресс, 2002.
Учебное издание
МАТЕМАТИКА
часть I
ЛИНЕЙНАЯ АЛГЕБРА С ЭЛЕМЕНТАМИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ И ОСНОВЫ
МАТЕМАТИЧЕСКОГО АНАЛИЗА
Составитель:
доцент
Курзин Сергей Павлович
Корректор Шамонова А.М.
Технический редактор
Компьютерная верстка
Подписано в печать. Формат.
Бумага офсетная. Гарнитура New Roman. Печать .
Усл. печ. л. . Уч.-изд. л. . Тираж 100 экз. Заказ № .
Издательство «».
, Казань, ул. ого, .
Отпечатано в типографии «».
, г. , ул. , .
ISBN
© Составление. Курзин С.П. 2008
© Институт социальных и гуманитарных знаний, 2008