Реализация реактивных функций

Реализация реактивных функций

МО РБ

УО "Полоцкий государственный университет"

Кафедра радиоэлектроники

Расчётно-графическая работа

Реализация реактивных функций

Разработал: Антонов Е.А.

гр. 12-РТ

Проверила: Алиева С. П.

Новополоцк 2013 г.

Двухполюсником можно назвать любую электрическую цепь, взаимодействующую с внешней по отношению к ней схемой посредством двух зажимов. При этом свойства двухполюсников определяют характеристики всей цепи. Двухполюсник, как и любая линейная электрическая цепь, может быть как активным, так и пассивным. Пассивным он является в том случае, если энергия, отданная им во внешнюю цепь, ни при каких условиях не превышает той, что была подведена к нему за все предшествующее время. По количеству элементов, составляющих схему двухполюсника, они подразделяются на одноэлементные, двухэлементные (RL-, RC- и LC-двухполюсники), трехэлементные (RLC-двухполюсники) и т. д. Двухполюсники, схемы которых включают резистивные сопротивления, называются диссипативными. В них происходит потеря подводимой энергии за счет превращения ее в тепловую с дальнейшим рассеянием этой энергии в пространстве. Двухполюсники, схемы которых состоят только лишь из реактивных элементов (индуктивностей и емкостей), носят название реактивных двухполюсников. Любой двухполюсник может быть охарактеризован своей входной функцией K(jω), которая представляет собой либо входное сопротивление Z(jω), либо входную проводимость Y(jω).

Задача синтеза электрических цепей заключается в определении их схем и значений элементов, составляющих эти схемы, по известным характеристикам. Если эти характеристики являются функциями времени, то синтез осуществляется во временной области. Если же известная характеристика цепи представляет собой функцию частоты, синтез проводится в частотной области.

Независимо от степени сложности схемы двухполюсников можно указать ряд закономерностей, характеризующих их общие свойства:

) число резонансных частот любого реактивного двухполюсника на единицу меньше общего числа реактивных элементов в его схеме;

) частоты резонансов напряжений и токов реактивного двухполюсника чередуются: между любыми двумя резонансами напряжений имеется один резонанс токов, и между любыми двумя резонансами токов находится резонанс напряжений;

) при резонансе напряжений характер реактивности двухполюсника меняется с емкостного на индуктивный, а при резонансе токов - с индуктивного на емкостной. У многоэлементных реактивных двухполюсников характер реактивности контура изменяется с ростом частоты не один раз;

) при возрастании частоты реактивное сопротивление двухполюсника в точках непрерывности возрастает (с учетом знака реактивного сопротивления);

) если в схеме двухполюсника есть путь для прохождения постоянного тока, то первым наступает резонанс токов, а если такого пути нет, первым наступает резонанс напряжений;

) зависимость сопротивления любого реактивного двухполюсника от частоты можно представить формулой Фостера:

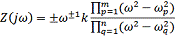
где m - число резонансов напряжений; n - число резонансов токов.

Степень множителя ω выбирается по условию: если первым наступает резонанс напряжений, то данный множитель должен стоять в знаменателе, т. е. показатель степени есть - 1.

В числителе формулы Фостера стоит произведение разностей квадратов текущей частоты и частот резонансов напряжений. Следовательно, число сомножителей в числителе дроби определяется количеством резонансов напряжений m в схеме двухполюсника. В знаменателе данной дроби стоит произведение разностей квадратов текущей частоты и частот резонансов токов. Значит, число сомножителей в этой части формулы определяется количеством резонансов токов n.

Если оно имеет емкостный характер, в схеме двухполюсника следует разомкнуть все ветви, содержащие индуктивности, и определить эквивалентную емкость C_экв полученной схемы, а затем приравнять k=1/C_экв. Если же сопротивление носит индуктивный характер, все емкости в схеме двухполюсника закорачиваются, и подсчитывается эквивалентная индуктивность L_экв образованной схемы. В этом случае k=L_экв.

Знак "+" или "-" перед формулой зависит от характера реактивности сопротивления двухполюсника в диапазоне частот от нуля до первого резонанса и от общего количества сомножителей в числителе и знаменателе дроби. Этот знак нетрудно установить, подставив произвольно выбранное значение текущей частоты из данного диапазона в формулу и определив тем самым знак дроби. При этом, если сопротивление имеет емкостный характер реактивности, а дробь отрицательна, то выбирается знак "+". В противном случае - знак "-". В случае индуктивного характера сопротивления отрицательное значение дроби предполагает знак "-", а положительное значение - знак "+".

Эквивалентные двухполюсники - эквивалентными называются двухполюсники, имеющие различную структуру (схему), но одинаковую характеристику Z(jω) на всем диапазоне частот.

Условие:

Осуществить реализацию реактивных функций разложением на элементарные дроби:

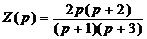
Решение: Для реализации входной функции т.е для того чтобы она была физически реализуема (состояла из элементов R,L,C с положительными действительными параметрами) необходимо и достаточно одновременное выполнение пяти условий:

1.       все коэффициенты полиномов должны быть положительными действительными числами;

2.      все полюсы должны лежать в левой полуплоскости и могут быть вещественными и комплексно-сопряженными;

3.      в бесконечно удалённой точке функция ведёт себя как Hp, H, ;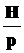

.        полюсы на мнимой оси могут быть только простыми(не кратными) с действительными положительными вычетами;

.        действительная часть функции на мнимой оси неотрицательна.

Проверим можно ли реализовать Y(p)

двухполюсник функция фостер дробь

1)     

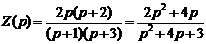
все коэффициенты полинома положительные действительные числа, первое условие выполняется;

2)      Найдем полюсы Z(p). Для этого приравняем знаменатель Z(p) к нулю:

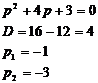
Все полюсы лежат в левой полуплоскости и являются вещественными и комплексно-сопряженными, второе условие выполняется;

Найдём

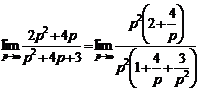
При , , то 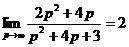, то есть на бесконечности функция Z(p) ведёт себя как H. Третье условие выполняется;

3)      Найдём вычеты функции Z(p), при p₁=-1 и p₂=-3

Т.к. схема с эл. RL, в вычетах функцию Z(p) умножим на :

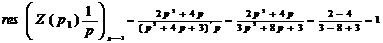
полюсы на мнимой оси простые (не кратные) с действительными положительными вычетами;

)        Считая,  найдём :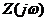

,

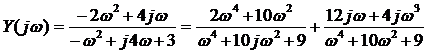Действительная часть всегда положительна, значит пятое условие выполняется. Схема с элементами RL т.к. высшая степень полинома числителя равна высшей степени полинома знаменателя . Нули и полюсы функции лежат на отрицательной вещественной полу оси, и первым к началу координат располагается ноль.

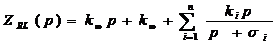
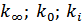
где  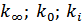- вычеты функции.

Схема реализации будет выглядеть следующим образом:

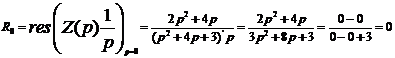
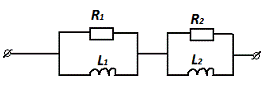
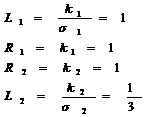
Вывод: в ходе работы были проверены условия физической реализации функции Z(p). Было выяснено, что двухполюсник состоит из L и R элементов. И была осуществлена реализация функции разложение на простейшие дроби.