Графический метод решения задач оптимального планирования
Лабораторная работа № 1
Тема: «Графический метод решения задач
оптимального планирования»
Часть 1.
Цель: реализовать на ЭВМ алгоритм решения
системы линейных уравнений размерностью M´N,
представленных в матричном виде. Рассмотреть случаи : M
< N, M=N,
M>N
с точки зрения существования и единственности решения.
Теоретические сведения.
Методы и модели для решения задач, в которых
необходимая информация однозначна и достоверна, называют детерминированными. В
данной работе рассматриваются детерминированные методы и модели математического
программирования - науки о методах отыскания и исследования экстремальных (max
и min) значений функций
цели, на неизвестные величины которой наложены ограничения.
Переменные величины, действуя на которые можно
достигнуть поставленной цели, называют планом, или вектором управления X=(x1,
x2, …, xn).
Для достижения цели имеются некоторые материальные, финансовые, трудовые и
другие ресурсы, технологии и способы производства. Обозначим вектор этих
ресурсов через A=(b1,
b2, …, bm).
Цель операции формализуется в виде критерия оптимальности и системы
ограничений.
Обозначим критерий оптимальности (целевую
функцию) через
= z(X).
Систему ограничений можно представить в виде : f
I (X)
R bi
, где I = 1, …, M,
а R- отношение порядка
(«=», «³»
, « £»).
На неизвестные величины могут быть наложены условия неотрицательности xj
³0,
j=1,.., N.
Объединение всех ограничений, накладываемых на
неизвестные величины, называют областью допустимых решений W,
т.е. XÎW.
Таким образом, общая детерминированная модель
математического программирования примет вид:
max (min) : Z = z(X), XÎW.
Допустимый план XÎW,
доставляющий критерию оптимальности Z
= z(X)
экстремальное значение, называется оптимальным и обозначается через X*,
экстремальное значение целевой функции - через Z*
= z(X*).
Задача оптимального использования ресурсов
Имеется M
видов ресурсов, заданных вектором A0=(b1,
b2, …, bm).
Задана матрица A=|| aij
|| , где aij - норма
расхода I-го ресурса на
единицу j-той продукции (I=1,…,m;
j=1,…,n).
Эффективность выпуска единицы j-той
продукции характеризуется, например, прибылью pj.
Требуется определить план выпуска продукции X=(x1,
x2, …, xn),
обеспечивающий максимальную прибыль предприятия при заданных ресурсах, т.е.

при ограничениях
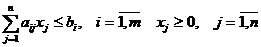
Модель задачи оптимального
использования ресурсов лежит в основе моделей оптимизации годовой
производственной программы предприятия.
Пример. Предприятие может
изготовлять 4 вида продукции П-1, П-2, П-3, П-4. Сбыт любого ее объема
обеспечен. Предприятие располагает в течение квартала трудовыми ресурсами в 100
человеко - смен, полуфабрикатами массой 260 кг, станочным оборудованием в 370
станко - смен. Нормы расхода ресурсов и прибыль от единицы каждого вида продукции
представлены в таблице:
|
Ресурсы
|
Продукция
|
Объем
ресурсов
|
|
П-1
|
П-2
|
П-3
|
П-4
|
|
|
Трудовые
ресурсы, чел - смен
|
2,5
|
2,5
|
2
|
1,5
|
100
|
|
Полуфабрикаты,
Кг
|
4
|
10
|
4
|
6
|
260
|
|
Станочное
оборудование, станко - смен
|
8
|
7
|
4
|
10
|
370
|
|
Прибыль
от ед-цы продукции
|
40
|
50
|
100
|
80
|
max Z
|
|
План
выпуска
|
X1
|
X2
|
X3
|
X4
|
|
Математическая модель задачи имеет вид:
Целевая функция - максимум прибыли:
max : Z
= 40 x1 + 50 x2
+ 100 x3 + 80 x4
при ограничениях:
на трудовые ресурсы:
,5 x1 + 2,5 x2
+ 2 x3 + 1,5 x4
£100
на полуфабрикаты:
x1 + 10 x2
+ 4 x3 + 6 x4
£ 260
на станочное оборудование:
x1 + 7 x2
+ 4 x3 + 10 x4
£370
условие неотрицательности:
xi ³
0, j=1, …,4.
Решение систем линейных уравнений.
В случае, если все ресурсы исчерпываются
полностью, получим систему линейных уравнений в общем случае размерностью M´N.
Система линейных уравнений легко решается стандартными математическими
методами. Здесь каждое уравнение соответствует гиперплоскости (прямой в случае
двух переменных) в пространстве.
Если система линейных уравнений независимая
(т.е. никакое уравнение нельзя выразить линейно через другие), то решением
системы будет :
а) точка пересечения плоскостей пространства
(или точка пересечения прямых в случае двух переменных) X=(x1,
x2, …, xn)
- единственное решение (случай M=N);
б) прямая пресечения плоскостей - множество
решений ( случай M>N);
в) нет решений (случай M<N).
В данном случае будем рассматривать только
линейно - независимые системы линейных уравнений (остальные случаи лучше
реализовать специальными методами линейного программирования, которые будут
рассмотрены позже).
Итак, для решения задачи оптимального управления
оптимален случай а), когда возможно единственное решение - X=(x1,
x2, …, xn).
Используя введенные ранее обозначения и принимая по определению M=N,
система ограничений примет вид:
a11 x1 + a12 x2 + … + a1n xn = b1x1
+ a22 x2 + … + a2n xn = b2
. . . . . .x1 + an2 x2 + … + ann xn
= bn
Существует множество стандартных способов
решения системы линейных уравнений. Рассмотрим один из наиболее удобных
способов, основанный на матричном методе решения. Анализируя внешний вид
матрицы и системы, можно сделать вывод - чтобы получить решение X=(x1,
x2, …, xn)
достаточно, например, получить коэффициенты, равные 1 перед диагональными
неизвестными, и 0 - перед остальными неизвестными. Тогда результаты последнего
столбца и будут решением системы. По правилам работы с матрицами, разрешается
выполнять со строками следующие действия:
а) умножение (деление) коэффициентов строки на
одно и тоже число;
б) сложение (вычитание) коэффициентов строк;
в) перемена строк местами.
Т.о. задача решения системы линейных уравнений
сводится к получению с помощью равносильных преобразований а) - б) - в) к
матрице вида:
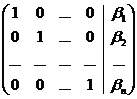
Переходя от данной матрицы к системе
линейных уравнений получим:
×x1 + 0× x2 + … + 0× xn = b1 или x1=b1
× x1 + 1× x2 + … +0× xn = b2 x2=b2
. . . . . . …
0× x1 + 0× x2 + … + 1× xn = bn
xn=bn
Так как по условию задачи план
является вектором управления X=(x1, x2, …, xn), то
решением задачи можно считать последний столбец расширенной конечной матрицы
(такую матрицу называют единичной).
Пример. Привести матрицу к виду
единичной матрицы с помощью равносильных преобразований:
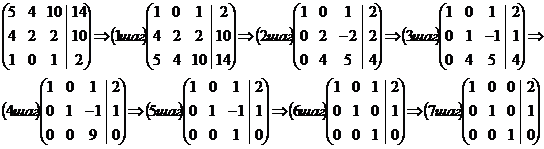
шаг. Чтобы получить 1 на главной
диагонали 1-й строки, поменяем местами 1-ю и 3-ю строки
шаг. Получим 0 под диагональным
коэффициентом 1-й строки во 2-й и 3-й строках. Для этого умножим 1-ю строку на
4 и вычтем из 2-й строки, а затем умножим 1-ю строку на 5 и вычтем из 3-й
строки.
шаг. Чтобы получить 1 на главной
диагонали 2-й строки, разделим коэффициенты 2-й строки на 2.
шаг. Получим 0 под диагональным
коэффициентом 2-й строки в 3-й строке. Для этого умножим коэффициенты 2-й
строки на 4 и вычтем из 3-й строки.
шаг. Чтобы получить 1 на главной
диагонали 3-й строки, разделим коэффициенты 3-й строки на 9.
шаг. Чтобы получить 0 во 2-й строке
над диагональным коэффициентом 3-й строки, сложим коэффициенты 3-й и 2-й
строки.
шаг. Чтобы получить 0 в 1-й строке
над диагональным коэффициентом 2-й строки, вычтем из 1-й строки коэффициенты
3-й строки.
Результатом задачи является
последний столбец матрицы. Действительно, если произвести проверку, решение (2,
1, 0) является верным для каждой строки матрицы.
Замечание. Необходимо отметить, что
приведенные действия для решения матрицы не являются единственными. Например,
чтобы получить 1 на главной диагонали 1-й строки, можно было просто разделить
все коэффициенты 1-й строки на 5. Решение задачи от выбора действий не
изменится.
Т.о. приведение матрицы к
диагональному виду можно свести к двум общим правилам:
получить 1 на главной диагонали
матрицы и 0 под главной диагональю, начиная с первой строки;
получить 0 во всех строках над
главной диагональю, начиная преобразования с последней строки.
Задание
Реализовать на ЭВМ алгоритм решения
системы линейных уравнений, применяя матричный способ (см. пример).
Замечания. 1) Рекомендуется
производить вывод всех промежуточных матриц на экран.
Учесть случай, когда после
преобразования на главной диагонали получается 0.
После окончания преобразования
произвести проверку результата и вывести на экран.
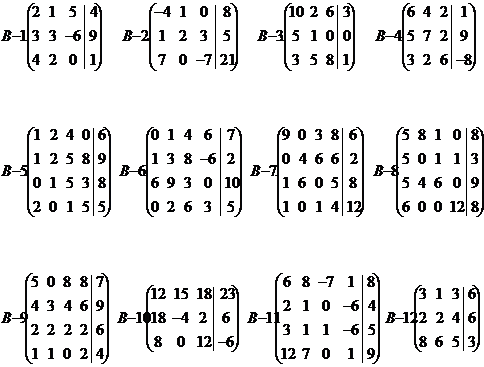
литература
1. Банди
Б. Основы линейного программирования. Москва, «Радио и связь», 1989
2. Балашевич
В.А. Основы математического программирования.
3. Ларионов
А.И., Юрченко Т.И., Новоселов А.Л. Экономико-математические методы в
планировании. Москва, «Высшая школа» , 1991
4. Вентцель
Е.С. Исследование операций.
лабораторная работа № 2
Тема: «Графический метод решения задач
оптимального планирования с двумя переменными»
Часть 2.
Цель: Провести анализ графических построений
решения задачи оптимального планирования и реализовать на ЭВМ алгоритм решения
задачи в случае двух переменных, используя графический метод решения.
Теоретические сведения.
Напомним, что задача линейного программирования
сводится к нахождению некоторой совокупности переменных xj, j=1, 2, …, n,
доставляющих линейной функции цели экстремальное значение и удовлетворяющих
системе ограничений в форме равенств или неравенств, т.е. необходимо найти план
=(x1, x2, …, xn),
который придает экстремальное значение линейной
функции
(min) : Z = z(X), ( 1 )
при системе ограничений:
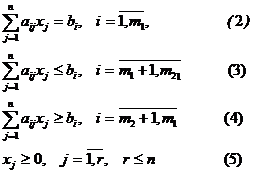
Линейная функция (1) называется
целевой, множество планов X, удовлетворяющих системе ограничений (2) - (5) -
множеством допустимых решений и обозначается W, XÎW.
Допустимый план X, доставляющий
целевой функции (1) экстремальное значение, называют оптимальным X*.
Задача (1) - (5) включает общую
постановку задачи линейного программирования.
Основная теорема линейного
программирования.
Следующая теорема позволяет выбрать
единственное решение задачи при наличии множества допустимых решений:
Теорема. Если целевая функция задачи
линейного программирования достигает экстремального значения в некоторой точке
области допустимых решений W,
то она принимает это значение в угловой (крайней) точке.
Базисные и опорные планы.
Допустимые планы задачи линейного
программирования считаются базисными, если в многограннике решений им
соответствуют соответствующие угловые (крайние) точки.
Базисные планы с неотрицательными
компонентами - опорные.
Геометрическая интерпретация задачи
линейного программирования.
В случае двух переменных область
допустимых решений превращается в многоугольную выпуклую область или (при
ограниченности) в выпуклый многоугольник на плоскости.
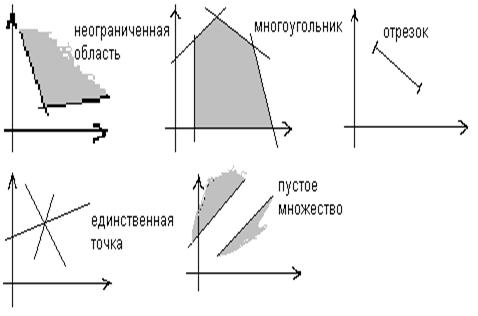
Пример.
Пусть 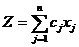 . Зафиксируем Z. Тогда целевая
функция будет представлять гиперплоскость, во всех точках которой значение Z не
меняется. При изменении Z получим семейство гиперплоскостей уровня цели. Так
как при изменении Z коэффициенты cj не меняются, то семейство гиперплоскостей
уровня цели есть множество параллельных гиперплоскостей. При этом вектор C=(c1,
c2, …, cn) называют вектором максимального возрастания целевой функции или
градиентным направлением. При перемещении некоторой фиксированной
гиперплоскости уровня цели в градиентном направлении C=(c1, c2, …, cn) значение
Z возрастает скорейшим образом.
. Зафиксируем Z. Тогда целевая
функция будет представлять гиперплоскость, во всех точках которой значение Z не
меняется. При изменении Z получим семейство гиперплоскостей уровня цели. Так
как при изменении Z коэффициенты cj не меняются, то семейство гиперплоскостей
уровня цели есть множество параллельных гиперплоскостей. При этом вектор C=(c1,
c2, …, cn) называют вектором максимального возрастания целевой функции или
градиентным направлением. При перемещении некоторой фиксированной
гиперплоскости уровня цели в градиентном направлении C=(c1, c2, …, cn) значение
Z возрастает скорейшим образом.
В случае двух переменных при
изменении Z получаем семейство параллельных прямых - линии уровня цели: c1+c2 .
Геометрическое решение задачи в
случае двух переменных.
Если задача линейного
программирования имеет две переменные, т.е.
(min) :
Z=c1x1+c2x2;x1+ai2x2 R bi, i=1, …, m; x1 ³ 0, x2 ³ 0,
то ее графически можно решить в
следующей последовательности:
Построить множество допустимых решений
W, с учетом
системы ограничений.
Построить вектор градиентного
направления C=(c1, c2, …, cn).
Построить произвольную линию уровня
цели Z=const (например, Z=0), перпендикулярно к вектору C=(c1, c2, …, cn).
При решении на max переместить
прямую Z=const в направлении вектора C=(c1, c2, …, cn) так, чтобы она заняла
крайнее положение.
В случае на min линию уровня цели
Z=const переместить в антиградиентном направлении.
Определить оптимальный план.
Возможны следующие случаи:
а) оптимальный план единственный. Тогда
линия уровня цели Z и область W
в крайнем положении будут иметь одну общую точку.
б) оптимальных планов может быть
бесконечное множество. В этом случае в крайнем положении линия уровня цели
проходят через грань области.
в) Целевая функция не ограничена.
Линия уровня цели не занимает крайнее положение с областью допустимых решений.
г) Задача решения не имеет. Область
допустимых решений - пустое множество, т.е. система не совместна.

Пример. Предприятие изготавливает
два вида продукции, используя два вида ресурса. Прибыль от реализации и затраты
представлены в таблице. Определить план выпуска, при котором прибыль
максимальна.
|
Ресурсы
|
Затраты
на ед.
|
Объем
ресурсов
|
|
П-1
|
П-2
|
|
|
1-й
2-й
|
3
1
|
1
4
|
15
16
|
|
Прибыль
|
2
|
1
|
max
Z
|
|
План
|
x1
|
x2
|
|
Модель задачи имеет вид:
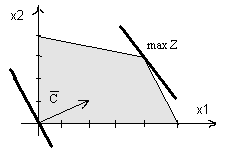
: Z=2x1+x2
при ограничениях:
x1+x2 £ 15+4x2 £ 16³ 0; x2 ³ 0.
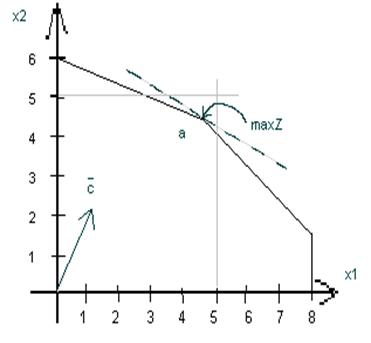
Исходя из графического решения
задачи, оптимальный план соответствует угловой точке многоугольника с
координатами X=(4; 3). Значение целевой функции в данной точке составляет Z=11.
Проверка: по теореме линейного программирования наилучшие решения задачи
представляют собой угловые точки многоугольника решений. Таким образом,
достаточно проверить значение целевой функции в каждой угловой точке и выбрать
максимальное:=(0; 0) Z=0=(5: 0) Z=10=(4; 3) Z=11=(0; 4) Z=4.
Итак, оптимальное решение X*= (4; 3)
и Z (X*) = 11.
Замечание. Каждое неравенство
ai1x1+ai2x2 £ bi, в
ограничениях представляет с точки зрения геометрии полуплоскость, ограниченную
прямой, заданной уравнением ai1x1+ai2x2 = bi. Пересечение прямых есть точка,
координаты которой делают уравнения этих прямых верными равенствами. Отсюда
следует, что любую угловую точку многоугольника можно вычислить как точку
пересечения соответствующих двух прямых, взятых из ограничений со знаком «=». В
свою очередь, точка пересечения двух прямых - это решение системы двух линейных
уравнений с двумя переменными (программу решения системы линейных уравнений
рекомендуется взять из лабораторной работы № 1 - случай матрицы 2´2). Таким
образом, вычислив все точки пересечения как решение систем линейных уравнений
каждой пары прямых, получим все угловые точки. Затем, вычислив в каждой точке
значение целевой функции, достаточно выбрать ту, в которой значение максимально
(или минимально по условию).
Задание
Реализовать на ЭВМ алгоритм решения
задачи определения оптимального плана выпуска 2-х видов продукции X=(x1, x2) .
Объемы ресурсов предприятия представлены вектором A=(b1, b2, …,bm), прибыль
(затраты) на единицу продукции представлены вектором C=(c1, c2), а нормы затрат
ресурсов на единицу продукции представлены матрицей || aij || , i=1,...,m ; j=1,2.
Определить оптимальный план выпуска 2-х видов продукции, используя графический
метод решения задачи с 2-мя переменными.
Замечание. Критерий оптимальности
задачи должен быть задан с клавиатуры, т.е. задача должна определять максимум
или минимум целевой функции по выбору пользователя.
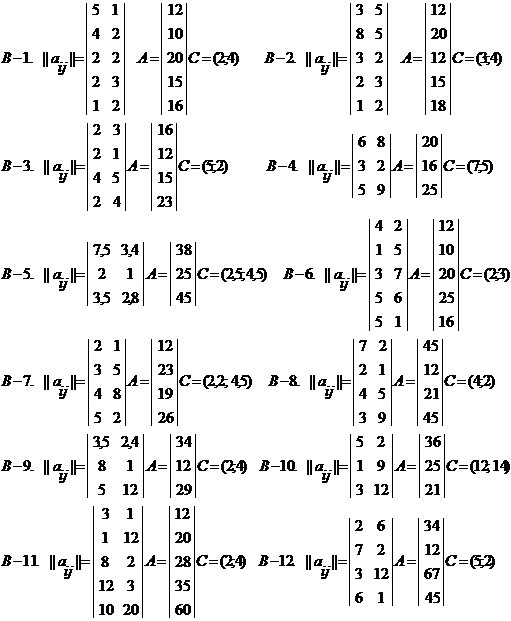
литература
1. Банди
Б. Основы линейного программирования. Москва, «Радио и связь», 1989
2. Балашевич
В.А. Основы математического программирования.
3. Ларионов
А.И., Юрченко Т.И., Новоселов А.Л. Экономико-математические методы в
планировании. Москва, «Высшая школа» , 1991
4. Вентцель
Е.С. Исследование операций.
лабораторная работа № 3
Тема: «Симплекс-метод. Построение
симплекс-таблицы»
Цель: научиться задавать систему ограничений в
предпочтительном виде и строить начальную симплекс-таблицу; реализовать на ЭВМ
симплекс-метод построения оптимального плана управления с помощью улучшения
симплекс-таблицы; провести анализ и определить случаи невозможности улучшения
плана.
Теоретические сведения.
Построение начального опорного плана.
Рассмотрим задачу линейного программирования с
системой ограничений, представленных в каноническом виде:
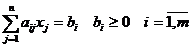
Ограничение имеет предпочтительный
вид, если при неотрицательности правой части левая содержит переменную,
входящую с коэффициентом 1, а остальные ограничения - равенства с коэффициентом
0.
Пример. В системе ограничений
x1 + 2x2 - 4x4 = 5 - предпочтительный вид
x2 + x3 + 2x4 = 8 - предпочтительный вид- 3x4 =
3 - нет
Если каждое ограничение системы ограничений -
равенств имеет предпочтительный вид, то и система представлена в предпочтительном
виде. В этом случае легко найти ее опорное (базисное) решение. Все переменные,
кроме предпочтительных, нужно приравнять к нулю. Тогда предпочтительные
переменные примут значения, равные правым частям. Полученный план будет опорным
(базисным).
При приведении системы ограничений к
предпочтительному виду рассмотрим два случая:
случай. Пусть
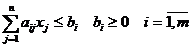
Добавим к левым частям
дополнительные переменные xn+i ³0, i = 1, ..., m и получим
расширенную задачу. В расширенной задаче система ограничений имеет
предпочтительный вид:
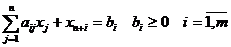
Следовательно, начальный опорный
план преобразуется в вектор X0 = (0, ..., 0, b1, b2, ..., bm). В целевую
функцию дополнительные переменные вводятся с коэффициентом 0.
случай. Пусть
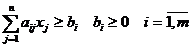
Вычтем из левых частей
дополнительные переменные xn+i ³0, i = 1, ..., m и получим
расширенную задачу, эквивалентную исходной. Однако теперь система ограничений
не имеет предпочтительного вида, так как дополнительные переменные входят в
левую часть с коэффициентами -1. Поэтому план X0 = (0, ...,
0, b1, b2, ..., bm)
недопустим. В этом случае вводят так называемый искусственный базис:
к левым частям системы ограничений -
равенств, не имеющих предпочтительного вида, добавляют искусственные переменные
wi. В целевую
функцию wi вводят с
коэффициентом (+М) в случае решения задачи на минимум и (-М) - на максимум, где
М - большое положительное число.
Полученная задача называется М -
задачей, соответствующей исходной:
(min) : Z=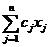
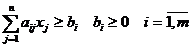
Если ни одно из ограничений не имеет
предпочтительный вид, то М - задача запишется:
(min) : Z=

Начальный опорный план X0 = (0, ...,
0, b1, b2, ..., bm).
Между оптимальным планом исходной
задачи и оптимальным планом М-задачи существует следующая связь:
если в оптимальном плане М-задачи
X*=(x1*, x2*, ... , xn*, w1*, ..., wm*) все искусственные
переменные равны 0, то план X*=(x1*, x2*, ... , xn*) оптимален для исходной
задачи.
Признак оптимальности начального
опорного плана. Симплекс - таблицы.
Так как исходную задачу линейного
программирования всегда можно представить в эквивалентом предпочтительном виде,
то рассмотрим эту задачу в виде:
(min) : Z=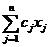
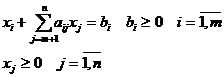
Решая ограничения - равенства
относительно базисных переменных xi, и подставив их значения в
целевую функцию, получим следующие равенства:
D0
= c1b1+c2b2+...+cmbm=CбA0, где Cб - вектор
коэффициентов целевой функции, стоящих у базисных переменных; А0 - вектор
свободных элементов у системы ограничений, представленных в предпочтительном
виде.
После подстановки в целевую функцию
значений базисных переменных, выраженных через свободные переменные, получим:
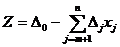 , где
, где
D0
= CбA0,
Dj
= CбAj - cj
Из данных выражений можно выяснить
признак оптимальности опорного плана: при начальном опорном плане X0 = (b1, b2,
...,bm, 0, ... , 0) значение целевой функции Z (X0)= D0. Так как xj ³0, при Dj£0 целевая
функция достигает минимума в точке X0. Если же Dj³0, то в
точке X0 целевая
функция достигает максимума.
Значения Dj называют оценками свободных
переменных.
Для решения задачи обычно данные
заносят в таблицу, называемую симплекс-таблицей.
Перед занесением систему ограничений
приводят к предпочтительному виду.
Пример. Модель задачи имеет вид:
: Z=2x1-x2+3x3-2x4+x5 при
ограничениях:
x2 + 0,5x3 + 0,5x5 = 1,5+ x4 = 2-0,5x3 + 0,5x5 =
0,5
Система ограничений данной задачи имеет
предпочтительный вид. Заносим ее условие в симплекс-таблицу, где n+3
столбцов (n - число переменных
в предпочтительном виде), m+2
строк, где m - число
ограничений - равенств.
|
Б.п.
|
Сб
|
А0
|
x1
|
x2
|
x3
|
x4
|
x5
|
|
|
|
2
|
-1
|
3
|
-2
|
1
|
|
x2 x4
x1
|
-1
-2 2
|
1,5
2 0,5
|
0
0 1
|
1
0 0
|
0,5
1 -0,5
|
0
1 0
|
0,5
0 0,5
|
|
Функция
цели
|
-4,5
|
0
|
0
|
-6,5
|
0
|
-0,5
|
Столбец Сб содержит коэффициенты целевой
функции, стоящие у базисных переменных. Столбец А0 свободных элементов системы
ограничений в предпочтительном виде. На пересечении столбцов и строк
расположена матрица коэффициентов системы ограничений || aij
||. Z - строкой или
индексной строкой называют последнюю строку таблицы, в которой расположены
коэффициенты:
D0 = CбA0,
Dj = CбAj - cj
Начальный опорный план задачи X0 = (0,5; 1,5; 0;
2; 0) - столбец А0, начальное значение функции цели Z
(X0) =-4,5.
Так как все оценки индексной строки Dj
неположительны, то план X0 = (0,5; 1,5; 0; 2; 0) - оптимален.
Переход к нехудшему опорному плану. Симплексные
преобразования.
Рассмотрим задачу:
max (min) : Z=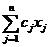
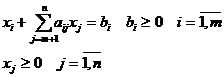
Пусть она решается на минимум.
Начальный опорный план X0 = ( b1, b2, ..., bm, 0, ...., 0), Z (X0)= D0= CбA0. Если для
всех оценок свободных переменных Dj£0, то X0 -
оптимальный.
Теперь пусть существуют
положительные оценки свободных переменных, т.е. Z не
минимальна.
1) Выберем
наибольшую из положительных свободных переменных:
j = j0>0
Столбец j0
называют разрешающим.
2) Соответствующую
переменную xj0 введем в
базис. Для этого нужно вывести из базиса одну из переменных.
3) Так
как Dj0
>0, то уменьшить функцию цели Z
можно, увеличивая xj0.
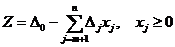
Значение xj0 можно увеличивать так,
чтобы ни одно из значений базисных переменных xj не было отрицательным: xj0 ³ 0.
1) Так
как для нахождения начального опорного плана все свободные переменные xj =0, то
получим:
= bi
- aij0 xj0
Z = D0
случай. Пусть все aij0 разрешающего столбца неположительны,
т.е. aij0£0, i=1,m. Тогда из вышеуказанной
формулы следует, что xi³0 при любом xj0³0,
т.е. целевая функция неограничена снизу.
Вывод.
а) Если при решении задачи на минимум в
индексной строке имеются положительные оценки свободных переменных, а в столбце
переменной xj0 нет ни одного положительного элемента, то Z не ограничена снизу
на множестве допустимых планов задачи.
б) пусть задача решается на максимум. Если среди
оценок свободных переменных имеются отрицательные, а в столбце переменной xj0
нет ни одного положительного элемента, то Z не ограничена сверху на множестве
допустимых планов задачи.
случай. Пусть среди элементов разрешающего
столбца имеются положительные, например, первые k.
Тогда xj0 можно
увеличивать до тех пор, пока не нарушается система неравенств:
= bi - aij0 xj0 ³0,
aij0 >0, i=1,k.
Отсюда следует:
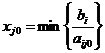
Пусть вышеуказанное равенство
выполняется при некотором i=i0. Обозначим
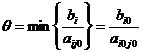
Если равенство выполняется при
нескольких i, то в
качестве i0 можно
выбрать любое. Строку i0, для которой выполняется указанное
равенство, называют разрешающей.
В результате преобразований получен
новый опорный план X1, в котором переменная xi0 заменена
на xj0. Целевая
функция Z
уменьшилась, т.е. приблизилась к необходимому минимуму целевой функции.
Формальные правила для перехода к
следующей симплекс-таблице (симплексные преобразования):
Элементы разрешающей строки определяются
по формулам:
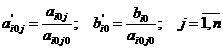
Элементы разрешающего столбца j0 новой
таблицы равны 0 за исключением ai0j0’=1, т.к. xj0 стала
базисной переменной и не входит в правую часть системы ограничений.
Чтобы найти любой другой элемент
новой симплекс-таблицы, используется правило прямоугольника:

По этому правилу могут быть
вычислены все элементы индексной строки, т.е. коэффициенты D’j целевой
функции:
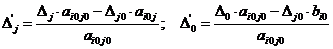
Коэффициенты целевой функции могут
быть рассчитаны по формулам:
D’j=СбАj - cj, D’0=CбA0 , которые
можно применить для контроля вычислений после каждого шага симплексных
преобразований.
Пример. (Задача оптимального
использования ресурсов)
Модель задачи имеет вид:
Расширенная задача:
,5x1+2,5x2+2x3+1,5x4 +x5 = 100
x1+10x2+4x3+6x4 +x6 = 260
x1+7x2+4x3+10x4 +x7= 370
Max : Z
= 40x1+50x2+100x3+80x4
,5x1+2,5x2+2x3+1,5x4
£ 100
x1+10x2+4x3+6x4
£ 260
x1+7x2+4x3+10x4
£ 370
Симплекс-таблица задачи имеет вид:
|
Б.п.
|
Сб
|
А0
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
|
|
|
40
|
50
|
100
|
80
|
0
|
0
|
0
|
|
X5
|
0
|
100
|
2,5
|
2,5
|
2
|
1,5
|
1
|
0
|
0
|
|
X6
|
260
|
4
|
10
|
4
|
6
|
0
|
1
|
0
|
|
X7
|
0
|
370
|
8
|
7
|
4
|
10
|
0
|
0
|
1
|
|
Max Z
|
0
|
-40
|
-50
|
-100
|
-80
|
0
|
0
|
0
|
Анализ: в индексной строке есть неотрицательные
элементы, задача решается на максимум Þ начальный опорный
план можно улучшить.
шаг. Выбираем разрешающий столбец:
в индексной строке выбираем минимальный элемент
из всех отрицательных элементов. Разрешающим столбцом принимаем j0=3
( минимум -100 соответствует столбцу x3).
шаг. Выбираем разрешающую строку:
в каждой строке найдем минимальное из отношений
соответствующих значений столбца А0 и неотрицательных значений разрешающего
столбца j0=3:
/ 2 = 50 - минимум
/ 4 = 65
/ 4 = 92,5
Разрешающая строка - i0
= 1.
шаг. Заменим x5
на x3 и пересчитаем
новую симплекс-таблицу по правилу прямоугольника:
а) разрешающую строку разделить на разрешающий
элемент;
б) разрешающий столбец (за исключением
разрешающего элемента) заменить на 0.
в)
|
Б.п.
|
Сб
|
А0
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
|
|
|
40
|
50
|
100
|
80
|
0
|
0
|
0
|
|
X3
|
100
|
50
|
1,25
|
1,25
|
1
|
0,75
|
0,5
|
0
|
0
|
|
X6
|
0
|
60
|
-1
|
5
|
0
|
3
|
-2
|
1
|
0
|
|
X7
|
0
|
170
|
3
|
2
|
0
|
7
|
-2
|
0
|
1
|
|
Max Z
|
5000
|
85
|
75
|
0
|
-5
|
50
|
0
|
0
|
4 шаг. Анализируем индексную строку последней
таблицы: в столбце х4 есть отрицательный элемент - оптимальный план может быть
улучшен. Повторить шаги 1-3. В результате получается таблица:
|
Б.п.
|
Сб
|
А0
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
|
|
|
40
|
50
|
100
|
80
|
0
|
0
|
0
|
|
X3
|
100
|
35
|
1,5
|
0
|
1
|
0
|
1
|
-0,25
|
0
|
|
X4
|
80
|
20
|
-1/3
|
5/3
|
0
|
1
|
-2/3
|
1/3
|
0
|
|
X7
|
0
|
30
|
16/3
|
-29/3
|
0
|
0
|
8/3
|
-7/3
|
1
|
|
Max Z
|
5100
|
250/3
|
250/3
|
0
|
0
|
140/3
|
5/3
|
0
|
max Z=5100 X*=(0;
0; 35; 20; 0; 0; 30)
Замечание. Оптимальный план выпуска продукции
выбирается в столбце А0 для соответствующих переменных (переменные, которых нет
в базисе равны 0).
Задание
Реализовать на ЭВМ алгоритм решения задачи
определения оптимального плана выпуска n
видов продукции X=(x1, x2, …, xn)
. Объемы ресурсов предприятия представлены вектором A=(b1,
b2, …,bm),
прибыль (затраты) на единицу продукции представлены вектором C=(c1, c2, …, cn),
а нормы затрат ресурсов на единицу продукции представлены матрицей || aij
|| , i=1,...,m
; j=1,n.
Определить оптимальный план выпуска n
видов продукции, используя симплекс-метод решения задачи (симплекс-таблицы).
Замечания.
Критерий оптимальности задачи должен быть задан
с клавиатуры, т.е. задача должна определять максимум или минимум целевой
функции по выбору пользователя.
Число переменных не превышает 10, а число
ограничений - не больше 5.
Все ограничения имеют знак отношения £
(программа самостоятельно представляет систему ограничений в предпочтительном
виде).
литература
1. Банди
Б. Основы линейного программирования. Москва, «Радио и связь», 1989
2. Балашевич
В.А. Основы математического программирования.
3. Ларионов
А.И., Юрченко Т.И., Новоселов А.Л. Экономико-математические методы в
планировании. Москва, «Высшая школа» , 1991
4. Вентцель
Е.С. Исследование операций.
оптимальный ресурс линейный опорный
Лабораторная работа №4
Тема: «Целочисленное программирование».
Цель: изучить специальные методы решения задач
дискретного программирования (метод Баллаша и метод Фора и Мальгранжа) с
применением их для решения задач оптимального планирования с целочисленными
переменными, реализовать методы на ЭВМ.
Теоретические сведения.
В задачах дискретного программирования также как
и в задачах линейного программирования есть ограничения на переменные и целевая
функция, однако переменные принимают только целые значения 0, 1, 2, …, и.т.д.
Простое округление результата, полученного с помощью методов линейного
программирования, может привести к значительным плановым просчетам. Поэтому
задачи целочисленного программирования требуют применения специальных методов
решения.
Различают задачи:
целочисленного программирования с булевыми
переменными;
дискретного программирования.
Применение булевых переменных удобно в практике
плановых расчетов (задачи о включении заказа в план или отказа от выполнения
заказа в данном плановом периоде).
Решение задач целочисленного программирования с
булевыми переменными.
Рассмотрим специальные методы решения задач с
булевыми переменными на примере следующей задачи:
На заводе необходимо сформировать
производственную программу, исходя из набора заказов, в которых имеется 5
различных типов станков. Известны технологические процессы и нормы затрат
времени на основных операциях технологического процесса, прибыль от реализации
каждого заказа:
|
№
тех. операции
|
Нормы
затрат времени по операциям тех .процесса на изготовление заказа
|
Фонд
времени
|
|
1
|
2
|
3
|
4
|
5
|
|
|
1
2 3
|
25
31 29
|
38
18 32
|
41
28 34
|
14
36 24
|
18
25 18
|
96
90 100
|
|
Прибыль
на заказ
|
16
|
12
|
11
|
8
|
6
|
max Z
|
Модель решения задачи имеет вид:
Max
Z=16x1
+ 12x2 + 11x3
+ 8x4 + 6x5
при ограничениях:
x1 + 38x2
+ 41x3 + 14x4
+ 18x5 £
96
x1 + 18x2
+ 28x3 + 36x4
+ 25x5 £
90
x1 + 32x2
+ 34x3 + 24x4
+ 18x5 £
100,
где xj
- признак включения j- го заказа
в план производства.
Задача относится к классу задач дискретного
программирования с булевыми переменными:
- заказ будет изготовлен в плановом периоде;
- в противном случае.
В качестве специальных методов решения задач
дискретного программирования с булевыми переменными, основанных на случайном
поиске, рассмотрим
а) метод Баллаша;
б) метод Фора и Мальгранжа.
Метод Баллаша.
шаг. Расположить переменные т.о., чтобы
коэффициенты в целевой функции составляли неубывающую последовательность.
Примем R=0 (индекс плана).
шаг. Примем x1=0;
xj=0; j=2,n.
План XR=(1; 0; … ;
0).
шаг. Для данного варианта решения рассчитать Z0.
Это значение приравнивается max:
= Z0.
шаг. С помощью генератора сочетаний сформировать
очередное решение XR.
шаг. Вычислить ZR.
шаг. Проверить: если ZR
< max, то данное
решение хуже, чем полученное ранее рекордное; переход к 9 шагу. В противном
случае - переход к 7 шагу.
шаг. Проверить выполнение ограничений задачи для
решения XR. Если какое
- либо из ограничений не выполняется, то XR
не рассчитывается; переход к 9 шагу. Если все ограничения выполняются, т.е.
решение допустимое, то переход к 8 шагу.
шаг. Запомнить полученное решение XR
и max := ZR.
шаг. Проверить: все ли варианты решений просмотрены:
нет - переход к 10 шагу;
да - переход к 11 шагу.
шаг. Примем R
:= R + 1. Переход к 4
шагу.
шаг. Расчет закончен. Оптимальный вариант
расчета соответствует max.
Количество вариантов решений равно 2n.
|
№
плана
|
Значения
переменной
|
max
|
Выполнение
(+) или невыполнение (-) ограничений
|
ZR
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
2
|
3
|
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
+
|
+
|
+
|
0
|
|
1
|
1
|
0
|
0
|
0
|
0
|
16
|
+
|
+
|
+
|
16
|
|
2
|
0
|
1
|
0
|
0
|
0
|
16
|
+
|
+
|
+
|
12
|
|
3
|
0
|
0
|
1
|
0
|
0
|
16
|
+
|
+
|
+
|
11
|
|
4
|
0
|
0
|
0
|
1
|
0
|
16
|
+
|
+
|
+
|
8
|
|
5
|
0
|
0
|
0
|
0
|
1
|
16
|
+
|
+
|
+
|
6
|
|
6
|
1
|
1
|
0
|
0
|
0
|
28
|
+
|
+
|
+
|
28
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
|
32
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
В процессе счета ограничения проверялись 17 раз
вместо 96, т.е. экономия составила 96 - 17 = 79 расчетов. Максимальное значение
было получено на 18 плане и равно 36 тыс. д.е.
Замечание. Метод Баллаша может быть применим к
задачам как с линейными, так и с нелинейными критериями и ограничениями. Однако
генератор сочетаний предполагает проверять все возможные комбинации 0 и 1, т.е.
2n вариантов, что не
всегда удобно (особенно при вычислении «вручную» ) при больших n.
Метод Фора и Мальгранжа.
Метод Фора и Мальгранжа можно разделить на 2
этапа:
этап. Поиск исходного плана.
этап. Улучшение исходного плана.
этап. Коэффициенты целевой функции должны быть
расположены в порядке убывания их величин. Определяется max
c1 и x1:=1.
Аналогично определяются xj:
если при некотором xj
ограничения не выполняются, то xj:=0.
Таким образом, получается некоторый план X0=(x10;
x20; …; xn0)
и max:=Z(X0).
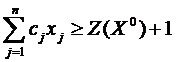
При этом к исходным ограничениям
присоединяют ограничение вида
Затем просматриваются ранее
сделанные выборы xj=1, начиная с последнего. Полагают xj=0 и
пытаются придать последующим значениям переменных 1.
Если добиться улучшения плана не
удается, то оптимальное решение найдено.
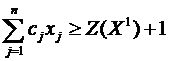
и процедура 2 этапа повторяется.
Если найдено решение X1=(x11, x12, …, x1n), то
ограничение (*) заменяется на
Пример. Сформировать
производственную программу работы сборочного участка, если известно, что фонд
времени равен 14 тыс. ч., а удельные характеристики изделий даны в таблице:
|
Характеристика
и размерность
|
Номера
изделий
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
Потребность
в затратах времени на сборку, тыс. ч.
|
5
|
8
|
7
|
4
|
2
|
3
|
1
|
2
|
|
Прибыль,
тыс. д. е.
|
12
|
10
|
9
|
7
|
6
|
5
|
3
|
1
|
Модель задачи имеет вид:
Max Z =
12x1+10x2+9x3+7x4+6x5+5x6+3x7+x8
При ограничении
x1+8x2+7x3+4x4+2x5+3x6+x7+2x8
£ 14
этап. Упорядочить переменные в порядке убывания
коэффициентов cj.
Присвоим
|
x1=1
|
Z=12
|
5 £ 14 -
допустимо
|
|
x2=1
|
Z=22
|
13 £ 14 -
допустимо
|
|
x3=0
|
|
20 £ 14 -
недопустимо
|
|
x4=0
|
|
|
|
x5=0
|
|
|
|
x6=0
|
|
|
|
x7=1
|
Z=25
|
14 £ 14 -
допустимо
|
|
x8=0
|
|
|
Добавим ограничение 5x1+8x2+7x3+4x4+2x5+3x6+x7+2x8
³ 25+1
этап. Улучшим план:
* Последнюю ненулевую переменную заменим на
нуль, т.е. x7=0 и попытаемся
заменить оставшиеся переменные на 1, т.е. x8=1.
Но данный план недопустим, т.к. ограничение
x1+8x2+7x3+4x4+2x5+3x6+x7+2x8
= 15 > 14 - недопустимо
* Снова последнюю ненулевую переменную заменим
на нуль, т.е. x2=0 и попытаемся
заменить оставшиеся переменные на 1, т.е.
|
x1=1
|
Z=12
|
5 £ 14 -
допустимо
|
|
x2=0
|
|
|
|
x3=1
|
Z=21 < 26 - не
улучшен
|
12 £ 14 -
допустимо
|
|
x4=0
|
|
16 £ 14 -
недопустимо
|
|
x5=1
|
Z=27 > 26 - улучшен
|
14 £ 14 -
допустимо
|
|
x6=0
|
|
|
|
x7=0
|
|
|
|
x8=0
|
|
|
Новый план X1
= (1, 0, 1, 0, 1, 0, 0, 0) и Z1=27.
Заменим дополнительное ограничение на 5x1+8x2+7x3+4x4+2x5+3x6+x7+2x8
³ 27+1 и попытаемся улучшить план:
|
x1=1Z=125 £ 14 -
допустимо
|
|
|
|
x2=0
|
|
|
|
x3=1
|
Z=21 < 26 - не
улучшен
|
12 £ 14 -
допустимо
|
|
x4=0
|
|
16 £ 14 -
недопустимо
|
|
x5=0
|
|
|
|
x6=0
|
|
15
£
14
- недопустимо
|
|
x7=1
|
Z=24 < 28 - не
улучшен
|
13
£
14
- допустимо
|
|
x8=0
|
|
15
£
14
- недопустимо
|
Новый план допустим по ограничению, но он не
улучшил значение целевой функции, т.к. ее значение 24 меньше предыдущего 28.
Значит, нужно повторить улучшение без изменения ограничений:
а)
|
x1=1Z=125 £ 14 -
допустимо
|
|
|
|
x2=0
|
|
|
|
x3=1
|
Z=21 < 26 - не
улучшен
|
12 £ 14 -
допустимо
|
|
x4=0
|
|
16 £ 14 -
недопустимо
|
|
x5=0
|
|
|
|
x6=0
|
|
|
|
x7=0
|
|
|
|
x8=1
|
Z=22 < 28 - не
улучшен
|
14
£
14
- допустимо
|
б)
|
x1=1Z=125 £ 14 -
допустимо
|
|
|
|
x2=0
|
|
|
|
x3=0
|
|
|
|
x4=1
|
Z=19 < 28 - не
улучшен
|
9 £ 14 -
допустимо
|
|
x5=1
|
Z=25 < 28 - не
улучшен
|
11
£
14
- допустимо
|
|
x6=1
|
Z=30 > 28 - улучшен
|
14
£
14
- допустимо
|
|
x7=0
|
|
|
|
x8=0
|
|
|
Новый план X2
= (1, 0, 0, 1, 1, 1, 0, 0) и Z2=30.
Заменим дополнительное ограничение на 5x1+8x2+7x3+4x4+2x5+3x6+x7+2x8
³ 30+1 и попытаемся улучшить план аналогично.
Решение задачи будет иметь вид: Xn
= (1, 0, 0, 1, 1, 1, 0, 0) и Zn=30.
Замечание. Для отыскания оптимального решения
было просмотрено 22 варианта, тогда как метод Баллаша требует 28 = 256
вариантов. Однако метод Фора и Мальгранжа применяется только к задачам с
линейными целевыми функциями и линейными ограничениями.
Задание
Реализовать на ЭВМ алгоритм решения задачи
целочисленного программирования с булевыми переменными на случай n
переменных (n
£ 10) и m
ограничений (m
£ 5):
а) методом Баллаша;
б) методом Фора и Мальгранжа.
Замечания.
План считается допустимым, если все ограничения
верны одновременно.
При решении указывать общее количество итераций
и порядок итерации, в которой был получен оптимальный вариант.
Предусмотреть случай выбора критерия
оптимальности решения задачи: максимум или минимум.

литература
1. Банди
Б. Основы линейного программирования. Москва, «Радио и связь», 1989
2. Балашевич
В.А. Основы математического программирования.
3. Ларионов
А.И., Юрченко Т.И., Новоселов А.Л. Экономико-математические методы в
планировании. Москва, «Высшая школа» , 1991
4. Вентцель
Е.С. Исследование операций.
Лабораторная работа № 5
Тема: «Методы целочисленного программирования»
Цель: изучить специальные методы решения задач
дискретного программирования (метод отсечений и метод ветвей и границ) с
применением их для решения задач оптимального планирования с целочисленными
переменными, реализовать методы на ЭВМ.
Теоретические сведения.
Напомним, что в задачах дискретного
программирования также как и в задачах линейного программирования есть
ограничения на переменные и целевая функция, однако переменные принимают только
целые значения 0, 1, 2, …, и.т.д. Простое округление результата, полученного с
помощью методов линейного программирования, может привести к значительным
плановым просчетам.
Поэтому задачи целочисленного
программирования требуют применения специальных методов решения.
Например, решая задачу (см. рис.) обычным
методом, приходим к решению а (4,55; 4,75) .
• Округление решения а по общим правилам
дает недопустимое решение (5; 5).
• Отсечение дробной части позволяет получить
внутреннюю точку, которая является допустимой, но не оптимальной (4; 4).
Задача целочисленного линейного программирования
состоит в том, чтобы найти оптимальное целочисленное решение. Например, в
данной задаче - (4; 5).
Для решения такого типа задач используют методы
дискретного программирования, наиболее распространенными из которых являются :
метод отсечений;
метод ветвей и границ.
Метод отсечений.
Алгоритм метода состоит из следующих шагов:
Отыскивается оптимальный план задачи без учета
ограничений на целочисленность неизвестных (например, симплекс-методом).
Полученный план анализируется на
целочисленность.
Если все переменные приняли целые значения, то
оптимальный план найден.
Если хотя бы одна компонента плана имеет дробную
часть, то к исходной системе ограничений добавляется неравенство вида:
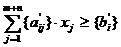
где xj -
переменная, имеющая наибольшую дробную часть
a’ij , b’i -
преобразованные исходные величины aij , bi , а {a’ij } , { b’i } - их
дробные части.
После решения задачи с
дополнительным ограничением анализируется, является ли полученный план
целочисленным.
если хотя бы одна переменная
принимает дробное значение, то вновь формируется дополнительное ограничение и
делается попытка отыскания целочисленного значения.
Конец алгоритма.
В случае, если требование
целочисленности относится лишь к некоторым переменным, то такие задачи называют
частично целочисленными. Для их решения строится дополнительное ограничение,
т.е. отсечение вида:
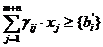
где γij
определяются следующим образом:
Для переменных, которые по условию
задачи могут принимать нецелочисленные значения, имеем:
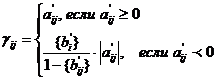 (*)
(*)
Для переменных, которые по условию
задачи должны принимать только целые значения:
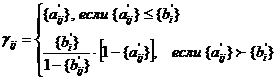 (**)
(**)
Пример.
На заводе энергетического
машиностроения изготавливаются паровые турбины двух типов. Мощности предприятия
лимитируются двумя цехами. Необходимо найти оптимальный выпуск турбин на
планируемый период.
|
Цех
|
Норма
расхода времени в i - м цехе, ч
|
Полезный
фонд времени работы цеха, ч
|
|
1
изделие
|
2
изделие
|
|
|
1
|
2,0
|
5,0
|
28,0
|
|
2
|
2,0
|
1,0
|
11,0
|
|
Прибыль
от реализации, тыс.д.е
|
3,0
|
2,0
|
maxZ
|
Модель задачи:
|
Прямая:
|
Расширенная:
|
|
MaxZ = 3x1 + 2x2 2x1+5x2 ≤
28 2x1+ x2 ≤
11 x1, x2 ≥
0 x1, x2 -
целочисленные
|
maxZ = 3x1 + 2x2 + 0x3+ 0x4
2x1+5x2 + x3 = 28 2x1+ x2 + x4 = 11 x1, x2 ≥
0 x1, x2 -
целочисленные
|
Решаем задачу без учета целочисленности симплекс
- методом.
|
Б.п.
|
Сб
|
А0
|
X1
|
X2
|
X3
|
X4
|
|
|
|
3
|
2
|
0
|
0
|
|
X3
|
0
|
28
|
2
|
5
|
1
|
0
|
|
X4
|
0
|
11
|
2
|
1
|
0
|
1
|
|
maxZ
|
0
|
-3
|
-2
|
0
|
0
|
разрешающий столбец
|
Б.п.
|
Сб
|
А0
|
X1
|
X2
|
X3
|
X4
|
|
|
|
3
|
2
|
0
|
0
|
|
X3
|
0
|
17
|
0
|
4
|
1
|
-1
|
|
X1
|
3
|
5,5
|
1
|
0,5
|
0
|
0,5
|
|
maxZ
|
16,5
|
0
|
-0,5
|
0
|
1,5
|
разрешающий столбец
|
Б.п.
|
Сб
|
А0
|
X1
|
X2
|
X3
|
X4
|
|
|
|
3
|
2
|
0
|
0
|
|
X2
|
2
|
4,25
|
0
|
1
|
0,25
|
-0,25
|
|
X1
|
3
|
27/8
|
1
|
0
|
-1/8
|
5/8
|
|
maxZ
|
149/8
|
0
|
0
|
1/8
|
11/8
|
Оптимальный план найден X=(27/8
; 4,25 ), но он нецелочисленный. Но по особенностям задачи план выпуска турбин
должен быть только целым.
По приведенным выше правилам построим
дополнительное ограничение:
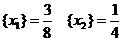
Так как дробная часть x1 больше
дробной части x2, то строим
ограничение по 2-й строке симплекс-таблицы (т.к. x1 стоит во
2-й строке).
Для переменных x1 и x2 строим g21 и g22 по формулам (**):g21 = 0; g22 = 0.
Для переменных x3 и x4 строим g23 и g24 по формулам (*):
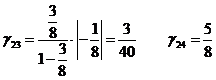
Дополнительное ограничение имеет
вид:
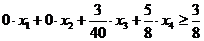
Приведем ограничение к
предпочтительному виду и добавим его в конечную симплекс-таблицу:
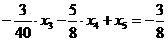
Расчет симплекс-таблицы проводится
по аналогичным правилам, но с небольшими изменениями:
а) при решении задачи на максимум в
индексной строке выбираем минимальный из ненулевых элементов
б) отношения элементов из столбца A0 и
разрешающего столбца должны быть положительными (но сами элементы могут быть и
отрицательными !)
Новая симплекс-таблица имеет вид:
|
Б.п.
|
Сб
|
А0
|
X1
|
X2
|
X3
|
X4
|
X5
|
|
|
|
3
|
2
|
0
|
0
|
0
|
|
X2
|
2
|
4,25
|
0
|
1
|
0,25
|
-0,25
|
0
|
|
X1
|
3
|
27/8
|
1
|
0
|
-1/8
|
5/8
|
0
|
|
X5
|
0
|
-3/8
|
0
|
0
|
-3/40
|
-5/8
|
1
|
149/8
|
0
|
0
|
1/8
|
11/8
|
0
|
разрешающий столбец
|
Б.п.
|
Сб
|
А0
|
X1
|
X2
|
X3
|
X4
|
X5
|
|
|
|
3
|
2
|
0
|
0
|
0
|
|
X2
|
2
|
3
|
0
|
1
|
0
|
-7/3
|
10/3
|
|
X1
|
3
|
4
|
1
|
0
|
0
|
5/3
|
-5/3
|
|
X3
|
0
|
5
|
0
|
0
|
1
|
25/3
|
-40/3
|
|
maxZ
|
18
|
0
|
0
|
0
|
1/3
|
5/3
|
Итак, план, ближайший к наилучшему, и имеющий
целые значения будет таким: X=
(4 ; 3). При этом прибыль составит max
Z= 18.
Метод ветвей и границ.
Основой метода ветвей и границ является
симплекс-метод.
Решение начинается с отыскания нецелочисленного
решения задачи.
На одну из переменных, принявших в оптимальном
плане нецелочисленное значение, накладываются ограничения, исключающие
полученные перед этим нецелочисленное значение.
В результате дополнения такими ограничениями
получаются две задачи, которые называют задачами - кандидатами.
Задачи - кандидаты решаются симплекс-методом, и
проводится оценка на возможность дальнейшего дробления каждой задачи -
кандидата на пару задач с дополнительными ограничениями:
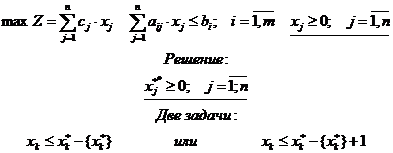
Деление очередной задачи на две
новые не проводится, если получено целочисленное значение или значение целевой
функции оказывается хуже.
Решение заканчивается, когда
дальнейшее ветвление невозможно. Оптимальное решение то, при котором получено
максимальное значение целевой функции к окончанию ветвления.
Задание
Составить программу определения
оптимального плана выпуска продукции N видов,
получая при этом максимум прибыли. Объем каждого вида продукции должен быть
только целым. Выбор метода решения задачи произвольный (метод отсечений или
метод ветвей и границ).

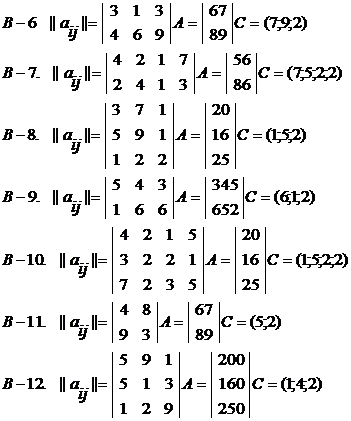
Литература
1. Банди
Б. Основы линейного программирования. Москва, «Радио и связь», 1989
2. Балашевич
В.А. Основы математического программирования.
3. Ларионов
А.И., Юрченко Т.И., Новоселов А.Л. Экономико-математические методы в
планировании. Москва, «Высшая школа» , 1991
4. Вентцель
Е.С. Исследование операций.
Лабораторная работа № 6
Тема: «Транспортная задача. Способы построения
начального опорного плана».
Цель: научиться строить математическую модель
транспортной задачи; уметь различать закрытую и открытую транспортные задачи, а
также приводить задачу открытого типа к виду расширенной закрытой транспортной
задачи. Уметь строить начальный опорный план задачи любым из способов (способ
северо-западного угла, способ минимального элемента, способ Фогеля), а также
различать преимущества и недостатки каждого из них.
Теоретические сведения.
Математическая модель задачи.
Пусть имеется m (i=1,m) поставщиков,
располагающих некоторым однородным продуктом в объемах по ai единиц, и n (j=1,n)
получателей с объемами по bj единиц.
Задана матрица C=|| cij
|| , где cij - стоимость перевозки единицы продукции от i- го поставщика j-му
потребителю.
Возникает задача определения плана перевозок X=
|| xij ||, где xij - количество
единиц продукции, поставляемой по коммуникации ( i, j ).
Условие задачи записывают в виде таблицы:
|
b1
|
b2
|
…
|
bj
|
…
|
bn
|
|
a1
|
x11
|
c11
|
x12
|
c12
|
…
|
x1j
|
c1j
|
…
|
x1n
|
c1n
|
|
|
|
|
|
|
|
|
|
|
|
|
a2
|
x21
|
c21
|
x22
|
c22
|
…
|
x2j
|
c2j
|
…
|
x2n
|
C2n
|
|
|
|
|
|
|
|
|
|
|
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
|
ai
|
xi1
|
c11
|
xi2
|
c11
|
…
|
xij
|
c11
|
…
|
xin
|
c11
|
|
|
|
|
|
|
|
|
|
|
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
|
am
|
xm1
|
c11
|
xm2
|
c11
|
…
|
xmj
|
c11
|
…
|
xmn
|
c11
|
|
|
|
|
|
|
|
|
|
|
|
Если  (1), то задача называется закрытой,
в противном случае - открытой.
(1), то задача называется закрытой,
в противном случае - открытой.
Математическая модель закрытой
задачи имеет вид:
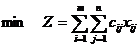 (2) - затраты на перевозку
продукции
(2) - затраты на перевозку
продукции
при ограничениях:
на запасы продукции у поставщиков,
которые по (1) должны быть полностью вывезены:
 (3) ;
(3) ;
на запросы потребителей, которые
должны быть полностью удовлетворены:
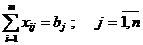 (4);
(4);
условия неотрицательности,
исключающие обратные перевозки:
≥ 0 (5).
Матрицу X= || xij ||, удовлетворяющую
условиям (3) - (5), называют допустимым планом перевозок, а переменные xij -
допустимыми перевозками.
Допустимый план X, доставляющий
целевой функции (2) минимальное значение, называется оптимальным. Матрицу C =
|| cij || - называют матрицей тарифов (матрицей транспортных издержек). Отрезок
или линия, соединяющая i - го поставщика с j -м потребителем называется
коммуникацией и обозначается ( i j ) или (Ai Bj). Если на
всех коммуникациях ( i j )
проставлены величины перевозок xij, то получим транспортную сеть.
Если условие (1) не выполняется, то
модель - открытая:
в случае, если запасы поставщиков
больше потребностей получателей, вводят n+1-го фиктивного потребителя, запросы
которых равны излишку запаса, т.е.
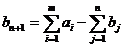
Тарифы ci n+1 = 0. Получим
расширенную закрытую задачу.
Если потребности превышают запасы,
вводят m+1 - го фиктивного поставщика. Его запасы считают равными недостающей
продукции:
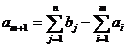
Тарифы cm+1 j равны
некоторому большому положительному числу М. Поставки xm+1 j в оптимальном плане
расширенной задачи покажут объемы недостачи продукции.
Структура системы ограничений.
Начальный опорный план.
Модель транспортной задачи - модель
линейного программирования. Ее оптимальный план всегда можно найти симплекс -
методом. Но матрица системы ограничений (3) - (4) имеет особенности:
Коэффициенты при неизвестных во всех
ограничениях равны 1.
Каждая неизвестная величина
встречается только в двух уравнениях: 1 раз в (3) и 2-й раз - в (4).
Система ограничений симметрична
относительно всех xij.
Исходя из данных особенностей, общая
процедура симплекс - метода упрощается.
этап. Как и при любом методе решение
задачи начинается с нахождения начального опорного плана. Наиболее
распространенными способами нахождения начального опорного плана являются:
а) способ северо - западного угла;
б) способ минимального элемента;
в) способ Фогеля.
Рассмотрим более подробно каждый из
способов.
Способ северо - западного угла
предполагает начать работу с клетки (1,1).
Положим x11 = min {a1, b1}.
если a1 > b1, то x11=b1;
вычеркнем из матрицы столбец j = 1;
если a1 < b1, то x11=a1; вычеркнем
из матрицы строку i = 1;
если a1 = b1, то x11=a1; вычеркнем
из матрицы или строку i = 1 или столбец j=1 (но не оба ряда
одновременно !)
Вычеркнув ряд, соответствующий min {a1, b1},
скорректируем ресурсы или потребности на величину x11 и с оставшейся матрицей
поступим аналогично.
На последнем шаге процесса получится
матрица 1×1,
в
которой одновременно вычеркиваем и столбец и строку.
План перевозок, построенный таким
способом, содержит m+n-1 заполненных клеток, т.е. является опорным.
Замечания:
а) при ai = bj, если сокращенная
матрица имеет одну строку и несколько столбцов, вычеркивается столбец; если
матрица имеет один столбец и несколько строк - то строку.
б) недостаток способа в том, что он
не учитывает матрицы тарифов (поэтому опорный план может оказаться далеким от
оптимального).
Способ минимального элемента
учитывает матрицу тарифов.
Находим min cij = c i0 j0.
если ai0 > bj0, то xi0 j0 = bjo; вычеркнем
из матрицы столбец j = j0 (запасы поставщика i0
корректируем, т.е. считаем равными ai0 - bj0);
если ai0 < bj0, то xi0 j0 = ai0; вычеркнем
из матрицы строку i = i0 ( запросы
потребителя j0 считаем равными bj0 - ai0 );
если ai0 = bj0, то xi0 j0 =ai0 = bj0 ;
вычеркнем из матрицы или строку i = i0 или
столбец j=j0
С оставшейся матрицей меньшего
размера поступаем аналогично.
На последнем шаге в матрице 1×1 одновременно
убираем и строку и столбец.
Способ Фогеля дает опорный план,
близкий к оптимальному. Его используют как приближенный метод решения
транспортной задачи.
Определим максимальную разность
между двумя минимальными элементами каждых строки и столбца.
Находим в ряду, соответствующем
максимальной разности всех строк и столбцов, клетку с минимальным тарифом (i0, j0). В нее
вписываем поставку xi0j0 = min {ai0, bj0}.
Вычеркиваем ряд, соответствующий min
{ai0, bj0}.
Корректируются запасы либо потребности.
С оставшейся матрицей поступаем
аналогично.
Построенный любым из способов
опорный план транспортной задачи является начальным. Занятые клетки
соответствуют базисным переменным, а незанятые - свободным.
Задание
Составить программу построения
начального опорного плана закрытой транспортной задачи, используя любой из
способов.
Указания.
Программа должна содержать меню для
выбора способа построения начального опорного плана (в меню должен быть включен
каждый из способов );
В случае открытой транспортной
задачи предусмотреть каждый из двух случаев (т.е. программа должна определять
самостоятельно тип задачи и при необходимости приводить ее математическую
модель к виду расширенной закрытой транспортной задачи);
Результатом работы программы должна
быть либо матрица допустимых планов перевозок, либо значения базисных
переменных с указанием их индексов в матрице X.

Литература
1. Банди
Б. Основы линейного программирования. Москва, «Радио и связь», 1989
2. Балашевич
В.А. Основы математического программирования.
3. Ларионов
А.И., Юрченко Т.И., Новоселов А.Л. Экономико-математические методы в
планировании. Москва, «Высшая школа» , 1991
4. Вентцель
Е.С. Исследование операций.
Лабораторная работа № 7
Тема: «Транспортная задача. Улучшение начального
опорного плана. Распределительный метод».
Цель: научиться строить математическую модель
транспортной задачи; уметь различать закрытую и открытую транспортные задачи, а
также приводить задачу открытого типа к виду расширенной закрытой транспортной
задачи. Уметь улучшать начальный опорный план задачи с помощью
распределительного метода.
Теоретические сведения.
Циклы. Свойства циклов и их построение.
Напомним, что транспортная задача строится
следующим образом:
пусть имеется m (i=1,m) поставщиков, располагающих
некоторым однородным продуктом в объемах по ai единиц, и n (j=1,n)
получателей с объемами по bj единиц.
Задана матрица C=|| cij
|| , где cij - стоимость перевозки единицы продукции от i- го поставщика j-му
потребителю.
Возникает задача определения плана перевозок X=
|| xij ||, где xij -
количество единиц продукции, поставляемой по коммуникации ( i, j ).
Условие задачи записывают в виде таблицы:
|
b1
|
b2
|
…
|
bj
|
…
|
bn
|
|
a1
|
x11
|
c11
|
x12
|
c12
|
…
|
x1j
|
c1j
|
…
|
x1n
|
c1n
|
|
|
|
|
|
|
|
|
|
|
|
|
a2
|
x21
|
c21
|
x22
|
c22
|
…
|
x2j
|
c2j
|
…
|
x2n
|
C2n
|
|
|
|
|
|
|
|
|
|
|
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
|
ai
|
xi1
|
c11
|
xi2
|
c11
|
…
|
xij
|
c11
|
…
|
xin
|
c11
|
|
|
|
|
|
|
|
|
|
|
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
|
am
|
xm1
|
c11
|
xm2
|
c11
|
…
|
xmj
|
c11
|
…
|
xmn
|
c11
|
|
|
|
|
|
|
|
|
|
|
|
Если  (1), то задача называется закрытой,
в противном случае - открытой.
(1), то задача называется закрытой,
в противном случае - открытой.
Математическая модель закрытой
задачи имеет вид:
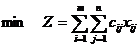 (2) - затраты на перевозку
продукции
(2) - затраты на перевозку
продукции
при ограничениях:
на запасы продукции у поставщиков,
которые по (1) должны быть полностью вывезены:
 (3) ;
(3) ;
на запросы потребителей, которые
должны быть полностью удовлетворены:
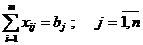 (4);
(4);
условия неотрицательности,
исключающие обратные перевозки:
≥ 0 (5).
Матрицу X= || xij ||,
удовлетворяющую условиям (3) - (5), называют допустимым планом перевозок, а
переменные xij - допустимыми перевозками.
Допустимый план X, доставляющий
целевой функции (2) минимальное значение, называется оптимальным. Матрицу C =
|| cij || - называют матрицей тарифов (матрицей транспортных издержек). Отрезок
или линия, соединяющая i - го поставщика с j -м потребителем называется
коммуникацией и обозначается ( i j ) или (Ai Bj). Если на
всех коммуникациях ( i j )
проставлены величины перевозок xij, то получим транспортную сеть.
Если условие (1) не выполняется, то
модель - открытая:
в случае, если запасы поставщиков
больше потребностей получателей, вводят n+1-го фиктивного потребителя, запросы
которых равны излишку запаса, т.е.
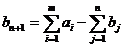
Тарифы ci n+1 = 0. Получим
расширенную закрытую задачу.
Если потребности превышают запасы,
вводят m+1 - го фиктивного поставщика. Его запасы считают равными недостающей
продукции:
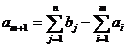
Тарифы cm+1 j равны
некоторому большому положительному числу М. Поставки xm+1 j в оптимальном плане
расширенной задачи покажут объемы недостачи продукции.
Наиболее распространенными способами
нахождения начального опорного плана являются:
а) способ северо - западного угла;
б) способ минимального элемента;
в) способ Фогеля.
Подробные алгоритмы каждого способа
были рассмотрены ранее.
Построенный любым из способов
опорный план транспортной задачи является начальным. Занятые клетки
соответствуют базисным переменным, а незанятые - свободным.
Одним из самых распространенных
методов улучшения начального опорного плана является распределительный метод.
Основой этого метода является построение так называемых циклов.
Циклом в матрице называется
непрерывная замкнутая ломаная линия, вершины которой находятся в клетках
матрицы, а звенья расположены вдоль строк и столбцов. Причем в каждой вершине
цикла встречается ровно два звена: одно из них располагается по строке, а
другое - по столбцу. Если цикл образует самопересекающаяся ломаная линия, то
точки ее самопересечения вершин не образуют !
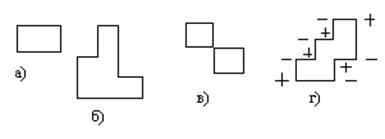
Примерами циклов могут служить
ломаные замкнутые линии:
Циклы в матрице тарифов
удовлетворяют следующим свойствам:
Число вершин в каждом цикле четно.
Рассмотрим произвольный цикл.
Выберем в качестве начальной произвольную его вершину и припишем ей знак +, а
затем, обходя цикл в любом направлении, будем в его вершинах расставлять
попеременно знаки + и - . Такой цикл называют означенным. (Пример означенного
цикла на рисунке г ). В означенном цикле число положительных вершин равно числу
отрицательных.
Пусть в матрице, состоящей из m
строк и n столбцов, произвольно отмечено m+n клеток. Тогда существует цикл,
вершины которого лежат в отмеченных клетках.
На заполненных клетках опорного
плана нельзя построить цикл, т.е. опорный план транспортной задачи является
ацикличным.
Улучшение плана перевозок.
Распределительный метод.
Назовем операцией сдвига по циклу на
величину θ
процесс
увеличения перевозок, стоящих в положительно означенных вершинах цикла, на
число θ
и
уменьшения на это число перевозок, стоящих в отрицательно означенных вершинах
цикла.
Пусть (i0, j0) -
свободная клетка. Построим цикл с вершиной (i0, j0), все
остальные вершины которого находятся в заполненных клетках. Присвоим свободной
вершине (i0, j0) знак + и
означим цикл.
Переместим по циклу величину θ. Очевидно,
значение θ
не
может превосходить min {x -ij}, где x -ij - значения
поставок, находящихся в отрицательно означенных вершинах цикла.
При сдвиге по циклу на величину θ допустимый
план остается допустимым. Стоимость же плана может увеличиваться или
уменьшаться.
Рассмотрим, какое изменение ∆Z
целевой функции вызывается сдвигом по циклу на величину θ. Это
изменение выразится формулой:
∆Z = θ ∙ ( ∑ {c+ij} - ∑{
c -ij}), где ∑
{c+ij} и ∑{
c -ij} -
соответственно сумма тарифов по положительно и отрицательно означенным клеткам
цикла.
Обозначим величину ∑ {c-ij} - ∑{
c +ij} = ∆i0 j0 и назовем
ценой цикла величину ∆Z = - θ ∙∆i0 j0.
Опорный план можно улучшить только в
том случае, если существует свободная клетка (i0, j0) , для
которой ∆Z < 0. Но так как θ > 0, то ∆Z
< 0, если ∆i0 j0 > 0.
Итак, опорный план можно улучшить,
если существуют свободные клетки с положительной оценкой. Сделав сдвиг по циклу
на величину θ
=
min {x -ij}, получим
новый опорный план. Свободная клетка (i0, j0)
становится заполненной , а клетка, для которой θ = min {x -ij}, считается
свободной. Если существует несколько клеток, для которых θ = min {x -ij}, то клетка
с максимальным тарифом считается свободной, а в остальных - нулевая поставка.
Таким образом, сдвиг по циклу на
величину θ
=
min {x -ij} позволяет
прийти к новому, улучшенному опорному плану. При этом значение целевой функции
изменится на величину ∆Z = - θ ∙∆i0 j0, т.е.
уменьшится.
Так как область допустимых решений
имеет конечное число опорных планов, то за коечное число шагов придем к
оптимальному решению.
Признаком оптимальности опорного
плана является неположительность оценок всех свободных клеток.
Рассмотрим процесс решения
транспортных задач, называемый распределительным методом.
Исходные данные заносятся в таблицу
(в случае необходимости модель задачи приводится к закрытой).
Строим начальный опорный план.
Занятыми должны быть m+n-1 клеток.
Находим оценки свободных клеток. Так
как к улучшению приводит сдвиг по циклу для свободной клетки с положительной
оценкой, то целесообразно испытывать их не все подряд, а выбирать в первую
очередь клетки, имеющие минимальные тарифы cij. Если ∆i j ≤ 0,
то оцениваем следующую свободную клетку и т.д., пока не найдем клетку с
положительной оценкой. Если же для всех свободных клеток ∆i j ≤ 0,
то найденный опорный план оптимален.
Пусть (i0, j0) - клетка
с положительной оценкой. Находим θ = min {x -ij}. Делаем сдвиг
по циклу на величину θ.
Получим
улучшенный опорный план и т.д.
|
10
|
20
|
30
|
15
|
|
30
|
|
3
|
20
|
1
|
|
4
|
10
|
4
|
|
|
|
|
|
|
|
|
|
|
20
|
10
|
2
|
|
4
|
10
|
3
|
|
6
|
|
|
|
|
|
|
|
|
|
|
25
|
|
7
|
|
5
|
20
|
8
|
5
|
4
|
|
|
|
|
|
|
|
|
|
В данной таблице с помощью способа минимального
элемента построен начальный опорный план X0, Z(X0) = 270.
Число заполненных клеток m + n -1 = 3
+ 4 -1 = 6.
Приступаем к улучшению опорного плана (если это
возможно).
Находим свободную клетку с минимальным тарифом -
(1,1). Для нее в таблице постоим означенный цикл пересчета.
|
10
|
20
|
30
|
15
|
|
30
|
+
|
3
|
20
|
1
|
|
4
|
-
10
|
4
|
|
|
|
|
|
|
|
|
|
|
20
|
-
10
|
2
|
|
4
|
+
10
|
3
|
|
6
|
|
|
|
|
|
|
|
|
|
|
25
|
|
7
|
|
5
|
-
20
|
8
|
+
5
|
4
|
|
|
|
|
|
|
|
|
|
С его помощью находим цену цикла ∆11=∑
{c-ij} - ∑{c +ij} = =(2+8+2) - (3+4+3) = 2.
Следовательно, сдвиг по циклу на величину θ
= min {10, 20, 10}=10 выгоден. Значение целевой функции
должно измениться на величину ∆Z = - θ ∙∆11=
-10 ∙ 2=-20.
Сделав сдвиг по циклу на величину θ
= 10, придем
к новому опорному плану Z=250.
|
10
|
20
|
30
|
15
|
|
30
|
10
|
3
|
20
|
1
|
|
4
|
|
4
|
|
|
|
|
|
|
|
|
|
|
20
|
0
|
2
|
|
4
|
20
|
3
|
|
6
|
|
|
|
|
|
|
|
|
|
|
25
|
|
7
|
|
5
|
10
|
8
|
15
|
4
|
|
|
|
|
|
|
|
|
|
Расположим свободные клетки в порядке
возрастания тарифов (1,4), (2,2), (1,3), (3,2), (2,4), (3,1).
Для клетки (1,4) цикл пересчета совпадает с
циклом (1,1). Следовательно, его цена = -2.
Далее находим:
∆22=(2+1) - (3+4) = -4.
∆13= (3+3) - (2+4) = 0
∆32= (8+2+1) - (5+3+3) = 0
∆24= (4+3) - (6+8) = -7
∆31= (2+8) - (7+4) = -1.
Так как для всех свободных клеток ∆i
j ≤
0, то найденный план в последней таблице оптимален. Очевидно, он не
единственный (об этом говорят нулевые оценки свободных клеток). Построив для
клеток ∆13 и ∆13 циклы пересчета и сделав сдвиг по циклу, получим
новые опорные планы.
Задание
Составить программу улучшения начального
опорного плана закрытой транспортной задачи с помощью распределительного
метода.
Указания.
Программа должна содержать меню для выбора
способа построения начального опорного плана (в меню должен быть включен каждый
из способов );
В случае открытой транспортной задачи
предусмотреть каждый из двух случаев (т.е. программа должна определять
самостоятельно тип задачи и при необходимости приводить ее математическую
модель к виду расширенной закрытой транспортной задачи);
Допускается построение простых циклов (т.е.
циклов из 4-х вершин). Программа должна определять оценки всех свободных клеток
и выполнять построение циклов до тех пор, пока хотя бы одна оценка
положительная.
Результатом работы программы должна быть либо
матрица оптимального плана перевозок, либо значения переменных с указанием их
индексов в матрице X.
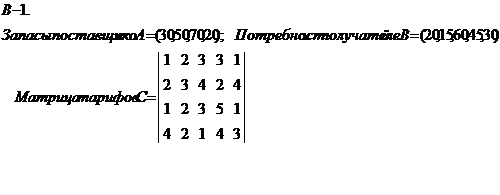
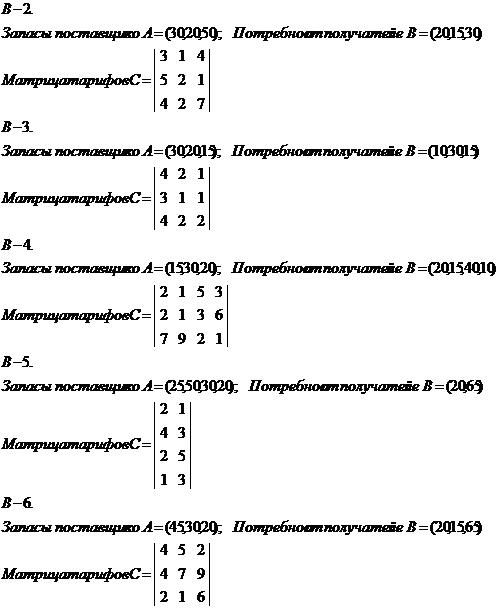
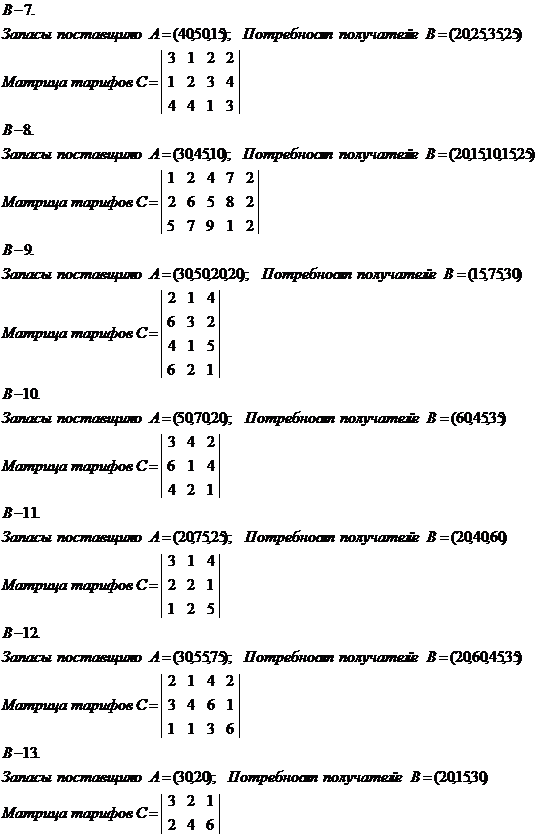
Литература
1. Банди
Б. Основы линейного программирования. Москва, «Радио и связь», 1989
2. Балашевич
В.А. Основы математического программирования.
3. Ларионов
А.И., Юрченко Т.И., Новоселов А.Л. Экономико-математические методы в
планировании. Москва, «Высшая школа» , 1991
4. Вентцель
Е.С. Исследование операций.
Лабораторная работа № 8
Тема: «Двухэтапная транспортная задача.»
Цель: научиться строить математическую модель
двухэтапной транспортной задачи; уметь приводить задачу к классическому виду, а
также применять способы решения транспортной задачи для построения начального
опорного плана и его улучшения распределительным методом с учетом особенностей
двухэтапной транспортной задачи.
Теоретические сведения.
Транспортная задача закрытого типа или ее
расширенный вид, вообще говоря, редко встречаются в реальном планировании,
однако они являются основой для решения задач более сложного вида, когда грузы
могут доставляться не только непосредственно от поставщиков к потребителям, но
и через промежуточные пункты.
Пусть m
( i = 1,m)
пунктов производства, n
( j = 1,n)
пунктов потребления и p
( r = 1,p)
промежуточных баз.
Как и в обычной транспортной задаче, обозначим
через ai, bj
соответственно объемы поставок и потребления.
Пусть dr
- мощность r -й базы; cir
и crj - соответственно
стоимость перевозки единицы продукции от поставщиков на базы и с базы к
потребителям.
Тогда модель задачи имеет вид:

Если суммарная пропускная мощность
баз равна суммарной мощности поставщиков и суммарному спросу потребителей, т.е.
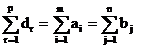
то пропускные емкости баз будут
использованы полностью, и следовательно, схема перевозок с баз к потребителям
не зависит от схемы перевозок от поставщиков на базы.
В таких случаях задачу можно решать
по частям:
составить оптимальный план поставок
от поставщиков к базам.
Составить оптимальный план поставок
с баз к потребителям.
Оптимальный план задачи будет
объединением двух оптимальных планов, составленных по частям.
Однако, в общем случае оптимальный
план двухэтапной транспортной задачи отличен от объединения двух оптимальных
планов.
Приведем двухэтапную транспортную
задачу к классической задаче. Для этого будем считать базы одновременно
поставщиками и потребителями. Для каждой базы в расширенной матрице (поставщики
+ базы) - (базы + потребители) отведем строку и столбец. Тогда матрица тарифов
будет состоять из 4-х блоков:
|
d1
|
…
|
dp
|
b1
|
…
|
bn
|
|
a1
|
|
|
|
|
|
|
|
…
|
|
|| cir ||
|
|
|
M
|
|
|
am
|
|
|
|
|
|
|
|
d1
|
0
|
|
M
|
|
|
|
|
…
|
|
0
|
|
|
|| crj ||
|
|
|
dp
|
M
|
|
0
|
|
|
|
В первом - левом верхнем блоке отражаются связи
поставщиков с базами (i
r), в 4-м - связи
баз с потребителями.
Так как по условию задачи непосредственные
перевозки от поставщиков к потребителям запрещены, то во 2-м блоке все тарифы
считают равными М (где М - некоторое заведомо большое число).
Аналогично, перевозки между базами также
запрещены по условию задачи, поэтому 3-й левый нижний блок - перевозки между
базами - также заполнен показателями М.
В клетках, где отражаются связи базы с самой
собой, тарифы равны 0. Поставки в этих клетках показывают величину
неиспользованной мощности базы. Диагональ из нулевых тарифов, отражающих связи
базы с самой собой, называют фиктивной.
Решение двухэтапной транспортной задачи имеет
некоторые особенности:
Изменение нахождения начального опорного плана:
а) необходимо распределить поставки в одном из
блоков (1-м или 4-м)
б) заполнить фиктивную диагональ.
в) распределить поставки в другом блоке (4-м или
1-м)
Если цикл пересчета проходит через фиктивную
диагональ, то он обязательно проходит через нее дважды: одна вершина цикла,
находящаяся на диагонали, будет всегда +, другая -.
Пример. Имеется два маслодельных завода А1, А2.
Сливочное масло поступает сначала в холодильники Д1, Д2, Д3, а из них - в
пункты потребления В1, В2, В3 и В4. Исходные данные представлены в таблицах:
Тарифы перевозок от поставщиков на базы
|
d1=240
|
d2=500
|
d3=260
|
|
a1=350
|
x11
|
20
|
x12
|
23
|
x13
|
16
|
|
|
|
|
|
|
|
|
a2=450
|
x21
|
15
|
x22
|
10
|
x23
|
24
|
|
|
|
|
|
|
|
Тарифы перевозок с баз к потребителям
|
b1=150
|
b2=250
|
b3=175
|
b4=225
|
|
d1=240
|
x11’
|
12
|
x12’
|
19
|
x13’
|
20
|
x14’
|
13
|
|
|
|
|
|
|
|
|
|
|
d2=500
|
x21’
|
10
|
x22’
|
15
|
x23’
|
14
|
x24’
|
12
|
|
|
|
|
|
|
|
|
|
|
d3=260
|
x31’
|
16
|
x32’
|
21
|
x33’
|
25
|
x34’
|
11
|
|
|
|
|
|
|
|
|
|
Получить оптимальный план перевозок с
минимальными расходами (при условии невозможности перевозок непосредственно от
поставщиков к потребителям, а также между базами).
Решение.
Так как 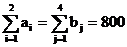 , то данные
таблиц сведем в одну матрицу (в случае неравенства задачу приводят к
расширенной закрытой транспортной задаче).
, то данные
таблиц сведем в одну матрицу (в случае неравенства задачу приводят к
расширенной закрытой транспортной задаче).
|
d1=240
|
d2=500
|
d3=260
|
b1=150
|
b2=250
|
b3=175
|
b4=225
|
|
a1=350
|
75
|
20
|
50
|
23
|
225
|
16
|
|
M
|
|
M
|
|
M
|
|
M
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2=450
|
|
15
|
450
|
10
|
|
24
|
|
M
|
|
M
|
|
M
|
|
M
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d1=240
|
165
|
0
|
|
M
|
|
M
|
|
12
|
75
|
19
|
|
20
|
|
13
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2=500
|
|
M
|
|
0
|
|
M
|
150
|
10
|
175
|
15
|
175
|
14
|
|
12
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d3=260
|
|
M
|
|
M
|
35
|
0
|
|
16
|
|
21
|
|
25
|
225
|
11
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим начальный опорный план способом
минимального элемента (распределение начато с 4-го блока).
а) x12=75
x21=150 x22=175
x23=175 x34=225
б) заполняем фиктивную диагональ (разность dr
- xrj)
в) заполняем 1-й блок. Так как на базах Д1 и Д3
после поставок потребителям остались неиспользованными мощности d1=165
и d3=35, то в блоке 1
конечное значение поставок на базы будут соответственно меньше на d1
и d3:
x11=75 x12=50
x13=225 x22=450
Улучшим план.
а) выбираем свободную клетку с минимальным
тарифом (3, 4) и строим цикл (3,4)-(3,5)-(4,5)-(4,4).
Δ34= 29 - 27 = 2 (план можно
улучшить)
Θ = min
{75, 150}=75
б) (4, 2) : строим цикл
(4,2)-(4,4)-(3,4)-(3,1)-(1,1)-(1,2)-(4,2).
Δ42= 33 - 32 = 1 (план можно
улучшить)
Θ = min
{75, 165, 50}=50
в) Проверяя оставшиеся свободные клетки,
получим, что больше план улучшить нельзя.
Итак, оптимальный план перевозок имеет вид:
x i =1 r =1=125 x i =1 r =3=225 x i
=2 r =2=450 x r =1 j =1=125 x r=2 j =1=25 x r=2 j =2=250 x r =2 j =3=175
r =3 j
=4=225
Z0 = 21225 д.е. и Zопт
= 21025 д.е. Таким образом, улучшение плана составило экономию денежных средств
на перевозку в объеме 200 д.е.
Замечание. Если решать задачу в 2 этапа, т.е.
находить сначала оптимальный план поставок поставщиков к холодильникам, а затем
задачу оптимальных поставок с холодильников к потребителям, суммарные потери
составят минимально 25350 д.е.
Задание
Составить программу улучшения начального
опорного плана закрытой транспортной задачи с помощью распределительного
метода.
Указания.
Программа должна содержать меню для выбора
способа построения начального опорного плана (в меню должен быть включен каждый
из способов );
В случае открытой транспортной задачи
предусмотреть каждый из двух случаев (т.е. программа должна определять самостоятельно
тип задачи и при необходимости приводить ее математическую модель к виду
расширенной закрытой транспортной задачи);
Допускается построение простых циклов (т.е.
циклов из 4-х вершин). Программа должна определять оценки всех свободных клеток
и выполнять построение циклов до тех пор, пока хотя бы одна оценка
положительная.
Результатом работы программы должна быть либо
матрица оптимального плана перевозок, либо значения переменных с указанием их
индексов в матрице X.
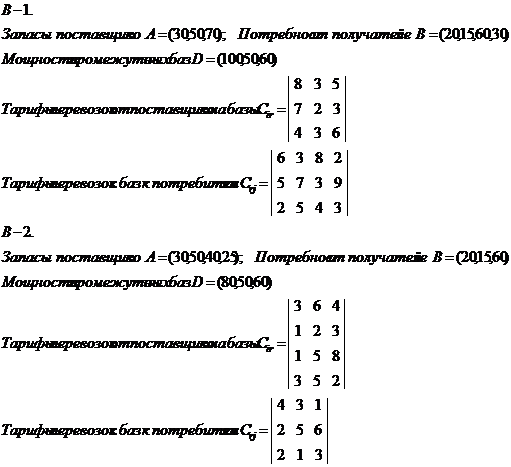
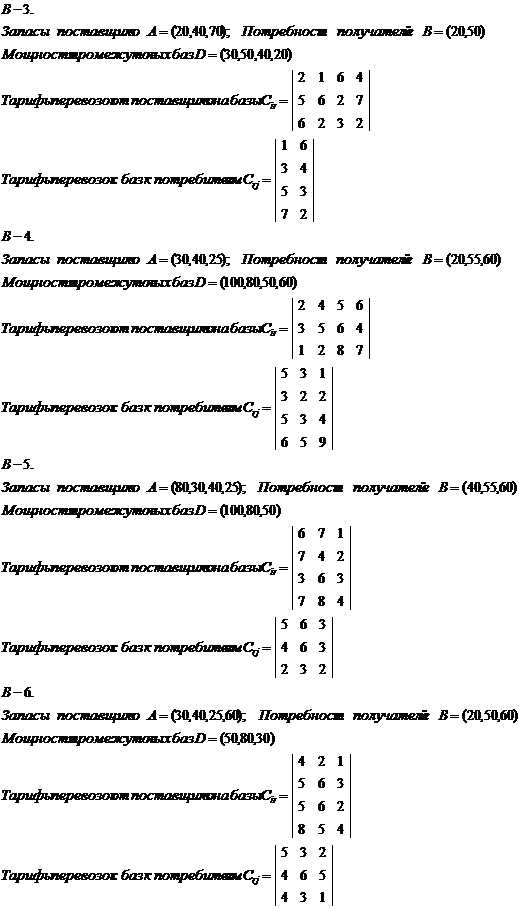
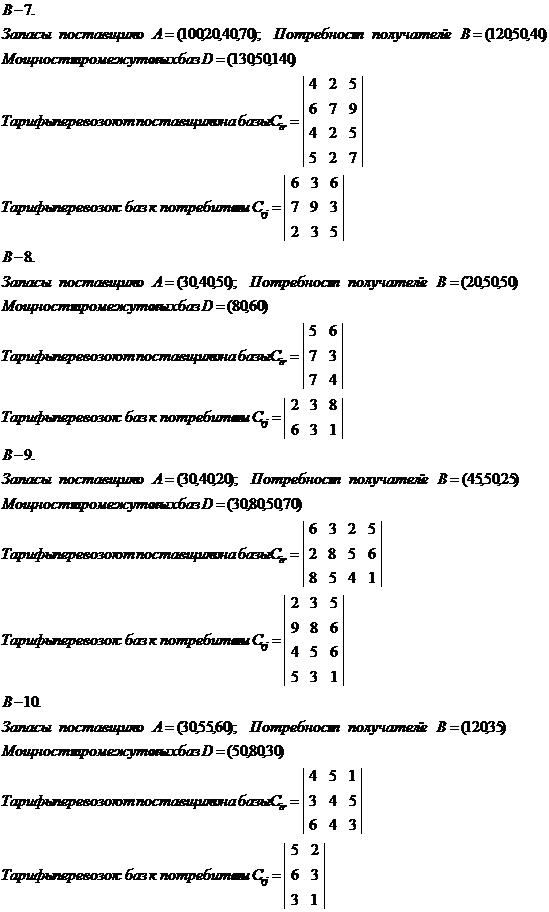
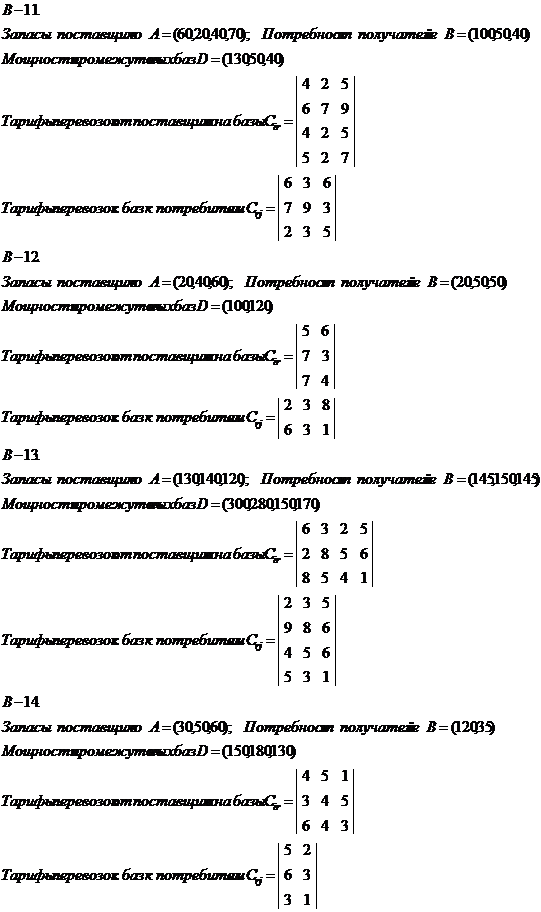
Литература
1. Волков
И.К., Загоруйко Е.А. Исследование операций: Учеб. для вузов / Под ред. В.С.
Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2000.
2. Таха,
Хемди А. Введение в исследование операций. - М.: Изд. дом «Вильямс», 2005
. Банди
Б. Основы линейного программирования. - Москва: «Радио и связь», 1989.
. Балашевич
В.А. Основы математического программирования. - Минск: «Высшая школа», 1985.
. Ларионов
А.И., Юрченко Т.И., Новоселов А.Л. Экономико - математические методы в
планировании.- М.: «Высшая школа», 1991.
. Сакович
В.А. Исследование операций - Минск: «Высшая школа», 1985